Lecture 00-02 线性代数基础回顾
主要内容
- 线性代数基础回顾
- 向量和点积
- 超平面和法向量
- 线性生成空间,基
- 特征向量和特征值
1. 向量
机器学习的几何解释和代数解释之间的联系
1.1 什么是向量?
考虑 $\boldsymbol u=[ u_1, u_2]’$,思考 $\boldsymbol u$ 在本质上代表着什么?
- 一组数字的有序集合 \(\{u_1, u_2\}\)
- 一个点的笛卡尔坐标
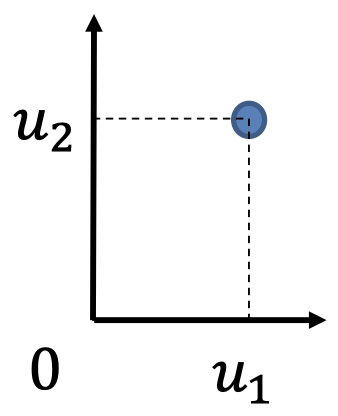
- 一个方向
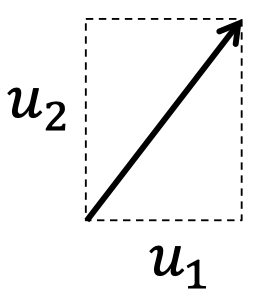
1.2 点积:代数定义
- 给定两个 $m$ 维向量 $\boldsymbol u$ 和 $\boldsymbol v$,它们的点积是 $\boldsymbol u \cdot \boldsymbol v \equiv \boldsymbol u’ \boldsymbol v \equiv \sum_{i=1}^{m}u_i v_i$
- 例如,一些项的加权和就是一个点积 $\boldsymbol x’ \boldsymbol w$
- 如果 $k$ 是一个标量,$\boldsymbol a, \boldsymbol b, \boldsymbol c$ 都是向量,那么
1.3 点积:几何定义
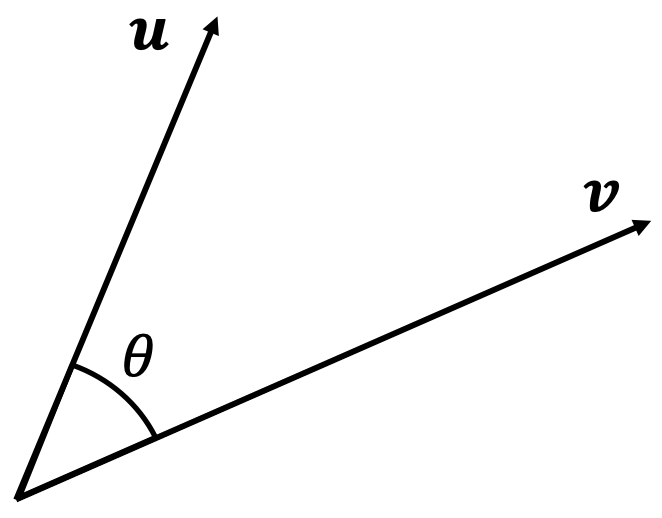
- 给定两个 $m$ 维的欧几里得向量 $\boldsymbol u$ 和 $\boldsymbol v$,它们的点积是 \(\boldsymbol u \cdot \boldsymbol v \equiv \boldsymbol u' \boldsymbol v \equiv \| \boldsymbol u \| \| \boldsymbol v \| \cos{\theta}\)

- \(\| \boldsymbol u \|, \| \boldsymbol v \|\) 是 \(\boldsymbol u, \boldsymbol v\) 的 $L_2$ 范数
-
$\theta$ 是这两个向量之间的夹角
$\boldsymbol u$ 在 $\boldsymbol v$ 上的标量投影由下式给出:
\[u_{\boldsymbol v}=\| \boldsymbol u\|\cos{\theta}\]因此,点积 为:
\[\color{red}{\fbox{$\color{black}{\boldsymbol u'\boldsymbol v=u_{\boldsymbol v}\|\boldsymbol v\|=v_{\boldsymbol u}\|\boldsymbol u\|}$}}\]
1.4 点积的几何性质
- 如果两个向量正交,那么 \(\boldsymbol u' \boldsymbol v =0\)
- 如果两个向量平行,那么 \(\boldsymbol u' \boldsymbol v = \| \boldsymbol u \| \| \boldsymbol v \|\),如果它们反向平行,那么 \(\boldsymbol u' \boldsymbol v = -\| \boldsymbol u \| \| \boldsymbol v \|\)
- \(\boldsymbol u' \boldsymbol u = \| \boldsymbol u \|^2\),所以,\(\| \boldsymbol u \|=\sqrt{u_1^2+\cdots+u_m^2}\) 定义了欧几里得向量长度。
1.5 超平面和法向量
- 一个 超平面 由参数 $\boldsymbol w$ 和 $b$ 定义,它是点 $\boldsymbol x$ 的一个集合,满足 $\boldsymbol x’ \boldsymbol w+b=0$
-
在 2 维空间中,一个超平面就是一条直线:该直线是一个点集,满足 $w_1x_1+w_2x_2+b=0$
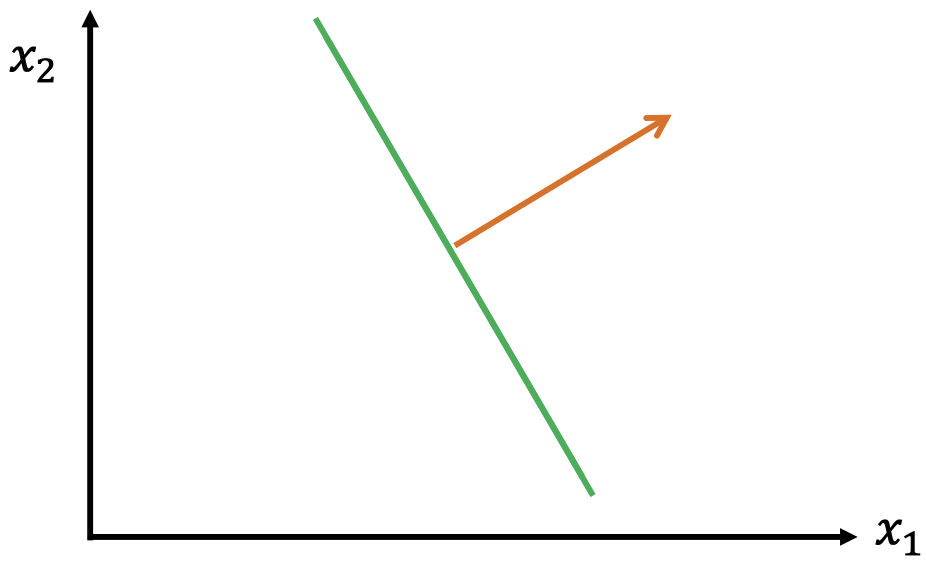
一个超平面的 法向量 是一个与该超平面垂直的向量。
- 考虑一个由参数 $\boldsymbol w$ 和 $b$ 定义的超平面。注意, $\boldsymbol w$ 本身是一个向量。
- 引理: 向量 $\boldsymbol w$ 是该超平面的一个法向量。
- 简略证明:
- 选择超平面上的任意两个点 $\boldsymbol u$ 和 $\boldsymbol v$。注意,向量 $(\boldsymbol u-\boldsymbol v)$ 位于该超平面上。
-
考虑点积
\[\begin{eqnarray}(\boldsymbol u-\boldsymbol v)'\boldsymbol w &=& \boldsymbol u'\boldsymbol w-\boldsymbol v'\boldsymbol w\\ &=& (\boldsymbol u'\boldsymbol w+b)-(\boldsymbol v'\boldsymbol w+b)=0\end{eqnarray}\] - 因此,$(\boldsymbol u-\boldsymbol v)$ 位于该超平面上,但是它又与 $\boldsymbol w$ 垂直,所以,$\boldsymbol w$ 是该超平面的一个法向量。
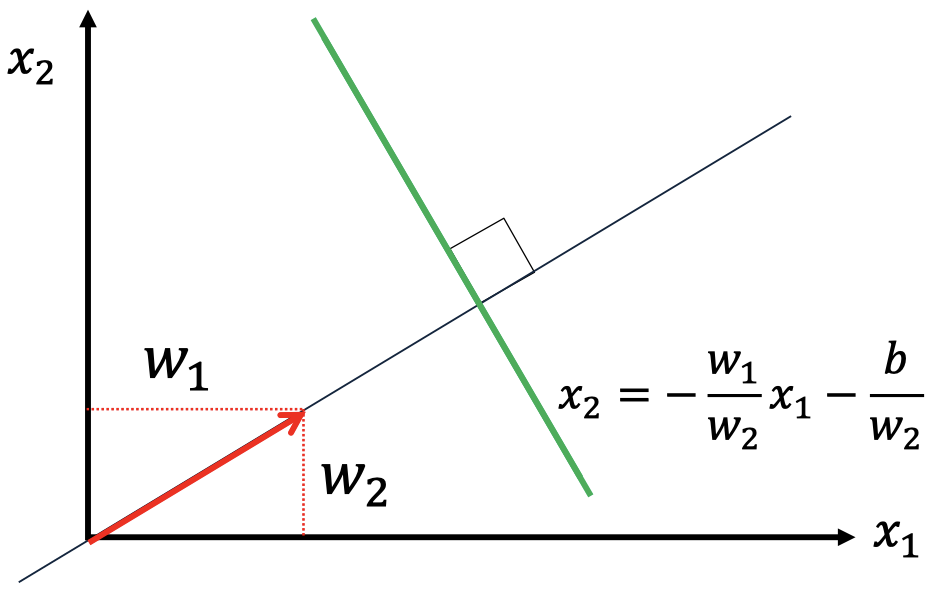
- 2 维空间中的例子
- 考虑一条由 $w_1, w_2$ 和 $b$ 定义的一条直线
- 向量 $\boldsymbol w=[ w_1, w_2]’$ 是一个法向量
2. 向量空间和基
在解释矩阵和某些算法(例如:PCA)时非常有用
2.1 线性组合,独立性
- 关于 向量空间 的正式定义,请参考:
https://en.wikipedia.org/wiki/Vector_space#Definition - 向量 $v_1,…,v_k\in V$(某向量空间)的一个 线性组合,是一个新的向量 $\sum_{i=1}^{k}a_iv_i$,其中,$a_1,…,a_k$ 是一些标量。
-
一个向量集合 \(\{v_1,...,v_k\}\subseteq V\) 被称为 线性相关,如果一个元素 $v_j$ 可以被写作其他元素的线性组合。
- 如果一个集合不是线性相关,我们称其为 线性独立。
2.2 线性生成空间,基
- 向量 $v_1,…,v_k\in V$ 的 线性生成空间,是这些向量的所有可得的线性组合(覆盖所有标量系数)的集合。
- 一个向量集合 \(\{v_1,...,v_k\}\subseteq V\),被称为一个向量子空间 $V’\subseteq V$ 的一个 基,如果:
- 该集合是线性独立的;并且
- 每一个 $v\in V’$ 都是该集合的一个线性组合。
- 一个 标准正交基 需要满足:
- 每一对基向量都是正交的(点积为零);并且
- 每一个基向量的范数都等于 $1$。
3. 矩阵
一些对于机器学习非常有用的事实
3.1 基本矩阵
- 想了解更多,请参考:https://en.wikipedia.org/wiki/Matrix_(mathematics)
- 包括 矩阵-矩阵积 和 矩阵-向量积
- 一个矩形数组,通常用大写字母表示,包含两个索引:第一个用于行,第二个用于列
- 方阵 的各维度(行和列的数量)都相等
- 一个 $m\times n$ 的矩阵 $A$ 的 转置矩阵 $A’$ 或 $A^T$ 是一个 $n\times m$ 的矩阵,其中,项 $A’{ij}=A{ji}$
- 如果一个方阵 $A$ 满足 $A=A’$,那么我们称其为 对称的
- 单位矩阵 $I$ 是一个方阵,其对角线上的元素均为 $1$,非对角线上的元素均为 $0$
- 方阵 $A$ 的 逆矩阵 $A^{-1}$(如果存在的话)满足 $A^{-1}A=I$
3.2 矩阵特征谱
- 标量-向量对 $(\lambda, v)$ 被称为 方阵 $A$ 的一个 特征值-特征向量 对,如果 $Av=\lambda v$
- 直觉上,矩阵 $A$ 没有对 $v$ 进行旋转,只是将其 拉伸 了
- 直觉上,特征值代表了拉伸因子
- 通常,特征值可能为零、负数,或者甚至为复数(虚数)
3.3 常见矩阵谱
- 对称矩阵 的特征值始终是实数(无虚部)
- 包含 线性相关 列的矩阵具有一些零特征值(称为秩亏)$\rightarrow$ 不存在逆矩阵
3.4 正定(半正定)矩阵
- 一个 对称方阵 $A$ 是 半正定的,如果对于所有的非零向量 $\boldsymbol v$,都满足 $\boldsymbol v’ A\boldsymbol v\ge0$。
- 然后,$A$ 具有 非负特征值。
- 例如,任何 $A=X’X$,因为:\(\boldsymbol v'X'X \boldsymbol v=\|X \boldsymbol v\|^2\ge0\)
- 更进一步,如果 $\boldsymbol v’ A\boldsymbol v>0$ 严格满足不等性,那么 $A$ 被称为 正定的。
- 然后,$A$ 具有(严格的)正特征值。
总结
- 线性代数基础回顾
- 向量和点积
- 超平面和法向量
- 线性生成空间,基
- 特征向量和特征值
下节内容:概率论基础
本作品采用知识共享署名-非商业性使用-相同方式共享 4.0 国际许可协议进行许可。 欢迎转载,并请注明来自:YEY 的博客 同时保持文章内容的完整和以上声明信息!