Lecture 5 正则化
主要内容
正则化是通过引入其他信息以解决病态问题或防止过拟合的过程。
- 贯穿机器学习的主要技术和主题
- 解决以下一个或多个相关问题
- 避免病态(计算问题)
- 避免过度拟合(统计问题)
- 将先验知识引入建模过程
- 这是通过在目标函数上增加一些项来实现的
在本节中:我们涵盖了前两个方面。我们将在整个课程中涵盖更多的正规化。
1. 例子 1:特征的重要性
1.1 特征的重要性
问题:哪个特征更重要?

- 线性模型有三个特征
- $\boldsymbol X$ 是 $n=4$ 个实例(行)的矩阵
- 模型:$y=w_1x_1+w_2x_2+w_3x_3+w_0$
- $\boldsymbol X$ 的前两列完全一样
- 特征 2(或者 1)是 不相关 特征
- 扰动对模型预测的影响?
- $w_1$ 增加 $\Delta$
- $w_2$ 减少 $\Delta$

1.2 不相关特征的问题
- 例子中,假设 $[\hat w_0,\hat w_1,\hat w_2,\hat w_3]’$ 是 “最优的”
- 对任意 $\delta$,新的 $[\hat w_0,\hat w_1+\delta,\hat w_2-\delta,\hat w_3]’$ 得到
- 同样的预测结果
- 同样的平方和误差
- 问题突显了
- 解不是唯一的
- 缺乏解释能力
- 优化学习参数是病态问题
1.3 一般不相关(共线性)的特征
- 极端情况:特征完全一样
- 对于线性模型,更一般地
- 特征 $\boldsymbol X_{.j}$ 是不相关的,如果
-
$\boldsymbol X_{.j}$ 是其他列的一个线性组合: $\boldsymbol X_{.j}=\sum_{l\ne j}\alpha_l\boldsymbol X_{.l}$
其中,$\boldsymbol X_{.j}$ 代表 $\boldsymbol X$ 的第 $j$ 列,$\alpha_l$ 代表某些标量,这也被称为多重共线性
- 等价于:$\boldsymbol {X’X}$ 的某些特征值为零
- 即使是接近不相关 / 共线性也会造成困难
- $\boldsymbol {X’X}$ 的某些特征值 $V$ 非常小
- 不止是病态的极端;事实上,很容易发生这类情况
2. 例子 2:数据缺失
2.1 数据缺失

- 极端例子:
- 模型有两个参数(斜率和截距)
- 只有一个数据点
- 欠定组
2.2 病态问题

- 在前面的两个例子中,寻找最优参数变成了一个病态问题。
- 这意味着问题的解没有被定义好
- 在我们的例子中,$w_1$ 和 $w_2$ 无法被唯一确定
-
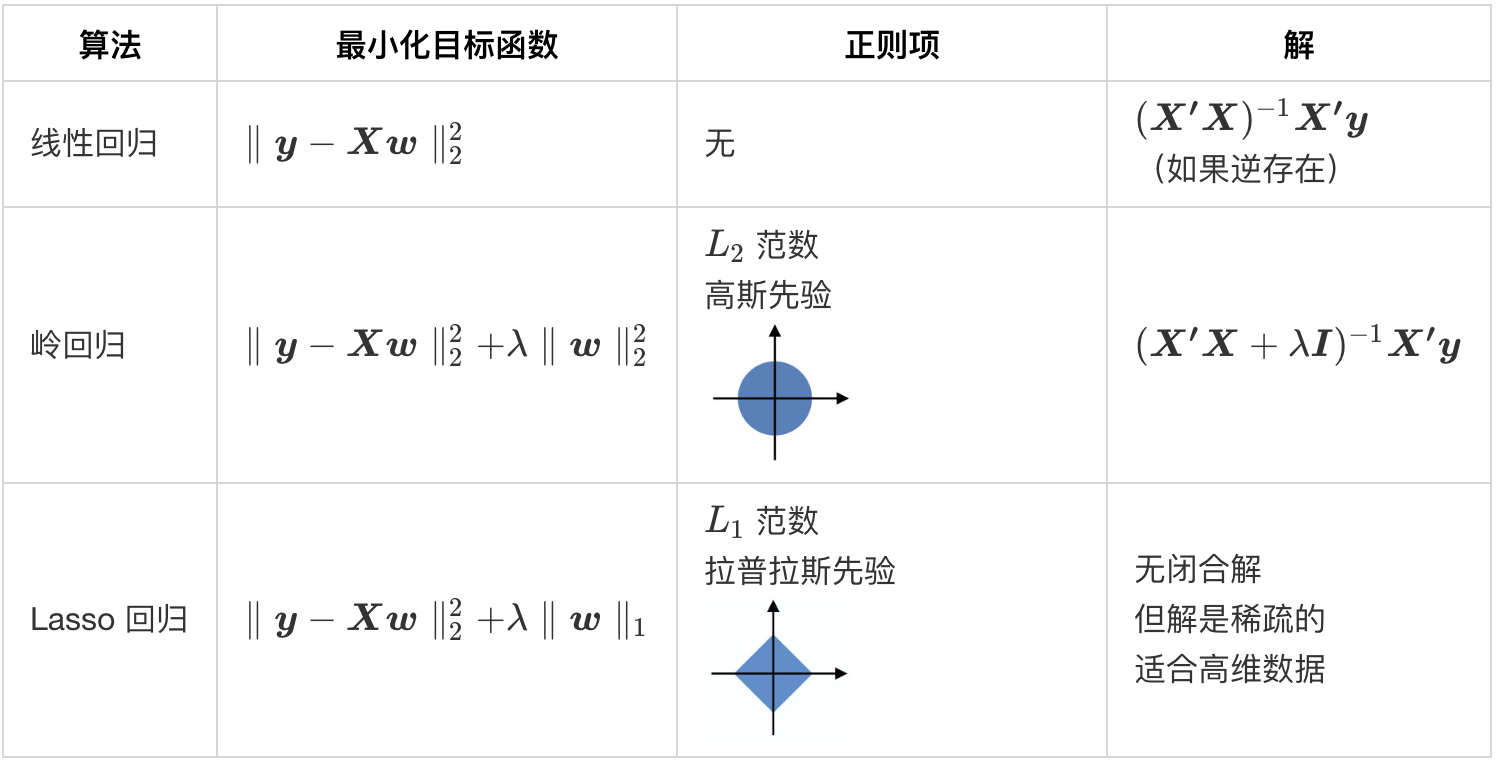
回忆线性回归中正规方程的解:
$\hat{\boldsymbol w}=(\boldsymbol{X’X})^{-1}\boldsymbol{X’y}$
- 由于存在不相关 / 多重共线性特征,矩阵 $\boldsymbol{X’X}$ 的逆不存在
2.3 重新设置问题条件

- 正则化:向系统中引入一个额外条件。
-
原始问题是最小化:
$\|\boldsymbol y -\boldsymbol {Xw}\|_2^2$
-
正则化后的问题是最小化:
$\|\boldsymbol y -\boldsymbol {Xw}\|_2^2+\color{red}{\lambda \|\boldsymbol w\|_2^2}$ 对于$\lambda>0$
-
现在,正规方程的解变成了:
$\hat{\boldsymbol w}=(\boldsymbol{X’X}+\color{red}{\lambda \boldsymbol I})^{-1}\boldsymbol{X’y}$
- 这种形式称为 岭回归
- 将山脊变为山顶
- 在 $\boldsymbol{X’X}$ 的特征值上增加 $\lambda$:使其变为可逆
2.4 正则项作为先验
- 如果没有正则化,寻找参数完全建立在训练集 $\boldsymbol X$ 中包含的信息上
- 正则化引入了额外信息
- 回忆我们的概率模型:$Y=\boldsymbol {x’w}+\varepsilon$
- 这里 $Y$ 和 $\varepsilon$ 是随机变量,其中 $\varepsilon$ 代表噪声
- 现在假设 $\boldsymbol w$ 也是一个随机变量(记为 $\boldsymbol W$),服从一个正态先验分布:
$\boldsymbol W\sim N(0,1/\lambda)$
- 我们期望较小的权重,没有一个特征占明显的主导地位
- 这总是合适的吗?例如:数据中心化和缩放
- 我们可以编码更多详尽的问题知识
2.5 利用贝叶斯规则计算后验
-
先验在随后被用来计算后验:

- 相比最大似然估计(MLE),这里我们采用最大后验估计(MAP)
-
采用 Log 技巧,可以得到:
$\log(posterior)=\log(likelihood)+\log(prior)-\color{red}{\require{cancel}\cancel{\log(marg)}}$
(注:该项对于优化没有影响) -
现在,问题转变为最小化:
$\|\boldsymbol y -\boldsymbol {Xw}\|_2^2+\lambda \|\boldsymbol w\|_2^2$
3. 非线性模型的正则化
机器学习中的模型选择
3.1 例子:回归问题

问题:我们应该使用多复杂的模型?
3.1.1 欠拟合(线性回归)

模型类别 $\Theta$ 可能 太简单 而无法拟合真实模型。
3.1.2 过拟合(非参数平滑)

模型类别 $\Theta$ 可能 过于复杂 导致拟合了真实模型 + 噪声。
3.1.3 实际模型($x\sin x$)

正确的模型类别 $\Theta$ 会为了测试误差而牺牲一些训练误差。
3.2 如何 “改变” 模型的复杂度
- 方法 1:显式模型选择
- 方法 2:正则化
- 通常,方法 1 可以视为方法 2 的特例
3.2.1 显式模型选择
- 尝试不同类别的模型。例如,尝试不同等级 $d$ 的多项式模型(线性、二次、三次…)
- 采用支持的验证方法(交叉验证)选择模型
- 将训练数据分割为训练集 $D_{train}$ 和验证集 $D_{validate}$
- 对于每个等级 $d$,我们有模型 $f_d$
- 在 $D_{train}$ 上训练 $f_d$
- 在 $D_{validate}$ 上测试 $f_d$
- 选择测试分数最佳的等级 $\hat d$
- 用全部数据重新训练模型 $f_{\hat d}$
3.2.2 通过正则化改变模型复杂度
-
增加问题:
$\hat{\boldsymbol{\theta}}\in\mathop{\operatorname{arg\,min}}\limits_{\boldsymbol\theta\in\Theta}(L(data,\boldsymbol\theta)+\color{red}{\lambda R(\boldsymbol\theta)})$
-
例如,岭回归:
$\hat{\boldsymbol w}\in\mathop{\operatorname{arg\,min}}\limits_{\boldsymbol w\in W}(\|\boldsymbol y -\boldsymbol {Xw}\|_2^2+\color{red}{\lambda \|\boldsymbol w\|_2^2})$
- 注意:正则项 $ R(\boldsymbol\theta)$ 不依赖于数据
- 采用支持的验证 / 交叉验证选择 $\lambda$
3.3 例子:多项式回归

- 9 阶多项式回归
- 模型形式: $\hat f=w_0+w_1x+…+w_9x^9$
- 引入正则项 $\lambda\|\boldsymbol w\|_2^2$

3.4 正则项作为约束
- 为了便于说明,考虑一个修正后的模型: 最小化 $|\boldsymbol y-\boldsymbol{Xw}|_2^2$ 满足 $|\boldsymbol w|_2^2\le\lambda$(对于 $\lambda>0$)

- Lasso($L_1$ 正则化)促使最优解落在坐标轴上 $\rightarrow$ 某些权重设为零 $\rightarrow$ 解是稀疏的
3.5 正则化线性回归
4. 偏差与方差之间的权衡
训练误差,测试误差与模型复杂度之间的关系分析
4.1 评估泛化能力
- 监督学习:在现有数据上训练模型,然后对新数据进行预测
- 训练模型:ERM /最小化训练误差
- 通过风险/测试误差来评估泛化能力
- 模型复杂度是影响模型泛化能力的主要因素
- 在本节中,我们主要目的是探索训练误差,测试误差与模型复杂性之间的关系。
4.2 训练误差与模型复杂度
- 模型越复杂 $\rightarrow$ 训练误差越低
- 有限数量的点 $\rightarrow$ 通常可以将训练误差减小到 0(这总是可能的吗?)

4.3 (另一种)偏差-方差分解
- 监督回归预测的平方损失函数为: $l\left(Y,\hat f(\boldsymbol X_0)\right)=\left(Y-\hat f(\boldsymbol X_0)\right)^2$
- 引理:偏差-方差分解
$\mathbb{E}\left[l\left(Y,\hat f(\boldsymbol X_0)\right)\right]=\left(\mathbb{E}[Y]-\mathbb{E}[\hat f]\right)^2+Var[\hat f]+Var[Y]$
$\boldsymbol x_0$ 的风险 / 测试误差 $=$ (偏差) 2 $+$ 方差 $+$ 无法减少的误差
预测的随机性来自测试数据特征和训练数据中的随机性。
4.4 将数据当成一个随机变量来训练


4.5 模型复杂度与方差
- 简单模型 $\rightarrow$ 低方差
- 复杂模型 $\rightarrow$ 高方差

4.6 模型复杂度与偏差
- 简单模型 $\rightarrow$ 高偏差
- 复杂模型 $\rightarrow$ 低偏差

4.7 偏差与方差之间的权衡
- 简单模型 $\rightarrow$ 高偏差,低方差
- 复杂模型 $\rightarrow$ 低偏差,高方差

4.8 测试误差与训练误差

总结
- 正则化
- 不相关 / 多重共线性特征 $\rightarrow$ 病态问题
- 模型复杂度
- 偏差与方差之间的权衡
下节内容:从感知器到神经网络
本作品采用知识共享署名-非商业性使用-相同方式共享 4.0 国际许可协议进行许可。 欢迎转载,并请注明来自:YEY 的博客 同时保持文章内容的完整和以上声明信息!