Lecture 11 核方法

主要内容

核化
- SVM 对偶公式的基扩展
- “核技巧”；特征空间点积的快速计算
模块化学习
- 从特征变换中分离出“学习模块”
- 表示定理
构造核函数
- 常见核函数及其特性概述
- Mercer 定理
- 学习非常规数据类型

1. SVM 核化

通过基扩展进行特征变换；通过对核进行直接评估来实现加速 —— “核技巧”

1.1 SVM 处理非线性数据

方法 1：软间隔 SVM（参考 Lecture 10）
方法 2：特征空间变换（参考 Lecture 4）
- 将数据映射到一个新的特征空间
- 在新的特征空间中运行硬间隔或者软间隔 SVM
- 决策边界在原始特征空间中是非线性的

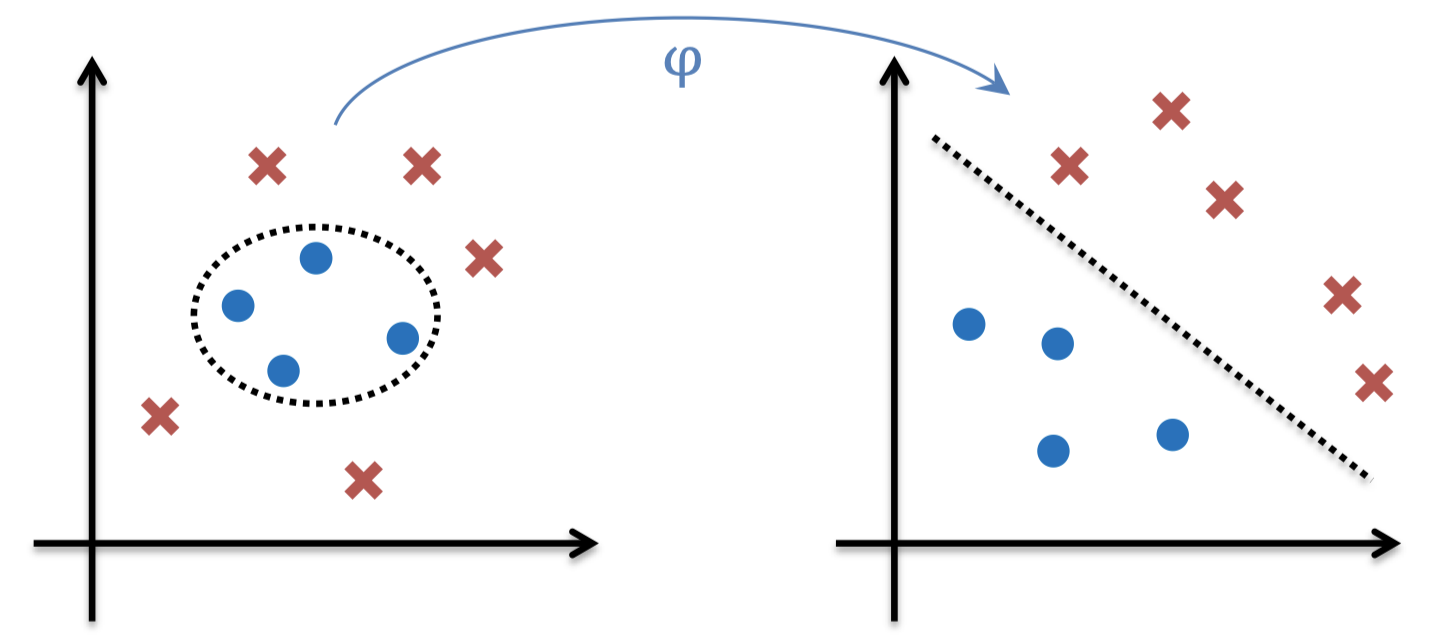
1.2 特征变换（基扩展）

考虑一个二分类问题
每个样本点具有特征 $[x_1, x_2]$
非线性可分
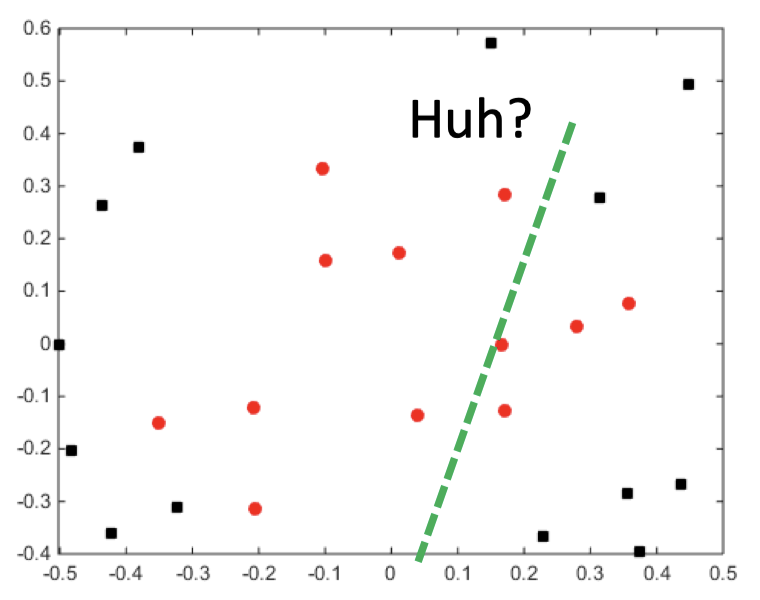
现在“增加”一个特征 $x_3=x_1^2+x_2^2$
每个样本点现在为 $[x_1, x_2, x_1^2+x_2^2]$
现在数据变成线性可分了

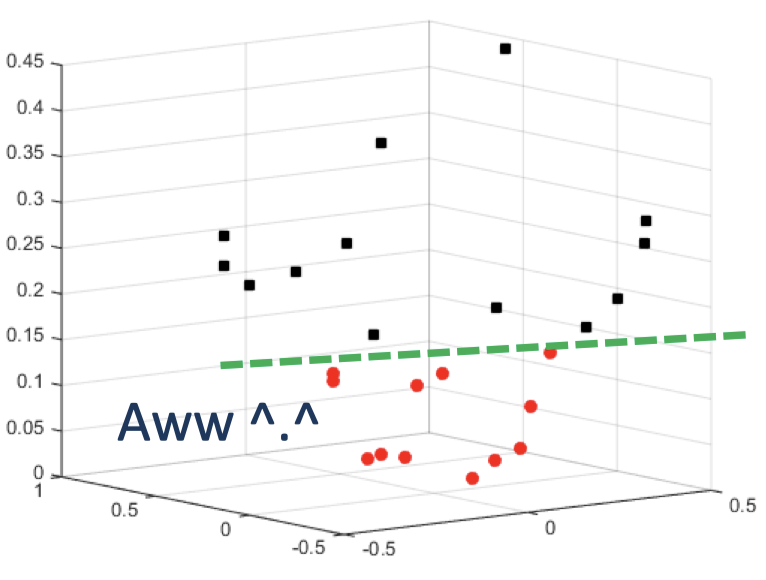
1.3 朴素工作流

选择 / 设计一个线性模型
选择 / 设计一个高维变换 $\varphi (\boldsymbol x)$
- 希望在添加了许多各种特征之后，其中一些特征将使数据变得线性可分
对于每个训练样本，以及每个新的实例，计算 $\varphi (\boldsymbol x)$
训练分类器 / 进行预测
问题： 对于高维 / 无限维的 $\varphi (\boldsymbol x)$，计算 $\varphi (\boldsymbol x)$ 是不现实 / 不可能的。

1.4 硬间隔 SVM 的对偶公式

训练： 寻找 $\boldsymbol \lambda$ 使得

\[\begin{array}{cc}\mathop{\operatorname{arg\,max}}\limits_{\boldsymbol \lambda}\sum_{i=1}^{n}\lambda_i-\dfrac{1}{2}\sum_{i=1}^{n}\sum_{j=1}^{n}\lambda_i \lambda_j y_i y_j \color{red}{\underbrace{\fbox{$\color{black}{\boldsymbol x_i' \boldsymbol x_j}$}}_{\text{点积}}}\\\\ \text{s.t.}\quad \lambda_i\ge 0 \;\text{and}\;\sum_{i=1}^{n}\lambda_i y_i=0 \end{array}\]

预测： 根据 $s$ 的符号对实例 $\boldsymbol x$ 进行分类

\[s=b^*+\sum_{i=1}^{n}\lambda_i^* y_i \color{red}{\underbrace{\fbox{$\color{black}{\boldsymbol x_i' \boldsymbol x}$}}_{\text{点积}}}\]

注意：对于任意支持向量 $j$，通过求解 $y_j(b^{*}+\sum_{i=1}^{n}\lambda_i^* y_i \color{red}{\fbox{$\color{black}{\boldsymbol x_i' \boldsymbol x_j}$}})=1$ 来找到 $b^*$

1.5 特征空间中的硬间隔 SVM

训练： 寻找 $\boldsymbol \lambda$ 使得

\[\begin{array}{cc}\mathop{\operatorname{arg\,max}}\limits_{\boldsymbol \lambda}\sum_{i=1}^{n}\lambda_i-\dfrac{1}{2}\sum_{i=1}^{n}\sum_{j=1}^{n}\lambda_i \lambda_j y_i y_j \color{red}{\fbox{$\color{black}{\varphi (\boldsymbol x_i)' \varphi (\boldsymbol x_j)}$}}\\\\ \text{s.t.}\quad \lambda_i\ge 0 \;\text{and}\;\sum_{i=1}^{n}\lambda_i y_i=0 \end{array}\]

预测： 根据 $s$ 的符号对实例 $\boldsymbol x$ 进行分类

\[s=b^*+\sum_{i=1}^{n}\lambda_i^* y_i \color{red}{\fbox{$\color{black}{\varphi (\boldsymbol x_i)' \varphi (\boldsymbol x)}$}}\]

注意：对于任意支持向量 $j$，通过求解 $y_j(b^{*}+\sum_{i=1}^{n}\lambda_i^* y_i \color{red}{\fbox{$\color{black}{\varphi (\boldsymbol x_i)' \varphi (\boldsymbol x_j)}$}})=1$ 来找到 $b^*$

1.6 观察：核表示

参数估计和计算预测都仅依赖于点积形式的数据
- 在原始特征空间：$\boldsymbol u’ \boldsymbol v=\sum_{i=1}^{m}u_i v_i$
- 在经过特征变换后的空间：$\varphi(\boldsymbol u)’ \varphi(\boldsymbol v)=\sum_{i=1}^{l}\varphi(\boldsymbol u)_i \varphi(\boldsymbol v)_i$
核函数是可以在某些特征空间中表示为点积的函数
\[K(\boldsymbol u, \boldsymbol v)=\varphi(\boldsymbol u)' \varphi(\boldsymbol v)\]

1.7 核函数是一种捷径：例子

对于某些 $\varphi(\boldsymbol x)$，直接对核函数进行计算 要比先映射到特征空间然后再计算点积更快。
例如，考虑两个向量 $\boldsymbol u =[ u_1 ]$ 和 $\boldsymbol v =[ v_1 ]$，以及变换 $\varphi(\boldsymbol x)=[ x_1^2, \sqrt{2c} x_1, c ]$，其中 $c$ 是某个常数
- 所以，$\varphi(\boldsymbol u)=[ u_1^2, \sqrt{2c} u_1, c ]’$（2 步操作）和 $\varphi(\boldsymbol v)=[ v_1^2, \sqrt{2c} v_1, c ]’$（+2 步操作）
- 然后，$\varphi(\boldsymbol u)’\varphi(\boldsymbol v)=(u_1^2 v_1^2+2cu_1 v_1+c^2)$ （+5 步操作 = 9 步操作）
这可以通过 直接计算核函数 来代替
\[\varphi(\boldsymbol u)' \varphi(\boldsymbol v)=(u_1 v_1 +c)^2\]
- 现在只需 3 步操作
- 这里，$K(\boldsymbol u, \boldsymbol v)=(u_1 v_1 +c)^2$ 是相应的核函数

1.8 更通用的：“核技巧”

考虑两个训练数据点 $\boldsymbol x_i$ 和 $\boldsymbol x_j$，以及它们在经过变换后的特征空间中的点积。
$k_{ij}\equiv \varphi(\boldsymbol x_i)’\varphi(\boldsymbol x_j)$ 核矩阵可以按如下步骤计算：
1. 计算 $\varphi(\boldsymbol x_i)’$
2. 计算 $\varphi(\boldsymbol x_j)$
3. 计算 $k_{ij}=\varphi(\boldsymbol x_i)’\varphi(\boldsymbol x_j)$
然而，对于某些变换 $\varphi$，存在一种“捷径”函数可以得到与 $K(\boldsymbol x_i,\boldsymbol x_j)=k_{ij}$ 完全相同的答案：
- 不包含上面的 1-3 步，而且没有计算 $\varphi(\boldsymbol x_i)$ 和 $\varphi(\boldsymbol x_j)$
- 通常，计算 $k_{ij}$ 的时间复杂度为 $O(m)$，但是计算 $\varphi(\boldsymbol x)$ 的时间复杂度为 $O(l)$，其中 $l \gg m$（计算上不现实）甚至 $l=\infty$（计算上不可行）

1.9 核函数硬间隔 SVM

训练： 寻找 $\boldsymbol \lambda$ 使得
\[\begin{array}{cc}\mathop{\operatorname{arg\,max}}\limits_{\boldsymbol \lambda}\sum_{i=1}^{n}\lambda_i-\dfrac{1}{2}\sum_{i=1}^{n}\sum_{j=1}^{n}\lambda_i \lambda_j y_i y_j \color{red}{\underbrace{\fbox{$\color{black}{K(\boldsymbol x_i, \boldsymbol x_j)}$}}_{\text{核函数}}}\\\\ \text{s.t.}\quad \lambda_i\ge 0 \;\text{and}\;\sum_{i=1}^{n}\lambda_i y_i=0 \end{array}\]
特征映射通过核函数实现
预测： 根据 $s$ 的符号对实例 $\boldsymbol x$ 进行分类
\[s=b^*+\sum_{i=1}^{n}\lambda_i^* y_i \color{red}{\underbrace{\fbox{$\color{black}{K(\boldsymbol x_i, \boldsymbol x)}$}}_{\text{核函数}}}\]
特征映射通过核函数实现
这里，我们注意到，对于任意支持向量 $j$，都有 $y_j(b^{*}+\sum_{i=1}^{n}\lambda_i^* y_i \color{red}{\fbox{$\color{black}{K(\boldsymbol x_i, \boldsymbol x_j)}$}})=1$，可以以此来找到 $b^*$

1.10 非线性的处理方法

ANN
- $\boldsymbol u=\varphi(\boldsymbol x)$ 中的元素是输入 $\boldsymbol x$ 经过变换得到的
- 该 $\varphi$ 具有从数据中学习得到的权重
SVM
- 对核函数 $K$ 的选择决定了特征空间 $\varphi$
- 不学习 $\varphi$ 的权重
- 但是，甚至不需要计算 $\varphi$ 就可以支持高维
- 同样支持任意数据类型
思考：
1. 所有的用到了特征空间变换 $\varphi(\boldsymbol x)$ 的方法都用到了核函数吗？
不是的，虽然对于 SVM 是这样，但是回忆之前 Lecture 04 的内容，我们还在更为一般的条件下讨论过基扩展和特征映射，同样在神经网络中我们也可以使用特征映射。我们总是可以在进行特征映射之后应用机器学习算法，而有些算法并不需要涉及到点积的计算，记住核函数是对应于点积的，我们并不一定需要在机器学习中使用核函数。

2. 支持向量是来自于训练集中的点吗？
是的，支持向量是训练的样本，它们具有 非零对偶变量（即拉格朗日乘子 $\lambda_i\ne 0$）。所以当我们用 SVM 进行预测时（参考 “1.9 核函数硬间隔 SVM”）：
\[s=b^*+\sum_{i=1}^{n}\lambda_i^* y_i \color{red}{\underbrace{\fbox{$\color{black}{K(\boldsymbol x_i, \boldsymbol x)}$}}_{\text{核函数}}}\]
如果我们用对偶方程训练 SVM，我们不会得到任何 $w$，我们会得到很多不同的 $\lambda_i$，其中每一个都对应于一个训练样本，所有的 $\lambda_i$ 都要求非负（当然，其中很多可能为 $0$，这取决于你的数据和你所采用的特征映射），而其中那些 $\lambda_i$ 为 $0$ 的训练样本是那些落在最大间隔之外的点，它们并不 “支持着” 决策边界，因为 $\lambda_i$ 为 $0$ 会使得原始问题中约束条件失效，它们并不涉及 $w$ 的计算（事实上，它们并不涉及有关预测值的计算）。通过观察上面的式子，可以发现不论核函数 $K(\boldsymbol x_i, \boldsymbol x)$ 等于多少，只要 $x_i$ 对应的 $\lambda_i=0$，那么在求和时该项就会被消掉，这就是为什么 支持向量 非常重要的原因。它们之所以重要不是因为有一个时髦的名称，它们从实质上来帮助 SVM 进行预测，它们实际上是一些对于 SVM 的训练非常重要的样本。所以，如果在非支持向量的训练样本中存在一些噪声，通常不会对结果有什么影响；只有那些属于支持向量的训练样本是至关重要的。

3. 我们总是可以通过特征映射 $\varphi(\boldsymbol x)$ 使得数据完美线性可分吗？
不是的，假如我不告诉你关于数据的任何信息，可能存在两个不同的样本 $\boldsymbol x_i$ 对应相同的 $y_i$ 的情况，这是有可能发生的，其原因可能不是由于测量数据的方法导致的，它有可能是由于存在隐变量，或者 $y$ 的噪声导致的。所以，问题中的说法并不准确，更恰当的说法是：通常情况下，我们都可以通过特征映射 $\varphi(\boldsymbol x)$ 使得数据更加线性可分。

2. 模块化学习

SVM 之外的核化；将 “学习模块” 从特征空间变换中分离出来

2.1 模块化学习

与特征映射相关的所有信息都浓缩在核函数中
为了使用一种不同的特征映射，只需要简单地更换核函数即可
算法设计可以分为：选择 “学习方法”（例如，SVM vs Logistic 回归）和选择特征空间映射，即核函数。

2.2 核化感知器

当分类正确时，权重不会更新
当分类错误时：$\boldsymbol w^{k+1}=-\eta(\pm \boldsymbol x)$（其中，$\eta>0$ 被称为 学习率）
- 如果 $y=1$，但是 $s<0$
  $w_i\leftarrow w_i+\eta x_i$
  $w_0\leftarrow w_0+\eta$
- 如果 $y=-1$，但是 $s\ge 0$
  $w_i\leftarrow w_i-\eta x_i$
  $w_0\leftarrow w_0-\eta$

假设所有权重的初始值都设为 $0$

第一次更新：$\boldsymbol w=\eta y_{i_1}\boldsymbol x_{i_1}$
第二次更新：$\boldsymbol w=\eta y_{i_1}\boldsymbol x_{i_1}+\eta y_{i_2}\boldsymbol x_{i_2}$
第三次更新：$\boldsymbol w=\eta y_{i_1}\boldsymbol x_{i_1}+\eta y_{i_2}\boldsymbol x_{i_2}+\eta y_{i_3}\boldsymbol x_{i_3}$
…

权重总是具有形式 $\boldsymbol w=\sum_{i=1}^{n}\alpha_i y_i\boldsymbol x_i$，其中 $\boldsymbol \alpha$ 是一些系数
感知器的权重总是数据的线性组合
回忆一个新的数据点 $\boldsymbol x$ 的预测是基于 $w_0+\boldsymbol w’\boldsymbol x$ 的符号
将 $\boldsymbol w$ 进行替换，我们得到 $w_0+\sum_{i=1}^{n}\alpha_i y_i\boldsymbol x_i’\boldsymbol x$
点积 $\boldsymbol x_i’\boldsymbol x$ 可以被替换为一个核函数

算法描述：
选择初始权重 $\boldsymbol w^{(0)}, k=0$
设定 $\boldsymbol \alpha=\boldsymbol 0$
对于 $t$ 从 $1$ 到 $T$（轮）：
$\qquad$ 对于每个训练样本 $\{\boldsymbol x_i,y_i\}$：
$\qquad \qquad$ 基于 $w_0+\sum_{j=1}^{n}\alpha_j y_j \color{red}{\underbrace{\fbox{$\color{black}{\boldsymbol x_i' \boldsymbol x_j}$}}_{\text{核矩阵} k_{ij}}}$
$\qquad \qquad$ 如果分类错误，更新 $\alpha_i \leftarrow \alpha_i+1$

2.3 表示定理

定理： 对于任何训练集 $\{\boldsymbol x_i,y_i\}_{i=1}^{n}$，任何经验风险函数 $E$，单调递增函数 $g$，然后任何解
\[f^* \in \mathop{\operatorname{arg\,min}}\limits_f E(\boldsymbol x_1,y_1,f(\boldsymbol x_1),...,\boldsymbol x_n,y_n,f(\boldsymbol x_n))+g(\|f\|)\]
都有对应某些系数的表示：
\[f^*(\boldsymbol x)=\sum_{i=1}^{n}\alpha_i k(\boldsymbol x,\boldsymbol x_i)\]
注：$f$ 位于再生核希尔伯特空间（RKHS）
表示定理告诉我们（决策理论）学习器什么时候可以核化
对偶告诉我们该线性核表示的形式
SVM 只是一个例子，其他还包括诸如：
- 岭回归
- Logistic 回归
- 主成分分析（PCA）
- 典型相关分析（CCA）
- 线性判别分析（LDA）
- 还有很多…

3. 构造核函数

一些流行的核函数及其属性概述

3.1 多项式核

函数 $K(\boldsymbol u,\boldsymbol v)=(\boldsymbol u’\boldsymbol v+c)^d$ 被称为 多项式核
- 这里 $\boldsymbol u$ 和 $\boldsymbol v$ 都是 $m$ 维的向量
- $d \ge 0$ 是一个整数，$c\ge 0$ 是一个常数
不失一般性地，假设 $c=0$
- 如果并非如此，将 $\sqrt{c}$ 作为哑变量特征添加到 $\boldsymbol u$ 和 $\boldsymbol v$
推导如下：
$\begin{eqnarray} (\boldsymbol u'\boldsymbol v)^d &=& (u_1v_1+\cdots+u_mv_m)(u_1v_1+\cdots+u_mv_m)...(u_1v_1+\cdots+u_mv_m)\\ &=& \sum_{i=1}^{l}(u_1v_1)^{a_{i_1}}...(u_mv_m)^{a_{i_m}}\qquad \color{red}{\text{（这里}\, 0\le a_{ij}\le d \,\text{和}\, l \,\text{都是整数）}}\\ &=& \sum_{i=1}^{l} (u_1^{a_{i_1}}...u_m^{a_{i_m}})(v_1^{a_{i_1}}...v_m^{a_{i_m}})\\ &=& \sum_{i=1}^{l}\varphi(\boldsymbol u)_i \varphi(\boldsymbol v)_i \end{eqnarray}$
特征映射 $\varphi: \Bbb R^m \rightarrow \Bbb R^l$，其中 $\varphi_i(\boldsymbol x)=(x_1^{a_{i_1}}…x_m^{a_{i_m}})$

3.2 检查核函数的合法性

方法 1： 给定合法的核函数 $K_1(\boldsymbol u, \boldsymbol v), K_2(\boldsymbol u, \boldsymbol v)$，常数 $c>0$，并且 $f(\boldsymbol x)$ 是一个实值函数。那么，下面的每个函数都是一个合法的核函数：
- $K(\boldsymbol u,\boldsymbol v)=K_1(\boldsymbol u,\boldsymbol v)+K_2(\boldsymbol u,\boldsymbol v)$
- $K(\boldsymbol u,\boldsymbol v)=cK_1(\boldsymbol u,\boldsymbol v)$
- $K(\boldsymbol u,\boldsymbol v)=f(\boldsymbol u)K_1(\boldsymbol u,\boldsymbol v)\,f(\boldsymbol v)$
- 更多实例，请参考 PRML by Bishop
方法 2： 利用 Mercer 定理

3.3 径向基函数核

函数 $K(\boldsymbol u,\boldsymbol v)=\exp(-\gamma \| \boldsymbol u-\boldsymbol v\|^2)$ 被称为 径向基函数核（又称 高斯核）
- 这里 $\gamma>0$ 是 spread 参数
推导如下：
$\begin{eqnarray} \exp(-\gamma \| \boldsymbol u-\boldsymbol v\|^2) &=& \exp\left(-\gamma (\boldsymbol u-\boldsymbol v)'(\boldsymbol u-\boldsymbol v)\right)\\ &=& \exp\left(-\gamma (\boldsymbol u'\boldsymbol u-2\boldsymbol u'\boldsymbol v+\boldsymbol v'\boldsymbol v)\right)\\ &=& \exp(-\gamma \boldsymbol u'\boldsymbol u)\exp(2\gamma \boldsymbol u'\boldsymbol v)\exp(-\gamma \boldsymbol v'\boldsymbol v)\\ &=& f(\boldsymbol u)\exp(2\gamma \boldsymbol u'\boldsymbol v)\,f(\boldsymbol v)\\ &=& f(\boldsymbol u)\left(\sum_{d=0}^{\infty}r_d(\boldsymbol u'\boldsymbol v)^d\right)\,f(\boldsymbol v) \qquad \color{red}{\text{（指数函数的泰勒展开）}} \end{eqnarray}$
这里，每个 $(\boldsymbol u’\boldsymbol v)^d$ 都是一个 多项式核。利用核函数的性质，可知中间部分也是一个合法的核函数，因此，最终整个表达式是一个合法的核函数。

3.4 Mercer 定理

问题：给定一个映射 $\varphi(\boldsymbol u)$，是否存在一个合法的核函数？
逆问题：给定某个函数 $K(\boldsymbol u,\boldsymbol v)$，它是一个合法的核函数吗？换而言之，是否存在一个映射 $\varphi(\boldsymbol u)$ 是由这个核函数实现的？
Mercer 定理：
- 考虑一个有限序列 $\boldsymbol x_1,…,\boldsymbol x_n$
- 构造一个由成对的值 $K(\boldsymbol x_i,\boldsymbol x_j)$ 组成的 $n\times n$ 的矩阵
- 如果这个矩阵是 半正定的，那么 $K(\boldsymbol x_i,\boldsymbol x_j)$ 是一个合法的核函数，这一点对于所有可能的序列 $\boldsymbol x_1,…,\boldsymbol x_n$ 都满足

3.5 各种不同类型的输入数据

到目前为止，本课程 COMP90051 涉及的数据都是由数字组成的向量
但是，如果我们想在不同类型的数据上应用机器学习该怎么办？
图
- Facebook, Twitter, …
可变长度序列
- “science is organized knowledge”, “wisdom is organized life”, …
- “CATTC”, “AAAGAGA”
歌曲，电影等等

3.6 处理任意数据结构

核函数是一种强大的方法可以处理很多不同的数据类型
可以在可变长度的字符串上定义相似度函数：
$K($“science is organized knowledge”, “wisdom is organized life”$)$
然而，不是所有的作用在两个对象上的函数都是一个合法的核函数
记住，我们需要核函数 $K(\boldsymbol u,\boldsymbol v)$ 在某个特征空间实现点积的计算

总结

核函数
- 基扩展处理非线性
- 核技巧加速计算
模块化学习
- 将 “学习模块” 从特征变换中分离出来
- 表示定理
构造核函数
- 一些流行的核函数及其属性概述
- Mercer 定理
- 将机器学习扩展到常规数据结构之外

下节内容：集成学习

本作品采用知识共享署名-非商业性使用-相同方式共享 4.0 国际许可协议进行许可。欢迎转载，并请注明来自：YEY 的博客同时保持文章内容的完整和以上声明信息！

统计机器学习 11：核方法

墨尔本大学 COMP90051 课程笔记