Lecture 00-03 线性文本分类
参考资料:Natural Language Processing: Chapter 2 - Linear text classification (p.13-46) —— by Jacob Eisenstein
引言
我们从 文本分类 问题开始:给定一个文本文档,为其分配一个离散标签 $y\in \mathcal Y$,其中 $\mathcal Y$ 是可能标签的集合。文本分类有着很广泛的应用,从垃圾邮件过滤到电子健康记录分析等等。本章从数学的角度描述了一些最著名的应用和最高效的文本分类算法,这应该有助于你理解这些算法的作用以及为什么起作用。文本分类也是更复杂的自然语言处理任务的基础。对于没有机器学习或统计学背景的读者来说,本章中的材料要比后面的大部分内容花费更多的时间来消化。但是,这些投入的时间终将获得回报,因为这些基本分类算法背后的数学原理会在本书其他章节的内容中反复出现。
1. 词袋模型
为了实现文本分类,第一个问题是如何表示每个文档或实例。一种常见方法是使用单词计数的列向量,例如 $\boldsymbol x = [0,1,1,0,0,2,0,1,13,0…]^{\mathrm{T}}$,其中 $x_j$ 是单词 $j$ 的计数。$\boldsymbol x$ 的长度为 $V\triangleq |\mathcal V|$,其中 $\mathcal V$ 是词汇表中可能单词的集合。在线性分类中,分类决策基于单个特征计数(例如,单词计数)的加权和。
对象 $\boldsymbol x$ 是一个向量,但通常称为一个 词袋(bag of words),因为它仅包含每个单词计数的相关信息,而不包含单词出现的顺序信息。在词袋表示法下,我们将忽略语法、句子边界、段落 —— 等等除了单词之外的一切。然而,词袋模型对于文本分类却出奇地有效。如果你在某个文档中看到 “$whale$(鲸鱼)” 一词,那么该文档是 $\rm{fiction}$(虚构的) 还是 $\rm{nonfiction}$(非虚构的)?如果你看的是 “$molybdenum$(钼)” 这个词呢?对于许多标签问题,单个单词可以作为强大的预测指标。
为了从一个词袋中预测出一个标签,我们可以为词汇表中的每个单词分配一个分数,以衡量与该标签的兼容性。例如,对于标签 $\rm{F\scriptsize{ICTION}}$,我们可以分配一个正的分数给单词 $whale$ ,分配一个负的分数给单词 $molybdenum$。这些得分称为 权重,它们被排列在一个列向量 $\boldsymbol \theta$ 中。
现在,假设你想要一个多分类器,其中,$K\triangleq |\mathcal Y|>2$。例如,你可能想对有关体育、名人、音乐和商业的新闻报道进行分类。目标是在给定词袋 $\boldsymbol x$ 的情况下,利用权重 $\boldsymbol \theta$ 预测出一个标签 $\hat y$。对于每个标签 $y\in \mathcal Y$,我们计算出一个分数 $\Psi(\boldsymbol x,y)$,这是词袋 $\boldsymbol x$ 与标签 $y$ 之间兼容性的一个标量度量。在线性词袋分类器中,该分数是权重 $\boldsymbol \theta$ 与 特征函数 $\boldsymbol f(\boldsymbol x,y)$ 的输出之间的向量内积:
\[\Psi(\boldsymbol x,y)= \boldsymbol \theta \cdot \boldsymbol f(\boldsymbol x,y)=\sum_{j}\theta_j f_j(\boldsymbol x,y) \tag{1}\label{(1)}\]如上所示,$\boldsymbol f$ 函数具有两个参数,单词计数 $\boldsymbol x$ 和标签 $y$,并且返回一个向量输出。例如,给定参数 $\boldsymbol x$ 和 $y$,该特征向量的元素 $j$ 可能为:
\[f_j(\boldsymbol x,y)=\begin{cases}x_{whale}, & \text{if}\; y= \rm{F\scriptsize{ICTION}}\\ 0, & \rm{otherwise}\end{cases} \tag{2}\]如果标签为 $\rm{F\scriptsize{ICTION}}$,则此函数返回单词 $whale$ 的计数,否则返回零。索引 $j$ 取决于 $whale$ 在词汇表中的位置,以及 $\rm{F\scriptsize{ICTION}}$ 在可能的标签集合中的位置。然后,相应的权重 $\theta_j$ 对单词 $whale$ 和标签 $\rm{F\scriptsize{ICTION}}$ 之间的兼容性进行打分。正的分数表示该单词使得该标签可能性更大。
特征函数的输出可以形式化为一个向量:
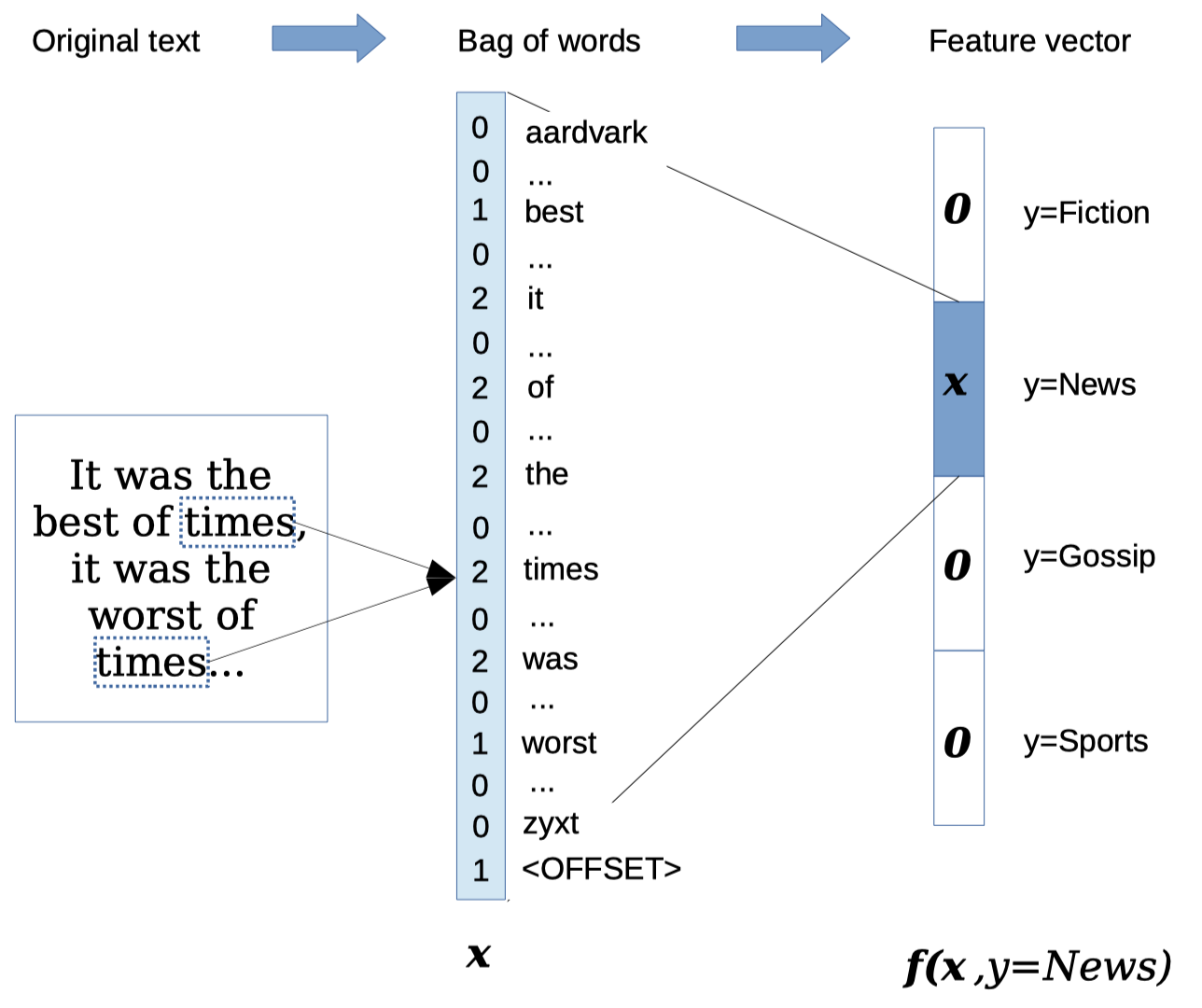
\[\begin{align} \boldsymbol f(\boldsymbol x,y=1) &= [\boldsymbol x;\underbrace{0;0;...;0}_{(K-1)\times V}] \tag{3}\label{(3)}\\ \boldsymbol f(\boldsymbol x,y=2) &= [\underbrace{0;0;...;0}_{V} ;\boldsymbol x;\underbrace{0;0;...;0}_{(K-2)\times V}] \tag{4}\\ \boldsymbol f(\boldsymbol x,y=K) &= [\underbrace{0;0;...;0}_{(K-1)\times V};\boldsymbol x] \tag{5}\label{(5)} \end{align}\]其中,$[\underbrace{0;0;…;0}_{(K-1)\times V}]$ 是由 $(K-1)\times V$ 个零组成的一个列向量,分号表示垂直串联。对于 $K$ 个可能标签中的每一个,特征函数都会返回一个向量,该向量中的大多数元素都为零,而在其中某个位置则会插入一个单词计数 $\boldsymbol x$ 的列向量,插入的位置与某个特定的标签 $y$ 有关。这种表示方式如 图 1 所示。这种表示方法初看可能有些笨拙,但是它将学习设定推广到了一个令人印象深刻的范围,尤其是 结构预测。
给定一个权重向量 $\boldsymbol \theta \in \mathbb R^{VK}$,我们现在可以通过公式 $\eqref{(1)}$ 计算出分数 $\Psi(\boldsymbol x,y)$。该内积给出了观测 $\boldsymbol x$ 与标签 $y$ 之间兼容性的一个标量度量。对于任何文档 $\boldsymbol x$,我们预测标签 $\hat y$:
\[\hat y=\mathop{\operatorname{arg\,max}}\limits_{y\in \mathcal Y}\Psi(\boldsymbol x,y) \tag{6}\] \[\Psi(\boldsymbol x,y)=\boldsymbol \theta \cdot \boldsymbol f(\boldsymbol x,y) \tag{7}\]这种内积的表示方法清晰地将数据($\boldsymbol x$ 和 $y$)和参数($\boldsymbol \theta$)分割开来。
在表示和分析时,我们采用向量符号;而在代码中,权重和特征向量可以通过字典实现。然后内积可以通过循环计算。在python中:
1
2
3
4
5
def compute_score(x,y,weights):
total = 0
for feature,count in feature_function(x,y).items():
total += weights[feature] * count
return total
这种表示方法有很多好处,它避免了在大量计数为零的特征上的存储与迭代。
通常,会在单词计数向量 $\boldsymbol x$ 的末尾增加一个 偏置特征,通常是 $1$。然后,我们需要在每个零向量中增加一个额外的零,使得向量的长度匹配。这使得完整特征向量 $\boldsymbol f(\boldsymbol x,y)$ 的长度为 $(V+1)\times K$。而与该偏置特征相关联的权重可以被想象成一个作用在每个标签上的正或负偏差。例如,如果我们预期大部分的邮件都是 SPAM(垃圾邮件),那么 $y=\rm{S\scriptsize{PAM}}$ 的偏置特征的权重应当大于 $y=\rm{N\scriptsize{OT}}\text{-}\rm{S\scriptsize{PAM}}$ 的偏置特征的权重。
回到权重 $\boldsymbol \theta$,它们是从哪里来的?一种可能性是手动设置它们。 如果我们想将英语与西班牙语区分开,则可以使用英语和西班牙语词典,并将出现在相关词典中的每个单词的权重设置为 $1$。例如:
\[\begin{align} \theta_{(E,bicycle)} &= 1 & \quad \theta_{(S,bicycle)} &= 0\\ \theta_{(E,bicicleta)} &= 0 & \quad \theta_{(S,bicicleta)} &= 1\\ \theta_{(E,con)} &= 1 & \quad \theta_{(S,con)} &= 1\\ \theta_{(E,ordinateur)} &= 0 & \quad \theta_{(S,ordinateur)} &= 0\\ \end{align}\]类似地,如果我们想区分正面情感和负面情感,可以使用社会心理学家(Tausczik 和Pennebaker,2010)定义的正面和负面 情感词汇表。
但是,由于单词数量众多以及对精确数值权重的选择困难,往往使得手动设置分类权重并不容易。相反,我们将从数据中学习权重。电子邮件用户手动将消息标记为 $\rm{\scriptsize{SPAM}}$(垃圾邮件);报纸将它们自己的文章标记为 $\rm{\scriptsize{BUSINESS}}$(商业) 或 $\rm{\scriptsize{STYLE}}$(风格)。使用此类 实例标签,我们可以通过 有监督机器学习 自动获得权重。本章将讨论几种用于分类的机器学习方法。第一种是基于概率。有关概率知识的回顾,请参阅 自然语言处理 00-01:概率论基础。
2. 朴素贝叶斯
一个词袋 $\boldsymbol x$ 及其真实标签 $y$ 的 联合概率 记为 $\text{p}(\boldsymbol x,y)$。假设我们有一个包含 $N$ 个带标签实例的数据集 \(\{(\boldsymbol x^{(i)},y^{(i)})\}_{i=1}^{N}\),我们假设它们服从 独立同分布(IID)。那么整个数据集的联合分布记为 $\text{p}(\boldsymbol x^{(1:N)},y^{(1:N)})$,它等于 $\prod_{i=1}^{N}\text{p}_{X,Y}(\boldsymbol x^{(i)},y^{(i)})$。
而这与分类有什么关系呢?一种分类方法是设置权重 $\boldsymbol \theta$,使得一个带标签文档 训练集 的联合概率最大化。这被称为 最大似然估计:
\[\begin{align} \hat{\boldsymbol \theta} &= \mathop{\operatorname{arg\,max}}\limits_{\boldsymbol \theta}\text{p}(\boldsymbol x^{(1:N)},y^{(1:N)};\boldsymbol \theta) \tag{8}\\ &= \mathop{\operatorname{arg\,max}}\limits_{\boldsymbol \theta} \prod_{i=1}^{N}\text{p}(\boldsymbol x^{(i)},y^{(i)};\boldsymbol \theta) \tag{9}\\ &= \mathop{\operatorname{arg\,max}}\limits_{\boldsymbol \theta} \sum_{i=1}^{N}\log \text{p}(\boldsymbol x^{(i)},y^{(i)};\boldsymbol \theta) \tag{10} \end{align}\]记法 $\text{p}(\boldsymbol x^{(i)},y^{(i)};\boldsymbol \theta)$ 表示 $\boldsymbol \theta$ 是概率函数的一个 参数。概率的乘积可以用对数概率之和代替,因为对数函数在正参数上是单调递增的,所以相同的 $\boldsymbol \theta$ 可以同时使概率函数和它的对数最大化。从数值稳定性的角度考虑,使用对数也会更好一些:在大型数据集上,许多概率相乘可能会导致结果 下溢 为零。
概率 $\text{p}(\boldsymbol x^{(i)},y^{(i)};\boldsymbol \theta)$ 通过 生成式模型 定义 —— 它是一种已生成观测数据的理想的随机过程。算法 1 描述了 朴素贝叶斯 分类器下的生成式模型,参数 \(\boldsymbol \theta=\{\boldsymbol \mu,\boldsymbol \phi\}\)
-
该生成式模型的第一行编码了 “实例之间是相互独立的” 这一假设:文档 $i$ 的标签或文本不会影响文档 $j$ 的标签或文本。此外,实例都服从相同的分布:标签 $y^{(i)}$ 和文本 $\boldsymbol x^{(i)}$(以 $y^{(i)}$ 为条件)上的分布对于所有的实例 $i$ 都是相同的。换而言之,我们假设每个文档在标签上的分布是相同的,并且每个文档在单词上的分布仅取决于标签,而不是文档中的其他任何内容。我们还假设这些文档之间不会互相影响:如果单词 $whale$ 出现在文档 $i=7$ 中,并不会使得它在文档 $i=8$ 中再次出现的可能性更大或者更小。
-
该生成式模型的第二行表明随机变量 $y^{(i)}$ 是来自一个带有参数 $\boldsymbol \mu$ 的类别分布。类别分布就像一个带权重的骰子:列向量 $\boldsymbol \mu=[\mu_1;\mu_2;…;\mu_K]$ 给出了每个标签的概率,因此掷出标签 $y$ 的概率等于 $\mu_y$。例如,如果 $\mathcal Y=\{\rm{\scriptsize{POSITIVE, NEGATIVE, NEUTRAL}}\}$,我们可能有 $\boldsymbol \mu=[0.1;0.7;0.2]$。我们要求 $\sum_{y\in \mathcal Y}\mu_y=1$ 和 $\mu_y \ge 0,\; \forall y\in \mathcal Y$:每个标签的概率都是非负的,并且这些概率之和等于 $1$。
-
第三行描述了词袋计数 $\boldsymbol x^{(i)}$ 是如何生成的。通过写成 $\boldsymbol x^{(i)}\mid y^{(i)}$,这行表明单词计数是以标签为条件的,因此联合概率可以使用链式法则进行因式分解:
这个特定的分布 ${\rm{p}}_{X\mid Y}$ 是 多项式分布,它是非负计数向量上的一个概率分布。该分布的概率质量函数为:
\[\begin{align} {\rm p_{mult}}(\boldsymbol x;\boldsymbol \phi) &= B(\boldsymbol x)\prod_{j=1}^{V}\phi_j^{x_j} \tag{12}\\ B(\boldsymbol x) &= \dfrac{\left(\sum_{j=1}^{V}x_j\right)!}{\prod_{j=1}^{V}(x_j!)} \tag{13} \end{align}\]就像在类别分布中一样,参数 $\phi_j$ 可以被解释为一个概率:具体来说,就是文档中任何给定的 token 是单词 $j$ 的概率。多项式分布涉及到单词上的乘积,而乘积中的每一项都等于概率 $\phi_j$ 的单词计数 $x_j$ 次幂。那些计数为零的单词在该乘积中不起作用,因为 $\phi_j^0=1$。系数项 $B(\boldsymbol x)$ 被称为 多项式系数。它不取决于 $\boldsymbol \phi$,并且通常可以忽略。你知道为什么在这里我们需要它吗?
记法 ${\rm p}(\boldsymbol x\mid y;\boldsymbol \phi)$ 表明给定标签 $y$ 和参数 $\boldsymbol \phi$,单词计数 $\boldsymbol x$ 的条件概率等于 ${\rm p_{mult}}(\boldsymbol x;\boldsymbol \phi_y)$。通过指定该多项式分布,我们描述了一个 多项式朴素贝叶斯 分类器。为什么是 “朴素的”?因为该多项式分布会独立地对待每个单词 token,以类别作为条件:概率质量函数在所有的计数上进行因式分解。
2.1 Types 和 tokens
算法 2 中展示了一个略微改进过的朴素贝叶斯生成式模型。相比生成一个 types 计数的向量 $\boldsymbol x$,该模型会生成一个 tokens 的序列 $\boldsymbol w=(w_1,w_2,…,w_M)$。Types 和 tokens 之间的区别很关键: $x_j\in \{0,1,2,…,M\}$ 是单词 type $j$ 在词汇表中的计数,例如,单词 $cannibal$ 出现的次数;而 $w_m\in \mathcal V$ 是 token $m$ 在文档中的身份信息,例如,$w_m=cannibal$。
序列 $\boldsymbol w$ 的概率是类别概率的乘积。算法 2 作出了一个条件独立假设:每个 token $w_m^{(i)}$ 都独立于所有其他 tokens $w_{n\ne m}^{(i)}$,以标签 $y^{(i)}$ 为条件。这与多项式分布中所暗含的 “朴素” 独立性假设相同,因此,该模型的最优参数与多项式朴素贝叶斯中的最优参数相同。对于任何实例,该模型给出的概率与多项式朴素贝叶斯下的概率成正比。这个比例常数就是多项式系数 $B(\boldsymbol x)$。因为 $B(\boldsymbol x)\ge 1$,计数向量 $\boldsymbol x$ 的概率至少与诱导相同计数的单词列表 $\boldsymbol w$ 的概率一样大:可能有许多个单词序列都对应于同一个计数向量。例如,$man\; bites\; dog$ 和 $dog\; bites\; man$ 对应于同一个计数向量 $\{bites:1,dog:1,man:1\}$,并且 $B(\boldsymbol x)$ 等于计数向量 $\boldsymbol x$ 可能的单词顺序的总数。
有些时候,将实例视为 types 的计数 $\boldsymbol x$ 会很有帮助;而另外一些时候,我们最好将其视为 tokens 的序列 $\boldsymbol w$。如果 tokens 是由一个假设条件独立的模型生成的,那么这两种视角得到的概率模型是相同的,除了一个和标签或参数无关的比例因子。
2.2 预测
朴素贝叶斯的预测规则是选择能够最大化 $\log \text p(\boldsymbol x,y;\boldsymbol \mu,\boldsymbol \phi)$ 的标签 $y$:
\[\begin{align} \hat y &= \mathop{\operatorname{arg\,max}}\limits_y \log \text p(\boldsymbol x,y;\boldsymbol \mu,\boldsymbol \phi) \tag{14}\\ &= \mathop{\operatorname{arg\,max}}\limits_y \log \text p(\boldsymbol x\mid y;\boldsymbol \phi)+\log \text p(y;\boldsymbol \mu) \tag{15} \end{align}\]现在我们可以根据生成的故事插入概率分布:
\[\begin{align} \log \text p(\boldsymbol x\mid y;\boldsymbol \phi)+\log \text p(y;\boldsymbol \mu) &= \log \left[B(\boldsymbol x)\prod_{j=1}^{V}\boldsymbol \phi_{y, j}^{x_j}\right]+\log \mu_y \tag{16}\\ &= \log B(\boldsymbol x)+\sum_{j=1}^{V}x_j \log \phi_{y, j}+\log \mu_y \tag{17}\\ &= \log B(\boldsymbol x)+\boldsymbol \theta \cdot \boldsymbol f(\boldsymbol x,y) \tag{18} \end{align}\]其中,
\[\begin{align} \boldsymbol \theta &= [\boldsymbol \theta^{(1)};\boldsymbol \theta^{(2)};;...;\boldsymbol \theta^{(K)}] \tag{19}\\ \boldsymbol \theta^{(y)} &= [\log \phi_{y,1};\log \phi_{y,2};...;\log \phi_{y,V};\log \mu_y] \tag{20} \end{align}\]特征函数 $\boldsymbol f(\boldsymbol x,y)$ 是一个由 $V$ 个单词计数和一个偏置组成的向量,其他不等于 $y$ 的标签则由零元素填补(请见等式 $\eqref{(3)}$-$\eqref{(5)}$ 和 图 1)。这种构造可以确保内积 $\boldsymbol \theta \cdot \boldsymbol f(\boldsymbol x,y)$ 仅激活权重在 $\boldsymbol \theta^{(y)}$ 中的特征。这些特征和权重就是我们在为每个 $y$ 计算联合对数概率 $\log \text p(\boldsymbol x,y)$ 时所需要的全部信息。这点很关键:通过这种记法,我们已经将计算文档标签对 $(\boldsymbol x,y)$ 的对数似然的问题转换成了计算向量内积。
2.3 估计
下节内容:
本作品采用知识共享署名-非商业性使用-相同方式共享 4.0 国际许可协议进行许可。 欢迎转载,并请注明来自:YEY 的博客 同时保持文章内容的完整和以上声明信息!