统计建模 MAST90139 课程笔记

数据科学统计建模 01：导论 (1)

墨尔本大学 MAST90139 课程笔记

Posted by YEY on March 3, 2020

Lecture 01 导论 (1)

1. 概览

1.1 线性模型

  • 线性（回归）模型 可以说是几乎所有统计应用中使用的最重要的统计模型。

  • 一个线性模型可以由下面的回归方程定义：

    \[\begin{align} Y &= \beta_0+\beta_1 X_1+\cdots+\beta_{p-1} X_{p-1}+\epsilon,\qquad 或者 \\\\ Y &= \mu+\varepsilon，\;\; 其中\;\; \mu=E(Y)=\beta_0+\beta_1 X_1+\cdots+\beta_{p-1} X_{p-1} \end{align}\]

    其中，

    • $Y$：响应变量（也称 “结果变量” 或者 “因变量”）；
    • $X_1,\cdots,X_{p-1}$：协变量（也称 “解释变量”、“预测变量” 或者 “自变量”）；
    • $\varepsilon$：随机误差，具有均值 $0$ 和未知的常数方差 $\sigma^2$；
    • $\beta_0,\beta_1,\cdots,\beta_{p-1}$：未知的回归参数，需要基于观测数据对其进行估计。


    注意：

    • 这里我们假设随机误差 $\varepsilon$ 的均值为 $0$ 可以从下面两个角度理解：
      • 直观上：假如其均值不为 $0$，说明它影响着 $Y$ 的均值（或者说预测值），进而说明随机误差项中仍然存在可以影响 $Y$ 的因素，比如遗漏的解释变量，因此模型仍有改进的必要。
      • 形式上：在不假设误差项 $0$ 均值（但是模型需要引入常数项 $\beta_0$）的情况下，我们会遇到模型识别的问题，此时我们无法区分常数项和随机误差项的均值。所以我们要么不引入常数项 $\beta_0$，要么假设误差项均值为 $0$。
    • 关于假设随机误差的方差 $\sigma^2$ 是一个未知常数还是未知函数则又引出了另外的讨论话题。但是，在线性模型中，我们将随机误差假设为一个未知常数，关于这点可以这样理解：
      由于存在随机变化，因此我们很难确定数据集中的所有数据是否具有相同的质量。然而，大多数建模过程在使用这些数据来估计模型中的未知参数时都会平等地对待所有数据。大多数方法还使用数据中随机变量的单个估计值来计算预测和校准不确定性。以相同的方式处理所有数据也会得到更简单、更易于使用的模型。反之，如果事实证明数据的质量并不均等，那么像这样处理数据的决定也会对结果模型的质量产生负面影响。

1.2 线性模型的向量 / 矩阵形式

  • 给定 $n$ 个观测数据点 $(Y,X_1,\cdots,X_{p-1})$，上面的回归方程可以写成向量 / 矩阵的形式：

    \[\begin{align} \mathbf y &= X\boldsymbol \beta + \boldsymbol \varepsilon,\qquad 或者\\\\ \mathbf y &= \boldsymbol \mu + \boldsymbol \varepsilon,\;\; 其中\;\; \boldsymbol \mu=E(\mathbf y)=X\boldsymbol \beta \end{align}\]

    其中，$\boldsymbol \mu=(\mu_1,\dots,\mu_n)^{\mathrm{T}},\;\boldsymbol \varepsilon=(\varepsilon_1,\dots,\varepsilon_n)^{\mathrm{T}},$

    \[\mathbf y=\begin{bmatrix} y_1 \\ \vdots \\ y_i \\ \vdots \\ y_n \end{bmatrix}_{\,n\times 1},\quad X=\begin{bmatrix}1 & x_{11} & \cdots & x_{1,p-1} \\ \vdots & \vdots & & \vdots\\ 1 & x_{i1} & \cdots & x_{i,p-1} \\ \vdots & \vdots & & \vdots\\ 1 & x_{n1} & \cdots & x_{n,p-1} \end{bmatrix}_{\,n\times p},\quad \boldsymbol \beta=\begin{bmatrix} \beta_0 \\ \beta_1 \\ \vdots \\ \beta_{p-1} \end{bmatrix}_{\,p\times 1}\]

  • 在一个线性模型中，$y_1,\dots,y_n$ 被假设为彼此之间相互独立，而 $X$ 被假设为已经确定的而非随机的。

    注意：

    • 这里我们假设 $X$ 是确定的有以下几点考虑：
      • 数学上更方便
      • 无论我们假设 $X$ 是随机的还是确定的，这并不会影响对于 $\boldsymbol \beta$ 的统计推断，因为 $\boldsymbol \beta$ 描述的是 $X$ 对于 $Y$ 的影响。所以我们选择了将 $X$ 视为确定的这一更简单的设定。

      另外，在后面的学习中，我们也会涉及到需要将 $X$ 假设为随机的情况。

1.3 线性模型的扩展

  • 线性模型是统计学中最重要的模型，但是当我们用它来解释复杂的现实世界时存在很多局限性。因此，我们需要对其进行扩展。关于线性模型的扩展有很多种方法，在本课程中，我们将主要从以下 4 个方面对线性模型进行扩展：
    • 将 $Y$ 的分布从正态扩展到一个指数族成员，引出 广义线性模型（GLM）。
      在线性模型中，我们假设 $Y$ 服从正态分布。在广义线性模型中，我们将这个假设放松到指数族成员，指数族涵盖了大部分常见分布：正态、二项式、泊松、Gamma、指数、Beta、负二项式等等。
    • 假设 $y_1,\dots,y_n$ 之间存在依赖关系，引出 多元广义线性模型（multivariate GLM）。
      线性模型中关于 $y_1,\dots,y_n$ 之间相互独立的假设也会带来很多局限。我们通过将其放松为允许彼此之间存在互相依赖关系，从而引出多元广义线性模型。
    • $\boldsymbol \mu=E(\mathbf y)$ 可能是 $X$ 和 $\boldsymbol \beta$ 的一个非参数函数，引出 非参数回归模型（nonparametric regression models）。
      线性模型中，响应变量 $Y$ 的均值 $\boldsymbol \mu=E(\mathbf y)=X\boldsymbol \beta$ 是一个关于 $\boldsymbol \beta$ 参数的线性函数。我们可以将其推广到非线性的情况，甚至非参数的情况。非参数可以有很多种形式，例如：回归树模型（我们几乎不可能写出一个树模型的数学函数）。分类树和回归树都是非参数回归模型的特例，此外，还存在很多其他的非参数回归模型，例如：核回归、局部多项式回归、样条回归（spline regression）等等。所以，从参数到非参数是一个巨大的扩展，这不仅仅是另外某个领域，而且衍生出了诸多相关学科，很多统计学家都长期致力于非参数模型的研究。
    • $X_1,\dots,X_{p-1}$ 作用在 $Y$ 上的某些效应（effects）可能是随机的，引出 随机 / 混合效应模型（random / mixed effects models）。
      在线性模型中，我们假设模型参数 $\boldsymbol \beta$ 只是一些未知的常数，它们并不是随机变量。在这种设定下，协变量 $X$ 作用在 $Y$ 上的效应被称为固定效应（fixed effects）。但是，在实践中，这种假设可能是不够的。
      例如：假如 $X_1$ 是一个分类变量（categorical variable），比如某个国家（世界上一共有超过 $200$ 个国家）。如果我们将 “国家” 这个分类变量作为线性回归模型中的一个协变量，我们需要将该分类变量编码为虚拟变量（dummy variables，也称 “哑变量”）。所以，如果一共有 $200$ 个国家，那么我们需要 $199$ 个虚拟变量来表示 “国家” 这个分类变量，这也意味着我们需要 $199$ 个参数来表示 “国家” 这个因素作用在 $Y$ 上的效应。可见，如果采用线性模型的设定，仅仅一个 “国家” 这样的协变量我们就需要如此多的参数，显然，这种低效的方法在实践中是不可行的。
      因此，我们将固定效应（fixed effects）推广到随机效应（random effects）。这意味着变量 $X$ 的某些系数可以是随机的，而其余的系数仍然是固定的。也就是说，一部分 $\beta$ 是随机的，另一部分 $\beta$ 是固定的，由此，我们可以得到随机效应模型，或者混合效应模型。


    由于时间限制，本课程中我们只会对以上几种扩展进行一些中等程度的学习，而不会深入到很高的层次。例如，仅仅对于随机效应模型就足够开设两到三门课程；对于多元广义线性模型也可以单独开设两门课程；而对于非参数回归模型，足够开设三到五门，或者甚至十门以上的课程进行深入研究。统计学是一个非常巨大的领域，其中很多内容对于初学者而言都比较困难，我们希望他们通过这门课程可以学习到尽可能多的知识而不会感到太大压力。


  • 本课程推荐参考教材为：Extending the Linear Model with R by Faraway, Julian
    另外，本课程需要使用统计软件 R 以及基于参考教材的 R package faraway

2. 通过一个案例回顾线性模型

对于本课程的所有章节，我们通常会以一个案例学习作为开始，通过结合真实数据的例子，我们可以对即将学习的那些线性模型扩展有一个更好的理解。

2.1 案例学习：2000年总统大选时佐治亚州缺计的选票

  • 2000 年的美国总统选举对当时的投票机制引起了很大争议。

  • 佐治亚州的投票数据在 Meyer（2002）中进行了介绍和分析。

    1
2
3
4
5

    library(faraway);
data(gavote);
help(gavote);
dim(gavote);
head(gavote)

    输出结果：

    1
2
3
4
5
6
7
8

    [1] 159  10  
         equip   econ perAA rural    atlanta gore bush other votes ballots  
APPLING  LEVER   poor 0.182 rural notAtlanta 2093 3940    66  6099    6617  
ATKINSON LEVER   poor 0.230 rural notAtlanta  821 1228    22  2071    2149  
BACON    LEVER   poor 0.131 rural notAtlanta  956 2010    29  2995    3347  
BAKER    OS-CC   poor 0.476 rural notAtlanta  893  615    11  1519    1607  
BALDWIN  LEVER middle 0.359 rural notAtlanta 5893 6041   192 12126   12785  
BANKS    LEVER middle 0.024 rural notAtlanta 1220 3202   111  4533    4773

    所以，在这个数据集中，我们的实验单元（experiment unit）是什么？
    答案是佐治亚州下辖的每个郡（county）：APPLING、ATKINSON、BACON 等等。

  • 前往投票站的选民如果已经完成了登记，那么他 / 她将会获得一张 ballot（选票）。
  • 但是，如果他 / 她没有投票选取总统，或者投票给一个以上的候选人，或者设备出现了故障，那么，不会产生 vote（投票）记录。
  • 例如：在 Appling 郡，有 $6617-6099=518$ 张 ballot 没有进入总统选举的 votes。这被称为 undercount（缺计）。
  • 我们的目标是通过线性模型和 R 分析出是什么因素影响了这种 undercount。

2.2 关于 gavote 数据的描述

  • 一个数据框，包含了以下 10 个变量的 159 个观测值。每个案例代表佐治亚州的一个郡。

    \[\begin{align} {\mathsf{equip:}} &\quad {\mathsf{采用的投票设备: LEVER, OS-CC, OS-PC, PAPER, PUNCH}}\\ {\mathsf{econ:}} &\quad {\mathsf{本郡的经济状况: middle poor rich}}\\ {\mathsf{perAA:}} &\quad {\mathsf{本郡非裔美国人的所占人口百分比}}\\ {\mathsf{rural:}} &\quad {\mathsf{本郡属于\; rural\; (乡村)\;还是\; urban\;(城市)}}\\ {\mathsf{atlanta:}} &\quad {\mathsf{本郡属于\;Atlanta\;地区还是\;notAtlanta\;地区}}\\ {\mathsf{gore:}} &\quad {\mathsf{Gore\;的\;votes\;数量}}\\ {\mathsf{bush:}} &\quad {\mathsf{Bush\;的\;votes\;数量}}\\ {\mathsf{other:}} &\quad {\mathsf{其他候选人的\;votes\;数量}}\\ {\mathsf{votes:}} &\quad {\mathsf{votes\;的总数}}\\ {\mathsf{ballots:}} &\quad {\mathsf{ballots\;的总数}}\\ \end{align}\]


  • Source: Meyer M. (2002) Uncounted Votes: Does Voting Equipment Matter? Chance, 15(4), 33-38

3. 关于 gavote 的初步数据分析

3.1 数值摘要

1

summary(gavote)

输出结果：

1
2
3
4
5
6
7
8
9
10
11
12
13
14

   equip        econ        perAA          rural           atlanta         gore       
 LEVER:74   middle:69   Min.   :0.0000   rural:117   Atlanta   : 15   Min.   :   249  
 OS-CC:44   poor  :72   1st Qu.:0.1115   urban: 42   notAtlanta:144   1st Qu.:  1386  
 OS-PC:22   rich  :18   Median :0.2330                                Median :  2326  
 PAPER: 2               Mean   :0.2430                                Mean   :  7020  
 PUNCH:17               3rd Qu.:0.3480                                3rd Qu.:  4430  
                        Max.   :0.7650                                Max.   :154509  
      bush            other            votes           ballots      
 Min.   :   271   Min.   :   5.0   Min.   :   832   Min.   :   881  
 1st Qu.:  1804   1st Qu.:  30.0   1st Qu.:  3506   1st Qu.:  3694  
 Median :  3597   Median :  86.0   Median :  6299   Median :  6712  
 Mean   :  8929   Mean   : 381.7   Mean   : 16331   Mean   : 16926  
 3rd Qu.:  7468   3rd Qu.: 210.0   3rd Qu.: 11846   3rd Qu.: 12251  
 Max.   :140494   Max.   :7920.0   Max.   :263211   Max.   :280975

可以看到，有些变量属于分类变量（例如：equip），对于这类变量，我们在 summary 中统计的是数据中该变量的各个类别出现的频率。有些变量属于数值变量（例如：perAA），对于这类变量，我们统计的是其均值、中位数、四分位数和最大最小值。

3.2 定义变量

我们感兴趣的是 undercount 是如何被影响的。但 undercount 并不在我们的观测数据中。因此，我们需要创造一个 undercount 的变量。我们观察到，不同的郡分配到的选票（ballots）数目差别很大，这表明为了更真实地反映出各郡的有效投票率，我们应当采用 relative undercount（相对缺计） 而不是 absolute undercount（绝对缺计）。我们可以定义一个代表 relative undercount 的变量 undercount 并将其添加到 gavote 数据框中。

方法 1：

1
2

gavote$undercount <- (gavote$ballots-gavote$votes)/gavote$ballots
summary(gavote$undercount)

输出结果：

1
2

   Min. 1st Qu.  Median    Mean 3rd Qu.    Max.
0.00000 0.02779 0.03983 0.04379 0.05647 0.18812

方法 2：

1

with(gavote, sum(ballots-votes)/sum(ballots)) #overall percent of undercount

输出结果：

1

[1] 0.03518021

上面给出了两种计算 relative undercount 的方法：

  • 方法 1 计算的是每个 county（郡）的 relative undercount（相对缺计），具体方法是用其对应的 ballots 的数量减去 votes 的数量，然后除以 ballots 的数量。
  • 方法 2 选择了直接在 ballots 和 votes 这两个向量上进行计算，对结果进行求和，然后再除以 ballots 向量中所有元素之和，其结果我们称为 overall percent of undercount（总体相对缺计），这种方法实际上忽略了 county（郡）这个因素对于 undercount 的影响。

我们对变量 undercount 很感兴趣，因此可以将其作为响应变量，其中每个郡对应的 undercount 计算公式如下（这里我们采用 方法 1）：

\[\text{undercount}=\dfrac{\text{number of ballots }-\text{ number of votes}}{\text{number of ballots}}\]

明白这些区别很重要，这并不涉及到高深的数学知识，但却反映了我们对于一个问题的分析思路。在实际项目中，合理地定义变量非常重要，它决定了我们是能够从数据中挖掘出很多有用的信息，还是简单地将这些信息忽略掉了。统计学不只是简单的数学计算，我们的目的是将其用于实践，因此，理解其中所涉及到的每个变量的物理意义（或者说，领域知识）是非常重要的，这是统计学的一个特性。

3.3 统计图摘要

我们还可以利用 R 绘制各种图表摘要，例如：直方图、概率密度图、饼图等。

1
2
3
4

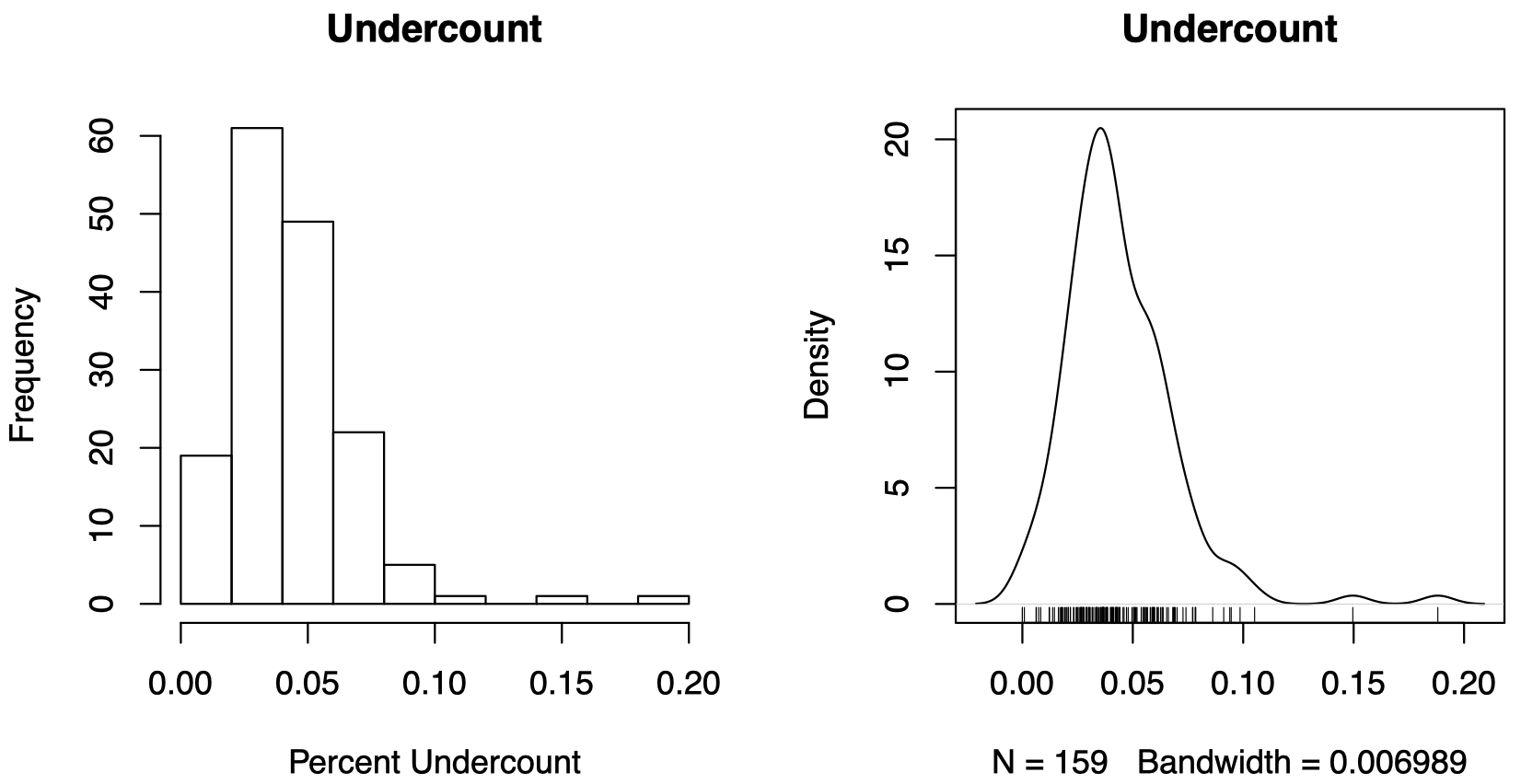
hist(gavote$undercount,main="Undercount",xlab="Percent Undercount")
plot(density(gavote$undercount),main="Undercount"); rug(gavote$undercount)
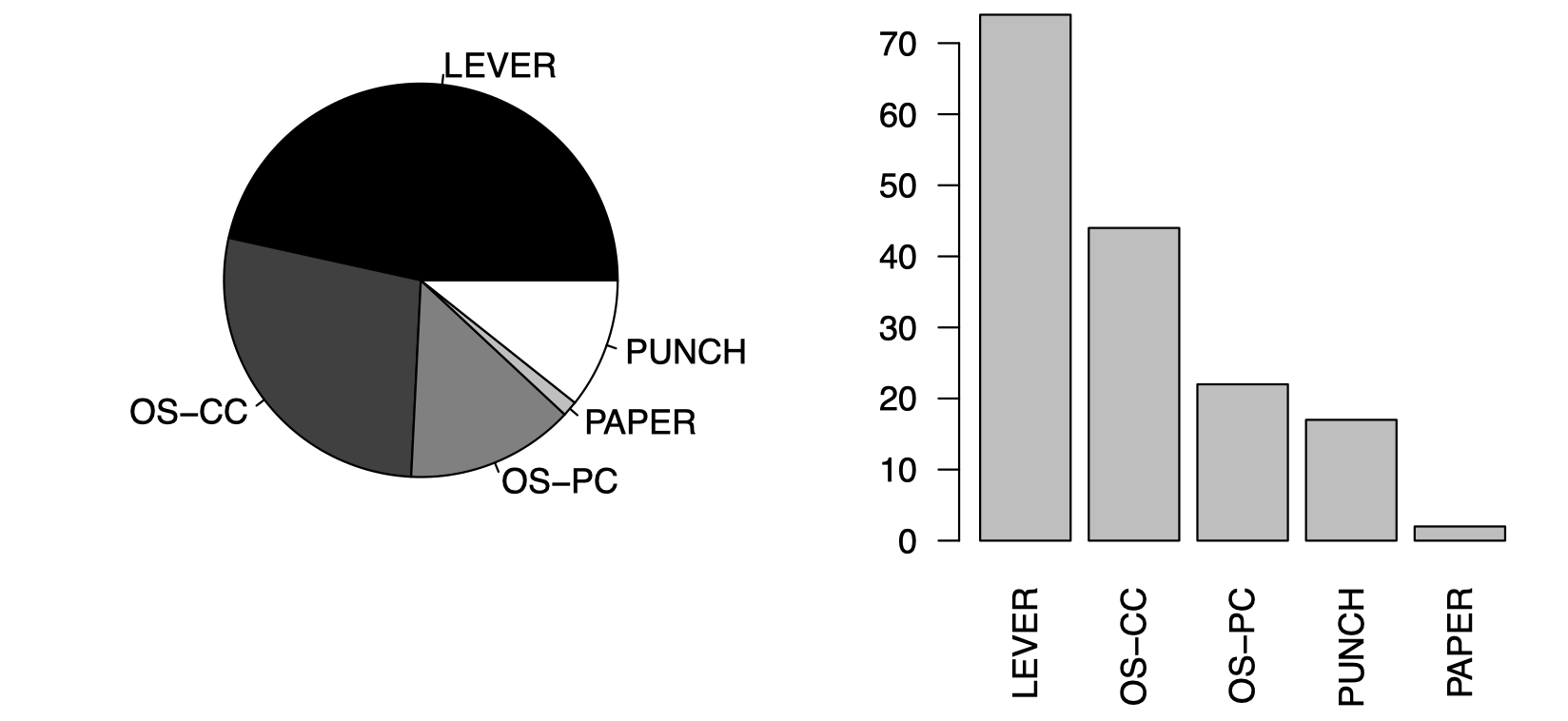
pie(table(gavote$equip),col=gray(0:4/4))
barplot(sort(table(gavote$equip),decreasing=TRUE),las=2)

图 1：左边是 undercount 的直方图；右边是带数据地毯的估计密度图。变量 undercount 是数值型的。

我们的数据中一共有 195 个郡，所以一共产生了 195 个 undercount 的值。从 图 1 左边的直方图可以看到，大部分郡的 undercount 的相对比重在 5% 附近，说明这些郡的大部分选民都投出的 ballots 都有效地计入了 votes；而极少数的郡的 undercount 的相对比重达到了 15% 甚至 20%，这说明这些郡的无效 ballots（即没有被计入 votes 的选票）占比很高。右边是密度图，形状和左边的直方图很像，但是更平滑。

图 2：左边是 equip（投票设备）的频率饼图；右边是 Pareto 图。变量 equip 是类别型的。

从 图 2 左边的饼图可以看到在这次选举中，LEVER 是最受欢迎的投票设备，而 PAPER 几乎没有什么郡采用。或者，我们可以将其转换为右边的柱状图，我们称之为 Pareto 图。

接下来，让我们看一下 “支持 Gore 的选民占比” 和 “非裔美国人占比” perAA 之间的关系。定义一个新的变量 pergore 代表支持 Gore 的选民占比，我们可以画出关于 pergore 和 perAA 二者的散点图。另外，并排箱型图提供了一种用于展示 定性变量（qualitative variables，例如：equip） 和 定量变量（quantitative variables，例如：undercount） 之间关系的方法。

1
2
3
4

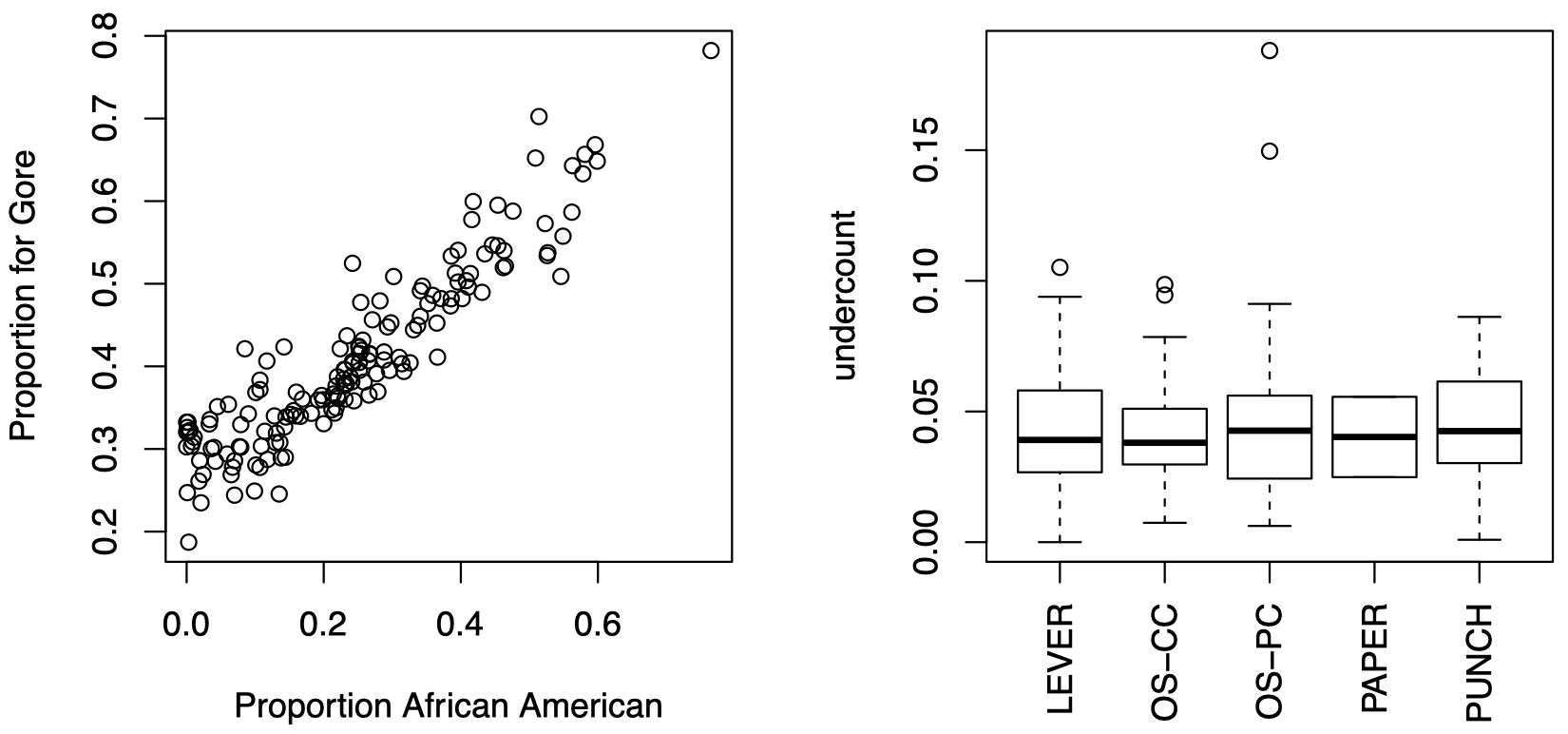
gavote$pergore <- gavote$gore/gavote$votes
plot(pergore ~ perAA, gavote, xlab="Proportion African American", 
       ylab="Proportion for Gore")
plot(undercount ~ equip, gavote, xlab="", las=3)

图 3：左边是每个郡内支持 Gore 的选民和非裔美国人比例的散点图。右边的箱型图显示了投票设备的 undercount 分布情况。

从 图 3 左边的散点图的趋势似乎可以得出某种结论：对于那些非裔美国人占比更高的郡，支持 Gore 的选民占比 pergore 也更有可能比较高。但这种结论也有可能并没有反映出真实情况，可能存在所谓的 虚假效应（spurious effect） 或者 混杂效应（confounding effect）。所以，虽然我们需要这些初步的数据分析来为我们提供一些信息，但是我们并不能简单地将所看到的信息直接作为最终结论。我们可以继续利用线性模型来分析 “非裔美国人占比” 和 “支持 Gore 的选民占比” 二者之间的关系。另外，我们希望根据右边的箱型图弄清楚 undercount 与每个郡所采用的投票设备 equip 之间的关系。从图上看，除了 OS-PC 存在两个比较高的异常值之外，几种 equip 对应的 undercount 分布之间没有特别明显的差异。所以，接下来我们可能会进一步去了解这两个异常点所代表的两个郡的情况，看看到底发生了什么。

如果我们想找出两个数值变量之间的关系，散点图会很有用；如果我们希望弄清楚一个数值变量和一个分类变量之间的关系，那么并列箱型图会很有帮助；而如果我们想知道两个分类变量之间的关系，统计图可能不会提供太多帮助，这种情况下，我们可以利用表格。

3.4 表格摘要

xtabs 函数可用于定性变量（qualitative variables，即 categorical variables）的交叉列表（cross-tabulations）。在此之前，我们需要将第 4 个变量的名称替换一下，“rural” 这个名称容易让人混淆因为它实际上包含 rural 和 urban 两个等级（levels），所以我们将其替换为 “usage”。接下来，我们基于 atlanta 和 usage 这两个变量对 undercount 进行交叉分类（cross classification）。这两个变量都各有 2 个等级，所以我们会得到一个 2 $\times$ 2 的表格。

R 代码：

1
2

names(gavote);
names(gavote)[4] <- "usage"

输出结果：

1
2

 [1] "equip"   "econ"    "perAA"     "rural"      "atlanta"    "gore"   "bush"      
 [8] "other"   "votes"   "ballots"   "undercount" "pergore"

R 代码：

1

xtabs(~ atlanta + usage, gavote)

输出结果：

1
2
3
4

            usage
atlanta      rural urban
  Atlanta        1    14
  notAtlanta   116    28

相关性（Correlations） 是对定性变量之间的关系进行数值化概括的标准方法。接下来我们将探寻 gavote 中的 3 号变量（perAA）、10 号变量（ballots）、11 号变量（undercount）和 12 号变量（pergore）之间的相关性。

R 代码：

1
2

nix <- c(3,10,11,12)
cor(gavote[,nix])

输出结果：

1
2
3
4
5

               perAA     ballots undercount    pergore
perAA      1.0000000  0.02773230  0.2296874 0.92165247
ballots    0.0277323  1.00000000 -0.1551724 0.09561688
undercount 0.2296874 -0.15517245  1.0000000 0.21876519
pergore    0.9216525  0.09561688  0.2187652 1.00000000

上面我们得到了一个 4 $\times$ 4 的相关系数矩阵。可以看到，大部分变量之间的相关系数都比较小。此外，pergore 与 perAA 的之间相关系数很大（正如我们在前面的散点图中所看到的），这说明这两个变量之间高度相关，而这可能会在解释线性（回归）模型的结果时带来一些麻烦。

下节内容：导论 (2)

知识共享许可协议本作品采用知识共享署名-非商业性使用-相同方式共享 4.0 国际许可协议进行许可。 欢迎转载，并请注明来自：YEY 的博客 同时保持文章内容的完整和以上声明信息！
CATALOG
    FEATURED TAGS
    随笔 课程笔记 统计机器学习 COMP90051 学习笔记 自然语言处理 COMP90042 PyTorch 人工智能伦理 COMP90087 数据科学多元统计学 MAST90138 AI 自动规划 COMP90054 数据分析 计算统计学与数据科学 MAST90083 高级数据库系统 COMP90050 统计建模 MAST90139 读书 📚 MySQL 学习索引 Hive 技术问题 Jekyll Workshop
    FRIENDS