Lecture 02 搜索算法 (1)
1. 基本模型算法
1.1 基本状态模型:经典规划
追求的目标:
状态模型 $S(P)$:
- 有限离散状态空间 $S$
- 一个 已知的初始状态 $s_0\in S$
- 一个目标状态的集合 $S_G\subseteq S$
- 每个 $s\in S$ 中可以采取的行动 $A(s)\subseteq A$
- 确定性转移函数(deterministic transition function) $s’=f(a,s) \;\;\text{for}\;\; a\in A(s)$
- 正的 行动代价(action costs) $c(a,s)$
$\color{blue}{\to}$ 一个 解 是将 $s_0$ 映射到 $S_G$ 内部的一个可行的行动序列,如果它能够最小化 行动代价之和(例
$\quad$如:移动步数),我们称其为 最优解。
$\color{blue}{\to}$ 通过放松 蓝色 部分的假设,我们可以得到不同的 模型 和 控制器
$\quad$例如:假设我们的转移函数不是确定性的(deterministic),而是概率性的(probabilistic),所
$\quad$以基于某个变量,某种情况下可能发生一种转移,而其他情况下可能发生另一种转移。我们并不
$\quad$知道到底会发生哪种情况,这其中存在着一些概率。
1.2 求解状态模型:图里面的寻路
用于规划的 搜索算法 利用了(经典)状态模型 $S(P)$ 与有向图之间的对应关系:
- 图中的 结点 代表模型中的 状态 $s$
- 图中的 边 $(s,s’)$ 代表模型中对应的具有相同代价的 转移
在 启发式搜索规划 中,问题 $P$ 通过在与模型 $S(P)$ 关联的 图 上的 路径查找 算法得以解决。
1.3 搜索算法的分类
盲目 搜索 vs. 启发式(或者 有信息)搜索:
- 盲目搜索算法:在一般搜索算法中仅使用基本的原始信息。
- 例如:深度优先搜索(DFS)、宽度优先搜索(BFS)、一致代价搜索(Uniform Cost Search, UCS,例如:Dijkstra)、迭代深化搜索(Iterative Deepening Search, IDS)
- 启发式搜索算法:额外使用 启发式函数 估计到目标的距离(或剩余代价)。
- 例如:A$^*$ 搜索、IDA$^*$ 搜索、爬山算法(Hill Climbing)、最佳优先搜索(Best First)、WA$^*$ 搜索、DFS B&B 算法、LRTA$^*$ 搜索……
系统 搜索 vs. 局部 搜索:
- 系统搜索算法:同时考虑大量搜索结点。
- 局部搜索算法:一次处理一个(或几个)候选解(搜索结点)。
$\to$ 这不是非黑即白的区别,可以存在混杂的情况。(例如,enforced hill-climbing)
1.4 是什么在规划中起作用
- 盲目搜索 vs. 启发式搜索:
- 对于达到最低满意度要求的规划,启发式搜索在任何情况下都大大优于盲目算法。
- 对于最优规划,启发式搜索也更好。(但差异不太明显)
- 系统搜索 vs. 局部搜索:
- 对于达到最低满意度要求的规划,两者都有一些成功的案例。
- 对于最优规划,需要系统算法。
$\to$ 在这里,我们介绍了在规划中最成功的搜索算法的子集。仅涵盖了某些盲搜索算法。(为此,请
$\quad$参阅 Russel&Norvig 第 3 和 4 章)
1.5 搜索算法中的术语
| 术语 | 定义 |
|---|---|
| 搜索结点 $n$ | 包含搜索所到达的 状态 (states),以及有关如何到达该状态的信息。 |
| 路径代价 $g(n)$ | 到达 $n$ 的路径代价。 |
| 最优代价 $g^*$ | 一个最优解路径的代价。对于一个状态 $s$,$g^*(s)$ 是到达 $s$ 的最便宜路径的代价。 |
| 结点扩展 | 生成一个结点的所有后继结点,通过应用适用于该结点状态的所有行动来实现。 在此之后,状态 $s$ 本身也被称为扩展过的(expanded)。 |
| 搜索策略 | 决定下一次扩展哪个结点的方法。 |
| Open List | 当前所有的候选待扩展 结点 (nodes) 的集合。又称 frontier(边缘)。 |
| Closed List | 所有已经扩展过的 状态 (states) 的集合。仅用于 图搜索,而不用于 树搜索。 又称 探索集(explored set) |
1.6 世界状态 vs. 搜索状态
一个(经典)搜索空间 通过下面三种操作定义:
- $\textrm{start}(\,)$:生成初始(搜索)状态。
- $\textrm{is-target} (s)$:测试一个给定的搜索状态是否是一个目标状态。
- $\textrm{succ} (s)$:生成搜索状态 $s$ 的后继状态 $(a,s’)$,其中 $a$ 是在生成该后继状态中所采取的行动。
搜索状态 $\ne$ 世界状态:
- 前进(Progression)规划
- 是,搜索状态 $=$ 世界状态
首先从问题的初始状态出发,考虑行动序列,直到找到一个能够得到目标状态的序列。
- 是,搜索状态 $=$ 世界状态
- 后退(Regression)规划
- 否,搜索状态 $=$ 世界状态的集合,表示为合取子目标(conjunctive sub-goals)
我们从目标状态开始,向后应用行动,直到找到一个能够达到初始状态的行动序列。
- 否,搜索状态 $=$ 世界状态的集合,表示为合取子目标(conjunctive sub-goals)
$\to$ 在整个课程中,除非另外说明,否则我们只考虑前进(Progression)规划。
$\quad$我们用 “$s$” 交替地表示 世界状态 / 搜索状态。
1.7 搜索状态 vs. 搜索结点
- 搜索状态 $s$:搜索空间中的状态(顶点)
- 搜索结点 $\sigma$:搜索状态,加上关于在搜索过程中在何处 / 何时 / 如何遇到这些状态的信息。
一个搜索结点中包含哪些信息?
不同的搜索算法在一个搜索结点 $\sigma$ 中存储了不同的信息,但是一般都包含以下几种典型的信息:
- $\textrm{state} (\sigma)$:关联的搜索状态。
- $\textrm{parent} (\sigma)$:指向该搜索结点 $\sigma$ 的来源(即父结点)的指针。
- $\textrm{action} (\sigma)$:一个导致 $\textrm{state} ( \textrm{parent} (\sigma))$ 变为 $\textrm{state} (\sigma)$ 行动。
- $g(\sigma)$:$\sigma$ 的代价。(从根结点到 $\sigma$ 的路径代价)
对于根结点,$\textrm{parent} (\sigma)$ 和 $\textrm{action} (\sigma)$ 无定义。
1.8 搜索策略的评估指标
- 保证
- 完整性:当一个解存在的时候,我们的策略能够保证找到这个解吗?
- 最优性:返回的解能够保证是最优解吗?
- 复杂度
- 时间复杂度:找到一个解需要花费多长时间?(在 生成状态 下进行测量)
- 空间复杂度:搜索需要占用多少内存?(在 状态 下进行测量)
- 典型状态空间特征控制复杂度
- 分支因子 $b$:每个状态有多少个继任者?
- 目标深度 $d$:到达最浅的目标状态所需行动的数量。
2. 盲目系统搜索算法
2.1 在我们开始之前
- 盲目搜索 vs. 有信息搜索
- 盲目搜索 不需要除了问题本身以外的任何输入。
- 优点:可以简单地直接从问题开始,不需要额外信息,不需要考虑启发函数等等。
- 缺点:求解过程比较盲目,会生成大量扩展,实践中计算量很大,效率很低。
- 有信息搜索 需要额外输入一个 启发函数 $h$,该函数将状态映射到它们 目标距离 的估计
- 优点:在实践中,通常比盲目搜索更加高效
- 缺点:需要 找到 / 实现 启发函数 $h$
- 注意:在 规划 中,启发函数 $h$ 是从声明式问题描述中自动生成的。
- 盲目搜索 不需要除了问题本身以外的任何输入。
- 关于盲目搜索,我们将讨论:
- 宽度优先搜索
- 优势:时间复杂度
- 变体:一致代价搜索(Uniform cost search)
- 深度优先搜索
- 优势:空间复杂度
- 迭代加深搜索(Iterative deepening search.)
- 结合了宽度优先搜索和使得优先搜索的优势
- 子过程中使用了 深度受限搜索(depth-limited search)
- 宽度优先搜索
- 关于盲目搜索,我们不会讨论:
- 双向搜索(Bi-directional search)
- 两个单独的搜索空间,一个从初始状态开始向前搜索,另一个从目标开始向后搜索。当两个搜索空间重叠时停止。
- 双向搜索(Bi-directional search)
2.2 宽度优先搜索
策略:按照生成顺序扩展结点(FIFO frontier)。
- 也就是说,先扩展根节点,接着扩展根节点的所有后继,然后再扩展它们的后继,以此类推。一般地,在下一层的任何结点扩展之前,搜索树上本层深度的所有结点都应该已经扩展过。
- 每次总是扩展深度最浅的结点,这可以通过将边缘(frontier)组织成 FIFO 队列来实现。
图例:

保证:
- 完整性 可以保证吗?
- 可以
- 最优性 可以保证吗?
- 对于一致行动代价(即每条边对应的代价都是一样的)而言,可以保证能够找到最优解。宽度优先搜索总是寻找一个最浅的目标状态。
- 如果每条边的代价不是一致的,则宽度优先搜索找到的解不一定是最优解。
例如:假如 B、F 都是目标状态,A 到 B 的代价是 5,而 A 到 C 和 C 到 F 的代价都是 1,宽度优先搜索会得到路径 A $\to$ B,而不是代价更小的 A $\to$ C $\to$ F。
动画演示:
时间复杂度:假设 $b$ 是最大分支因子,$d$ 是目标深度(最浅目标状态的深度)
- 生成结点数量的上界是多少?
- $b+b^2+b^3+\cdots +b^d$:在最坏情况下,该算法会生成第一个 $d$ 层中的所有结点。
- 所以,时间复杂度为 $O(b^d)$
- 如果算法是在选择要扩展的结点时而不是在结点生成时进行目标检测,那么时间复杂度为多少呢?
$O(b^{d+1})$,因为在目标被检测到之前,最坏情况下,之前深度 $d$ 上的其他结点已经被扩展,我们会生成第一个 $d+1$ 层中的所有结点。
空间复杂度:和时间复杂度相同,因为所有的生成结点都保留在内存中。
例子
- 设定:$b=10\; ;\quad 10000 \;\text{nodes/second}\; ;\quad 1000 \;\text{bytes/node}$
-
数据:

表 1:宽度优先搜索的时间和内存代价
$\to$ 所以,哪种问题更严重,时间还是内存?
- 内存。(根据我自身的经验,通常 RAM 内存在几分钟以内就会耗尽。)
从上表可以看出,内存需求是宽度优先搜索算法中相比它的执行时间更令人头疼的问题。要求解一个重要问题,人们可以忍受等待 13 天搜索到第 12 层,但是很少有计算机能具备高达 P 字节的内存支持其存储要求。幸运的是,我们还有其他对内存需求较小的搜索策略。 - 但是,时间需求依然是一个重要的因素。如果你的问题在第 16 层有一个解,那么(按照我们给的假定)宽度优先搜索(或者事实上任一盲目搜索算法)需要花费 350 年的时间来求解。一般来讲,指数级别复杂度的搜索问题不能采用盲目搜索算法求解,除非是规模很小的实例。
2.3 深度优先搜索
策略:扩展(LIFO frontier)中最近的结点。
- 深度优先搜索总是扩展搜索树的当前边缘结点集中最深的结点。搜索过程如图例所示,搜索很快推进到搜索树的最深层,那里的结点没有后继。当那些结点扩展完之后(如果还没有搜索到解),就从边缘结点集中去掉(减少内存资源的占用),然后搜索算法回溯到下一个还有未扩展后继的深度稍浅的结点。
- 相比宽度优先搜索使用的 FIFO 队列,深度优先搜索使用 LIFO 队列,即最新生成的结点最早被选择扩展。该结点一定是最深的未被扩展的结点,因为它比它的父结点深。
图例:
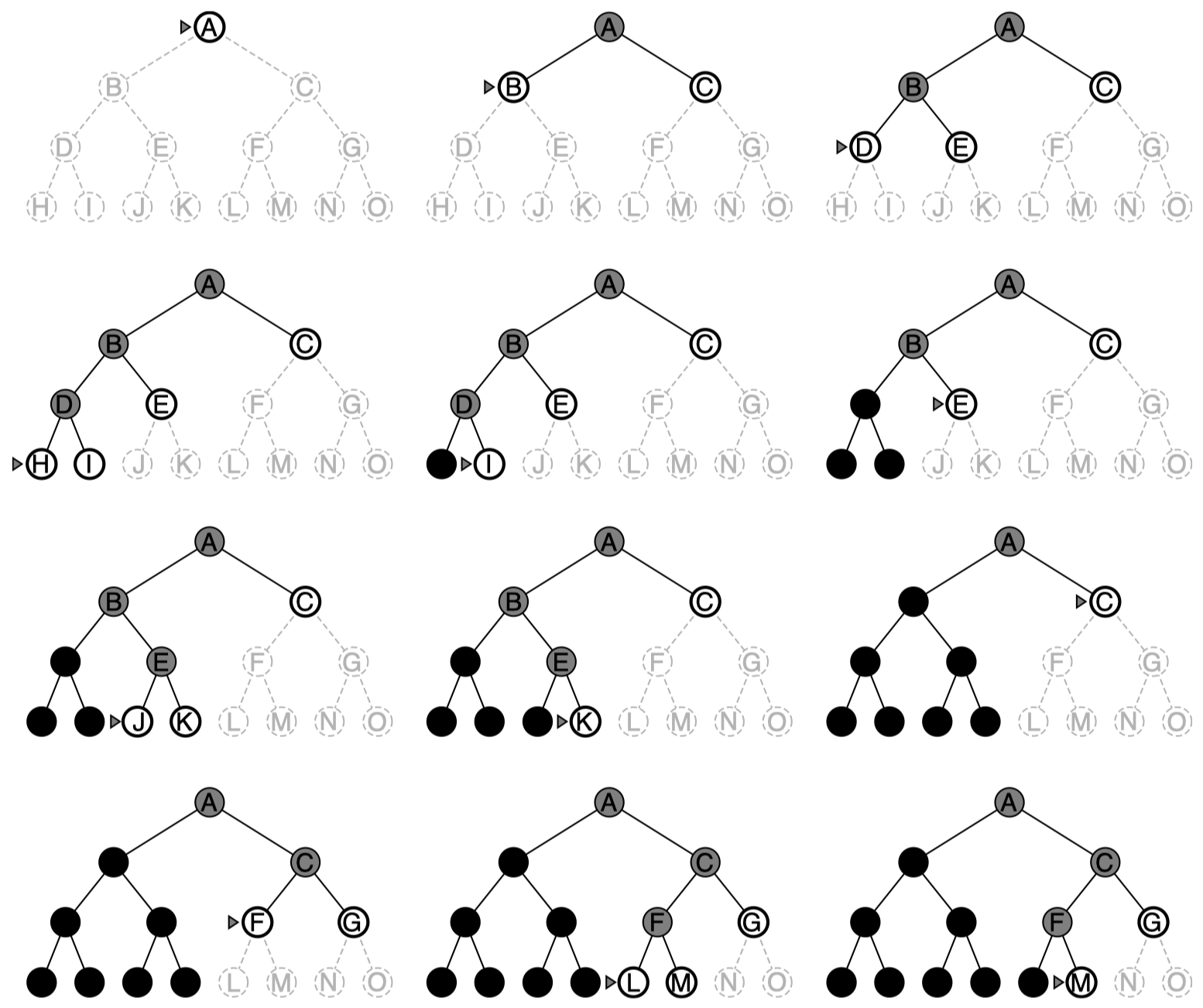
图 2:二叉树的深度优先搜索。未探索区域用浅灰色虚线表示。已经被探索并且在边缘中没有后代的结点可以从内存中删除。第三层的结点没有后继并且 M 是唯一的目标结点。
保证:
- 完整性 可以保证吗?
- 不能,因为搜索分支可能无限长度:没有检查沿分支方向上是否存在环(cycles)。
$\to$ 深度优先搜索可以保证完整性的前提是:状态空间是 无环的(acyclic),例如:约束满足问题(Constraint Satisfaction Problems, CSPs)。如果我们增加一个检查是否存在环的流程,那么该算法将能够保证在有限状态空间内的完整性。
- 不能,因为搜索分支可能无限长度:没有检查沿分支方向上是否存在环(cycles)。
- 最优性 可以保证吗?
- 不能。最终,算法只是 “选择某个方向并希望最优解在该方向上”。(深度优先搜索是一种 “希望依赖好运” 的方法。)
空间复杂度:存储(从当前结点出发)路径上的结点和可应用的行动。所以如果 $m$ 是到达的最大深度,空间复杂度为 $O(bm)$。(其中 $b$ 是分支因子)
时间复杂度:如果在状态空间中具有长度为 $m$ 的路径,将生成 $O(b^m)$ 个结点。即使可能存在深度仅为 $1$ 的解。
$\to$ 如果我们碰巧选择了 “正确的方向”,那么无论状态空间有多大,我们都可以在 $O(bl)$ 的时间复杂度内找到一个长度为 $l$ 的解。
2.4 迭代加深搜索
策略: 迭代加深的深度优先搜索(iterative deepening search)是一种常用策略,它经常和深度优先搜索结合使用来确定最佳深度界限。做法是不断地增加深度限制 —— 首先为 $0$,接着为 $1$,然后为 $2$,以此类推 —— 直到找到目标。当深度界限达到 $d$,即最浅的目标结点所在深度时,就能找到目标结点。
图例:

迭代加深搜索看上去是一个糟糕的算法,因为它似乎做了很多重复的工作。但事实上,这种算法有诸多优势。
保证:
- 完整性 可以保证吗?
- 可以(在假设分支因子 $d$ 有限的情况下)
- 最优性 可以保证吗?
- 可以(在假设一致代价的前提下)
空间复杂度:$O(bd)$。(其中 $b$ 是分支因子,$d$ 是最浅目标状态的深度)
时间复杂度:$O(b^d)$,与宽度优先搜索相近,重复生成上层结点需要付出额外代价,但不是很大。
- 也许迭代加深搜索看起来比较浪费:状态被多次重复生成。但是,事实上这种代价并没有多大,原因是在分支因子相同(或者近似)的搜索树中,绝大多数的结点都在底层,所以上层的结点重复生成多次影响不大。
-
在迭代加深的深度优先搜索中,底层(深度 $d$)结点只被生成一次,倒数第二层结点被生成两次,以此类推,一直到根结点的子结点,它被生成 $d$ 次。因此,生成结点的总数为:
\[N(\text{IDS})=(d)b+(d-1)b^2+\cdots +(1)b^d\] -
对比宽度优先搜索:
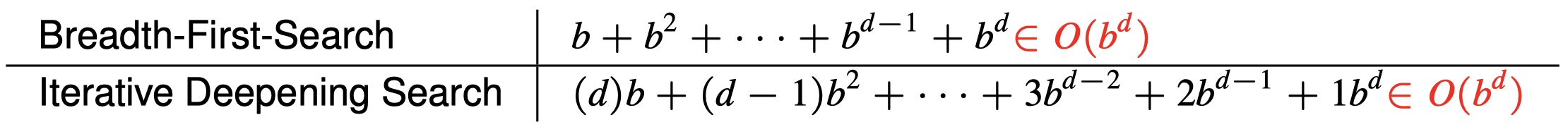
-
例子:$b=10,\,d=5$
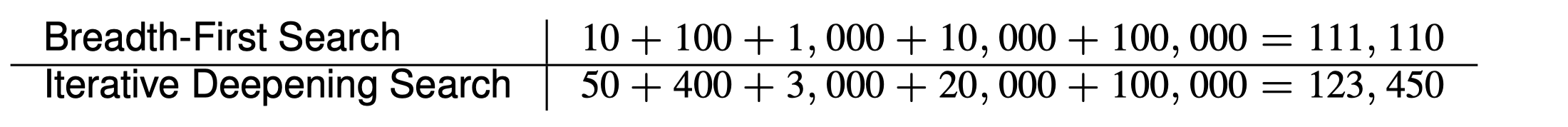
$\to$ 迭代加深搜索(IDS)结合了宽度优先和深度优先搜索的优势。当搜索空间较大并且解所在的深度未知时, IDS 是首选的盲目搜索方法。另外,如果你确实担忧状态的重复生成,可以先用宽度优先搜索直到有效内存耗尽,然后对边缘集中的所有结点应用迭代加深的深度优先搜索。
下节内容:搜索算法 (2)
本作品采用知识共享署名-非商业性使用-相同方式共享 4.0 国际许可协议进行许可。 欢迎转载,并请注明来自:YEY 的博客 同时保持文章内容的完整和以上声明信息!