Lecture 03 导论 (3)

我们将用两周来回顾之前在 MAST90104 中学习过的线性模型的相关内容，上周我们已经回顾了包括如何拟合线性模型、如何解释线性模型等在内的一部分内容，本周我们将继续回顾线性模型中余下的内容。

在这节课中，我们将主要回顾以下内容：

• 线性模型中的假设检验
• 线性模型中的置信区间
• 模型诊断

7. 线性模型中的假设检验

7.1 假设检验

假设检验可以用来决定一个线性模型中的预测变量 $X$ 组成的任何集合的显著性。

假设误差项 $\varepsilon_i$ 之间服从 i.i.d. 正态分布。

假设我们希望知道：在不损失较大的拟合优度的前提下，一个模型 $\Omega$ 是否可以用它的子模型 $\omega$ 来替代。而这可以通过假设检验来确认：

其中，$\boldsymbol \beta_{\Omega-\omega}$ 是参数 $\boldsymbol \beta$ 的一个子集，它存在于模型 $\Omega$ 中，但是不在其子模型 $\omega$ 中。

在线性模型中，我们希望知道预测变量的某个特定集合的显著性，我们希望知道这个预测变量的特定集合对于响应变量的效应。这可以通过构建两个模型来进行验证：模型 $\Omega$ 及其子模型 $\omega$。如果 $H_0$ 成立，说明两个模型之间的预测变量的差异构成的集合对于响应变量没有显著效应（即这部分预测变量的系数均为 $0$），因此，模型 $\Omega$ 可以用其子模型 $\omega$ 来替代。反之，如果 $H_1$ 成立，说明两个模型之间的预测变量的差异构成的集合对于响应变量有显著效应，我们不能用模型 $\omega$ 代替模型 $\Omega$。

假设样本数量为 $n$，模型 $\Omega$ 的参数数量为 $\text{dim}(\boldsymbol \beta_{\Omega})=p$，模型 $\omega$ 的参数数量为 $\text{dim}(\boldsymbol \beta_{\omega})=q$。那么当模型 $\omega$ 正确时（即 $H_0$ 为真），$F$ 统计量为：

如果 $F>F_{p-q,n-p}^{(\alpha)}$，我们将在显著性水平 $\alpha$ 上拒绝 $H_0$ 假设。

这也被称为 方差分析检验（ANOVA test）。当然，在这两个模型中，模型 $\omega$ 的残差平方和要更大一些，因为它包含的参数数量更少。$F$ 统计量是由 R.A. Fisher 提出的，它告诉了我们从模型 $\Omega$ 转换到模型 $\omega$ 的过程中，残差平方和 $\textsf{RSS}$ 的相对减少量，如果这个减少量非常显著，则意味着当我们将包含全部参数的模型缩减为包含参数子集的模型时，被移除的那部分预测变量对于响应变量的效应实际上是非常显著的，因此，我们不能将其移除。

7.2 假设检验的例子

回忆之前我们之前讨论过的 2000 年美国总统大选时佐治亚州选票的例子，现在我们比较之前拟合的两个模型：$\omega=$lmod 和 $\Omega=$lmodi。其中，模型 $\omega$ 只包含 pergore 和 perAA 两个预测变量，而模型 $\Omega$ 增加了 usage 和 equip，以及一些交互项：

R 代码：

1
sumary(lmod)

输出结果：

1
2
3
4
5
6
            Estimate Std. Error t value Pr(>|t|)
(Intercept) 0.032376   0.012761  2.5370  0.01216
pergore     0.010979   0.046922  0.2340  0.81531
perAA       0.028533   0.030738  0.9283  0.35470

n = 159, p = 3, Residual SE = 0.02445, R-Squared = 0.05

R 代码：

1
sumary(lmodi)

输出结果：

1
2
3
4
5
6
7
8
9
10
11
12
                      Estimate Std. Error t value  Pr(>|t|)
(Intercept)          0.0432973  0.0028386 15.2529 < 2.2e-16
cperAA               0.0282641  0.0310921  0.9090  0.364786
cpergore             0.0082368  0.0511562  0.1610  0.872299
usageurban          -0.0186366  0.0046482 -4.0095 9.564e-05
equipOS-CC           0.0064825  0.0046799  1.3852  0.168060
equipOS-PC           0.0156396  0.0058274  2.6838  0.008097
equipPAPER          -0.0090920  0.0169263 -0.5372  0.591957
equipPUNCH           0.0141496  0.0067827  2.0861  0.038658
cpergore:usageurban -0.0087995  0.0387162 -0.2273  0.820515

n = 159, p = 9, Residual SE = 0.02335, R-Squared = 0.17

我们可以通过 R 命令 anova(model1, model2) 完成 ANOVA 检验：

R 代码：

1
anova(lmod, lmodi)

输出结果：

1
2
3
4
5
6
7
8
9
Analysis of Variance Table

Model 1: undercount ~ pergore + perAA
Model 2: undercount ~ cperAA + cpergore * usage + equip
  Res.Df      RSS Df Sum of Sq      F   Pr(>F)   
1    156 0.093249                                
2    150 0.081775  6  0.011474 3.5077 0.002823 **
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

计算得到的 $F$ 统计量为：

这里，我们在模型 $\omega$ 中使用的是 pergore 和 perAA，而在模型 $\Omega$ 中我们对这两个变量进行了中心化，即 cpergore 和 cperAA。事实上，是否中心化对于残差平方和 RSS 没有影响，它们影响的其实是参数 $\boldsymbol \beta$ 的估计，所以在计算 $F$ 统计量时无需担心这一点。另外，可以看到 p 值为 $0.002823$，小于 $0.05$，因此我们拒绝 $H_0$ 假设。这意味着和模型 $\omega$ 相比，模型 $\Omega$ 多出来的 usage、equip 和 cpergore:usage 这几个预测变量对于响应变量的效应是比较显著的，我们应当拒绝模型 $\omega$。

因此，当我们希望检验 预测变量的某个集合 作用在响应变量上的效应时，可以采用 $F$ 检验。

而有些时候，我们只是希望检验 单个预测变量 对于响应变量的效应，我们当然还是可以使用一般的 $F$ 检验方法：拟合一个包含该预测变量的模型和一个不包含该预测变量的模型，并计算 $F$ 统计量。但是，非常重要的一点是我们需要知道模型中还包含哪些其他的预测变量，并且如果这些预测变量也发生了改变，那么结果可能会有所不同。

如果我们希望检验的这个 单独的预测变量 是 数值变量 时，我们可以用 $t$ 检验 替代。我们用以下假设来检验预测变量 $X_i$ 对于响应变量的效应：

在 $H_0$ 假设下，$t$ 统计量为：

注意，这里 $t$ 检验和 $F$ 检验实际上是等价的：$t_{n-p}^2=F_{1,n-p}$

这种方法得到的 p 值和 $F$ 检验中得到的完全一样。例如，在模型 lmodi 中，非裔美国人占比 cperAA 的显著性给出的 p 值为 $0.364786$。这表明在调整其他预测变量对响应变量的效应之后，cperAA 这个预测变量并不具有统计显著性。

注意，通常我们应该避免将 $t$ 检验应用于包含 $2$ 个以上 levels 的 分类变量。因为对于一个包含 $2$ 个以上 levels 的分类变量，我们需要不止一个虚拟变量来编码这个分类变量（例如：对于一个包含 $3$ 个 levels 的分类变量，我们需要用 $2$ 个虚拟变量来编码它），这意味着我们实际上检验的预测变量的数量不止一个，在这种情况下，我们应该使用 $F$ 检验而不是 $t$ 检验。

在 R 中，我们可以使用 drop1(model, test="F") 来实现对于单个预测变量的 $F$ 检验，它每次从原始模型中移除 1 个预测变量，来检验这种移除对于响应变量的效应的显著性：

R 代码：

1
drop1(lmodi, test="F")

输出结果：

1
2
3
4
5
6
7
8
9
10
11
Single term deletions

Model:
undercount ~ cperAA + cpergore * usage + equip
               Df Sum of Sq      RSS     AIC F value  Pr(>F)  
<none>                      0.081775 -1186.1                  
cperAA          1 0.0004505 0.082226 -1187.2  0.8264 0.36479  
equip           4 0.0054438 0.087219 -1183.8  2.4964 0.04521 *
cpergore:usage  1 0.0000282 0.081804 -1188.0  0.0517 0.82051  
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

可以看到，移除 cperAA 对应的 p 值为 $0.36479>0.05$，此时我们接受 $H_0$，即可以认为 cperAA 这个预测变量对于响应变量的效应不具有统计显著性，我们可以将其移除，这和我们之前在 $t$ 检验中得到的结论是一致的。而对于分类变量 equip，它包含 $5$ 个 levels，所以我们用 $4$ 个虚拟变量来编码它，如果我们将它移除，可以看到对应的 p 值为 $0.04521<0.05$，此时我们拒绝 $H_0$ 假设，这意味着 equip 这个分类变量对于响应变量的效应具有统计显著性，我们不应该将其移除。同理，交互项 cpergore:usage 对应的 p 值为 $0.82051>0.05$，我们可以将其移除。

另外，我们注意到在原始模型中一共有 $5$ 个预测变量，而在这里只尝试移除了其中的 $3$ 个，drop1 命令并没有对单独的 cpergore 和 usage 进行检验，因为这里涉及到一个隐式的原则，我们称之为 等级原则（hierarchy principle）：一个交互项对应的所有低阶项都应当被保留在模型中。也就是说，无论交互项 cpergore:usage 对于响应变量是否具有显著效应，其对应的预测变量 cpergore 和 usage 在这里都不会被移除。所以，接下来我们需要对移除交互项 cpergore:usage 之后的模型再进行一次 drop1 检验。

在解释假设检验的结果时存在很多困难，其中可能涉及到一些操作顺序导致的误差，在真正理解问题之前，我们需要避免只是简单地从字面上解读这些结果。

8. 线性模型中的置信区间

对于模型参数 $\boldsymbol \beta$ 中的任何一个元素，我们都可以得到一个对应的置信区间：

其中，$t_{n-p}^{(\alpha/2)}$ 是一个自由度为 $(n-p)$ 的 $t$ 分布中的上 $(\alpha/2)$ 分位数。

注意：这样一个 $t$ 置信区间是基于线性模型的正态假设得到的。如果正态假设不能满足，那么我们会将 $t$ 区间替换为渐进正态区间。

在 R 中，使用 confint(model) 命令可以查看模型中各个参数项的置信区间：

R 代码：

1
confint(lmodi)

输出结果：

1
2
3
4
5
6
7
8
9
10
                            2.5 %       97.5 %
(Intercept)          0.0376884415  0.048906189
cperAA              -0.0331710614  0.089699222
cpergore            -0.0928429315  0.109316616
usageurban          -0.0278208965 -0.009452268
equipOS-CC          -0.0027646444  0.015729555
equipOS-PC           0.0041252334  0.027153973
equipPAPER          -0.0425368415  0.024352767
equipPUNCH           0.0007477196  0.027551488
cpergore:usageurban -0.0852990903  0.067700182

从参数项的置信区间中，我们可以得到和之前假设检验对于同一个参数检验结果的等价结论。例如：对于变量 usageurban，它是预测变量 usage 编码后的一个虚拟变量，它对应的参数 $\beta_{\text{usageurban}}$ 的 $95\%$ 置信区间为 $(-0.0278208965,-0.009452268)$，可以看到 $0$ 并不在这个区间内，这意味着我们将在 $5\%$ 的显著性水平上拒绝假设 $H_0:\beta_{\text{usageurban}}=0$。同理，对于 cperAA，$0$ 包含在其置信区间中，因此我们不拒绝 $H_0:\beta_{\text{cperAA}}=0$。

置信区间和对应的 $t$ 检验之间存在一种等价效应，我们称之为 对偶性（duality）：如果某个预测变量的假设检验 p 值大于 $0.05$，那么 $0$ 将落在其对应参数的 $95\%$ 置信区间内，反之亦然。

置信区间为参数提供了一系列看似合理的值，并且在判断某个预测变量影响的大小时，要比仅仅反映统计显著性而非实际显著性的 p 值更有用。

我们可以给每个参数单独构造置信区间，但是当我们要同时检验很多个参数时，就会遇到和之前的顺序检验中同样的问题。这些置信区间分别来看都是正确的，但是并不是说有 $95\%$ 的概率使得所有这些真实参数全部都落在它们对应的置信区间内。这种 多元比较（multiple comparisons） 的问题在投票设备 equip 这个分类变量上显得尤其严重，$5$ 个不同的 levels 引出了 ${5\choose 2}=10$ 个成对的比较项，远比这里单独来看的 $4$ 个虚拟变量要多。

一般地，给定一个 $p$ 维向量 $\mathbf a$，参数 $\boldsymbol \beta$ 的一个线性组合 $\mathbf a^{\mathrm{T}}\boldsymbol \beta$ 的 $100(1-\alpha)\%$ 置信区间为：

其中，$\mathrm{se}(\mathbf a^{\mathrm{T}}\hat{\boldsymbol \beta})=s\sqrt{\mathbf a^{\mathrm{T}}(X^{\mathrm{T}}X)^{-1}\mathbf a}$，而 $s$ 为样本标准差。

这个置信区间的对偶形式对应的 $t$ 检验为 $H_0:\mathbf a^{\mathrm{T}}\boldsymbol \beta=\mathbf 0$。

注意：上面的 $\mathrm{se}(\mathbf a^{\mathrm{T}}\hat{\boldsymbol \beta})$ 的公式是由 $\hat{\boldsymbol \beta}$ 的最小二乘估计推导得到的。推导过程如下：

总体方差 $\sigma^2$ 对于我们是未知的，所以我们用样本方差作为其估计值代替：$\hat{\sigma}^2=s^2$，从而得到：

R 中 doBy package 中的函数 esticon() 可以用来计算 $\mathbf a^{\mathrm{T}}\boldsymbol \beta$ 的置信区间，及其对应的假设检验。

9. 线性模型中的诊断

线性模型中的 诊断（Diagnostics） 是整个导论部分最重要的一节内容，因为它是对其他理论部分的直接实践。

9.1 相关概念

推论的有效性取决于有关线性模型的假设。然而，我们永远无法知晓我们的假设是真实成立的还是无法满足的，因为我们永远无法知道真相，但是我们可以利用模型诊断来帮助我们发现假设中是否存在某些问题。

一种假设是 $E \mathbf y=X\boldsymbol \beta$ 是正确的：它包含了所有正确的变量，并且正确地变换和组合它们。

另一种假设是关于 $\boldsymbol \varepsilon$：它里面的元素具有相同的方差，彼此之间不存在相关性，并且服从一个正态分布。

我们还对 离群点（outliers） 的检测感兴趣，因为这些点对应的 响应变量的值 对于其余大部分数据所拟合出的模型来说属于异常点。

理想情况下，我们希望每个样例都对拟合的模型具有同等的贡献；但是有时候，某些点对应的 预测变量的值 对于模型的影响要远大于其他点，这些点被称为 影响点（influential points）。

诊断工具旨在检测数据与拟合值之间的差异；以及少数几个数据点与其余数据点之间的差异。这些技术大多数基于 残差、帽子矩阵 和 案例删除度量（case deletion measures） 的图形表示。

9.2 杠杆效应

考虑一个线性模型：

其中，$X$ 是一个 $n\times p$ 的矩阵，$\boldsymbol \beta$ 是一个 $p\times 1$ 的参数向量。

• $\boldsymbol \beta$ 的 最小二乘估计量 为：$\hat{\boldsymbol \beta}=(X^{\mathrm{T}}X)^{-1}X^{\mathrm{T}}\mathbf y$

• 残差 向量：$\hat {\boldsymbol \varepsilon}=\mathbf r=\mathbf y-\hat{\mathbf y}$，其中 $\hat{\mathbf y}=X\hat{\boldsymbol \beta}$ 是 拟合值 向量。残差向量为我们揭示了那些病态拟合的数据点，通常这些数据点的残差都非常大。

• 帽子矩阵：$H=X(X^{\mathrm{T}}X)^{-1}X^{\mathrm{T}}$

我们可以得到：

可以看到，$\hat{\mathbf y}$ 实际上是 $\mathbf y$ 的一个线性变换。所以，我们用预测变量的的观测值 $X$ 拟合了一个线性模型，而模型给出的拟合值实际上是响应变量的观测值 $\boldsymbol y$ 的一个线性组合，这个线性组合的系数是一个特殊的矩阵 $X(X^{\mathrm{T}}X)^{-1}X^{\mathrm{T}}$，我们称之为帽子矩阵 $H$（因为在使用它对 $\mathbf y$ 进行线性变换后，我们得到了一个戴帽子的 $\hat{\mathbf y}$）。因此，$\hat{\mathbf y}=H\mathbf y$。

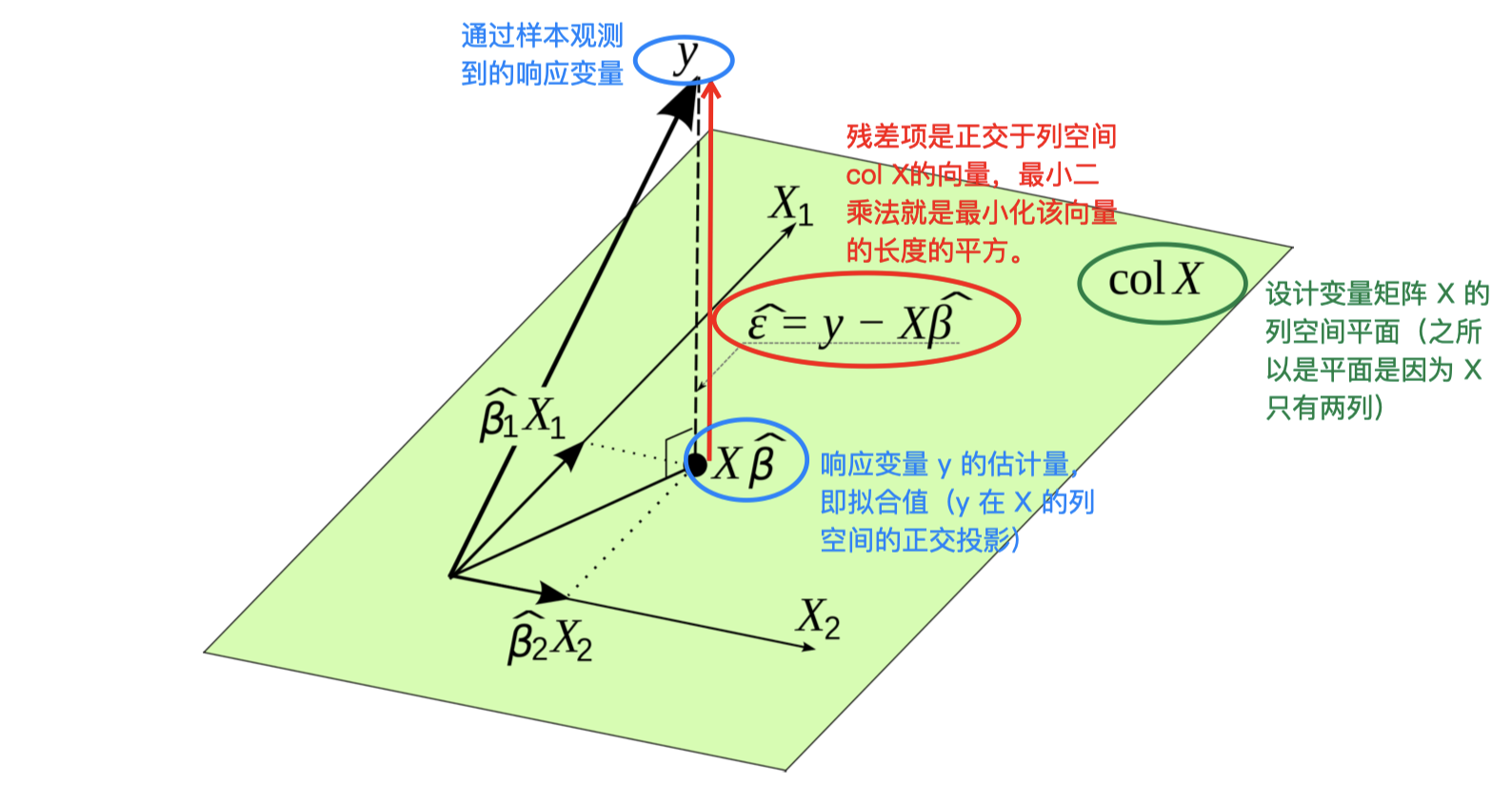
从几何上，观测值 $\hat{\mathbf y}$ 可以被解释为观测值的 $n$ 维向量 $\mathbf y$ 在 $p$ 维子空间 \(\{X\boldsymbol \beta, \boldsymbol \beta \in \mathbb R^p\}\) 内的正交投影。投影之后得到的观测值 $\hat{\mathbf y}$ 仍然是一个 $n$ 维向量，但是被附加了一个线性约束，使得其被约束在一个 $p$ 维子空间内。帽子矩阵 $H$ 的秩等于响应变量 $X$ 的数量，即 $\mathrm{rank}(H)=p$，虽然 $H$ 本身是一个 $n \times n$ 的矩阵，但是它的秩 $\mathrm{rank}(H)=p< n$，所以 $H$ 是一个降秩矩阵。另外，通过线性代数我们还可以证明 $H$ 的迹等于其对角线上的元素之和，也就是 $H$ 的迹：$\mathrm{rank}(H)=\mathrm{tr}(H)=p$。此外，$H$ 还具有 对称性 和 幂等性，即 $H^2=H$。

$H=(h_{ij})$ 决定了数据作用在拟合值 $\hat {\mathbf y}$ 上的 影响（influence）或者 杠杆效应（leverage）的大小。具体来说，帽子矩阵 $H$ 中第 $i$ 行第 $j$ 列的元素 $h_{ij}$ 反映了响应变量的第 $j$ 个观测值 $y_{j}$ 施加在第 $i$ 个拟合值 $\hat y_i$ 上的杠杆或者影响的大小。请注意，这种影响是来自 $X$ 而不是 $\mathbf y$。我们可以观察一下，如果用矩阵 $H$ 的第 $i$ 行乘以向量 $\mathbf y$，则相当于用$H$ 中第 $i$ 行的 $n$ 个元素 $h_{i1},\dots,h_{in}$ 分别乘以 $\mathbf y$ 中对应的 $n$ 个元素 $y_1,\dots,y_n$ 并求和，从而得到 $\hat {\mathbf y}$ 的第 $i$ 个预测值 $\hat y_i=\sum_{j=1}^{n}h_{ij}y_j$。

我们可以将 $H$ 对角线上的第 $i$ 个元素 $h_{ii}$ 简记为 $h_i$，它反映了第 $i$ 和观测值 $y_i$ 作用在其自身拟合值 $\hat y_i$ 上的杠杆，这也是我们最感兴趣的影响。由于 $\mathrm{tr}(H)=\sum_{i=1}^{n}h_{ii}=p$ 并且 $0\le h_{ii}\le 1$，因此，$H$ 的对角线上所有元素的平均大小为 $\dfrac{p}{n}$。根据经验，如果一个观测数据点 $\mathbf x$ 对应的 $h_{ii}>\dfrac{2p}{n}$，我们可以认为它是一个 高杠杆点（high-leverage point），这意味着对应的观测值 $y_i$ 对于其拟合值 $\hat y_i$ 具有较大影响。

注意：高杠杆点不一定是异常点，例如上面左图中的 $\blacktriangle$ 属于高杠杆点，但不属于异常点；低杠杆点也有可能是异常点，例如中间图里的 $\blacktriangle$；而右图中的 $\blacktriangle$ 则同时属于高杠杆点和异常点。具体关于某个点是否是异常点可以通过计算库克距离进行判断。

9.3 残差

如果 $\mathbf r=(r_1,\dots,r_n)^{\mathrm{T}}$ 是基本的残差向量，其中 $r_i=y_i-\hat y_i$，利用线性代数知识可以推出 $r_i$ 的方差为：$\mathrm{Var}(r_i)=(1-h_{ii})\sigma^2$，对应的 第 $i$ 个标准化残差（$i$-th standardized residual） 为：

可以证明，\(\mathrm{Var}(r_i^*)=\sigma^2\) 或者 \(\mathrm{Var}\left( \dfrac{r_i^*}{\sigma} \right)=1\)，而 $\sigma^2$ 的 一致估计量（consistent estimator） 为 $\hat \sigma^2=\dfrac{\mathbf r^{\mathrm{T}}\mathbf r}{n-p}=\dfrac{\textsf{RSS}}{n-p}$。现在，第 $i$ 个学生化残差（$i$-th studentized residual） 为：

因为 $\mathrm{Var}\left( \dfrac{r_i^*}{\sigma} \right)=1$，所以学生化残差的方差 $\mathrm{Var}(r_i^{(t)})=\mathrm{Var}\left( \dfrac{r_i^*}{\hat \sigma} \right)\simeq 1$。

通常，学生化残差的解释性更强一些，因为在模型是充分的（adequate）情况下，通常大约 $95\%$ 的标准化残差 $r_i^*$ 落在正负 $2$ 倍的标准误 $s$ 的范围内 $[-2s,2s]$，而对残差进行学生化之后，可以知道在模型充分的情况下，通常大约 $95\%$ 的学生化残差会落在区间 $[-2,2]$ 内，这在实践中会给估计带来更多便利。

残差向量 $\mathbf r$ 和帽子矩阵 $H$ 所扮演的角色也可以通过移除单个观测数据点对于模型的影响来体现。

我们对于 $\boldsymbol \beta$ 的估计是基于所有的 $n$ 个观测数据点。但是假如我们希望知道第 $i$ 个观测值对于估计值的效应，我们可以将第 $i$ 个观测值移除，然后重新拟合模型，那么参数 $\boldsymbol \beta$ 的最小二乘估计的变化为：

其中，$\hat{\boldsymbol \beta}_{(i)}$ 基于移除第 $i$ 个观测之后的数据的 $\boldsymbol \beta$ 的最小二乘估计。

可以看到，$\Delta_i \hat{\boldsymbol \beta}$ 会随着残差 \(r_i\) 和杠杆 \(h_{ii}\) 的增大而增大，所以，它是衡量第 $i$ 个观测数据对于模型拟合过程的影响的一个非常好的指标。

9.4 统计诊断图

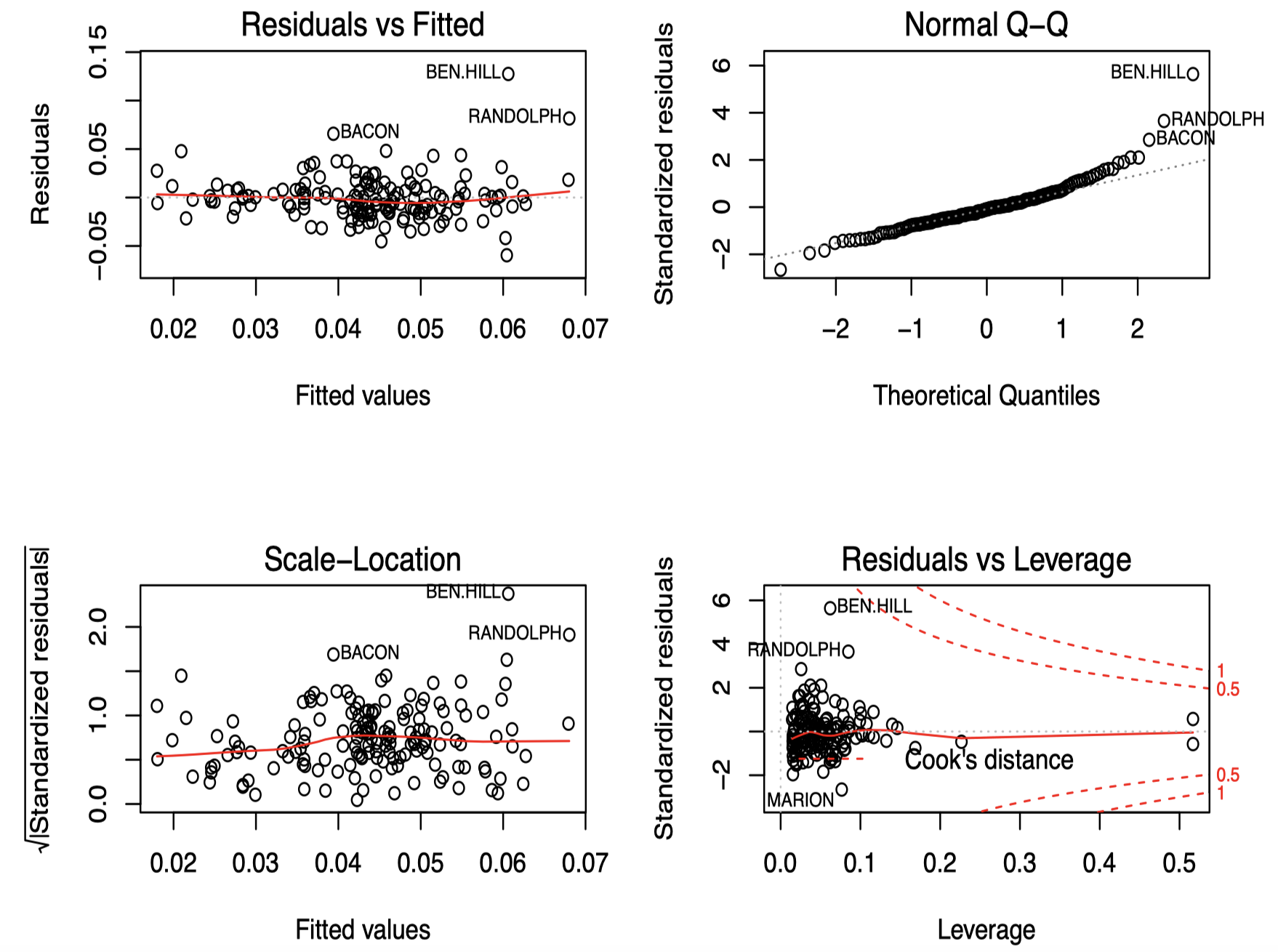
图形诊断方法提供了更加丰富的信息，因此很受欢迎。事实上，我们几乎不可能判断一个给定模型是否完全正确。诊断更多的是为了检查模型是否存在严重错误。事实上，一个成功的数据分析应当将更多精力放在避免大的错误上，而不是一味地对拟合进行优化。R 中的 plot() 命令提供了四种有用的诊断集合：

R 代码：

1
plot(lmodi)

输出结果：

可以看到，plot() 命令生成了四张诊断图。

左上角 是残差与拟合值的关系图，可以用来检验模型是否存在欠拟合（lack of fit）。如果残差呈现一种曲线的趋势，说明模型需要调整，通常是对变量中的某一个进行转换。另外，图中增加了一条红色的平滑曲线用来帮助我们进行判断。可以看到，在这里所有的点基本都落在一条水平带中间，说明我们的模型不存在这方面的问题。此外，该图还可以用来检查误差项的常数方差假设。在这张图中，我们可以看到随着拟合值的变化，方差基本上保持不变。

假设误差是对称的，我们可以通过绘制残差绝对值与拟合值的关系图来有效地将分辨率提高一倍。而由于 $|\hat \varepsilon|$ 倾向于偏斜，我们最好采用 $\sqrt{|\hat \varepsilon|}$ 来代替。左下角 展示了这种标准化残差绝对值的平方根与拟合值之间的关系图，进一步确认了我们已经观察到的关于方差恒定性的信息。注意图中还标注出了一些具有较大残差的数据点。

我们还可以利用 QQ 图检验残差的正态性。它将残差与 “理想的” 正态观测进行对比。对于每个观测数据 $i=1,\dots,n$，我们绘制排序后的残差与理论正态分位数 $\Phi^{-1}\left(\frac{i}{n+1}\right)$ 之间的关系图，如 右上角 所示。可以看到，图中的数据点总体上服从一种线性趋势（除了个别案例外），这表明我们对于模型的正态性假设是合理的。如果我们观察到一条曲线，则表明模型拟合过程中存在偏斜，表明我们可能需要对响应变量进行某种转换；而如果两边尾部的数据点偏离线性则表明存在长尾误差，这表明我们应该考虑使用更具鲁棒性的拟合方法。特别是对于较大的数据集，正态性假设并不需要非常严格，因为尽管存在非正态性，但推断仍然是近似正确的。只有在明显偏离正态性的情况下，才必须采取措施改变模型。

由于 $\mathrm{Var}(\hat \varepsilon_i)=\sigma^2(1-h_i)$，较大的 $h_i$ 将导致 $\mathrm{Var}(\hat \varepsilon_i)$ 较小。这种情况下，拟合值将 “被迫” 靠近 $y_i$。这是一种检验杠杆的有效手段，来决定哪些样例可能具有影响力。那些落在预测变量空间的边界上的点将具有最大的杠杆值。

库克统计量（Cook statistics）是一种流行的推断诊断，因为对于每个样例，它们减少了单个值的信息。它们可以被定义为：

它们代表了如果将单个样例 $i$ 从数据中移除，对于拟合的变化的一种规模度量。可以发现，库克距离 $D_i$ 实际上是一个关于标准化残差 $\dfrac{\hat \varepsilon_i}{\hat \sigma}$ 与杠杆值 $h_i$ 的一个函数。

右下角 的图展示了模型 lmodi 的杠杆和库克统计量相关信息，它描述了每个数据点的标准化残差与杠杆值的关系图。可以看到大部分的标准化残差都集中在一个 $[-2,2]$ 的正常范围内，但是也存在少数比较大的标准化残差，以及少数的高杠杆点，为了综合考虑大的标准化残差和高杠杆的影响，我们需要借助库克距离：一个大的残差结合一个大的杠杆将导致一个较大的库克统计量。图中还显示了库克统计量的两组轮廓线（红色虚线），它们是关于标准化残差 $\frac{\hat \varepsilon_i}{\hat \sigma}$（图中的纵轴）与杠杆值 $h_i$（图中的横轴）的一个函数，即 $D_i$。也就是说， 对于所有落在 “0.5” 的红色轮廓线上的数据点，其库克距离 $D_i=0.5 $；对于所有落在 “1” 的红色轮廓线上的数据点，其库克距离 $D_i=1$。

可以看到，图中有些数据点超出了正常范围，我们需要进一步调查这些点在模型拟合中可能产生的影响。我们可以通过下面的命令选取最具影响力的两个样例点：

R 代码：

1
gavote[cooks.distance(lmodi) > 0.1,]

输出结果：

1
2
3
4
5
6
         equip econ perAA usage    atlanta gore bush other votes ballots undercount
BEN.HILL OS-PC poor 0.282 rural notAtlanta 2234 2381    46  4661    5741  0.1881205
RANDOLPH OS-PC poor 0.527 rural notAtlanta 1381 1174    14  2569    3021  0.1496193
           pergore   cpergore     cperAA
BEN.HILL 0.4792963 0.07097452 0.03901887
RANDOLPH 0.5375633 0.12924148 0.28401887

可以看到，BEN.HILL 和 RANDOLPH 这两个郡（counties）采用的投票设备都是 OS-PC，并且它们的响应变量 undercount 都很高，分别为 0.1881205 和 0.1496193。回忆之前的第一节课中的初步数据分析，我们可以发现，这两个数据点和之前 第一节课图 3 的箱型图 中设备 OS-PC 中的两个异常点是相同的。这两个点是影响点，因为它们具有远高于平均值的 undercount。但是，从上面右下角的标准化残差与杠杆值关系图中可以看到，BEN.HILL 和 RANDOLPH 这两个数据点的杠杆值并不高，这说明它们的预测变量的取值都是在正常范围内。另外，从图中还可以看到，BEN.HILL 的标准化残差超过了 $5$。通常来说，当标准化残差超过 $3.5$ 时，我们就应该进一步关注该数据点，所以在这里，BEN.HILL 这个数据点应当引起我们的注意。

判断某些杠杆是否异常极端的一种有用技术是 半正态图（half-normal plot），它描述的是排序后的杠杆值与理论的正态分位数 $\Phi^{-1}\left(\frac{n+i}{2n+1}\right)$ 之间的关系。

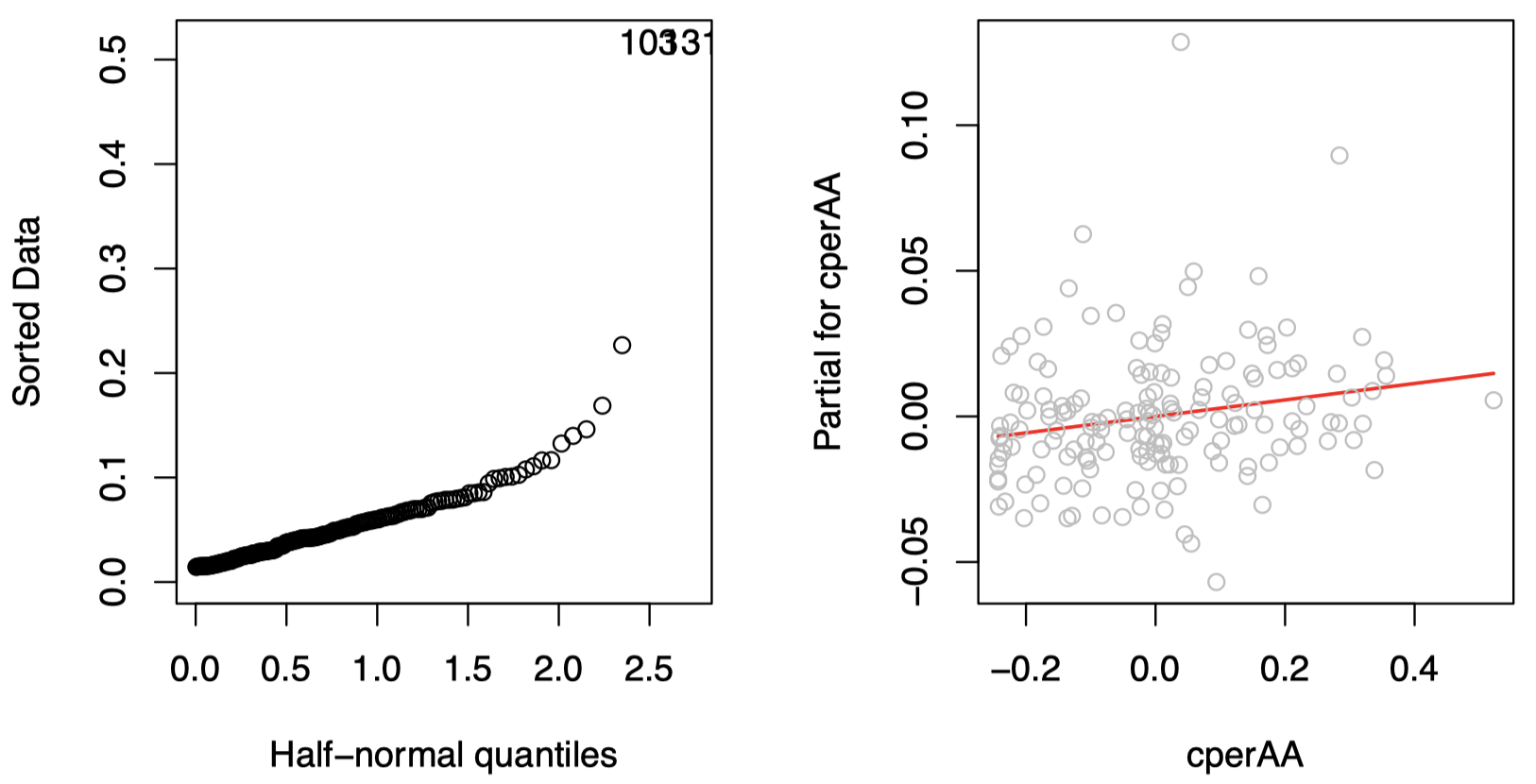
图 4 中，左边是模型 lmodi 的杠杆值的半正态图。可以看到有两个数据点的杠杆值要明显高于其他数据点，它们是：

R 代码：

1
2
halfnorm(hatvalues(lmodi))
gavote[hatvalues(lmodi)>0.3,]

输出结果：

1
2
3
4
5
6
           equip econ perAA usage    atlanta gore bush other votes ballots undercount
MONTGOMERY PAPER poor 0.243 rural notAtlanta 1013 1465    31  2509    2573 0.02487369
TALIAFERRO PAPER poor 0.596 rural notAtlanta  556  271     5   832     881 0.05561862
             pergore     cpergore       cperAA
MONTGOMERY 0.4037465 -0.004575261 1.886792e-05
TALIAFERRO 0.6682692  0.259947458 3.530189e-01

这是仅有的两个投票设备为 PAPER 的郡，因此它们也是仅有的两个可以决定变量 PAPER 的系数的样例。由于其余的预测变量值全部都不显着，因此足以为这两个点提供高杠杆。注意，我们并没有将这两个数据点确定为影响点 —— 仅仅具有高杠杆值并不足以使其成为影响点。

部分残差图（Partial residual plots）描述了 $\hat \varepsilon+\hat \beta_i \tilde{\mathbf x}_i$ 与 $\tilde{\mathbf x}_i$ 之间的关系，其中 $\tilde{\mathbf x}_i$ 是预测变量 $X_i$ 的 $n$ 个观测值。

这样做是动机是我们希望观察其他的预测变量 $X$ 被移除后，对于响应变量的预测效应（也就是单独的预测变量 $X_i$ 对于响应变量的效应）：

图 4 中，右边是变量 cperAA 的部分残差图：

R 代码：

1
termplot(lmodi,partial=TRUE,terms=1)

图中的红色直线表示最小二乘法在对于该数据的拟合结果，其具有和模型 lmodi 中的 cperAA 项相同的斜率，即 $\hat \beta_{\texttt{perAA}}$。该图为我们提供了该预测变量和响应变量之间的边缘关系的简单印象。在该样例中，我们看到的是一种线性关系，这表明我们不需要再为预测变量 cperAA 寻找任何转换。此外，没有迹象表明图中的少数几个离该直线较远的点对这种线性关系造成了不适当的影响。

下节内容：导论 (4)

本作品采用知识共享署名-非商业性使用-相同方式共享 4.0 国际许可协议进行许可。 欢迎转载，并请注明来自：YEY 的博客 同时保持文章内容的完整和以上声明信息！

• Previous
  数据科学研究项目 01：论文阅读
• Next
  自然语言处理 Workshop 02：BPE 算法