Lecture 04 导论 (4)
上节课中我们回顾了线性模型中的假设检验、置信区间和模型诊断的相关内容,这节课是导论中的最后一部分,我们将回顾线性模型中余下的内容。
在这节课中,我们将主要回顾以下内容:
- 鲁棒回归
- 加权最小二乘
- 变量转换
- 变量选择
- 给出结论
10. 鲁棒回归
正常情况下,如果随机误差项服从正态分布,那么我们可以采用正态线性回归模型。但是有时,我们在数据集中会碰到一些具有高杠杆值的点或者影响点,这种情况下,正态线性回归模型可能没有办法很好地拟合数据。也就是说,普通最小二乘法对于长尾误差(lon g -tailed errors)的表现非常差。因此,这种情况下,我们可以采用一种更具鲁棒性的方法替代最小二乘法。
普通最小二乘法的损失函数为平方损失函数:$\text{LS loss}=(\hat{\mathbf y}-\mathbf y)^2$
在鲁棒回归中,我们不会采用平方损失函数。对于鲁棒回归,有很多不同的损失函数,其中使用最广泛的一种是 Huber 损失函数:
\[\text{Huber loss}=\begin{cases}c\cdot|\hat{\mathbf y}-\mathbf y|, &\quad \text{if}\;\;|\hat{\mathbf y}-\mathbf y|> a\\ (\hat{\mathbf y}-\mathbf y)^2 , &\quad \text{if}\;\;|\hat{\mathbf y}-\mathbf y|< a \\ -c\cdot|\hat{\mathbf y}-\mathbf y|, &\quad \text{if}\;\;|\hat{\mathbf y}-\mathbf y|< -a \end{cases}\]两种损失函数的图像如下:
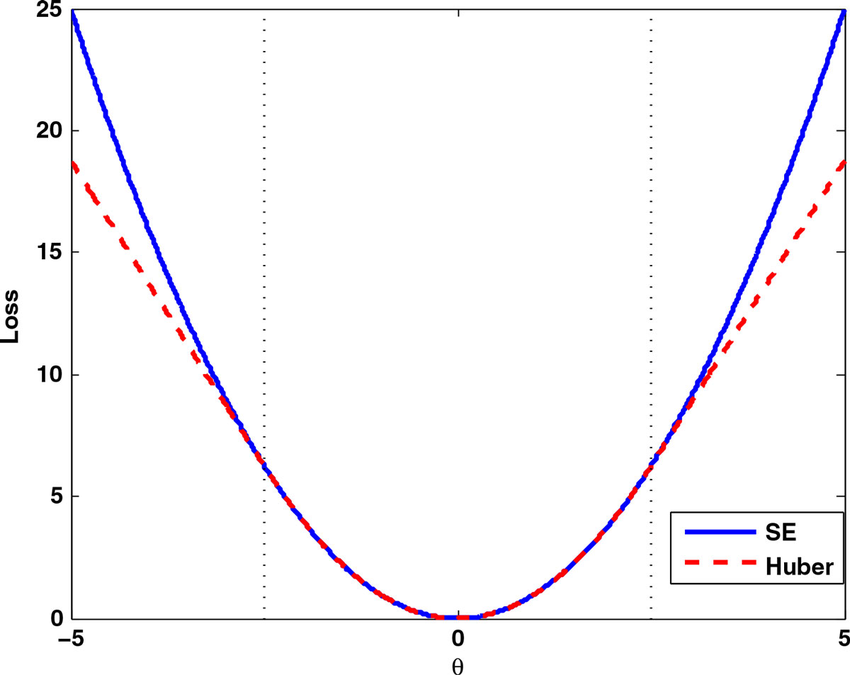
可以看到,平方损失函数的图像是一条抛物线,而 Huber 损失函数的图像在 $[-a,a]$ 之间是抛物线,而在 $[-\infty,-a]$ 和 $[a,\infty]$ 之间为直线。
我们先回顾一下之前的普通最小二乘法拟合的线性模型 lmodi:
R 代码:
1
summary(lmodi)
输出结果:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
Call:
lm(formula = undercount ~ cperAA + cpergore * usage + equip,
data = gavote)
Residuals:
Min 1Q Median 3Q Max
-0.059530 -0.012904 -0.002180 0.009013 0.127496
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 0.043297 0.002839 15.253 < 2e-16 ***
cperAA 0.028264 0.031092 0.909 0.3648
cpergore 0.008237 0.051156 0.161 0.8723
usageurban -0.018637 0.004648 -4.009 9.56e-05 ***
equipOS-CC 0.006482 0.004680 1.385 0.1681
equipOS-PC 0.015640 0.005827 2.684 0.0081 **
equipPAPER -0.009092 0.016926 -0.537 0.5920
equipPUNCH 0.014150 0.006783 2.086 0.0387 *
cpergore:usageurban -0.008799 0.038716 -0.227 0.8205
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.02335 on 150 degrees of freedom
Multiple R-squared: 0.1696, Adjusted R-squared: 0.1253
F-statistic: 3.829 on 8 and 150 DF, p-value: 0.0004001
在 R 中,我们可以使用 MASS package 中的 rlm() 命令来构建鲁棒线性模型。
R 代码:
1
2
3
library(MASS)
rlmodi <- rlm(undercount ~ cperAA+cpergore*usage+equip, gavote)
summary(rlmodi)
输出结果:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
Call: rlm(formula = undercount ~ cperAA + cpergore * usage + equip,
data = gavote)
Residuals:
Min 1Q Median 3Q Max
-6.026e-02 -1.165e-02 -6.587e-06 1.100e-02 1.379e-01
Coefficients:
Value Std. Error t value
(Intercept) 0.0414 0.0023 17.8662
cperAA 0.0327 0.0254 1.2897
cpergore -0.0082 0.0418 -0.1972
usageurban -0.0167 0.0038 -4.4063
equipOS-CC 0.0069 0.0038 1.8019
equipOS-PC 0.0081 0.0048 1.6949
equipPAPER -0.0059 0.0138 -0.4269
equipPUNCH 0.0170 0.0055 3.0720
cpergore:usageurban 0.0073 0.0316 0.2298
Residual standard error: 0.01722 on 150 degrees of freedom
对比之前的模型 lmodi,我们可以发现预测变量 equipOS-PC 的系数从之前的 $0.015640$ 下降到了 $0.0081$,几乎减小了一半。回忆上节课中 库克距离的诊断图,我们知道图中两个高影响点 BEN.HILL 和 RANDOLPH 都采用了 OS-PC 作为投票设备。因此,在鲁棒回归中,我们减小了该项的系数。
当我们使用鲁棒评估方法时,推断方法的应用将更加困难。因此,与之前对应的 lmodi 模型的输出结果相比,上面的 rlmodi 模型的输出信息要更少一些。最有趣的变化是,OS-PC 的系数现在只有原先的一半。回想一下,我们使用 treatment 编码了不同类别的设备,而这种变化代表了 OS-PC 设备和作为参考 level 的设备之间的差异。其他项的系数也有一些小的波动,但不足以改变我们对于重要效应的印象。这里,鲁棒拟合降低了两个离群点所代表的郡对于模型的影响。
下节内容:导论 (4)
本作品采用知识共享署名-非商业性使用-相同方式共享 4.0 国际许可协议进行许可。 欢迎转载,并请注明来自:YEY 的博客 同时保持文章内容的完整和以上声明信息!