Lecture 04 规划导论

如何描述任意搜索问题？

上节课我们讨论了一些搜索算法，本节课我们将介绍如何将它们作为工具来解决一些通用问题。

你可能已经见过很多 AI 应用，例如：从 1997 年 IBM 国际象棋程序 “深蓝” 击败当时最顶尖的人类棋手卡斯帕罗夫，到 2017 年 Google DeepMind 开发的围棋程序 AlphaGo 击败排名世界第一的柯洁，不过短短二十年。

但是，这些程序有一个通用的缺陷，就是它们只能在特定应用上取得非常好的成绩，而一旦切换到其他领域，表现将非常糟糕。这意味着，你在除了围棋之外的 任何方面 都要强过 AlphaGo。

这能够算是（人工）“智能” 吗？

$\to$ 如何构建一个可以解决 新问题 的机器

动机：如何开发可以自己做决策的系统或者 agents。

1. AI 中的自治行为

问题的关键在于选择接下来的行动（action），也就是所谓的控制问题（control problem）。一般有以下三种方法：

基于编程（Programming-based）：手动指定控制。
基于学习（Learning-based）：从经验中学习控制。
基于模型（Model-based）：手动指定问题，自动推导控制。

$\color{blue}{\to}$ 各方法并不正交，每种都有各自的优劣。
$\color{blue}{\to}$ 不同的模型（models）会产生不同类型的控制器（controllers）。

1.1 基于编程的方法

首先是基于编程的方法，它是能够解决任何任务的最简单的方法，可以想象，为了解决问题，无论 angent 需要遵循的规则是什么，我们都可以一步步通过编程实现。

$\color{blue}{\to}$ 控制由程序员指定。

例如，假设现在我们需要编写程序玩超级马里奥游戏，我们可以设定并编写如下规则：

如果马里奥发现没有危险，那么奔跑……
如果出现了危险，并且马里奥是变大的状态，那么跳跃并击杀……
……

优点：领域知识（domain-knowledge）可以很容易表达。
缺点：并不是真正意义上的通用求解器，无法处理程序员没有预见到的情况。

1.2 基于学习的方法

目前，研究的核心领域主要集中在基于学习的方法。

$\color{blue}{\to}$ 从经验或者通过模拟来学习得到一个控制器。通常包括以下三种：

无监督（强化学习）：
在无监督学习中，angent 可以根据行动得到不同的反馈（惩罚或者奖励），通过不断重复这一过程，angent 可以学习到在特定情况下采取哪种行动是正确的。
例如，在马里奥游戏中，我们可以设定：
- 每次在马里奥 “死亡” 时，对 agent 施加惩罚（例如，分数减少 1000）。
- 每次敌人 “死亡” 或者到达目的地时，对 agent 进行奖励（例如，分数增加 1000）。
如果我们不断重复这一方法，我们将发现马里奥能够学习到如何在特定情况下做出正确选择。在过去十年中，无监督学习这一领域取得了很多进展，尤其是在我们有了更强大的硬件后，该方法的可行性将大大提高，我们可以通过运行非常多次来提升学习效果。但是，该方法也存在一些问题：在模型训练过程中，会消耗大量的计算时间，尤其是，如果我们不知道应该采用哪些特征进行学习时，该方法将变得更加困难。
有监督（分类）：
与无监督学习相对的另一种方法是有监督学习。同样，假如我们希望让马里奥学习如何选择行动，相比简单地对 agent 施加惩罚/奖励，我们可能知道，对于各种特定情况应该采取什么行动。又或者，假如我们希望构建一个可以实现图像分类（例如，人、动物、植物）的 agent，我们可以给每张图标都添加真实的类别标签，然后让 agent 基于这些信息进行学习，从而构建一个分类模型，这样，当给定一张新的测试图像时，该模型就能够对其进行分类。
- 基于监督者提供的信息，学习对正确和错误的行动进行分类。
演化（Evolutionary）：
第三种方法是演化算法，这里我们不会对其展开太多讨论。
- 从一系列可能的控制器中：对它们进行试验，选择其中表现最好的，然后通过多次迭代进行变异和重组，保留最优的控制器。

优点：不需要太多关于规则的知识。
缺点：在实践中，很难知道应该学习哪些特征，并且训练过程很慢。

1.3 通用问题求解

这里，我们将关注如何用基于模型的方法，来求解通用问题。这个领域已经被研究了数十年，最早的相关研究可以追溯到开始于 1959 年的 GPS 研究项目。

目标：写出一个可以解决所有问题的程序。
$\color{blue}{\to}$ 写出 $X\in\{算法\}$：对于所有的 $Y\in\{问题\}$，$X$ 都能够解决 $Y$。
$\color{blue}{\to}$ 那么，什么叫做一个 “问题”？怎样定义 “解决” 一个问题？
显然，这个目标过于宏大，实践上存在诸多困难，因此我们将目标改为专注某一类问题。
目标 2.0：写出一个可以解决一个大类的问题的程序。
随着时间的推移和研究的深入，我们不再满足于仅仅解决某一类问题，我们还希望知道如何更高效地解决这些问题。
目标 3.0：写出一个可以有效解决一个大类的问题的程序。
（一些新问题）$\leadsto$（描述问题 $\to$ 使用现成的求解器）$\leadsto$（和人类专家程序竞争解决方案）
所以，通常采用的方法是：我们得到了一些新问题，我们希望用一些通用目标规划语言来描述这些问题，然后我们用一些现成的通用求解器对其进行求解，我们希望它能够和人类专家利用专业知识得到的解决方案相当，甚至更好。

$\color{blue}{\to}$ 用巧妙的解决方法击败人类。
参考链接：始于 1959 年的通用求解器 GPS

1.4 基于模型的方法

$\color{blue}{\to}$ 为问题指定模型：行动 (actions)、初始状态 (initial situation)、目标 (goals)、传感器 (sensors)。

$\color{blue}{\to}$ 让一个求解器自动计算得到控制器。

我们得到了一些领域信息：行动、传感器、目标。我们希望利用这些信息来构建一个求解器，以便我们可以自动计算得到一个控制器，该控制器描述了 angent 在任何给定状态下应当如何采取行动。

优点：

强大：在某些应用中，泛化性能是非常必要的。
快速：可以快速搭建原型。10 行 PDDL 语言描述问题 vs. 1000 行 C++ 代码（语言生成任务）
灵活和清晰：修改 / 保留描述。
智能和领域独立性：可以自动决定如何有效对一个复杂问题进行求解。

缺点：需要一个模型；计算困难

效率损失：如果没有任何关于国际象棋的特定领域知识，我们不可能击败卡斯帕罗夫。

$\color{blue}{\to}$ 二者之间的权衡：“自动且通用” vs. “手动但高效”

基于模型的方法实现的智能行为称为 AI 中的 规划（Planning）。

如何高效实现全自动算法？

1.5 例子：经典搜索问题

我们来看一个例子：纸牌接龙（Solitaire）

我们可以将其建模为一个经典搜索问题：

状态（States）：描述了域中的所有可能的配置，这里可以理解为纸牌位置。
例如：上图中，“黑桃 J” 位于 “红桃 Q” 上方，而 “红桃 Q” 位于面板上方第二列，“梅花 A” 则位于 “家” 中的第一列。我们可以通过描述每张纸牌的位置来描述某种可能的配置（状态），而所有可能的状态构成了这个域的状态空间。
行动（Actions）：我们可以通过行动从一个状态映射到另一个状态，即移动纸牌。
例如：将 “黑桃 J” 移动到倒数第二列的空位上。
初始状态（Initial state）：初始配置，即游戏开始时关于所有纸牌的位置描述。
目标状态（Goal states）：所有纸牌都 “回家”。
解（Solution）：如果我们将问题传入规划器，那么将得到一个移动纸牌的序列来完成游戏。

2. 模型

2.1 基本状态模型：经典规划

目标：写出一个能解决所有经典搜索问题的程序。

状态模型：

有限离散状态空间 $S$
一个已知的初始状态 $s_0\in S$
一个目标状态的集合 $S_G\subseteq S$
在每个状态 $s\in S$ 中可能采取的行动 $A(s)\subseteq A$
一个确定性转移函数 $s’=f(a,s)$，对于所有的 $a\in A(s)$
正的行动代价 $c(a,s)$

$\color{blue}{\to}$ 一个解是一个可能的行动序列，它将初始状态 $s_0$ 映射到目标状态 $S_G$，并且，如果它使得 行动代价之和（例如：行动步数）最小化，那么我们称之为 最优解。

$\color{blue}{\to}$ 通过放松上面蓝色部分的假设，我们可以得到不同模型和 控制器。

2.2 不确定性但是无反馈：一致规划

除了经典规划，但是还有很多其他类型的规划模型，例如：一致规划（Conformant Planning）。

一致规划的模型假设大部分都和之前经典规划一样，区别是现在我们的初始状态是一个可能的状态集合。想象一下，假设现在房间内有一个移动机器人和目标点，如果机器人知道自己的初始位置，那么这是一个经典规划问题，但是假如现在房间内的灯是关着的，机器人并不知道自己的具体位置，只知道一些可能的初始位置，这种情况下机器人仍然需要到达目标点，那么我们可以用一致规划模型求解，它将比经典规划更复杂一些。

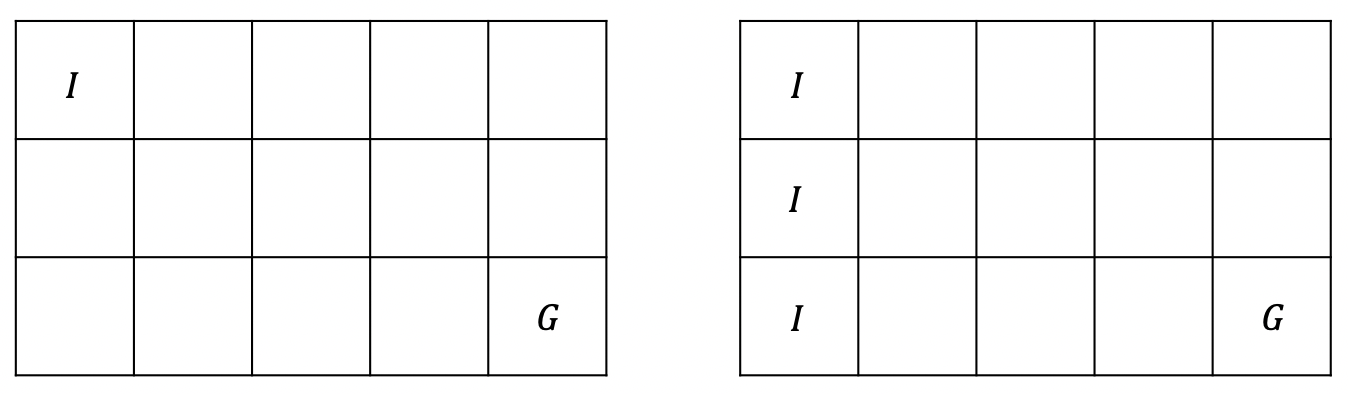
例如，在上面左边的图中，我们已知初始位置 $I$ 和目标位置 $G$，那么可以视为一个经典规划问题。而在右边的图中，已知目标位置 $G$，而初始位置 $I$ 有三个可能的位置，但是我们并不知道具体是其中哪个，这是一个更复杂的规划问题，但是我们仍然可以对其求解。例如，我们可以有一个这样的解：机器人总是先向右移动 4 步，再向下移动 2 步，如果因为碰到墙壁无法继续移动则停止，显然，这个解对于右图中的一致规划问题也是适用的。

状态模型：

有限离散状态空间 $S$
一个可能的初始状态集合 $S_0\in S$
一个目标状态的集合 $S_G\subseteq S$
在每个状态 $s\in S$ 中可能采取的行动 $A(s)\subseteq A$
一个非确定性转移函数 $F(a,s)\subseteq S$，对于所有的 $a\in A(s)$
一致行动代价 $c(a,s)$

$\color{blue}{\to}$ 一个解还是一个 行动序列，但对于 任何可能的初始状态和转移，都必须能够到达目标状态。

$\color{blue}{\to}$ 比 经典规划 更复杂，在最坏的情况下，我们比较难以验证一个规划的 一致性；但在特殊情况下，具有 部分可观测性的规划 是可行的。

2.3 基于马尔可夫决策过程（MDPs）的规划

AI 中的另一类常见问题是 马尔可夫决策过程（Markov Decision Processes，MDPs），它是一种 完全可观测 的概率状态模型：

一个状态空间 $S$
初始状态 $s_0\in S$
一个目标状态的集合 $S_G\subseteq S$
在每个状态 $s\in S$ 中可能采取的行动 $A(s)\subseteq A$
转移概率 $P_a(s’\mid s)$，其中 $s\in S, a\in A(s)$
行动代价 $c(a,s)>0$

它和经典规划的区别在于：经典规划中我们采用的是一个确定性转移函数，即当我们执行某个行动时，我们能够确切地知道该行动将导致的状态变化；而 MDPs 采用的是一个概率函数，即当我们采取某个行动时，我们并不知道它将具体导致哪种状态变化，我们只知道这个状态转移的概率是多少。

$\color{blue}{\to}$ 解是将状态映射到行动的 函数（策略）。

$\color{blue}{\to}$ 最优解 是能够使得到达目标的 期望代价 最小化的解。

2.4 部分可观测马尔可夫决策过程（POMDPs）

POMDPs 是一种 部分可观测 的概率状态模型，它假设系统状态由MDP决定，但是智能体无法直接观察状态。相反的，它必须要根据模型的全域与部分区域观察结果来推断状态的分布：

状态 $s\in S$
行动 $A(s)\subseteq A$
转移概率 $P_a(s’\mid s)$，其中 $s\in S, a\in A(s)$
初始信念状态 $b_0$
最终信念状态 $b_f$
传感器模型由概率 $P_a(o\mid s)$ 给出，其中 $o\in Obs$

所以，这种情况下，我们不仅有概率转移函数，而且还有信念状态。也就是说，agent 可能并不知道自己的初始状态或者目标状态，只有关于它们的信念，它通过传感器得到有关周围环境的信息，并在此基础上对信念状态作出调整。

无论是 MDPs 和 POMDPs，想要完全求解都面临所谓 “维度诅咒” 问题：MDPs 的状态空间大小随状态变量的数目呈指数级增加；而 POMDPs 则要更加复杂，由于状态空间随状态变量的数目呈指数增加，因此，POMDPs 的复杂度随状态变量数目是呈双指数级增加的。

$\color{blue}{\to}$ 信念状态（Belief states） 是状态空间 $S$ 上的概率分布。

$\color{blue}{\to}$ 解是将信念状态映射到行动的策略。

$\color{blue}{\to}$ 最优解 是能够使得从 $b_0$ 到达 $G$ 的 期望代价 最小化的解。

2.5 例子

根据不同的问题类型，我们可能需要不同的求解器。

假设现在有一个路径规划问题：agent $\mathbf A$ 要达到目标 $\mathbf G$，在一个已知地图中每次移动一格。

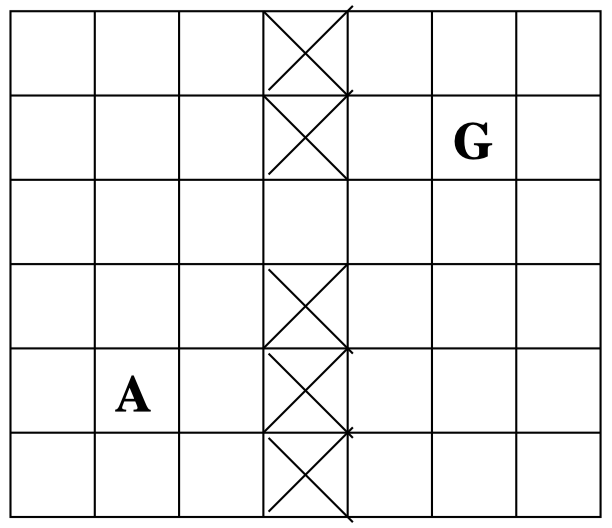
如果行动是确定性的，并且初始位置已知，那么这是一个 经典规划问题。
如果行动是随机性的，并且位置是可观测的，那么这是一个 MDP 问题。
如果行动是随机性的，并且位置是部分可观测的，那么这是一个 POMDP 问题。

不确定性和反馈机制的不同组合：三个问题，三个模型。

3. 语言

3.1 模型、语言和求解器

根据不同类型的问题，我们希望得到一个规划器，可以求解该类型下的所有问题（例如 MDPs）。

一个规划器是一个某一类模型上的求解器；它接收一个模型描述作为输入，计算得到对应的控制器。
很多模型，很多解的形式：不确定性、反馈、代价……
模型通过合适的规划语言（Strips，PDDL，PPDDL 等）描述，其中状态表示对该语言的解释。

3.2 经典规划问题的一种基本语言：Strips

最早的规划语言是 Strips，尽管这是一种起源于上世纪 50 年代的古老语言，但是它仍然是如今很多问题研究的基础。大部分的现代规划器，本质上都是基于 Strips 的扩展变体。

一个问题在 STRIPS 中表示为一个元组 $P=\langle F,O,I,G\rangle$：
- $F$ 表示所有原子（布尔变量）的集合
  - 变式（Fluents）$F$ 表示一个问题中的所有原子。例如，在一个规划问题中，一个 agent 可以处于很多不同位置中的一个，而一个 fluent 则可以指示该 agent 可能的位置。例如 “Chris 站在这个位置” 这句话可以是真或假；“Chris 站在那个位置” 也可以是真或假。域中的每个位置都可以有一个这样的 fluent，它是一个布尔变量。
- $O$ 表示所有算子（行动）的集合
  - 为了从初始状态到达目标状态，需要执行的一系列行动称为 算子（operators）。
- $I\subseteq F$ 表示初始状态
  - 初始状态（Initial situation）是 fluents 的一个子集，在初始时其结果为真。例如，当 Chris 进入房间时，“Chris 站在这个位置” 可能是一个初始状态。
- $G\subseteq F$ 表示目标状态
  - 假设 Chris 试图寻找一条到达房间右上角的路径，“Chris 站在房间右上角” 就是一个 目标状态（goal situation），同样，它也是 fluents 的一个结果为真的子集。
算子 $o \in O$ 表示为：
- 添加列表（Add list）$Add(o)\subseteq F$
  - 行动执行后结果为真。
- 删除列表（Delete list）$Del(o)\subseteq F$
  - 行动执行后结果为假。
- 前置条件列表（Precondition list）$Pre(o)\subseteq F$
  - 为了行动能够执行，必须为真。
所以，回到之前的例子，假如 Chris 希望移动到房间右上角，采取这些步骤将对域产生影响，我们会添加一个 fluent（“Chris 站在房间左下角”），而当 Chris 移动之后，之前的 fluent 会被删除。而要执行这一行动，前提条件是之前的 “Chris 站在房间左下角” 这一陈述为真。

3.3 从语言到模型（STRIPS 语义学）

一个 STRIPS 问题 $P=\langle F,O,I,G\rangle$ 决定了 状态模型 $S(P)$，其中：

状态 $s\in S$ 是变式 $F$ 中原子的某种集合。$S=2^F$。
初始状态 $s_0$ 为 $I$
目标状态 $s$ 满足 $G\subseteq s$
$A(s)$ 中的行动 $a$ 是 $O$ 中的 $o$，满足 $Pre(a)\subseteq s$
后继状态为 $s’=s-Del(a)+Add(a)$
行动代价 $c(a,s)$ 均为 $1$

$\color{blue}{\to}$ $P$ 的（最优）解是 $S(P)$ 的（最优）解

$\color{blue}{\to}$ 轻度的语言扩展通常很方便：求反（negation）、条件效应（conditional effects）、非布尔变量（non-boolean variables）；描述更丰富的模型所需的一些信息（代价、概率等）。

3.4 例子：砖块世界

我们将通过一个具体例子来了解如何描述问题域。砖块世界（The Blocksworld）是 AI 规划中最著名的例子之一，在这个游戏中，我们有一个钩爪和一些砖块，钩爪可以用来拾取和放下砖块，我们希望通过钩爪将这些砖块堆叠成某个目标状态。

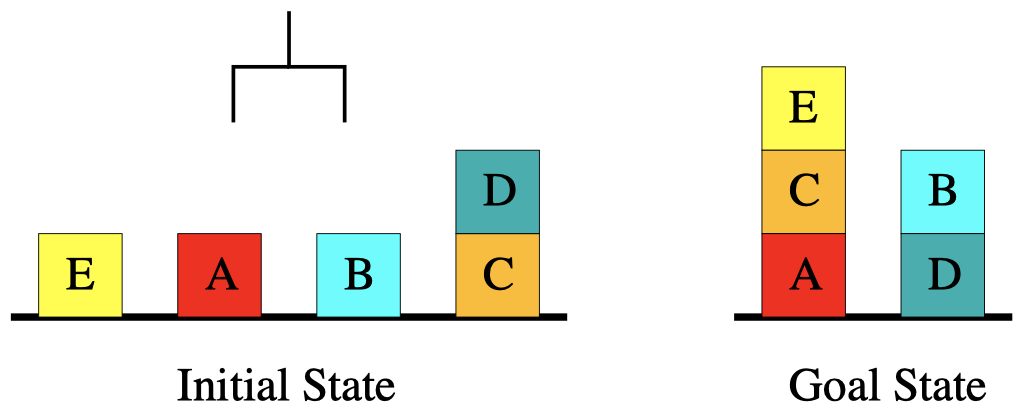
我们将用 Strips 来描述这个问题：

命题（Propositions）
- $on(x,y)$：砖块可以堆叠在另一个砖块上方，例如左图中砖块 D 在砖块 C 上方。
- $onTable(x)$：砖块可以位于桌面上方，例如左图中砖块 E、A、B、C 都在桌面上方。
- $clear(x)$：砖块上方没有物体，例如左图中的砖块 E、A、B、D。
- $holding(x)$：表示钩爪正在抓取的砖块。
- $armEmpty()$：钩爪是否为空闲状态。
初始状态
- 例如，左图的初始状态为：
  $\{onTable(E),clear(E),\dots,onTable(C),on(D,C),clear(D),armEmpty()\}$
目标状态
- 例如，右图的目标状态为：
  $\{on(E,C),on(C,A),on(B,D)\}$
动作
我们通过执行一系列动作来改变域的状态。在几乎所有的规划任务中，一般都遵循 封闭世界假定（closed-world assumption），即所有没有被指定的事物都可以认为是假命题。例如，在上面的例子中，我们没有指定除了 A、B、C、D、E 之外的其他砖块的状态，那么我们可以认为不存在其他砖块，即关于其他砖块的命题都是假命题。
- $stack(x, y)$：实现一个堆叠状态。
- $unstack(x, y)$：解除一个堆叠状态。
- $putdown(x)$：拾起砖块。
- $pickup(x)$：放下砖块。
$stack(x, y)$ ？
我们来看一下堆叠（stacking）操作，如果我们要完成一个 $stack(x,y)$ 操作（即将砖块 $x$ 叠放在砖块 $y$ 上方），那么前置条件列表是什么？显然，砖块 $x$ 应该在钩爪上，并且砖块 $y$ 上方没有其他物体。另外，添加列表应该是什么呢？显然，在堆叠 $stack(x,y)$ 完成后，命题 $on(x,y)$、$armEmpty()$、$clear(x)$ 将被加入域中。最后，删除列表应该是什么呢？也就是说，在完成 $stack(x,y)$ 后，之前的哪些命题将不再为真。显然，在完成堆叠后，$holding(x)$ 和 $clear(y)$ 将不再为真，因此我们将它们加入删除列表。
- $Pre: \{holding(x),clear(y)\}$
- $Add: \{on(x,y),armEmpty(),clear(x)\}$
- $Del: \{holding(x),clear(y)\}$
可以看到，在这个例子中，删除列表和前置条件列表相同，虽然这并非总是成立，但在很多实际的域中，这属于很常见的情况。

3.5 PDDL

前面我们介绍了 Strips 语言，并且用它描述了砖块世界的问题。PDDL（规划域定义语言）是基于 Strips 语言的一种扩展，如今在规划领域被广泛采用。

PDDL 不是一种命题语言：

通过从一个对象的有限集合中将对象变量实例化，增强了表示能力。（类似于谓词逻辑）
行动图式（Action schemas）通过对象实现参数化。
谓词（Predicates）通过对象完成实例化。

一个 PDDL 规划任务可以分为两部分：

域文件（Domain ﬁle）和问题文件（problem ﬁle）。
域文件给出谓词（predicates）和算子（operators）；每个基准域（benchmark domain）都有一个域文件。域文件基本上描述了规则，例如在之前的砖块世界中，可以移动、堆叠砖块的前置条件等等。
问题文件给出对象、初始状态和目标状态。问题文件指定了需要处理的情况，例如初始状态、目标状态等等。

PDDL 的这种设计非常强大，这意味着对于很多相似的问题，我们可以有一个通用的域文件，然后对于不同问题采用不同的问题文件来编码。

3.6 PDDL 描述砖块世界

域文件：

(deﬁne (domain blocksworld)
(:predicates (clear ?x) (holding ?x) (on ?x ?y)
             (on-table ?x) (arm-empty))
(:action stack
 :parameters (?x ?y)
 :precondition (and(clear ?y) (holding ?x))
 :effect (and (arm-empty) (on ?x ?y)
              (not (clear ?y)) (not (holding ?x)))
)
...

在上面的域文件中，我们在 predicates 中定义了 5 种基本命题：$clear(x)$、$holding(x)$、$on(x,y)$、$onTable(x)$ 和 $armEmpty()$。其中冒号 : 表示定义，问号 ? 表示参数。然后，我们定义了行动 $stack(x,y)$：参数为 $x$ 和 $y$；前置条件为 $\{clear(y),holding(x)\}$，其中 and 表示后面的所有命题同时满足；在 PDDL 中，添加列表和删除列表一并用 effect 表示，其中命题前加 not 表示删除。我们可以通过这种方式定义域中的所有规则。

问题文件：

(deﬁne (problem bw-abcde)
(:domain blocksworld)
(:objects a b c d e)
(:init (on-table a) (clear a)
       (on-table b) (clear b)
       (on-table e) (clear e)
       (on-table c) (on d c) (clear d)
       (arm-empty))
(:goal (and (on e c) (on c a) (on b d))))

在问题文件中，我们定义了所有对象变量：砖块 $a$、$b$、$c$、$d$、$e$。然后我们还分别定义了初始状态和目标状态。

4. 复杂度

4.1 规划中的算法问题

满意规划（Satisﬁcing Planning）
输入：一个规划任务 $P$
输出：关于 $P$ 的一个规划；或者 “不可解”，如果关于 $P$ 的规划不存在。

最优规划（Optimal Planning）
输入：一个规划任务 $P$
输出：关于 $P$ 的一个最优规划；或者 “不可解”，如果关于 $P$ 的规划不存在。

尽管两者看上去非常相似，但是相应的求解技术之间存在很大差异。

$\color{blue}{\to}$ 对于这两种规划问题中的任何一种，其相关的成功技术都几乎是错综复杂的。
$\color{blue}{\to}$ 在实践中，满意规划通常更为有效。
$\color{blue}{\to}$ 解决这些问题的程序被称为（最优）规划器 / 规划系统 / 规划工具。

4.2 规划中的决策问题

定义（PlanEx）：通过 PlanEx，我们可以表示为一个判定问题，给定一个规划任务 $P$，判断是否存在一个关于 $P$ 的规划。

$\color{blue}{\to}$ 对应满意规划。

定义（PlanLen）：通过 PlanLen，我们可以表示为一个判定问题，给定一个规划任务 $P$ 和一个整数 $B$，判断是否存在一个关于 $P$ 的最大长度为 $B$ 的规划。

$\color{blue}{\to}$ 对应最优规划。

4.3 NP 和 PSPACE

图灵机：工作在由磁带单元（tape cells）组成的磁带（tape）上，其读/写头（R/W head）在其中移动。机器具有内部状态（internal states）。转移规则（transition rules）指定了，在给定当前单元内容和内部状态的情况下，后继内部状态将是什么，以及读写头是向左还是向右移动，或者保持原位。有一些内部状态是接受状态（“是”；否则为“否”）。

NP：关于存在一个非确定性图灵机的判定问题，该图灵机在按其输入大小的多项式时间内运行。如果在可能的运行中至少有一种能接受，则接受。

PSPACE：关于存在一个确定性图灵机的判定问题，该图灵机在按其输入大小的多项式空间内运行。

关系：可以在确定性多项式空间中模拟非确定性多项式空间。因此 PSPACE $\boldsymbol{=}$ NPSPACE，所以 (通常) NP 是 PSPACE 的子集。

$\color{blue}{\to}$ 更多细节请参见教材，个人推荐 Garey and Johnson (1979)。

4.4 PlanEx 和 PlanLen 的计算复杂度

定理：PlanEx 和 PlanLen 是 PSPACE-完全 问题。

$\color{blue}{\to}$ 至少和其他 PSPACE 中包含的问题一样困难。

$\color{blue}{\to}$ 更多细节请参阅 Bylander (1994)。

4.5 特定域的 PlanEx vs. PlanLen

通常，两者具有相同的复杂度。
在特定的应用程序中，有界长度规划的存在性问题通常要比规划存在性问题更加困难。
这在许多 IPC 基准域中都会发生：PlanLen 是 NP-完全 问题，而 PlanEx 是 P 问题。
- 例如：砖块世界 vs. 物流问题

$\color{blue}{\to}$ 实际上，最优规划（几乎）永远不会很 “简单”。

例如，在砖块世界中，我们几乎总是可以得到这样一个解：先将所有砖块移动到桌面上，然后再堆叠成目标状态。但是想找到最优解就明显困难得多。

4.6 例子：砖块世界

$n$ 个砖块，$1$ 个钩爪。
一次单独的行动要么是用钩爪拾取一个砖块，要么是将钩爪上的砖块放置在其他砖块/桌面上。

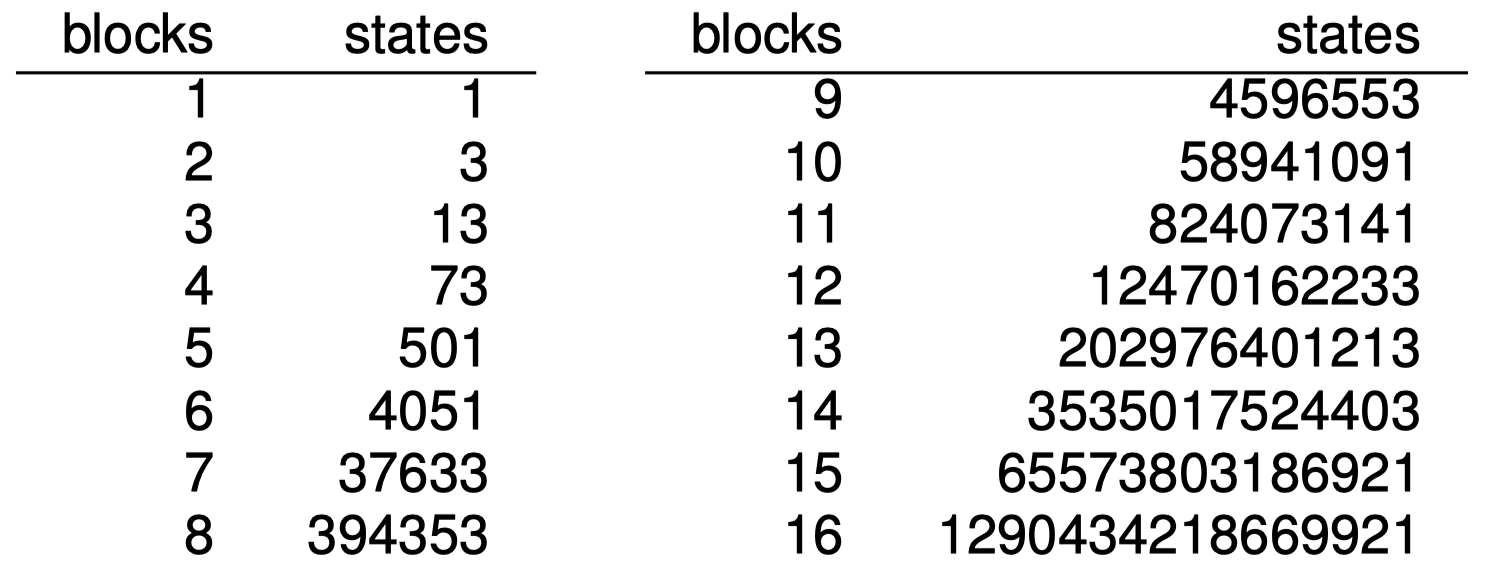
$\color{blue}{\to}$ 状态空间可能非常大。特别是，状态空间通常基于指定的输入大小呈指数级增加。

$\color{blue}{\to}$ 换而言之：搜索问题通常都是计算困难的（例如，砖块世界的最优解是一个 NP-完全 问题）。

5. 计算方法

5.1 计算：如何解决 STRIPS 规划问题？

关键问题：使用 PDDL 语言 的两个主要好处：

说明：简洁的模型描述。
在前面的砖块世界的例子中，我们仅用非常短的 PDDL 文件就可以定义 domain，即便是很复杂的问题，我们也可以很容易地将其编码为 domain 文件来表示，这将带来诸多好处：因为否则的话，我们将不得不编写每一个单独的 对象（object）和每一条单独的 规则（rule），PDDL 语言为我们提供了一种更灵活的选择。
计算：揭示有用的启发式信息（结构）
另一个问题是计算。语言让我们得以描述问题，使得程序可以理解问题的结构，并且在结构之外加入启发式信息。例如，在吃豆人问题中，我们可以在 PDDL 规划器之外加入启发式搜索来引导搜索树。

为了达到上述目的，通常有 两种传统方法：搜索 vs. 分解

对状态模型 $S(P)$ 直接进行显式搜索，但是通常效率较低，直到最近才有所改善。
如今我们采用的最常见的方法是显示搜索：我们有初始状态、目标状态，以及搜索算法（例如：$\mathbf A^*$ 算法）来发现从初始状态到目标状态的路径。
另一种方法是分解（decomposition）问题。
相比只是找出一条从初始状态到目标状态的路径，我们试图将规划问题分解为一些启发式的子问题，如果我们可以找到这些子问题的解，我们可以将其组合，得到原规划问题的解。通常，这种方法更好一些，因为规划问题的状态空间通常很大，即使采用很好的启发式算法，搜索空间依然很大。

5.2 经典规划的计算方法

通用问题求解器（General Problem Solver, GPS）和 Strips（50-70 年代）：均值分析、分解、回归……
偏序（Partial Order, POCL）规划（80 年代）：处理任何开放的子目标、解决威胁；UCPOP 1992
图规划（Graphplan）（1995-2000）：建立包含一定长度内的所有可能的并行规划的图；然后通过从目标向后搜索整个图来提取规划。
可满足性规划（Planning as Satisfiability, SATPlan）（1996-）：将规划问题映射为 SAT 问题；使用最前沿的 SAT 求解器。
启发式搜索规划（Heuristic Search Planning）（1996-）：从问题 $P$ 中提取的具有启发函数 $h$ 的搜索状态空间 $S(P)$。
模型检查规划（Model Checking Planning）（1998-）：使用 “符号” 宽度优先搜索来搜索状态空间 $S(P)$，其中状态集由 BDD 实现的公式表示。

5.3 经典规划中的最新技术

自图规划以来取得重大进展
经验主义方法
- 标准 PDDL 语言
- 提供规划器和基准；比赛
- 专注于性能和可扩展性
解决了大问题（非最优）
不同的构想和想法
- 启发式搜索 规划
- SAT 规划
- 其他：局部搜索（LPG），蒙特卡洛搜索（Arvand），…

这里，我们将主要关注启发式搜索规划，部分关注 SAT 规划。

6. 国际规划竞赛 IPC

什么是国际规划竞赛（The International Planning Competition，IPC）？

在一系列由 IPC 组织者设计的基准上运行参赛的规划器。对其中最高效的规划器颁发奖励。

1998, 2000, 2002, 2004, 2006, 2008, 2011, 2014
PDDL [McDermott 等（1998）；Fox and Long（2003）; Hoffmann and Edelkamp（2005）]
$\approx$ 40 domains, $>$ 1000 instances, 74 planners in 2011
最优轨迹 vs. 满意轨迹
其他各种：不确定性、学习……

历届冠军

IPC 2000: Winner FF, heuristic search (HS)
IPC 2002: Winner LPG, HS
IPC 2004: Winner satisﬁcing SGPlan, HS; optimal SATPLAN, compilation to SAT
IPC 2006: Winner satisﬁcing SGPlan, HS; optimal SATPLAN, compilation to SAT
IPC 2008: Winner satisﬁcing LAMA, HS; optimal Gamer, symbolic search
IPC 2011: Winner satisﬁcing LAMA, HS; optimal Fast-Downward, HS
IPC 2014: Winner satisﬁcing IBACOP, HS Portfolio; optimal SymbA^*, symbolic search
IPC 2018: Winner satisﬁcing FD/BFWS-LAPKT, HS Portfolio/Width-Based planning; optimal Delﬁ, HS portfolio

$\color{blue}{\to}$ 在接下来的部分，我们将关注启发式搜索规划。
$\color{blue}{\to}$ 上面是一段关于 IPC 历史的简短摘要，还有许多不同的类别和奖项。

问题：如果规划器 $x$ 和 $y$ 同时竞争 IPC’YY，并且 $x$ 获胜了，那么 $x$ 比 $y$ 更好吗？

$\color{blue}{\to}$ 是的，但是这仅仅是对于 IPC’YY 的标准而言，并且仅适用于这种情况下获胜方的决定标准。在其他 domain 或根据其他标准下，使用 “失败方” 有可能会更好。

$\color{blue}{\to}$ 这很复杂，过度简化是非常危险的。（但是，当然，我们一直都在这么做）

7. 总结

通用问题求解尝试开发在某一大类问题上都能够表现良好的求解器。
如前所述，规划是一种专门针对经典搜索问题的一般问题解决形式。（实际上，我们还解决了无法访问、随机、动态、连续和 multi-agent 设置。）
经典搜索问题需要找到一条从初始状态到目标状态的行动路径。
他们假设一个 single-agent、完全可观察、确定性的静态环境。尽管存在诸多条件限制，它们在实践中还是无处不在。
启发式搜索规划已经主导了国际计划竞赛（IPC），这也是我们目前比较关注的。
对于我们的目的而言，STRIPS 是最简单的语言，同时它还具有合理的表达能力。它使用布尔变量（事实），并根据前置条件（precondition）、添加列表（add list）和删除列表（delete list）来定义行动（actions）。
对于 STRIPS，规划是否存在（有界或无界）是一个 PSPACE-完全 问题。
事实上，PDDL 是用于描述规划问题的标准语言。

8. 扩展阅读

阅读材料： Everything You Always Wanted to Know About Planning (But Were Afraid to Ask) [Joerg Hoffmann, 2011]

地址: http://fai.cs.uni-saarland.de/hoffmann/papers/ki11.pdf

内容: Joerg personal perspective on planning. Very modern indeed. Excerpt from the abstract:

The area has long had an afﬁnity towards playful illustrative examples, imprinting it on the mind of many a student as an area concerned with the rearrangement of blocks, and with the order in which to put on socks and shoes (not to mention the disposal of bombs in toilets). Working on the assumption that this “student” is you – the readers in earlier stages of their careers – I herein aim to answer three questions that you surely desired to ask back then already:

What is it good for? Does it work? Is it interesting to do research in?

补充材料： Introduction to STRIPS, from simple games to StarCraft:
http://www.primaryobjects.com/2015/11/06/artificial-intelligence-planning-with-strips-a-gentle-introduction/

PDDL 在线建模编辑器：
http://editor.planning.domains

下节内容：生成启发函数

本作品采用知识共享署名-非商业性使用-相同方式共享 4.0 国际许可协议进行许可。欢迎转载，并请注明来自：YEY 的博客同时保持文章内容的完整和以上声明信息！

人工智能自动规划 04：规划导论

墨尔本大学 COMP90054 课程笔记