Lecture 06 序列标注:隐马尔可夫模型
本节课我们将学习一种自动词性标注模型:隐马尔可夫模型(Hidden Markov Models, HMM)。尽管在本节内容中我们将学习如何将 HMM 应用于词性标注,但实际上它是一种通用的机器学习模型,可以应用于任何序列标签问题。
1. 从局部分类器到隐马尔可夫模型
1.1 词性标注(POS Tagging)重新回顾
- $\textit{Janet will back the bill}$
- $\textit{Janet}$/NNP $\textit{will}$/MB $\textit{back}$/VP $\textit{the}$/DT $\textit{bill}$/NN
- 局部分类器:我们可以将每个单词的词性预测作为一个分类问题。
- 例如:现在,我们希望预测 “$\textit{bill}$” 这个单词的词性,我们可以将其当成一个分类问题。输入为 “$\textit{bill}$”,以及一些其他特征,例如前面的单词 “$\textit{the, back}$” 以及它们已经预测出的词性 “DT, VP”。然后进行预测,从所有的候选词性标签中对单词 “$\textit{bill}$” 进行词性分类。
- 容易发生 错误传播(error propagation)。
因为在预测过程中,我们将前面单词词性的预测结果作为当前预测单词的输入特征之一,所以,如果前面单词的词性预测错误,会影响后续单词词性的预测。
- 如果将 整个序列当成一个 “类别(class)” 会怎么样?
- 输出:“NNP_MB_VP_DT_NN”
- 在之前的局部(单词)层面处理词性分类会碰到错误传播的问题,我们可以尝试在句子层面进行词性标注以避免这个问题。这里,我们将整个单词序列的词性预测作为一个分类问题。例如,输入是一个单词序列 “$\textit{Janet will back the bill}$”,输出是整个单词序列的标签类别 “NNP_MB_VP_DT_NN”。
- 但是,这种方法实现起来非常困难,因为存在以下问题:
- 可能的组合数量会呈指数增长:
候选词性数量为 $|Tags|$,序列长度为 $M$,可能的标签序列类别数量为 $|Tags|^M$。
例如:有 $80$ 个可选词性,序列中包含 $20$ 个单词,可能的类别数量为 $80^{20}$。
所以,无论我们的训练集有多大,都不可能覆盖所有可能的类别。 - 另一个问题是如何处理不同长度的句子:
即便我们的训练集可以覆盖 $80^{20}$ 种序列类别,但是,当新的预测序列包含其他数量的单词时(例如:$5$ 个 或者 $40$ 个单词),该方法会再次失效。
- 可能的组合数量会呈指数增长:
1.2 一种更好的方法
- 标注(Tagging)是一个句子层面的任务,因为我们并不是单独对每个单词进行词性标注,而是需要考虑全局上下文,结合整个句子的语境来判断单词的词性。但是作为人类,我们可以将其 分解(decompose) 为若干个小的单词层面的任务:对于一个句子,我们倾向于先大致理解其含义,例如哪些是主语,哪些是主要的动词等,然后再深入每个单词,看一下其最有可能的词性是什么。
- 解决方案:
- 定义一个模型,可以将整个过程分解为单个单词层面的步骤。
- 但是在学习和预测的时候考虑整个序列(没有错误传播),即预测的标签序列对于整个句子的概率是最优的。
因此,我们仍然是从句子层面考虑这个问题,但是我们的模型能够将其分解为一些更小的单词层面的子任务。
- 这就是 序列标注(sequence labelling) 的思想,或者更一般地说,结构预测(structured prediction)。
1.3 一种概率模型
现在,我们介绍一种概率模型,并在此基础上推导出隐马尔可夫模型。
- 目标:从句子 $\boldsymbol w$ 中获得最佳标签序列 $\boldsymbol t$。
-
$\hat{\boldsymbol t}=\mathop{\operatorname{arg\,max}}\limits_{\boldsymbol t}P(\boldsymbol t\mid \boldsymbol w)$
-
$\hat{\boldsymbol t}=\mathop{\operatorname{arg\,max}}\limits_{\boldsymbol t}\dfrac{P(\boldsymbol w\mid \boldsymbol t)P(\boldsymbol t)}{P(\boldsymbol w)}=\mathop{\operatorname{arg\,max}}\limits_{\boldsymbol t}P(\boldsymbol w\mid \boldsymbol t)P(\boldsymbol t)$ $\qquad$ (贝叶斯定理)
-
- 让我们将其分解:
-
$P(\boldsymbol w\mid \boldsymbol t)=\prod_{i=1}^{n}P(w_i\mid t_i)$ $\qquad$ (一个单词仅依赖于其词性标签的概率)
-
$P(\boldsymbol t)=\prod_{i=1}^{n}P(t_i\mid t_{i-1})$ $\qquad$ (一个词性标签仅依赖于其前一个词性标签的概率)
-
- 这里,我们采用了两个类似于 bi-gram 语言模型中的非常强的 独立假设:
- 假设单词 $w_i$ 出现的概率仅取决于其词性 $t_i$
- 假设词性 $t_i$ 出现的概率仅取决于其前一个词性 $t_{i-1}$
- 这就是 隐马尔可夫模型(Hidden Markov Model, HMM)
2. 隐马尔可夫模型
\[\hat{\boldsymbol t}=\mathop{\operatorname{arg\,max}}\limits_{\boldsymbol t}P(\boldsymbol w\mid \boldsymbol t)P(\boldsymbol t)\] \[P(\boldsymbol w\mid \boldsymbol t)=\prod_{i=1}^{n}P(w_i\mid t_i)\] \[P(\boldsymbol t)=\prod_{i=1}^{n}P(t_i\mid t_{i-1})\]- 为什么是 “马尔可夫(Markov)”?
因为该模型假设序列服从一个 马尔可夫链(Markov chain):一个事件(词性标签 tag)的概率仅取决于前一个事件(词性标签 tag)。 - 为什么是 “隐(Hidden)”?
因为这些事件(词性标签 tags)是不可见的:我们仅仅能看到单词序列,而需要预测的词性标签 tags 是未观测到的,我们的目标是寻找最佳的词性标签序列。
2.1 HMM 的训练过程
- 参数是单独的概率 $P(w_i\mid t_i)$ 和 $P(t_i\mid t_{i-1})$
分别对应 发射(emission)$(O)$ 和 转移(transition)$(A)$ 概率 - 训练过程利用 最大似然估计(MLE)
在朴素贝叶斯和 n-gram 语言模型中,这一步可以通过简单地计算不同类别的词频完成。 -
在 HMM 中,我们采用 完全相同的做法,例如:
-
$P(\textit{like}\mid \text{VB})=\dfrac{count(\text{VB},\textit{like})}{count(\text{VB})}$
-
$P(\text{NN}\mid \text{DT})=\dfrac{count(\text{DT},\text{NN})}{count(\text{DT})}$
对于发射概率 $P(\textit{like}\mid \text{VB})$,我们计算语料库中所有词性被标注为 $\text{VB}$ 的单词 “$\textit{like}$” 的数量,然后除以所有的 $\text{VB}$ 词性的数量。对于转移概率 $P(\text{NN}\mid \text{DT})$,我们计算语料库中词性 $\text{DT, NN}$ 的共现次数,除以 $\text{DT}$ 出现的总次数。这里和之前的语言模型相比,唯一的差别就是语言模型的语料库仅包含文本,而这里的语料库包含文本以及相应的词性标注。
-
- 序列中的第一个 tag 应该如何处理呢?
和之前 n-gram 模型的处理方式一样,我们引入一个起始符号 “\(\texttt{<s>}\)” 代表一个序列的开始。
例如:\(P(\text{NN}\mid \texttt{<s>})=\dfrac{count(\texttt{<s>},\text{NN})}{count(\texttt{<s>})}\) - 序列中的最后一个 tag 应该如何处理呢?
同样地,我们引入一个结束符号 “\(\texttt{</s>}\)” 代表一个序列的结束。 - 如何处理没有见过的 (word, tag) 和 (tag, previous tag) 组合?
和之前朴素贝叶斯和 n-gram 模型的处理方式一样,引入 平滑(smoothing)技术。
2.3 转移矩阵
这里是一个 转移矩阵(transition matrix)的例子:
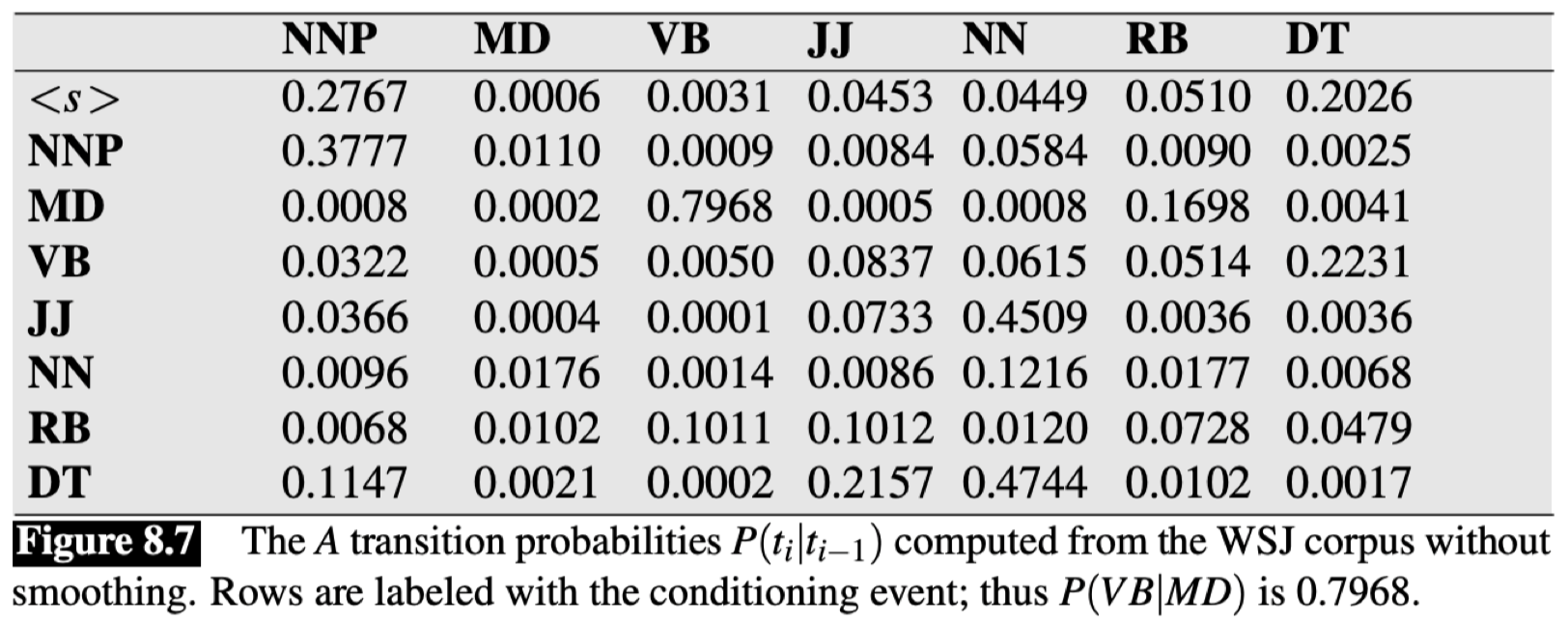
该矩阵描述了 转移概率(transition probabilities)。这里的转移概率来自 WSJ(华尔街日报)语料库,其中的文本都已经过词性标注,所以我们可以在此基础上计算这些转移概率。其中,第一列表示条件。所以,如果我们想知道最有可能出现在句子开头的词性,我们可以读取表中第一行,可以看到其中最大值为 \(P(\text{NNP}\mid \texttt{<s>})=0.2767\),所以句子中第一个单词词性最有可能是 NNP。同理,$\text{VB}$ 出现在 $\text{MD}$ 之后的概率 $P(\text{VB}\mid \text{MD})=0.7968$。
2.4 发射矩阵
这里是一个 发射矩阵(emission/observation matrix)的例子:
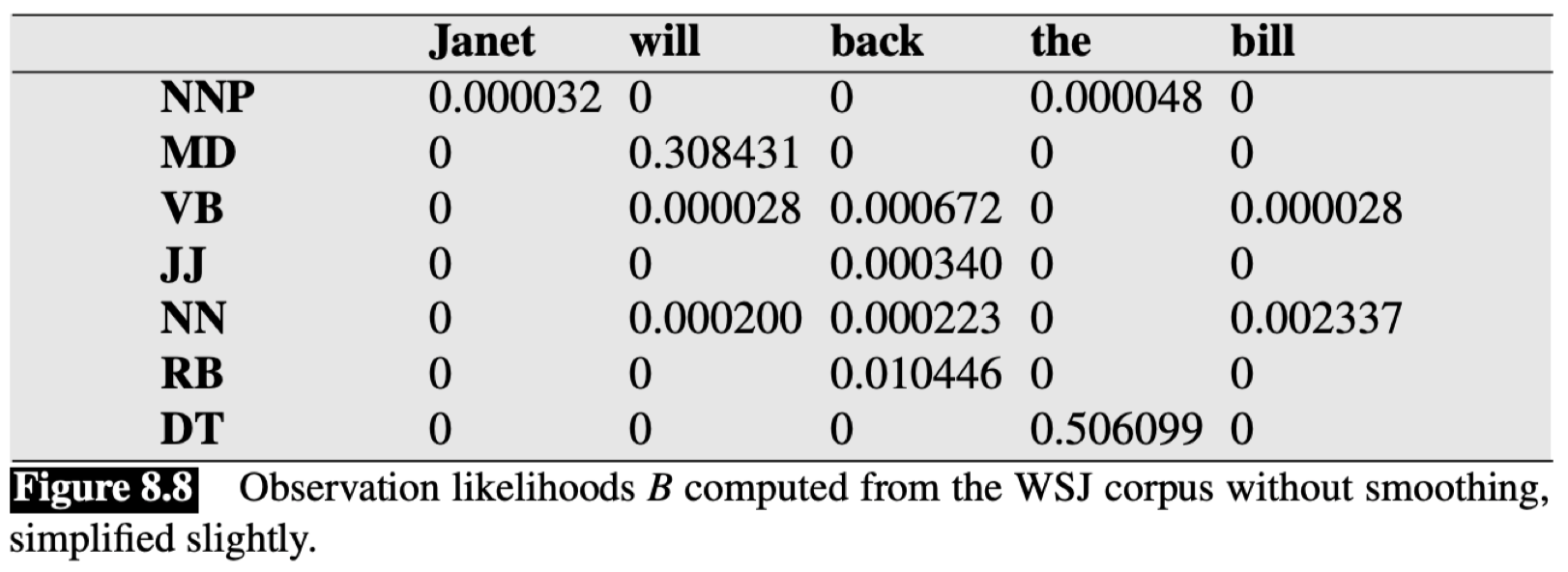
该矩阵描述了 发射概率(emission probabilities),即基于一个特定的词性标注生成相应单词的概率。同样,第一列代表条件,即给定的词性。所以,在没有采取任何平滑方法的前提下,可以看到对于词性 $\text{NNP}$,仅有两个单词 “$\textit{Janet}$” 和 “$\textit{the}$” 具有非零概率。我们还可以从另一个角度来看,有哪些词性可以生成单词 “$\textit{Janet}$”?可以看到,“$\textit{Janet}$” 对应的那一列只有 $\text{NNP}$ 不为 $0$,所以,这里单词 “$\textit{Janet}$” 只可能来自词性 $\text{NNP}$。
2.5 HMM 的预测过程(Decoding)
\[\begin{align} \hat{\boldsymbol t}&=\mathop{\operatorname{arg\,max}}\limits_{\boldsymbol t}P(\boldsymbol w\mid \boldsymbol t)P(\boldsymbol t)\\ &= \mathop{\operatorname{arg\,max}}\limits_{\boldsymbol t}\prod_{i=1}^{n}P(w_i\mid t_i)P(t_i\mid t_{i-1}) \end{align}\]- 简单思路:对于每个单词,选择使得 $P(w_i\mid t_i)P(t_i\mid t_{i-1})$ 最大化的 tag。从左至右,以 贪婪 形式进行。
- 这种做法是错误的,因为我们要寻找的是使得整个词性序列概率最大的 tags,即 $\mathop{\operatorname{arg\,max}}\limits_{\boldsymbol t}$,而不是使得单个单词词性概率最大的 tag,即 $\mathop{\operatorname{arg\,max}}\limits_{t_i}$。
上面的思路实际上等价于局部分类器,存在 错误传播 的问题。 - 正确的方法:考虑 所有 可能的 tag 组合,并对它们进行评估,然后选择概率最大的 tags 序列(类似朴素贝叶斯)。
但是有一个问题:序列数量会呈指数增长。
2.6 维特比算法
实际上,我们还有一种更好的选择:维特比算法(The Viterbi Algorithm)
-
维特比算法实际上是一种 动态规划(Dynamic Programming)方法。
我们可以计算一个单词序列的最优 tags 组合,但不必穷尽计算所有的可能组合。 - 我们将通过一个很简单的例子来说明,假设现在有一个只包含两个单词的句子:
“$\textit{can play}$” $\to \textit{can}$/MD $\textit{play}$/VB
我们希望给出的结果是 MD 和 VB。 - 对于单词 $\textit{can}$ 而言,找出其最优 tag 很简单:\(\mathop{\operatorname{arg\,max}}\limits_{t}P(\textit{can}\mid t)P(t\mid \texttt{<s>})\)
我们之所以可以这样做是因为第一个 “tag” 总是 “\(\texttt{<s>}\)”。我们只需要尝试所有可能的 tags,然后选择使得概率乘积最大的 tag 作为单词 “$\textit{can}$” 的 tag。 - 假设单词 “$\textit{can}$” 的最佳 tag 是 NN。为了得到单词 “$\textit{play}$” 的 tag,我们可以像之前一样,选择 \(\mathop{\operatorname{arg\,max}}\limits_{t}P(\textit{play}\mid t)P(t\mid \text{NN})\) 作为单词 “$\textit{play}$” 的 tag,但是这种做法是错误的,因为这又回到了局部分类器上面。
- 正确的做法是,我们保持追踪单词 “$\textit{can}$” 的 每个 tag 的得分,并且检查当 “$\textit{can}$” 具有一个不同的 tag 时 将会发生什么。所以我们可以直接利用之前的计算得分的结果而不必重复计算。
2.7 维特比算法的例子
我们将通过一个例子来看维特比算法是如何计算单词序列的 tags 的,回顾之前的 WSJ 语料库的例子,我们现在有如下的转移矩阵和发射矩阵:
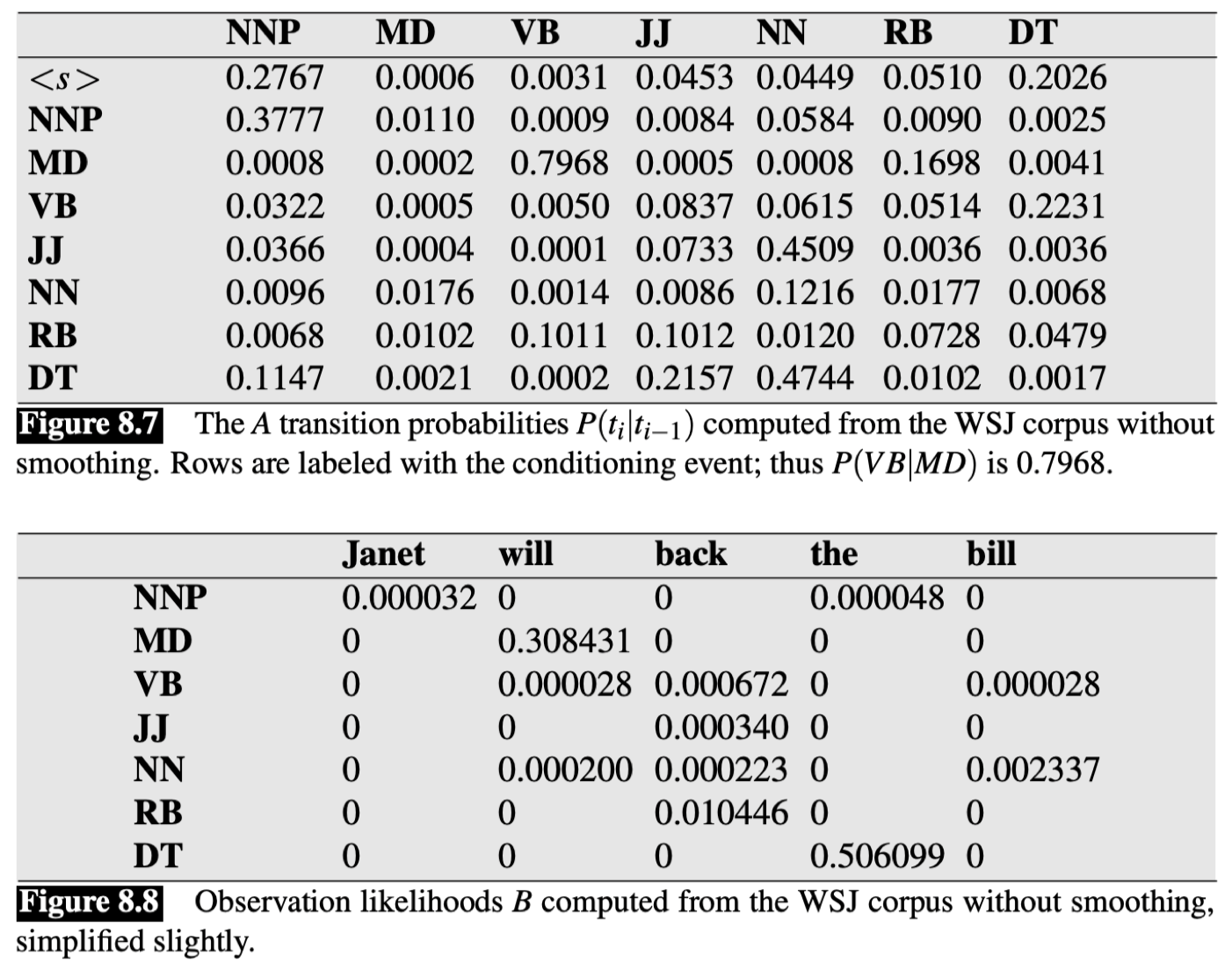
假如我们现在要预测句子 “$\textit{Janet will back the bill}$” 的 tags 序列。
我们先构建一个表,第一列代表所有可能的 tags 的集合,第一行代表句子中的每一个单词:
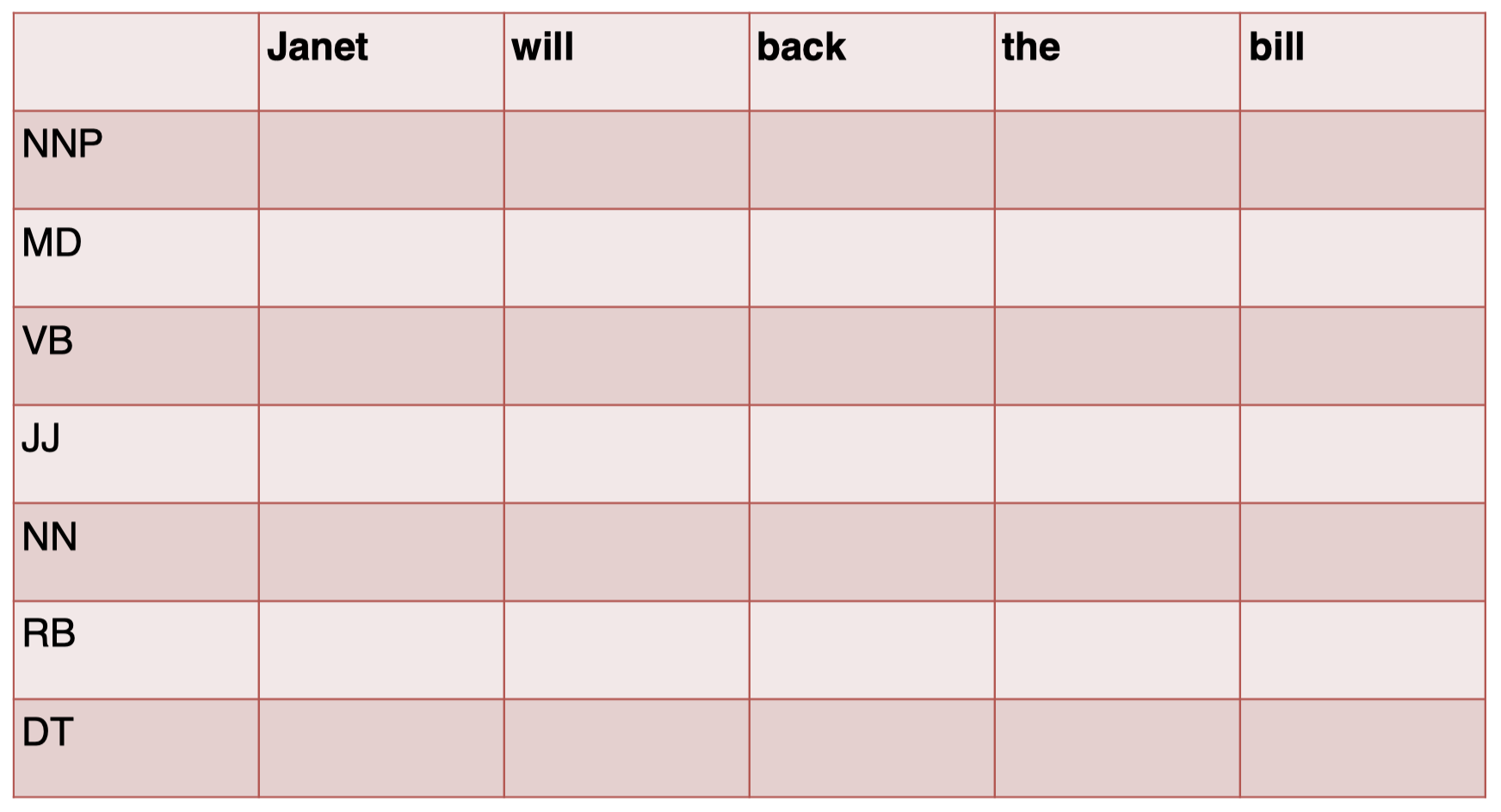
首先,我们对句子中的第一个单词 “$Janet$” 的 tag 进行预测:
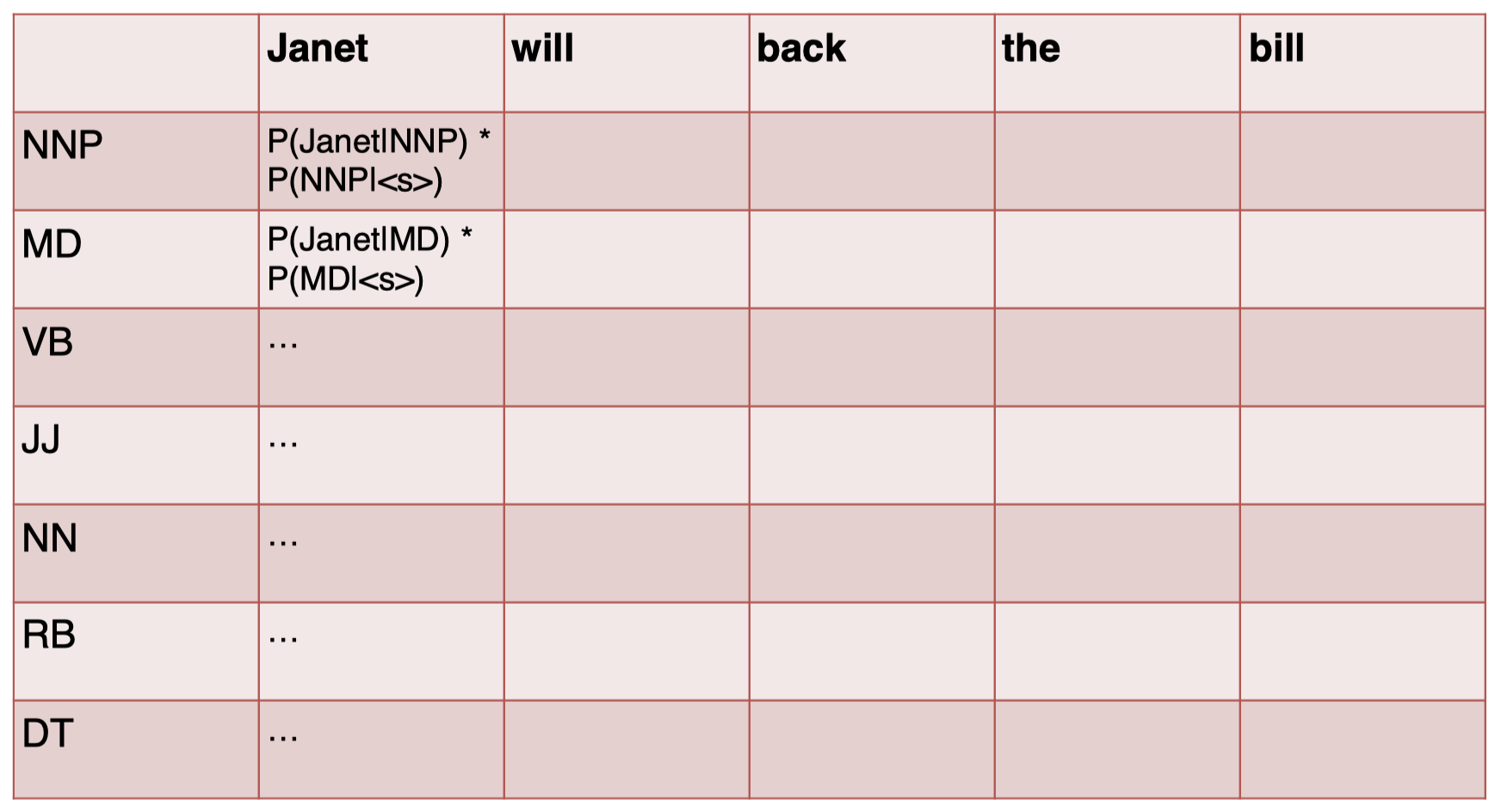
通过查看转移矩阵和发射矩阵的表格,进行计算,得到结果:
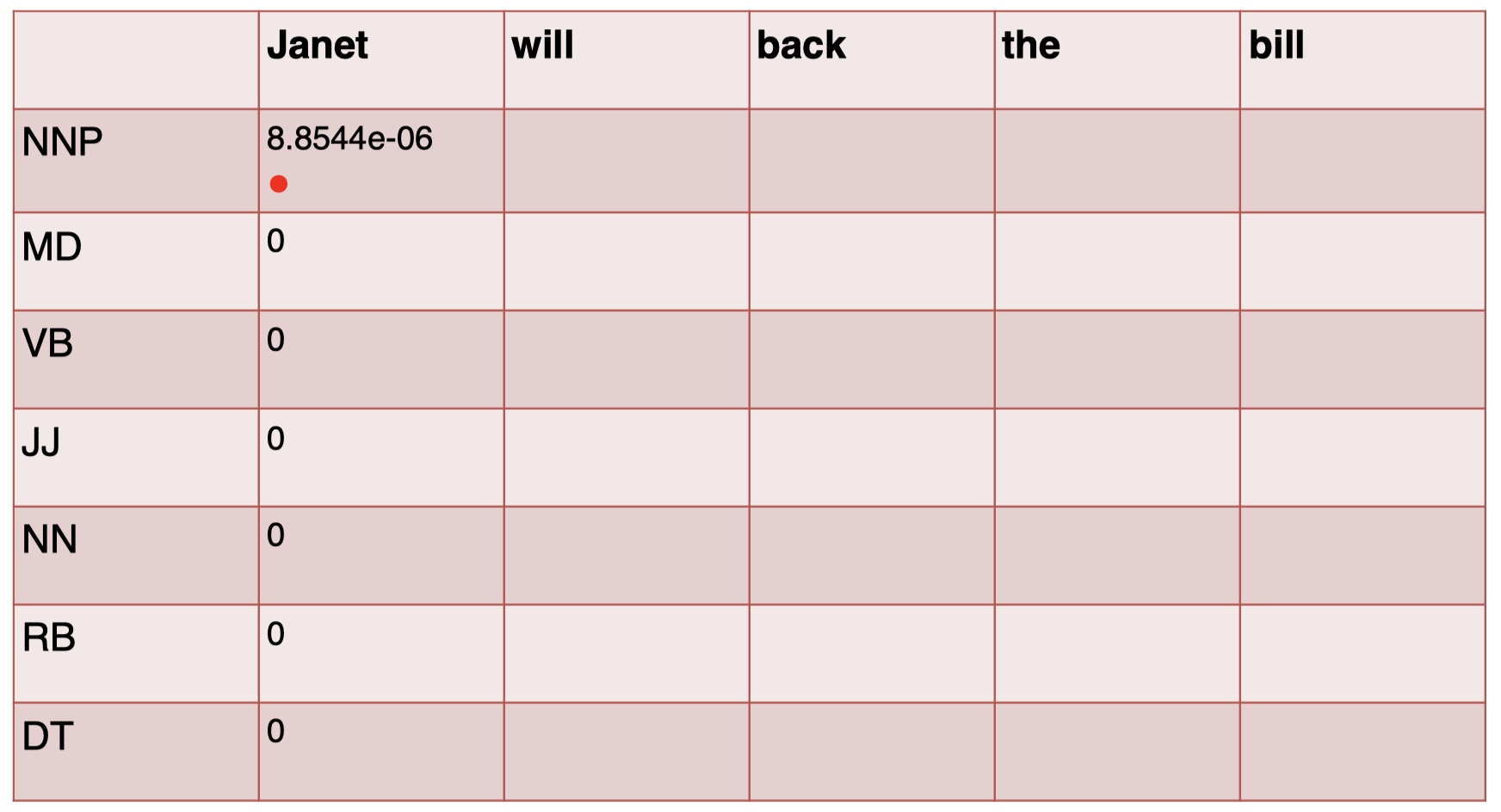
接下来,我们计算单词 “$\textit{will}$” 的 tag,注意,这里我们还乘以了一个得分项 $s(t_{\textit{Janet}}\mid \textit{Janet})$,它表示前一个单词 “$\textit{Janet}$” 对应的 tag 得分,也就是 “$\textit{Janet}$” 那一列中对应的 tag 行的结果,所以如果这里 $t_{\textit{Janet}}$ 为 NNP,那么该项等于 $8.8544\times 10^{-6}$,如果 $t_{\textit{Janet}}$ 为其他的 tag,该项为 $0$:
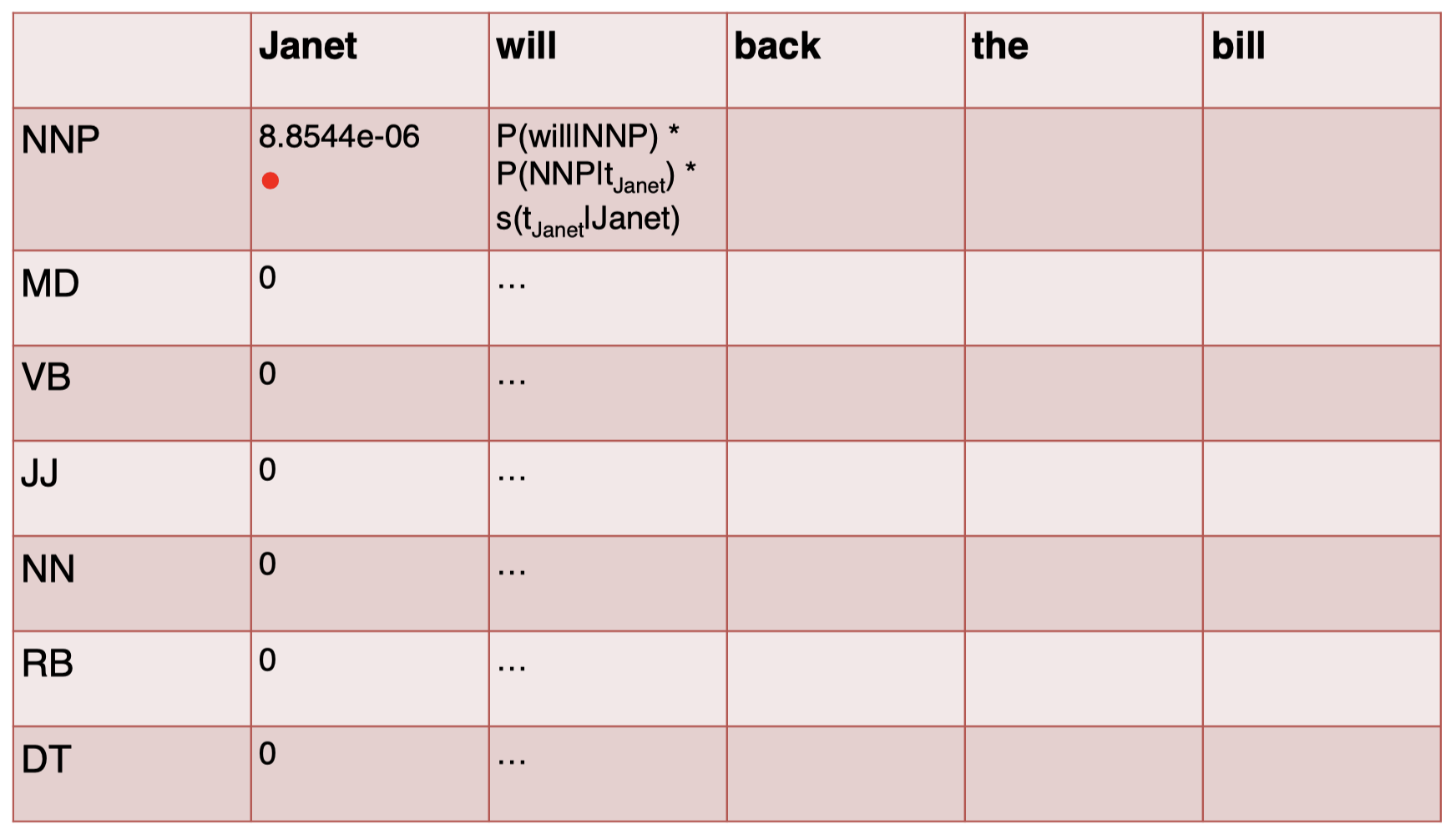
但是,$t_{\textit{Janet}}$ 在这里究竟是什么呢?我们不能简单地直接取得分最大的 tag,而是需要计算所有可能的 $t_{\textit{Janet}}$ 对应的 $P(\textit{will}\mid \text{NNP})\times P(\text{NNP}\mid t_{\textit{Janet}})\times s(t_{\textit{Janet}}\mid \textit{Janet})$ 的结果,并取其最大值作为单词 “$\textit{will}$” 在 NNP 上的得分 $s(\text{NNP}\mid \textit{will})$:

对于其余 tag 项按照相同方式进行计算,然后将单词 $\textit{will}$ 所有结果中的非零得分项连接到前一个单词 “$Janet$” 对应 tag 的得分项,得到下面的 3 条轨迹:
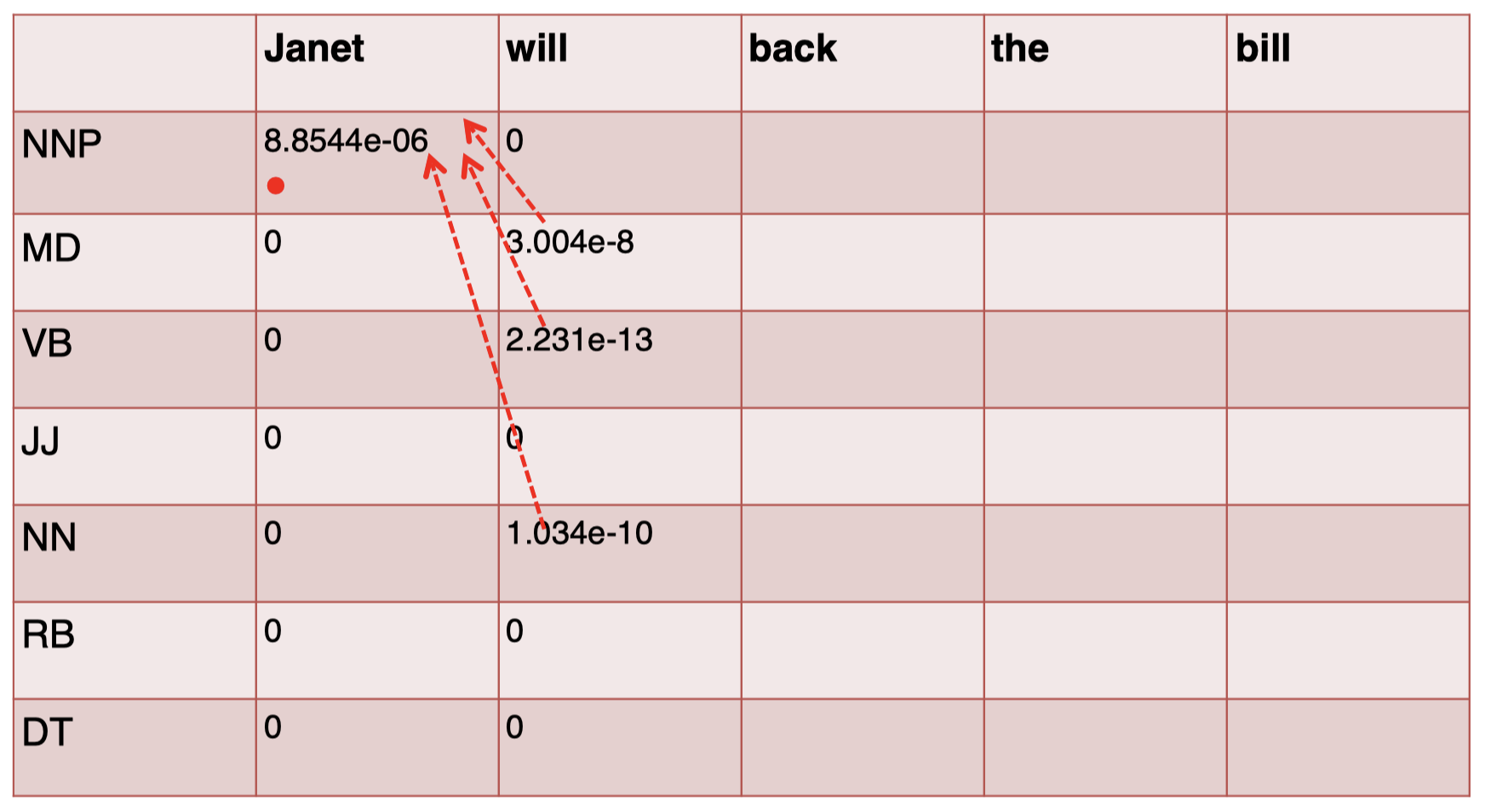
同理,对于第 3 个单词 “$\textit{back}$”,我们按照同样方式进行计算,注意,这里我们在实际计算时只需要考虑非零项即可。例如,对于 NNP 和 MD 我们无需计算,因为在发射矩阵中,单词 “$\textit{back}$” 对应的这两项为 $0$,而对于 VB,我们在计算时也只需考虑前一个单词 “$\textit{will}$” 为 MD、VB 和 NN 的 3 种情况,因为 “$\textit{will}$” 只有这 3 个 tag 的得分项是非零的,所以只需选择三者中最大值即可:
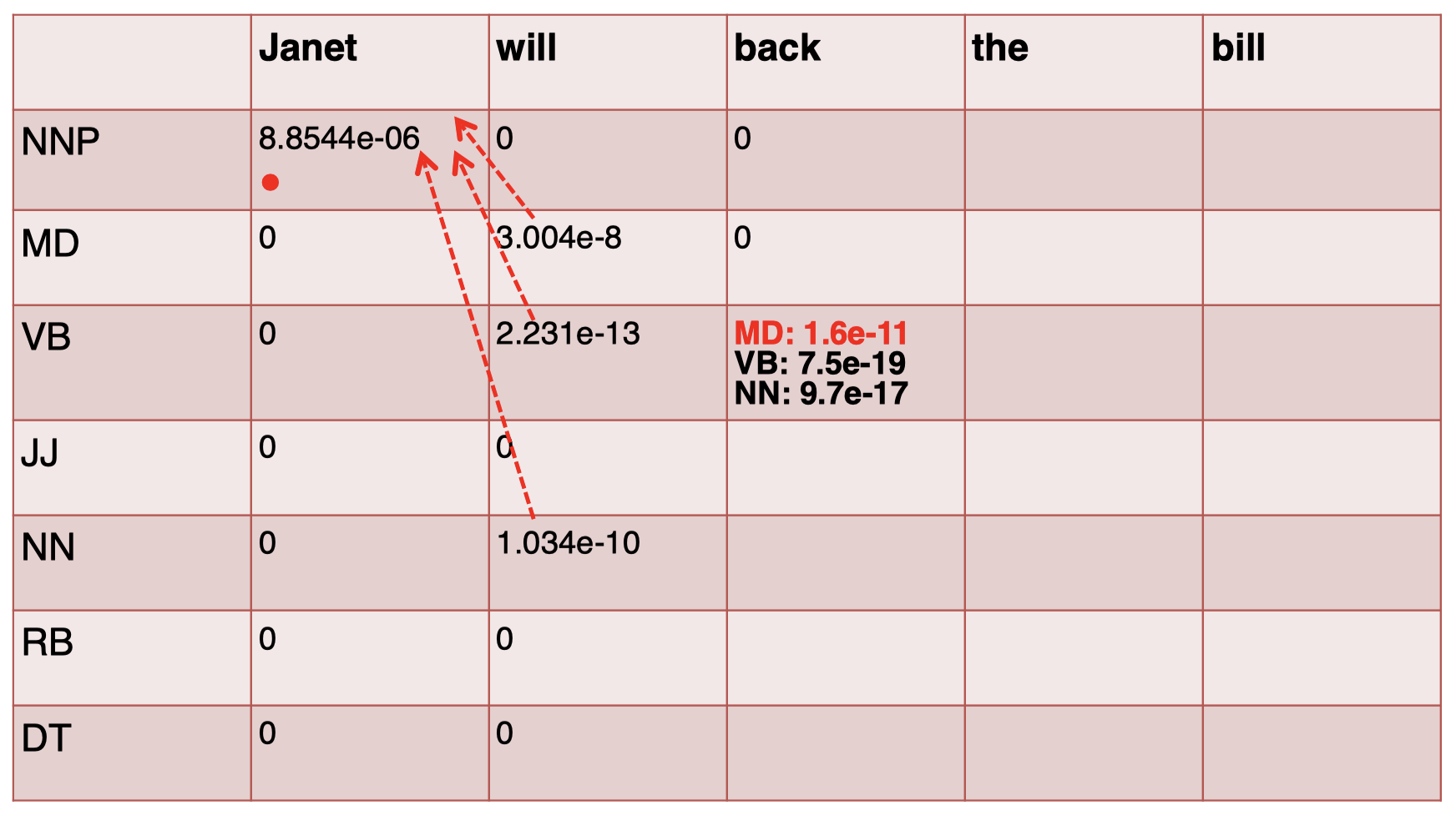
其余 tag 项也按照同样的方法进行计算,然后将结果轨迹进行连接:

同理,对于第 4 个单词 “$\textit{the}$”,我们有:
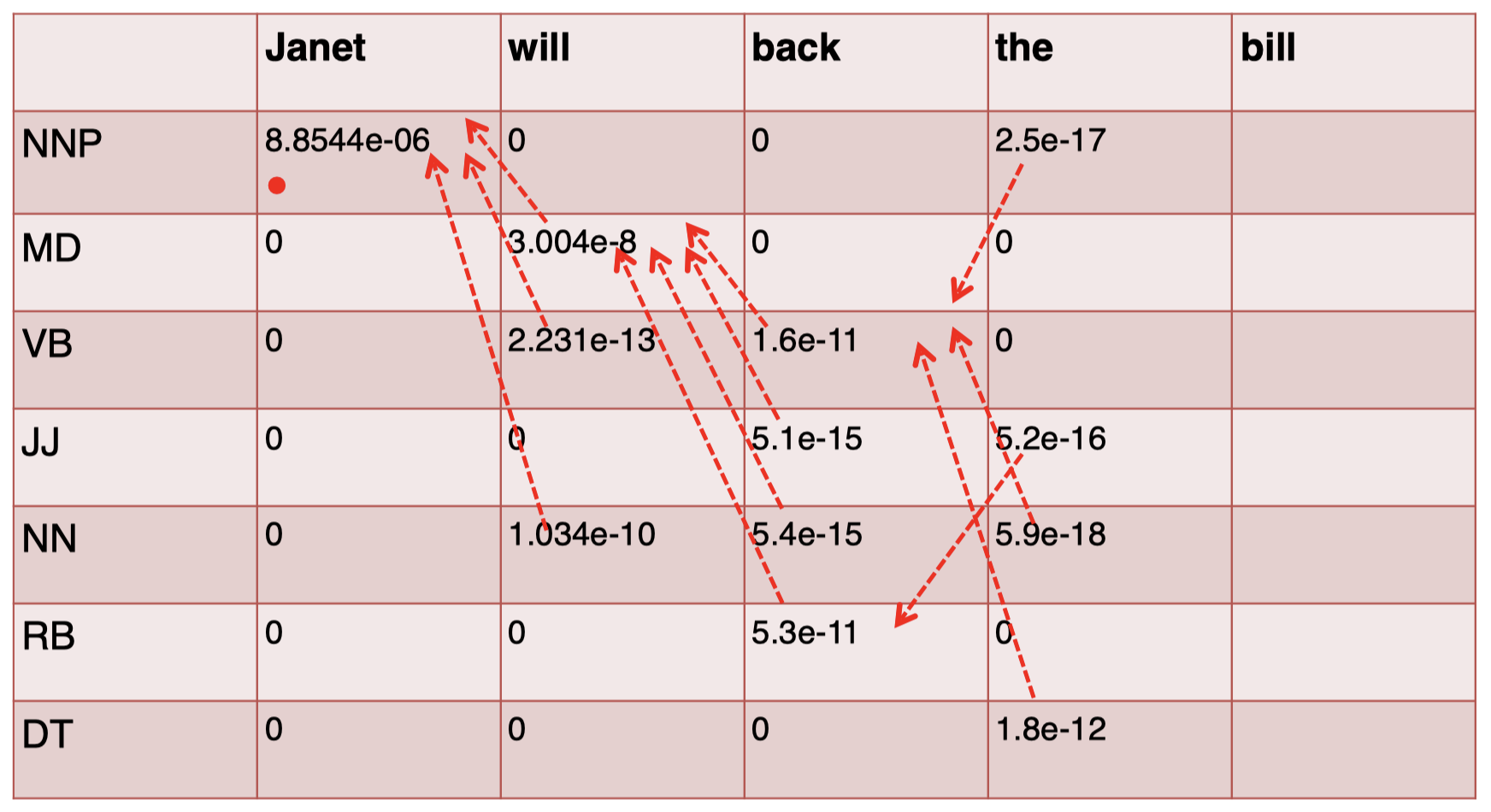
对于最后一个单词 “$\textit{bill}$”,我们有:
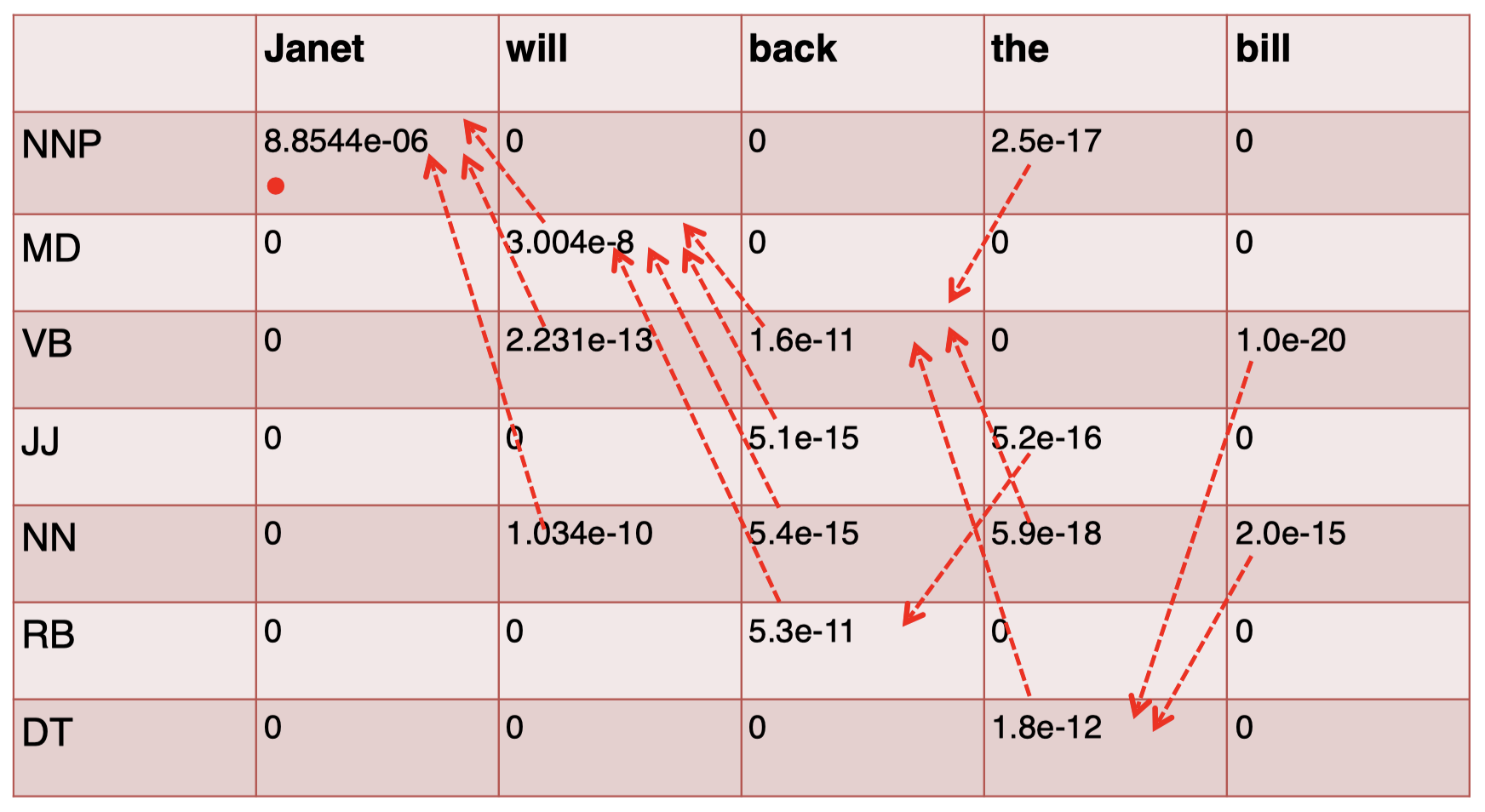
现在,我们计算出了整个矩阵,接下来只需要 按照轨迹回溯,为各单词选择相应的 tag 即可。我们 从最后一个单词 “$\textit{bill}$” 开始,选择其中 得分最高的 tag,即 NN,然后按照箭头轨迹回溯到前一个单词 “$\textit{the}$”,得到其对应的 tag,即 DT,以此类推,直到得到第一个单词的 tag:
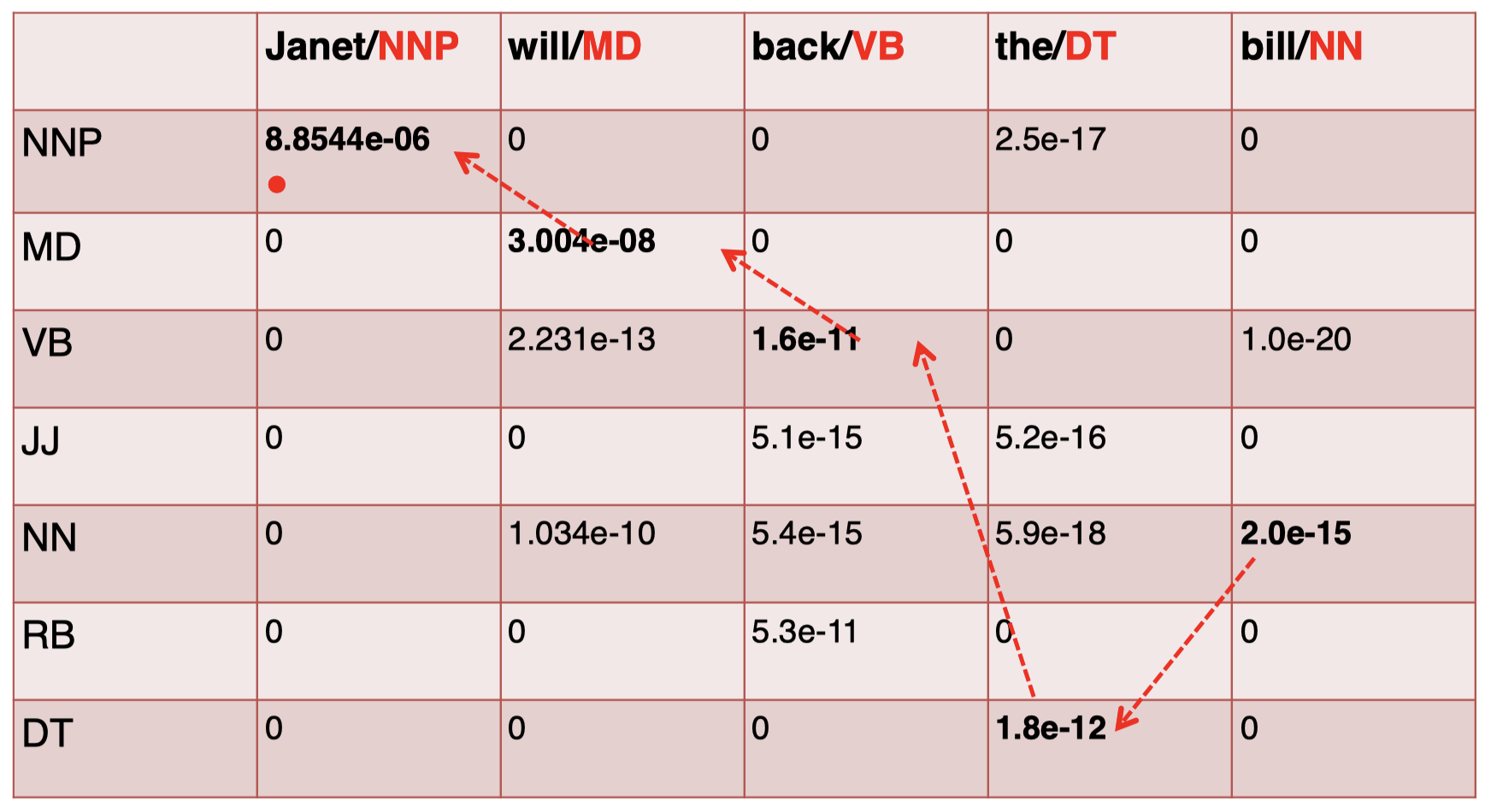
最终,我们得到的轨迹就是整个句子对应的概率最大的 tag 序列,即最优标签序列:
2.8 维特比算法的评估
-
维特比算法的时间复杂度是多少?
$O(T^2N)$,其中 $T$ 是 tagset 的大小(即所有可能 tag 类别的数量),$N$ 是单词序列的长度。
因为我们计算的是一个 $T\times N$ 的矩阵,而矩阵中的每个元素我们都进行 $T$ 次操作(因为我们要考虑前一个单词的所有可能的 tags)。 -
为什么维特比算法是可行的?
因为我们采用了 独立性假设:1. 每个单词的概率仅取决于其词性;2. 每个词性的概率仅取决于前一个词的词性。这使得我们可以对整个序列标注问题进行分解(具体来说,就是所谓的 马尔可夫性质)。如果没有这些假设,我们就无法应用动态规划求解最优序列标签。
2.9 维特比算法的伪代码
下面是维特比算法的伪代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
alpha = np.zeros(M, T)
for t in range(T):
alpha[1, t] = pi[t] * O[w[1], t]
for i in range(2, M):
for t_i in range(T):
for t_last in range(T): # t_last means t_{i-1}
s = alpha[i-1, t_last] * A[t_last, t_i] * O[w[i], t_i]
if s > alpha[i, t_i]:
alpha[i, t_i] = s
back[i, t_i] = t_last
best = np.max(alpha[M-1,:])
return backtrace(best, back)
- 在实践中,我们通常计算的是 log 概率以避免数值下溢(将乘积转换成累加),因为直接计算概率乘积可能会导致最后结果非常接近于 $0$。
- 另外,计算时我们可以采用 向量化(Vectorisation),即用 矩阵-向量 操作替代循环操作,这样可以在一定程度上实现行列级别的并行计算,从而使计算过程加速。
2.10 实践中的 HMM
-
我们已经介绍了基于 bigrams 的 HMM taggers,而目前实际应用最广的是基于 trigrams 的 HMM taggers。
\[P(\boldsymbol t)=\prod_{i=1}^{n}P(t_i\mid t_{i-1},t_{i-2})\]这种情况下,维特比算法的时间复杂度变为 $O(T^3N)$。
-
需要处理 稀疏性(sparsity)问题:某些 tag trigram 序列可能没有在训练数据中出现过。
\[P(t_i\mid t_{i-1},t_{i-2})=\lambda_3 \hat P(t_i\mid t_{i-1},t_{i-2})+\lambda_2 \hat P(t_i\mid t_{i-1})+\lambda_1 \hat P(t_i)\]
同之前 n-grams 模型的处理方法一样,我们可以结合 Backoff 和 Interpolation 方法进行处理:其中,$\lambda_1 + \lambda_2 + \lambda_3=1$。
-
结合其他特征,HMM 在 Penn Treebank 上可以达到 $96.5\%$ 的准确率。(Brants, 2000)
在上节课中,我们提到过 unigram tagger 可以达到大约 $90\%$ 的准确率,这里我们可以看到,通过构建更加复杂的模型,我们将准确率提升了近 $7\%$。
2.11 HMM 的其他变体 Taggers
-
HMM 是 生成式(generative)模型。
\[\begin{align} \hat T&=\mathop{\operatorname{arg\,max}}\limits_{T}P(T\mid W)\\ &=\mathop{\operatorname{arg\,max}}\limits_{T}P(W\mid T)P(T)\\ &=\mathop{\operatorname{arg\,max}}\limits_{T}\prod_{i}P(word_i\mid tag_i)\prod_{i}P(tag_i\mid tag_{i-1}) \end{align}\]为什么是生成式?
回到 HMM 最初的公式,我们希望根据给定的单词序列 $W$ 找到最优的标签序列 $T$。然后,我们利用贝叶斯定理逆转条件,对原问题进行分解,使得模型学习一些发射概率和转移概率。HMM 是生成式的意味着一旦我们完成了 HMM 的训练,我们可以让模型生成一些单词序列和相应的标签序列。具体来说,我们可以让模型先生成一个标签序列(因为我们已经有了转移矩阵,所以可以逐一生成 tag,从而生成一个 tag 序列),然后对于序列中的每一个 tag,我们可以随机抽样一个对应的单词。所以,HMM 模型是生成式的,因为只要我们愿意,我们可以在训练完成后以这种方式生成更多的输入。假设现在有一个语料库,我们可以利用训练好的 HMM 对语料库进行扩充(尽管这些新的生成数据可能不完美或者存在一些噪音)。 -
我们还可以训练无监督的 HMM:即模型在学习过程中不需要任何标注过的数据。
这种情况下,我们的训练数据中没有标注词性,我们只是让模型试图发现可能的标签序列。我们不会在这里展开讨论,大致来说,我们可以假设一些贝叶斯先验,然后随机分配 tag,然后缓慢地进行迭代以找到最佳 tag 序列。 -
另外一种是 判别式(Discriminative) 模型
\[\begin{align} \hat T&=\mathop{\operatorname{arg\,max}}\limits_{T}P(T\mid W)\\ &=\mathop{\operatorname{arg\,max}}\limits_{T}\prod_{i}P(t_i\mid w_i,t_{i-1}) \end{align}\]相比之前生成式 HMM 中利用贝叶斯定理逆转条件概率,这里我们只是利用给定的单词序列寻找最有可能的标签序列。因此,我们可以增加更多的特征,我们现在不止关注单词 $w_i$,我们还关注前一个单词的词性 $t_{i-1}$,实际上,我们还可以在条件项中增加更多的特征,这样我们会得到一个判别式模型,因为这类模型直接描述了在给定观测事件的条件下,未观测事件的概率。此外,判别式模型无法生成新的输入,因为它们能做的仅仅是在给定单词序列的情况下,给出相应的标签序列。判别式模型并不能自己生成序列,所以它们只能用于判别任务,而无法用于生成任务。但是,判别式模型的准确率通常要高于生成式模型,部分原因是判别式模型很容易增加特征:例如我们现在的特征为 $w_i$ 和 $t_{i-1}$,假设我们希望增加更多的特征,只需要将其加入条件项中即可。但是对于生成式模型,我们不能通过这种简单的方式完成,因为生成式模型中我们的条件项包含未观测事件,所以不能简单地将观测特征直接加入其中。
-
判别式模型直接描述条件概率 $P(t\mid w)$
- 支持更丰富的特征集,通常在大型有监督数据集上训练得到的准确率要高于生成式模型。
- 判别式 HMM 变体的例子:
最大熵马尔可夫模型(Maximum Entropy Markov Model,MEMM)
条件随机场(Conditional random field,CRF)
联结主义时间分类(Connectionist Temporal Classification,CTC) - 大部分 深度学习 的序列模型都属于判别式模型(例如:用于翻译任务的编码-解码器),类似于 MEMM。
- 如今我们使用的大部分模型都属于判别式模型,因为其表现更好,但是生成式模型也有其特定的应用场景,例如文本生成任务。
2.12 HMM 在 NLP 任务中的表现
我们可以看一下 HMM 的不同变体在 NLP 任务中的表现。
- HMM 在词性标注(part-of-speech tagging)任务中非常高效。
- Trigram HMM 可以达到 $96.5\%$ 的准确率(TnT)
- 相关的模型也都有着目前几乎最佳的表现:
- MEMMs:$97\%$
- CRFs:$97.6\%$
- Deep CRF:$97.9\%$
- 更多最新的 Englisn Penn Treebank tagging accuracy 相关信息可以参考:
https://aclweb.org/aclwiki/index.php?title=POS_Tagging_(State_of_the_art)
- 此外,除了词性标注,HMM 还可以应用于其他序列标注任务。
- 命名实体识别(named entity recognition)、浅层解析(shallow parsing)、对齐(alignment)等等。
- 其他领域:DNA、蛋白质序列、晶格图像等等。
3. 总结
- 对于序列标注任务,HMM 是一种简单高效的方法。
- 非常有竞争力,并且训练过程很快(利用维特比译码算法),可以作为其他序列标注任务的 natural baseline。
- 主要缺点:与 MEMMs 和 CRFs 这类判别式模型相比,HMM 在特征表示方面不是非常灵活。
4. 扩展阅读
- JM3 Appendix A A.1-A.2, A.4
- See also E18 Chapter 7.3
- 参考资料:
- Rabiner’s HMM tutorial: http://tinyurl.com/2hqaf8
- Lafferty et al, Conditional random fields: Probabilistic models for segmenting and labeling sequence data (2001)
下节内容:NLP 深度学习:前馈网络
本作品采用知识共享署名-非商业性使用-相同方式共享 4.0 国际许可协议进行许可。 欢迎转载,并请注明来自:YEY 的博客 同时保持文章内容的完整和以上声明信息!