Lecture 05 生成启发函数
现在,我们来看一下如何生成启发函数。主要内容如下:
- 动机
- 非正式松弛
- 正式松弛
- 在搜索时松弛
- 结论
1. 动机
想象一下,你已经毕业了,并且入职了一家商业软件开发公司。
老板:这里有一个问题需要解决。
你(想):嗯,我觉得启发式搜索可能会有用。
你(想):嗯,我需要一个启发函数,问题是 怎么得到呢?
想象一下,你是一个规划系统。
某人:嘿,这是 PDDL 输入,请解决它。
你(想):嗯,我唯一知道的方法就是启发式搜索。
你(想):嗯,我需要一个启发函数。
你:问题是 怎么得到呢?
因此,我们希望能够提出一种自动生成启发函数的方法,可以适用于所有的规划问题,而不是针对某个特定问题的启发进行硬编码。
“松弛”(Relaxation)是一种构造启发函数的方法。
- 在为需要解决的问题编写解决方案时,可以使用它。
- 规划系统可以使用它从规划任务描述(PDDL 输入)自动生成启发函数。
- 注意 1:如果用户必须手动提供启发函数,那么我们将失去两个主要优点(通用性、自治性、灵活性和快速原型设计,请参阅 $\to$ Lecture 1-2)。
- 注意 2:当然可以使用户有 可能(方便地)提供其他启发函数。(本课程未涵盖)
2. 非正式松弛
2.1 如何非正式松弛
如何松弛:
- 我们有一个问题 $\mathcal P$,我们希望估计它的完美启发 $h^*$。
- 我们定义了一个 更简单的问题 $\mathcal P’$,它的完美启发 $h’^*$ 可以用来 估计 $h^*$。
- 我们定义了一个转换 $r$,可以将 $\mathcal P$ 中的实例 简化为 $\mathcal P’$ 的实例。
- 给定实例 $\Pi \in \mathcal P$,我们用 $h’^*(r(\Pi))$ 来估计 $h^*(\Pi)$。
$\to$ 松弛意味着简化问题,并将对较简单问题的解决方案作为对实际问题的解决方案的启发式估计。
2.2 例子:寻路问题中的松弛
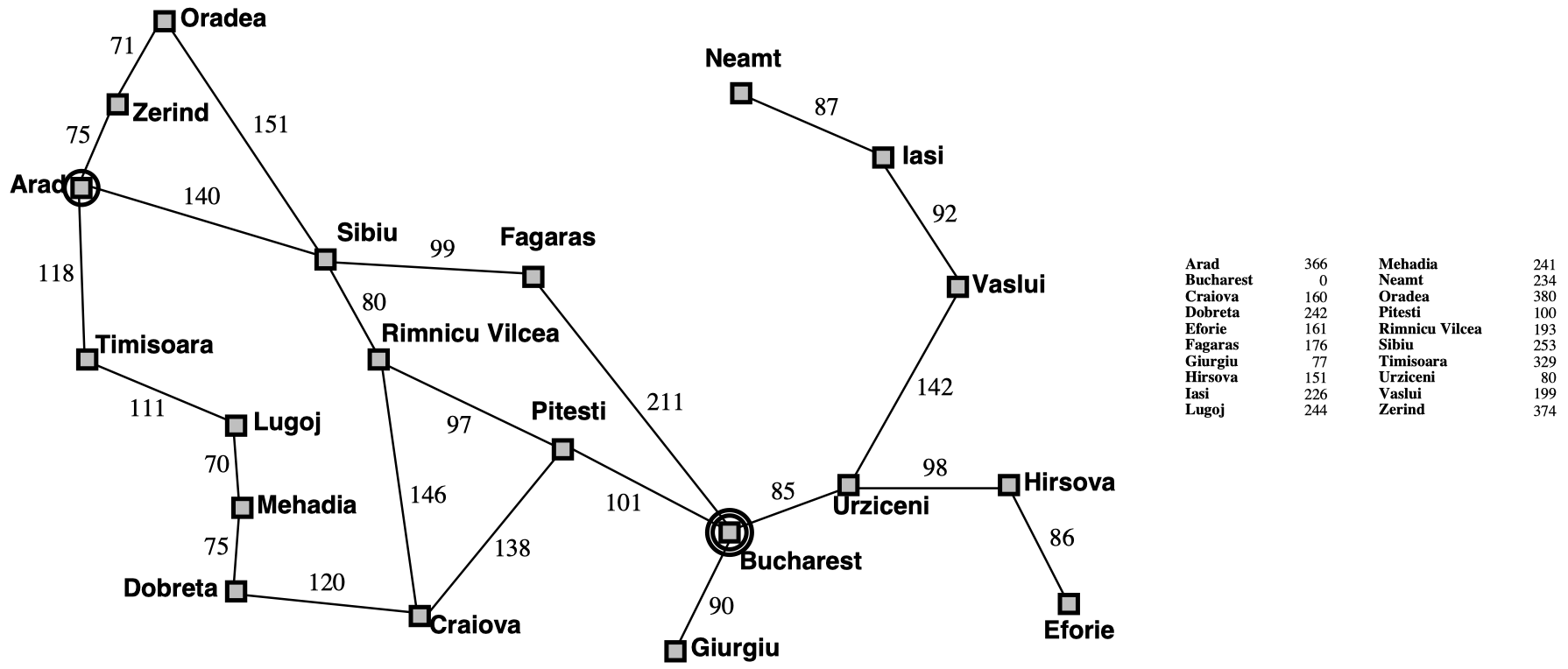
如果我希望找到一条从一个点到另一个点的路径,这可能是一个相当复杂的问题,具体取决于不同的点之间有多少条链接。该原始问题的简化问题可以是:寻找一条从一个点到另一个点的欧几里得距离,或者说,一只鸟从起点 飞到终点的路径。
如何通过松弛推导出直线距离?
- 问题 $\mathcal P$:寻找路径。
- 简化问题 $\mathcal P’$:为一只鸟寻找路径。
- $\mathcal P’$ 的完美启发 $h’^*$:直线距离。
- 转换 $r$:假装你是一只鸟。
2.3 例子:八数码问题中的松弛
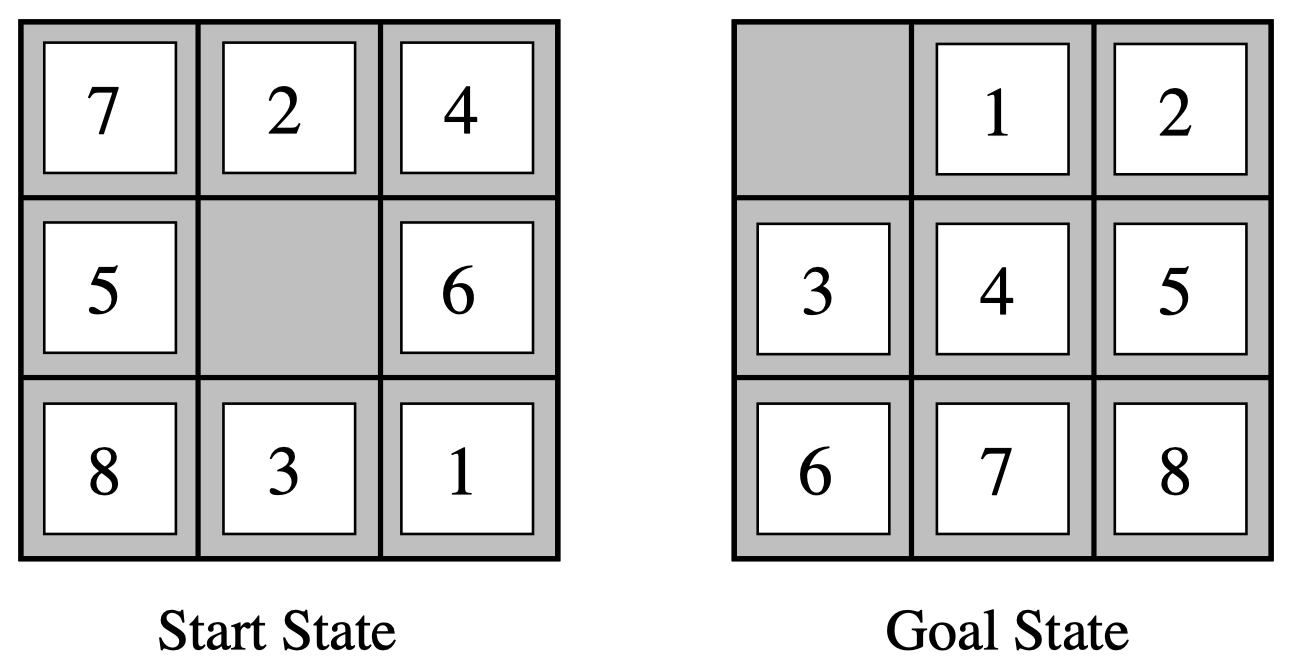
$\mathcal P$ 的完美启发 $h^*$:行动(Actions)$=$ “一个码块可以从 A 方槽移动到 B 方槽,如果 A和 B 是邻接的,并且 B 是空的。”
-
如何推导出曼哈顿距离启发(Manhattan distance heuristic)?
$\mathcal P’$:行动(Actions)$=$ “一个码块可以从 A 方槽移动到 B 方槽,如果 A和 B 是邻接的。”我们可以将问题简化为:只要两个方槽邻接即可移动码块,而不必考虑目标方槽是否为空。基于这样的假设,我们可以得到曼哈顿距离启发。例如:上图中,码块 1 从初始状态中的位置移动到目标状态中的位置,其曼哈顿启发为 3(即向上移动 2 格,再向左移动 1 格)。
-
如何推导出错位码块启发(misplaced tiles heuristic)?
$\mathcal P’$:行动(Actions)$=$ “一个码块可以从 A 方槽移动到 B 方槽。”一种更简单的考虑是:码块可以从一个方槽移动到其他任意一个方槽。即码块 1 可以从初始状态中的位置直接 1 步移到目标状态中的位置。
- 两种方法中的 $h’^*$(对应于 $r$):$\mathcal P’$ 中的最优代价(对应于采取不同的行动)。
- 这里:曼哈顿距离 $=18$,错位码块 $=8$。
2.4 例子:目标计数问题中的松弛
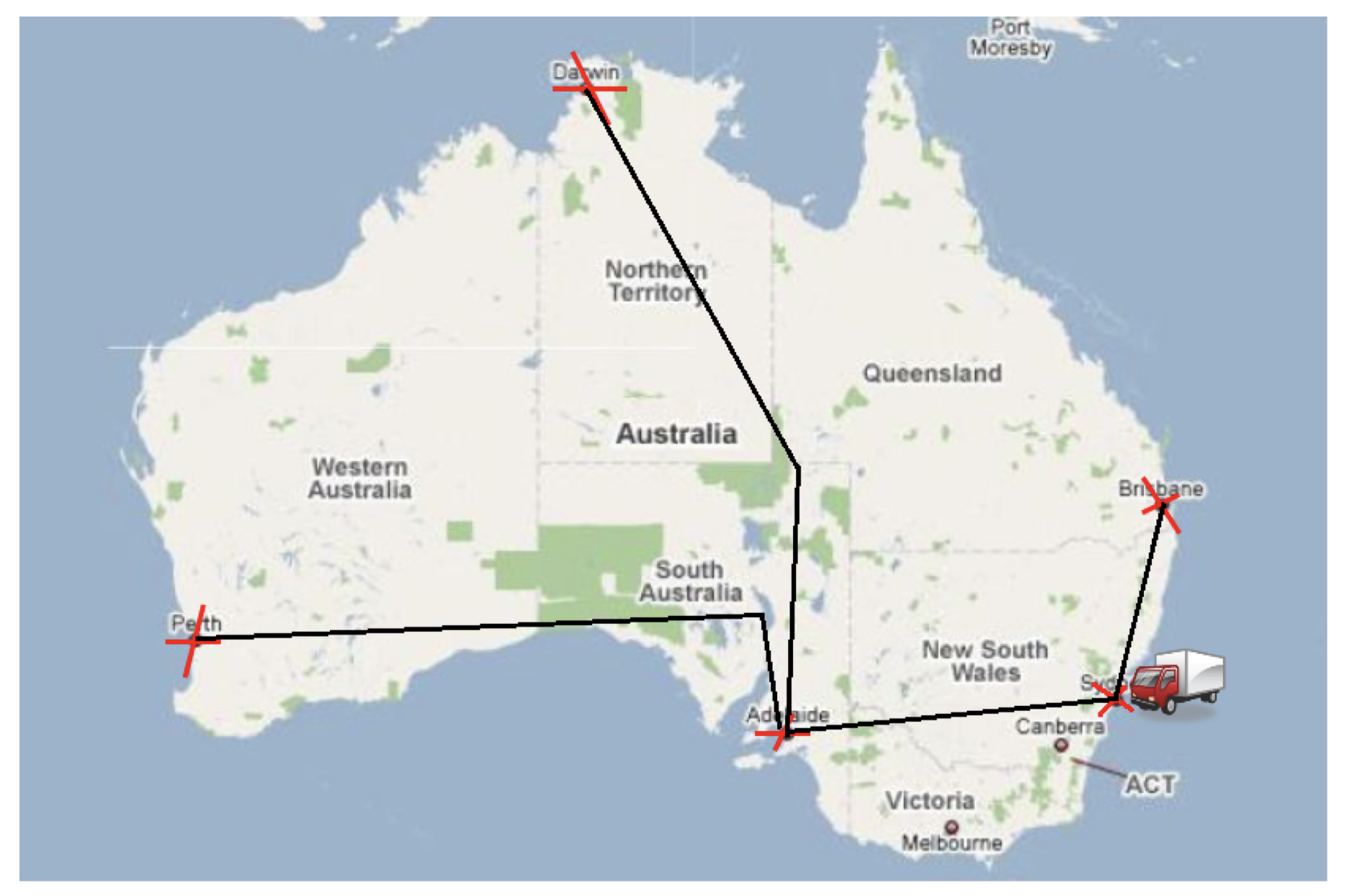
一共 5 个城市:悉尼(Sydney, Sy)、阿德莱德(Adelaide, Ad)、布里斯班(Brisbane, Br)、珀斯(Perth, Pe)、达尔文(Darwin, Da)。一辆卡车从悉尼出发,途径所有城市,最后返回悉尼。
- 命题(Propositions)$P$:$at(x)$ 表示所在城市,$v(x)$ 表示已访问过的城市,其中,\(x\in \{Sy, Ad, Br, Pe, Da\}\)。
- 行动(Actions)$a\in A$:$drive(x,y)$ 表示从城市 $x$ 前往城市 $y$,其中,$x$ 和 $y$ 之间存在道路;前置条件 \(pre_a=\{at(x)\}\),添加列表 \(add_a=\{at(y),v(y)\}\),删除列表 \(del_a=\{at(x)\}\)。
- 初始状态(Initial state)$I$:$at(Sy),v(Sy)$。
- 目标状态(Goal state)$G$:$at(Sy)$,$v(x)$ 对于所有的 $x$。
下里是一种可以采用的松弛,考虑我们还需要到达的目标数量,假设我们可以直接到达每个城市:
- 问题 $\mathcal P$:所有的 STRIPS 规划问题。
- 简化问题 $\mathcal P’$:所有的 STRIPS 规划问题,其中,前置条件和删除列表都是空集。
- $\mathcal P’$ 的完美启发 $h’^$</span>:最优规划代价($=h^$)。
- 转换 $r$:移除前置条件和删除列表。
- 这里的启发值是多少?$4$(因为我们在初始状态时已经到达了悉尼)。
$\to$ 前置条件和删除列表为空集的最优 STRIPS 规划仍然是一个 NP-困难 问题。(通过添加列表设定的目标,从 MINIMUM COVER 中减少。)
$\to$ 需要 近似 $\mathcal P’$ 的完美启发 $h’^*$。因此,目标计数(goal counting):用尚未访问的目标数近似估计 $h’^*$。
3. 正式松弛
3.1 如何正式松弛:在我们开始之前
- 在下一小节 3.2 中给出的定义不存在于任何课本或者论文中。
- 生成启发函数的方法各不相同,很难(或者说几乎不可能)仅通过一个定义就能(自然地)捕获所有的启发函数。
- 但是,一个正式的定义对于准确说明实际问题中的相关区分线是有用的。
- 目前的定义在这方面做得很好。
$\to$ 它很适合规划中当前使用的内容。
$\to$ 它在区分线中很灵活,它抓住了所有松弛思想的基本构造和本质。
3.2 松弛
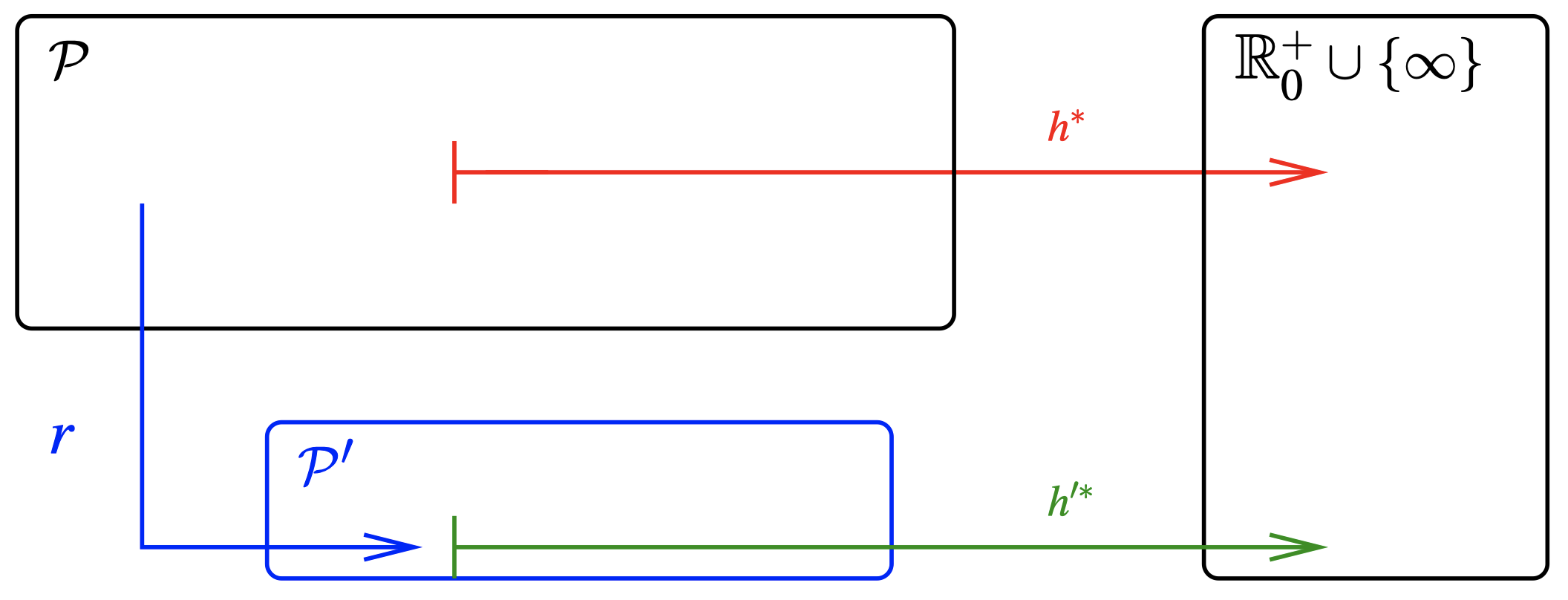
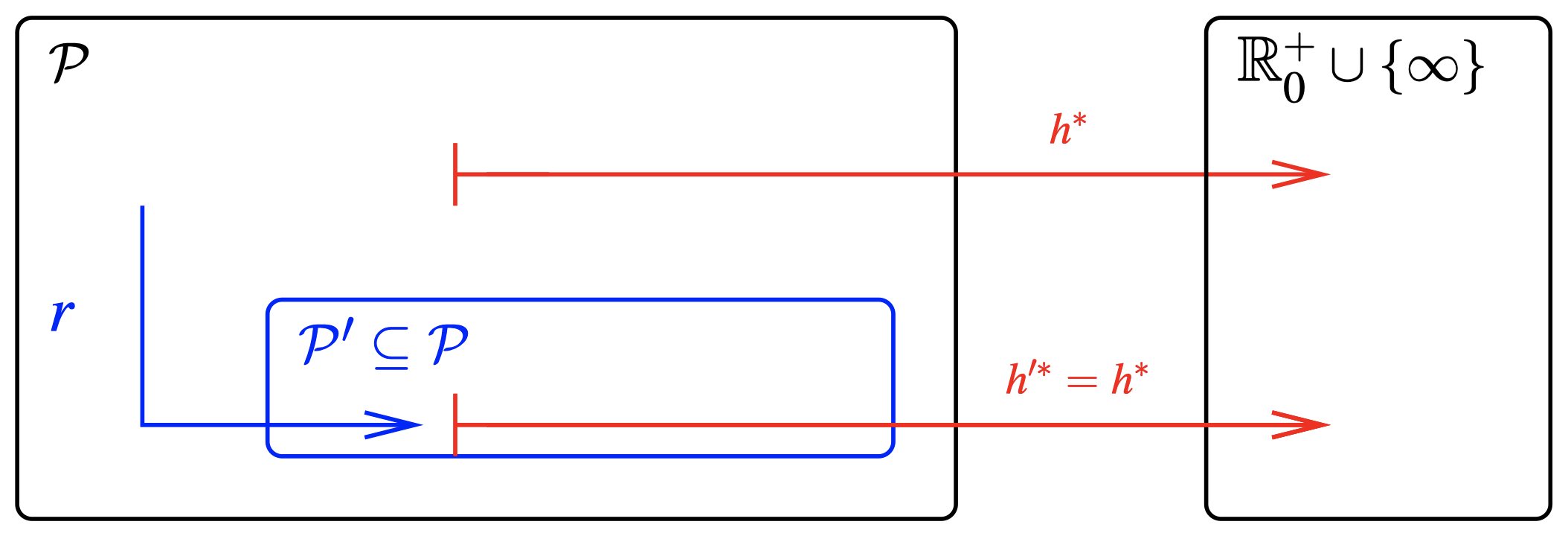
定义(松弛 Relaxation)
令 \(h^*: \mathcal P \to \mathbb R_0^+ \cup \{\infty\}\) 为一个函数。一个 $h^*$ 的 松弛 是一个三元组 $\mathcal R=(\mathcal P’,r,h’^*)$,其中,$\mathcal P’$ 是一个任意集合,并且 $r:\mathcal P \to \mathcal P’$ 和 \(h'^* : \mathcal P' \to \mathbb R_0^+ \cup \{\infty\}\) 都是函数,使得对于所有的 $\Pi \in \mathcal P$,松弛启发 \(h^{\mathcal R}(\Pi):= h'^*(r(\Pi))\) 满足 \(h^{\mathcal R}(\Pi)\le h^*(\Pi)\)。松弛为:
- 自然的(native):如果 \(\mathcal P' \subseteq \mathcal P\) 并且 \(h'^*=h^*\)。
- 有效构造(efficiently constructible):如果存在一个多项式时间算法,在给定 $\Pi \in \mathcal P$ 的情况下计算 $r(\Pi)$。
- 有效计算(efficiently computable):如果存在一个多项式时间算法,在给定 $\Pi’ \in \mathcal P’$ 的情况下计算 $h’^*(\Pi’)$。
提示:
- 我们有一个问题 $\mathcal P$,我们希望估计它的完美启发 $h^*$。
- 我们定义了一个更简单的问题 $\mathcal P’$,它的完美启发 $h’^$ 可以用来 (可采纳地) 估计 $h^$。
- 我们定义了一个转换 $r$,从 $\mathcal P$ 到 $\mathcal P’$。
- 给定 $\Pi \in \mathcal P$,我们用 $h’^*(r(\Pi))$ 来估计 $h^*(\Pi)$。
3.3 松弛(Relaxations):说明
寻找路径的例子:
- 问题 $\mathcal P$:寻找路径。
- 简化问题 $\mathcal P’$:为一只鸟寻找路径。
- $\mathcal P’$ 的完美启发 $h’^*$:直线距离。
- 转换 $r$:假装你是一只鸟。
3.4 自然松弛(Native Relaxations):说明
目标计数的例子:
- 问题 $\mathcal P$:所有的 STRIPS 规划问题。
- 简化问题 $\mathcal P’$:所有的 STRIPS 规划问题,其中,前置条件和删除列表都是空集。
- $\mathcal P’$ 的完美启发 $h’^*$:最优规划代价($=h^*$)。
- 转换 $r$:移除前置条件和删除列表。
3.5 寻路问题中的松弛:性质

松弛 $\mathcal R=(\mathcal P’,r,h^{‘*})$:假装你是一只鸟。
- 是自然的(native)吗?
不是,鸟不会寻路(这相当于琐碎的地图,到处都有直接的路线。) - 是有效构造(efficiently constructible)吗?
是的(假装你是鸟)。 - 是有效计算(efficiently computable)吗?
是的(测量直线距离)。
3.6 八数码问题中的松弛

松弛 \(\mathcal R=(\mathcal P',r,h'^{*})\):使用更宽泛的动作规则来获取曼哈顿距离。
- 是自然的(native)吗?
不是,由于对规则进行了修改,这不再是 “相同的智力游戏”。(在定义 “相同的智力游戏” 时可以宽泛一点。) - 是有效构造(efficiently constructible)吗?
是的(设置了交换操作)。 - 是有效计算(efficiently computable)吗?
是的(计算错位的码块/总计曼哈顿距离)。
3.7 我们应当如何松弛?
- 如果松弛 $\mathcal R$ 不是有效构造(efficiently constructible)会怎样?
- (a) 近似 $r$ 或者 (b) 以某种方式设计 $r$ 使得其通常是可行的,或者 (c) 干脆不管它,寄希望于运气。
- 绝大多数已知的松弛(在规划中)都是有效构造的。
- 如果松弛 $\mathcal R$ 不是有效计算(efficiently computable)会怎样?
- (a) 近似 $h’^{*}$ 或者 (b) 以某种方式设计 $h’^{*}$ 使得其通常是可行的,或者 (c) 干脆不管它,寄希望于运气。
- 绝大多数已知的松弛(在规划中)都是有效计算的,但有些不是。对于后者,我们采用方法 (a);方法 (b) 和 (c) 在这里不适用。
3.8 目标计数问题中的松弛:性质

- 命题(Propositions)$P$:$at(x)$ 表示所在城市,$v(x)$ 表示已访问过的城市,其中,\(x\in \{Sy, Ad, Br, Pe, Da\}\)。
- 行动(Actions)$a\in A$:$drive(x,y)$ 表示从城市 $x$ 前往城市 $y$,其中,$x$ 和 $y$ 之间存在道路;前置条件 \(pre_a=\{at(x)\}\),添加列表 \(add_a=\{at(y),v(y)\}\),删除列表 \(del_a=\{at(x)\}\)。
- 初始状态(Initial state)$I$:$at(Sy),v(Sy)$。
- 目标状态(Goal state)$G$:$at(Sy)$,$v(x)$ 对于所有的 $x$。
松弛 $\mathcal R=(\mathcal P’,r,h^{‘*})$:移除前置条件和删除列表,然后使用 $h^{*}$。
- 是自然的(native)吗?
是的,带有空的前置条件和删除列表的规划是原规划的一个特例(即 $\mathcal P$ 的一个子类)。 - 是有效构造(efficiently constructible)吗?
是的(移除前置条件和删除列表)。 - 是有效计算(efficiently computable)吗?
不是,这种情况下,最优规划仍然是一个 NP-困难 问题(基于添加列表的目标集合的 最小覆盖 问题)。
我们应该怎样采取松弛?
$\to$ 使用 方法 (a):通过计算当前不正确的目标数,来近似问题 $P’$ 中的 $h^*$。
4. 在搜索期间松弛
4.1 如何在搜索期间松弛:示意图
在搜索期间使用松弛 $\mathcal R=(\mathcal P’,r,h^{‘*})$
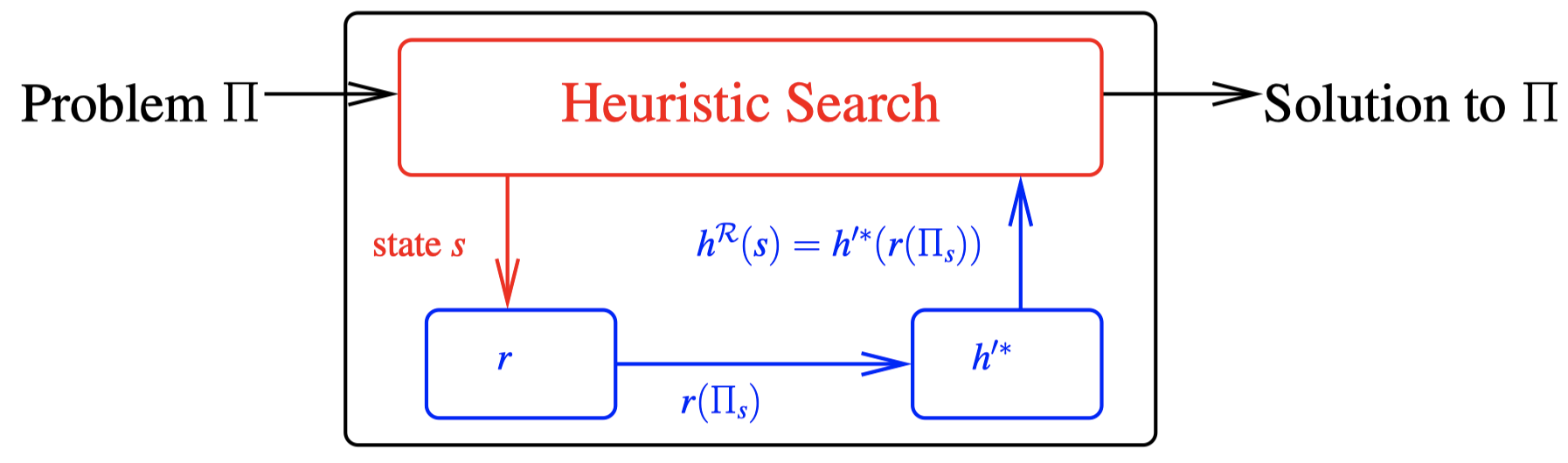
$\to$ $\Pi_s$:$\Pi$ 由初始状态被替换为状态 $s$,即 $\Pi=(F,A,c,I,G)$ 变为 $(F,A,c,s,G)$。
$\to$ 任务是为搜索状态 $s$ 寻找规划。
$\to$ 在本课程中,我们将采用这种表示方式。
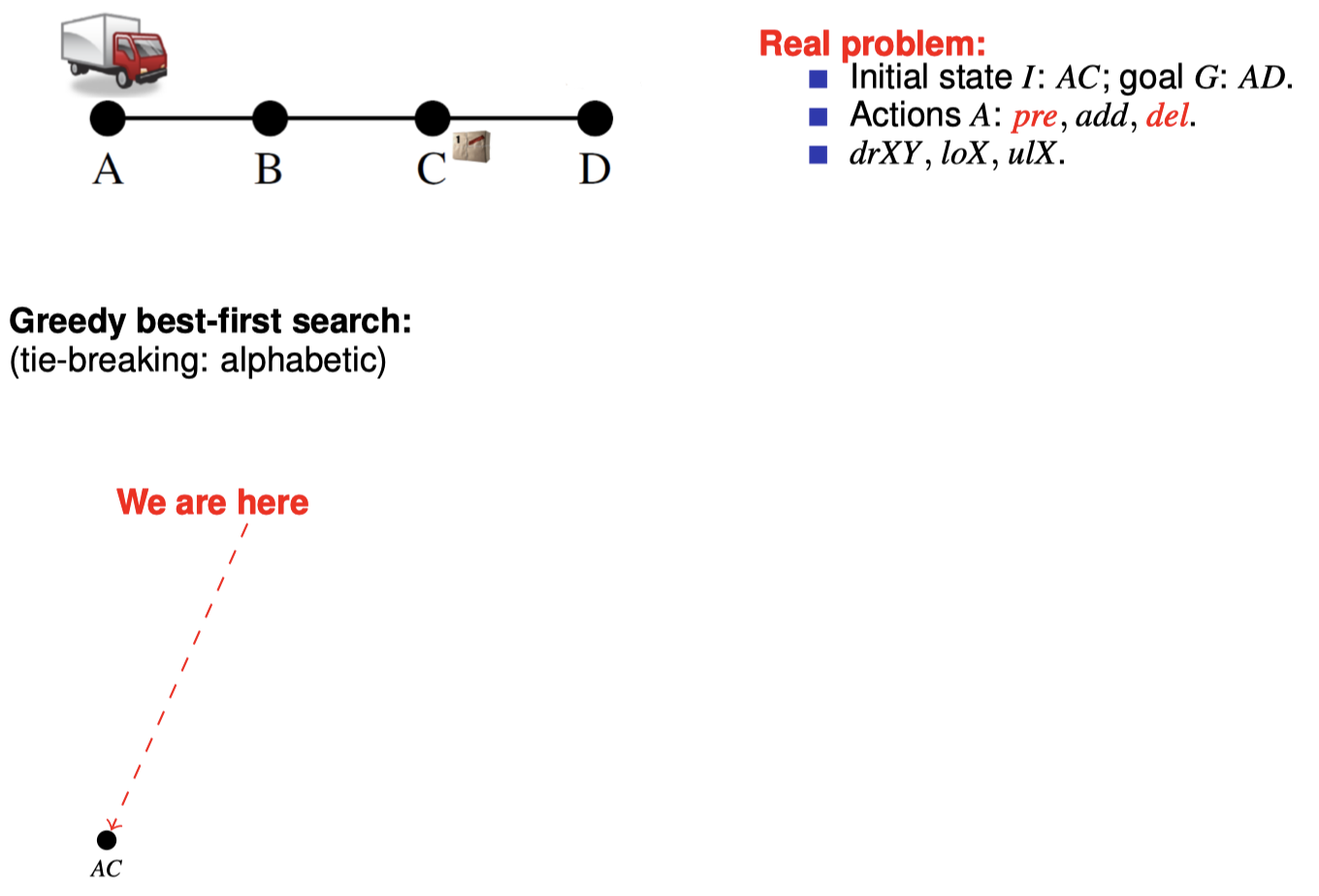
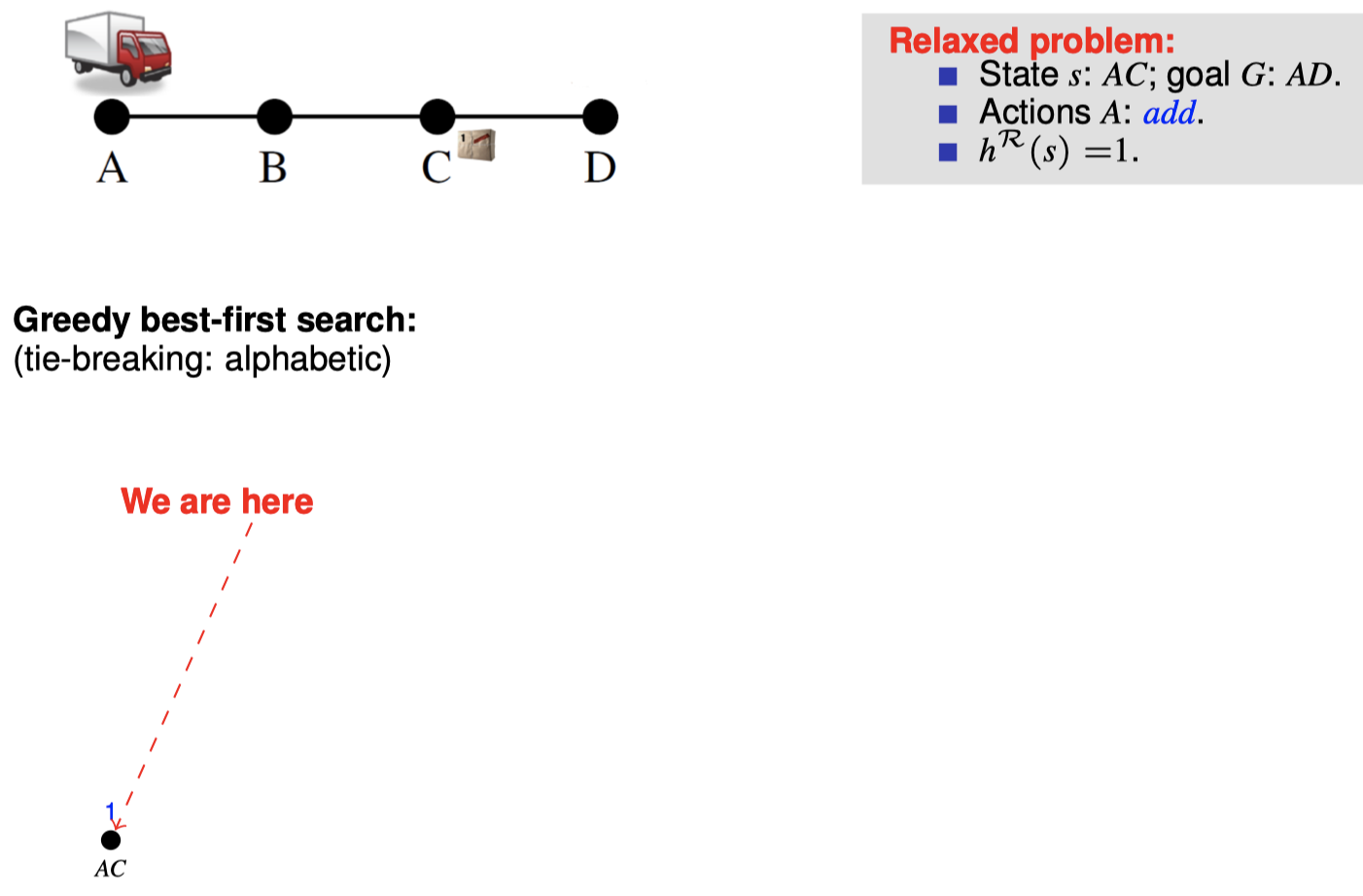
4.2 如何在搜索期间松弛:目标计数
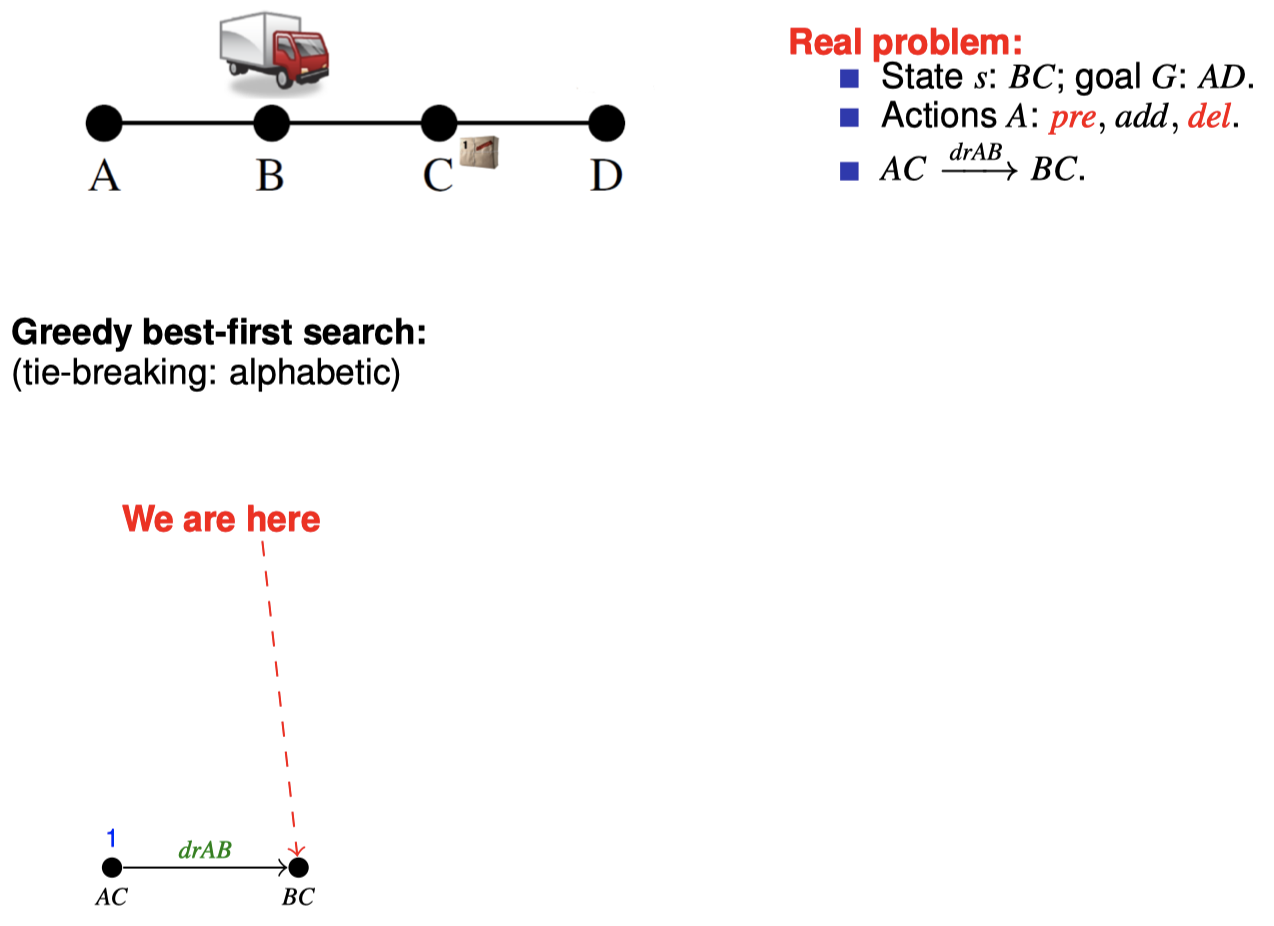
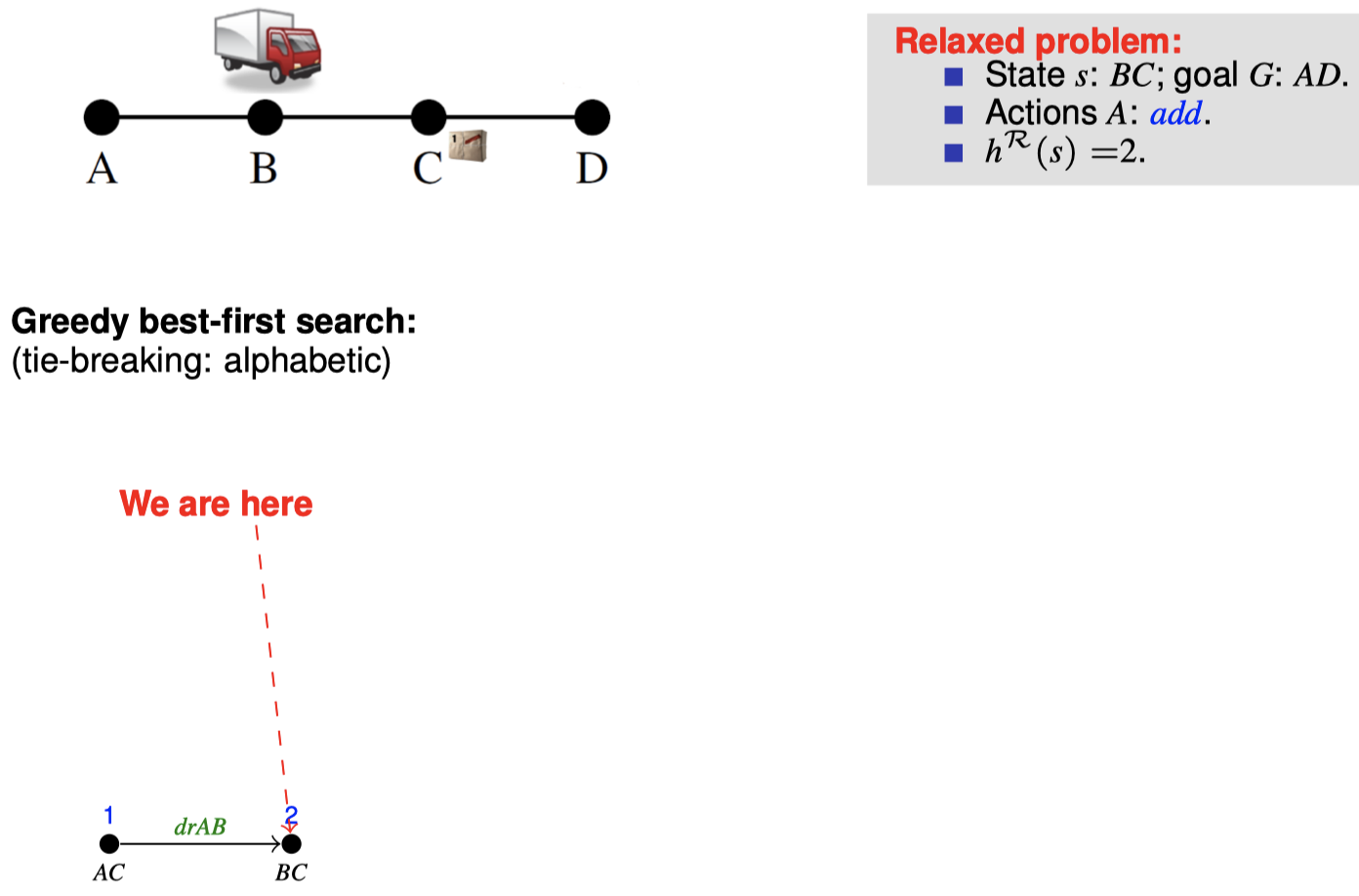
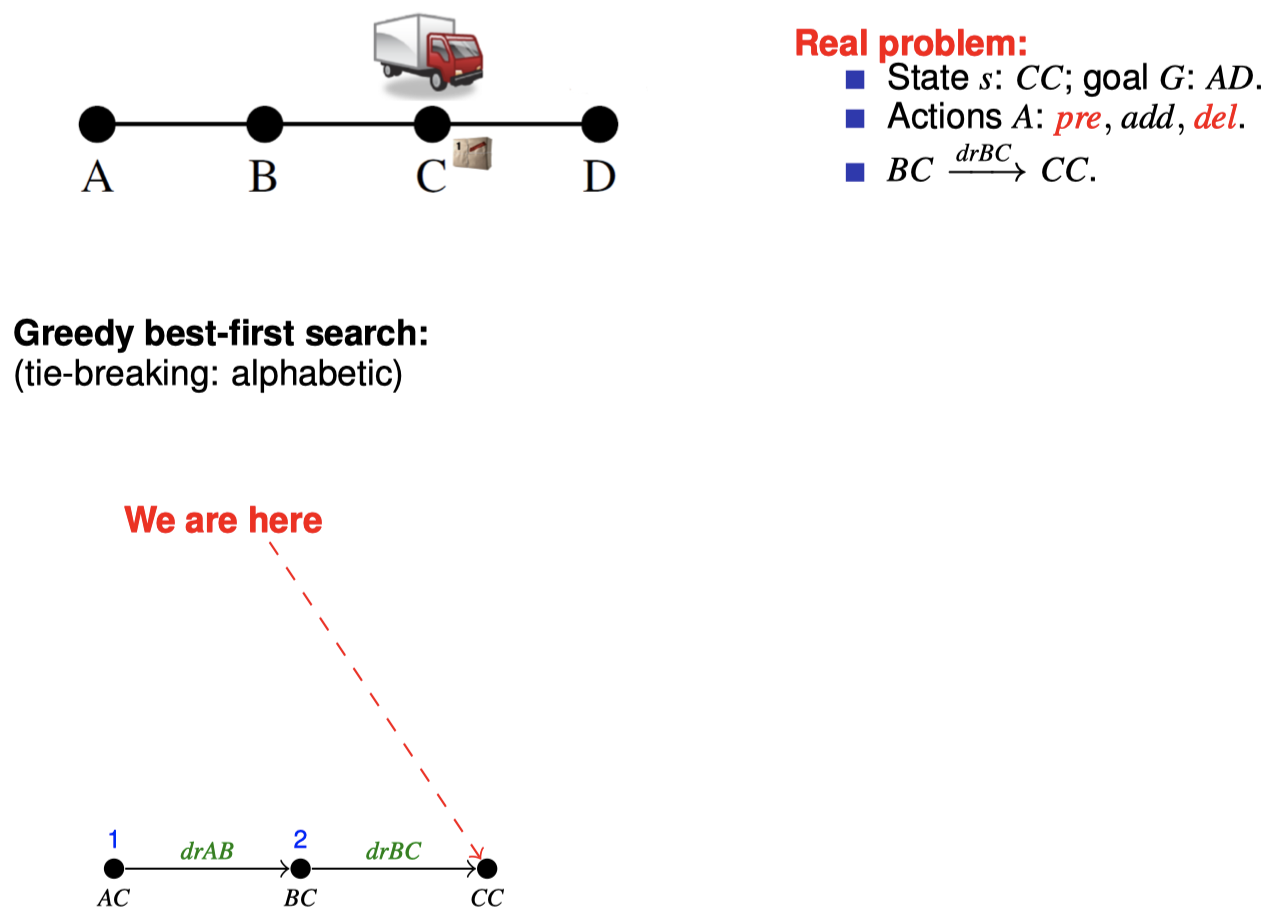
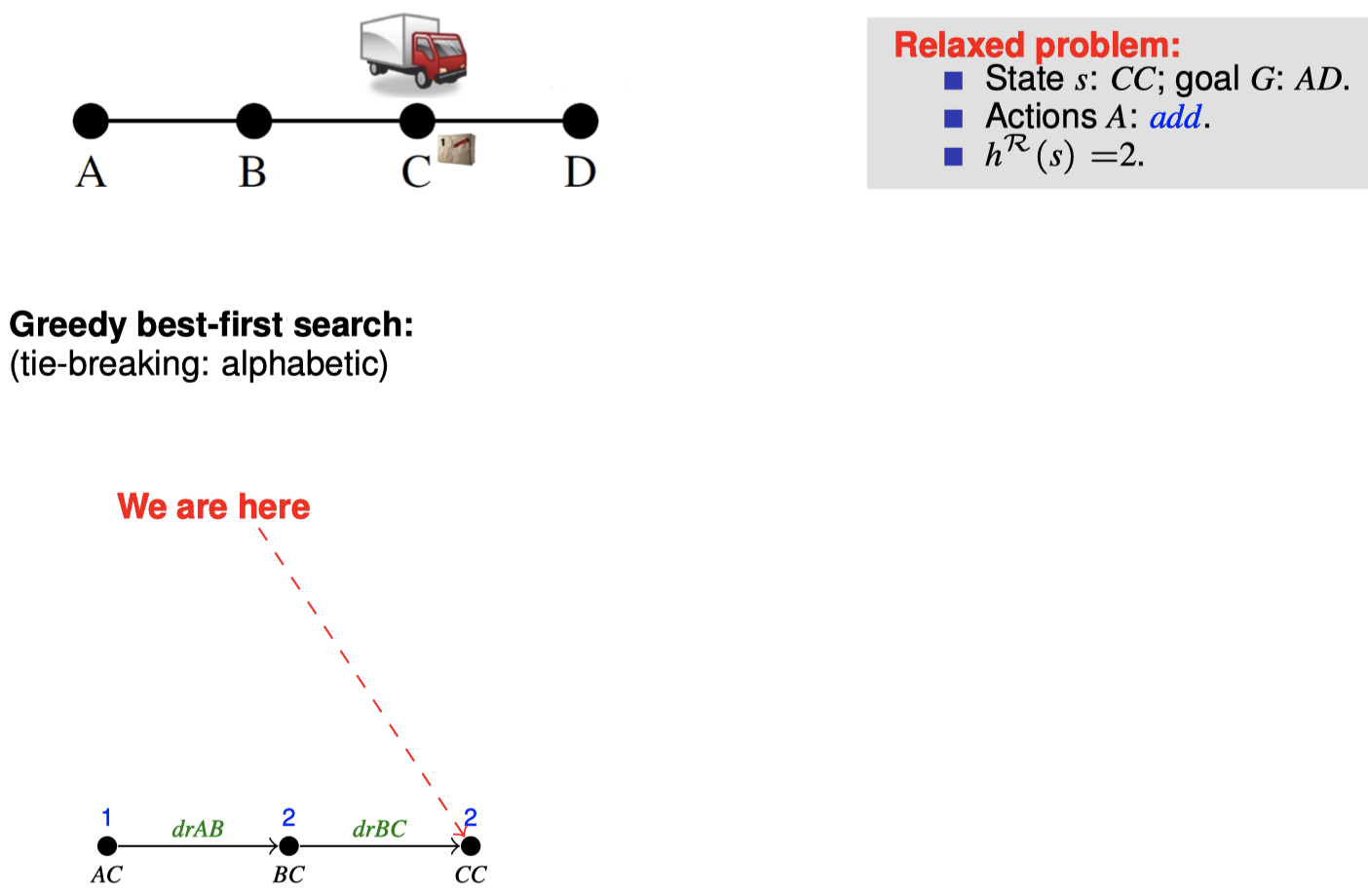
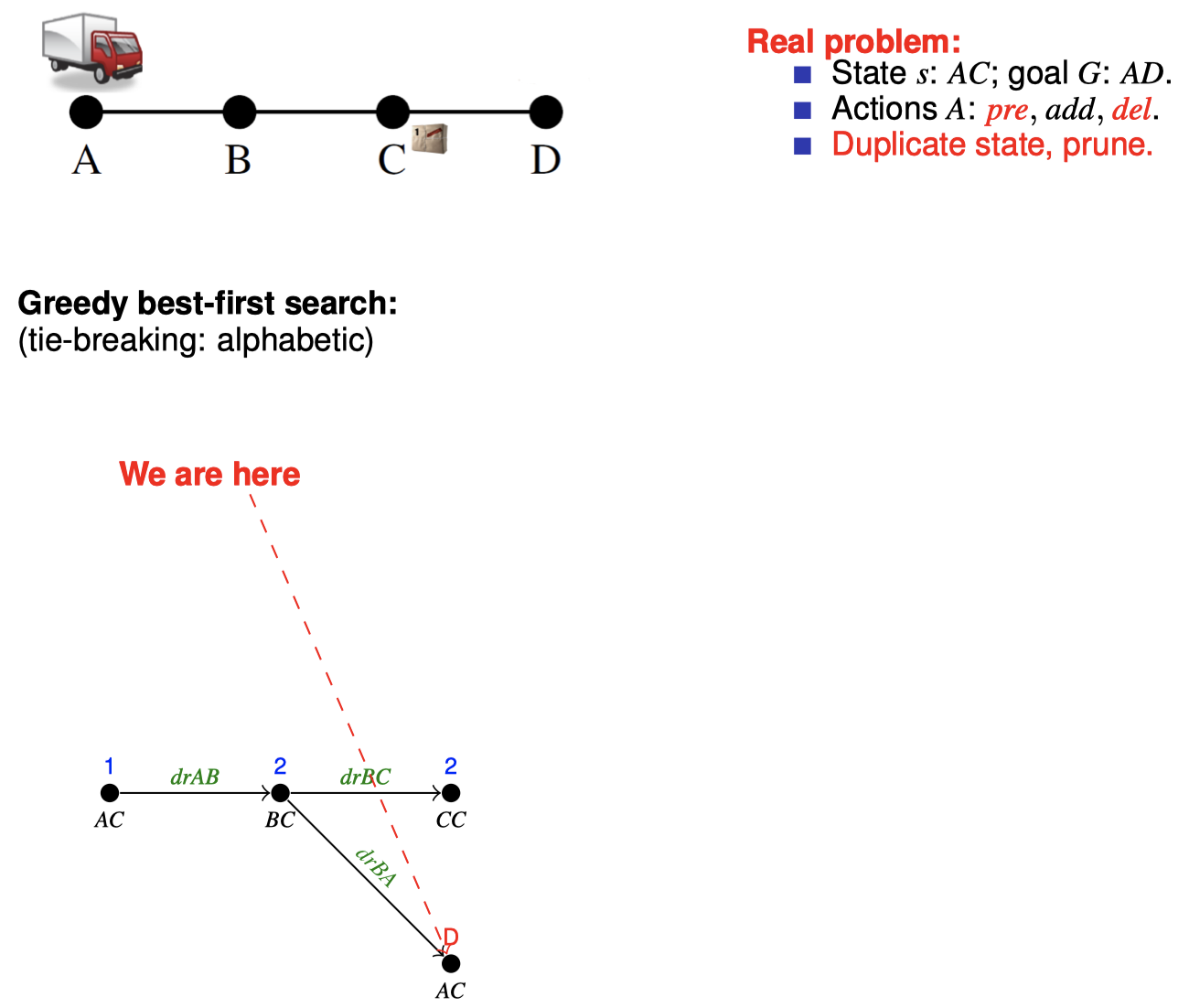

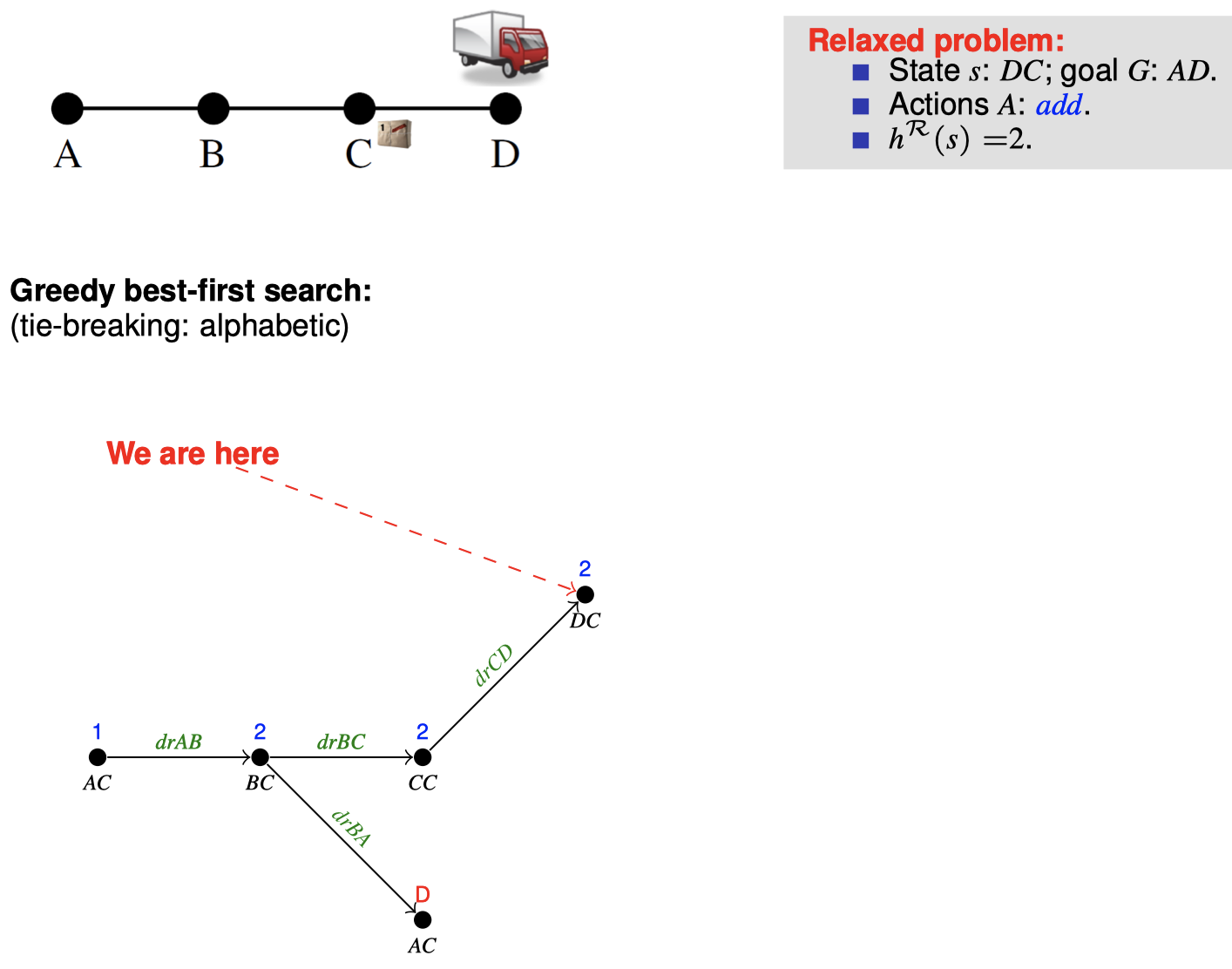
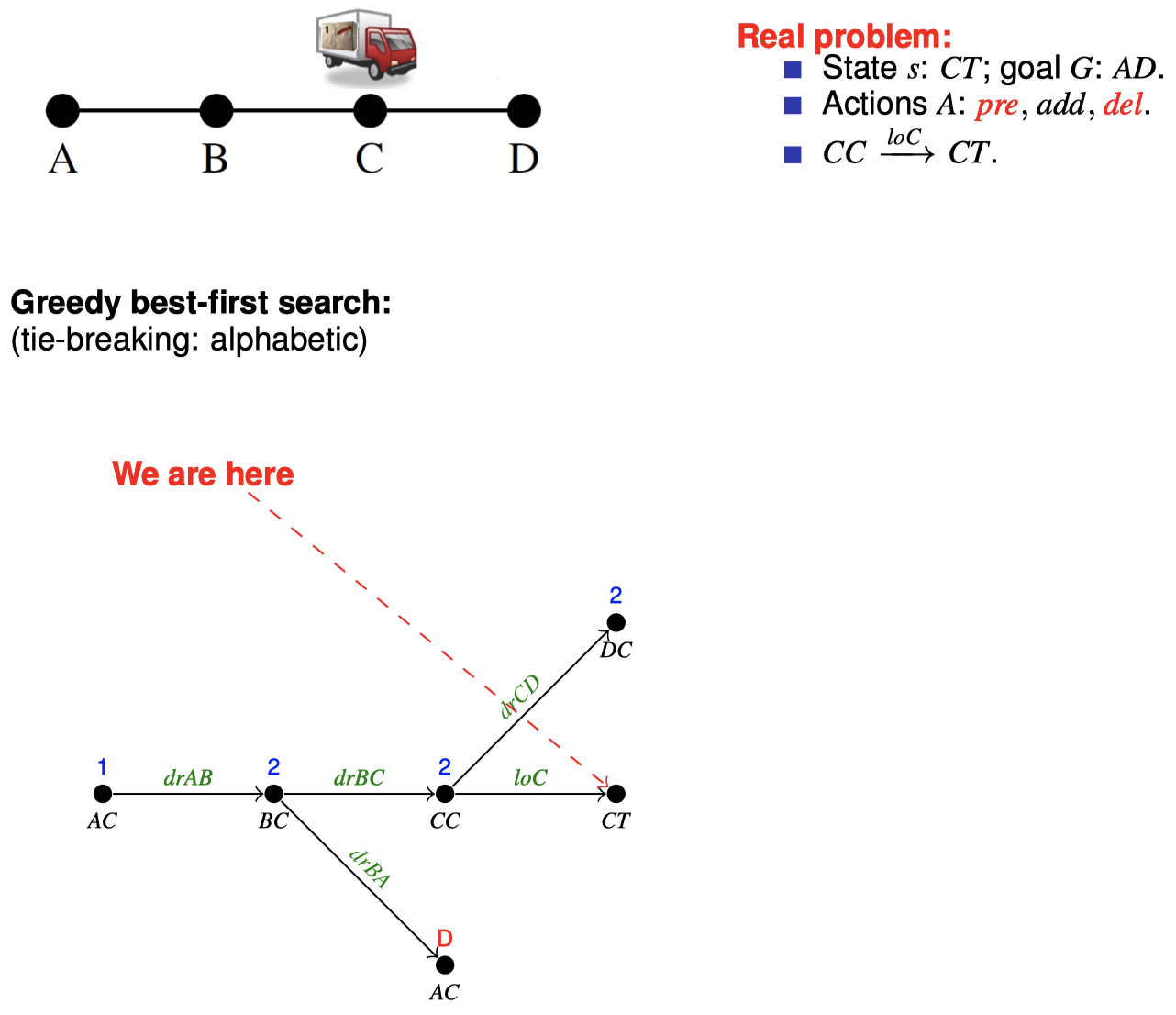
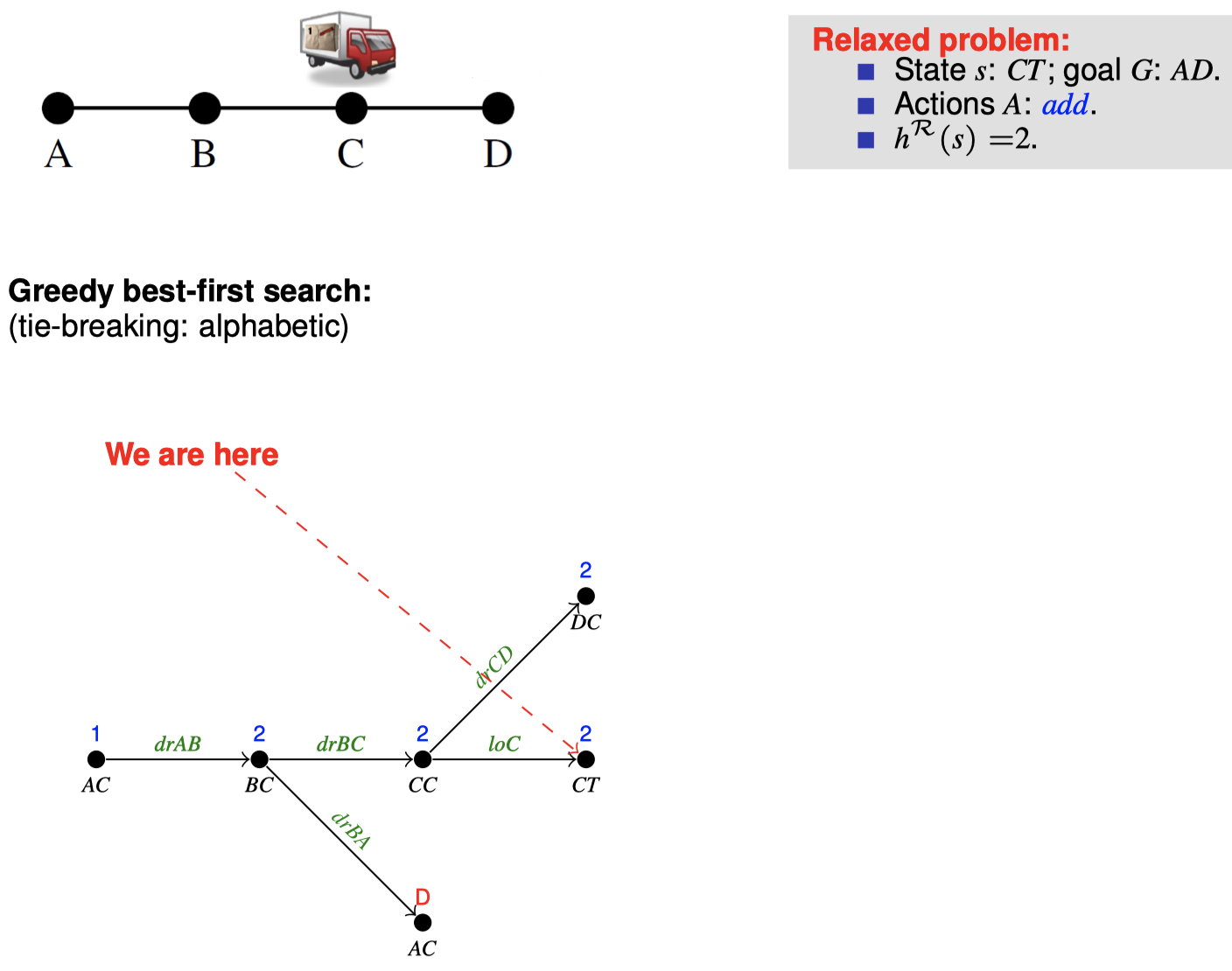
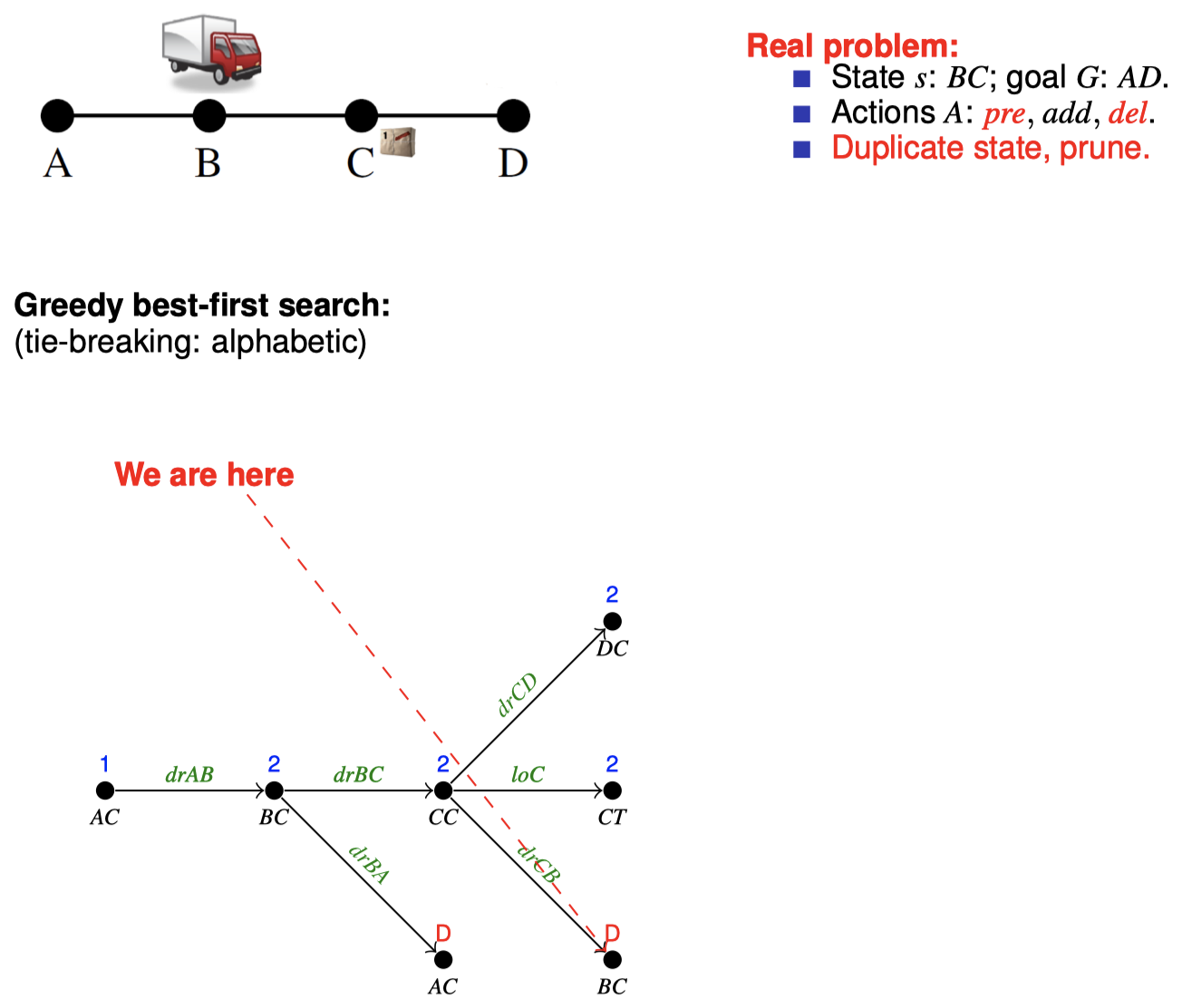
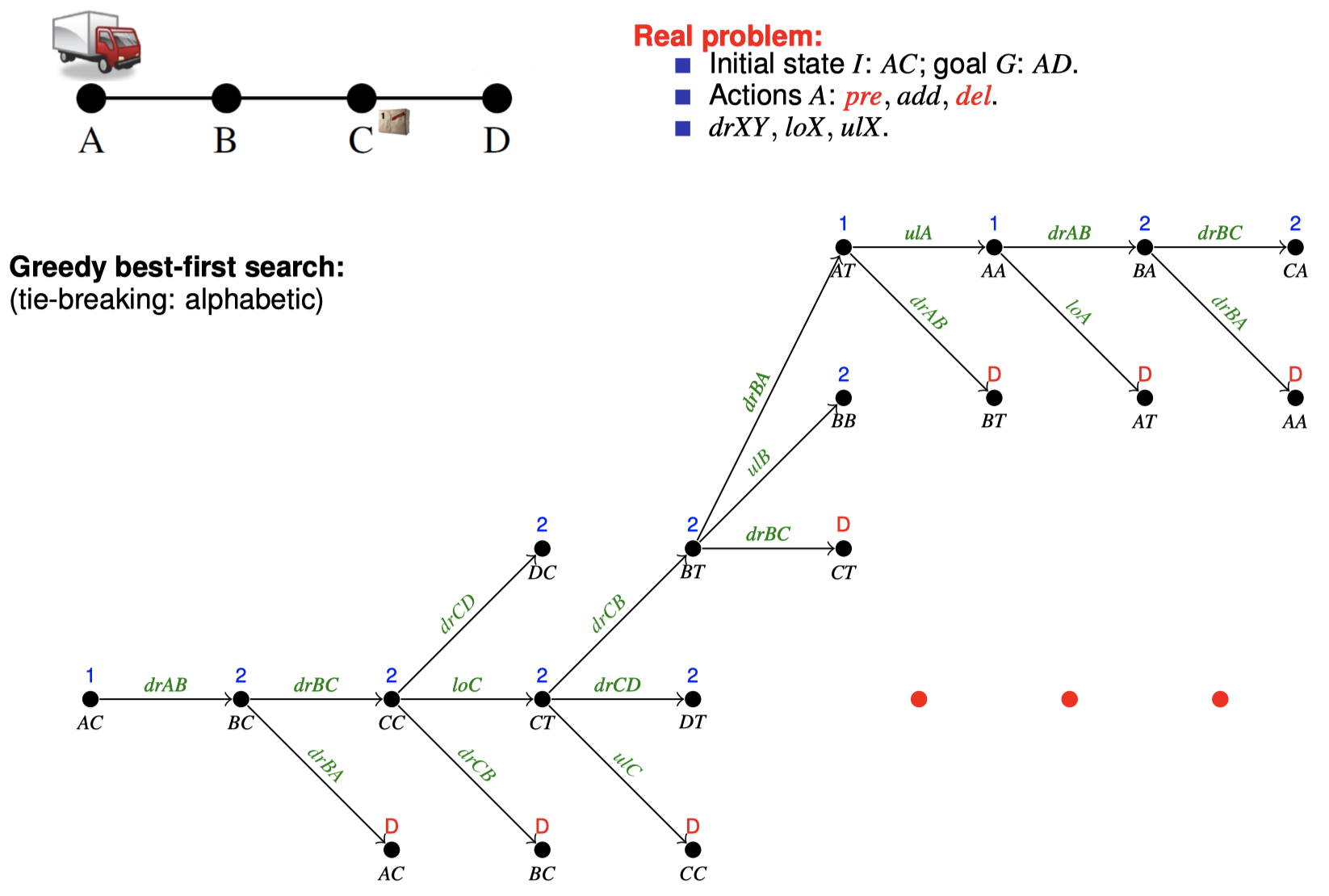
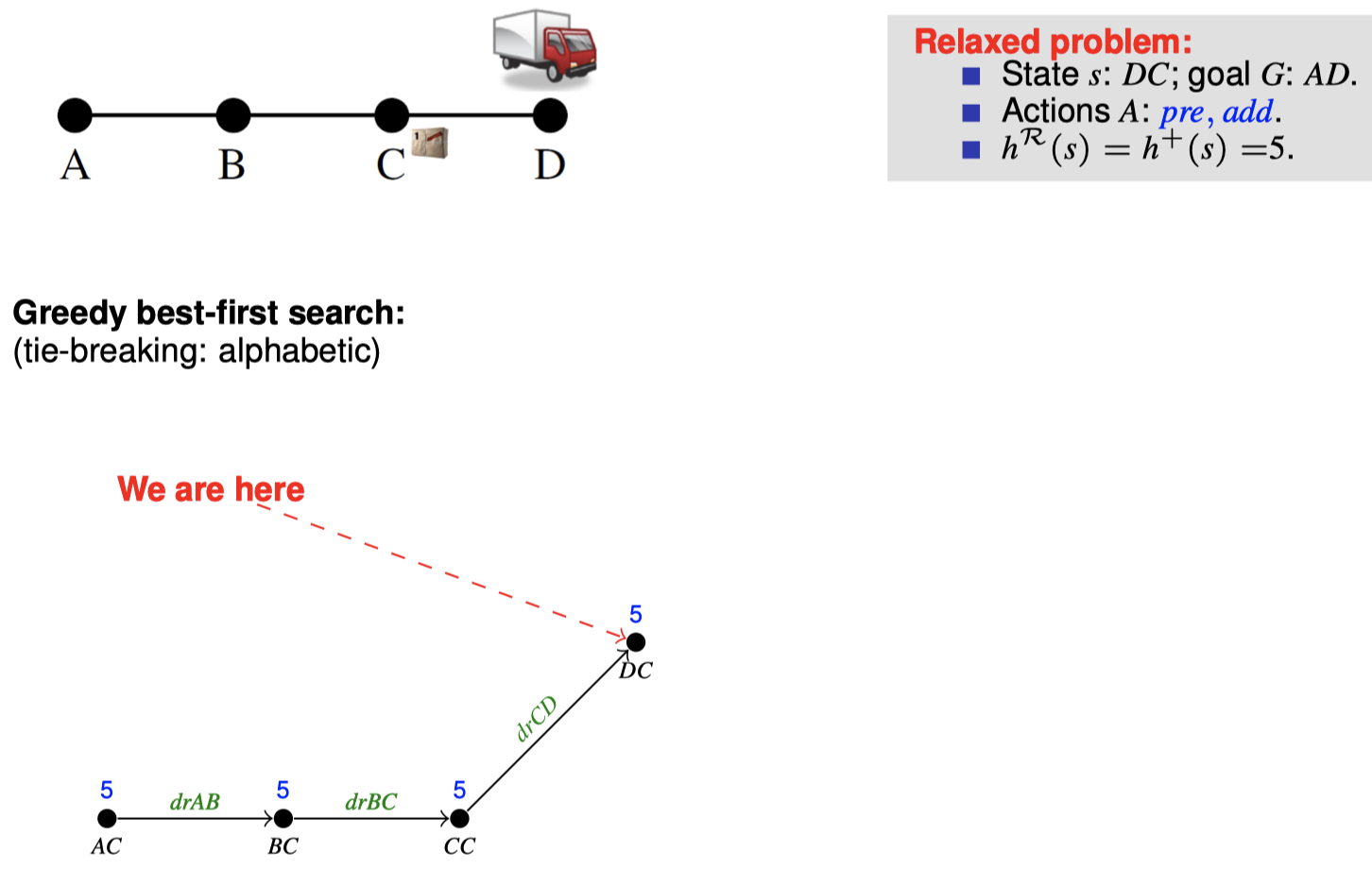
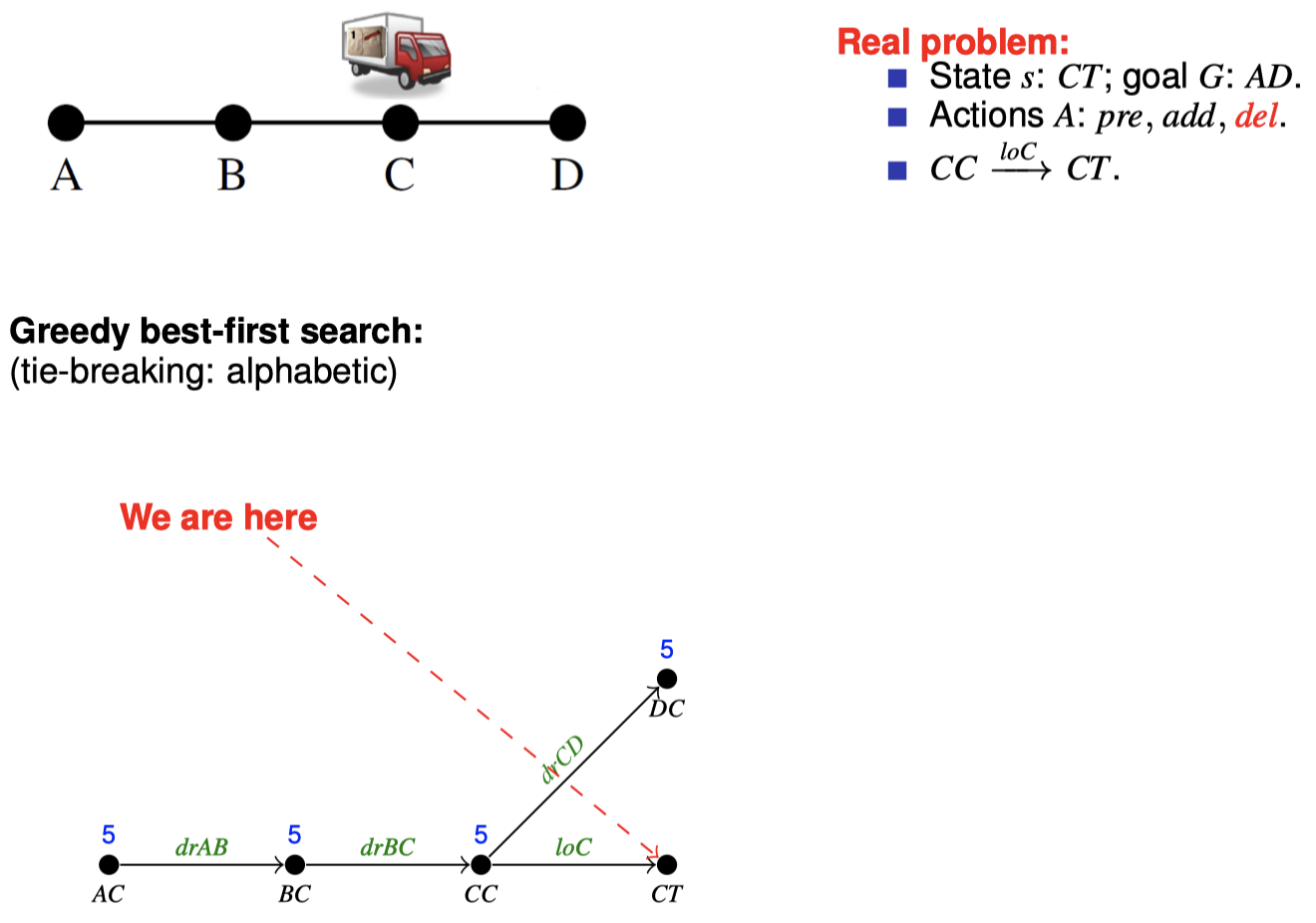
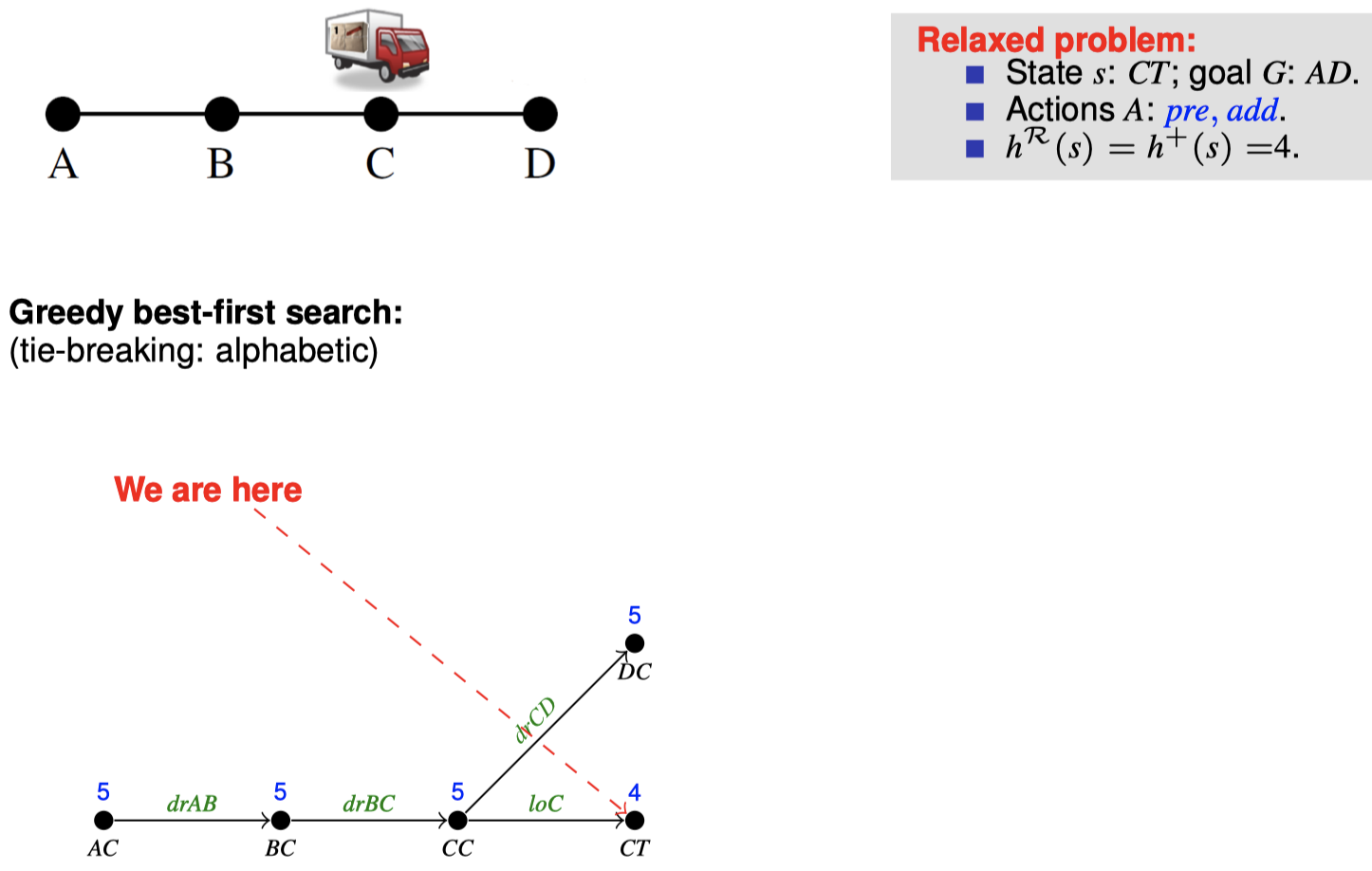
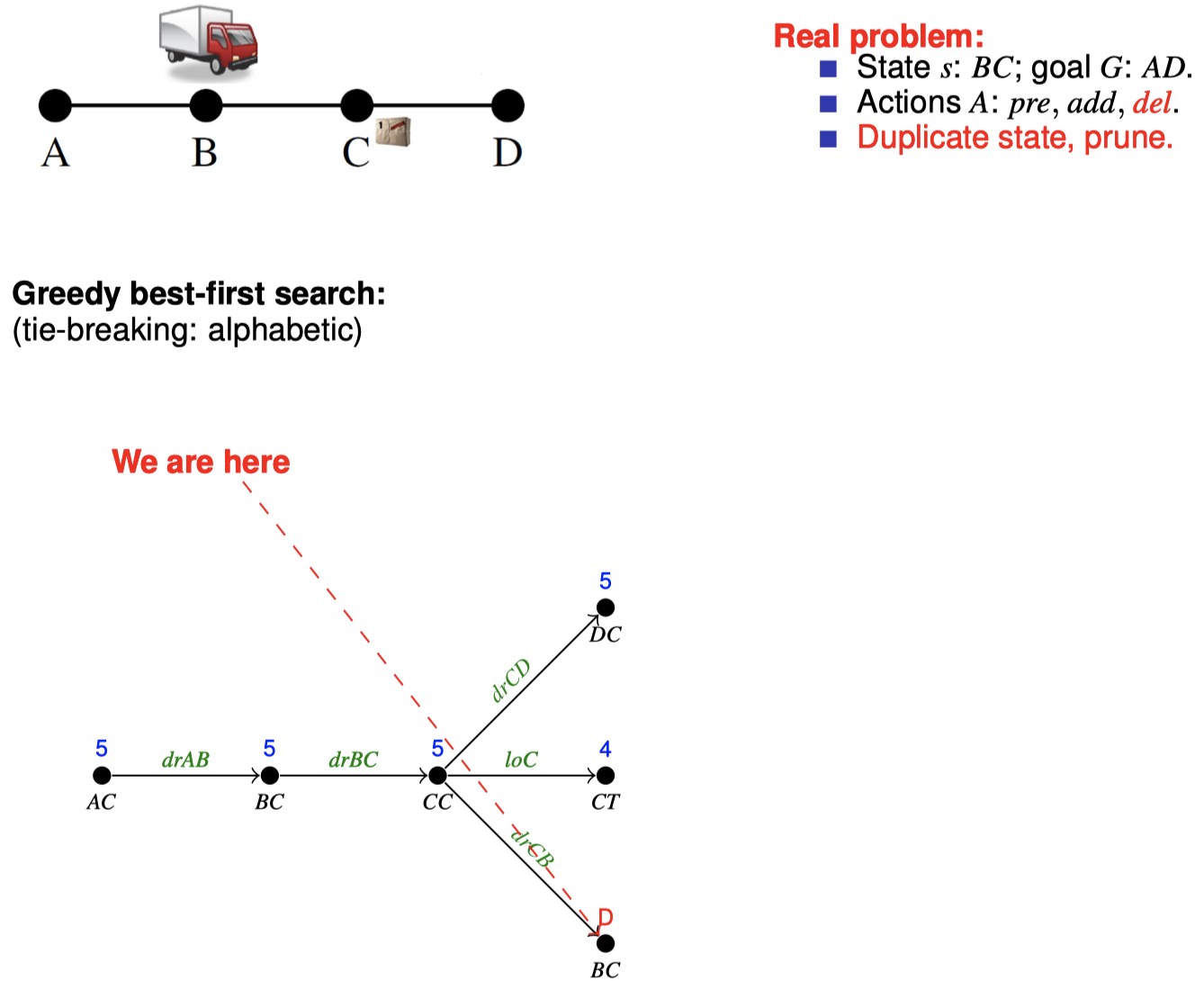
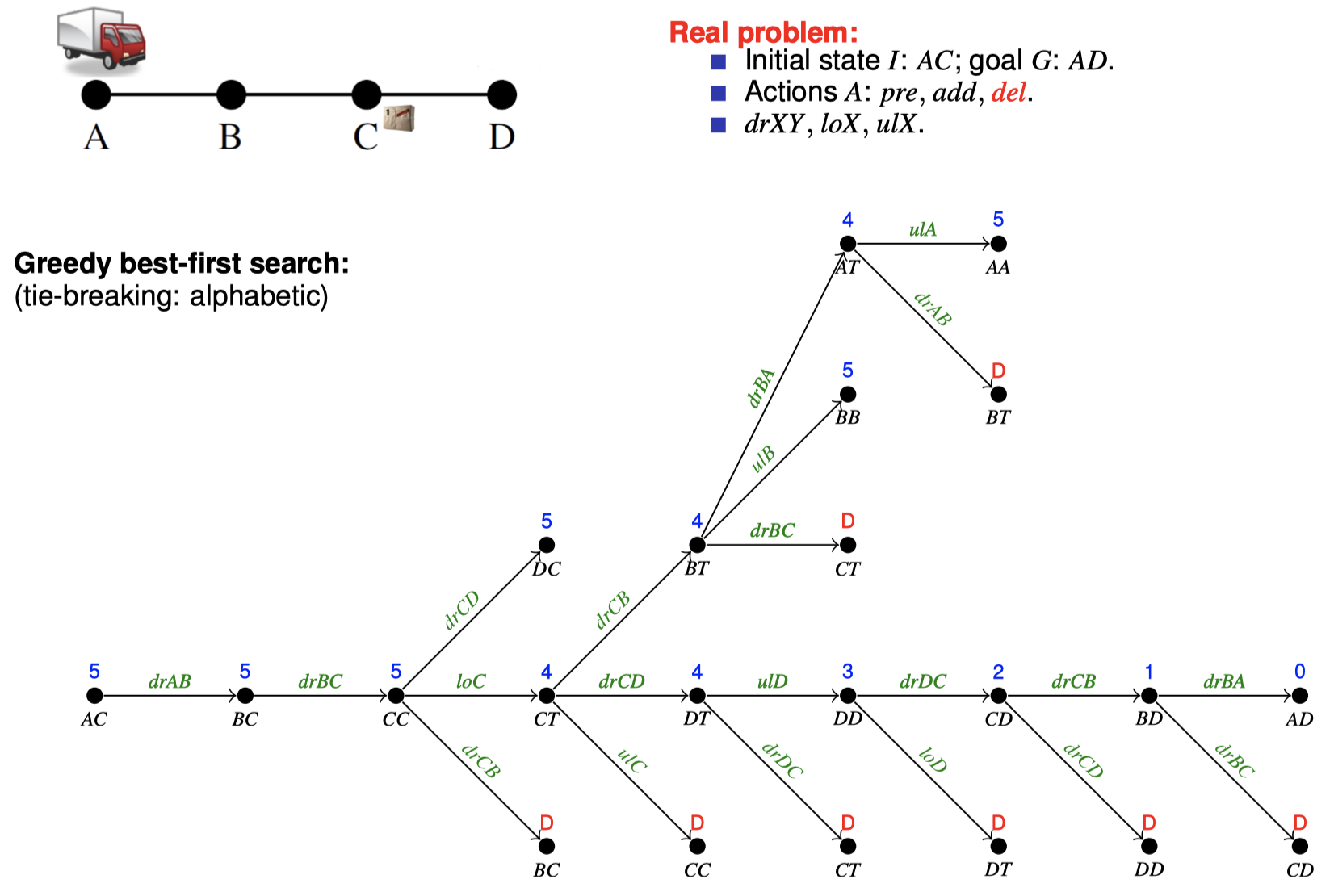
4.3 如何在搜索期间松弛:忽略删除列表
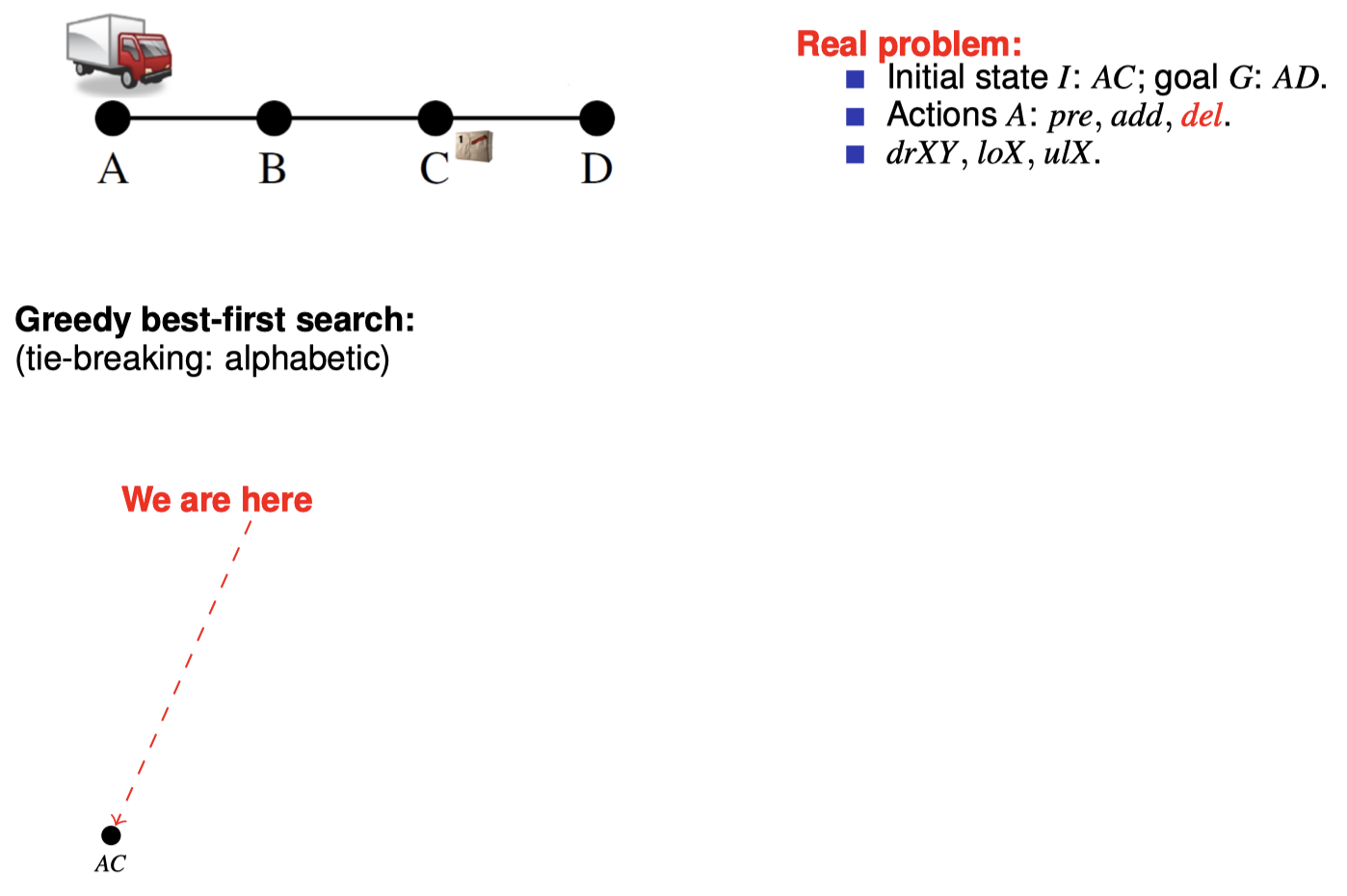
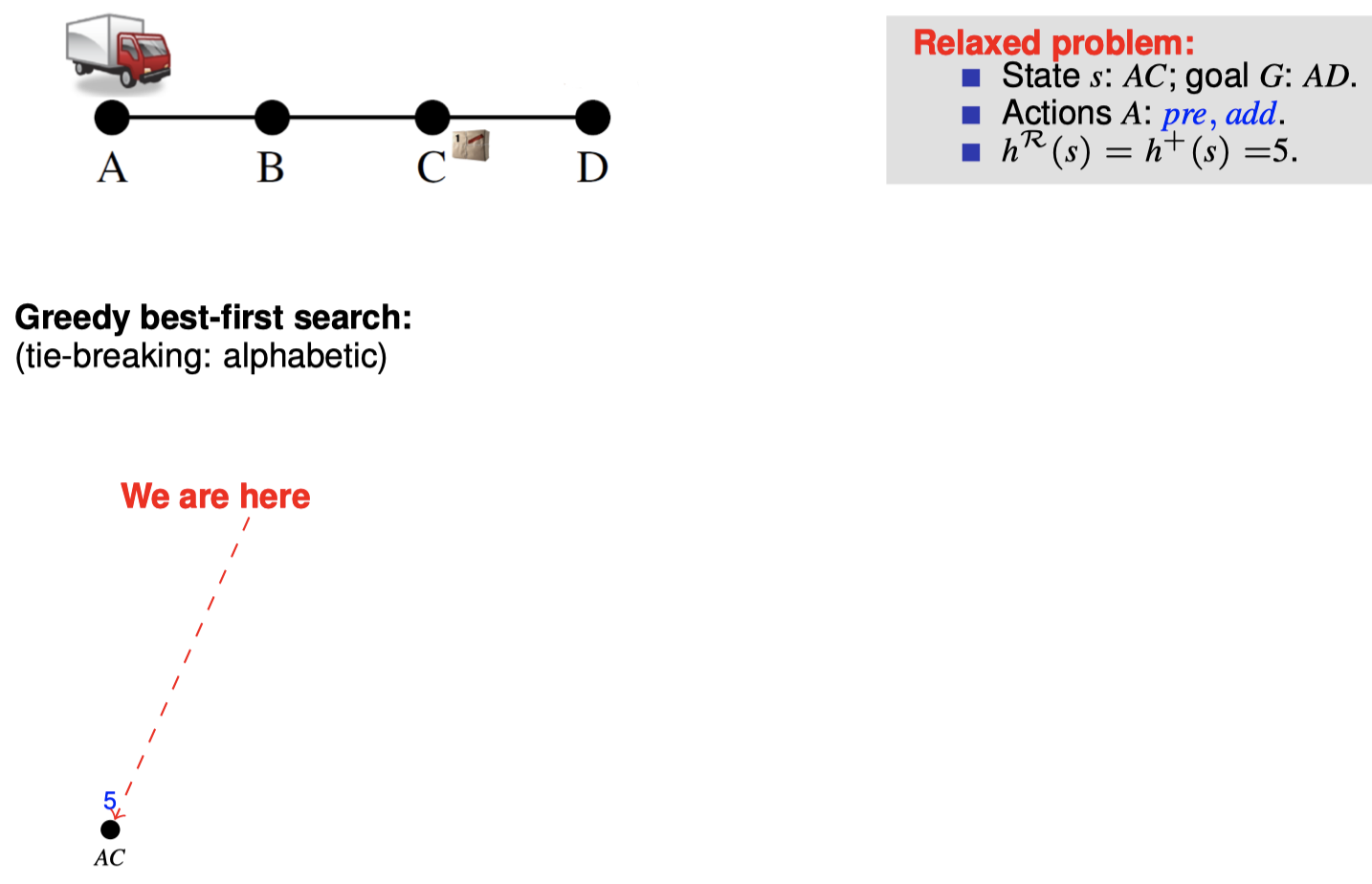
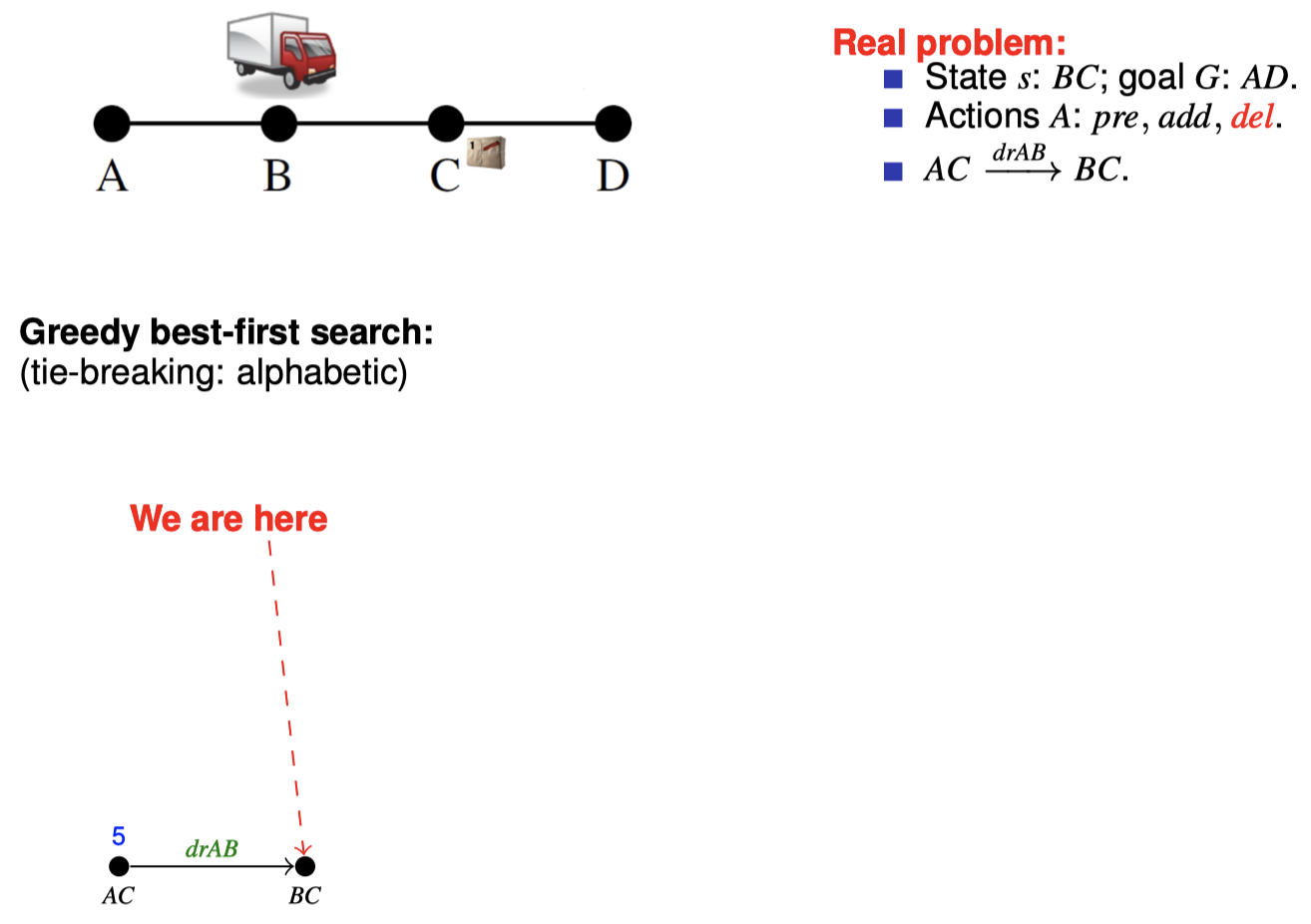

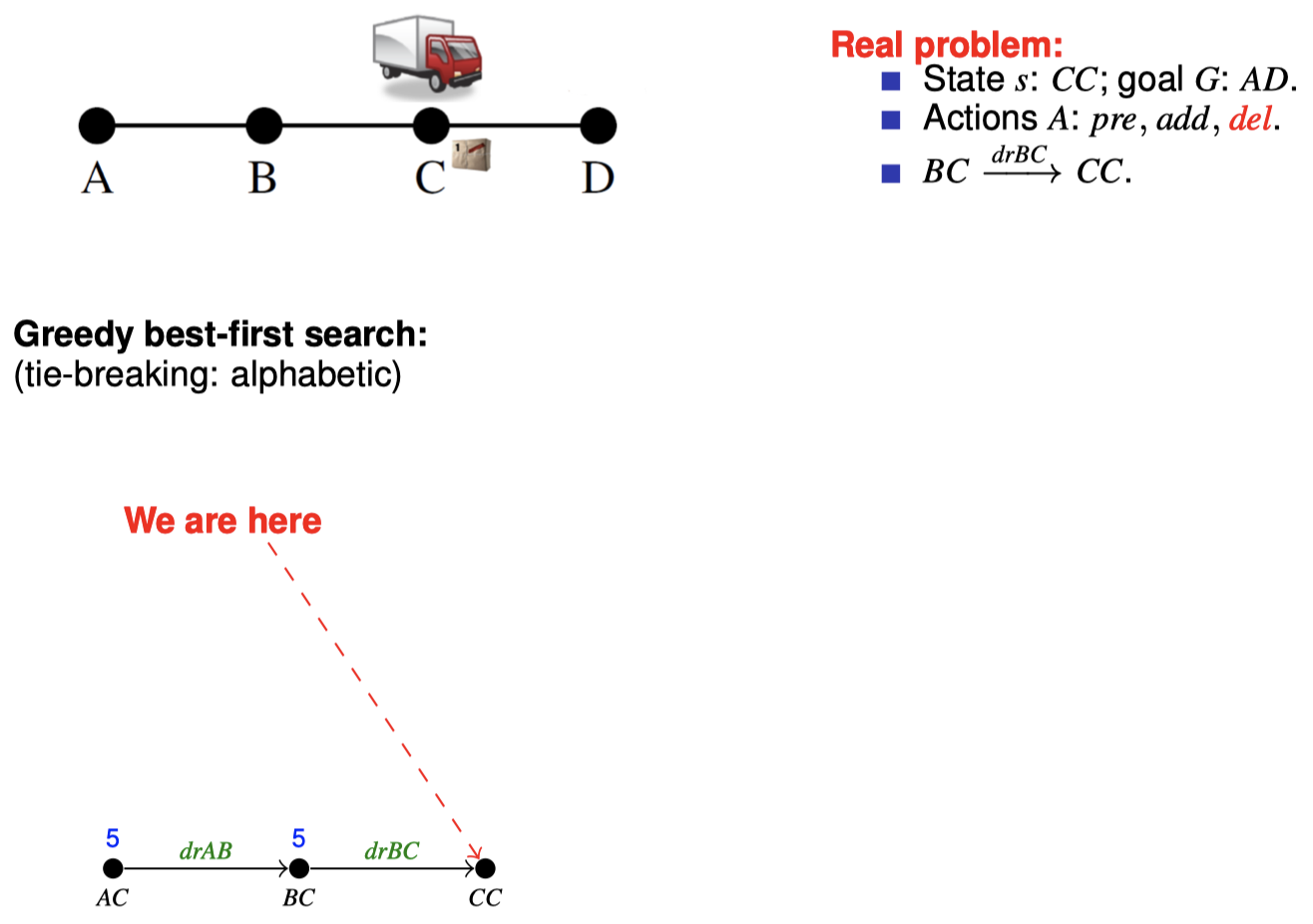

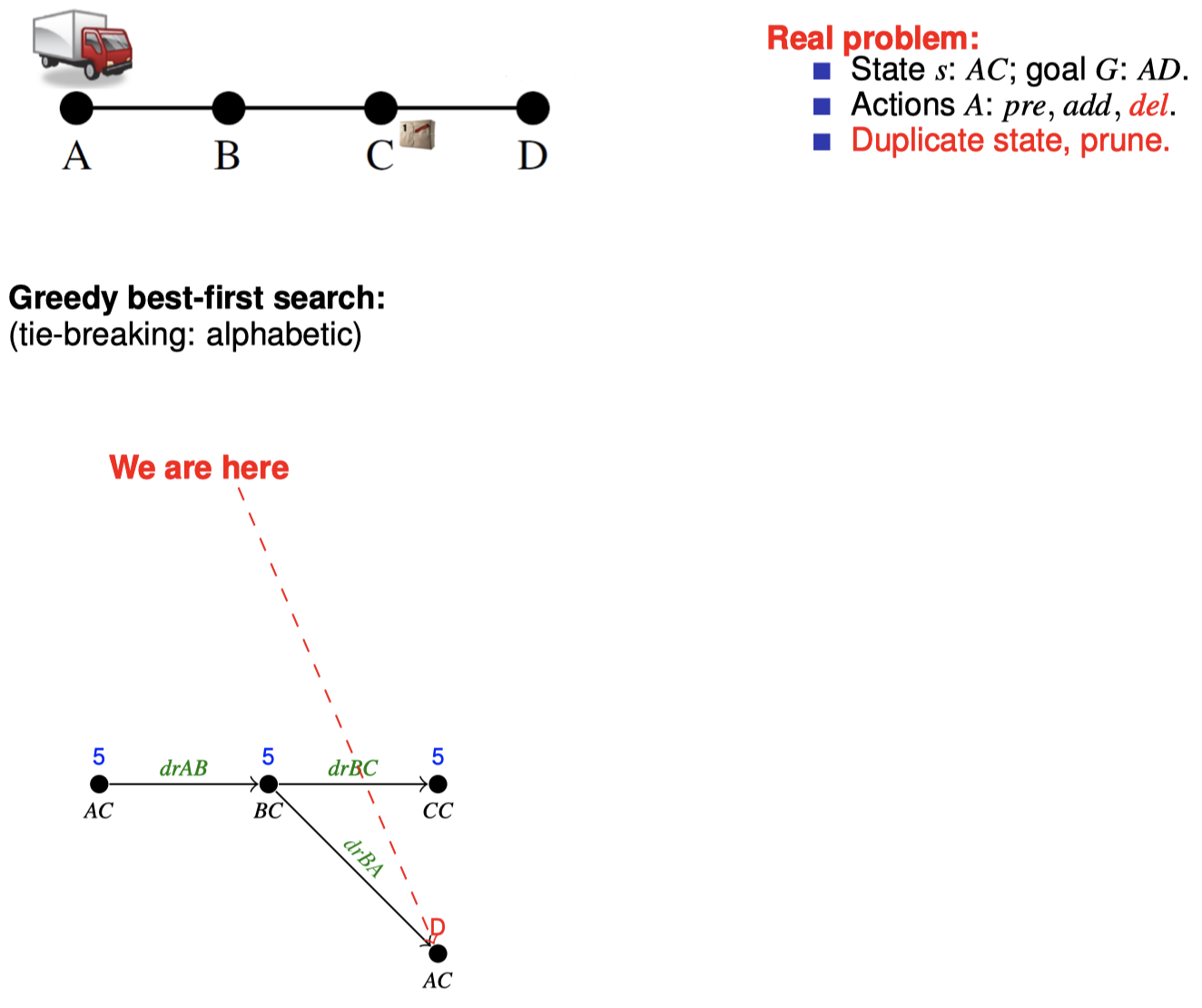
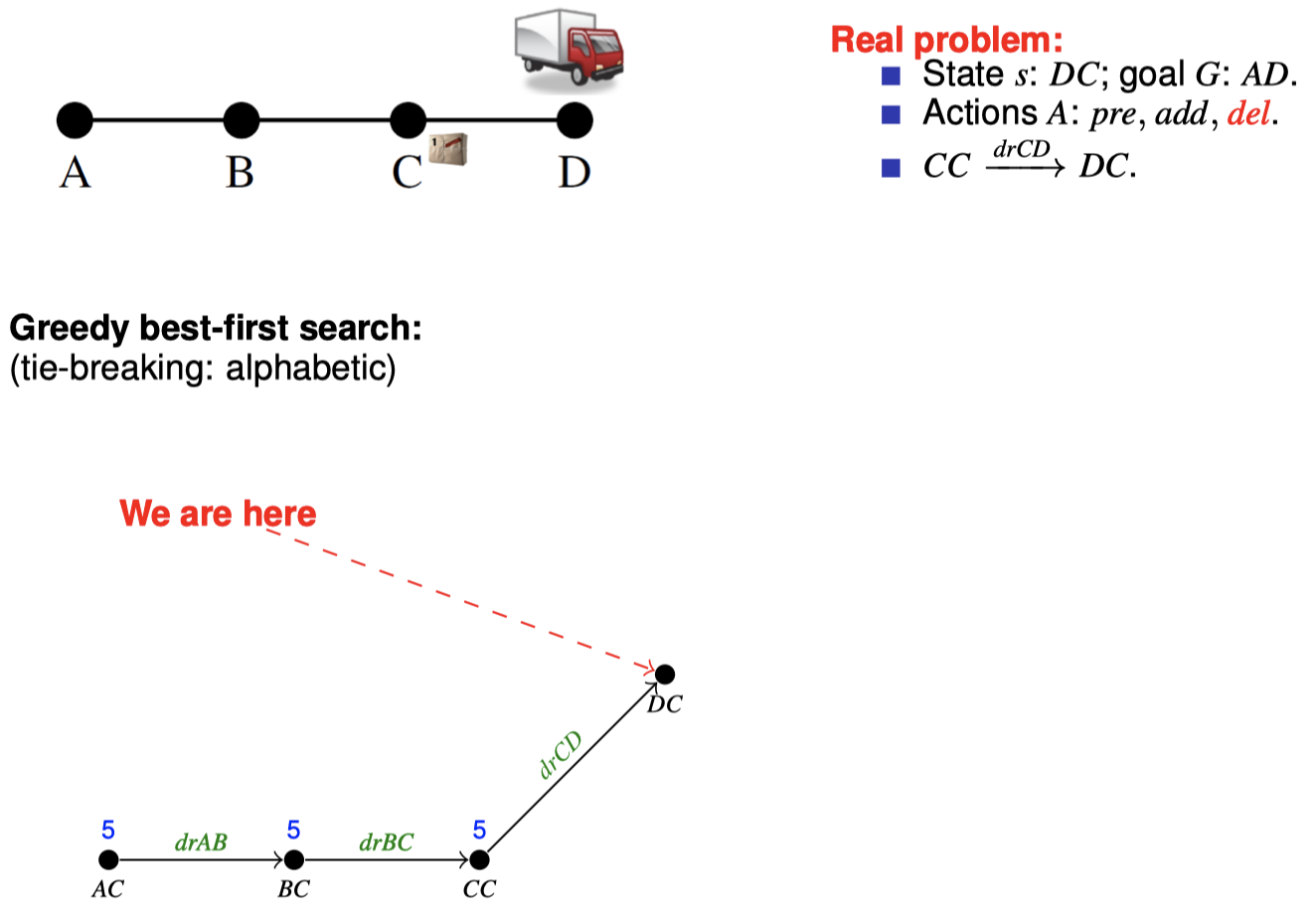
5. 扩展阅读
下节内容:生成启发函数
本作品采用知识共享署名-非商业性使用-相同方式共享 4.0 国际许可协议进行许可。 欢迎转载,并请注明来自:YEY 的博客 同时保持文章内容的完整和以上声明信息!