Lecture 07 NLP 深度学习：前馈网络

什么是深度学习？

机器学习的一个分支。
它是神经网络的另一个名字。
神经网络：灵感来源于大脑的工作机制，包含被称为 神经元 的计算单元。
为什么是深度？因为在现代深度学习模型中，有很多连接在一起的层。

1. 前馈神经网络

1.1 总体结构

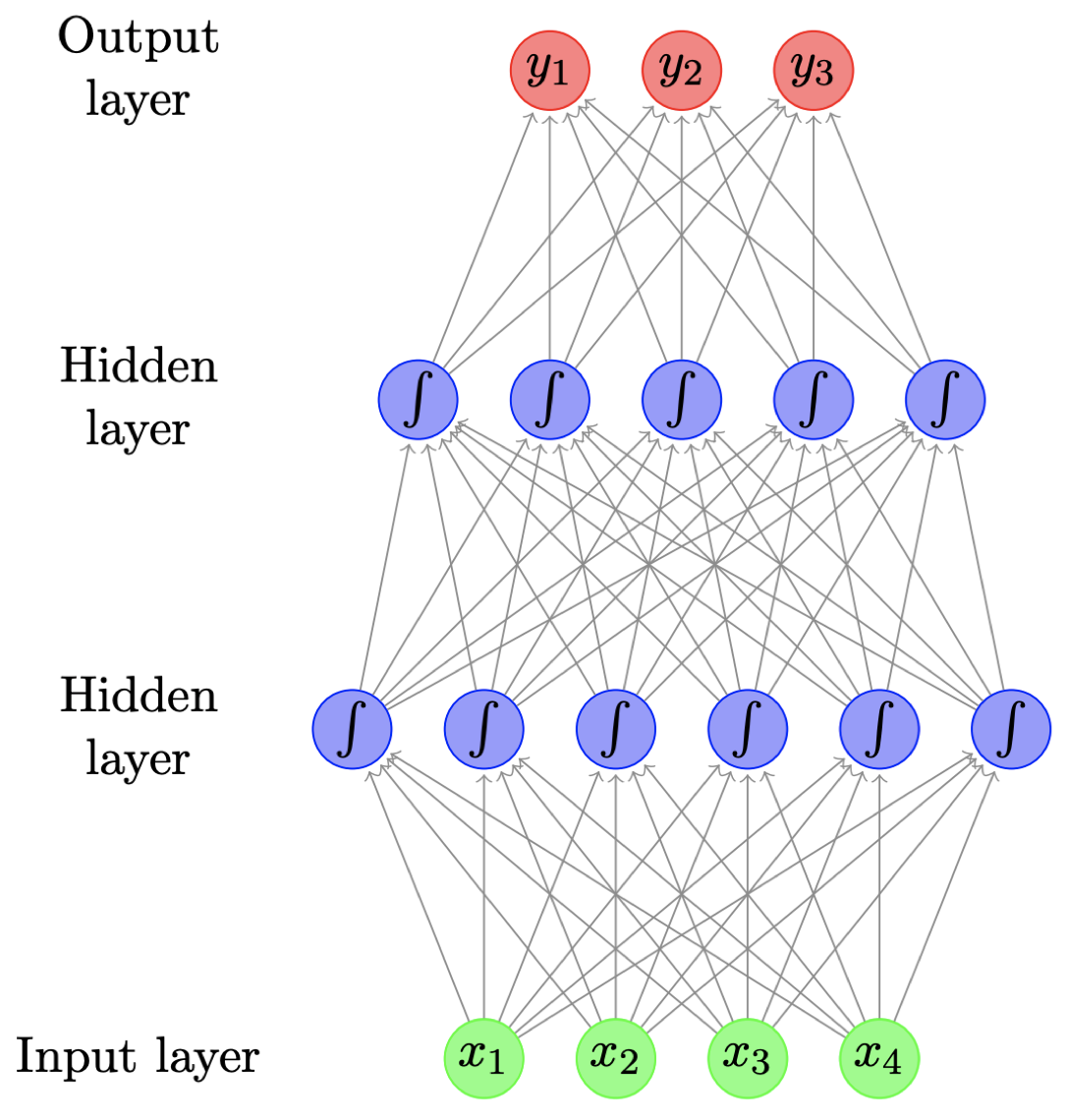
又称 多层感知器（multilayer perceptrons）
上图是一个包含两个隐藏层的前馈神经网络，图中的每个圆圈表示一个神经元，它实际上对应着某个函数，该函数通常是一个非线性函数（例如：Sigmoid 函数），其输入来自前一层的输出的线性加权组合，而每个神经元的输出的线性组合将作为下一层的输入。以此类推，直到输出层，输出层通常是根据实际问题定制的，例如：处理一个三分类问题时，通常可以将输出层神经元个数设为 3 个。
图中的每个箭头都携带一个权重，其大小取决于输入变量的重要程度。
Sigmoid 函数在这里引入了非线性。

1.2 神经元

每个 神经元 都是一个函数

给定输入（向量） $\mathbf x$，计算实值（标量）$h$
\[h=\tanh \left(\sum_{j}w_jx_j+b\right)\]
对输入进行缩放（乘以权重，$\mathbf w$），并且加上偏移量（偏置，$b$）
采用 非线性函数，例如：logistic sigmoid, hyperbolic sigmoid（tanh），或者 ReLU

1.3 矩阵向量表示

通常会有很多个隐藏神经元，即
\[h_i=\tanh \left(\sum_{j}w_{ij}x_{j}+b_i\right)\]
每个神经元都有属于自己的权重向量 $\mathbf w_i$ 和偏置项 $b_i$
某一层的计算结果可以用矩阵和向量操作表示
\[\mathbf h=\tanh (W\mathbf x + \mathbf b)\]
其中，$W$ 是一个由权重向量 $\mathbf w_i$ 构成的矩阵，$\mathbf x$ 是输入向量，$\mathbf b$ 是所有偏置项组成的向量。
此时，非线性函数实际上作用在每个元素上。

1.4 输出层

二分类问题（例如：对一条推文进行正面/负面情感分类）
- 使用 Sigmoid 激活函数（又称 Logistic 函数）
多分类问题（例如：对一个文档的主题进行分类）
- 使用 Softmax 函数，确保概率大于 $0$，并且和为 $1$。
  \[\left[\dfrac{\exp(v_1)}{\sum_i\exp(v_i)},\dfrac{\exp(v_2)}{\sum_i\exp(v_i)},\dots,\dfrac{\exp(v_m)}{\sum_i\exp(v_i)} \right]\]

1.5 前馈神经网络

让我们回到之前的例子，上图是一个包含 1 个输入层、2 个隐藏层和 1 个输出层的前馈神经网络。它可以表示为：

\[\mathbf h_1=\tanh (W_1\mathbf x + \mathbf b_1)\] \[\mathbf h_2=\tanh (W_2\mathbf h_1 + \mathbf b_2)\] \[\mathbf y=\text{softmax}(W_3\mathbf h_2)\]

权重矩阵 $W$ 和偏置向量 $\mathbf b$ 就是该模型的所有参数，我们通过定义目标函数，利用梯度下降等方法对其进行训练。

1.6 从数据中学习

如何从数据中学习参数？

本质上，模型试图尽可能地 “拟合” 训练数据，我们可以通过其分配给正确输出的概率来衡量：
\[L=\prod_{i=0}^{m}P(y_i\mid x_i)\]
- 最大化 所有训练数据的总概率 $L$
- 等价于 最小化 $\log L$，对于参数而言
训练采用梯度下降
- 很多工具，例如 tensorflow、pytorch、dynet 等，利用自动微分来自动计算梯度。

2. 应用

现在，我们来看一些如何为下游应用构建神经网络的例子。

2.1 主题分类

给定一个文档，基于一个预定义的主题集合（例如：经济、政治、体育等）对其进行分类。

输入：词袋（bag-of-words）

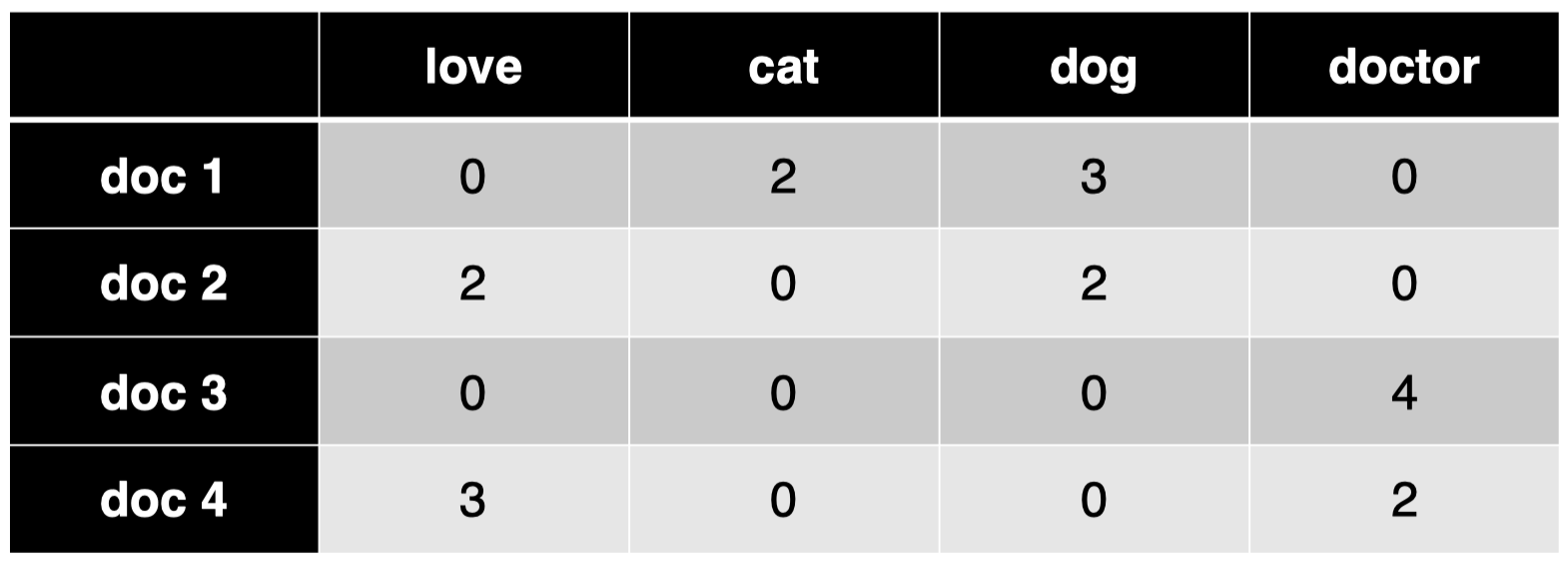
模型：考虑之前的两层模型，假设输出的主题类别一共有 3 类：

\[\mathbf h_1=\tanh (W_1\mathbf x + \mathbf b_1)\] \[\mathbf h_2=\tanh (W_2\mathbf h_1 + \mathbf b_2)\] \[\mathbf y=\text{softmax}(W_3\mathbf h_2)\]

对于第一个文档 doc 1：
输入向量 $\mathbf x=[0,2,3,0]$ 代表文档的词袋表示
输出向量 $\mathbf y=[0.1,0.6,0.3]$ 代表该文档在 3 个类别上的概率分布

训练过程：
得到模型输入后，向前传播拟合数据：依次计算第一个隐藏层、第二个隐藏层以及输出层，然后我们可以得到一个输出类别的概率分布，然后我们查看每个类别的正确标签，并计算当前概率分布下的类别交叉熵（例如：假设第一个文档的正确标签是类别 2，我们可以在其概率 $0.6$ 上计算 $\log$ 损失），我们试图告诉模型的是：对于每一个训练样本，我们希望模型对于该样本的正确标签类别分配的概率为 $1.0$。对于概率小于 $1.0$ 的情况，我们基于反向传播计算梯度并且更新模型参数。

预测过程：
当模型训练完成后，预测过程非常直接：仅涉及单向的向前传播过程。将测试文档转换为词袋表示作为输入向量，然后向前传播，计算得到输出类别的概率分布，并且将其中概率最大值对应的类别标签作为该文档的预测类别。

改进：

使用 bag-of-ngrams 作为输入。
文本预处理：词形还原、移除停用词等。
相比原始计数，我们可以用 TF-IDF 或者指示器（$0$ 或 $1$，取决于该单词是否存在）来进行单词加权。

2.2 作者身份识别

给定一段文本，识别其作者或者作者相关特点（例如：性别、年龄、母语等）。

在该任务中，文本的风格特征要比单词内容本身更重要。
- POS tags 和功能词（例如：$\textit{on, of, the, and}$）
关于功能词，我们可以从特定的词典获得（因为功能词通常是一个封闭集合）。或者，另一种关于功能词很好的近似方法是：挑选一个大的语料库中出现频率最高的 300 个单词。
输入：bag of function words, bag of POS tags, bag of POS bigrams/trigrams
单词权重：密度（例如：在一个文本窗口内，功能词和内容词之间的数量比例）
其他特征：连续功能词之间距离的分布

3. 前馈神经网络语言模型

尽管存在很多不同的下游应用，但是它们对应的语言模型可以是通用的。

3.1 语言模型回顾

目标：为一个单词序列分配概率。
基本框架：可以视为句子上的 “滑动窗口”，根据有限的上下文对每个单词进行预测。
例如，$n=3$ 时，一个 trigram 模型为：
\[P(w_1,w_2,\dots,w_m)=\prod_{i=1}^{m}P(w_i\mid w_{i-2} w_{i-1})\]
训练（估计）来自频率计数
- 难以处理罕见单词 $\to$ 平滑处理

3.2 语言模型作为分类器

语言模型可以被视为简单的 分类器，对一个序列中下一个可能出现的单词进行分类。

\[P(w_i\mid w_{i-2}=“\textit{cow}”,w_{i-1}=“\textit{eats}”)\]

例如，在 trigram 模型中，我们给定当前的两个上下文单词 “$\textit{cow}$” 和 “$\textit{eats}$”，我们希望预测接下来出现的单词。分类任务是从词汇表（总的类别）中选择可能性最高的一个作为下一个出现的单词。

3.3 前馈神经网络语言模型

使用神经网络作为模型的一个分类器
\[P(w_i\mid w_{i-2}=“\textit{cow}”,w_{i-1}=“\textit{eats}”)\]
- 输入特征：前面的两个单词
- 输出类别：下一个单词
怎样表示一个单词？
我们可以像之前一样采用 one-hot 向量表示，但是，更好的方法是 嵌入（Embeddings）。

3.4 词嵌入（Word Embeddings）

将离散的单词符号映射为一个相对低维空间中的连续向量。
词嵌入允许模型捕获单词之间的相似度。
- $\textit{dog}$ vs. $\textit{cat}$
- $\textit{walking}$ vs. $\textit{running}$
缓解数据稀疏问题。
例如，考虑语料库中有一个句子：
\[\textit{dog is walking}\]
现在，我们有一个新的句子：
\[\textit{cat is running}\]
词嵌入模型对于 “$\textit{dog}$” 和 “$\textit{cat}$” 这两个单词给出了相似的词嵌入，同理，对于 “$\textit{walking}$” 和 “$\textit{running}$” 也给出了相似的词嵌入。然后，我们的模型会意识到既然 “$\textit{dog is walking}$ ” 是一个可能的句子序列，那么，“$\textit{cat is running}$” 也应当是一个可能的句子序列。

而对于没有采用词嵌入的模型，例如 n-grams 模型，它们很难进行这种泛化，因为在这类模型看来，“$\textit{dog}$” 和 “$\textit{cat}$” 仅仅是两个离散的单词，它们之间并没有什么关联。
你可能会问，之前我们表示输入向量 $\mathbf x$ 采用的是词袋模型，而并没有采用词嵌入。事实上，这里词嵌入已经在整个神经网络架构中被隐式地定义了。可以看到，在输入层和第一个隐藏层之间的 权重向量本质上就是一种嵌入。

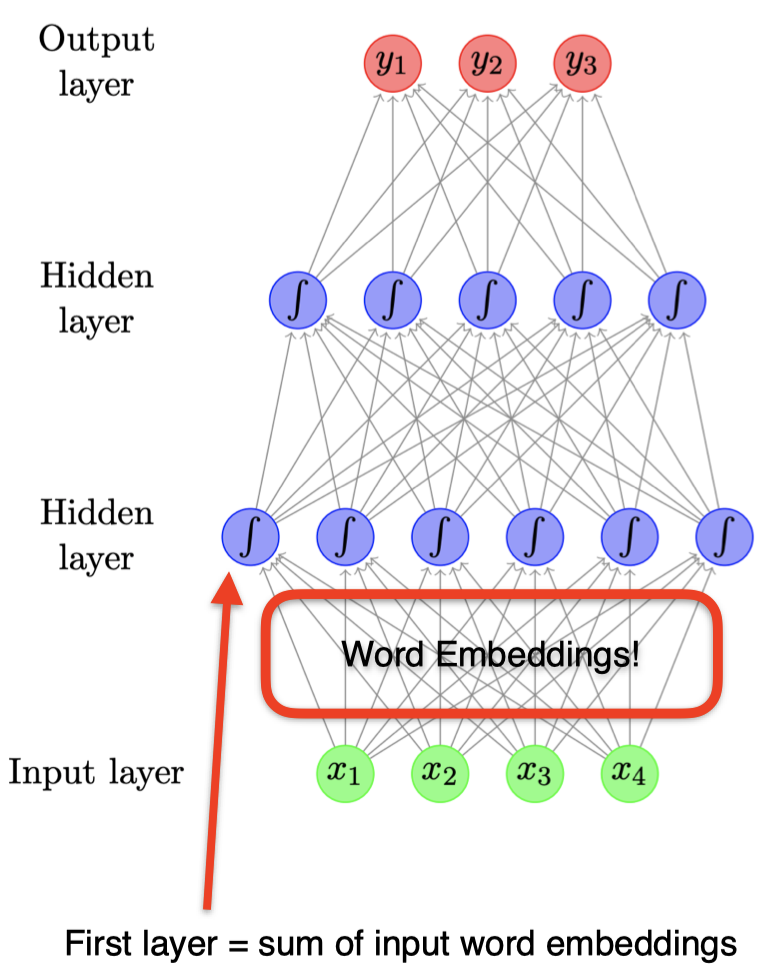
3.5 语言模型架构

那么，怎样用神经网络构建语言模型呢？下图是一个用神经网络构建语言模型的例子。

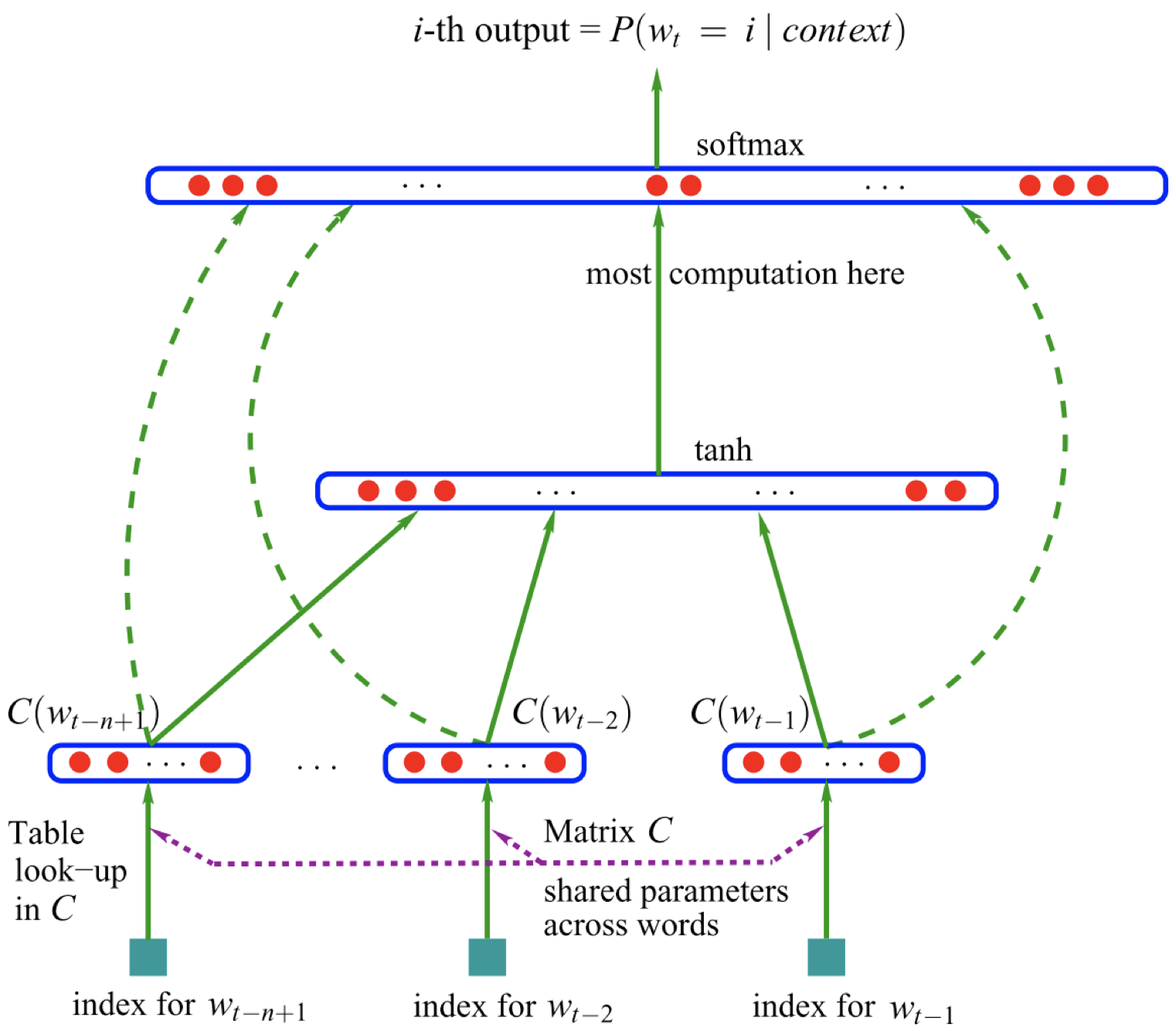
这里，我们采用 n-grams 语言模型。首先，我们观察 $(n-1)$ 个上下文单词：

\[w_{t-n+1},\dots,w_{t-2},w_{t-1}\]

并对它们进行嵌入，得到相应的词嵌入：

\[C(w_{t-n+1}),\dots,C(w_{t-2}),C(w_{t-1})\]

然后，我们将这些词嵌入连接起来，输入非线性激活函数 $\tanh$ 函数。之后，再进行解除嵌入或者进行另一个线性转换来生成输出层。很重要的一点是，我们试图预测的是一个单词，输出类别的大小实际上等于词汇表的大小，所以输出层中的单元数量实际上等于词汇表中的唯一单词数量。最后，我们在这些值上应用一个 $\text{softmax}$ 函数，从而得到一个关于所有单词概率的向量。之后，当我们要根据上下文预测下一个单词时，我们只需要选择概率向量中的最大值对应的单词作为预测单词即可。

3.6 例子

现在，我们来看一个简单的例子，输入是前面上下文的两个单词 “$\textit{cow}$” 和 “$\textit{eats}$”，然后我们试图估计下一个单词为 “$\textit{grass}$” 的概率：

\[P(w_i=“\textit{grass}”\mid w_{i-2}=“\textit{cow}”,w_{i-1}=“\textit{eats}”)\]

查看单词 “$\textit{cow}$” 和 “$\textit{eats}$” 的词嵌入：

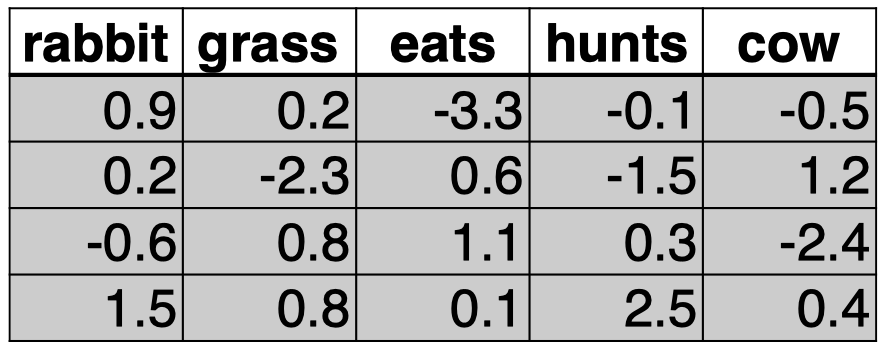
可以看到，在这个例子中，我们的词汇表中大小为 $|V|=5$，词嵌入的维度 $d=4$。
将它们连接起来，输入网络中。
\[\mathbf x=\mathbf v_{\textit{cow}}\oplus \mathbf v_{\textit{eats}}\] \[\mathbf h_1=\tanh(W_1\mathbf x+\mathbf b_1)\] \[\mathbf y=\text{softmax}(W_2\mathbf h_1)\]
首先，我们将单词 “$\textit{cow}$” 和 “$\textit{eats}$” 的词嵌入 $\mathbf v_{\textit{cow}}$ 和 $\mathbf v_{\textit{eats}}$ 连接起来作为输入向量 $\mathbf x$。然后通过权重矩阵 $W_1$ 进行加权，并加上偏置向量 $\mathbf b_1$，将结果作为非线性函数 $\tanh$ 的输入，得到隐藏层的表示 $\mathbf h_1$。利用权重矩阵 $W_2$ 对 $\mathbf h_1$ 加权，并作为函数 $\text{softmax}$ 的输入，最终得到预测结果 $\mathbf y$。
输出：$\mathbf y$ 给出了词汇表中所有单词的概率分布。

\[P(w_i=“\textit{grass}”\mid w_{i-2}=“\textit{cow}”,w_{i-1}=“\textit{eats}”)=0.8\]
该前馈神经网络模型的大部分参数都在词嵌入（即所有单词的词嵌入表，维度为 $d\times |V|$）和输出嵌入（即 $W_2$，维度为 $|V|\times d$）中。

3.7 为什么要用神经网络构建语言模型

N-grams 语言模型
- 训练成本低（只需要计算频数）
- 稀疏性问题，扩展到更大的上下文时存在问题
- 无法充分捕获单词特性（语法和语义上的相似度)，例如：$\textit{film}$ vs. $\textit{movie}$
神经网络语言模型（NNLMs）更具鲁棒性
- 强迫将单词用低维的嵌入表示
- 自动捕获单词特性，在计算句子概率时，使得估计更具鲁棒性
- 灵活性：只需稍加改变就可以适用于其他任务（例如：词性标注）

3.8 词性标注

词性标注（POS tagging）也可以被归为分类问题：
- 例如，给定当前单词 “$\textit{eats}$”，和它的前一个上下文单词 “$\textit{cow}$”，我们的目标是预测当前单词 “$\textit{eats}$” 的词性：
  \[P(t_i\mid w_{i-1}=\textit{“cow”},w_{i}=\textit{“eats”})\]
  对当前单词 “$\textit{eats}$” 的可能词性分类。
为什么不用一种更时髦的分类器呢？（神经网络）
神经网络语言模型架构可以直接适用于该任务。

3.9 前馈神经网络用于词性标注

最大熵马尔可夫模型（Maximum Entropy Markov Model, MEMM） 标注器：
- 输入：
  - 最近的单词：$w_{i-2},w_{i-1},w_{i}$
  - 最近的 tag：$t_{i-2},t_{i-1}$
- 输出：
  - 当前单词 tag：$t_{i}$
神经网络 框架：
- 输入：
  - 5 项：3 个词嵌入，2 个 tag 嵌入
- 输出：
  - 1 项：长度为 $|T|$ 的向量（$T$ 为可能的 tags 集合），使用 $\text{softmax}$ 函数
- 训练过程：
  - 最小化：$-\sum_{i}\log P(t_i\mid w_{i-2},w_{i-1},w_{i},t_{i-2},t_{i-1})$
  这里，我们有 3 个单词：$w_{i-2}=\textit{“one”},w_{i-1}=\textit{“small”},w_{i}=\textit{“step”}$，我们将其编码为词嵌入，它们共用一个嵌入矩阵。同时，我们有上下文单词 $w_{i-2},w_{i-1}$ 对应的词性标签：$t_{i-2}=\text{“CD”},t_{i-1}=\text{“JJ”}$，同理，我们将其编码为 tag 嵌入，它们共用另一个嵌入矩阵。然后，我们将得到的 5 个嵌入向量（3 个词嵌入，2 个 tag 嵌入）连接得到一个长的向量，然后作为 $\tanh$ 函数的输入，然后将计算结果传入输出层。输出层的隐藏单元数量等于所有可能的 tags 组成的集合的大小。然后，我们将 $\text{softmax}$ 函数作用于该向量上，然后我们将得到所有可能的 tags 对应的概率向量，然后只需要取其中的最大值对应的 tag 作为当前单词 $w_{i}$ 的词性标签 $t_{i}$ 即可。

3.10 卷积神经网络

最后，我们简单介绍一下卷积神经网络。

通常用于 计算机视觉（Computer Vision, CV），但也可以用于 NLP 任务。
在 CV 任务中，输入为一张图片，它由很多 像素（pixel）组成。卷积神经网络的工作机制是：每次观察图片中的一小块区域，然后用 卷积核（convolution kernel）产生一个特征方阵。对于图片中的每一个小的区域，我们都可以进行这样的操作，这样我们得到了该图片的另一种表示。如果我们采用不同的卷积核，那么将得到不同的图片表示。为什么要使用不同的卷积核呢？因为这样我们可以从不同的潜在角度（例如：颜色、边缘锐度等）来捕获图片特征。之后，我们可以进行 最大池化（max pooling）操作，同样，我们观察图片表示中的一小块区域，取其中的最大值作为该区域的表示，对其他图片表示的每个小区域都进行同样的操作，这样我们得到一些新的特征表示。最后，将得到的特征表示喂给一个全连接层，然后我们将得到分类预测的结果。
识别有代表性特征的局部预测器。
这种方法之所以效果很好的原因在于，相比一次分析整张图片，我们采用了每次只分析其中的一小块区域，本质上看，我们每次只对这一小块区域进行预测，而最大池化操作使得模型可以只保留这块区域最明显的特征。
将这些局部预测器进行结合，生成一个固定大小的表示。

3.11 卷积神经网络用于 NLP 任务

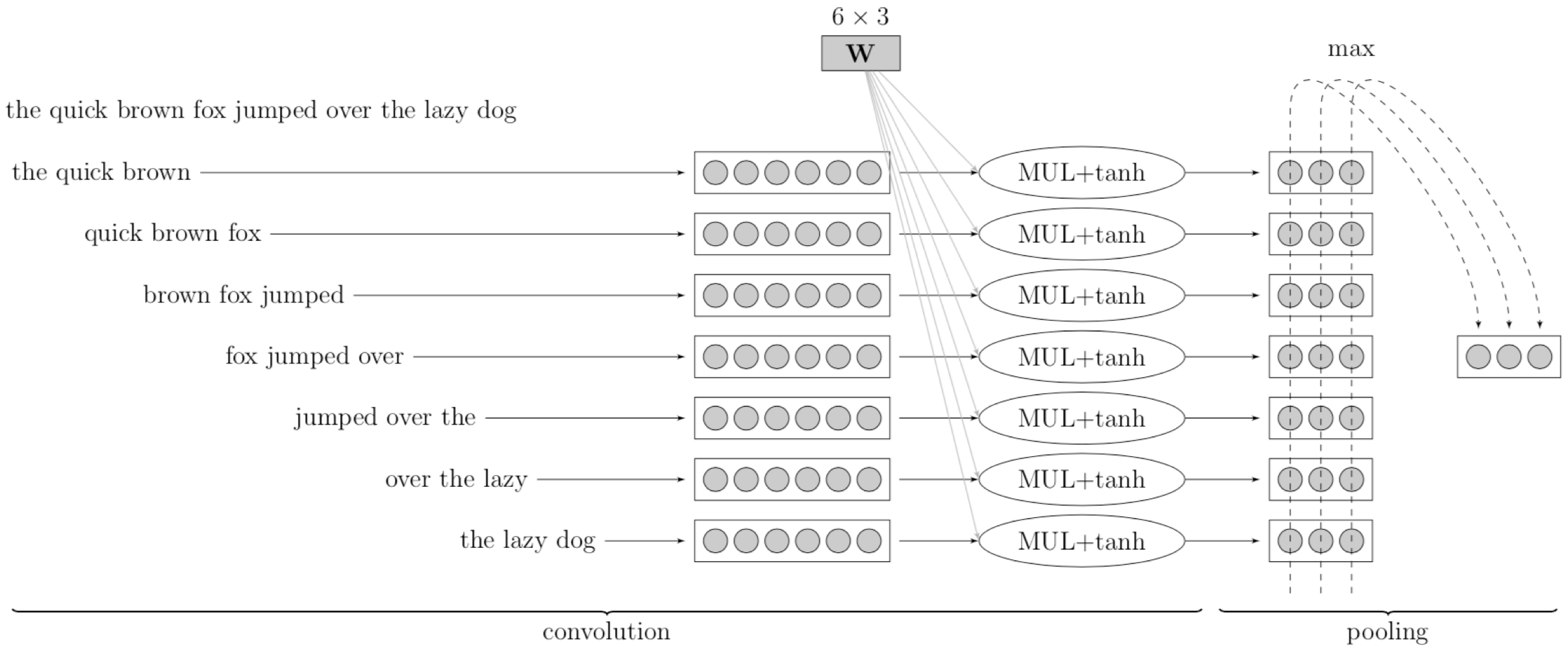
这里是一个将卷积神经网络用于 NLP 任务的例子，相比 CV 任务中的像素矩阵，在 NLP 任务中我们的数据是句子。

在整个句子上的滑动窗口（例如：$3$ 个单词）
$W$ 相当于卷积核（线性变换 + $\tanh$ 函数）
最大池化生成了一个固定大小的表示

我们可以采用和之前相同的思路：
每次观察句子的一小部分，即 滑动窗口（例如，这里窗口大小为 $3$ 个单词），窗口每次向前移动一个单词的距离。对于窗口中的每个单词，我们可以将其转换为词嵌入（例如：这里每个词嵌入的维度为 $2$），并且将其连接为一个长的向量（例如：这里该向量长度为 $3\times 2=6$）。然后，对这些连接向量进行卷积核运算（线性变换 + $\tanh$ 函数），我们将得到该窗口对应的一个隐藏特征表示（例如：这里是一个长度为 $3$ 的向量）。对每个滑动窗口进行同样操作，我们将得到一系列的隐藏特征向量。之后，进行最大池化操作，我们观察每个向量中的第一个元素，取其中最大的元素作为输出向量中的对应位置的元素，然后对第二个、第三个元素执行同样的操作。

为什么要进行最大池化操作呢？
有两个原因：1. 由于我们的句子长度是变化的，这样我们得到的特征向量的数量也是变化的，所以，通过最大池化，我们总是可以得到一个固定大小的表示。2. 另一个原因就是之前提到过的，最大池化可以帮助模型识别特征向量中最具代表性的特征。当我们进行 NLP 话题分类任务时，直觉上，我们可以想象某些特定单词对于识别话题是有帮助的，这正是最大池化所做的事情。

4. 总结

神经网络
- 鲁棒性（例如：单词变体、拼写错误等）。
- 优秀的泛化能力。
- 灵活性 —— 基于不同任务定制不同的神经网络架构。
缺点
- 训练过程比传统机器学习方法要慢得多，但是可以通过 GPU 加速。
- 参数数量很多，主要受词汇表大小、嵌入、网络深度等因素影响。
- 对数据量需求很大（data hungry），在小型数据集上表现不是很好。
- 在大型语料库上的预训练模型（例如：BERT）可以缓解数据饥饿问题。

5. 扩展阅读

Feed-forward network: G15, section 4
Convolutional network: G15, section 9

下节内容：NLP 深度学习：循环网络

本作品采用知识共享署名-非商业性使用-相同方式共享 4.0 国际许可协议进行许可。欢迎转载，并请注明来自：YEY 的博客同时保持文章内容的完整和以上声明信息！

自然语言处理 07：NLP 深度学习：前馈网络

墨尔本大学 COMP90042 课程笔记