自然语言处理 COMP90042 课程笔记

自然语言处理 13：形式语言理论和有限状态自动机

墨尔本大学 COMP90042 课程笔记

Posted by YEY on April 15, 2020

Lecture 13 形式语言理论和有限状态自动机

在接下来的两周，我们将学习 句法（syntax）相关内容。和目前为止我们学过的内容相比，这部分内容会比较偏理论。

1. 形式语言理论

1.1 什么是语言？

目前为止，我们见过了一些处理单词、句子和文档等符号序列的方法：

  • 语言模型
  • 隐马尔可夫模型
  • 循环神经网络

但是，这些模型都没有涉及到语言的本质，因为它们可以用于处理任何符号序列，而不仅限于单词、句子等。

1.2 形式语言理论

形式语言理论 (Formal Language Theory) 为我们提供了一种定义语言的框架，它是一种数学框架。

在形式语言理论中：

  • 一种语言 $=$ 字符串 (strings) 的集合
  • 一个字符串 $=$ 来自一个有限 字母集 (alphabet) 的 元素 (element) 所组成的序列
    • 字母集可以视为 词典 (vocabulary)
    • 元素可以视为 单词 (words)

1.3 动机

形式语言理论研究的是语言的 类别 (classes) 和它们的计算特性。这门课中，我们将主要介绍以下两种形式语言：

  • 正则语言 (Regular Language)
  • 上下文无关语言 (Context Free Language)

这两种语言构成了形式语言理论中的前两个类别，之后还有更复杂的 上下文敏感语言 (Context Sensitive Language) 等，但是这门课中我们不会对其进行过多展开。

主要目的是为了解决 从属问题 (membership problem)：一个字符串是否属于某种语言。

那么，我们应该怎样做呢？我们可以定义该语言的 语法 (grammar)，然后检查该字符串是否符合该语法规则。

1.4 例子

  • 二进制串（Binary strings）以 0 开头，以 1 结尾
    • \(\{01, 001, 011, 0001, \dots\}\) ⭕️
    • \(\{1, 0, 00, 11, 100, \dots\}\) ❌
  • 来自字母集 \(\{a, b\}\) 的偶数长度的序列
    • \(\{aa, ab, ba, bb, aaaa, \dots\}\) ⭕️
    • \(\{aaa, aba, bbb, \dots\}\) ❌
  • 以 wh- 类型的单词作为开头，问号 ？结尾的英文句子
    • \(\{\textit{what }?, \textit{where my pants }?, \dots\}\) ⭕️

1.5 除了从属问题之外的问题

  • 从属问题（Membership）
    • 某个字符串是否属于某种语言？是/否
  • 记分（Scoring）
    • 具有记分等级的从属关系
    • 某个字符串在多大程度上可以被接受？（语言模型）
  • 转导（Transduction）
    • 将一个字符串转变为另一个字符串（词干提取 stemming）

1.6 概览

本节课，我们主要涉及以下内容：

  • 正则语言（Regular languages）
  • 有限状态接收器 & 转换器（Finite state acceptors & transducers）
  • 单词形态学建模（Modelling word morphology）

2. 正则语言

2.1 正则语言

  • 正则语言（Regular language）：语言中最简单的类别。
  • 任何 正则表达式（regular expression）都是一种正则语言。
    • 描述了什么样的字符串是该语言的一部分
  • 正式地，一个正则表达式包含以下运算：
    • 从字母集中抽样得到的符号：$\Sigma$
    • 空字符串：$\varepsilon$
    • 两个正则表达式的连接：$RS$
    • 两个正则表达式的交替：$R\mid S$
    • 星号表示出现 0 次或者重复多次：$R^*$
    • 圆括号定义运算的有效范围：$()$

2.2 正则语言的例子

  • 二进制串（Binary strings）以 0 开头，以 1 结尾
    • $0 \,(0\mid 1)^* 1$
  • 来自字母集 \(\{a, b\}\) 的偶数长度的序列
    • $((aa)\mid (ab)\mid (ba)\mid (bb))^*$
  • 以 wh- 类型的单词作为开头，问号 ？结尾的英文句子
    • $((what)\mid (where)\mid (why)\mid (which)\mid (whose)\mid (whom))\Sigma^*?$

2.3 正则语言的性质

  • 封闭（Closure）：如果我们对正则语言 L1 和 L2 进行合并，得到的结果仍然是正则语言吗？如果是，那么我们将该运算称为 封闭运算（closed operation）。
  • 在以下运算中，正则语言是封闭的：
    • 连接（concatenation）和 求并（union）：来自封闭的定义。
    • 求交（intersection）：在正则语言 L1 和 L2 中都合法的字符串。
    • 求反（negation）：不在正则语言 L 中的字符串。
  • 这种性质非常万金油，可以有不同的正则语言来描述语言的不同性质，然后将它们合并起来。
    • 可以使用相同的核心算法来完成这些事。

3. 有限状态接收器（FSA）

3.1 有限状态接收器

  • 正则表达式定义了一个正则语言。
  • 但是，它并没有给出一种算法来检查某个字符串是否属于该语言。
  • 有限状态接收器（Finite state acceptors，FSA）给出了检查某个成员（字符串）是否属于某个正则语言的算法。
  • FSA 包含：
    • 输入符号的字母集：$\Sigma$
    • 状态集合：$Q$
    • 起始状态：$q_0\in Q$
    • 最终状态：$F\subseteq Q$
    • 转移函数：符号和状态 $\to$ 下一个状态
  • 如果存在一条从 $q_0$ 到最终状态的 路径（path），并且转移函数与路径上的每个符号都匹配，则接受该字符串。
    • Djisktra 最短路径算法，$O(V\log V +E)$

3.2 FSA 的例子

  • 输入字母集：\(\{a,b\}\)
  • 状态：\(\{q_0,q_1\}\)
  • 起始状态：$q_0$
  • 最终状态：\(\{q_1\}\)
  • 转移函数：\(\{(q_0,a) \to q_0, \;(q_0,b) \to q_1, \;(q_1,b) \to q_1\}\)
  • 注意：如果在 $q_1$ 状态下应用 $a$ 符号会导致失败。
  • 接受 $a^*bb^*$

3.3 派生形态

使用词缀（affixes）将一个单词变为另外一种语法类别：

  • $\textit{grace} \to \textit{graceful} \to \textit{gracefully}$
  • $\textit{grace} \to \textit{disgrace} \to \textit{disgracefully}$
  • $\textit{allure} \to \textit{alluring} \to \textit{alluringly}$
  • $\textit{allure} \to *\textit{allureful}$
  • $\textit{allure} \to *\textit{disallure}$

注：$*$ 表示无效派生

3.4 FSA 用于单词形态学

为什么 FSA 可以用于单词形态学？

因为可以看到，FSA（几乎）具有一致的处理流程。那么，我们可以将其描述为一种正则语言吗？

  • 希望接受有效形式，拒绝无效形式（带 $*$ 标记）
  • 泛化到其他单词，例如：表现类似 $\textit{grace}$ 或者 $\textit{allure}$ 的名词

下面是一个 FSA 用于单词形态学的例子：

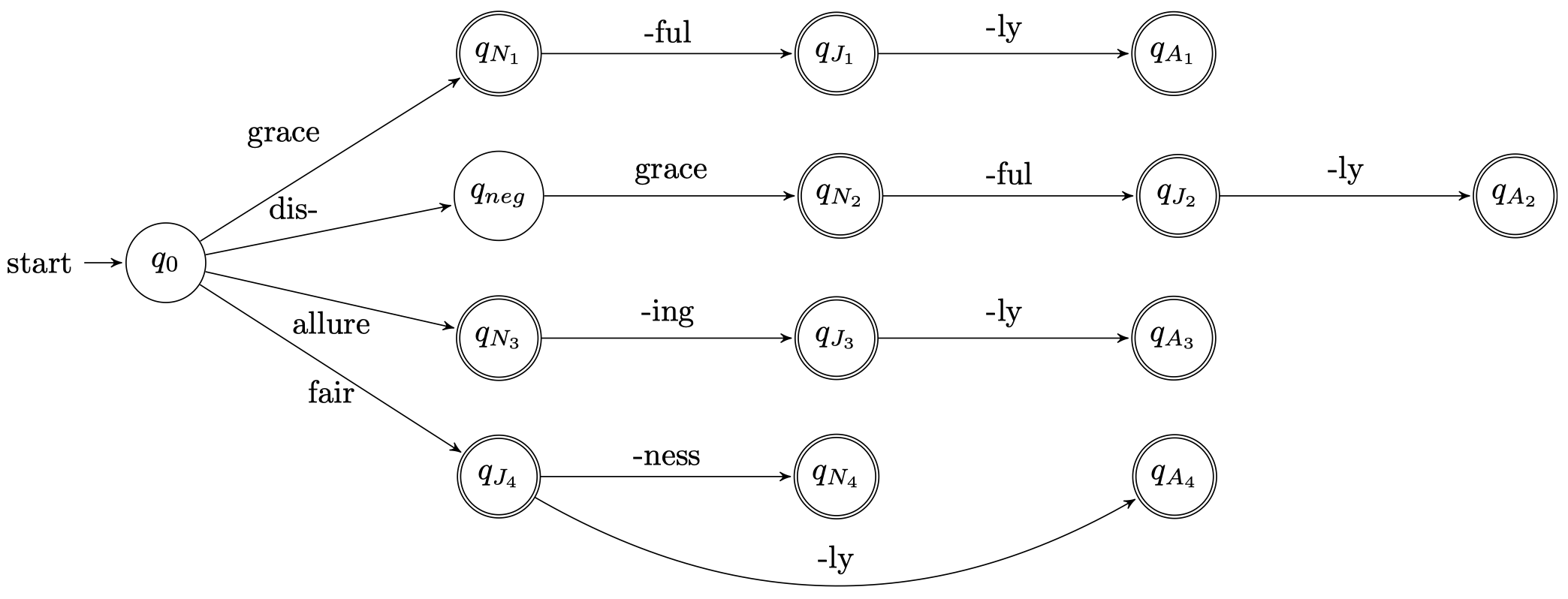
我们可以将上图进行一些压缩处理，合并一些具有共同路径的分支：

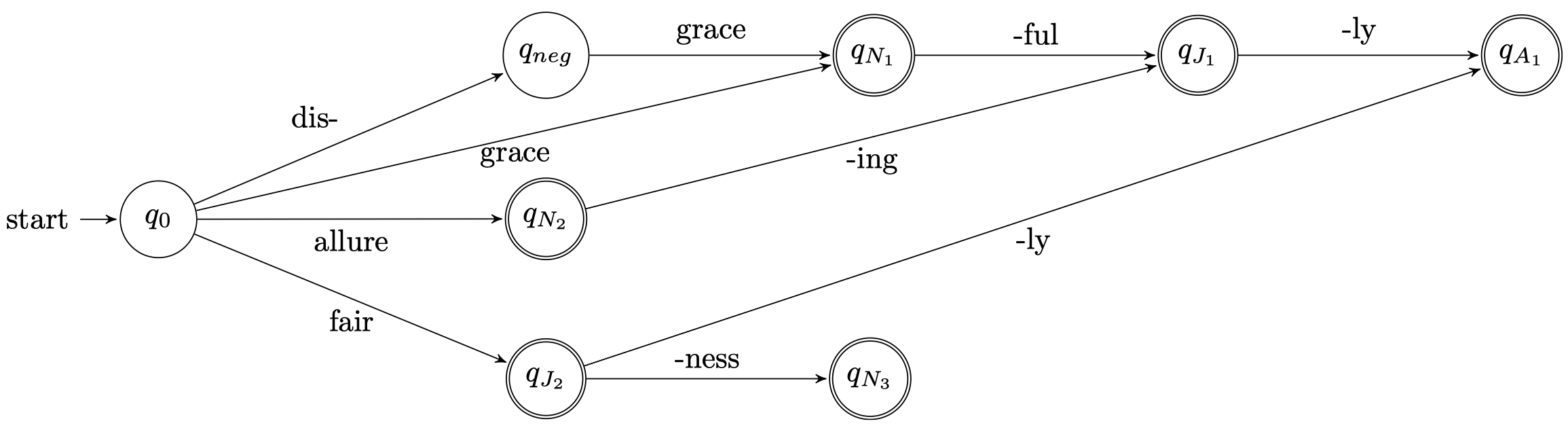
我们还可以加入更多的单词，并对其中具备相似性质的单词进行合并，当我们构建了这样一个非常复杂的 FSA 之后，我们就可以检查某个单词是否可以派生出一些其他合法的形态。

4. 加权 FSA

4.1 加权 FSA

我们已经介绍了 FSA 作为一种从属问题的二分类检测器，即某个单词是否可以添加相应的词缀来生成新的合法单词。但是，有时我们希望这个过程可以具有更多的记分性质，不仅仅是单纯的非此即彼的二分类问题。

  • 有些单词比其他单词更有可能被接受：
    • $\textit{fishful}$ vs. $\textit{disgracelyful}$
      虽然二者都不是合法的英文单词，但是，从某种程度上，我们可以认为 $\textit{fishful}$ 要比 $\textit{disgracelyful}$ 更有可能作为一个合法英文单词，因为其从字面上更容易理解一些。
    • $\textit{musicky}$ vs. $\textit{writey}$
      同理，$\textit{musicky}$ 要比 $\textit{writey}$ 更有可能成为一个形容词。所以，有些单词作为合法单词的可能性要高于其他一些单词，语言和单词并不仅仅是二元类别的。
  • 关于可接受程度的记分方式 —— 加权 FSA：
    • 状态集合：$Q$
    • 输入符号的字母集：$\Sigma$
    • 起始状态加权函数：$\lambda: Q \to \mathbb R$
    • 最终状态加权函数：$\rho: Q \to \mathbb R$
    • 转移函数：$\delta: (Q,\Sigma, Q) \to \mathbb R$

4.2 WFSA 最短路径

对于路径 $\pi=t_1,\dots, t_N$，现在其总分为：

\[\lambda(t_0)+\sum_{i=1}^{N}\delta(t_i)+\rho(t_N)\]

其中，每个 $t$ 都是一条边，因此在分数计算中，更正式的方式是使用转移前后的状态和边的标签。

利用 最短路径算法 来找到具有最小代价的路径 $\pi$，计算复杂度和之前一样，为 $O(V\log V+E)$。

4.3 N-gram 语言模型作为 WFSA

这里，我们使用 n-gram 语言模型作为一个例子，来看一下如何利用 WFSA 来衡量 n-gram 概率。

回忆一下，在 n-gram 语言模型中， 我们采用如下方式对字符串（句子）进行记分：

\[P(w_1,\dots,w_M)\approx \prod_{m=1}^{M}P_n(w_m\mid w_{m-1},\dots,w_{m-n+1})\]

现在，我们用 FSA 表示 Unigram 语言模型：

  • 一个状态：$q_0$
  • 状态转移得分：$\delta(q_0,w,q_0)=\log P_1(w)$
  • 初始状态和最终状态得分 $=0$

  • 序列 $w_1, w_2, \dots, w_M$ 的路径得分为：

    \[0+\sum_{m}^{M}\delta(q_0,w_m,q_0)+0=\sum_{m}^{M}\log P_1(w_m)\]

现在，让我们再来看一下 Bigram 语言模型：

\[P(w_1,w_2,\dots,w_M)=\prod_{i=1}^{M}P(w_i\mid w_{i-1})\]

Bigram 语言模型的 WFSA 实现：

  • 输入符号的字母集：$\Sigma=$ 单词 types 的集合（即词汇表 vocabulary）
  • 状态集合：$Q=\Sigma$（状态数量 $=$ 单词 types 的数量）
    因为在 Bigram 语言模型下，我们需要一个状态来记住当前单词的前一个上下文单词。
  • 起始状态加权函数：\(\lambda(q_i)=\log P(w_1=i\mid w_0 = \texttt{<s>})\)
  • 最终状态加权函数：\(\rho(q_i)=\log P(w_{M+1}=\texttt{</s>}\mid w_M=i)\)

  • 转移函数：

    \[\delta(q_i,w,q_j)=\begin{cases} \log P(w_m=j\mid w_{m-1}=i),& \; w=j\\-\infty,& \; w \ne j \end{cases}\]

5. 有限状态转换器（FST）

5.1 有限状态转换器

很多时候，我们并不希望只是接受字符串或者对其进行记分，我们还希望可以将其转换为另一种语言，并且进行相应的语法修正，并从句法上分析其结构等等。

回顾之前将 FSA 用于单词形态学的例子：

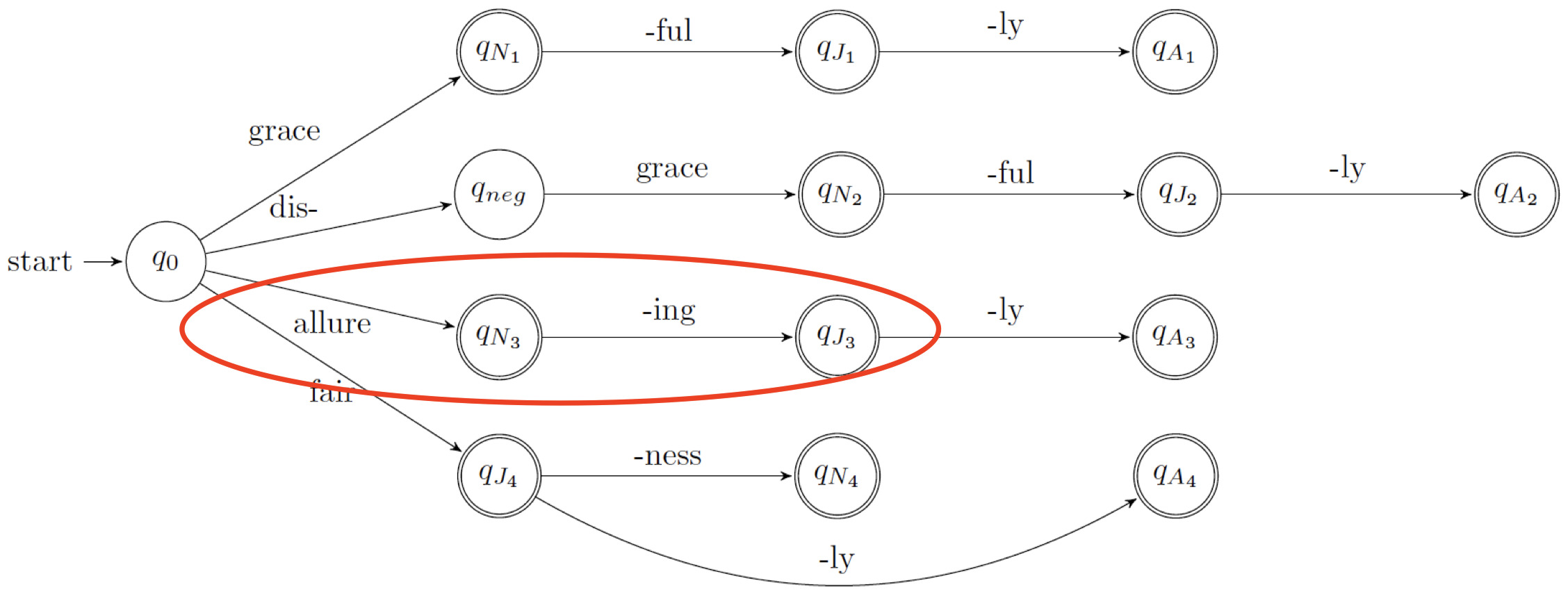
  • FSA：$\textit{allure}+\textit{ing}=\textit{allureing}$
  • FST：$\textit{allure}+\textit{ing}=\textit{alluring}$

可以看到，FSA 可以为单词添加词缀，将 $\textit{allure}$ 变为 $\textit{allureing}$，但是 $\textit{allureing}$ 并不是一个合法的英文单词，我们需要将其中的 “$e$” 去掉，而 FSA 并不能做到这点，因为 FSA 不会替换任何东西，而 FST 可以很好地处理这种情况。

有限状态转换器（Finite State Transducers，FST）：

  • FST 在 FSA 的基础上增加了字符串的输出能力：
    • 包含一个 输出字母集（output alphabet）
    • 现在，转移函数会采用输入符号并发出输出符号 $(Q,\Sigma, \Sigma, Q)$
      其中，第一个 $Q$ 表示输入状态，最后一个 $Q$ 表示输出状态，第一个 $\Sigma$ 表示输入字母集，第二个 $\Sigma$ 表示输出字母集。
  • 可以进行 加权 $=$ WFST
    • 为转移函数进行记分
  • 例如：将 编辑距离（edit distance）作为 WFST，它接受一个输入字符串和一个输出字符串，并返回从输入字符串转变为输出字符串的代价。
    • 只有当两个字符串相同时，代价才为 0。

5.2 编辑距离自动机

这里是一个 编辑距离自动机 (Edit Distance Automata) 的例子：

\[\begin{align} \delta(q,a,a,q) &= \delta(q,b,b,q)=0 \\ \delta(q,a,b,q) &= \delta(q,b,a,q)=1 \\ \delta(q,a,\varepsilon,q) &= \delta(q,b,\varepsilon,q)=1 \\ \delta(q,\varepsilon,a,q) &= \delta(q,\varepsilon,b,q)=1 \end{align}\]

其中，$\delta$ 是状态转移的记分函数，在编辑距离的 WFST 实现下，我们只需要一个状态 $q$。上面的式子表明：将 $a$ 替换为 $a$ 或者将 $b$ 替换为 $b$ 的代价为 $0$；将 $a$ 替换为 $b$ 或者将 $b$ 替换为 $a$ 的代价为 $1$；将 $a$ 删除或者将 $b$ 删除的代价为 $1$；插入一个 $a$ 或者 $b$ 的代价为 1。

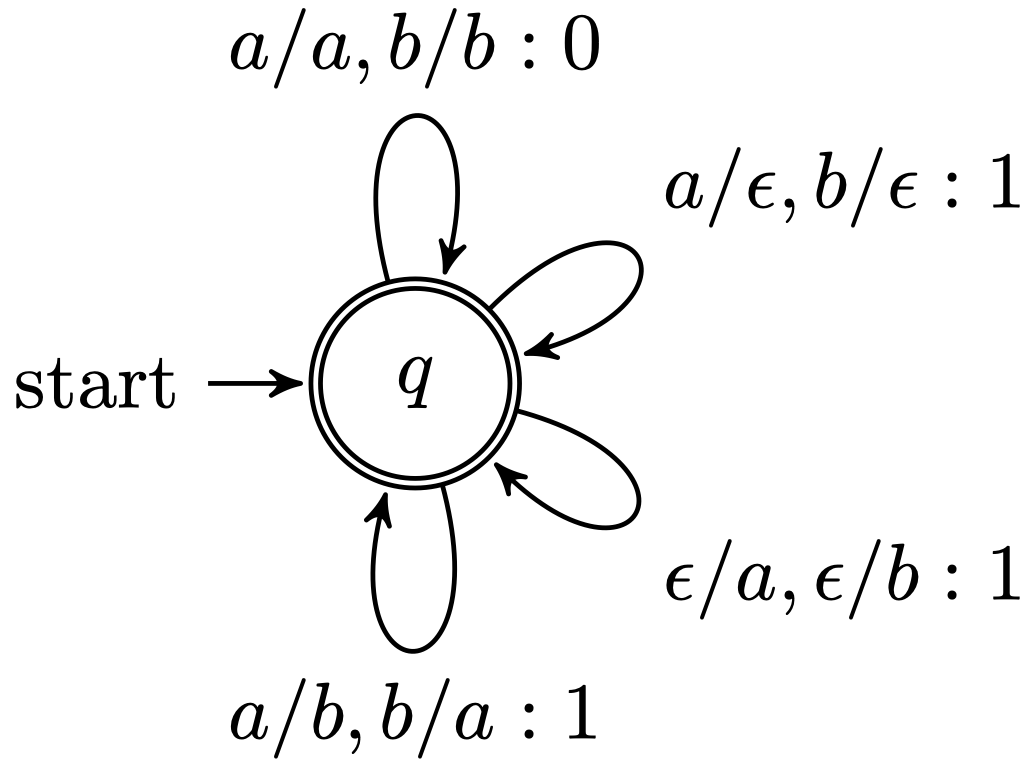
例如：

  • 输入字符串为 $ab$，输出字符串为 $bb$：
    $ab \to bb: 1$
  • 输入字符串为 $ab$，输出字符串为 $aaab$：
    $ab \to aaab: 2$

5.3 FST 用于屈折形态

我们还可以将 FST 用于单词的 屈折形态（Inflectional Morphology）。

在西班牙语中，动词的屈折形态必须和主语在人称和数量上保持一致。

可以看到，在西班牙语中，动词的屈折形态要比英语中更加复杂，不同的人称和数量的组合会产生不同的屈折形态（$canto$、$cantas$、$canta$ 等），而英语中只有两种不同形态（$sing$ 和 $sings$）。

我们可以采用 FST 来进行 形态学分析（morphological analysis）。这里，我们的目标为：

\[\textit{canto}\to \textit{cantar} + \text{VERB} + \text{present} + 1\text{P} + \text{singular}\]

即给定单词 $canto$，我们希望知道它是如何得到的。例如，它可以由 $cantar$，加上动词（VERB）属性，加上现在时态（present），加上第一人称（1P），加上单数形式（singular）得到。

5.4 FST 用于西班牙语屈折形态

现在，假设我们已经花费了很多时间构建了下面的 FST 树用于西班牙语的屈折形态分析。这棵 FST 树将告诉我们如何对每个字母进行替换，并得到最终的屈折形态。

例如，给定单词 $\textit{canto}$，上面的 FST 树可以生成 2 种屈折形态：

  • $\textit{canto} \to \textit{canto} + \text{Noun} + \text{Masc} + \text{Sing}$
  • $\textit{canto}\to \textit{cantar} + \text{Verb} + \text{PresInd} + 1\text{P} + \text{Sing}$

5.5 FST 压缩

给定两个 FST，我们可以将其中一个 FST $T_1$ 的输出，作为另外一个 FST $T_2$ 的输入，来对其进行压缩。

  • 记为 $T_1\circ T_2$，压缩两个 FST 会产生一个新的 FST
  • 另外，我们也可以将 FST 和 FSA 进行压缩，结果为一个新的 FST

我们为什么对 FST 的压缩感兴趣呢？

因为就像正则表达式一样，通过对相近的 FST 其进行合并，我们可以为语言中的不同部分构建不同的 FST 树。

下面是一个对 FST 进行压缩的例子：

  • 在英语中，-$ed$ 用于单数过去时态
    • $\textit{cook}\to \textit{cooked}$
    • $\textit{want}\to \textit{wanted}$
  • 但是，当单词以 “$e$” 结尾时，我们希望避免产生连续的 “$e$”（例如：$\textit{bakeed}$）
  • 解决方案：构建 2 个 FST
    • FST $T_1$：$\textit{bake}+\text{PAST}\to \textit{bake}+\textit{ed}$
    • FST $T_2$：$\textit{bake}+\textit{ed}\to \textit{baked}$

6. 自然语言是正则语言吗？

我们已经学习了很多关于正则语言的知识，包括如何通过正则表达式定义其语法等等。现在，我们思考一个问题：自然语言是正则语言吗？或者说，我们可以用正则表达式定义自然语言吗？

6.1 正则语言

某些情况下，我们可以将自然语言视为正则语言。例如：

  • 句子长度是无界的（递归的），但是结构是 局部的 $\to$ 可以采用 FSA 描述 $=$ 正则语言。
  • $(\text{Det Noun Prep Verb})^*$

6.2 非正则语言

现在，我们来看一下非正则语言的情况。

带有完整圆括号的算术表达式可以视为非正则语言：

  • $\color{orange}{(} a+\color{blue}{(}b\times \color{red}{(} c\,/\,d \color{red}{)} \color{blue}{)} \color{orange}{)}$
  • 算术表达式可以具有任意多的开放圆括号。
  • 需要记住出现了多少个开放圆括号，以产生相同数量的闭合圆括号。
  • 无法用有限数量的状态描述。

同理，对于 $a^n b^n$ 这种形式的语言，如果 $a$ 出现了 $n$ 次，那么 $b$ 同样需要出现 $n$ 次，这和上面算术表达式中的圆括号是一样的情况，我们无法用正则表达式对其进行描述。

6.3 中心嵌入

在自然语言中，还有一种被称为 中心嵌入（Center Embedding）的现象：相关的从句是以中心方式嵌入的。例如：

  • $\textit{The cat loves Mozart}$
  • $\textit{The cat }\color{red}{\textit{the dog chased }}\textit{loves Mozart}$
  • $\textit{The cat }\color{red}{\textit{the dog }}\color{blue}{\textit{the rat bit }}\color{red}{\textit{chased }}\textit{loves Mozart}$
  • $\textit{The cat }\color{red}{\textit{the dog }}\color{blue}{\textit{the rat }}\color{orange}{\textit{the elephant admired }}\color{blue}{\textit{bit }}\color{red}{\textit{chased }}\textit{loves Mozart}$

需要记住 $n$ 个主语名词，以确保其后紧跟 $n$ 个动词。例如：假如我们有 2 个名词 $\textit{cat}$ 和 $\textit{dog}$，那么其后也必须跟 2 个动词 $\textit{chased}$ 和 $\textit{loves}$。这和之前 $a^n b^n$ 的情况非常类似，因此，这种情况下，我们的语言不再是正则的。

因此，我们需要（至少是）上下文无关语法 (context-free grammar) 来描述这种情况，和正则语言相比，它具有更少的约束，可能捕获更多的自然语言的特性。

7. 总结

本节课，我们学习了：

  • 在形式语言理论的框架下，语言和语法的概念
  • 正则语言
  • 有限状态自动机：接收器和转换器
  • 封闭性质
  • 加权变体 & 最短路径推断
  • 将 FSA/FST 应用于编辑距离和单词形态学

8. 扩展阅读

  • E18, Chapter 9.1

下节内容：上下文无关语法

知识共享许可协议本作品采用知识共享署名-非商业性使用-相同方式共享 4.0 国际许可协议进行许可。 欢迎转载，并请注明来自：YEY 的博客 同时保持文章内容的完整和以上声明信息！
CATALOG
    FEATURED TAGS
    随笔 课程笔记 统计机器学习 COMP90051 学习笔记 自然语言处理 COMP90042 PyTorch 人工智能伦理 COMP90087 数据科学多元统计学 MAST90138 AI 自动规划 COMP90054 数据分析 计算统计学与数据科学 MAST90083 高级数据库系统 COMP90050 统计建模 MAST90139 读书 📚 MySQL 学习索引 Hive 技术问题 Jekyll Workshop
    FRIENDS