Lecture 12 博弈论:正则形式博弈
本节课我们将对博弈论中的一些基础知识进行简单介绍。当然,这里讨论的材料只是冰山一角,而且有许多其他资料对于这个主题的介绍更加全面,这里将仅介绍一些最基本的概。更多相关内容可参考:http://www.stanford.edu/∼jacksonm/
进行 非合作博弈论分析(noncooperative game-theoretic analysis)的基本要素是:
- 根据玩家可采取的 行动(actions)及其 收益(payoffs)作为 行动的函数(a function of actions)来 确定情境(framing the situation);
- 使用各种 均衡概念(equilibrium notions)来进行描述性或指示性的预测。
在构建分析框架时,有一些很重要的问题需要考虑:
- 首先,谁是 玩家(players)?
他们可能是人、公司、组织、政府、种族团体等等。 - 其次,他们有哪些 可采取的行动(available actions)?
我们应当列出这些玩家可能采取的那些对任何玩家的收益可能产生影响的所有行动。 - 第三,互动的时间限制(the timing of interactions)是多久?是 同时(simultaneously)采取行动还是 按顺序(sequentially)采取行动?是否重复互动?
游戏的顺序也很重要。对于玩家 $i$ 而言,在另一位玩家之后行动可以让其知道另一位玩家做了什么;但是相应地,从失去时机和某些行动的可采取性而言,这也可能使玩家 $i$ 处于劣势。当不同的玩家在采取行动时,他们会获得什么信息? - 第四,互动给各玩家带来的 收益(payoffs)是什么?
确定收益(Ascertaining payoffs)涉及到对所有参与者的每种潜在选择集的成本和收益进行估计。许多情况下,估计某些玩家(例如,自己)的收益可能比其他玩家容易,并且我们可能并不清楚其他玩家是否也在按策略思考,我们可以进行 敏感性分析(sensitivity analysis)。
一旦我们确定了情况框架,我们就可以从不同玩家的视角出发,分析哪些行动对他们而言是最优的。我们可以使用不同的标准来衡量这种最优性。
1. 正则形式博弈(Games in Normal Form)
让我们从一个博弈的标准表示开始,这被称为 正则形式博弈(normal form game),或者 战略形式博弈(strategic form game):
- 玩家集合 \(N=\{1,\dots,n\}\)
- 玩家 $i$ 具有一个可选行动集合 $a_i$;这些通常称为 纯策略(pure strategies)(这里,“纯” 策略表示选择了一个行动,相对的,混合策略会对一系列行动进行随机分配)。该集合可以是有限的或者无限的。
- 令 $a=a_1\times \cdots \times a_n$ 是纯策略或行动的所有 配置(profiles)的集合,其通用元素由 $a =(a_1,\dots,a_n)$ 表示。
- 玩家 $i$ 的收益是所采取的行动向量的一个函数 $u_i: A\to \mathbb R$,其中,$u_i(a)$ 是玩家 $i$ 的收益,如果 $a$ 是该环境下中所选择的行动配置。
正则形式博弈通常可以用一张表来表示。此类博弈中最著名的例子是所谓的 囚徒困境(prisoners’ dilemma),如表 1 所示。在此博弈中,有两个玩家各自具有两种纯策略,其中 \(a_i= \{C,D\}\),$C$ 代表 “合作(cooperate)”,而 $D$ 代表 “背叛(defect)”。表中每个单元格的第一个数字表示行玩家(或玩家 1)的收益,它是行动对的一个函数,而第二个数字表示列玩家(或玩家 2)的收益。
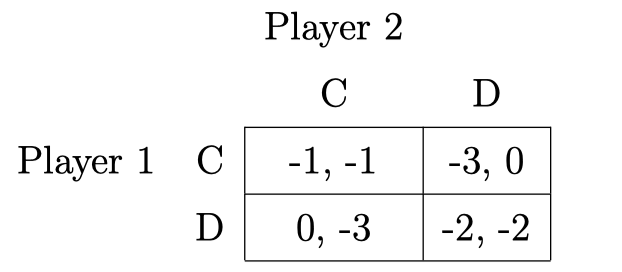
在囚徒困境中,收益背后的故事通常如下:这两名玩家犯了罪,现在在警察局的不同房间里。检察官分别告诉他们:“如果你认罪并同意举证对方,而对方不认罪的话,我可以立即释放你。如果你们两人都认罪,那么你们两人都会被判处 $2$ 年刑期。如果你不认罪而对方认罪了,那么你将被判处 $3$ 年刑期。如果你们之中没有人认罪,那么我将根据目前手上的证据以较轻的罪行起诉你们,而你们每人都将被判处 $1$ 年刑期。” 因此,矩阵中的收益是以服刑年限表示的损失时间。合作(C)是指与其他玩家合作,而背叛(D)是指认罪并举证其他玩家。
注意,我们还可以将每个收益乘以一个缩放因子,然后加上一个常数,这样,我们将得到一个等效表示形式(只要对所有给定玩家的收益都以相同方式进行缩放)。例如,在表 2 中,我将每个数字翻倍并加上 $6$。在这种转换下,游戏的战略方面将保持不变。
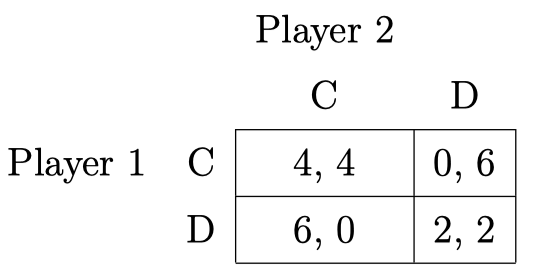
还有许多博弈可能有着不同的描述版本,但就博弈的战略方面而言,它们具有相似的正则形式。另一个与囚徒困境属于相同博弈的例子是 古诺双头垄断(Cournot duopoly),故事如下:两家公司生产相同的商品,他们都有两种不同级别的产能,高或低。如果他们以高产能生产,他们将有很多商品要卖,而在低产能时它们将卖得少。如果他们选择合作,则他们同意以低产能生产各自的商品。在这种情况下,该商品将由于稀有而在市场上卖到很高的价格,这种情况下,两家公司各自的利润为 $4$。而如果它们各自以高产能生产商品(或者说选择背叛),那么商品价格将被压低,即使他们因此能卖出更多的商品,由于商品价格的大幅下降,他们的整体利润将降低到 $2$。而如果一方选择背叛而另一方选择合作,那么该商品价格将处于中间范围,此时,选择较高产能的公司将通过销售更多商品获得较高利润为 $6$,而选择较低产能的公司仅能覆盖其成本,即获得利润为 $0$。
1.1 占优策略(Dominant Strategies)
给定正则形式博弈,我们便可以预测哪些行动将会被选择。当存在 “占优策略” 时,预测会变得特别容易。对于一名玩家来说,一个占优策略就是 在其他玩家的每一个可能行动中 都能产生最高收益的策略。也就是说,策略 $a_i\in a_i$ 是玩家 $i$ 的一个 占优(或者弱占优)策略(dominant / weakly dominant strategy),如果 $u_i(a_i,a_{-i})\ge u_i(a_i’,a_{-i})$ 对于所有的 $a_i’$ 并且 $a_{-i}\in a_{-i}$。
下节内容:更高效的强化学习:回报设计和 $Q$-函数逼近
本作品采用知识共享署名-非商业性使用-相同方式共享 4.0 国际许可协议进行许可。 欢迎转载,并请注明来自:YEY 的博客 同时保持文章内容的完整和以上声明信息!