Lecture 01 导论
参考教材:
- Gareth, J., Daniela, W., Trevor, H., & Robert, T. (2013). An intruduction to statistical learning: with applications in R. Spinger.
- Hastie, T., Tibshirani, R., & Friedman, J. (2009). The elements of statistical learning: data mining, inference, and prediction. Spinger Science & Business Media.
1. 导论
1.1 内容安排
本课程中,我们将尝试覆盖以下 6 个主题:
- 回归与分类
- 重采样和模型选择
- 样条 (Splines) 和 广义加性模型 (GAMs)
- 基于树的方法和 SVMs
- 无监督学习
- 神经网络
1.2 统计学习概览
统计学习 (Statistical Learning) 是一套以 理解数据 (understanding data) 为目的的庞大工具集。
统计学习的工具可以分为两大类:有监督的 (supervised) 和 无监督的 (unsupervised)。
有监督统计学习 主要有两种用途:1. 构建统计模型用于预测;2. 对一个或多个给定的 输入 (input) 估计某个 输出 (output)。
在 无监督统计学习 中,有输入但无监督输出;但是,我们可以从这些数据中学习 关系和结构。
1.3 有监督学习:回归与分类
- 像工资数据这类涉及预测连续或定量的输出值。这通常称为 回归 (regression) 问题。
- 但是,在某些情况下,我们可能希望预测的是一个非数值的值,即一个类别或定性输出。这称为 分类 (classification) 问题。例如:股市数据。
回归的例子:工资预测
这个例子中,我们将考察与美国中部大西洋地区男性收入相关的几个因素。具体来说,我们希望理解员工的 age (年龄)、education (受教育程度)、year (工龄) 与其历年 wage (工资)的关系。
- 输入 (特征):
age,year和education - 输出 (标签):
wage
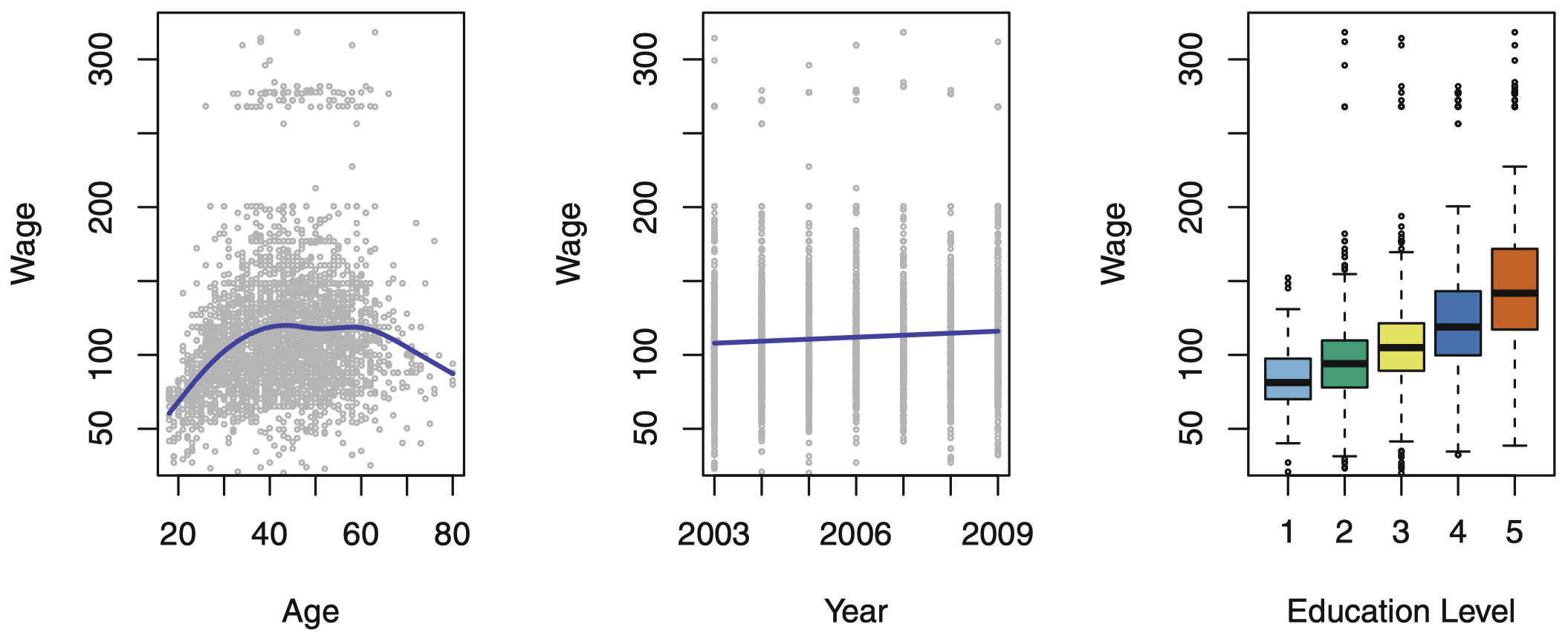
图 1:Wage 数据,其中包含美国大西洋中部地区男性收入调查信息。左图:wage 与 age 的函数关系,平均来看,随着 age 的增长 wage 是增加的,这种趋势在 60 岁左右终止,之后 wage 开始下降。中图:wage 与 year 的函数关系,呈现出缓慢而稳定的增长,2003 ~ 2009 年平均 wage 约增加了 10,000 美元。右图:箱型图反映了 wage 与 education 的函数关系,其中最低的教育水平取值 1 (没有高中文凭) ,最高的教育水平取值 5 (高级研究生学位) ,平均来说,wage 随受教育水平呈现递增关系。
分类的例子:股市数据
这里,我们将考察一个股票市场数据集 Srnarket,它收集了 2001 年至 2005 年间的标准普尔 500 股票指数 (S&P) 每日股指变动数据。我们的目标是用过去 3 天指数的变动比例预测 3 天后股指的涨跌状态。这个问题中的统计学习模型不是对数值类型的变量预测,而是关注某一天的股市业绩是掉进 Up 桶还是 Down 桶。我们希望能够精准预测市场行情的变动方向。
- 输入 (特征):过去 3 天的标准普尔指数 (S&P Index) 的变动比例
- 输出 (标签):
Up(上涨) 或者Down(下跌)

图 2:左图:前一天标准普尔股指百分比变化,箱线图表示由 Smarket 数据所得到的市场上涨和下跌的情况。中图和右图:内容与左图类似,分别显示的是 2 天和 3 天前标准普尔股指百分比变化情况。
1.4 无监督学习:聚类
前面两个应用的数据集中既有输入变量也有输出变量。然而,还有另一类不同的重要问题,即观察到的只有输入变量却没有相应的输出变量。例如,在营销领域中,可以采集到现有客户或潜在客户的人口信息。建模的目标是希望理解哪些类型的客户在他们所被观察到的属性上彼此相似,并形成一个族群。这就是一个 聚类(clustering) 问题。不同于之前的例子,这里我们并不打算预测输出变量。
聚类的例子:基因表达数据
这里,我们以 NCI60 (基因表达) 数据集为例,其中包含了 64 个癌症细胞系 6830 个基因表达测量数据。这个例子中我们感兴趣的并不是要对某个指定的输出预测,而是在基因表达测量上的细胞系数据中是否有集群存在。
这 64 个细胞系可以通过两个变量 Z1 和 Z2 来表达,这 两个变量是数据中的前两个 主成分 (principal component),综合了各个细胞系 6830 个基因表达测量信息。虽然降维可能导致部分信息损失,但却使得能进行验证聚类合理性的可视化分析。
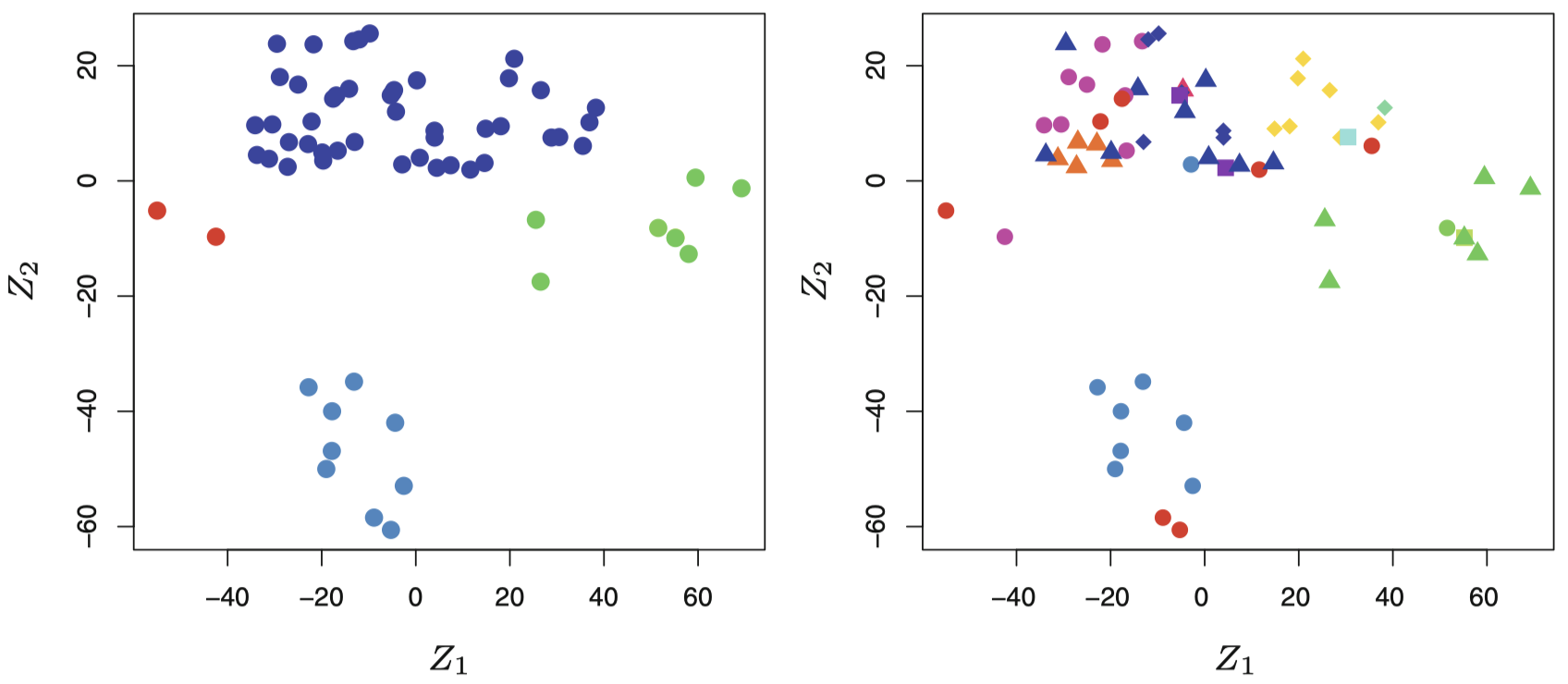
图 3:左图:NCI60 数据集在一个由 Z1 和 Z2 构成的 2 维空间中的表示。每个点对应于 64 个细胞系中的一个。图上显示有 4 组细胞系,我们用不同的颜色表示它们。右图:与左图同理,14 个不同类型的癌症每一类使用不同颜色符号表示。对应于同一癌症类型的细胞系在这个 2 维空间中往往也是较为邻近的。
2. 表示方法
$n$:不同数据点或样本观测的个数。
$p$:用于预测的变量个数。
例如,Wage 数据集包含 3000 个人的 12 个变量信息,因此,我们有 $n=3000$ 个观测,以及 $p=12$ 个变量 (例如:year、age、sex 等)。
一般地,$x_{ij}$ 代表第 $i$ 个观测的第 $j$ 个变量值,$i=1,2,\dots,n$ 并且 $j=1,2,\dots,p$。在本课程中,$i$ 用于索引样本或观测 (从 $1$ 到 $n$),$j$ 用于索引变量 (从 $1$ 到 $p$)。我们用 $\mathbf{X}$ 表示一个 $n\times p$ 的矩阵,其中位置 $(i,j)$ 上的元素为 $x_{ij}$。即,
\[\mathbf{X}=\begin{pmatrix} x_{11} & x_{12} & \cdots & x_{1p} \\ x_{21} & x_{22} & \cdots & x_{2p} \\ \vdots & \vdots & \ddots & \vdots \\ x_{n1} & x_{n2} & \cdots & x_{np} \\ \end{pmatrix}\]有时,我们会对 $\mathbf{X}$ 的行进行研究,通常将其记为 $x_1,x_2,\dots,x_n$。这里,$x_i$ 是长度为 $p$ 的向量,包含了第 $i$ 个观测中的 $p$ 个变量测量。即,
\[x_i=\begin{pmatrix} x_{i1}\\ x_{i2}\\ \vdots\\ x_{ip}\\ \end{pmatrix}\]向量默认用列表示。例如,对于 Wage 数据集,$x_i$ 是一个长度为 12 的向量,包含第 $i$ 个个体的 year、age、sex 和其他变量值。
有时,我们也会研究 $\mathbf{X}$ 的列,将其记为 $\mathbf{x}_1,\mathbf{x}_2,\dots,\mathbf{x}_p$。其中每一个都是长度为 $n$ 的向量。即,
\[\mathbf{x}_j=\begin{pmatrix} x_{1j}\\ x_{2j}\\ \vdots\\ x_{nj}\\ \end{pmatrix}\]例如,在 Wage 数据集中包含 $n=3000$ 个 year 的值。
使用这种方式,矩阵 $\mathbf{X}$ 可以写成
\[\mathbf{X}=(\mathbf{x}_1 \quad \mathbf{x}_2 \quad \cdots \quad \mathbf{x}_p)\]或者
\[\mathbf{X}=\begin{pmatrix} x_{1}^{\mathrm T}\\ x_{2}^{\mathrm T}\\ \vdots\\ x_{n}^{\mathrm T}\\ \end{pmatrix}\]右上角记号 $\mathrm T$ 表示矩阵或向量的 转置 (transpose)。例如,有 $x_i^{\mathrm T}=(x_{i1} \quad x_{i2} \quad \cdots \quad x_{ip})$,以及
\[\mathbf{X}=\begin{pmatrix} x_{11} & x_{21} & \cdots & x_{n1} \\ x_{12} & x_{22} & \cdots & x_{n2} \\ \vdots & \vdots & & \vdots \\ x_{1p} & x_{2p} & \cdots & x_{np} \\ \end{pmatrix}\]$y_i$ 表示待预测的变量 (比如 wage) 的第 $i$ 个观测值。待预测变量的全部 $n$ 个观测值的集合,用如下向量表示:
观测数据集为 $\{(x_1,y_1),(x_2,y_2),\dots,(x_n,y_n)\}$,其中每个 $x_i$ 都是一个长度为 $p$ 的向量 (如果 $p=1$,则 $x_i$ 就是一个简单的标量)。
总体来说,在本课程中我们将采用以下几种表示方式:
- 向量:长度为 $n$,使用小写加粗字母表示,例如 $\mathbf{a}$。
- 向量:长度不为 $n$ (比如为特征数 $p$),使用小写常规字母表示,例如 $a$。
- 标量:也用小写常规字母表示,例如 $a$。
- 矩阵:使用大写加粗字母表示,例如 $\mathbf{A}$。
- 随机变量:不论维数,一律使用大写常规字母表示,例如 $A$。
有时需要指出对象的维数。记号 $a\in \mathbb R$ 表明对象是一个标量。记号 $a\in \mathbb R^k$ 表明对象是一个向量,其长度为 $k$ (若长度为 $n$,则用 $\mathbf a\in \mathbb R^n$ 表示)。记号 $\mathbf A\in \mathbb R^{r\times s}$ 表明对象是一个 $r\times s$ 的矩阵。
我们尽可能地避免矩阵代数的使用。但在少数情况下,完全回避矩阵代数会使计算变得缓慢冗长。在这些情况下,理解矩阵乘法的概念是很重要的。设 $\mathbf A\in \mathbb R^{r\times d}, \; \mathbf B\in \mathbb R^{d\times s}$,则 $\mathbf A$ 和 $\mathbf B$ 相乘的结果记为 $\mathbf{AB}$。矩阵 $\mathbf{AB}$ 的第 $(i,j)$ 个元素等于 $\mathbf{A}$ 中第 $i$ 行和 $\mathbf{B}$ 中第 $j$ 列的对应元素乘积之和,即 \((\mathbf{AB})_{ij}=\sum_{k=1}^{d}a_{ik}b_{kj}\)。举例来说,设
\[\mathbf{A}=\begin{pmatrix} 1 & 2 \\ 3 & 4 \\ \end{pmatrix}, \quad \mathbf{B}=\begin{pmatrix} 5 & 6 \\ 7 & 8 \\ \end{pmatrix}\]则
\[\mathbf{AB}=\begin{pmatrix} 1 & 2 \\ 3 & 4 \\ \end{pmatrix} \begin{pmatrix} 5 & 6 \\ 7 & 8 \\ \end{pmatrix}= \begin{pmatrix} 1\times 5+ 2\times 7 & 1\times 6+ 2\times 8 \\ 3\times 5+ 4\times 7 & 3\times 6+ 4\times 8 \\ \end{pmatrix}= \begin{pmatrix} 19 & 22 \\ 43 & 50 \\ \end{pmatrix}\]注意到运算结果是一个 $r \times s$ 的矩阵。仅当 $\mathbf{A}$ 的列数与 $\mathbf{B}$ 的行数相同时,才能计算 $\mathbf{AB}$。
3. 主要内容和数据集
本课程中,我们将尝试覆盖以下内容:
- 基本术语 (K 近邻分类器和一些相关问题)
- 线性回归
- 经典分类方法 (逻辑回归和线性判别分析)
- 交叉验证和 bootstrap (估计多种不同方法的准确性,以便选择最佳方法)
- 标准线性回归的潜在改进方式 (stepwise 选择、岭回归、主成分回归、偏最小二乘和 lasso)
- 非线性统计学习
- 基于树的方法,包括 bagging、boosting 和随机森林。
- 支持向量机
- 无监督学习:主成分分析、K 均值聚类和层次聚类
- 神经网络
用于实验和习题的数据集:

表 1:教材中实验和习题所需要的数据集列表。所有的数据集都包含在 ISLR 软件包中,但 Boston (MASS 程序包的一部分)和 USArrests (R 基础模块的一部分) 除外。
下节内容:统计学习
本作品采用知识共享署名-非商业性使用-相同方式共享 4.0 国际许可协议进行许可。 欢迎转载,并请注明来自:YEY 的博客 同时保持文章内容的完整和以上声明信息!