Lecture 02 统计学习
参考教材:
- Gareth, J., Daniela, W., Trevor, H., & Robert, T. (2013). An intruduction to statistical learning: with applications in R. Spinger.
- Hastie, T., Tibshirani, R., & Friedman, J. (2009). The elements of statistical learning: data mining, inference, and prediction. Spinger Science & Business Media.
1. 什么是统计学习
1.1 案例学习
例子1:广告预算与产品销量
我们先来看一个简单的例子,比如受客户委托做统计咨询,为某产品的销量提升提供策略咨询建议。Advertising (广告) 数据集记录了该产品在 200 个不同市场的销售情况及该产品在每个市场中 3 类广告媒体的预算,这 3 类媒体分别为: TV (电视)、radio (广播) 和 newspaper (报纸)。
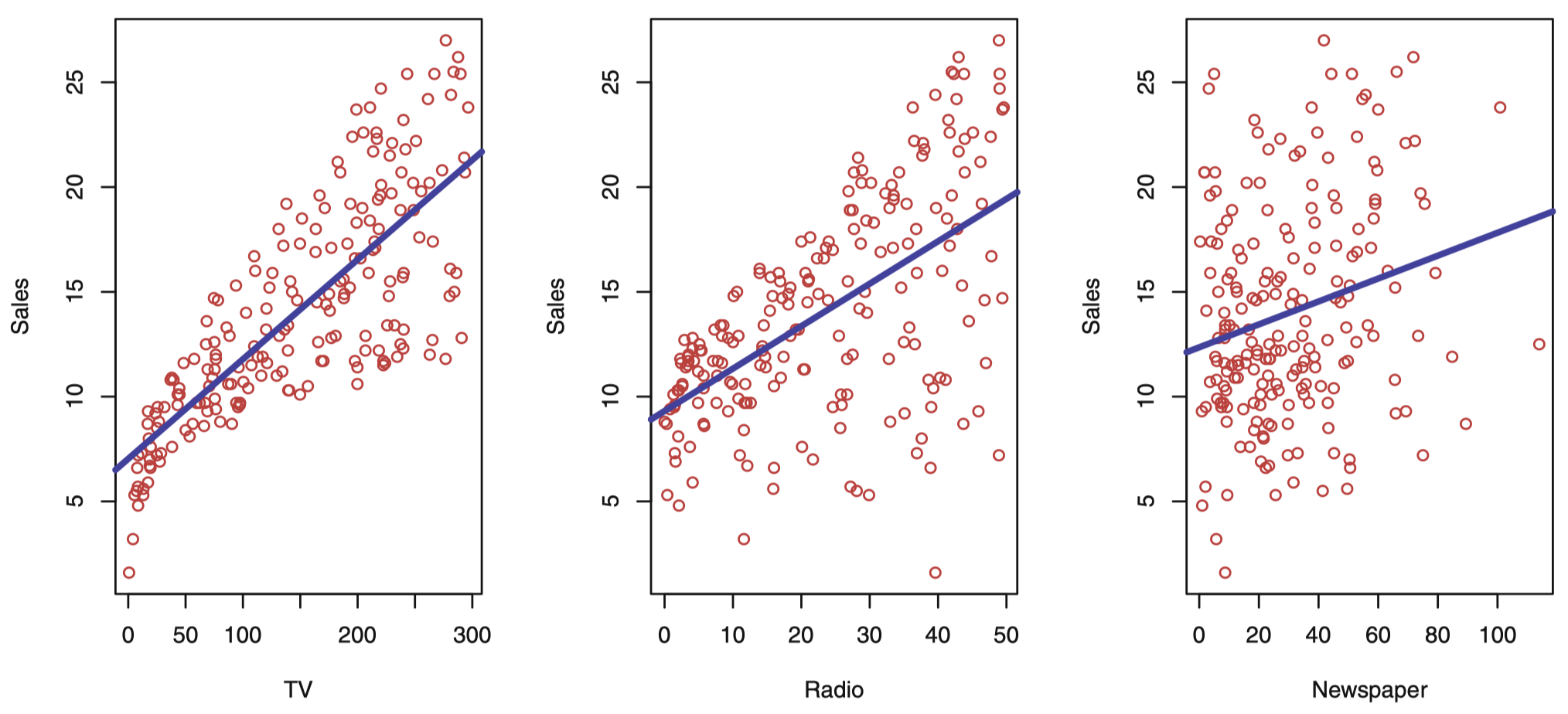
图 1:Advertising (广告) 数据集。这个散点图绘制了 200 个不同市场的 sales (单位: 千) 关于 TV、radio 和 newspager 三种媒体广告预算 (单位: 千美元) 的函数。每个散点图我们都给出了 sales 这个变量通过普通最小二乘法的拟合线,拟合的这个结果将在下节课详解。换句话说,在每个图中的蓝线代表一个简单的模型,这条线可以用来预测 TV、radio 和 newspager 的 sales。
一般情况,假设观察到一个定量的响应变量 $Y$,以及 $p$ 个不同的预测变量 $X_1,X_2,\dots,X_p$。假设 $Y$ 和 $X=(X_1,X_2,\dots,X_p)$ 之间存在某种关系,可以用下面的一般形式表示:
\[Y=f(X)+\epsilon\]这里,$f$ 是某个关于 $X_1,X_2,\dots,X_p$ 的固定的未知函数,并且 $\epsilon$ 是一个独立于 $X$ 且均值为零的随机 误差项 (error term)。这种形式下,$f$ 代表了由 $X$ 提供的关于 $Y$ 的 系统 (systematic) 信息。
例子2:个人收入与受教育年限
我们再来看另一个例子,图 2 表示了 Income (收入) 数据集中 30 个人的 Income (收入) 与各自 years of education (受教育年限) 的关系。

图 2:Income 数据集。左图:图中的点为 income 观测值 (单位: 千美元) 和 30 个人 的 years of education。右图:曲线代表真实的 income 和 years of education 的关系,一般情况下该线是未知的 (但这里是己知的,因为收入数据是模拟的)。竖线表示与每个观测值有关的误差。若观测点落在曲线上方,则误差为正,若观测点落在曲线的下方,则误差为负。总体来看,误差的均值接近于 0。
一般而言,估计函数 $f$ 会涉及多个输入变量,如图 3 所示,作 income 对 years of education 和 seniority (专业资质) 的函数 $f$。这里 $f$ 是一个基于观测值估计的二维曲面。
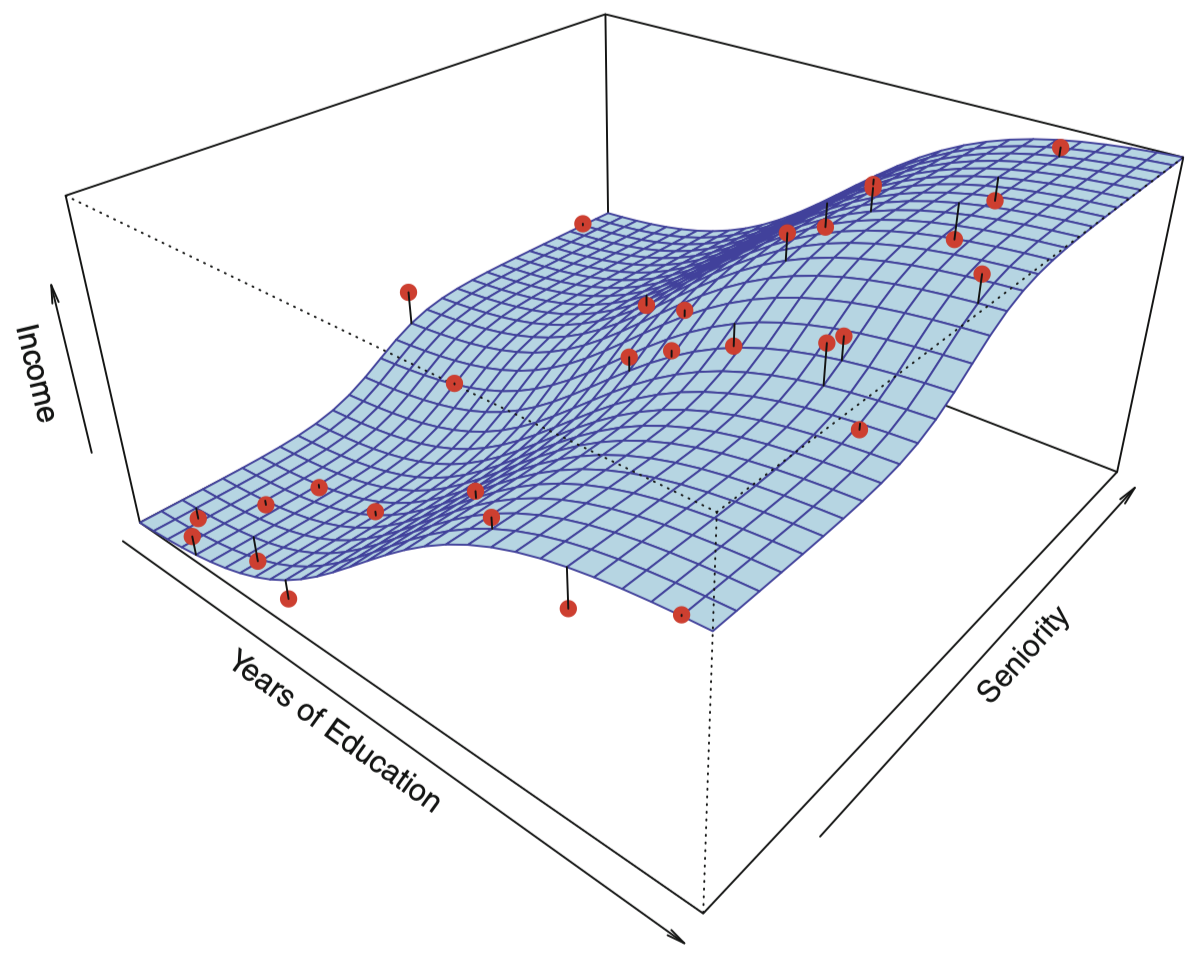
图 3:该图表示的是 Income 数据集中 income 关于 years of education 和 seniority 的函数,曲面代表实际的 income 与 years of education 和 seniority 的关系,它是己知的,这是因为这个数据是模拟得到的。其中,图中的点表示 30 个人的模拟观测值。
实际上,统计学习是关于估计 $f$ 的一系列方法。在节课中我们将集中介绍几个在估计 $f$ 时所需要的关键理论概念,这些概念将用于估计 $f$,同时这些概念也用于对所得估计进行评价。
1.2 为什么需要估计 $f$
估计 $f$ 的主要原因有两个:预测 (prediction) 和 推断 (inference)。
预测
许多情形下,输入集 $X$ 是现成的,但输出 $Y$ 是不易获得的。这时,由于误差项的均值是 $0$ ,那么可通过下式预测 $Y$:
\[\hat Y=\hat f(X)\]这里 $\hat f$ 表示 $f$ 的估计,$\hat Y$ 表示 $Y$ 的预测值。在这种设定下,$\hat f$ 通常被视为一个 黑箱 (black box),这表示一般意义下,如果该黑箱能提供准确的关于 $Y$ 的预测,则并不十分追求 $\hat f$ 的确切形式。
$\hat Y$ 作为响应变量 $Y$ 的预测,其准确性依赖于两个量:可减小误差 (reducible error) 和 不可减小误差 (irreducible error)。通常,$\hat f$ 并不是 $f$ 的一个完美估计,这种不准确性也会引入一些误差,但这类误差是 可减小的,因为我们实际上有能力提高 $f$ 的准确性,只要选择更合适的统计学习技术去估计 $f$ 就可能降低这种误差。然而,即使有可能构造出一个 $f$ 的完美估计,使得我们的估计响应取得 $\hat Y=f(X)$ 的形式,我们的预测中仍然会存在一些误差。这是因为 $Y$ 还是一个关于 $\epsilon$ 的函数,并且按照定义,$\epsilon$ 无法通过 $X$ 来预测。因此,与 $\epsilon$ 相关的可变性同样影响着我们预测的准确性。这部分误差就被称为 不可减小 误差,因为 无论我们对 $f$ 估计得多么好,我们都无法减小由 $\epsilon$ 引入的误差。
考虑一个给定的估计 $\hat f$ 和一组预测变量 $X$,将产生预测 $\hat Y=\hat f(X)$。假设 $\hat f$ 和 $X$ 是固定的,于是很容易证明:
\[\begin{align} E(Y-\hat Y)^2 &= E[\,f(X)+\epsilon -\hat f(X)]^2 \\ &= \underbrace{[\,f(X)-\hat f(X)]^2}_{可减小误差} + \underbrace{\mathrm{Var}(\epsilon)}_{不可减小误差} \end{align}\]其中,$E(Y-\hat Y)^2$ 代表了 $Y$ 的预测值和实际值之差的平方的均值,或者 期望值,而 $\mathrm{Var}(\epsilon)$ 代表了和误差项 $\epsilon$ 相关的 方差。
为什么不可减小误差会大于零呢?
- 首先,$\epsilon$ 可能包含了某些 未测量变量 (unmeasured variables),它们对于预测 $Y$ 有用:由于没有测量它们,所以 $f$ 在预测时无法使用这些变量。
- 其次,$\epsilon$ 可能还包含了一些 不可测量的差异 (unmeasurable variation)。例如,某天某个特定患者对于某种药物的不良反应风险可能会有所不同,具体取决于药物本身在制造过程中产生的差异,或者患者当天的情绪状态等。
推断
很多情况下,我们对当 $X_1,X_2,\dots,X_p$ 变化时对 $Y$ 产生怎样的影响比较感兴趣。在这种情形下,我们想要估计 $f$,但我们的目的并不一定是为了预测 $Y$,而是希望理解 $X$ 和 $Y$ 之间的关系,更确切地,是去理解 $Y$ 作为一个关于 $X_1,X_2,\dots,X_p$ 的函数是如何变化的。这种情况下,$\hat f$ 不能再被视为黑箱,因为我们需要知道它的具体形式。在这种设定下,我们可能对以下问题感兴趣:
-
哪些预测变量与响应变量相关? 通常情况下用于预测的变量中只有一小部分与 $Y$ 充分相关,从一大组可能的变量中根据应用的需要识别一些重要的预测变量是极其有必要的。
-
响应变量与每个预测变量之间的关系是什么? 一些预测变量与 $Y$ 正相关,这意味着,当增加相应的预测变量的值时,$Y$ 的值也会增加。而另一些预测变量则与 $Y$ 呈 负相关。取决于 $f$ 的复杂性,响应变量与某个给定的预测变量之间的关系也可能依赖于其他预测变量的值。
-
$Y$ 与每个预测变量的关系是否能用一个线性方程概括,或者需要更复杂的形式? 过去,大多数估计 $f$ 的方法都采用线性形式。在一些情况下,这种假设是合理的甚至是比较理想的方式。但更一般的情况下,真正的关系 可能更为复杂,此时,线性模型可能无法提供一种准确的表达。
如果我们的问题是推断,我们无法使用神经网络或者深度学习。因为在神经网络和深度学习中,我们的案例是复杂的网络,这种情况下,我们无法理解问题背后的发生的事情,我们能够理解的只有结果。因此,问题的类型决定了我们需要使用的工具,所以,在数据科学中,我们首先需要弄清 决策者的意图是什么:预测、推断,或者两者皆有。
1.3 如何估计 $f$
假设己观测到一组 $n$ 个不同的点。例如在图 2 中,我们观测到 $n=30$ 个数据点。这些观测点称为 训练数据,因为我们要用这些观测点去训练或引导我们的方法怎样估计 $f$。令 $x_{ij}$ 表示观测点 $i$ 的第 $j$ 个预测变量或输入的值,其中 $i = 1,2,\dots,n$ 并且 $j =1,2,\dots,p$。相应地,令 $y_i$ 表示第 $i$ 观测点的响应变量值。训练数据记为 $\{(x_1,y_1),(x_2,y_2),\dots,(x_n,y_n)\}$,其中 $x_i=(x_{i1},x_{i2},\dots,x_{ip})^{\mathrm T}$。
我们的目标是对训练数据应用统计学习方法来估计未知函数 $f$。换而言之,我们希望找到一个函数 $\hat f$,使得对任意观测点 $(X,Y)$ 都有 $Y=\hat f(X)$。一般而言,该任务涉及的大多数统计学习方法都可分为两大类:参数方法 和 非参数方法。
参数方法
参数方法是一种基于模型估计的两阶段方法。
-
首先,我们对函数 $f$ 的形式或形状给出一个假设。例如,一个常用假设是 $f$ 关于 $X$ 是线性的:
\[f(X)=\beta_0+\beta_1 X_1 +\beta_2 X_2 +\cdots + \beta_p X_p\]这是一个 线性模型 (linear model),我们将在下节课展开讨论。一旦假设 $f$ 是线性的,估计 $f$ 的问题将被大大简化:我们不必去估计一个完全任意的 $p$ 维函数 $f(X)$,而只需估计 $p+1$ 个系数 $\beta_0,\beta_1,\dots,\beta_p$。
-
在选定一个模型后,我们需要用训练数据集去 拟合 或 训练 模型。在上面的线性模型中,我们需要估计参数 $\beta_0,\beta_1,\dots,\beta_p$。这就是说,我们希望找到这些参数的值使得:
\[Y\approx \beta_0+\beta_1 X_1 +\beta_2 X_2 +\cdots + \beta_p X_p\]对于该模型,最常用的拟合方法称是 普通最小二乘法 (ordinary least squares, OLS),具体细节将在下节课中讨论。然而,最小二乘法只是众多用于拟合线性模型的方法中的一种,在后面的课程中,我们会讨论一些其他用来估计该模型参数的方法。
基于模型的方法统称为 参数法 (parametric);参数法把估计 $f$ 的问题简化为估计一组参数。对 $f$ 假设一个具体的参数形式将简化对 $f$ 的估计,因为估计参数是更为容易的,比如线性模型只需要估计 $\beta_0,\beta_1,\dots,\beta_p$,而不需要拟合一个任意函数 $f$。参数方法的缺陷是选定的模型与真实的 $f$ 在形式上并非是一致的。假如我们选择的模型与真实的 $f$ 差距太大,我们的估计效果将很差。此类问题的一种解决思路是尝试通过选择 灵活的 (flexible) 模型 拟合很多不同形式的函数 $f$。但一般来说,拟合灵活度更强的模型需要更多的参数估计。拟合复杂的模型会导致 过拟合 (overfitting),即模型拟合了错误或 噪声 (nosie)。
图 4 给出了一个参数模型的例子,其中数据来自于图 3 中的 Income 数据集。一个线性拟合如下所示:
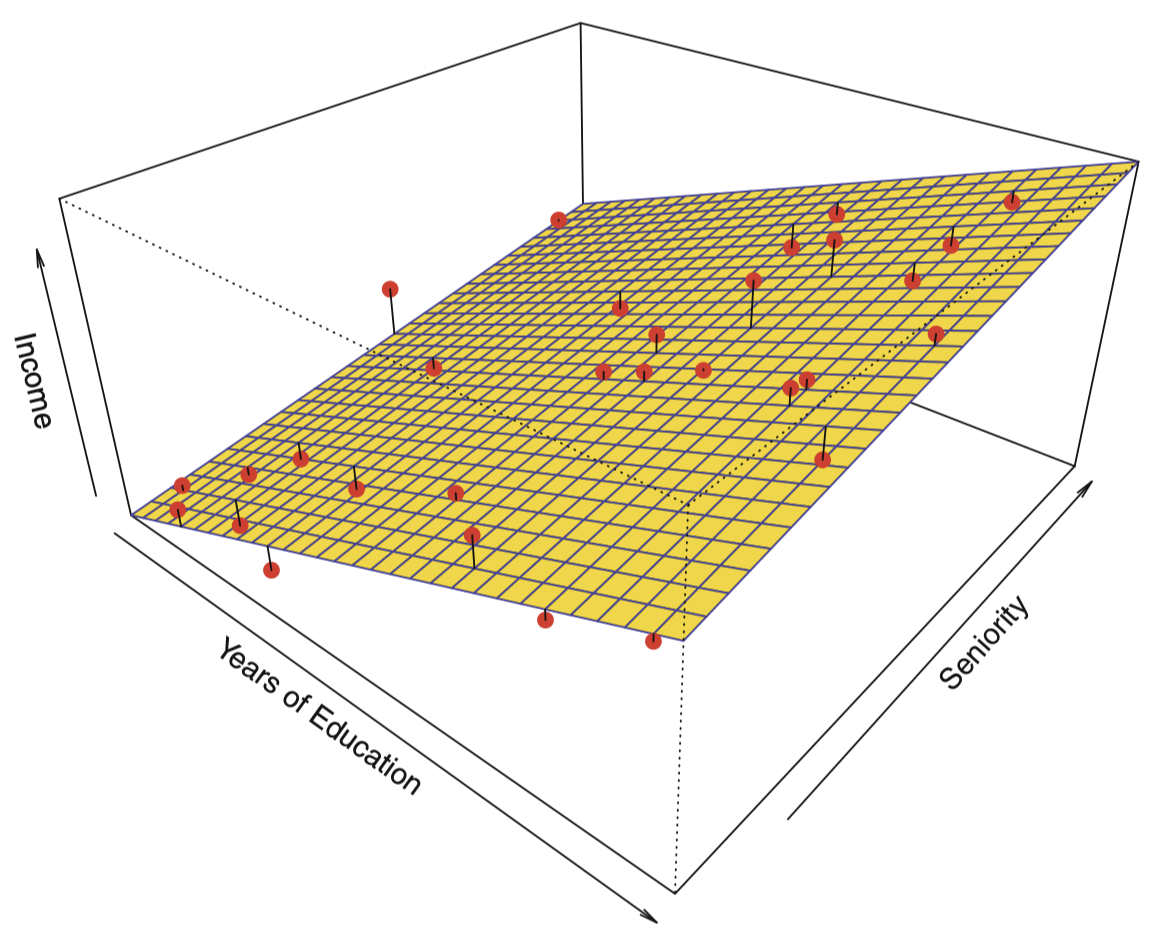
图 4:对图 3 中的 Income 数据进行最小二乘线性模型拟合。图中观测值用红色点标识,平面表示对数据进行最小二乘拟合图形。
由于假设响应变量与两个预测变量之间的关系是线性的,整个拟合问题就简化为用最小二乘线性回归去估计参数 $\beta_0,\beta_1$ 和 $\beta_2$。对比图 3 和图 4,我们发现图 4 中 的线性拟合不够精确:真实的 $f$ 有一定的曲率,线性拟合无法抓住这些特征。然而,线性拟合看上去仍然是一个比较合理的估计,因为它捕获了 year of education 和 income 之间的正相关关系,以及 seniority 和 income 之间微弱的正相关关系。可能是由于观测的数据量太少,这已经是该模型能够得到的最优结果了。
非参数方法
- 非参数方法不需要对函数 $f$ 的形式事先做明确的假设。
- 非参数方法的优点:不限定函数 $f$ 的具体形式,可以在更大范围内选择更适宜 $f$ 形状的估计。
- 非参数方法的主要缺点:由于没有将估计 $f$ 的问题简化为估计一组参数,因此,为了获得一个关于 $f$ 的准确估计,需要大量的观测数据 (通常远超参数方法所需要的数据量)。
图 5 展示了用非参数方法对 Income 数据应用 薄板样条 (thin-plate spline) 估计 $f$ 的拟合结果。这种方法不会在 $f$ 强加任何预设的模型形式,相反,它会尝试使 $f$ 的估计值尽可能接近观测数据,并且要使拟合(即图 5 中的黄色表面)保持光滑。在这种情况下,非参数拟合对图 3 所示的真实 $f$ 生成了一个非常准确的估计。

图 5:黄色曲面代表对 Income 数据的一个光滑薄板样条拟合;红色点表示观测数据点。我们将在后面课程中详细讨论样条方法。
可以看到,years of education 与 income 之间存在明显的正相关关系,而 seniority 和 income 之间的正相关关系较弱。
为了拟合一个薄板样条,数据分析师必须选择一个 光滑度 (smoothness) 水平。图 6 显示了采用一个较低的光滑度水平拟合出的较为粗糙的薄板样条。
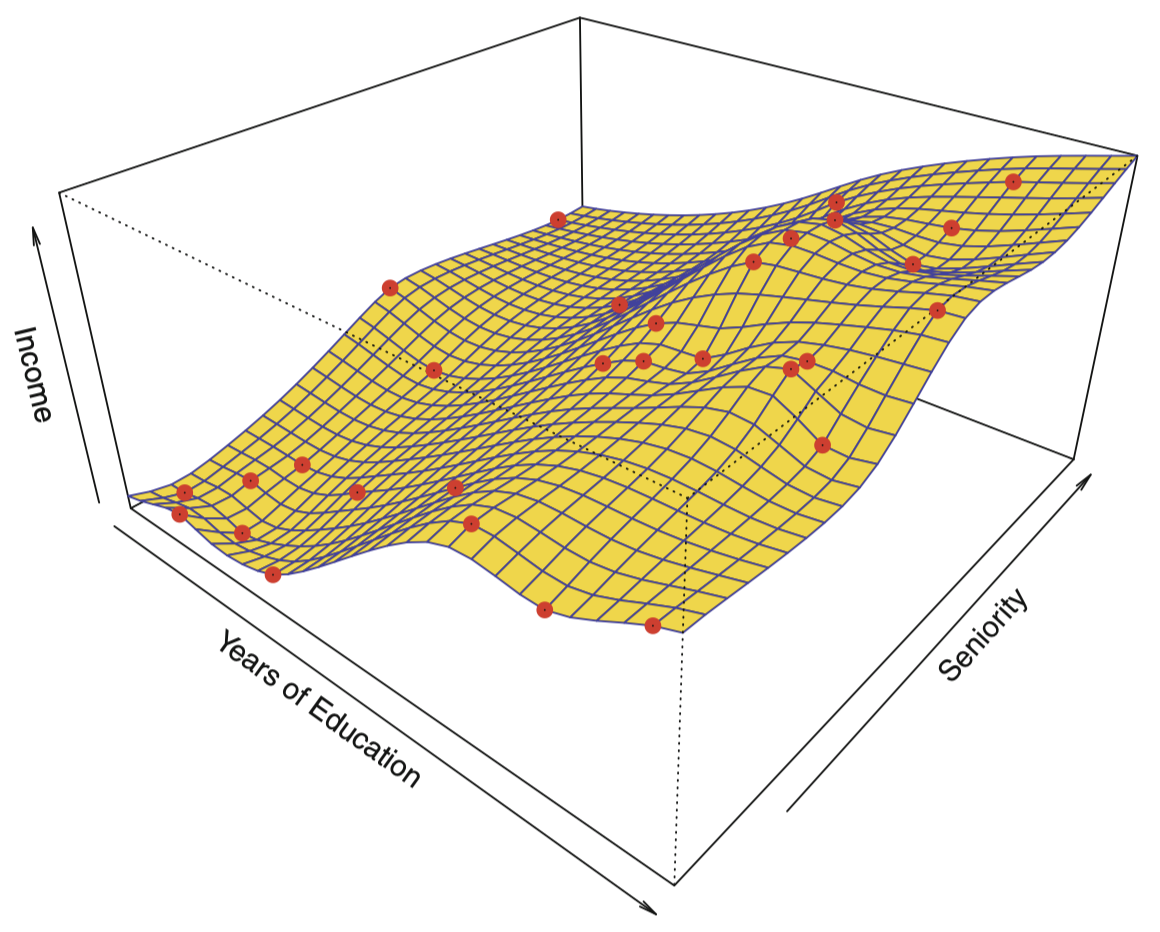
图 6:对 Income 数据进行粗糙薄板样条拟合,该拟合使得训练数据集上的误差为零。
可以看到,图 6 的估计结果完美拟合了每一个观测数据点,这说明模型发生了过拟合。
1.4 预测准确率和模型解释性的权衡
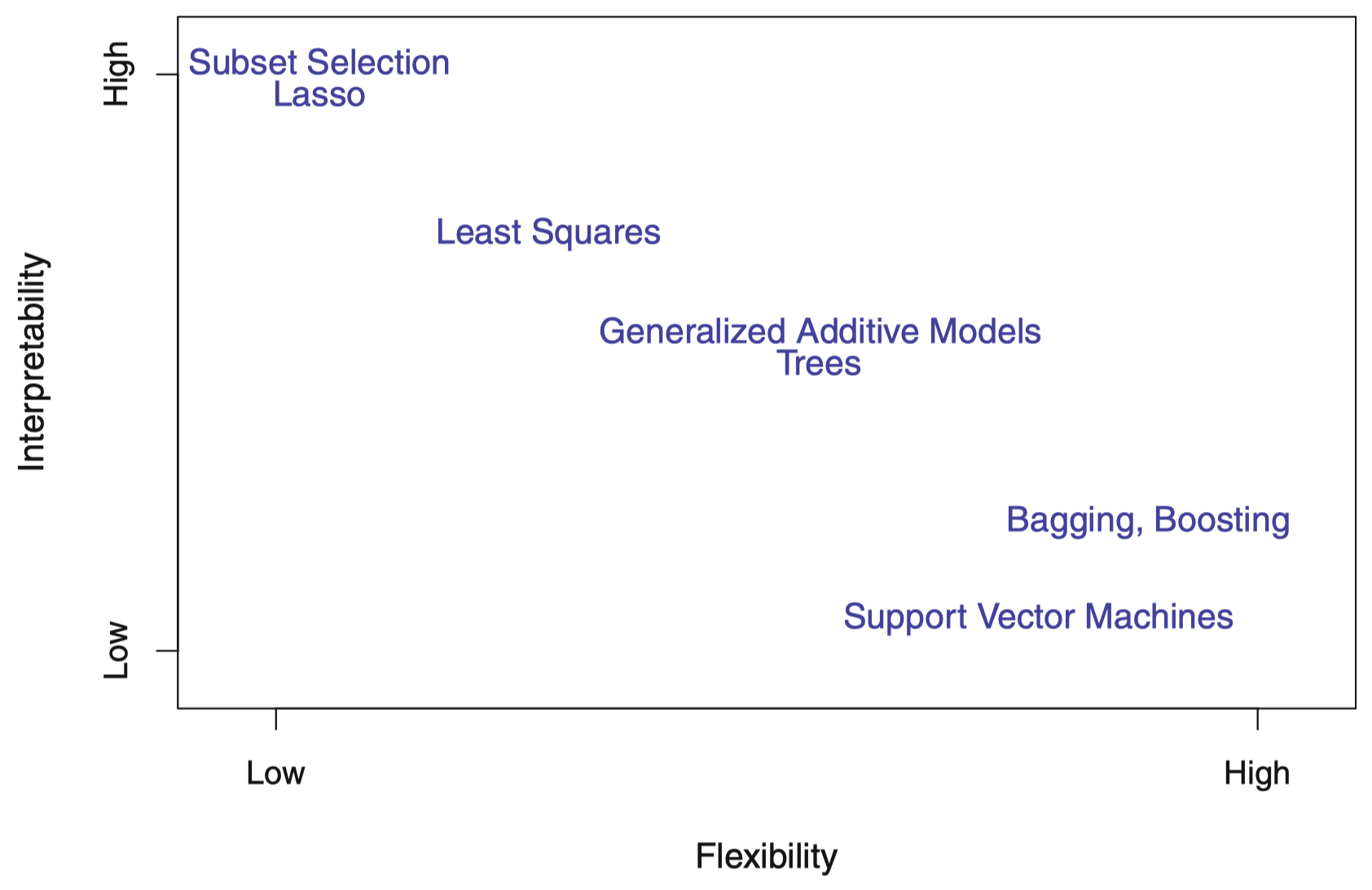
图 7:几种统计学习方法在灵活性和解释性之间的权衡。一般而言,当一种方法的灵活性增强时,其解释性将减弱。
图 7 比较了几种方法在灵活性和解释性之间的权衡。最小二乘线性回归 是一种光滑度较低但解释性较强的方法。Lasso 回归 依赖于线性模型,但相比估计系数 $\beta_0,\beta_1,\dots,\beta_p$,其使用另外一种拟合程序代替。新的估计过程在估计系数时具有更强的约束性,以使得大多数的系数估计正好为零。因此,在这种情况下,Lasso 回归方法要比线性拟合灵活度更低;同时相对于线性模型而言在解释性上更强,因为在最终模型中,响应变量将仅仅与预测变量集的一个小的子集相关,即那些非零系数估计。广义可加模型 (generalized additive model, GAM) 将线性模型扩展到允许一定的非线性关系,因此,GAM 比线性回归更加灵活。另外,GAM 的解释性方面不如线性回归,因为每个预测变量和响应变量之间的关系是用曲线来建模的。最后,完全非线性模型,例如 bagging、boosting、非线性核 SVM、神经网络等,具有非常高的灵活性,并且难以解释。
1.5 监督学习 VS. 无监督学习
大部分统计学习问题都可以分为两种类型:监督学习 和 无监督学习。
监督学习
目前,我们已经讨论过的例子都属于监督学习范畴。对每一个预测变量观测值 $x_i (i=1,\dots,n)$ 都有相应的响应变量的观测 $y_i$。我们希望拟合一个模型来建立预测变量和响应变量之间的联系,目的是精准预测未来观测数据的响应值,或者更好地理解响应变量与预测变量的关系。许多古典统计学习方法 (例如线性回归和逻辑回归) 以及一些更加现代的方法 (例如 GAM、boosting 和 SVM),都属于监督学习范畴。
无监督学习
无监督学习在一定程度上更具挑战性。对于每个观测 $i=1,\dots,n$,我们只有一个预测变量的观测向量 $x_i$,而没有相应的响应变量 $y_i$。这种情况下,无法拟合线性回归模型,因为缺少用于预测的响应变量。在这种设定下,建模工作在某种意义上来看带有一定的盲目性,这种情形被称为无监督,因为缺少一个响应变量来指导数据分析。那么,哪些统计分析可能需要采用无监督学习呢?比如需要理解变量 (或者观测) 之间的关系,可以采用 聚类。
图 8 简要说明了聚类的工作原理。图中将 150 个观测点绘制在由两个变量 $X_1$ 和 $X_2$ 张成的二维坐标系中。每一个观测点对应 3 个集群中的一个。
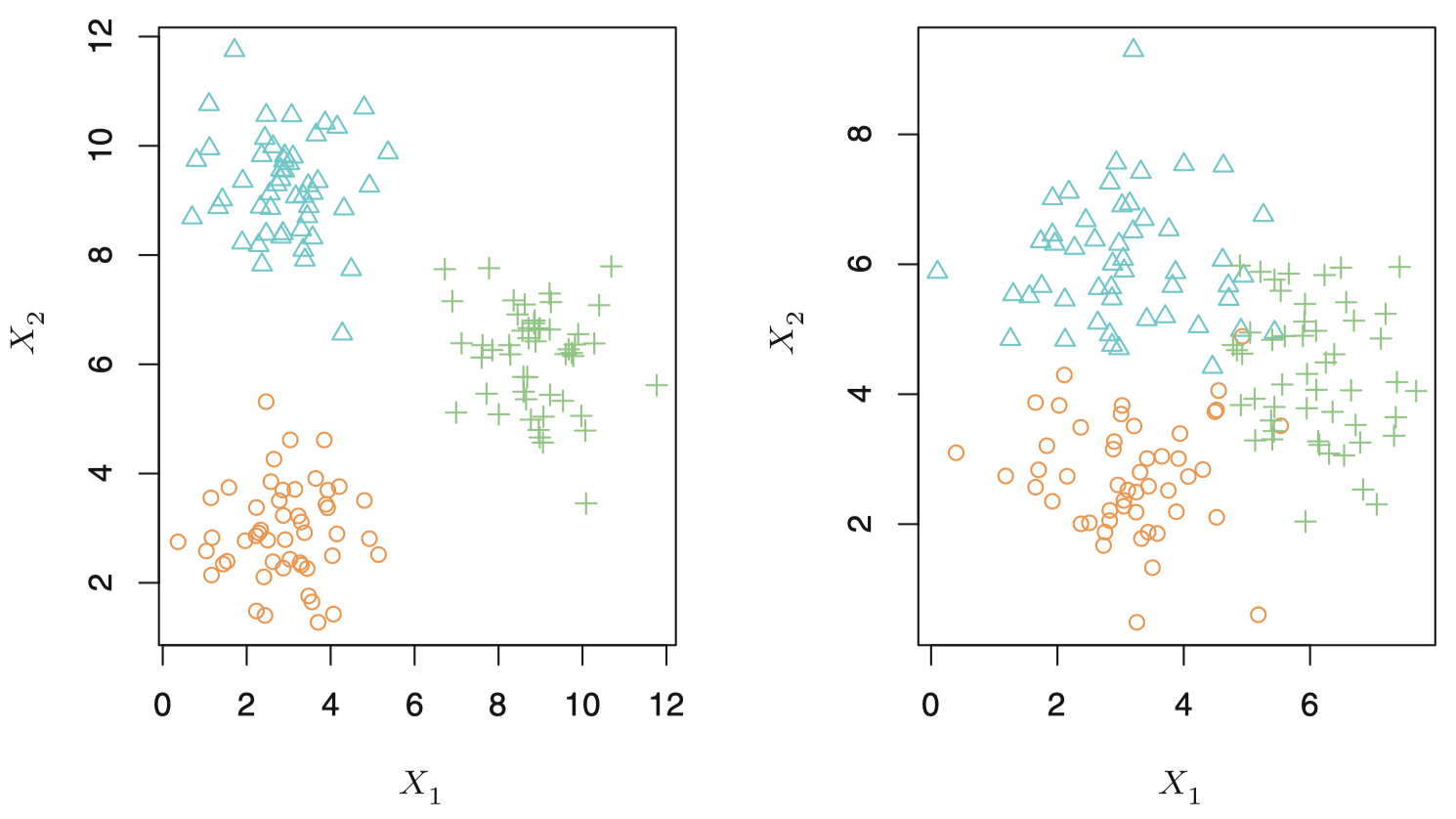
图 8:涉及三个集群的聚类数据集。每个集群都使用不同的颜色和标志符。左图:这三个集群己经被分割。此时,聚类方法能成功识别这三个集群。右图:不同集群之间有重叠部分,这是一个较难的聚类任务。
大部分统计学习方法都可以自然地归类为监督学习或者无监督学习。但是,有时也存在例外。例如,假设我们有 $n$ 个观测,其中 $m (m< n)$ 个观测点同时包含预测变量和响应变量,而其余 $n-m$ 个观测点只有预测变量而没有响应变量。当预测变量的采集相对简单,而相应的响应变量的采集较为困难时,就会出现这种情况。这类问题被称为 半监督学习,但是我们不会在这门课中对此展开讨论。
1.6 回归 VS. 分类
变量通常可以分为 定量 (quantitative) 和 定性 (qualitative) 两类。其中,定性变量也被称为 分类 (categorical) 变量。
定量变量呈现数值性。例如:年龄、身高、收入、房屋价值、股票价格等。
定性变量取值为 $K$ 个不同类别中的一个。例如:性别 (男性或女性)、所购买产品的品牌 (品牌 A、B 或 C)、是否拖欠债务 (是或否) 或癌症诊断 (急性骨髓性白血病、淋巴细胞白血病或无白血病)。
通常,我们将具有 定量 响应的问题称为 回归 问题,而将涉及 定性 响应的问题称为 分类 问题。但是,两类问题之间的区分界限并非如此绝对,一些统计学习方法 (例如 KNN) 既可以用于定量问题,也可以用于定性问题。
通常,我们会根据响应变量是定性还是定量,来选择相应的统计学习方法。例如:我们可以选择线性回归用于定量问题,选择逻辑回归用于定性问题。
2. 评价模型准确率
2.1 拟合效果检验
为了评价统计学习方法在某个数据集上的效果,对于一个给定的观测,我们需要定量测量预测的响应值与真实响应值之间的接近程度。在回归中,最常用的评价准则是 均方误差 (mean squared error, MSE)。
训练 MSE:
\[\mathrm{MSE}=\dfrac{1}{n}\sum_{i=1}^{n}(y_i-\hat f(x_i))^2\]测试 MSE:
\[\mathrm{Ave} (y_0-\hat f(x_0))^2\]我们并不十分关心该方法在 训练数据 上的效果如何。相反,我们感兴趣的是该方法在 测试数据 (未来数据) 上预测结果的准确率。测试数据不会用于统计学习方法的训练过程。
我们选择模型时应该 使测试 MSE 尽可能小。
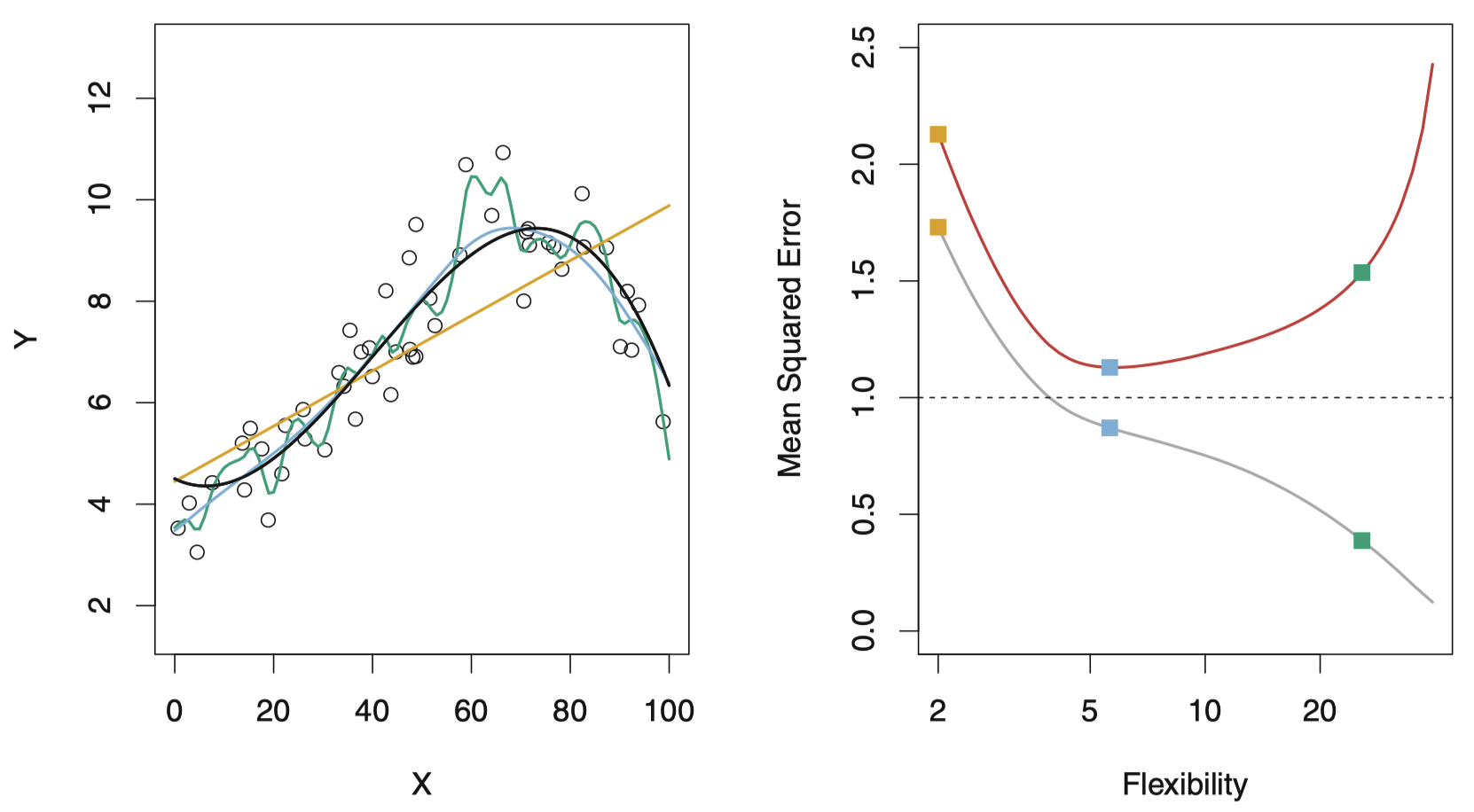
图 9:左图:小圆点代表由由真实函数 $f$ (黑色曲线) 模拟 (加上随机噪声) 产生的数据。三种 $f$ 的估计:线性回归 (橙色曲线),两条光滑样条拟合 (绿色和蓝色曲线)。右图:训练均方误差 (灰色曲线) 和测试均方误差 (红色曲线),所有方法都己使测试均方误差尽可能最小。三种颜色的小方块分别对应左图的三种拟合的训练均方误差和测试均方误差。
右图展示了均方误差关于模型灵活度的函数图像,灵活度在平滑样条曲线中又被称为 自由度。限定性强且曲线平坦的模型要比锯齿形曲线具有更小的自由度。
可以看到,右图的灰色曲线表示的训练 MSE 随模型灵活度增加而持续减小,而红色曲线代表的测试 MSE 则先减小再增大。左图中的橙色和绿色曲线都有一个较大的测试 MSE,蓝色曲线具有最小的测试 MSE,因此,这里蓝色曲线表示的光滑样条是三者中最优的。图中水平虚线表示的是不可减小误差 $\mathrm{Var}(\epsilon)$,它表示所有可能的方法中测试 MSE 的最小值。
当模型的灵活度增加时,训练 MSE 将降低,但测试 MSE 不一定会降低 (通常呈 U 形)。当拟合模型具有较小的训练 MSE 和较大的测试 MSE 时,就称该数据被 过拟合。无论过拟合是否发生,我们总是可以预期训练 MSE 要比测试 MSE 更小,其原因是许多统计学习方法要么直接要么间接,其目标函数都是最小化训练 MSE。
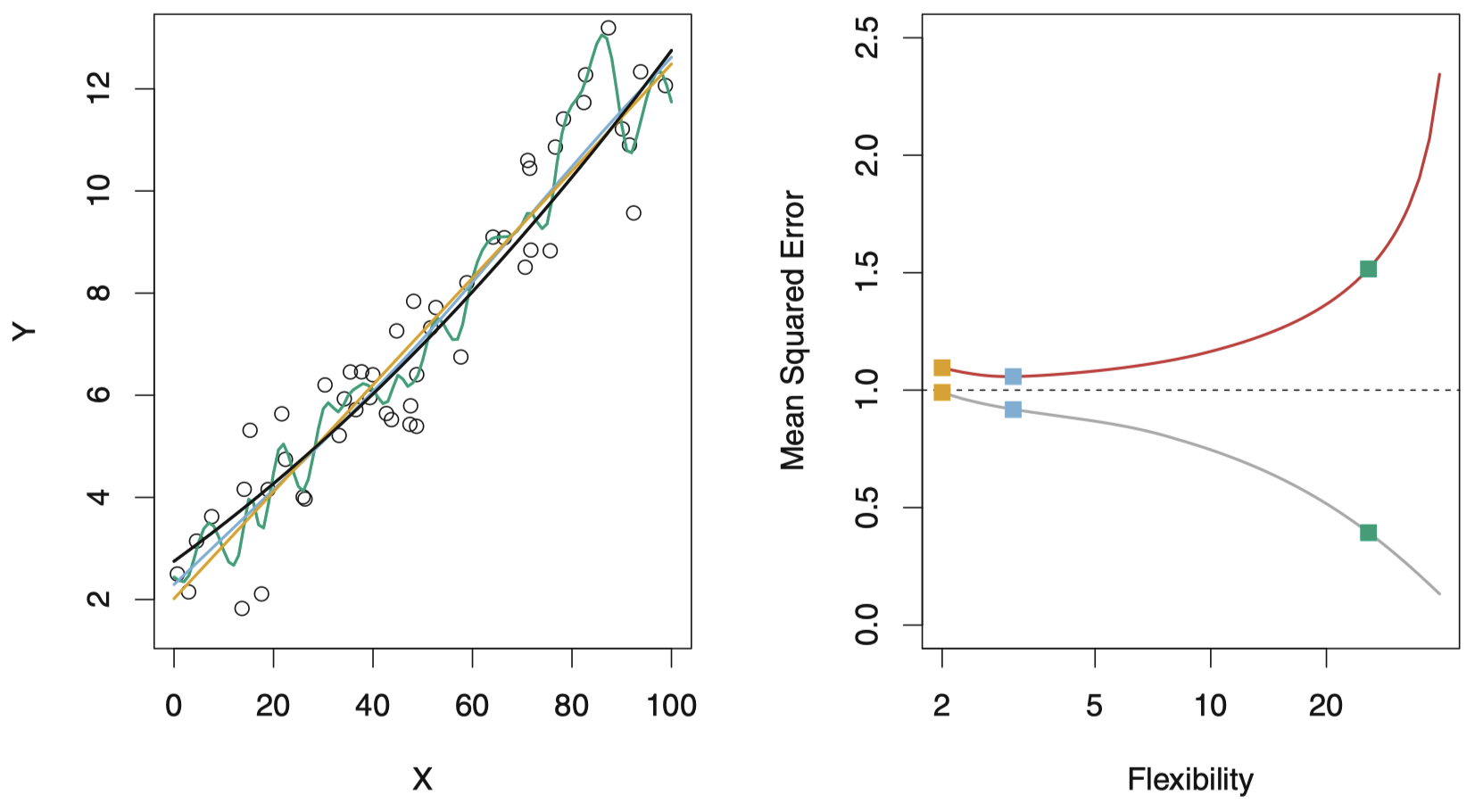
图 10:与图 9 类似,这里真实的 $f$ 是一条接近线性的函数。所以,线性回归是对于该数据较好的拟合。
图 10 给出了另外一个例子,真实的 $f$ 接近于线性。随着模型灵活度的增加,模型的训练 MSE 呈单调递减,测试 MSE 呈 U 形趋势。然而,由于真实函数接近于线性,测试 MSE 在上升之前只出现了一段小幅度的下降,导致最小二乘拟合的模型比高灵活度的绿色曲线更好。
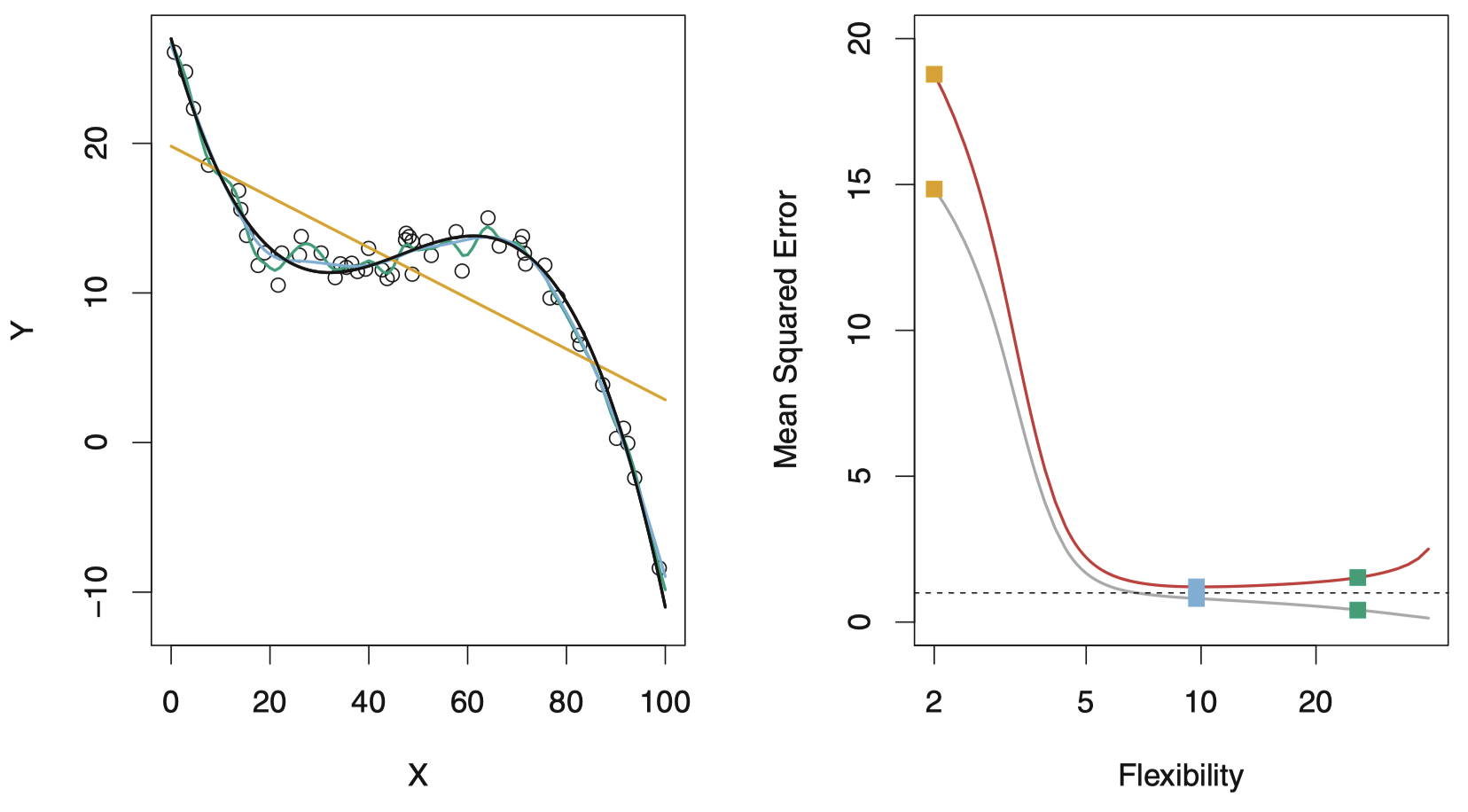
图 11:与图 9 类似,使用了一个完全不同于线性函数的真实 $f$。此时,线性回归是一个对该数据而言较差的拟合。
最后,图 11 展示了一个例子,此时 $f$ 是非线性的。训练 MSE 和测试 MSE 曲线呈现相似的变化模式,在测试 MSE 缓慢上升之前,两者都经历了一段快速下降的过程。
实践中,计算训练 MSE 相对容易,而估计测试 MSE 则相对困难,原因是预先准备可用的测试集并非易事。在前面的的三个例子中,不同灵活度模型的最小测试 MSE 存在很大差异。我们将在后面课程中探讨如何在实际问题中估计这个最小点。一个重要的方法是 交叉验证,其基本原理是使用训练集估计测试 MSE。
2.2 偏差-方差权衡
测试 MSE 的 U 形曲线反映了统计学习方法两种性质之间的博弈。可以证明,对于一个给定的 $x_0$,期望测试 MSE 总是可以分解为三个基本量的和:$\hat f(x_0)$ 的 方差,$\hat f(x_0)$ 的 偏差 的平方,以及误差项 $\epsilon$ 的方差。即,
\[E\left(y_0 - \hat f(x_0)\right)^2=\mathrm{Var}(\hat f(x_0))+[\mathrm{Bias}(\hat f(x_0))]^2 + \mathrm{Var}(\epsilon)\]这里,$E\left(y_0 - \hat f(x_0)\right)^2$ 表示 期望测试 MSE,它实际上是通过使用大量训 练数据重复估计 $f$,然后在 $x_0$ 上测试得到的 平均测试 MSE。另外,总体期望测试 MSE 可以通过对测试集中 $x_0$ 的所有可能取值计算出的 $E\left(y_0 - \hat f(x_0)\right)^2$ 取平均值得到。
可以看到,为使期望测试 MSE 达到最小,需要选择一种统计学习方法使方差和偏差同时达到最小。由于方差和偏差的平方本身都是非负的,因此,期望测试 MSE 不可能比不可约误差 $\mathrm{Var}(\epsilon)$ 更小。
一个统计学习方法的方差和偏差指的是什么?
-
方差 是指如果使用不同的训练数据集,所估计的 $\hat f$ 的变化量。如果一个模型有较大的方差,那么训练数据集微小的变化则会导致 $\hat f$ 较大的改变。通常,灵活度越高的统计模型具有更高的方差。
-
偏差 是指通过一个简单模型去逼近真实函数的过程中引入的误差,其构成可能非常复杂。通常,灵活度越高的方法所产生的偏差越小。
一般而言,灵活度越高的模型具有更高的方差和更低的偏差。
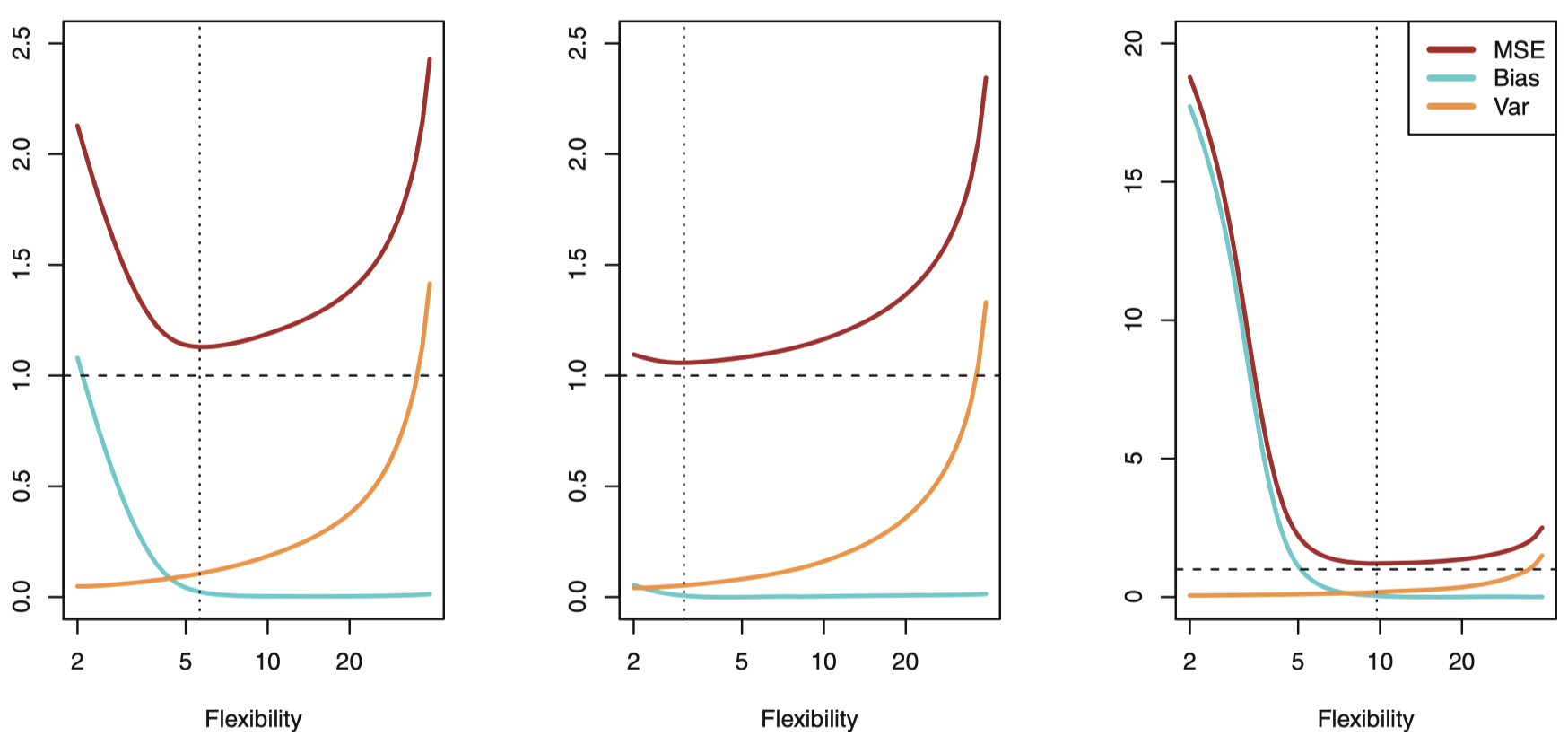
图 12:分别表示图 9 ~ 图 11 中的三个数据集的平方偏差 (蓝色曲线)、方差 (橙色曲线)、不可减小误差 (虚线)、测试 MSE (红色曲线)。垂直的点划线表示最小测试 MSE 所对应的灵活度。
图 12 展示了 偏差-方差权衡。如果一个统计学习模型在测试集上表现很好,则要求该模型同时具有有较低的方差和偏差。这就会涉及权衡的问题,因为我们很容易得到具有极低偏差但高方差的方法 (例如,绘制一条经过所有训练观测点的曲线),或者具有很低方差但高偏差的方法 (例如,对数据拟合一条水平线)。挑战在于寻找一种方法使得方差和偏差都很低。
2.3 分类模型
目前,对模型准确率的讨论主要集中在回归模型。这里,由于 $y_i$ 不再是数值变量,之前提到的一些基本概念 (例如:偏差-方差权衡) 仅需要略做修改就可以移植到分类模型中。假定我们要在训练集 $\{(x_1,y_1),\dots,(x_n,y_n)\}$ 上估计 $f$,其中 $y_1,\dots,y_n$ 现在是定性变量。量化估计 $\hat f$ 准确率最常用的方法是 训练错误率,即当我们将估计 $f$ 应用于训练观测数据时的错误比例:
\[\dfrac{1}{n}\sum_{i=1}^{n}I(y_i \ne \hat y_i)\]其中,$\hat y_i$ 是使用 $\hat f$ 对第 $i$ 个观测点进行预测的类别标签。$I(y_i \ne \hat y_i)$ 是一个 指示变量:当 $y_i \ne \hat y_i$ 时,其值为 $1$;当 $y_i = \hat y_i$ 时,其值为 $0$。如果 $I(y_i \ne \hat y_i)=0$,则说明第 $i$ 个观测数据点在该模型下实现了正确分类,否则说明它被错误分类了。因此,上式计算了训练集上的错误分类比例。
类似于回归模型,我们真正感兴趣的是将分类器应用于未在训练中使用的测试观测所产生的错误率。对于一组形式为 $(x_0,y_0)$ 的测试观测,其 测试错误率 为:
\[\mathrm{Ave}(I(y_0 \ne \hat y_0))\]其中,$\hat y_0$ 是将模型应用于预测变量为 $x_0$ 的测试观测所得到的预测类别标签。一个好的分类器应使测试错误率最小。
贝叶斯分类器
通过一个非常简单的分类器,可以将测试错误率平均最小化:将每个观测值分配到它最大可能所在类别中,将这个类作为它的预测值即可。换句话说,将一个待判的 $x_0$ 分配到下式最大的那个 $j$ 类上是合理的:
\[\Pr (Y=j\mid X=x_0)\]注意,这是一个 条件概率。它是给定了观测向量 $x_0$ 条件下 $Y=j$ 的概率。这就是 贝叶斯分类器 (Bayes classifier)。
对于二分类问题,只有两个可能的响应值:类别 1 和类别 2。如果 $\Pr (Y=1 \mid X=x_0)>0.5$,贝叶斯分类器会将该观测的类别预测为 1 ,否则预测为类别 2。
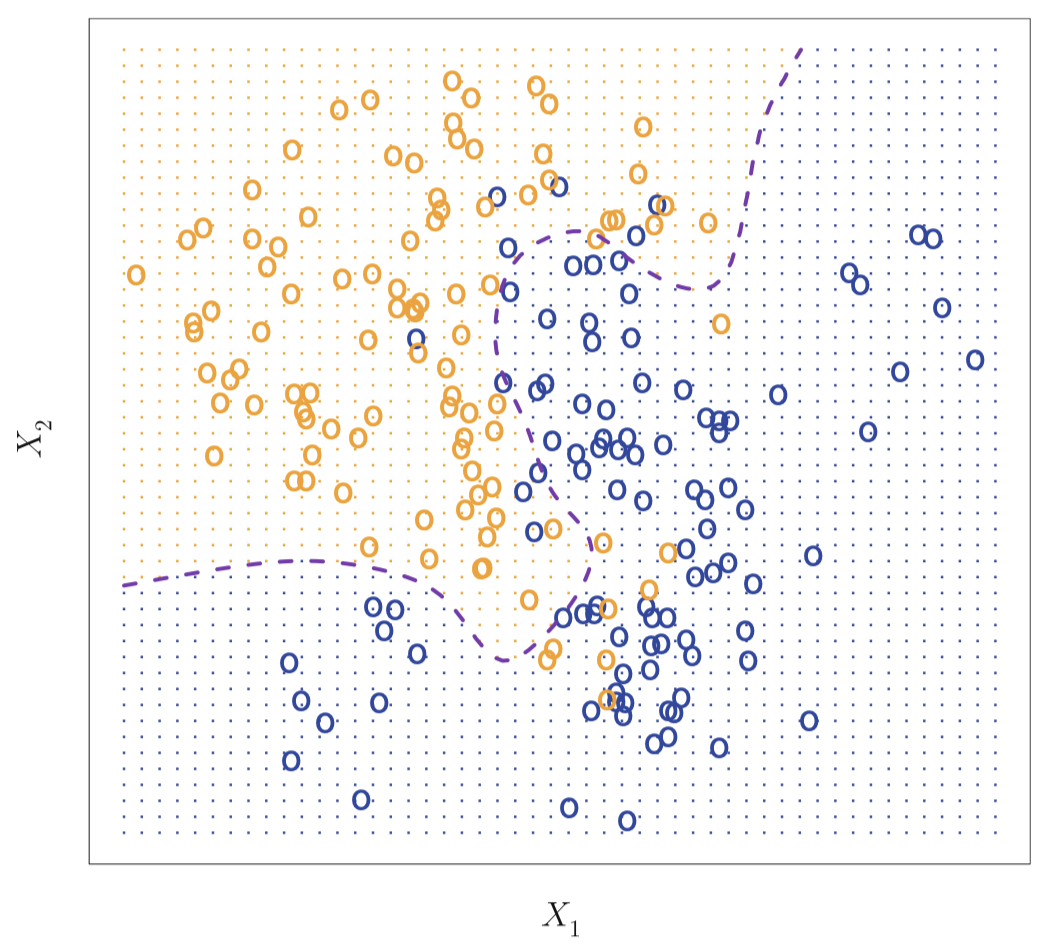
图 13:由两个类别各 100 个观测值组成的模拟数据集,分别用蓝色和橙色表示。紫色虚线代表贝叶斯决策边界。橙色背景网格表示该区域的测试观测将被分配给橙色类别,蓝色背景网格表示该区域的测试观测将被分配给蓝色类别。
图 13 给出了一个由预测变量 $X_1$ 和 $X_2$ 构成的二维空间的一个模拟数据集的例子。由于是模拟数据,所以我们事先知道数据的产生机制,于是每个点在 $X_1$ 和 $X_2$ 空间的条件概率是可以计算的。橙色阴影部分代表 $\Pr(Y = \text{orange} \mid X)$ 大于 $50\%$ 的点,而蓝色区域代表此概率低于 $50\%$ 的点。紫色虚线代表概率等于 $50\%$ 的点,这条线称为 贝叶斯决策边界 (Bayes decision boundary)。
贝叶斯分类器将产生最低的可能的测试错误率,称为 贝叶斯错误率。因为贝叶斯分类器总是选择条件概率最大的类,在 $X=x_0$ 处的错误率为 $1-\max_j \Pr(Y=j\mid X=x_0)$。一般情况下,整体贝叶斯错误率为:
\[1-E\left(\max_j \Pr(Y=j\mid X)\right)\]其中,期望平均了 $X$ 的所有可能取值上的概率。这里,模拟数据的贝叶斯错误率为 $0.1304>0$,因为真实群体中的类别之间存在重叠区域,因此对于某些 $x_0$ 值,$\max_j \Pr(Y=j\mid X=x_0)<1$。贝叶斯错误率在概念上类似于先前讨论的不可减小误差。
K 最近邻方法
通常,对于真实数据,我们并不知道给定 $X$ 后 $Y$ 的条件分布,从而无法对贝叶斯分类器进行计算。因此,贝叶斯分类器相较于其他方法而言更像是一种难以达到的黄金标准。许多方法尝试在给定 $X$ 后先估计 $Y$ 的条件分布,然后将一个给定观测分配给具有最大估计概率的类别。其中一个方法就是 K 最近邻 (KNN) 分类器。
给一个正整数 $K$ 和一个测试观测值 $x_0$,KNN 分类器首先识别出训练集中最靠近 $x_0$ 的 $K$ 个点的集合,记为 $\mathcal N_0$。然后对于每个类别 $j$,使用 $\mathcal N_0$ 中真实类别为 $j$ 的点所占比例作为该类别的条件概率的估计:
\[\Pr(Y=j\mid X=x_0)=\dfrac{1}{K}\sum_{i\in \mathcal N_0} I(y_i=j)\]最终,KNN 将应用贝叶斯规则,并且将测试观测 $x_0$ 分配给概率最大的类别。
下图描述了在一个较为简单的小型模拟训练数据集上的 KNN 方法的实现过程,这里 $K=3$,数据集由 6 个蓝色和 6 个橙色观测值组成:
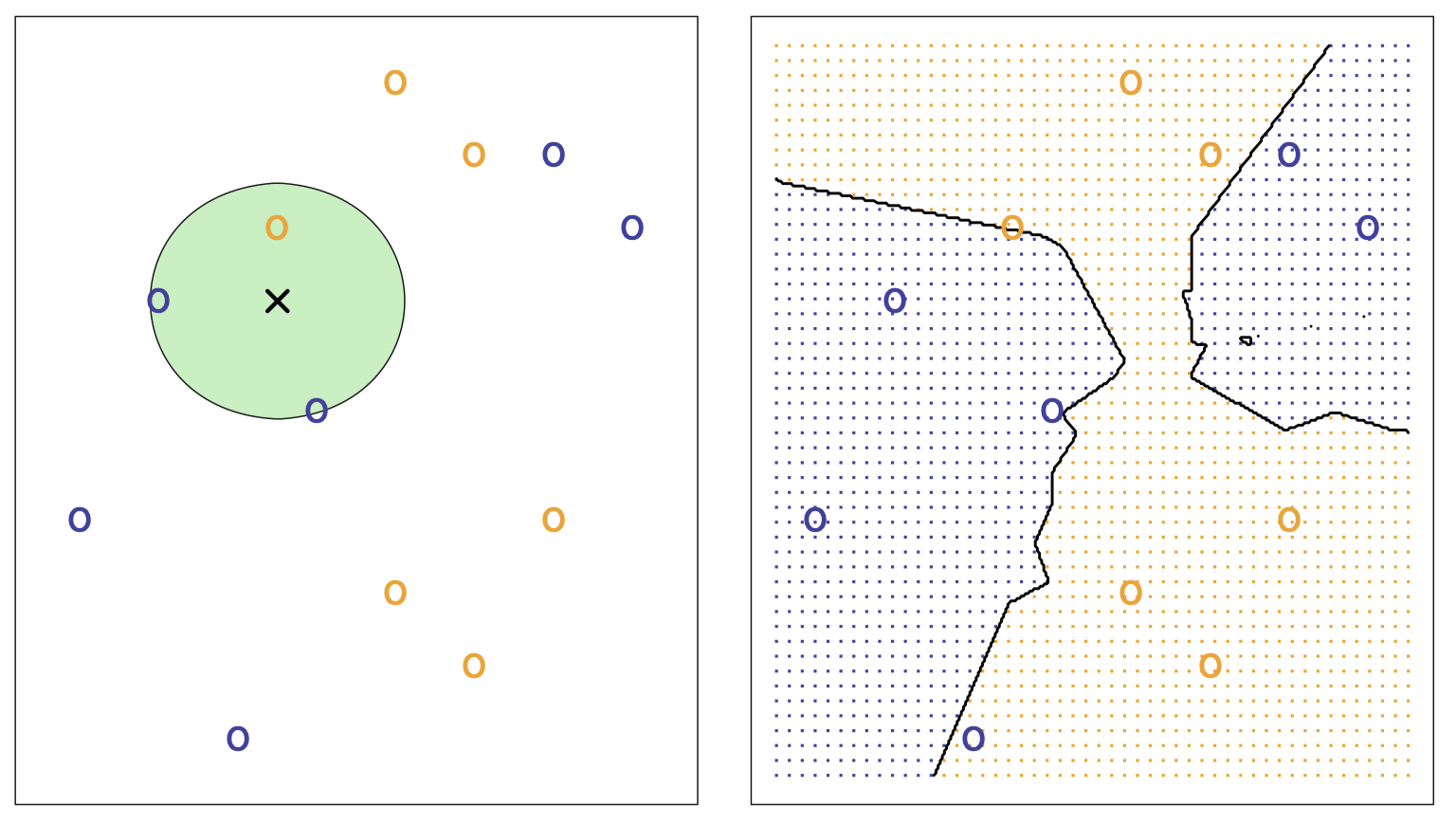
图 14:左图:一个测试观测点 (黑色十字交叉点) 和其可能的预测类标签。首先对测试观测点附近的三个点进行识别,将测试观测点预测为其最可能出现的类别 (这里为蓝色)。右图:黑色曲线代表 KNN 决策边界,蓝色网格阴影表示测试观测值将被分配到蓝色类别里,橙色网格阴影表示测试观测值将被分配到橙色类别里。
尽管这种方法原理简单,但 KNN 往往能够产生一个非常接近最优贝叶斯分类器的分类器。图 15 显示了在一个更大的模拟数据集 (图 13 所使用的数据集) 上用 $K=10$ 的 KNN 方法所生成的决策边界。注意,即使 KNN 分类器并不知道数据的真实分布,KNN 的决策边界仍然非常接近贝叶斯分类器的边界。该例中,KNN 方法的测试错误率为 $0.1362$,非常接近贝叶斯错误率 $0.1304$。
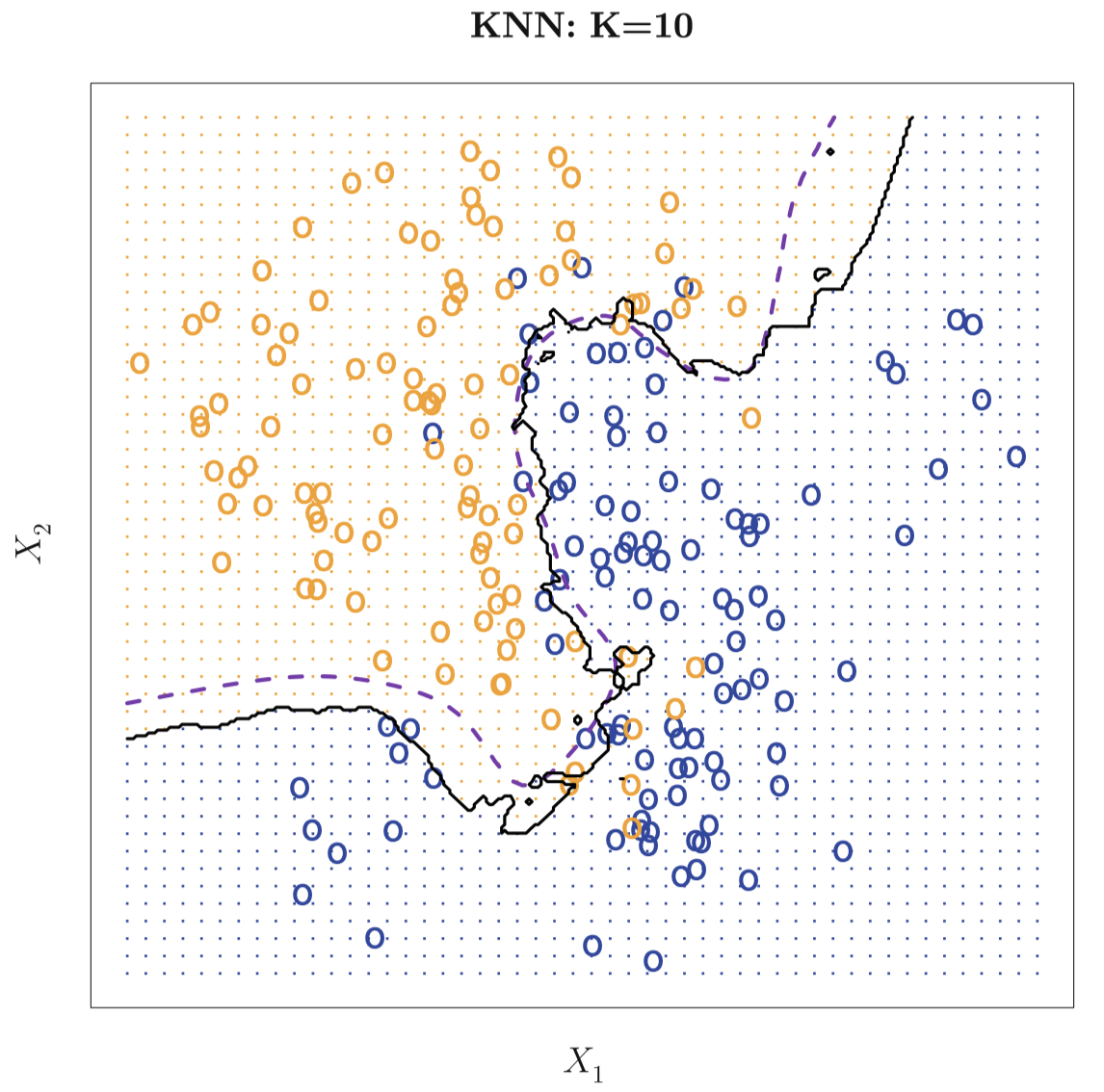
图 15:黑色实线表示 KNN 方法用于图 13 中的数据生成的决策边界,这里 $K=10$。紫色虚线代表贝叶斯决策边界。可以看到,图中这两个边界非常接近。
$K$ 的选择对 KNN 分类器的性能具有决定性影响。图 16 展示了对同一数据集应用不同 $K$ 值的情况:
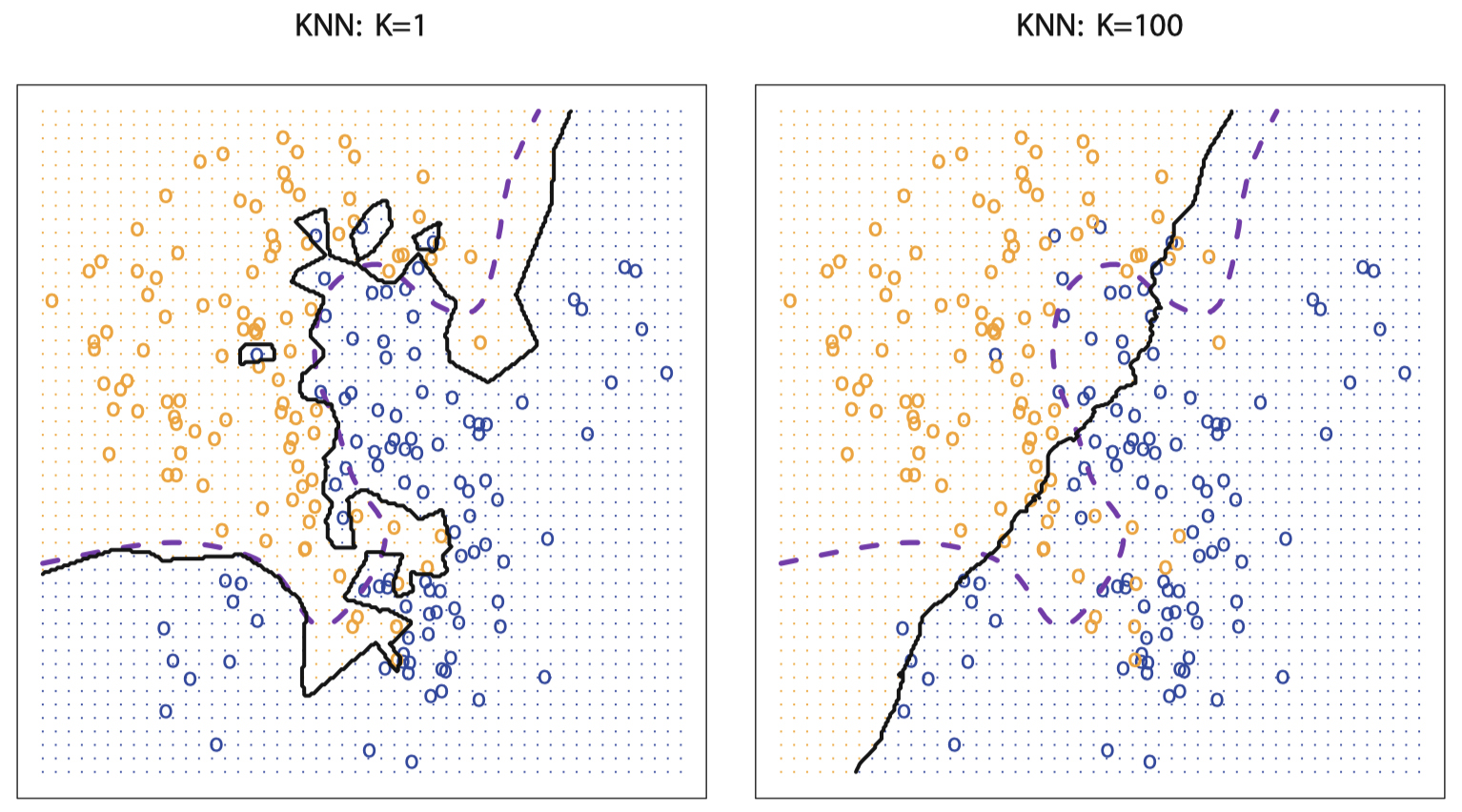
图 16:用图 13 的数据在 $K=1$ 和 $K=100$ 两种设置下 KNN 决策边界 (黑色实线) 的对比。当 $K=1$ 时,决策边界相当不规则,而 $K= 100$ 时,模型的灵活度下降。其中,紫色虚线代表贝叶斯决策边界。
当 $K=1$ 时,决策边界很不规则,数据拟合的模型不能与贝叶斯决策边界完全契合,模型具有低偏差、高方差。当 $K$ 增加时,模型的灵活性降低,得到一个接近线性的决策边界,模型具有低方差、高偏差。在模拟数据集中,无论 $K=1$ 或 $K=100$ 都没有产生较好的预测:两者的测试错误率分别为 $0.1695$ 和 $0.1925$。
和回归问题中一样,训练错误率和测试错误率之间没有一个很明确的关系。当 $K=1$ 时,KNN 方法的训练错误率为 $0$,但测试错误率也许相当的高。一般而言,当使用灵活度较高的分类方法时,训练错误率将减小,但测试错误率则不一定。图 17 描述了 KNN 训练错误率和测试错误率关于 $\frac{1}{K}$ 的变化函数:
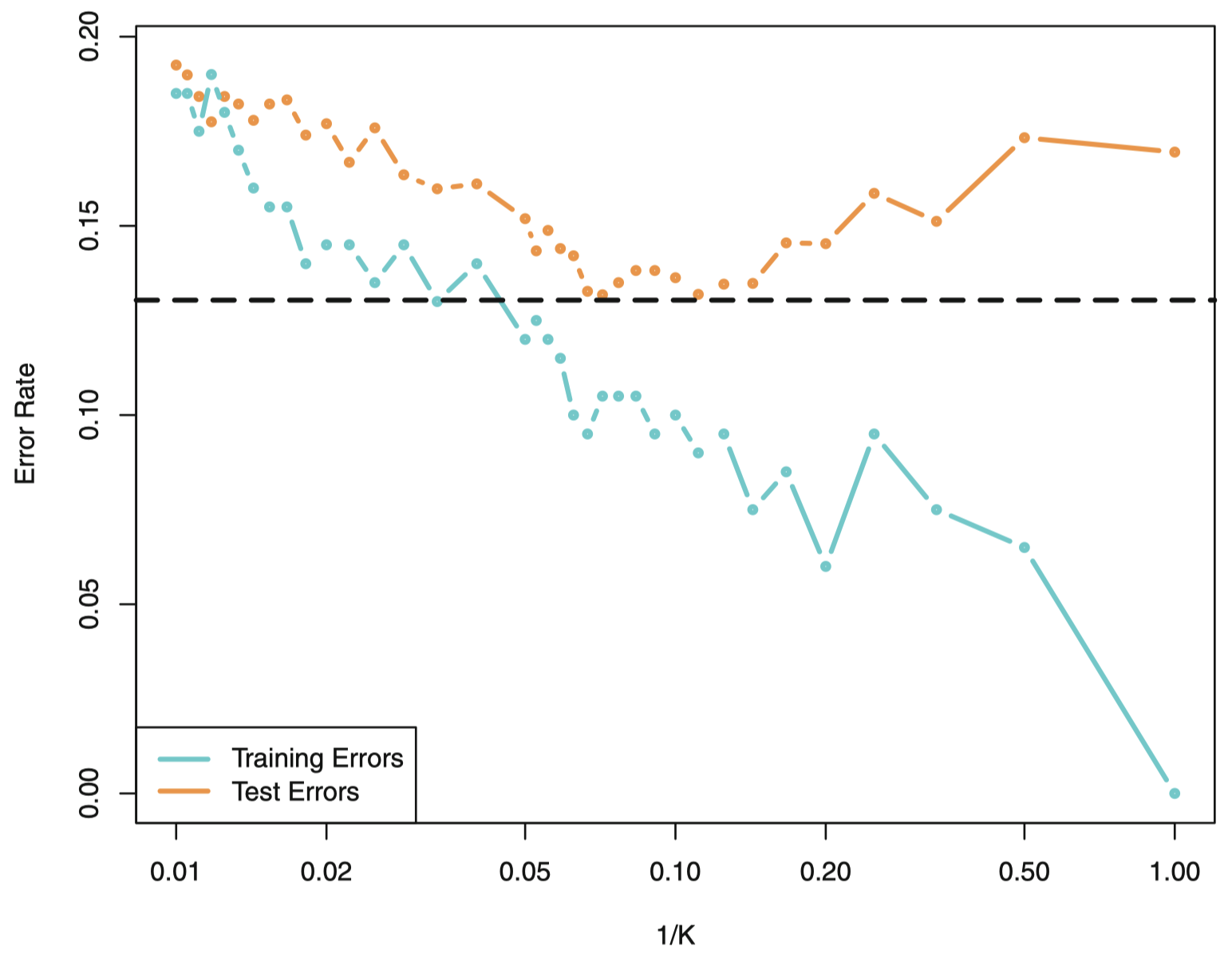
图 17:用图 13 数据所生成的 KNN 分类器的训练错误率 (蓝色,200 观测点) 和测试错误率 (橙色,5000 观测点) 相对模型灵活度的变化曲线,灵活度增加 (这里用 $1/K$ 近似表示) 时等价于 $K$ 值递减。黑色虚线表示贝叶斯错误率。曲线的跳跃波动现象是由于训练数据集的样本量小所造成的。
随着 $\frac{1}{K}$ 的增加,模型灵活性增加。与回归问题一样,随着灵活性的提高,训练错误率也持续下降。但是,测试误差呈现出典型的 U 形,先下降 (最小值大约在 $K=10$),然后随着模型变得过于灵活和过拟合而上升。
从回归和分类问题中,我们发现对于任何统计学习方法,选择合适的灵活度是成功建模的关键。偏差-方差权衡以及导致测试错误率产生 U 形曲线都使建模成为一项困难的任务。在后面课程中,我们将讨论各种估计测试错误率的方法,以及如何选择最优灵活度。
3. 思考
在下面几种情况中,高灵活度 统计学习方法与 低灵活度 的方法哪种更好:
(a) 样本量 $n$ 非常大,预测变量 $p$ 的数量很少。
(b) 预测变量 $p$ 的数量非常多,而观测数量 $n$ 很少。
(c) 预测变量与响应之间的关系是高度非线性的。
(d) 误差项的方差即 $\sigma^2=\mathrm{Var}(\epsilon)$ 非常大。
答案:(a) 高灵活度模型,因为样本数量足够大,而预测变量本身并不多,不会导致太高的模型复杂度,过拟合风险较低。(b) 低灵活度模型,过多的预测变量会导致过于复杂的模型,加上观测数量不足,选择灵活模型很容易发生过拟合。(c) 高灵活度模型,适用于高度非线性的情况,如果采用低灵活度模型,则容易发生欠拟合。(d) 低灵活度模型,不可减小误差 $\mathrm{Var}(\epsilon)$ 很大说明测试错误率的 U 型曲线较早到达底部,因此,为了使得测试错误率尽可能低,应选择低灵活度模型。
下节内容:线性回归
本作品采用知识共享署名-非商业性使用-相同方式共享 4.0 国际许可协议进行许可。 欢迎转载,并请注明来自:YEY 的博客 同时保持文章内容的完整和以上声明信息!