Lecture 02 几何观点和高维数据
参考教材:
- Hardle, W. and Simar, L (2015). Applied multivariate statistical analysis, 4th edition.
- Hastie, T. Tibshirani, R. and Friedman, J. (2009). The elements of statistical learning, 2nd edition
1. 几何观点
1.1 距离
-
两个向量 $x,y\in \mathbb R^p$ 之间的 欧几里得距离 (Euclidian distance) $d(x,y)$ 被定义为:
\[d(x,y)=\sqrt{\sum_{i=1}^{p}(x_i-y_i)^2}=\sqrt{(x-y)^{\mathrm T}(x-y)}\]二维空间 $\mathbb R^2$ 中的例子,其中 $x=(x_1,x_2)$,$y=(y_1,y_2)$:
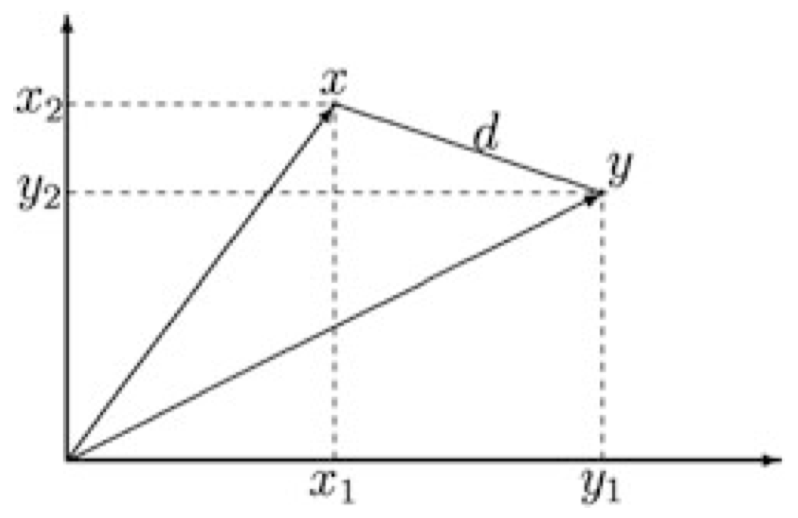
图 1:距离 $d$ -
该距离的一个 加权版本 可以被定义为:
\[d(x,y)=\sqrt{\sum_{i=1}^{p}w_i(x_i-y_i)^2}=\sqrt{(x-y)^{\mathrm T}\mathcal W(x-y)}\]其中,每个 $w_i>0$,并且 $\mathcal W=\mathrm{diag}(w_1,\dots,w_p)$。
-
这可以被进一步推广到下面的距离:
\[d(x,y)=\sqrt{(x-y)^{\mathrm T}\mathcal A(x-y)}\]其中,$\mathcal A$ 是一个 正定 矩阵。
1.2 范数
-
一个向量 $x\in \mathbb R^p$ 的 (欧几里得) 范数 (Norm) 被定义为:
\[\|x\|=\sqrt{\sum_{i=1}^{p}x_i^2}=\sqrt{x^{\mathrm T}x}\] -
一个 单位向量 是一个范数为 $1$ 的向量。
-
可以推广到关于一个 正定 矩阵 $\mathcal A$ 的范数:
\[\|x\|_{\mathcal A}=\sqrt{x^{\mathrm T}\mathcal A x}\]
1.3 两个向量的夹角
-
两个向量 $x,y\in \mathbb R^p$ 之间的夹角 $\theta$ 由 $\theta$ 的余弦值定义:
\[\cos(\theta)=\dfrac{x^{\mathrm T}y}{\|x\|\|y\|}\]在二维空间 $\mathbb R^2$ 中的例子:
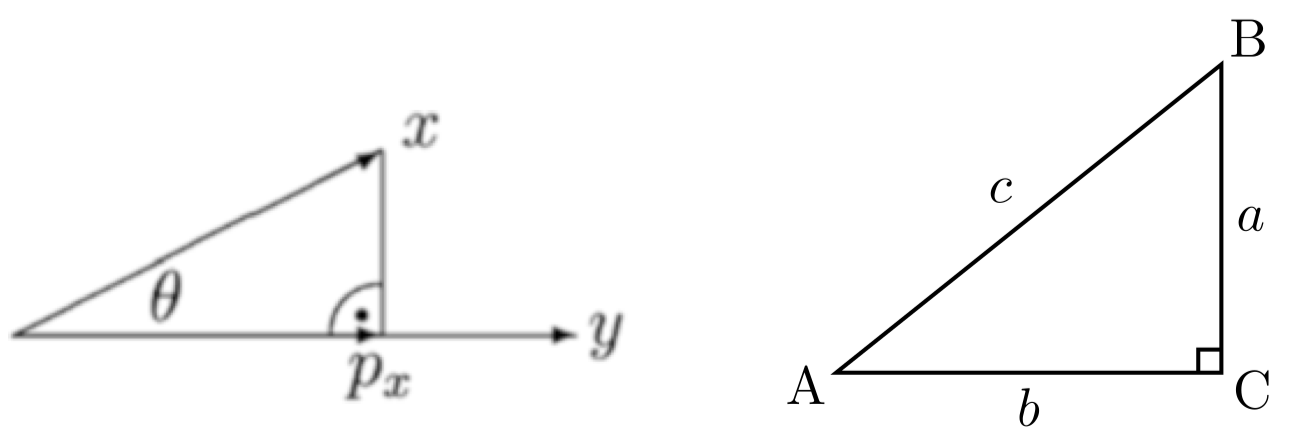
图 2:向量夹角和投影 -
根据三角学我们知道,在角 $C$ 为直角的直角三角形 $ABC$ 中,角 $A$ 的余弦值等于 $AC$ 段的长度 $b$ 除以 $AB$ 段的长度 $c$,因此
\[\cos(\theta)=\dfrac{p_x}{\|x\|}\]其中,$p_x$ 被称为 $x$ 在 $y$ 上的 投影 (Projection)。回归之前的两个向量夹角的余弦定义,我们可以计算出 $p_x$ 为:
\[p_x=\cos(\theta)\|x\|=\dfrac{x^{\mathrm T}y}{\|y\|}\]
1.4 旋转
-
对于 $p$ 维空间 $\mathbb R^p$ 中的向量,我们通常使用 $p$ 轴系统 来描述它们,并给出 $x$ 在该 $p$ 坐标系中的坐标。
-
在多元统计学中,有时将轴 (所有轴同时) 旋转 一个角度 $\theta$ 会很有用,可以通过这种方式创建一个新的 $p$ 轴坐标系。
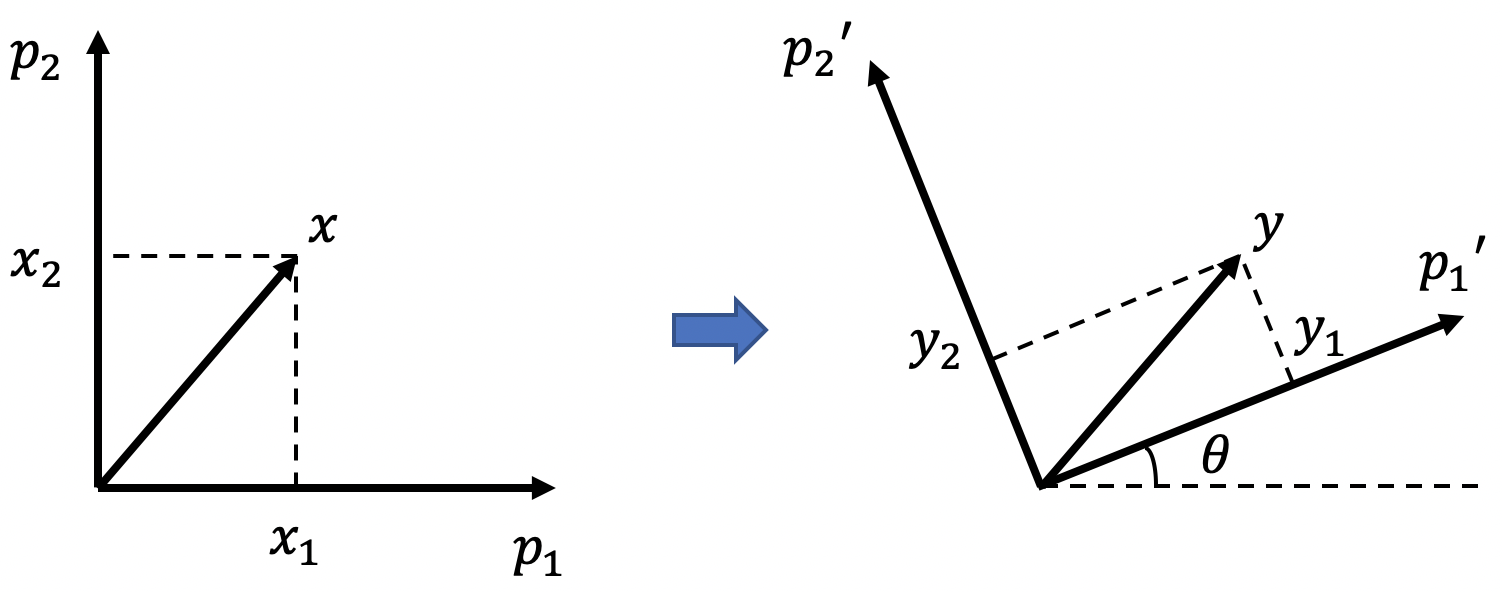
图 3:坐标轴旋转 -
在二维空间 $\mathbb R^2$ 中,我们可以通过 正交矩阵 来描述一个角度为 $\theta$ 的旋转:
\[\Gamma = \begin{pmatrix}\cos(\theta) & \sin(\theta) \\ -\sin(\theta) & \cos(\theta)\end{pmatrix}\]具体来说,如果坐标轴的原始集合 以原点为中心逆时针旋转 一个角度 $\theta$,则原始坐标轴系统中坐标为 $x$ 的点的新坐标 $y$ 为:
\[y=\Gamma x\]如果是 顺时针旋转,则为:
\[y=\Gamma^{\mathrm T}x\] -
更一般地,在向量 $x$ 左边乘以一个 正交矩阵 $\Gamma$ 在几何上对应于坐标轴系统的一次旋转。
2. 均值、协方差和相关系数
2.1 均值
-
一个随机向量 $X=(X_1,\dots,X_p)^{\mathrm T}$ 的 均值 (Mean) $\mu\in \mathbb R^p$ 被定义为:
\[\mu=\begin{pmatrix}\mu_1 \\ \vdots \\ \mu_p\end{pmatrix}=\begin{pmatrix}E(X_1) \\ \vdots \\ E(X_p)\end{pmatrix}\] -
在实践中,我们无法计直接对 $\mu$ 进行计算 (因为我们无法观测到总体),但是我们可以根据来自一个样本 $X_1,\dots,X_n$ 的 样本均值 来估计它:
\[\overline X=\begin{pmatrix}\overline X_1 \\ \vdots \\ \overline X_p\end{pmatrix}\]其中,对于 $j=1,\dots,p$,
\[\overline X_j = \dfrac{1}{n}\sum_{i=1}^{n}X_{ij}\]是第 $j$ 个变量 $X_j$ 的样本均值。
-
回顾矩阵 $\mathcal X$ 的表示形式:
\[\mathcal X=\begin{pmatrix} X_{11} & \cdots & X_{1p} \\ X_{21} & \cdots & X_{2p} \\ & \vdots & \\ X_{n1} & \cdots & X_{np} \end{pmatrix}\]以及一个长度为 $n$ 的列向量 $1_n=(1,\dots,1)^{\mathrm T}$。我们可以将 $\overline X$ 表示为 矩阵形式:
\[\overline X=n^{-1}\mathcal X^{\mathrm T}1_n\]
2.2 协方差矩阵
-
两个随机变量 $X$ 和 $Y$ 之间的 协方差 (Covariance) $\sigma_{XY}$ 是这两个随机变量之间的 线性依赖性 (linear dependence) 的一种度量:
\[\sigma_{XY}=\mathrm{Cov}(X,Y)=E(XY)-E(X)E(Y)\]- $\sigma_{XX}=\mathrm{Var}(X)$
- 如果 $X$ 和 $Y$ 彼此独立,则 $\sigma_{XY}=0$
- 但是反之则不然,$\sigma_{XY}=0$ 并不意味着 $X$ 和 $Y$ 彼此独立 (有可能存在非线性依赖)

图 4:协方差为正 
图 5:协方差为负 -
如果 $X=(X_1,\dots,X_p)^{\mathrm T}$ 是一个 $p$ 维随机向量,我们可以计算每一对 $X_i$ 和 $X_j$ 之间的协方差,并将所有结果汇总到一个 $p\times p$ 的 协方差矩阵 $\Sigma$ 中:
\[\Sigma = \begin{pmatrix}\sigma_{X_1X_1} & \cdots & \sigma_{X_1X_p} \\ & \vdots & \\ \sigma_{X_pX_1} & \cdots & \sigma_{X_pX_p}\end{pmatrix}= \begin{pmatrix}\sigma_{11} & \cdots & \sigma_{1p} \\ & \vdots & \\ \sigma_{p1} & \cdots & \sigma_{pp}\end{pmatrix}\]- 我们可以将 $X$ 的协方差记为 $\Sigma_X$
- 注意 $\Sigma$ 是对称的:$\Sigma=\Sigma^{\mathrm T}$
-
在 矩阵表示 下,我们可以将其写为:
\[\Sigma=E\{(X-\mu)(X-\mu)^{\mathrm T}\}\]其中,$X$ 和 $\mu$ 被写成 $p$ 维列向量。
-
在实践中,我们无法直接计算 $\Sigma$,但是我们可以根据来自一个样本 $X_1,\dots,X_n$ 的 样本协方差矩阵 来估计它:
\[\mathcal S=\begin{pmatrix}s_{X_1X_1} & \cdots & s_{X_1X_p} \\ & \vdots & \\ s_{X_pX_1} & \cdots & s_{X_pX_p}\end{pmatrix}= \begin{pmatrix}s_{11} & \cdots & s_{1p} \\ & \vdots & \\ s_{p1} & \cdots & s_{pp}\end{pmatrix}\]其中,对于 $j,k=1,\dots,p$,
\[s_{X_jX_k}=s_{jk}=\dfrac{1}{n-1}\sum_{i=1}^{n}(X_{ij}-\overline X_j)(X_{ik}-\overline X_k)\]是变量 $X_j$ 和 $X_k$ 之间的样本协方差。
- 注意 $\mathcal S$ 是 对称的 ($\mathcal S=\mathcal S^{\mathrm T}$) 和 半正定的。
-
在 矩阵表示 下,我们可以将其写为:
\[\mathcal S=\dfrac{1}{n-1}\mathcal X^{\mathrm T}\mathcal X-\dfrac{n}{n-1}\overline X \,\overline X^{\mathrm T}\]其中,$\mathcal X$ 是 $n\times p$ 的数据矩阵,$\overline X$ 被写成 $p$ 维列向量。
- 提示:请始终检查矩阵尺寸是否兼容 (即矩阵乘积是否有意义等)。
2.3 相关系数矩阵
-
协方差矩阵的问题:它不是 单位不变的 (unit invariant)。如果我们更改变量的度量单位,则协方差也会随之更改。
-
相关系数 (Correlation) 是单位不变的线性相关性的量度。
-
一个 $p$ 维随机向量 $X=(X_1,\dots,X_p)^{\mathrm T}$ 的 相关系数矩阵 $\mathcal P$ 是一个 $p\times p$ 的矩阵,其定义如下:
\[\mathcal P=\begin{pmatrix}1 & \rho_{12} & \cdots & \rho_{1p} \\ \rho_{21} & 1 & \cdots & \rho_{2p} \\ & \vdots & & \\ \rho_{p1} & \rho_{p2} & \cdots & 1\end{pmatrix}\]其中,
\[\rho_{ij}=\dfrac{\sigma_{ij}}{\sqrt{\sigma_{ii}\sigma_{jj}}}\]是变量 $X_i$ 和 $X_j$ 之间的相关系数。
- 我们总是有 $-1\le \rho_{ij} \le 1$
- $\rho_{ij}$ 是变量 $X_i$ 和 $X_j$ 之间 线性关系 的一种度量
- $|\rho_{ij}|=1$ 意味着完美线性关系
- $\rho_{ij}=0$ 意味着不存在线性关系,但是这并不能说明两者是独立的
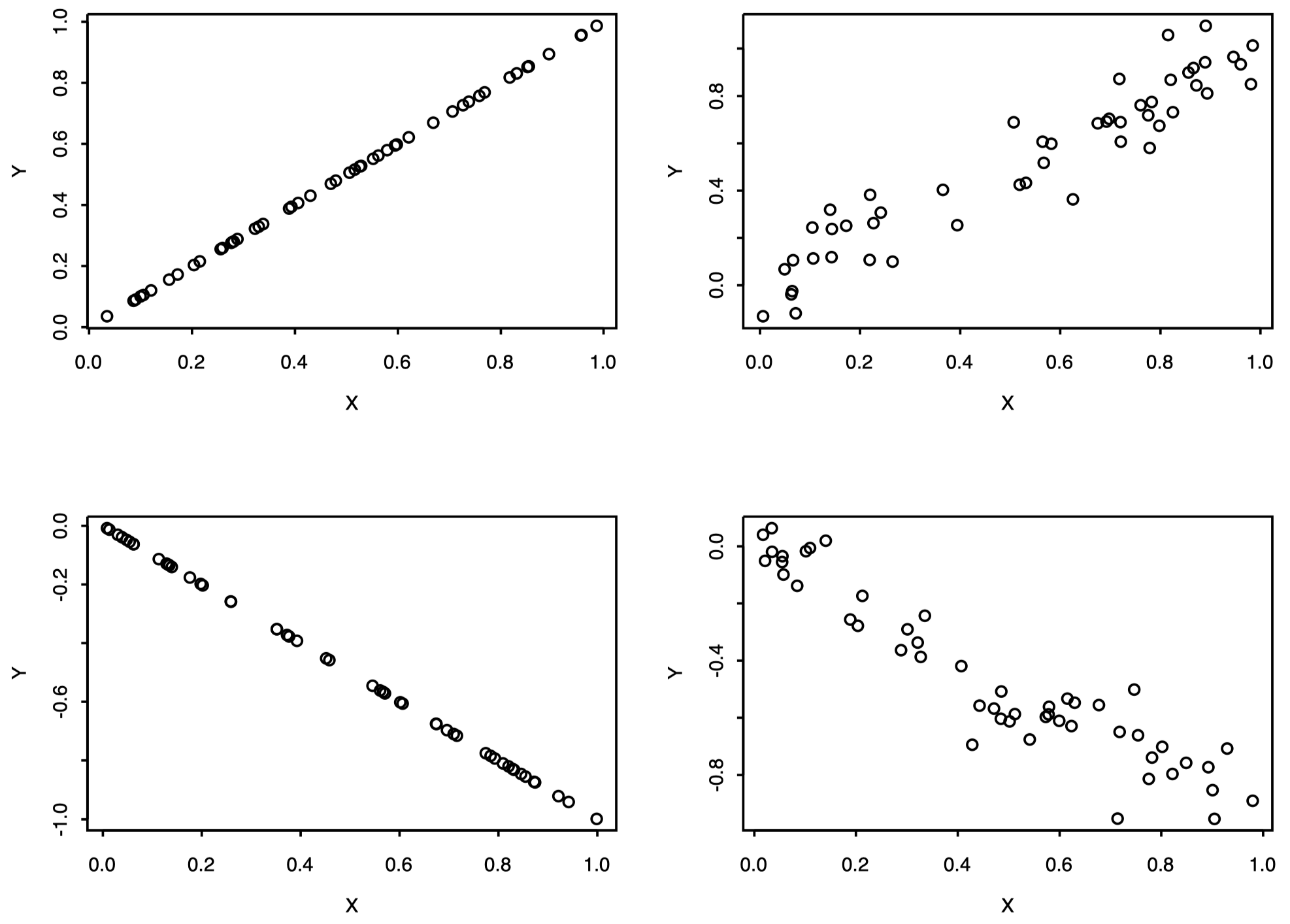
图 6:线性关系 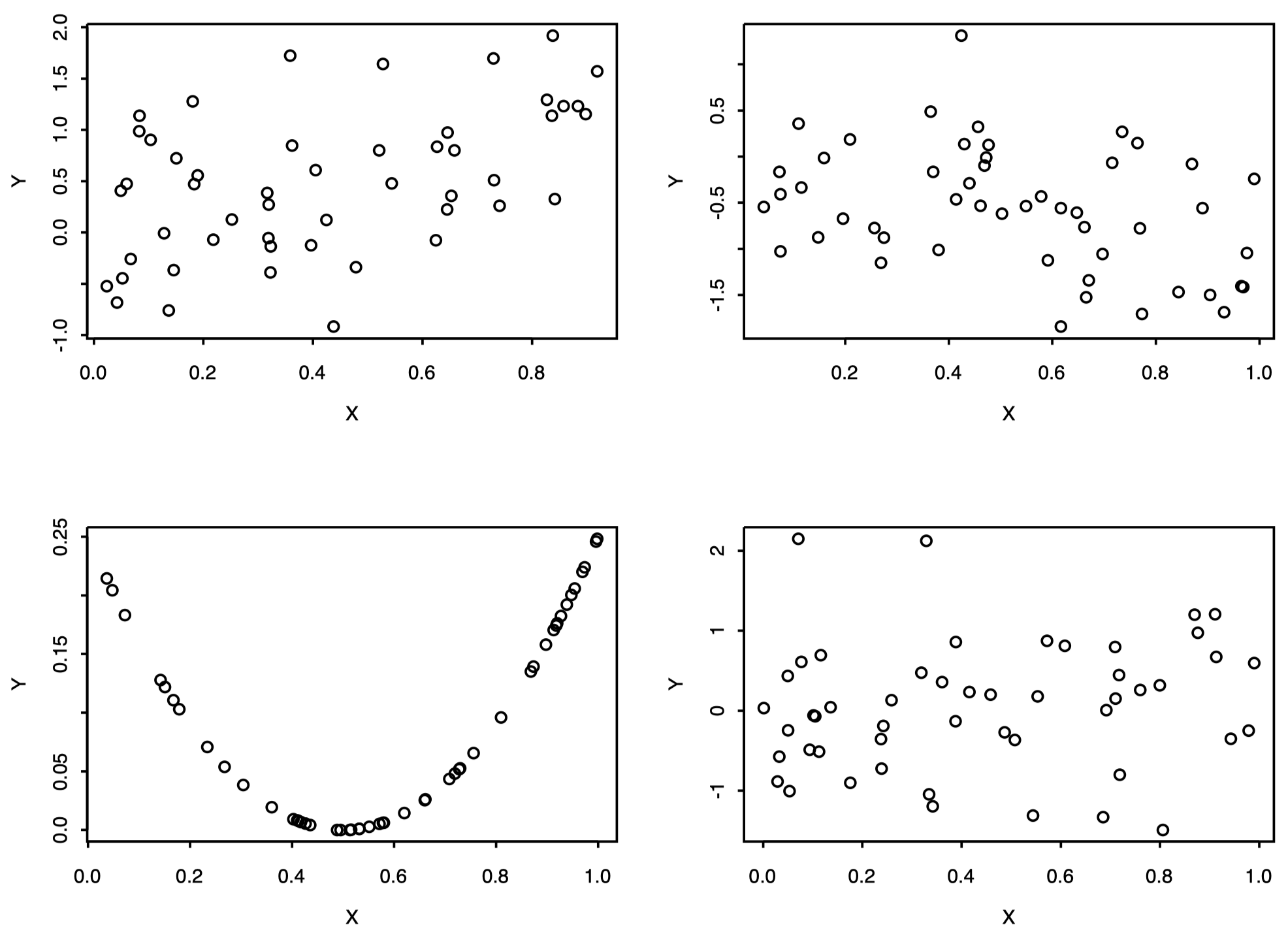
图 7:非线性关系 -
在 矩阵表示 下,我们可以将其写为:
\[\mathcal P=\mathcal D^{-1/2}\Sigma \mathcal D^{-1/2}\]其中,$\Sigma$ 是 $p\times p$ 的协方差矩阵,而
\[\mathcal D=\mathrm{diag}(\sigma_{11},\dots,\sigma_{pp})\]是 $p\times p$ 的对角矩阵,其对角线上的元素就是每个变量的方差。
-
在实践中,我们无法直接计算 $\mathcal P$,但是我们可以根据来自一个样本 $X_1,\dots,X_n$ 的 样本相关系数矩阵 来估计它:
\[\mathcal R = \begin{pmatrix}r_{11} & \cdots & r_{1p} \\ & \vdots & \\ r_{p1} & \cdots & r_{pp}\end{pmatrix}\]其中,对于 $j,k=1,\dots,p$,
\[r_{jk}=\dfrac{s_{jk}}{\sqrt{s_{jj}s_{kk}}}\]是变量 $X_i$ 和 $X_j$ 之间的样本相关系数。
-
在 矩阵表示 下,我们可以将其写为:
\[\mathcal R=\mathcal D^{-1/2}\mathcal S \mathcal D^{-1/2}\]其中,$\mathcal S$ 是 $p\times p$ 的样本协方差矩阵,而
\[\mathcal D=\mathrm{diag}(s_{11},\dots,s_{pp})\]是 $p\times p$ 的对角矩阵,其对角线上的元素就是每个变量的样本方差。
2.4 线性变换
令 $X=(X_1,\dots,X_p)^{\mathrm T}$ 为一个 $p$ 维向量,$Y$ 是一个 $q$ 维向量,其定义如下:
\[Y=\mathcal A X + b\]其中,$\mathcal A$ 是一个 $q\times p$ 的矩阵,$b$ 是一个 $q\times 1$ 的向量。那么,我们有:
\[\begin{align} E(Y) &= \mathcal A E(X) +b \\[2ex] \overline Y &= \mathcal A \overline X +b \\[2ex] \Sigma_Y &= \mathcal A \Sigma_X \mathcal A^{\mathrm T} \\[2ex] \mathcal S_Y &= \mathcal A \mathcal S_X \mathcal A^{\mathrm T} \end{align}\]- 提示:为了知道转置矩阵放置的位置,请始终检查矩阵尺寸是否兼容。
下节内容:多元分布
本作品采用知识共享署名-非商业性使用-相同方式共享 4.0 国际许可协议进行许可。 欢迎转载,并请注明来自:YEY 的博客 同时保持文章内容的完整和以上声明信息!