Lecture 03 多元分布
参考教材:
- Hardle, W. and Simar, L (2015). Applied multivariate statistical analysis, 4th edition.
- Hastie, T. Tibshirani, R. and Friedman, J. (2009). The elements of statistical learning, 2nd edition
1. 分布和密度函数
令 $X=(X_1,\dots,X_p)^{\mathrm T}$ 为一个随机向量。
1.1 累积分布函数
对于所有的 $x=(x_1,\dots,x_p)^{\mathrm T}\in \mathbb R^p$,$X$ 的 累积分布函数 (Cumulative Distribution Function, CDF) 被定义为:
\[F(x)=P(X\le x)=P(X_1\le x_1,\dots,X_p \le x_p)\]1.2 概率密度函数
如果 $X$ 是连续的,则 $X$ 的 概率密度函数 (Probability Density Function, PDF) $f$ 是一个非负函数,可以通过下式定义:
\[F(x)=\int_{-\infty}^{x}f(u)du\]它总是满足:
\[\int_{-\infty}^{\infty}f(u)du=1\]该积分是 $p$ 元的,$u\in \mathbb R^p$,但是 $f(u)\in \mathbb R$:
\[\int_{-\infty}^{x}f(u)du = \int_{-\infty}^{x_1} \cdots \int_{-\infty}^{x_p} f(u_1,\dots,u_p)du_1 \dots du_p\]1.3 边缘 CDF
$X$ 的某个子集的 边缘 CDF (Marginal CDF) 是通过在该子集上计算的 $X$ 的边缘得到的,从而使其他值等于无穷大。
-
例如,$X_1$ 的边缘 CDF 为:
\[\begin{align} F_{X_1}(x_1) &= P(X_1 \le x_1) \\[2ex] &= P(X_1 \le x_1, X_2 \le \infty,\dots,X_p \le \infty) \\[2ex] &= F_X(x_1,\infty,\dots,\infty) \end{align}\] -
$(X_1,X_3)$ 的边缘 CDF 为:
\[\begin{align} F_{X_1,X_3}(x_1,x_3) &= P(X_1 \le x_1,X_3 \le x_3) \\[2ex] &= P(X_1 \le x_1, X_2 \le \infty,X_3 \le x_3, X_4 \le \infty,\dots,X_p \le \infty) \\[2ex] &= F_X(x_1,\infty,x_3,\infty,\dots,\infty) \end{align}\]
1.4 边缘密度
对于一个连续的随机向量 $X$,$X$ 的某个子集的 边缘密度 (Marginal Density) 是通过 $X$ 的 联合密度 (Joint Density) $f$ 在其他分量上进行积分得到的。
-
例如,$X_1$ 的边缘密度为:
\[f_{X_1}(x_1)=\int_{-\infty}^{\infty}\cdots \int_{-\infty}^{\infty} f(x_1,u_2,\dots,u_p)du_2 \dots du_p\] -
$(X_1,X_3)$ 的边缘密度为:
\[f_{X_1,X_3}(x_1,x_3)=\int_{-\infty}^{\infty}\cdots \int_{-\infty}^{\infty} f(x_1,u_2,x_3,u_4,\dots,u_p)du_2 du_4 \dots du_p\]
1.5 条件 PDF
对于两个连续的随机变量 $X_1$ 和 $X_2$,在给定 $X_1$ 的情况下,$X_2$ 的 条件 PDF (Conditional PDF) 为:
\[f(x_2\mid x_1)=\dfrac{f(x_1,x_2)}{f_{X_1}(x_1)}\]该定义只对值 $x_1$ 满足 $f_{X_1}(x_1)>0$ 成立。
1.6 独立性
两个连续的随机变量 $X_1$ 和 $X_2$ 是 独立的 (Independent) 当且仅当它们满足
\[f(x_1,x_2)=f_{X_1}(x_1)f_{X_2}(x_2)\]如果 $X_1$ 和 $X_2$ 是独立的,那么
\[f_{X_2\mid X_1}(x_2\mid x_1)=\dfrac{f(x_1,x_2)}{f_{X_1}(x_1)}=\dfrac{f_{X_1}(x_1)f_{X_2}(x_2)}{f_{X_1}(x_1)}=f_{X_2}(x_2)\]因此,知道 $X_1$ 的值并不会改变对 $X_2$ 的概率评估,反之亦然。
1.7 期望和方差
一个随机向量 $X=(X_1,\dots,X_p)^{\mathrm T}$ 的 均值 (Mean) $\mu \in \mathbb R^p$ 被定义为:
\[\mu = \begin{pmatrix}\mu_1 \\ \vdots \\ \mu_p \end{pmatrix} = \begin{pmatrix}E(X_1) \\ \vdots \\ E(X_p) \end{pmatrix} = \begin{pmatrix}\int xf_{X_1}(x)dx \\ \vdots \\ \int xf_{X_p}(x)dx \end{pmatrix}\]-
如果 $X$ 和 $Y$ 是两个 $p$ 维向量,$\alpha$ 和 $\beta$ 是两个常数,那么
\[E(\alpha X + \beta Y)=\alpha E(X) + \beta E(Y)\] -
如果 $X$ 是一个 $p\times 1$ 的向量,$Y$ 是一个 $q\times 1$ 的向量,$X$ 和 $Y$ 相互独立,那么
\[E(XY^{\mathrm T})=E(X)E(Y^{\mathrm T})\]- 提示:请记住要始终检查矩阵尺寸是否兼容。
条件期望 (Conditional Expectation) $E(X_2\mid X_1=x_1)$ 被定义为:
\[E(X_2\mid X_1=x_1) = \int x_2 f_{X_2\mid X_1}(x_2\mid x_1)dx_2\]并且 条件方差 (Conditional Variance) $\mathrm{Var}(X_2\mid X_1=x_1)$ 被定义为:
\[\mathrm{Var}(X_2\mid X_1=x_1) = E(X_2X_2^{\mathrm T}\mid X_1=x_1)-E(X_2\mid X_1=x_1)E(X_2^{\mathrm T}\mid X_1=x_1)\]如果 $X_2$ 是一个列向量。
- 提示:如有疑问,请检查所得矩阵的维数,以查看是否正确。
1.8 协方差
如上节课中所述,一个均值为 $\mu$ 的随机向量 $X$ 的 协方差 (Covariance) $\Sigma$ 被定义为:
\[\Sigma = E\{(X-\mu)(X-\mu)^{\mathrm T}\}\]我们将一个均值为 $\mu$,协方差为 $\Sigma$ 的随机向量 $X$ 记为:
\[X \sim (\mu, \Sigma)\]对于一个均值为 $\mu$ 的 $p\times 1$ 向量 $X$ 和一个均值为 $\nu$ 的 $q\times 1$ 向量 $Y$,两者的 协方差矩阵 (Covariance Matrix) 被定义为:
\[\Sigma_{X,Y} = \mathrm{Cov}(X,Y)=E\{(X-\mu)(Y-\nu)^{\mathrm T}\}=E(XY^{\mathrm T})-E(X)E(Y^{\mathrm T})\]该矩阵的元素是 $X$ 和 $Y$ 中的分量之间的成对协方差。
-
我们有
\[\mathrm{Cov}(X+Y,Z)=\mathrm{Cov}(X,Z)+\mathrm{Cov}(Y,Z)\] -
我们有
\[\mathrm{Var}(X+Y)= \mathrm{Var}(X)+2\mathrm{Cov}(X,Y)+\mathrm{Var}(Y)\] -
对于矩阵 $\mathcal A$ 和 $\mathcal B$,以及随机向量 $X$ 和 $Y$,我们可以定义:
\[\mathrm{Cov}(\mathcal AX,\mathcal BY)=\mathcal A \mathrm{Cov}(X,Y) \mathcal B^{\mathrm T}\]
2. 多元正态分布
一个非常有用且经常遇到的分布是 多元正态分布 (Multinormal Distribution),也简称为 正态分布 (Normal Distribution)。
-
回顾在 单变量 (univariate) 情况下,一个正态分布 $N(\mu,\sigma^2)$ 的概率密度函数为:
\[f(x)=\dfrac{1}{\sqrt{2\pi}\sigma}\exp \left \{-\dfrac{(x-\mu)^2}{2\sigma^2} \right \}\] -
在 多变量 (multivariate) 情况下,需要考虑矩阵和向量。
-
回顾协方差矩阵:
\[\Sigma = \begin{pmatrix}\sigma_{11} & \cdots & \sigma_{1p} \\ & \vdots & \\ \sigma_{p1} & \cdots & \sigma_{pp}\end{pmatrix}= \begin{pmatrix}\sigma_{1}^2 & \cdots & \sigma_{1p} \\ & \vdots & \\ \sigma_{p1} & \cdots & \sigma_{p}^2\end{pmatrix}\]其中,$\sigma_j^2=\mathrm{Var}(X_j)$。
-
一个均值为 $\mu$,协方差为 $\Sigma$ 的多元正态分布的概率密度函数为:
\[f(x)=|2\pi \Sigma|^{-1/2}\exp \left\{ -\dfrac{1}{2}(x-\mu)^{\mathrm T}\Sigma^{-1}(x-\mu) \right\} \tag{1}\label{1}\] -
对于服从这样一个多元正态分布的 $p$ 维向量 $X$,我们将其记为:
\[X\sim N_p(\mu, \Sigma)\]如果 $X_i$ 是彼此独立的,那么
\[\Sigma = \begin{pmatrix} \sigma_1^2 & \cdots & 0 \\ & \vdots & \\ 0 & \cdots & \sigma_p^2\end{pmatrix}=\mathrm{diag}(\sigma_1^2,\dots,\sigma_p^2)\]因此,我们有
\[|2\pi \Sigma|=|\mathrm{diag}(2\pi \sigma_1^2,\dots, 2\pi \sigma_p^2)|=(2\pi)^p \sigma_1^2 \cdots \sigma_p^2\]以及
\[\Sigma^{-1}=\mathrm{diag}(\sigma_1^{-2},\dots,\sigma_p^{-2})\]所以,
\[\begin{align} f(x) &= \dfrac{1}{\sqrt{(2\pi)^p}\prod_{j=1}^{p}\sigma_j}\exp \left \{ -\dfrac{1}{2}\sum_{j=1}^{p}\dfrac{(x_j-\mu_j)^2}{\sigma_j^2}\right\} \\[2ex] &= \dfrac{1}{\sqrt{(2\pi)^p}\prod_{j=1}^{p}\sigma_j} \prod_{j=1}^{p}\exp\left \{ -\dfrac{(x_j-\mu_j)^2}{2\sigma_j^2}\right\} \\[2ex] &= \prod_{j=1}^{p} \left[ \dfrac{1}{\sqrt{2\pi}\sigma_j}\exp \left\{ - \dfrac{(x_j-\mu_j)^2}{2\sigma_j^2}\right\}\right] \end{align}\]等于 $p$ 个单变量正态分布 $N(\mu_j,\sigma_j^2)$ 的概率密度函数的乘积。
由等式 $\eqref{1}$ 可知,当 $(x-\mu)^{\mathrm T}\Sigma^{-1}(x-\mu)$ 是一个常数时,正态分布 $N_p(\mu,\Sigma)$ 的概率密度也是一个常数。
现在,对于一个正的常数 $c$,
\[(x-\mu)^{\mathrm T}\Sigma^{-1}(x-\mu)=c\]对应一个 椭球体 (ellipsoid)。
量
\[\sqrt{(x-\mu)^{\mathrm T}\Sigma^{-1}(x-\mu)}\]被称为 $x$ 和 $\mu$ 之间的 马氏距离 (Mahalanobis Distance)。
例如,在 $p=2$ 维情况下:
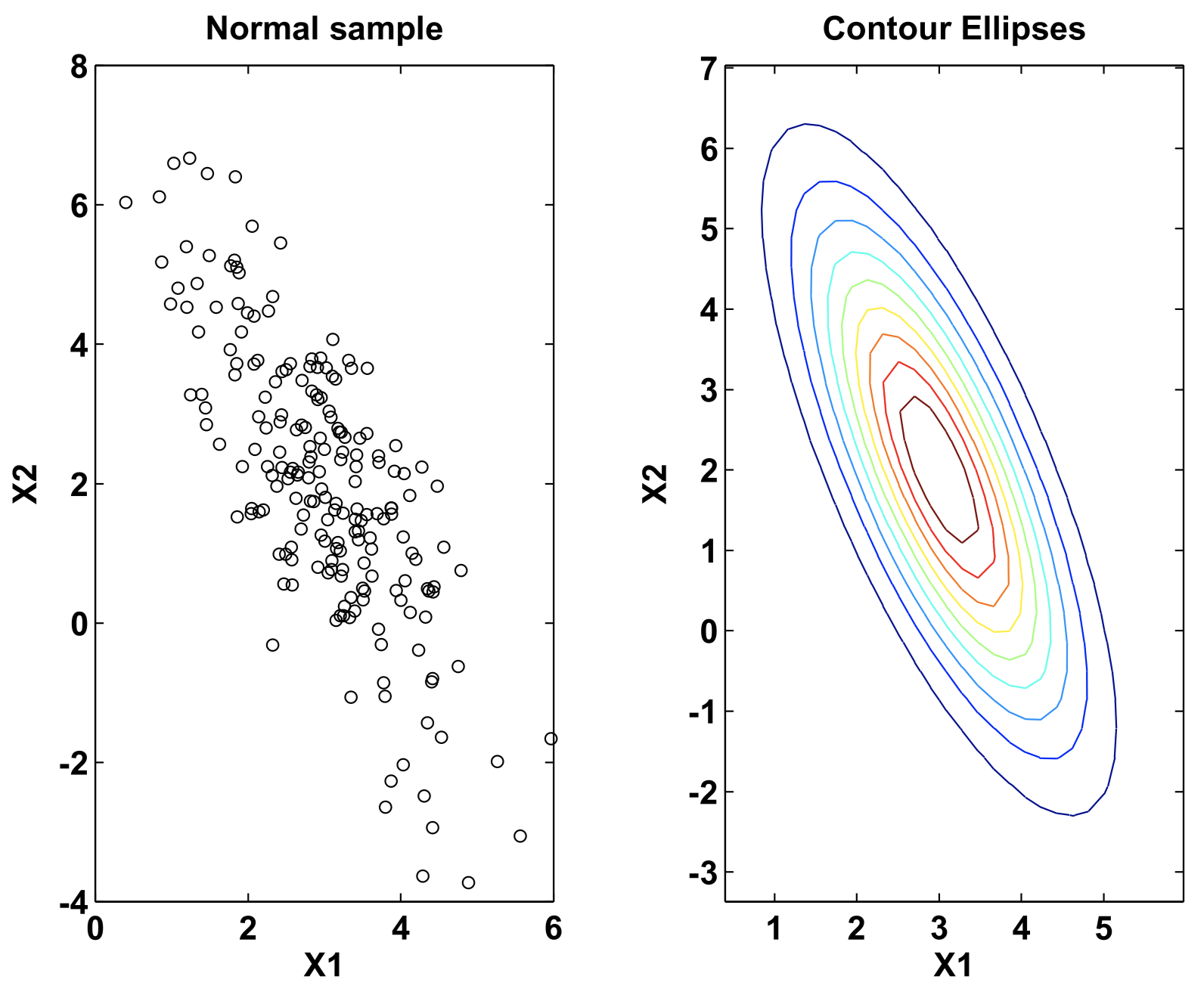
图 1:一个 $\mu=\begin{pmatrix}3 \\ 2\end{pmatrix}$ 和 $\Sigma=\begin{pmatrix}1 & -1.5 \\ -1.5 & 4\end{pmatrix}$ 的正态分布的样本散点图和椭圆轮廓线 -
令 $X\sim N_p(\mu, \Sigma)$,$\mathcal A$ 是一个 $q\times p$ 的矩阵,$b$ 是一个 $q\times 1$ 的向量。那么
\[Y=\mathcal AX+b \sim N_q(\mathcal A \mu +b,\mathcal A\Sigma \mathcal A^{\mathrm T})\] -
令 $X=(X_1^{\mathrm T},X_2^{\mathrm T})^{\mathrm T} \sim N_p(\mu, \Sigma)$,其中
\[\Sigma = \begin{pmatrix}\Sigma_{11} & \Sigma_{12}\\ \Sigma_{21} & \Sigma_{22}\end{pmatrix}\]并且
\[\mathrm{Var}(X_1)=\Sigma_{11},\;\mathrm{Var}(X_2)=\Sigma_{22}\]那么,
\[\Sigma_{12}=0 \quad \Longleftrightarrow \quad X_1 \text{ and } X_2 \text{ are independent.}\] -
如果 $X\sim N_p(\mu, \Sigma)$,并且 $\mathcal A$ 和 $\mathcal B$ 都是具有 $p$ 列的矩阵,那么
\[\mathcal AX \text{ and } \mathcal BX \text{ are independent} \quad \Longleftrightarrow \quad \mathcal A \Sigma \mathcal B^{\mathrm T}=0\] -
如果 $X\sim N_p(\mu, \Sigma)$,并且 $\Sigma$ 是可逆的,那么
\[Y=(X-\mu)^{\mathrm T}\Sigma^{-1}(X-\mu) \sim \chi_p^2\] -
如果 $X_1,\dots,X_n \sim \text{i.i.d. } N_p(\mu,\Sigma)$,那么
\[\overline X \sim N_p(\mu, \Sigma / n)\]
3. Wishart 分布
-
Wishart 分布 是 卡方分布 在多维空间上的一种推广。它取决于 3 个参数:维度 $p$,一个 $p\times p$ 的矩阵 $\Sigma$,以及自由度 $n$。记为:
\[W_p(\Sigma, n)\] -
回顾一下,如果 $Z_1,\dots,Z_n$ 服从独立标准正态分布 $N(0,1)$,那么
\[X=\sum_{k=1}^{n}Z_k^2 \sim \chi_n^2\]服从一个自由度为 $n$ 的卡方分布。
-
如果 $M$ 是一个 $p\times n$ 的矩阵,它的列之间都相互独立并且都服从一个 $N_p(0,\Sigma)$ 的分布,那么
\[\mathcal M = MM^{\mathrm T} \sim W_p(\Sigma,n)\] -
注意,在上面的定义中,$\Sigma$ 不需要是严格正定的,并且关于 $n$ 和 $p$ 也没有任何限制。
-
注意,$\mathcal M$ 服从 Wishart 分布,它必须是 非负定的 (Non-negative Definite) (根据定义,$\mathcal M$ 可以表示为 $MM^{\mathrm T}$,其中 $M$ 为所有列都服从独立正态分布的某个矩阵。因此,对于所有的 $p$ 维向量 $x$,必须满足 $x^{\mathrm T}\mathcal Mx = x^{\mathrm T}MM^{\mathrm T}x \ge 0$)。
-
此外,如果 $\mathcal M$ 总是 非奇异的 (即正定),则称其服从一个 非奇异 Wishart 分布。
-
在 Morris Eaton 的讲义的命题 8.2 中可以找到以下结果:
假设 $\mathcal M$ 服从参数为 $\Sigma、p、n$ 的 Wishart 分布。那么,当且仅当 $n\ge p$ 并且 $\Sigma>0$ 时,$\mathcal M$ 服从一个非奇异 Wishart 分布,其概率密度函数为:
\[f_{\Sigma,n}(\mathcal M)=\dfrac{|\mathcal M|^{\frac{n-p-1}{2}}\exp\left[-\frac{1}{2}\mathrm{tr}(\mathcal M\Sigma^{-1})\right]}{2^{pn/2}\pi^{p(p-1)/4}|\Sigma|^{n/2}\prod_{i=1}^{p}\Gamma\left[(n+1-i)/2\right ]}\] -
当 $\sigma$ 是一个标量时,一个 $W_1(\sigma^2,n)$ 分布等价于 $\sigma^2$ 乘以一个卡方分布 $\chi_n^2$。
-
如果有一个 $p\times p$ 的随机矩阵 $\mathcal Y\sim W_p(\Sigma,n)$ 和一个 $q\times p$ 的矩阵 $\mathcal B$,那么
\[\mathcal{BYB} \sim W_q(\mathcal B \Sigma \mathcal B^{\mathrm T},n)\] -
如果有一个 $p\times p$ 的随机矩阵 $\mathcal Y\sim W_p(\Sigma,n)$ 和一个 $p\times 1$ 的向量 $a$ 满足 $a^{\mathrm T}\Sigma a\ne 0$,那么
\[\dfrac{a^{\mathrm T}\mathcal Y a}{a^{\mathrm T}\Sigma a} \sim \chi_n^2\] -
回顾之前的无偏样本方差矩阵
\[S=\dfrac{1}{n-1}\sum_{i=1}^{n}(X_i-\overline X)(X_i-\overline X)^{\mathrm T}\]可以证明:
\[(n-1)S \sim W_p(\Sigma, n-1)\] -
上面本质上是在说如果 $X_1,\dots,X_n$ 是服从 $\text{i.i.d. } N(\mu, \Sigma)$ 的随机向量,其样本均值为 $\overline X$,那么
\[\sum_{i=1}^{n}(X_i-\overline X)(X_i-\overline X)^{\mathrm T}\]与 $\sum_{i=1}^{n-1}Z_iZ_i^{\mathrm T}$ 具有相同的分布,其中,$Z_i$ 是服从 $\text{i.i.d. } N(0,\Sigma)$ 分布的随机向量。
-
相关证明,请参阅 Anderson 在 An Introduction to Multivariate Statistical Analysis 一书中的 定理 3.3.2。
-
(提到 Eaton 和 Perlman 发表的关于 “非正态性” 的论文)
4. Hotelling 分布
-
Hotelling 分布 是自由度为 $n$ 的 学生 t 分布 $t_n$ 在多维空间上的一种推广。
-
在单变量情况下,一个变量 $X\sim t_n$,如果它可以被写为:
\[X=Y\sqrt{n/Z}\]其中,$Y$ 和 $Z$ 是相互独立的随机变量,$Y\sim N(0,1)$,$Z\sim \chi_n^2$。
-
Hotelling 的 T 方分布 $T^2(p,n)$ 定义为:如果 $X\sim N_p(0,\mathcal I_p)$ 和 $\mathcal M \sim W_p(\mathcal I_p,n)$ 之间相互独立,那么
\[nX^{\mathrm T}\mathcal M^{-1}X \sim T_{p,n}^2\] -
定理 (Hardle 和 Simar 教材第 193 页):如果 $X\sim N_p(\mu,\Sigma)$ 和 $\mathcal M\sim W_p(\Sigma,n)$ 相互独立,并且 $\mathcal M$ 是非奇异的,那么
\[n(X-\mu)^{\mathrm T} \mathcal M^{-1} (X-\mu)\sim T_{p,n}^2\]例如,如果 $X_1,\dots,X_n \sim \text{i.i.d. } N_p(\mu,\Sigma)$,那么样本均值向量 $\overline X$ 和样本协方差矩阵 $\mathcal S$ 满足:
\[n(\overline X-\mu)^{\mathrm T} \mathcal S^{-1}(\overline X-\mu) \sim T_{p,n-1}^2\]上述结果来自 $\mathcal S$ 独立于 $\overline X$ 这一事实,即 Cochran 定理 (Hardle 和 Simar 教材中的定理 5.7)。
证明:由于 $\overline X = \dfrac{1}{n}\sum_{i=1}^{n} X_i$,并且 $X_i \stackrel{\text{i.i.d.}}{\sim} N_p(\mu,\Sigma)$,所以 $\mathrm{Var}(\overline X) = \dfrac{1}{n}\mathrm{Var}(X_i) = \dfrac{\Sigma}{n}$
因此,我们有
\[\sqrt{n} (\overline X -\mu) \sim N_p(0,\Sigma)\]另外,我们知道
\[S=\dfrac{\sum_{i=1}^{n}(X_i - \overline X)(X_i - \overline X)^{\mathrm T}}{n-1} = \dfrac{Z}{n-1}\]其中,$Z=\sum_{i=1}^{n}(X_i - \overline X)(X_i - \overline X)^{\mathrm T} \sim W_p(\Sigma, n-1)$
因此,我们有
\[\begin{align} n(\overline X-\mu)^{\mathrm T} \mathcal S^{-1}(\overline X-\mu) &= \sqrt{n}(\overline X-\mu) ^{\mathrm T} S^{-1} \sqrt{n}(\overline X-\mu) \\[2ex] &= (n-1) \sqrt{n}(\overline X-\mu)^{\mathrm T} Z^{-1} \sqrt{n}(\overline X-\mu) \sim T^2_{p,n-1} \end{align}\] -
Hotelling 的 $T^2$ 分布 和 $F$ 分布 之间的关系是:
\[T_{p,n}^2=\dfrac{np}{n-p+1}F_{p,n-p+1}\] -
注意,自由度为 $n$ 的单变量 $t$ 分布的平方等价于一个 $F_{1,n}$ 分布。
-
Hotelling 的 $T^2$ 检验 通常用于以下假设检验问题 (Hardle 和 Simar 教材中的 7.1 章节):
假设 $X_1,\dots,X_n$ 是来自总体为 $N_p(\mu,\Sigma)$ 分布的 $\text{i.i.d.}$ 样本,其中 $\Sigma$ 是未知的。我们试图检验:
\[H_0: \mu = \mu_0 \quad \text{VS.} \quad H_1: \text{no constraints}\](这是使用 $t$ 统计量解决的普通单变量检验问题的多元版本。)
当 $H_0$ 为真时,我们有:
\[n(\overline X-\mu_0)^{\mathrm T}\mathcal S^{-1}(\overline X-\mu_0) \sim T_{p,n-1}^2\]当然,我们可以使用 $n(\overline X-\mu_0)^{\mathrm T}\mathcal S^{-1}(\overline X-\mu_0)$ 作为检验统计量,并根据 $T_{p,n-1}^2$ (或者 $F_{p,n-p}$) 分布校准截止阈值。
事实证明,对于该检验问题,我们也可以通过 似然比检验 推导出相同的检验 (参见 Hardle 和 Simar 教材中的 7.1 章节)。
下节内容:主成分分析 (一)
本作品采用知识共享署名-非商业性使用-相同方式共享 4.0 国际许可协议进行许可。 欢迎转载,并请注明来自:YEY 的博客 同时保持文章内容的完整和以上声明信息!