Lecture 04 分类
参考教材:
- Gareth, J., Daniela, W., Trevor, H., & Robert, T. (2013). An intruduction to statistical learning: with applications in R. Spinger.
- Hastie, T., Tibshirani, R., & Friedman, J. (2009). The elements of statistical learning: data mining, inference, and prediction. Spinger Science & Business Media.
1. 分类问题概述
上节课中我们所讨论的线性回归模型假设响应变量 $Y$ 是定量的,但很多情况下,响应变量是 定性的 (qualitative)。例如,眼睛颜色是定性变量,取值蓝色或棕色。定性变量又称 分类 (categorical) 变量。本节课我们将学习预测定性响应变量的方法及 分类 (classification) 过程。预测一个观测的定性响应值也指对观测 分类 (classify),因为它涉及将观测分配到一个类别中。另一方面,大部分的分类方法先从预测定性变量不同类别的概率开始,将分类问题作为概率估计的一个结果。从这个角度上看,分类与回归方法有许多类似之处。
如今许多 分类器 (calssifier) 已被开发出来用于预测定性响应变量值。我们之前已经接触过一部分,这节课中,我们将讨论三种应用最广泛的分类方法:逻辑回归 (logistìc regression)、线性判别分析 (linear discriminant analysis) 和 $K$ 最近邻 ($K$-nearest neighbours)。在后面课程中,我们将会讨论更多的数据密集型计算方法,例如广义可加模型、基于树的方法、随机森林、boosting,以及支持向量机。
定性变量取值为 无序集合 $\mathcal C$ 中的值,例如:
- $\texttt{eye color}\in\{\mathtt{brown, blue, green}\}$
- $\texttt{email}\in\{\mathtt{spam, ham}\}$
给定一个特征向量 $X$ 和一个定性响应 $Y$,其中响应变量 $Y$ 在集合 $\mathcal C$ 中取值。分类任务就是构建一个函数 $C(X)$,该函数将特征向量 $X$ 作为输入并预测其 $Y$ 值;即 $C(X) \in \mathcal C$。
通常,我们更感兴趣的是对 $X$ 属于 $\mathcal C$ 中每个类别的 概率 进行估计。
例如,对保险索赔是欺诈的概率进行估计要比将其直接分类为是否欺诈更具实际意义。
例子:信用卡违约
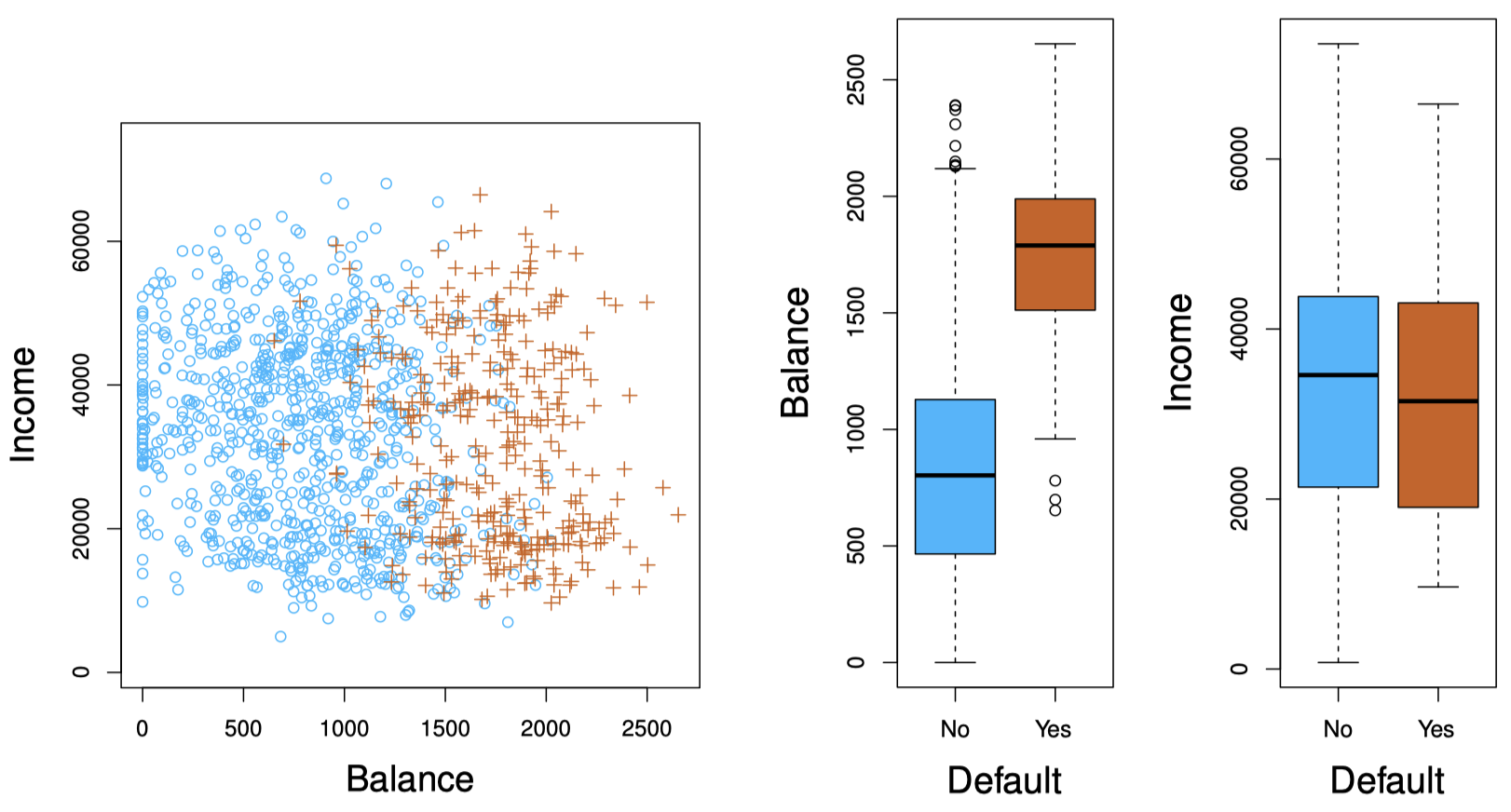
图 1:Default 数据集。左图:部分个体的年收入与月信用卡余额关系。信用卡违约的个体标记为 “$+$”,未违约的个体标记为 “$\circ$”。中图:default 关于 balance 函数的箱型图。右图:default 关于 income 函数的箱型图。
2. 为什么线性回归不可用
假设在上面的 Default 分类任务中,我们将响应变量编码为:
我们可以简单地对 $X$ 进行 $Y$ 的线性回归,并且如果 $Y> 0.5$ 就将其分类为 $\texttt{YES}$ 吗?
- 在这种二元结果的情况下,线性回归可以很好地用作分类器,并且它等效于我们稍后将讨论的 线性判别分析。
- 由于总体的 $E(Y\mid X=x)=\Pr (Y=1\mid X=x)$,我们可能认为回归可以完美解决此任务。
- 然而,线性 回归可能会产生小于 $0$ 或大于 $1$ 的概率。因此,逻辑回归 (logistic regression) 更为合适。

图 2:Default 数据分类。左图:线性回归估计的 default 概率。可以看到,其中一些数据上估计的概率值是负数。橙色标记表示按照 $0/1$ 编码的 default 值 ($\texttt{NO}$ 或 $\texttt{YES}$)。右图:逻辑回归预测的 default 概率,所有估计的概率均落在 $0$ 到 $1$ 之间。
橙色标记表示响应 $Y$ 为 $0$ 或 $1$。可以看到,线性回归无法很好地估计 $\Pr(Y=1\mid X)$,而逻辑回归似乎非常适合该任务。
现在,假设我们有一个具有三种可能值的响应变量。例如,对于急诊室中的病人,我们需要根据他们的症状对其进行分类:stroke (中风)、drug overdose (服药过量) 和 epileptic seizure (癫痫发作)。考虑用一个定量的响应变量 $Y$ 对这些值编码:
我们可以根据这些编码,并结合一系列预测变量 $X_1,\dots,X_p$ 通过最小二乘法建立线性回归模型来预测 $Y$。
但是,这种做法存在一个问题:上面的编码方式实际默认了一个有序的输出,它实际上暗示了 stroke 和 drug overdose 之间的差异与 drug overdose 和 epileptic seizure 之间的差异是相同的。然而,实际上并没有特别的原因必需这样,我们同样可以选择另一种编码顺序。对一个二元定性响应变量而言,这种做法不会影响最终结果,例如,病人的身体状况只有两种可能 stroke 和 drug overdose,这种情况下,即使我们改变编码顺序,线性回归最后依然会给出相同的结果。然而,对于两个以上水平的响应变量而言,不同的编码顺序将产生完全不同的线性模型,继而导致对于同一测试观测产生不同的预测类别。
如果响应变量值确实存在一个自然的程度顺序,例如温和、中等和剧烈,并且温和和中等的程度差距与中等和剧烈的程度差距是相近的,那么将其编码为 $1,2,3$ 是合理的。但是请注意,通常我们不能将一个定性的响应变量自然地转换为两个水平以上的定量变量来建立回归模型。
这种情况下,线性回归不再适用。多类别逻辑回归 (Multiclass Logistic Regression) 或者 判别分析 (Discriminant Analysis) 更为合适。
3. 逻辑回归
3.1 逻辑回归模型
为了简化,我们记 $p(X)=\Pr(Y=1\mid X)$。考虑利用 balance 预测 default。
如前所述,线性回归在处理分类问题时无法保证结果概率落在 $0$ 到 $1$ 之间,为避免这类问题,我们必须找到一个函数建立针对 $p(X)$ 的模型,使对任意 $X$ 值该函数的输出结果都在 $0$ 和 $1$ 之间。
有许多函数可以满足上述要求。在逻辑回归中,采用以下 逻辑函数 (logistic function) 形式:
\[p(X)=\dfrac{e^{\beta_0 + \beta_1 X}}{1+ e^{\beta_0 + \beta_1 X}}\]可以看到,无论 $\beta_0$、$\beta_1$ 或 $X$ 取值如何,$p(X)$ 的值始终落在 $0$ 到 $1$ 之间。
通过整理,可得
\[\log \left(\dfrac{p(X)}{1-p(X)}\right)=\beta_0 + \beta_1 X\]这种单调变换称为 $p(X)$ 的 对数几率 (log odds) 或 分对数 (logit)。
3.2 估计回归系数
我们使用 最大似然 (maximum likelihood) 对模型参数进行估计。
其基本思想是:寻找 $\beta_0$ 和 $\beta_1$ 的一个估计,使得通过逻辑函数得到的每个人的违约预测概率 $\hat p(x_i)$ 最大可能地与违约的观测情况接近。即,求出的估计 $\hat \beta_0$ 和 $\hat \beta_1$,使得所有违约人的值接近于 $1$ ,而未违约人的值接近于 $0$。
这可以通过 似然函数 (likelihood function) 表述,其形式如下:
\[\ell (\beta_0,\beta_1) = \prod_{i:y_i=1}p(x_i)\prod_{i:y_i=0}(1- p(x_i))\]它给出了在数据中已观察到的 $0$ 和 $1$ 的概率。我们选择能够使观测数据的似然函数最大化的 $\beta_0$ 和 $\beta_1$。
大多数统计软件包都可以通过最大似然拟合线性逻辑回归模型。在 R 中,我们可以使用 glm() 函数来拟合逻辑回归模型。
表 1 显示了 Default 数据中,建立用 balance 预测 default = YES 概率的逻辑回归模型的系数估计和其他相关信息。可以看到,$\hat \beta_1 =0.0055$,这表示信用卡余额 balance 越多,发生违约 default 的概率就越大。更准确地说,balance 每增加一个单位,default 的 log odds 就增加 $0.0055$ 个单位。
表 1:在 Default 数据中,建立用 balance 预测 default 概率的逻辑回归模型的系数估计。balance 每增加一个单位,default 的 log odds 增加 $0.0055$ 个单位。
| 系数 | 标准误 | $Z$ 统计量 | p 值 | |
|---|---|---|---|---|
Intercept |
$-10.6513$ | $0.3612$ | $-29.5$ | $< 0.0001$ |
balance |
$0.0055$ | $0.0002$ | $24.9$ | $< 0.0001$ |
表 1 中逻辑回归模型的输出结果与之前的线性回归输出的结果是类似的。例如,系数估计的准确性可通过计算标准误来衡量。表 1 中的 $Z$ 统计量和线性回归模型输出的 $t$ 统计量的作用是一样的,如 $\beta_1$ 的 $Z$ 统计量等于 $\hat \beta_1 / SE(\hat \beta_1)$。当 $Z$ 统计量的绝对值很大时,说明零假设 $H_0: \beta_1=0$ 不成立。零假设也就是 $p(X)=\frac{e^{\beta_0}}{1+e^{\beta_0}}$,表示 default 概率不依赖于 balance。由于表 1 中 balance 的 p 值很小,因此拒绝 $H_0$,表明 default 概率与 balance 之间确实存在关系。另外,这里截距项估计通常意义不大,主要作用是调节平均拟合概率使之与真实数据实际 odds 更接近。
3.3 预测
对于某个信用卡余额 balance 为 $1000$ 美元的个体,其估计的违约 default = YES 概率是多少?
对于 balance 为 $2000$ 美元的个体呢?
可见,对于某个个体,信用卡余额 (balance) 越高,其违约 (default = YES) 的概率也越高。
另外,我们还可以尝试用定性预测变量 student 来拟合逻辑回归模型。我们将 student 编码为一个虚拟变量 student [YES]:学生为 $1$,非学生为 $0$。表 2 给出了用 student 预测 default 概率的逻辑回归模型的结果,可以看出虚拟变量的系数值是正的,其 p 值也是显著的。这表明学生比非学生更容易违约。
表 2:在 Default 数据中,建立用 student 预测 default 概率的逻辑回归模型的系数估计。student 用一个虚拟变量 student [YES] 编码,$1$ 代表学生,$0$ 代表非学生。
| 系数 | 标准误 | $Z$ 统计量 | p 值 | |
|---|---|---|---|---|
Intercept |
$-3.5041$ | $0.0707$ | $-49.55$ | $< 0.0001$ |
student [YES] |
$0.4049$ | $0.1150$ | $3.52$ | $0.0004$ |
可以看到,学生比非学生违约概率更大。
3.4 多元逻辑回归
现在考虑预测一个二元响应变量受多个因素影响的情况。类似于之前的多元线性回归,我们可以将二元逻辑回归推广到多元情况:
\[\log \left(\dfrac{p(X)}{1-p(X)}\right)=\beta_0 + \beta_1 X_1 + \cdots + \beta_p X_p\]这里,$X=(X_1,\dots,X_p)$ 表示 $p$ 个预测变量,这种情况下,逻辑函数为:
\[p(X)=\dfrac{e^{\beta_0 + \beta_1 X_1 + \cdots + \beta_p X_p}}{1+ e^{\beta_0 + \beta_1 X_1 + \cdots + \beta_p X_p}}\]和之前一样,我们可以通过最大似然方法估计系数 $\beta_0,\beta_1,\dots,\beta_p$。
表 3 给出了用 balance、income 和 student 三个预测变量对 default 概率建立的逻辑回归模型的系数估计。
表 3:在 Default 数据中,结合 balance、income、student 三个预测变量建立的预测 default 概率的逻辑回归模型的系数估计。student 用一个虚拟变量 student [YES] 编码,$1$ 代表学生,$0$ 代表非学生。income 的单位为千美元。
| 系数 | 标准误 | $Z$ 统计量 | p 值 | |
|---|---|---|---|---|
Intercept |
$-10.8690$ | $0.4923$ | $-22.08$ | $< 0.0001$ |
balance |
$0.0057$ | $0.0002$ | $24.74$ | $< 0.0001$ |
income |
$0.0030$ | $0.0082$ | $0.37$ | $0.7115$ |
student [YES] |
$-0.6468$ | $0.2362$ | $-2.74$ | $0.0062$ |
表 3 的结果有点出乎意料。其中 balance 和 student [YES] 的 p 值很小,意味着两者对 default 概率是有影响的。然而这里 student [YES] 系数是负数,说明学生要比非学生的违约概率更低,这似乎和我们之前在单变量逻辑回归中得到的结论相矛盾。
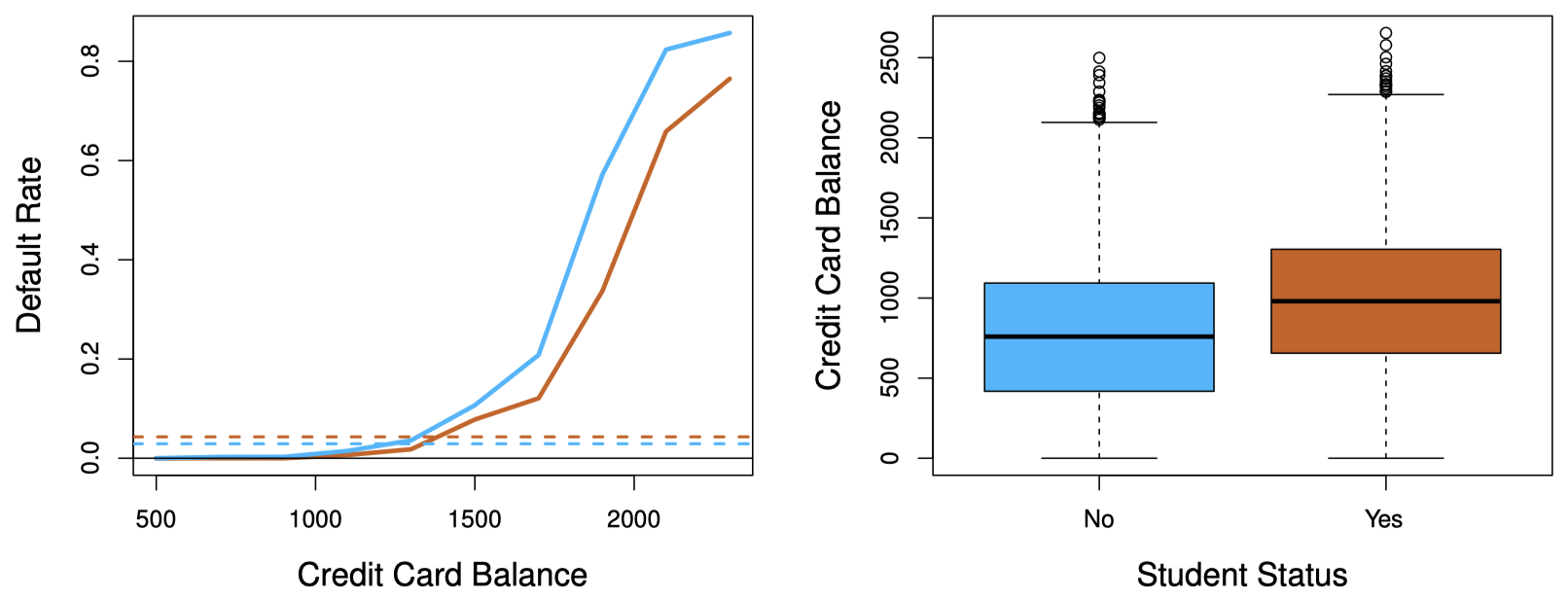
图 3:Default 数据集的混淆现象。左图:学生 (橙色) 与非学生 (蓝色) 的违约率。实线表示违约率与 balance 的函数关系,水平虚线是考虑所有变量时的违约率。右图:学生 (橙色) 与非学生 (蓝色) 的 balance 的箱型图。
图 3 对这个看似矛盾的问题从图像上给予解释:
- 通常,学生的信用卡余额 (
balance) 要比非学生高,而balance与违约率之间又存在正相关关系,因此,学生的 边缘违约率 (marginal default rate) 实际上要高于非学生。 - 但是,对于每个给定的
balance水平,学生的违约率都要低于非学生。 - 多元逻辑回归可以帮助我们发现这点。
例子:南非心脏病
- 80 年代初来自南非西开普的 $160$ 例 MI (心肌梗塞) 和 $302$ 例对照 (所有年龄在 15-64 岁的男性)。
- 该地区的总体患病率很高:$5.1\%$。图 4 中的散点图矩阵中显示了对 $7$ 个预测变量 (风险因素) 的测量。
- 目标是确定风险因素的相对强度和方向。
- 这是一项旨在对公众进行健康饮食教育的干预研究的一部分。
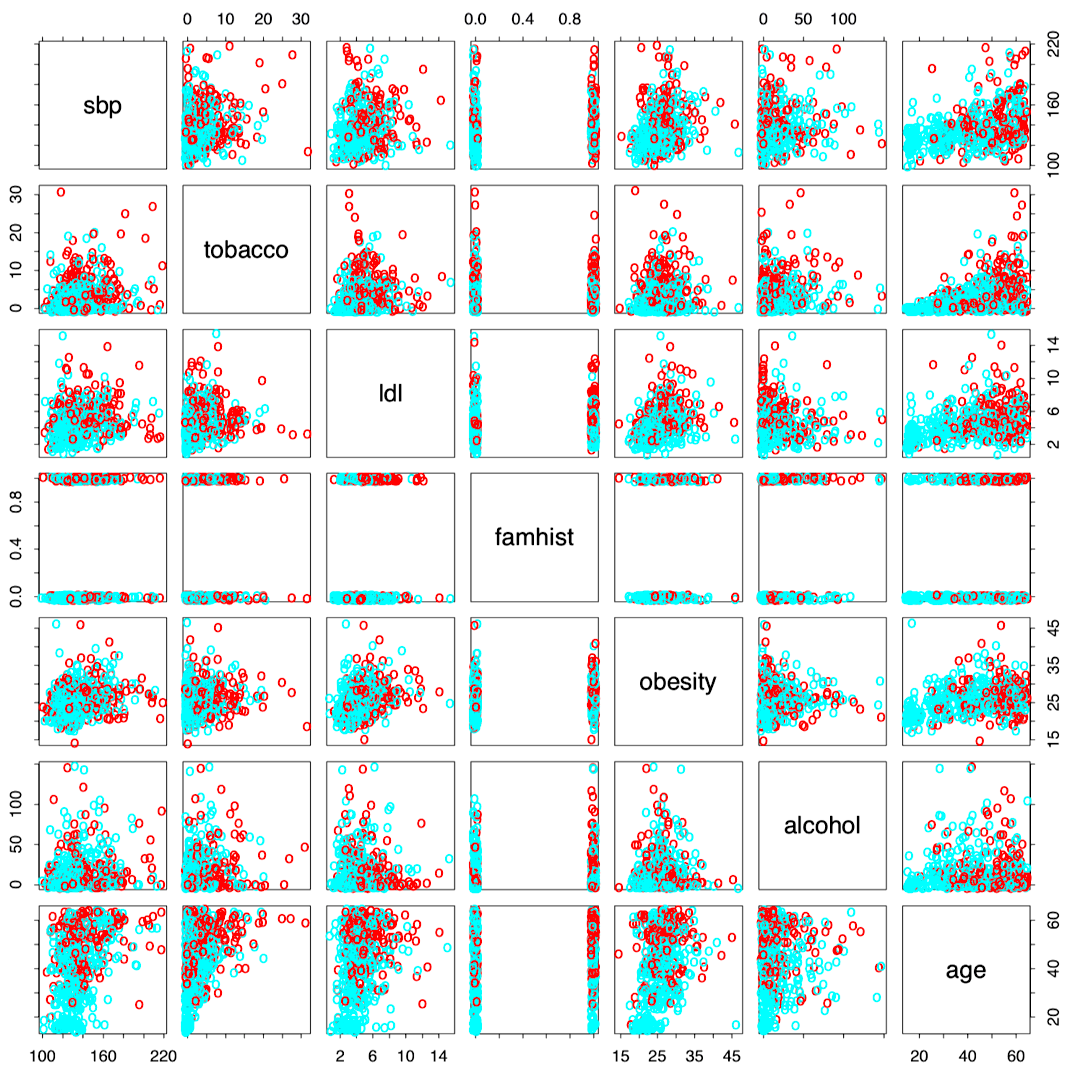
图 4:南非心脏病数据的散点图矩阵。响应采用颜色编码:病例 (MI) 为红色,控制组为青绿色。其中,famhist 是一个二元变量:$1$ 表示具有 MI 家族病史。
R 代码:
1
2
heartfit <-glm(chd∼.,data=heart ,family=binomial)
summary(heartfit)
输出结果:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
Call:
glm(formula = chd ∼ ., family=binomial, data=heart)
Coefficients :
Estimate Std. Error z value Pr(>|z|)
(Intercept) -4.1295997 0.9641558 -4.283 1.84e-05 ***
sbp 0.0057607 0.0056326 1.023 0.30643
tobacco 0.0795256 0.0262150 3.034 0.00242 **
ldl 0.1847793 0.0574115 3.219 0.00129 **
famhistPresent 0.9391855 0.2248691 4.177 2.96e-05 ***
obesity -0.0345434 0.0291053 -1.187 0.23529
alcohol 0.0006065 0.0044550 0.136 0.89171
age 0.0425412 0.0101749 4.181 2.90e-05 ***
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 596.11 on 461 degrees of freedom
Residual deviance: 483.17 on 454 degrees of freedom
AIC: 499.17
病例对照抽样和逻辑回归
- 在南非心脏病数据集中,有 $160$ 个病例和 $302$ 个控制对照,病例占比约 $\tilde \pi = 0.35$。然而,MI 在该地区的实际流行率为 $π= 0.05$。
- 使用病例-对照样本,我们可以准确地估计回归参数 $\beta_j$ (如果我们的模型是正确的);但是,对于常数项 $\beta_0$ 的估计不正确。
-
我们可以通过简单变换来校正估计的截距
\[\hat \beta_0^* = \hat \beta_0 + \log \dfrac{\pi}{1-\pi} - \log \dfrac{\tilde \pi}{1- \tilde \pi}\] - 通常,这种情况比较少见,我们一般对于系数和截距项的估计会全部接受。另外,一般而言,高达 (病例数) 五倍的控制组数量已经足够了。

图 5:与病例相比,对控制组进行更多采样可以减小参数估计的方差。但是在经过大约 5:1 的比率后,这种方差减小的趋势明显变小了。
3.5 多类别逻辑回归
到目前为止,我们已经讨论了二分类逻辑回归。我们可以很容易将其推广到多分类问题。其中,一种版本 (在 R 包 glmnet 中使用) 具有以下对称形式:
这里,每个 类都具有一个线性函数。
(我们可能已经意识到,像二分类类逻辑回归一样,这里实际上只需要 $K−1$ 个线性函数。)
我们将其称为 多类别逻辑回归 (multiclass/multinomial logistic regression)。
4. 判别分析
在二元响应变量的情况下,逻辑回归根据其逻辑函数直接对概率 $\Pr(Y=k\mid X=x)$ 建模。用统计语言说,即给定预测变量 $X$,建立响应变量 $Y$ 的条件分布模型。
现在,我们考虑另外一类间接估计这些概率的方法:
- 在这类方法中,我们分别对每种响应分类 (给定的 $Y$) 建模预测变量 $X$ 的分布 $\Pr(X\mid Y=k)$,然后运用 贝叶斯定理 (Bayes theorem) 翻转,来估计 $\Pr(Y=k\mid X=x)$。
- 当我们将每一类假设为正态 (高斯) 分布时,我们将得到线性或者二次判别分析。
- 但是,这种方法非常普遍,我们也可以使用其他版本。这里,我们将重点关注正态分布。
那么,为什么我们已经有了逻辑回归,还要使用另一类方法呢?
通常,有如下几个方面的原因:
- 当不同类别之间的区分度很高时,逻辑回归模型的参数估计不够稳定,而线性判别分析不存在这个问题。
- 如果样本数 $n$ 比较小,而且在每一类响应分类中预测变量 $X$ 都近似服从正态分布,那么线性判别分析要比逻辑回归更稳定。
- 如前所述,当响应变量的分类多于两类时,线性判别分析应用更普遍,因为它还提供了数据的低维视图。
4.1 运用贝叶斯定理进行分类
假设观测分成 $K$ 类,$K\ge 2$,即定性响应变最 $Y$ 可以取 $K$ 个不同的无序值。这种情况下,贝叶斯定理 (Bayes thcorem) 可以表述为:
\[\Pr(Y=k\mid X=x)=\dfrac{\Pr(X=x\mid Y=k)\cdot \Pr(Y=k)}{\Pr(X=x)}\]将其稍作变换以进行判别分析:
\[\Pr(Y=k\mid X=x)=\dfrac{\pi_k f_k(x)}{\sum_{l=1}^{K}\pi_l f_l(x)}\]其中,
- $f_k(x)=\Pr(X=x\mid Y=k)$ 表示第 $k$ 类观测的 $X$ 的 密度函数 (density function)。这里,我们将在每个类中分别使用正态密度。
- $\pi_k=\Pr(Y=k)$ 表示第 $k$ 类的 边缘 (marginal) 或者 先验 (prior) 概率。
我们将一个新的数据点分到其概率密度最高的类别中。
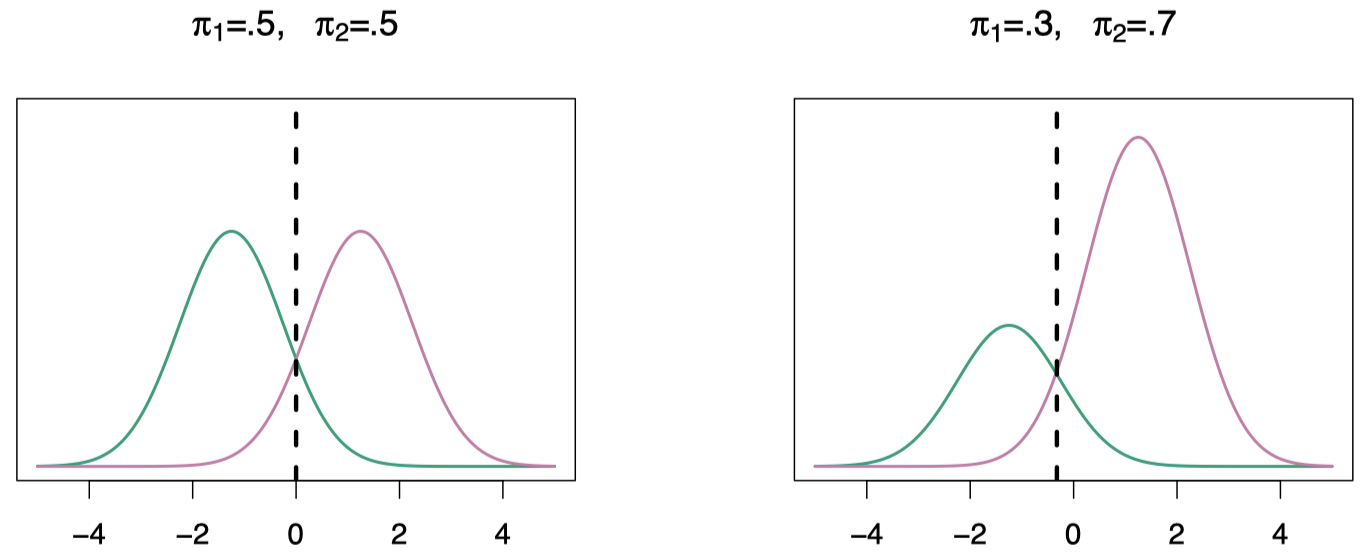
图 6:二元响应变量下,不同先验分布的情况。左图:类别 1 和 类别 2 的先验概率均为 $0.5$。右图:类别 1 和 类别 2 的先验概率分别为 $0.3$ 和 $0.7$。
当先验不同时,我们也会将其考虑在内,并比较 $\pi_k f_k(x)$。在右图中,我们将其分到粉红色表示的类别中,注意,此时决策边界已偏向左侧。
4.2 $p=1$ 情况下的线性判别分析
假设 $p = 1$,即只有一个预测变量。假设 $f_k(x)$ 是 正态的 (nonnal) 或 高斯的 (Gaussian)。在一维的情况下,正态密度函数形式为:
\[f_k(x)=\dfrac{1}{\sqrt{2\pi}\sigma_k}e^{-\frac{1}{2}\left(\frac{x-\mu_k}{\sigma_k}\right)^2}\]这里,$\mu_k$ 表示第 $k$ 类的均值,$\sigma_k^2$ 表示第 $k$ 类的方差。我们假设所有类别的方差都相同,即 $\sigma_k=\sigma$。
将其代入贝叶斯公式,我们得到一个关于 $p_k(x)=\Pr(Y=k\mid X=x)$ 的相当复杂的表达式:
\[p_k(x)=\dfrac{\pi_k \dfrac{1}{\sqrt{2\pi}\sigma}e^{-\frac{1}{2}\left(\frac{x-\mu_k}{\sigma}\right)^2}}{\sum_{l=1}^{K}\pi_l \dfrac{1}{\sqrt{2\pi}\sigma}e^{-\frac{1}{2}\left(\frac{x-\mu_l}{\sigma}\right)^2}}\]不过,我们可以对其进行一些简化。
判别函数
为了对 $X = x$ 进行分类,我们需要查看 $p_k(x)$ 中的最大值对应的 $k$。通过对上式两边取对数,并舍弃那些不依赖于 $k$ 的项,这等价于将 $x$ 分配到下面 判别得分 (discriminant score) 最大的类:
\[\delta_k(x)=x\cdot \dfrac{\mu_k}{\sigma^2}-\dfrac{\mu_k^2}{2\sigma^2}+\log(\pi_k)\]注意到,$\delta_k(x)$ 是一个关于 $x$ 的 线性函数,这也是 LDA 中线性名称的由来。
如果存在 $K = 2$ 个类别且 $\pi_1=\pi_2=0.5$,那么 决策边界 (decision boundary) 将位于:
\[x=\dfrac{\mu_1 + \mu_2}{2}\]例子
如图 7 的左图,显示了两个正态密度函数 $f_1(x)$ 和 $f_2(x)$,它们分别代表两个不同的分类,其均值和方差分别为 $\mu_1=-1.5, \mu_2=1.5, \sigma^2=1$。
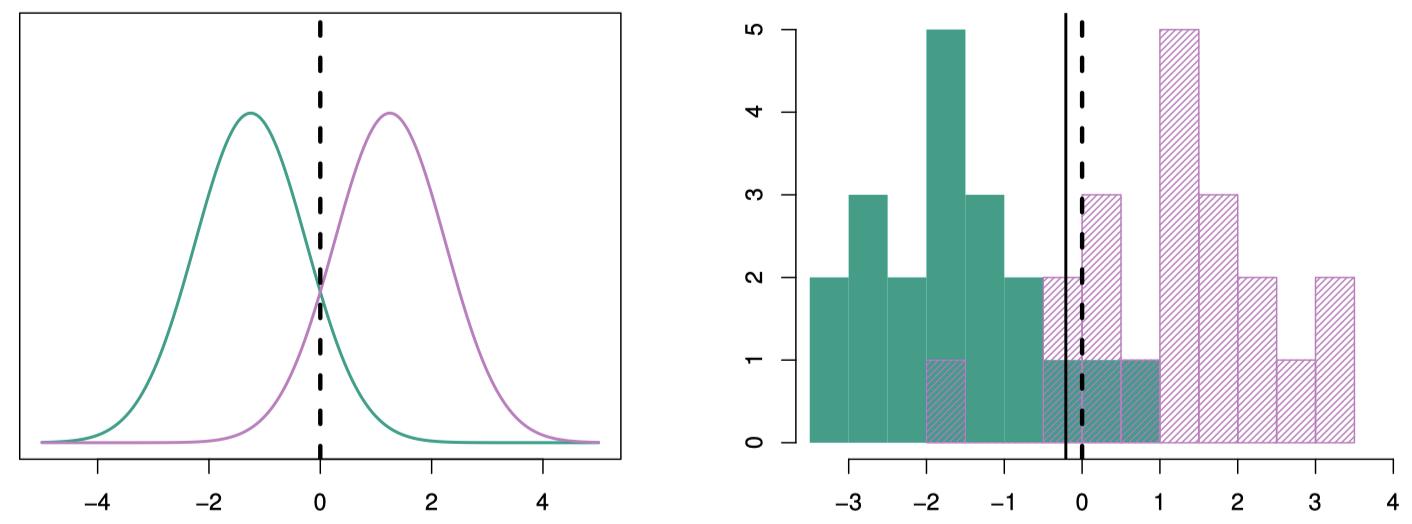
图 7:左图:两个一维的正态密度函数,竖直虚钱代表贝叶斯决策边界。右图:分别来自两类 $20$ 个观测的直方图,竖直虚钱代表贝叶斯决策边界,竖直实线代表通过训练数据得到的 LDA 决策估计边界。
可以看到,这两个密度函数存在重叠部分,所以给定观测 $X=x$,其响应类别存在不确定性。如果假设观测来自每一类的概率相等,即 $\pi_1=\pi_2=0.5$,那么根据之前的决策边界公式可知,如果 $x < 0$,则将观测分给第一类,否则分给第二类。
在这个例子中,我们事先知道每一类 $X$ 都服从高斯分布,且分布参数都是已知的,因此这里我们可以直接计算出贝叶斯分类器。
但在实践中,我们通常无法直接计算出贝叶斯分类器,因为我们并不知道这些参数;我们有的只是训练数据。在这种情况下,即使我们知道每个类中的 $X$ 确实来自高斯分布,我们仍然估计相关参数,并将其代入决策规则。
估计参数
线性判别分析 (linear discriminant analysis, LDA) 中,通常使用以下参数估计:
\[\begin{align} \hat \pi_k &= \dfrac{n_k}{n} \\[2ex] \hat \mu_k &= \dfrac{1}{n_k} \sum_{i:y_i=k} x_i \\[2ex] \hat \sigma^2 &= \dfrac{1}{n-K}\sum_{k=1}^{K} \sum_{i:y_i=k} (x_i-\hat \mu_k)^2 = \sum_{k=1}^{K}\dfrac{n_k-1}{n-K}\cdot \hat \sigma_k^2 \end{align}\]其中,$\hat \sigma_k^2=\frac{1}{n_k-1}\sum_{i:y_i=k}(x_i-\hat \mu_k)^2$ 是第 $k$ 类的估计方差的通常公式。
LDA 分类器将这些参数估计值代入判别得分 $\delta_k(x)$ 的公式中,并将观测 $X=x$ 分给能够使估计的判别函数 $\hat \delta_k(x)$ 最大化的类别 $k$:
\[\hat \delta_k(x)=x\cdot \dfrac{\hat \mu_k}{\hat \sigma^2}-\dfrac{\hat \mu_k^2}{2\hat \sigma^2}+\log(\hat \pi_k)\]4.3 $p> 1$ 情况下的线性判别分析
现在,我们将 LDA 分类器推广至多元预测变量的情况。假设 $X=(X_1,X_2,\dots,X_p)$ 服从一个均值 $\mu_k$ 不同、协方差矩阵 $\Sigma$ 相同的 多元高斯分布 (multivariate Gaussian)。
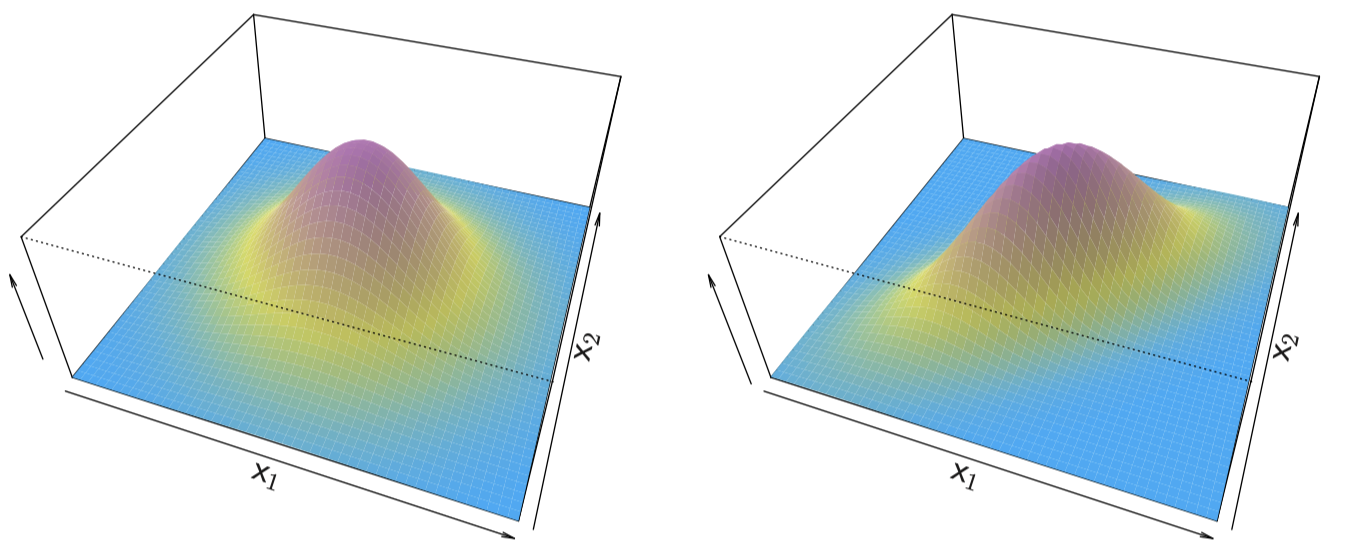
图 8:图中显示的是两个多元高斯密度函数,$p=2$。左图:两个预测变量之间是不相关的。右图:两个变量之间的相关系数为 $0.7$。
多元高斯分布的密度函数为:
\[f(x)=\dfrac{1}{(2\pi)^{p/2}|\Sigma|^{1/2}}e^{-\frac{1}{2}(x-\mu)^{\mathrm T}\Sigma^{-1}(x-\mu)}\]多元 LDA 判别函数为:
\[\delta_k(x)=x^{\mathrm T}\Sigma^{-1}\mu_k - \dfrac{1}{2}\mu_k^{\mathrm T}\Sigma^{-1}\mu_k + \log \pi_k\]尽管其形式相对复杂,但是 $\delta_k(x)=c_{k0} + c_{k1}x_1 +\cdots + c_{kp}x_p$ 仍然是一个关于 $x$ 的线性函数。
例子:$p=2$ 个预测变量,$K=3$ 个响应类别
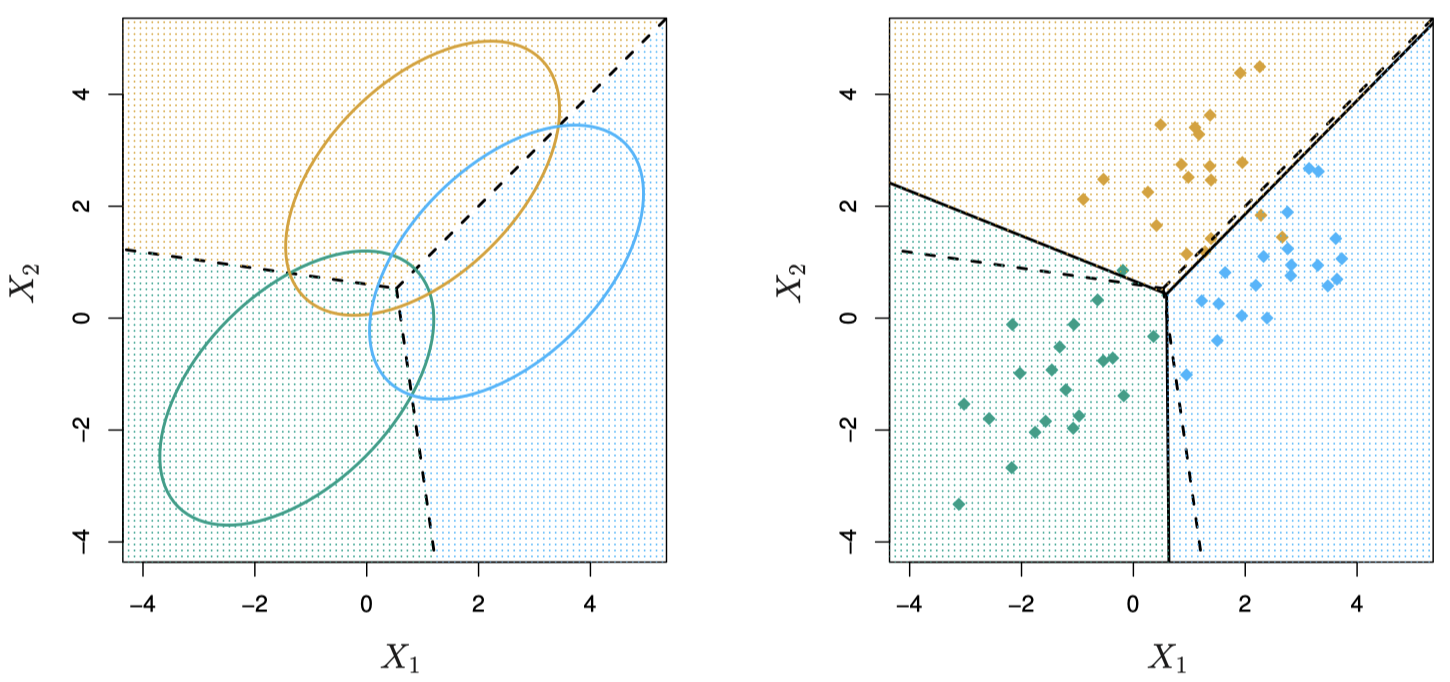
图 9:一个三类别响应变量的例子。每一类的观测均服从一个均值不同、协方差矩阵相同的多元高斯分布,其中 $p =2$。左图:显示的是包含每一类的 $95\%$ 概率的椭圆。虚线表示贝叶斯决策边界。右图:每一类各自生成 $20$ 个观测样本,黑色实线表示 LDA 决策边界,虚线表示贝叶斯决策边界。
这里,$\pi_1=\pi_2=\pi_3=1/3$。
图中虚线代表 贝叶斯决策边界 (Bayes decision boundaries)。如果能够知道,那么在所有可能的分类器中,它们将产生最少的误分类错误。
例子:Fisher 的鸢尾花数据集
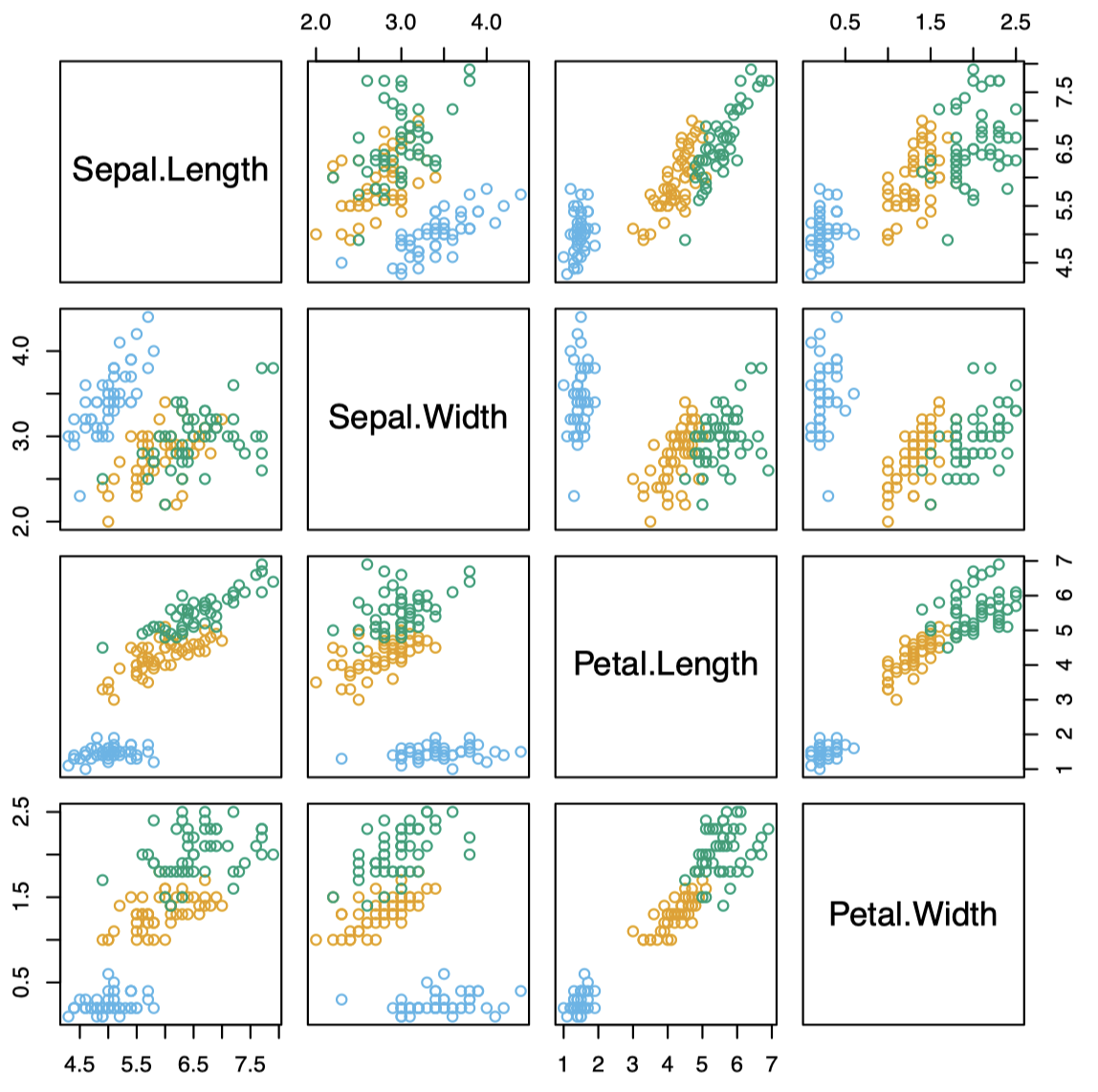
图 10:Fisher 的鸢尾花数据集 Iris 中各预测变量的散点图矩阵。其中包含 $4$ 个预测变量:Sepal.Length、Sepal.Width、Petal.Length、Petal.Width;$3$ 个响应类别:Setosa (蓝色)、Versicolor (黄色)、Virginica (绿色);并且每个类别包含 $50$ 个训练样本。
LDA 分类器对总共 $150$ 个训练样本中进行了分类,除了 $3$ 个误分类样本外,其余全部分类正确。

图 11:Fisher 的鸢尾花数据集 Iris 中,LDA 分类器得到的决策边界。
当响应变量有 $K$ 类时,线性判别分析的结果可以在 $K-1$ 维图中精确查看。
为什么? 因为 LDA 本质上将数据分类到最接近的中心点,并且它们跨越 $K−1$ 维平面,每条坐标轴表示一个类别 $k$ 的判别函数 $\delta_k(x)$。
即使当 $K> 3$ 时,我们仍然可以找到一个 “最佳” 的二维平面,使判别规则可视化。
4.4 从判别函数 $\delta_k(x)$ 到概率
一旦我们估计出了判别函数 $\hat \delta_k(x)$,我们就可以用它来估计不同类别的概率:
\[\widehat{\Pr}(Y=k\mid X=x)=\dfrac{e^{\hat \delta_k(x)}}{\sum_{l=1}^{K}e^{\hat \delta_l(x)}}\]因此,将 $X=x$ 分给最大 $\hat \delta_k(x)$ 对应的类等价于将其分给使概率 $\widehat{\Pr}(Y=k\mid X=x)$ 最大化的类。
当 $K=2$ 时,如果 $\widehat{\Pr}(Y=2\mid X=x) \ge 0.5$,则将其分到类别 2;否则,将其分到类别 1。
4.5 例子:LDA 对信用卡违约数据分类
现在,我们将 LDA 运用于 Default 数据上,根据一个人的信用卡余额和学生身份预测其违约情况。LDA 对 $10000$ 个训练数据进行拟合,结果如表 4 所示。
表 4:对 $10000$ 个 Default 数据集中的训练观测,LDA 预测与真实违约所组成的混淆矩阵。矩阵中主对角线上的元素为被正确分类的人数,而其余非对角线上的元素为被错误分类的人数。这里,LDA 对 23 个没有违约的人和 252 个违约的人的分类出现错误。
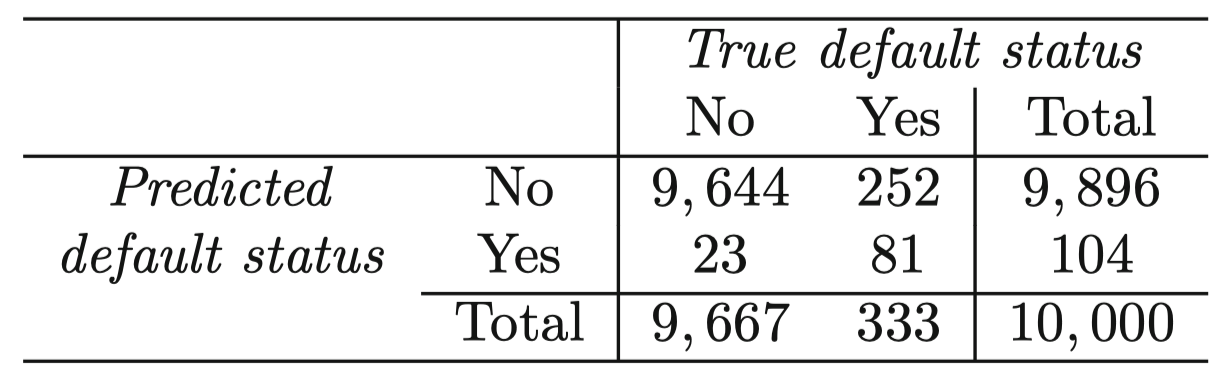
分类错误率:$(23 + 252)/10000 = 2.75\%$
注意事项:
- 上面计算的是 训练错误率,可能存在过拟合。在该例中,由于 $n = 10000, p=4$,所以并不需要担心这个问题。
- 如果我们总是将数据分类为 “
NO”,那么这里错误率也仅为 $333/10000=3.33\%$。所以,一个普通的 零分类器 (null classifier) 也可能达到仅比 LDA 错误率高一点的效果。 - 在真实的 “
NO” 中,错误率仅为 $23/9667 = 0.2\%$;在真实的 “YES” 中,错误率则高达 $252/333 = 75.7\%$。
混淆矩阵

图 12:混淆矩阵及各相关指标计算公式。
错误类型
- 假阳性率 (False positive rate):假阳性样本 (即被分类为阳性但实际为阴性的样本) 在全部真实阴性样本中所占的比例 (例如,前面计算的 $0.2\%$)。
- 假阴性率 (False negative rate):假阴性样本 (即被分类为阴性但实际为阳性的样本) 在全部真实阳性样本中所占的比例 (例如,前面计算的 $75.7\%$)。
上面的混淆矩阵是通过将满足以下条件的样本分类到 YES 得到的:
我们可以通过将阈值从 $0.5$ 更改为区间 $[0, 1]$ 中的某个其他值来改变以上两种错误率:
\[\widehat{\Pr}(\texttt{Default}=\texttt{YES}\mid \texttt{Balance},\texttt{Student}) \ge \text{threshold}\]调整阈值
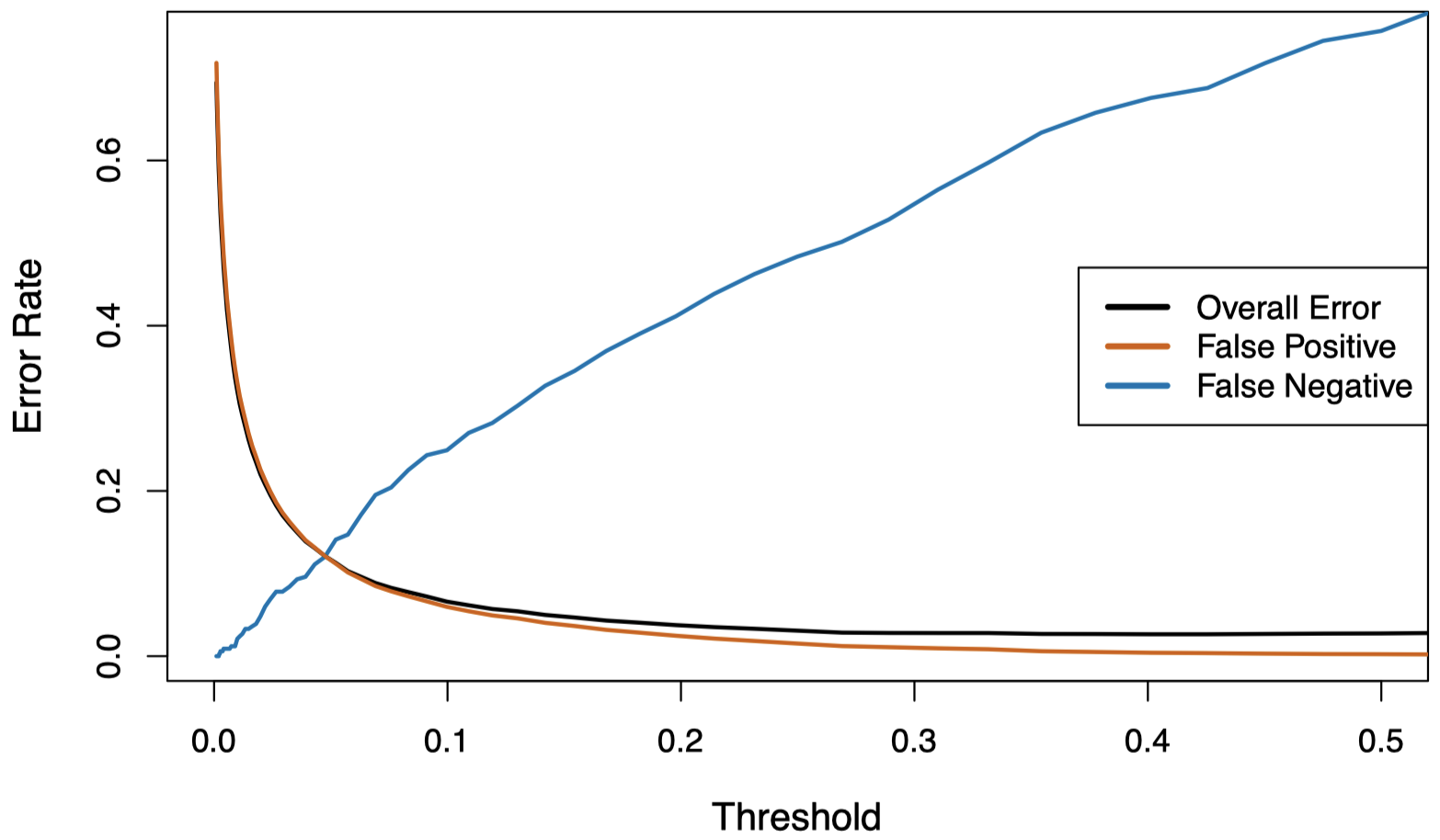
图 13:图中显示的是对 Default 数据集,错误率关于分类后验概率的阈值的函数。黑色曲线代表总的错误率,蓝色曲线代表假阴性率 (即违约者被错误分类的比例),而橙色曲线代表假阳性率 (即未违约者被错误分类的比例)。
这里,为了适当降低假阴性率,我们可能希望将阈值降低到 $0.1$ 或更小。
ROC 曲线
ROC 曲线可以同时展示出所有可能阈值出现的以上两类错误。图 14 表示了训练数据上 LDA 分类器的 ROC 曲线。分类器的性能表现是通过 ROC 曲线下方的面积 (area under the ROC curve, AUC) 来表示的,该曲线能够涵盖所有可能的阈值。一个理想的 ROC 曲线会紧贴左上角,通常我们可以认为,AUC 越大,分类器性能越好。
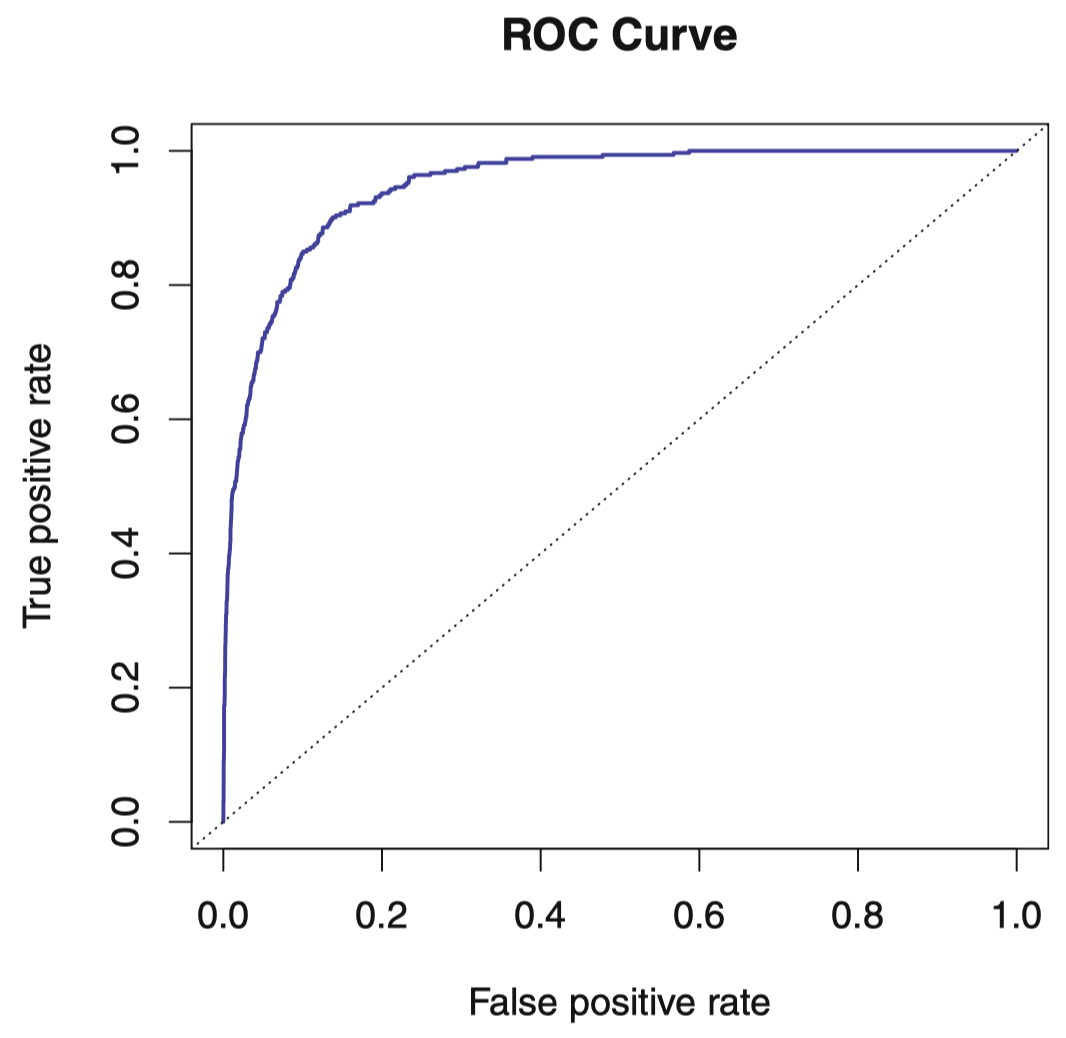
图 14:关于 Default 数据的 LDA 分类器的 ROC 曲线。改变后验违约概率的阈值,它追踪出两类错误。真实的阈值没有显示出来。真阳性率:在给定阈值下,违约者被正确判断的比例。假阳性率:同样调值下,未违约者被错误判断的比例。理想的 ROC 曲线应该紧贴左上角,即高的真阳性率,低的假阳性率。对角虚线代表 “没有信息” 的分类器,如果学生身份和信用卡余额对违约概率没有影响,那么该直线即是我们所期望的。
4.6 其他形式的判别分析
\[\Pr(Y=k\mid X=x)=\dfrac{\pi_k f_k(x)}{\sum_{l=1}^{K}\pi_l f_l(x)}\]当 $f_k(x)$ 为高斯密度,并且在每一类中具有相同的协方差矩阵 $\Sigma$ 时,上式将推导出 线性判别分析。通过改变 $f_k(x)$ 的形式,我们可以得到不同的分类器。
-
在每个类别都服从高斯分布,但各自具有不同 $\Sigma_k$ 的情况下,我们可以推导出 二次判别分析 (quadratic discriminant analysis, QDA)。
-
当每个类中 $f_k(x)=\prod_{j=1}^{p}f_{jk}(x_j)$ (条件独立模型) 时,我们可以得到 朴素贝叶斯分类器 (naive Bayes classifier)。对于高斯分布而言,这意味着 $\Sigma_k$ 是一个对角矩阵。
-
通过提出各种特定的密度模型 $f_k(x)$,我们可以得到许多不同形式的判别分析方法,包括非参数方法。
二次判别分析
与 LDA 一样, QDA 分类器也假设每一类观测都服从一个高斯分布,不同之处在于,QDA 假设每一类观测都有自己的协方差矩阵,即它假设来自第 $k$ 类的观测 $X \sim N(\mu_k,\Sigma_k)$。QDA 将样本分到能够使下面的判别函数最大化的类别 $k$ 中。
QDA 的判别函数为:
\[\delta_k(x)=-\dfrac{1}{2}(x-\mu_k)^{\mathrm T}\Sigma_k^{-1}(x-\mu_k) + \log \pi_k\]由于这里不同类别的 $\Sigma_k$ 是不同的,所以判别函数中包含 $x$ 的二次项。

图 15:左图:当 $\Sigma_1=\Sigma_2$ 时,二分类问题下的贝叶斯 (紫色虚线)、LDA (黑色点线)、QDA (绿色实线) 决策边界。阴影为 QDA 决策管辖部分。由于此时贝叶斯决策边界是线性的,所以 LDA 比 QDA 更加接近真实情况。右图:相关说明与左图一致,但 $\Sigma_1 \ne \Sigma_2$。由于此时贝叶斯决策边界不是线性的,所以 QDA 比 LDA 更加接近真实情况。
为什么假设 $K$ 类的协方差矩阵是否相同会产生如此大的差异呢?换句话说,为什么有些问题我们选择使用 LDA,而有些问题我们选择使用 QDA 呢?
这是一个关于偏差-方差权衡的问题。当有 $p$ 个预测变量时,预测协方差矩阵需要 $p(p+1)/2$ 个参数,QDA 需要对每一类分别估计协方差矩阵,即需要 $Kp(p+1)/2$ 个参数。如果我们有 $50$ 个观测变量,那么需要 $1225$ 个参数。然而,通过假设 $K$ 类的协方差矩阵相同,LDA 模型对 $x$ 来说是线性的,这就意味着有 $Kp$ 个线性系数需要估计。所以,LDA 没有 QDA 分类器灵活度高,因此具有更低的方差,该模型具有改善预测效果的潜力,但这里也需要权衡考虑:如果 $K$ 个类具有相同方差这一假设与实际情况严重不符,那么 LDA 将产生很大的偏差。一般而言,如果训练观测数据量相对较少,LDA 是一个比 QDA 更好的决策,此时降低模型的方差很有必要。相反地,如果训练集非常大,则更倾向于使用 QDA,此时分类器的方差不再是一个主要关心的问题,或者说 $K$ 个类的协方差矩阵相同这一假设与实际情况不符。
朴素贝叶斯
朴素贝叶斯假设每个类中的特征之间都是互相独立的。当特征数量 $p$ 非常大时,朴素贝叶斯非常有用,而诸如 QDA,甚至 LDA 等多元方法将无法工作。
高斯朴素贝叶斯 (Gaussian naive Bayes) 假设每个类的协方差矩阵 $\Sigma_k$ 都是对角矩阵:
\[\delta_k(x) \propto \log \left[\pi_k \prod_{j=1}^{p}f_{kj}(x_j)\right]=-\dfrac{1}{2}\sum_{j=1}^{p}\dfrac{(x_j-\mu_{kj})^2}{\sigma_{kj}^2} + \log \pi_k\]这也适用于 混合 特征向量 (定性和定量)。如果 $X_j$ 是定性的,则在离散类别上用概率质量函数 (直方图) 代替 $f_{kj}(x_j)$。
尽管有一些很强的假设,但朴素贝叶斯通常能够产生良好的分类结果。
5. 不同分类方法对比
5.1 逻辑回归 vs. LDA
对于二分类问题,可以证明,对于 LDA
\[\log \left(\dfrac{p_1(x)}{1-p_1(x)}\right)=\log \left(\dfrac{p_1(x)}{p_2(x)}\right)=c_0 + c_1 x_1 + \cdots + c_p x_p\]因此,它具有与逻辑回归相同的形式。
区别在于如何估计参数:
- 逻辑回归使用基于 $\Pr(Y\mid X)$ 的 条件似然 (conditional likelihood),又称 判别式学习 (discriminative learning)。
- LDA 使用基于 $\Pr(X,Y)$ 的 完全似然 (full likelihood),又称 生成式学习 (generative learning)。
尽管存在这些差异,但实际上二者的结果通常非常相似。
注意:逻辑回归也可以通过在模型中显式包含二次项来拟合 QDA 之类的二次边界。
5.2 线性场景 vs. 非线性场景
下面给出了 6 种不同场景下,不同分类器的测试错误率的箱型图,这里预测变量个数 $p=2$。
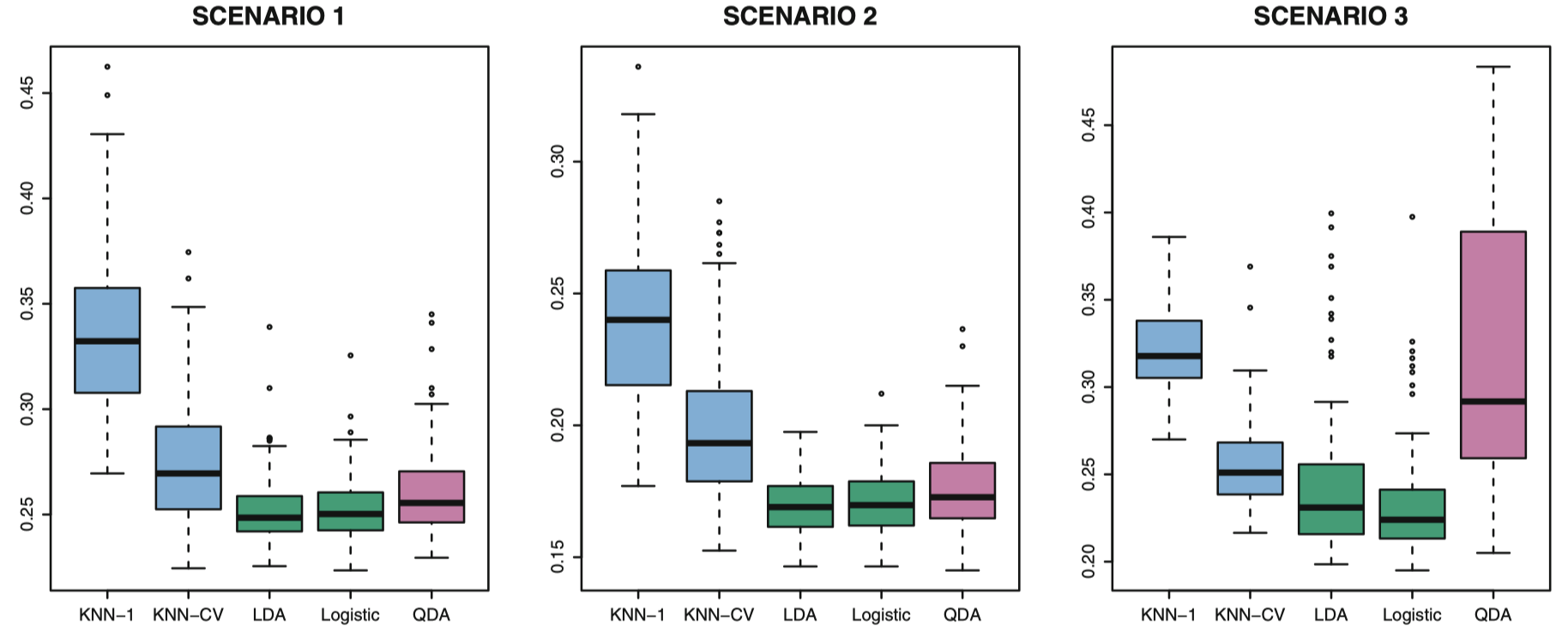
图 16:几种线性场景下,不同分类器的测试错误率的箱型图。
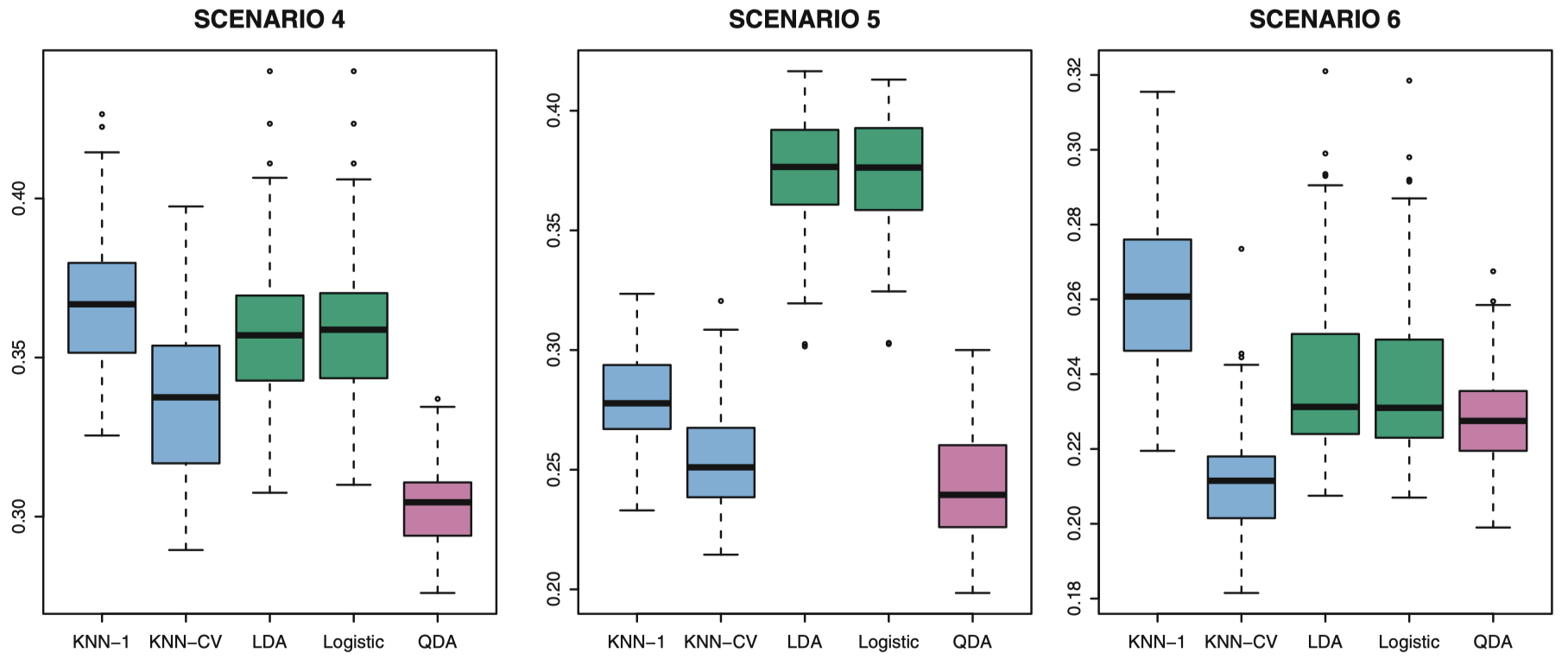
图 17:几种非线性场景下,不同分类器的测试错误率的箱型图。
场景 1:两个类分别有 $20$ 个训练观测。每一类的观测都是不相关的正态随机变量,且两类变量的均值不向。从图 16 中的左图可以看到在这种情况下 LDA 的表现良好,由于这里真实模型本身假设为 LDA 模型,所以结果与预期的一致。KNN 效果很差是因为它为了降低方差付出了代价,但却没有在偏差上获得相应补偿。QDA 也表现得比 LDA 要差,因为 QDA 适合灵活度更高的分类器,但在这里高灵活度模型并不适用。由于逻辑回归也假设线性决策边界,所以其结果只比 LDA 略微差一些。
场景 2:与场景 1 的假设一样,除了在每个类中,两个预测变量的相关性为 $-0.5$。图 16 中的中图显示了不同方法之间的效果比较,这些结果与场景 1 的情况几乎没有差异。
场景 3:从 $t$ 分布中产生 $X_1$ 和 $X_2$,每类 $50$ 个观测。$t$ 分布在形状上和正态分布很相似,但是它倾向于产生更多的极值点,也就是说,有更多的点远离均值。在这种情况下,决策边界仍然是线性的,所以逻辑回归模型比较适合。此时真实分布不符合 LDA 中的假设,由于观测并非来自正态分布,图 16 中的右图显示逻辑回归和 LDA 这两种方法明显优于其他方法,但逻辑回归比 LDA 效果要好一点。特别地,QDA 的效果差可以认为是非正态分布导致的结果。
场景 4:数据都由一个正态分布所产生,在第一类中预测变量的相关系数为 $0.5$,在第二类中预测变量的相关系数为 $-0.5$。这与 QDA 中的假设契合,并且产生了二次的决策边界。图 17 中的左图表明了 QDA 优于其他方法。
场景 5:每类中,观测来自正态分布,预测变量不相关。然而,响应值来自逻辑回归函数,预测变量为 $X_1^2,X_2^2,X_1\times X_2$。所以,这里有二次决策边界。图 17 中的中图表明了 QDA 再次呈现出最优的效果,KNN-CV 其次,线性模型的效果都很差。
场景 6:条件和场景 5 一样,但响应值来自一个更复杂的非线性函数,所以即使是 QDA 的二次决策边界也未能较好地拟合数据。图 17 中的右图表明 QDA 比线性方法略好些,而灵活度更高的 KNN-CV 方法是最好的。但是当 $K= 1$ 时,KNN 在所有方法里给出的结果最差。这表明了以下事实:即使数据显示出一个复杂的非线性关系,如果未能选择出一个合适的平滑度参数,非参数方法如 KNN 仍然可能给出较差的结果。
以上 6 种不同场景下的例子说明,没有哪种方法可以在各种不同场景下都明显优于其他方法:
- 当真实决策边界是线性时,LDA 和逻辑回归方法通常表现良好。
- 当真实决策边界是中等非线性时,QDA 可能会提供更好的结果。
- 最后,对于更复杂的决策边界,非参数方法 (例如:KNN) 可能会更好。但是,必须谨慎选择非参数方法的平滑度。
6. 总结
- 逻辑回归在分类问题中非常流行,尤其是当 $K = 2$ 时。
- 当训练样本数量 $n$ 很小,或者不同类被很好地分开,并且高斯假设合理时,LDA 会非常有用。这也适用于 $K> 2$ 的情况。
- 当特征数量 $p$ 很大时,朴素贝叶斯会非常有用。
- 更多有关逻辑回归、LDA 和 KNN 的一些比较,请参见教材第 4.5 节。
下节内容:重抽样方法
本作品采用知识共享署名-非商业性使用-相同方式共享 4.0 国际许可协议进行许可。 欢迎转载,并请注明来自:YEY 的博客 同时保持文章内容的完整和以上声明信息!