数据科学多元统计学 MAST90138 课程笔记

数据科学多元统计学 04：主成分分析 (一)

墨尔本大学 MAST90138 课程笔记

Posted by YEY on August 25, 2020

Lecture 04 主成分分析 (一)

参考教材：

  • Hardle, W. and Simar, L (2015). Applied multivariate statistical analysis, 4th edition.
  • Hastie, T. Tibshirani, R. and Friedman, J. (2009). The elements of statistical learning, 2nd edition

1. 引言

对于 1 维、2 维或 3 维数据的可视化要相对容易：我们可以在散点图中表示它们，从中我们可以学到很多有关数据的结构/属性的信息。

当数据具有较高维度时，我们很难对其进行可视化：

  • 我们可以找到一种数据摘要的方法吗？
  • 摘要应该更容易以图的形式表示。
  • 摘要仍应包含有关原始数据的尽可能多的信息。
  • 通常，我们可以通过降维来实现这一目标。
  • 接下来，我们来看一个将 2 维数据降维为单一维度数据的例子。

例子：将 2 维数据降维到 1 维数据

作为一个玩具示例，我们将首先看到如何将以下的 2 维数据降维到 1 维。

数据来自 i.i.d. 属性对 $(X_{i1}, X_{i2})^{\mathrm T} \sim (\mu, \Sigma)$，其中 $i = 1, \dots, n$，如图 1 所示。

图 1：2 维数据的散点图

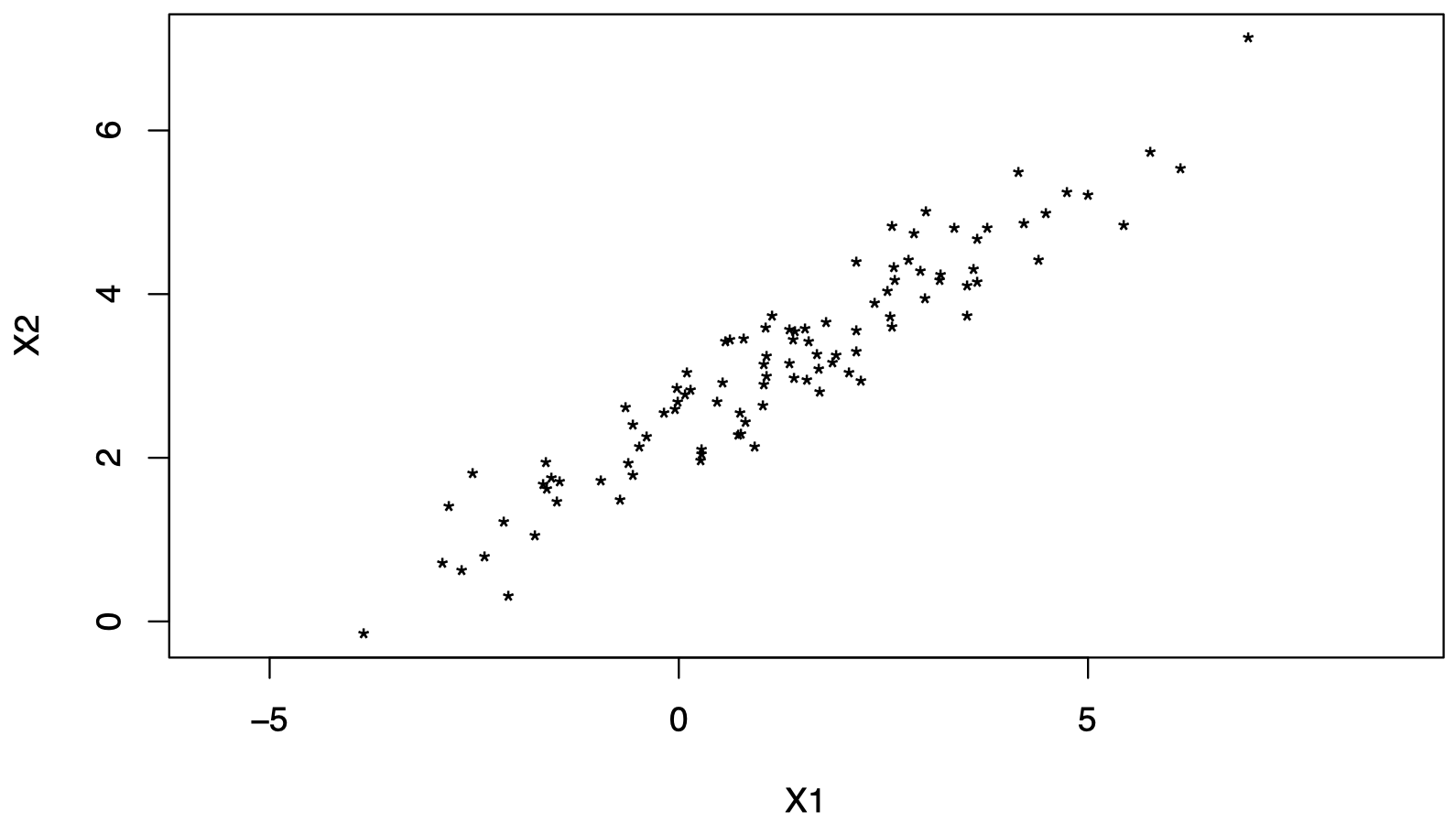
对于这类问题，通常首先需要进行 中心化数据 (中心化之后的数据从几何上更容易理解)。对于 $i = 1, \dots, n$，我们将 $(X_{i1}, X_{i2})^{\mathrm T}$ 替换为 $(X_{i1}- \overline X_1, X_{i2}- \overline X_2)^{\mathrm T}$，如图 2 所示：

图 2：中心化数据，可以看到，现在数据中心位于坐标原点处。

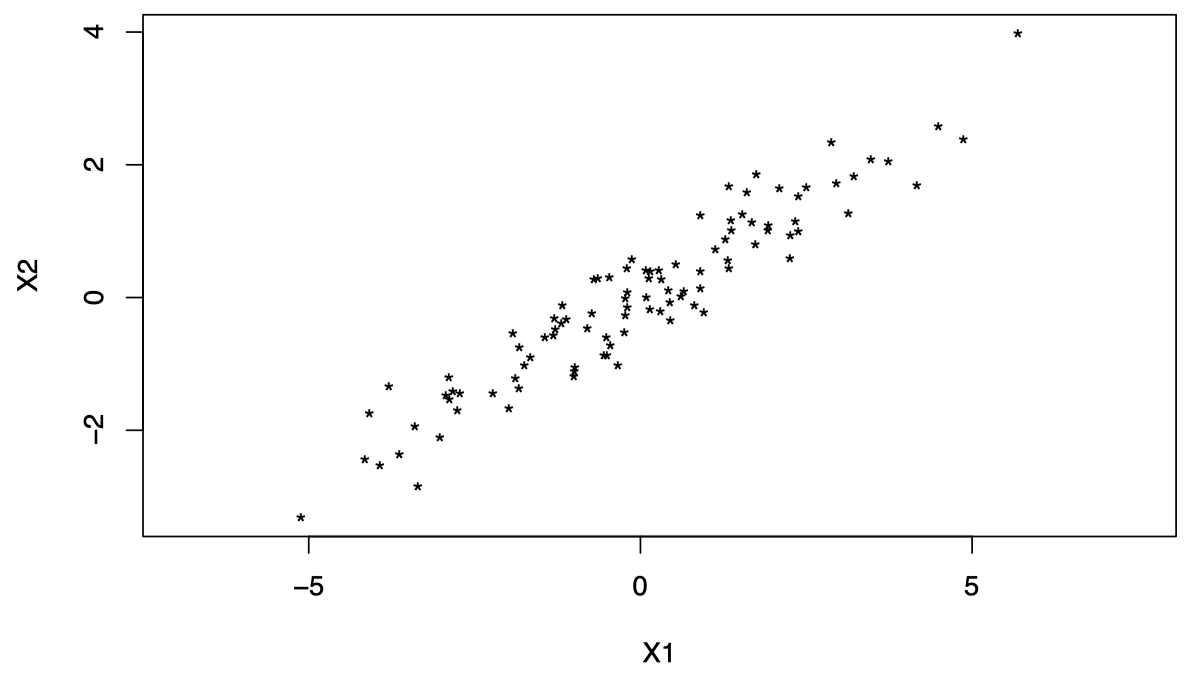
注意：从现在起，为避免繁琐的符号表示，当我们提到 $X_{ij}$ 时，我们实际上指的是 $X_{ij}-\overline X_j$。

为了将这些数据降维到一维，我们可以采取一些措施，例如：仅保留每个数据点的第一个成分 $X_{i1}$。

图 3：2 维数据中每个数据点在第一个成分方向 $X_{1}$ 上的投影

图 4：每个数据点仅保留第一个成分 $X_{i1}$，将数据降维到 1 维

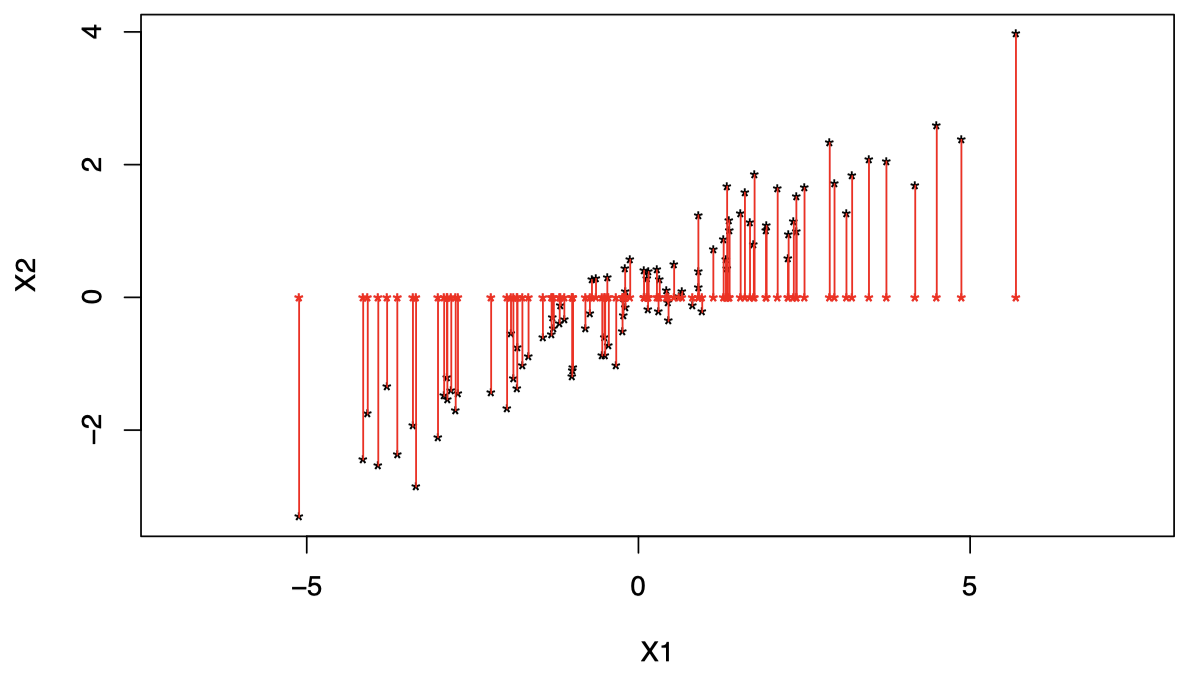
但这种降维方式并不是我们所期望的，因为我们丢失了原始数据中第二个成分 $X_2$ 的所有相关信息。

  • 例如，假设数据包含 $n = 100$ 个个体的年龄 ($X_1$) 和身高 ($X_2$)。
  • 那么，上面的降维方式将仅保留年龄，并完全丢弃身高相关的数据。

事实上，我们可以创建一个同时包含年龄和身高信息的 新变量。

一种简单的方法是对年龄和身高进行 线性组合。

  • 例如，对于 $i = 1, \dots, n$，我们可以创建一个新变量

    \[Y_i = \dfrac{1}{2}\text{age}_i + \dfrac{1}{2}\text{height}_i\]

    它相当于是对每个样本的年龄和身高数据的取平均值。其中，两个系数 $1/2$ 可以分别视为年龄和身高的权重。

  • 通常在这类问题中，我们会对线性组合的进行重新缩放，以使各权重系数的平方和等于 $1$。在这种情况下，我们有

    \[Y_i = \dfrac{1}{\sqrt 2}\text{age}_i + \dfrac{1}{\sqrt 2}\text{height}_i\]

因此，值 $Y_i = \dfrac{1}{\sqrt 2}X_{i1} + \dfrac{1}{\sqrt 2}X_{i2}$ 如图 5 所示：

图 5：通过创建一个各成分的线性组合实现降维

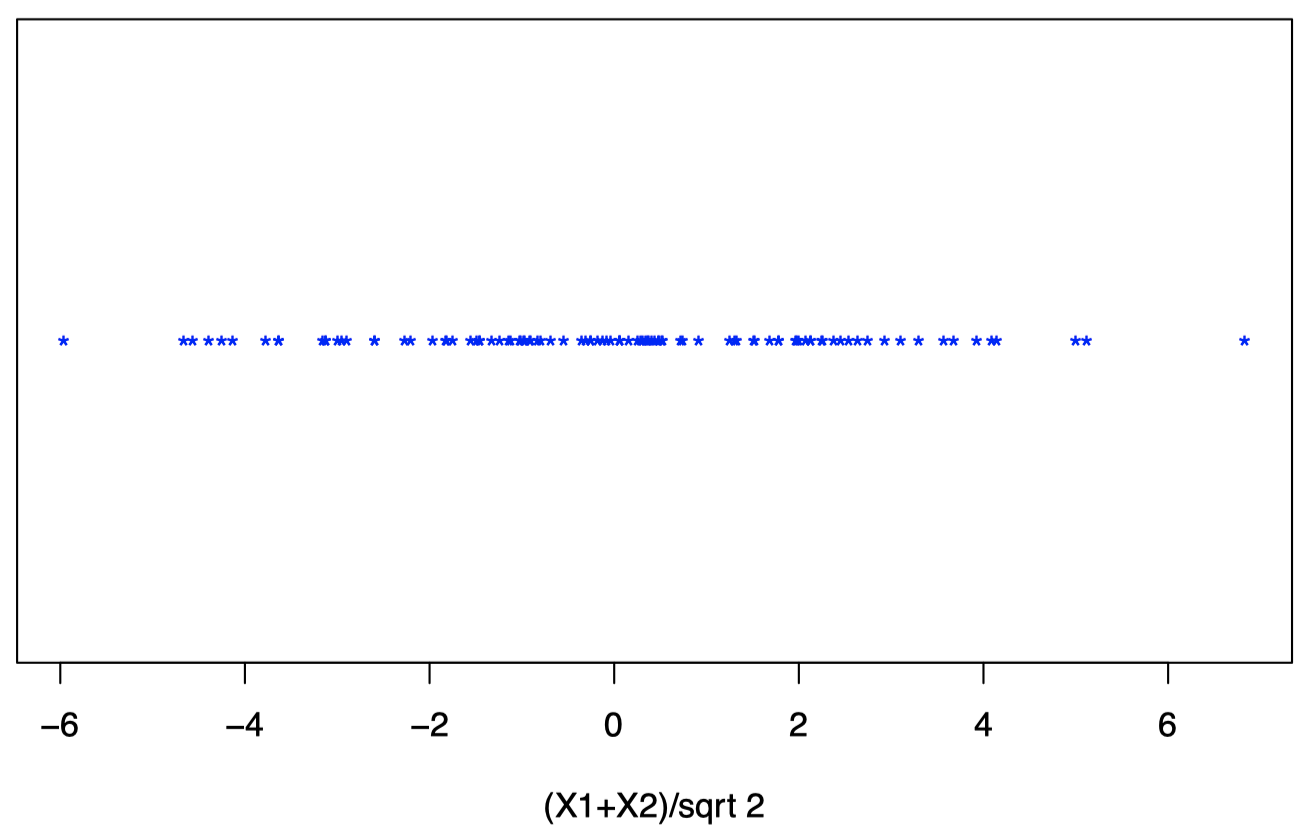
取两个成分的比例平均值相当于在原坐标系中将原始数据投影到图 6 中的红线 ($X_1 = X_2$) 上，并仅保留投影值 (蓝色)。

图 6：2 维数据中每个数据点在直线 $X_{1}=X_{2}$ 方向上的投影

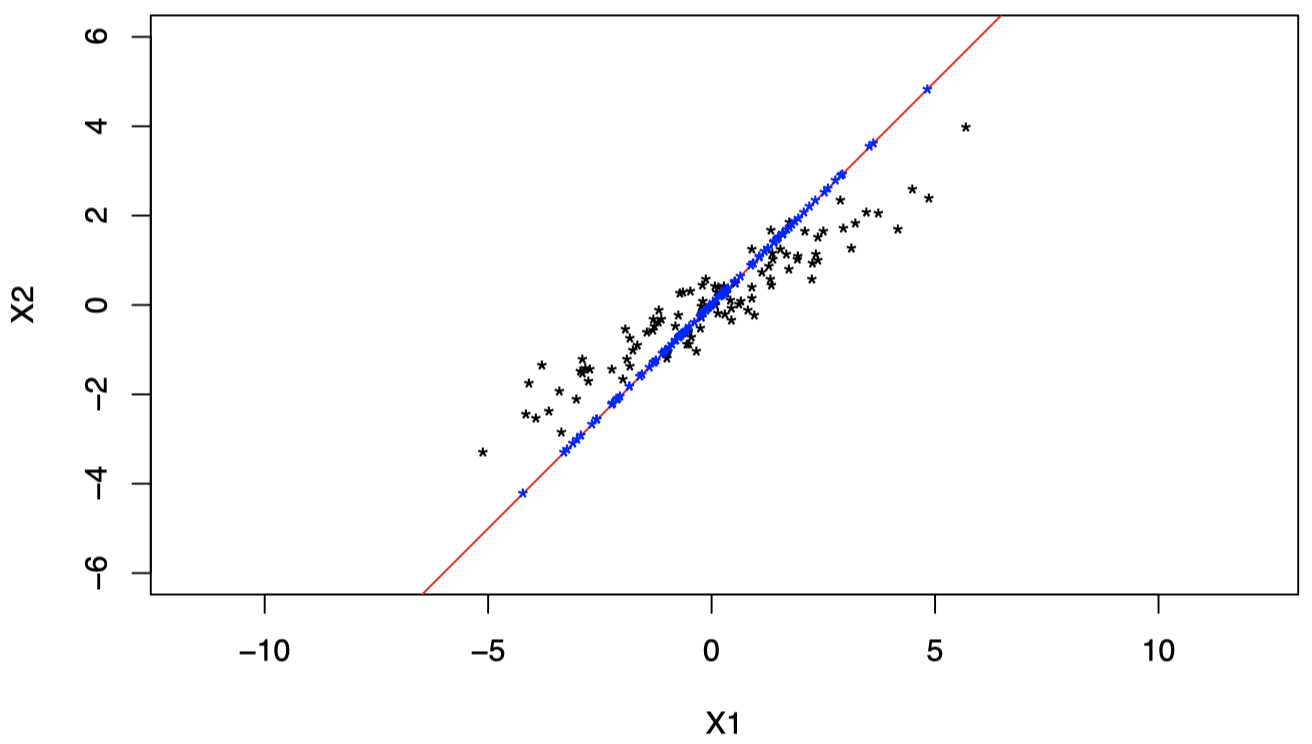
那么，上图是如何生成的呢？

  • 在前面的课程中我们已经介绍过，向量 $x$ 在向量 $y$ 上的正交投影 \(p_x = \dfrac{x^{\mathrm T} y}{\|y\|}\)，如图所示

  • 简而言之，点 $x$ 在通过原点和点 $y$ 的直线上的正交投影 $p_x$ 由下式给出

    \[p_x = \dfrac{x^{\mathrm T} y}{\|y\|} \tag {1}\]

  • 取线性组合 $Y_i = \dfrac{1}{\sqrt 2}X_{i1} + \dfrac{1}{\sqrt 2}X_{i2}$ 相当于

    \[Y_i = X_i^{\mathrm T}a\]

    其中，$X_i=(X_{i1},X_{i2})^{\mathrm T}$，$a=(\dfrac{1}{\sqrt 2}, \dfrac{1}{\sqrt 2})^{\mathrm T}$。

  • 由于 \(\|a\|=1\)，在式 $(1)$中 取 $y = a$，所以 $Y_i$ 是 $X_i$ 在通过原点和 $a$ 的直线上的正交投影。

图 7 中，红色直线经过原点和 $a= (1/\sqrt{2},1/\sqrt{2})^{\mathrm T}$，蓝色点表示每个 $X_i$ 在该直线上的正交投影。

图 7：红色直线经过原点和 $a= (1/\sqrt{2},1/\sqrt{2})^{\mathrm T}$，蓝色点表示每个 $X_i$ 在该直线上的正交投影。

图 8 显示了将投影后的数据点显示在新的一维坐标系中，原始二维空间中的数据点 $(X_1,X_2)$ 投影后在新坐标系中的坐标为 $(X_1+X_2)/\sqrt{2}$。

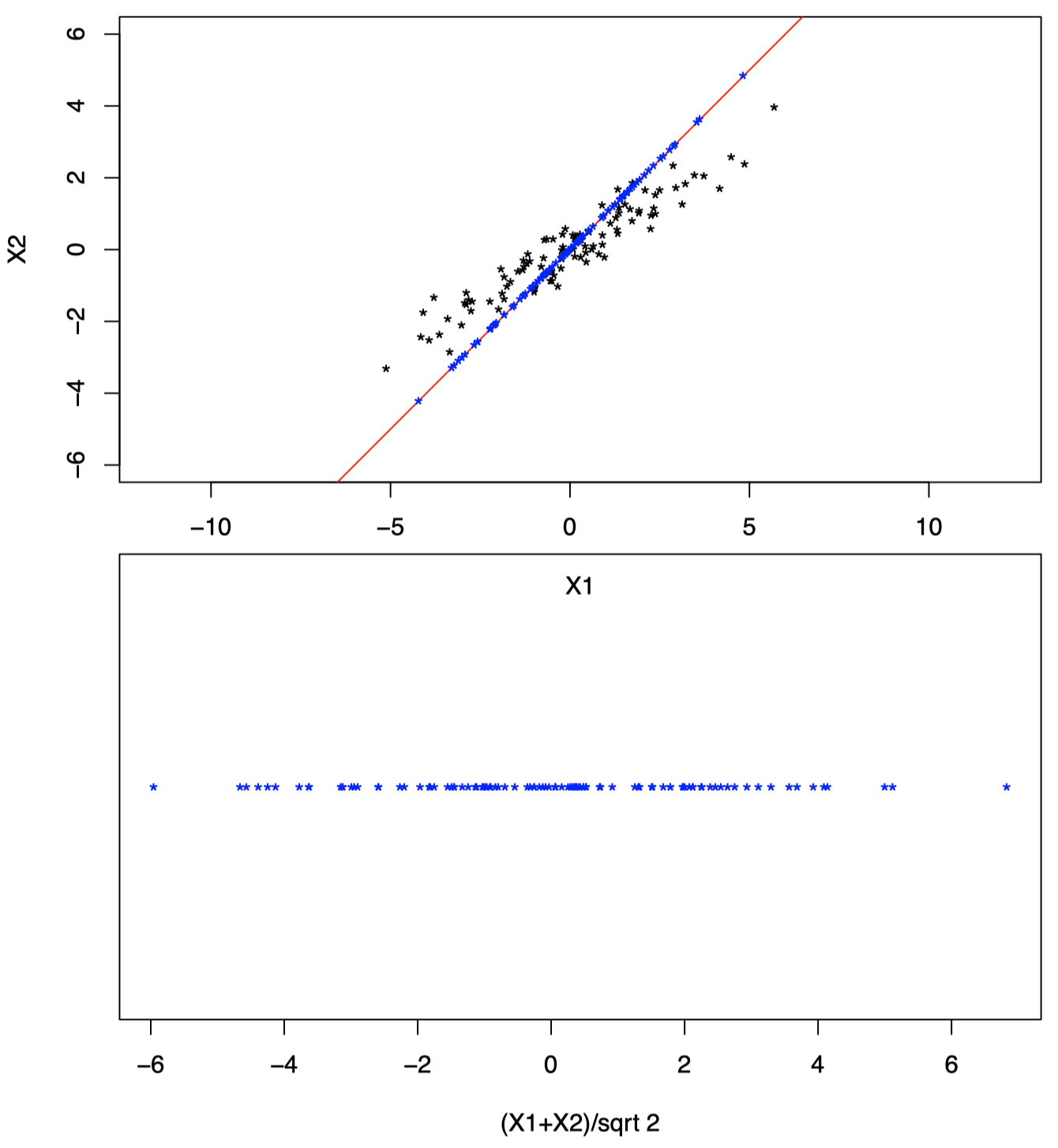
图 8：将投影后的数据点显示在新的一维坐标系中，原始二维空间中的数据点 $(X_1,X_2)$ 投影后在新坐标系中的坐标为 $(X_1+X_2)/\sqrt{2}$。

  • 但是，相比给 $X_i$ 的每个成分赋予相等的权重，我们希望找到一种方式能够在降维时尽量减少原始数据相关信息的丢失。
  • 这取决于我们如何定义 “损失信息 (lose information)”。
  • 在 主成分分析 (principal component analysis, PCA) 中，我们通过将数据投影到直线上来实现降维。
  • 此外，在 PCA 中，“尽可能少的信息损失” 被定义为 “尽可能多地保留原始数据的变化性”。
  • 在之前二维情况的例子中，当选择投影 $Y_i = X_i^{\mathrm T}a$ 所在的直线时，意味着我们希望找到一个 $a$ 使得投影的方差 $\mathrm{Var}(Y_i)$ 尽可能大。

为什么我们要最大化方差？图 9 显示了一个投影后的数据不具变化性的例子：将数据投影在图中红线上。

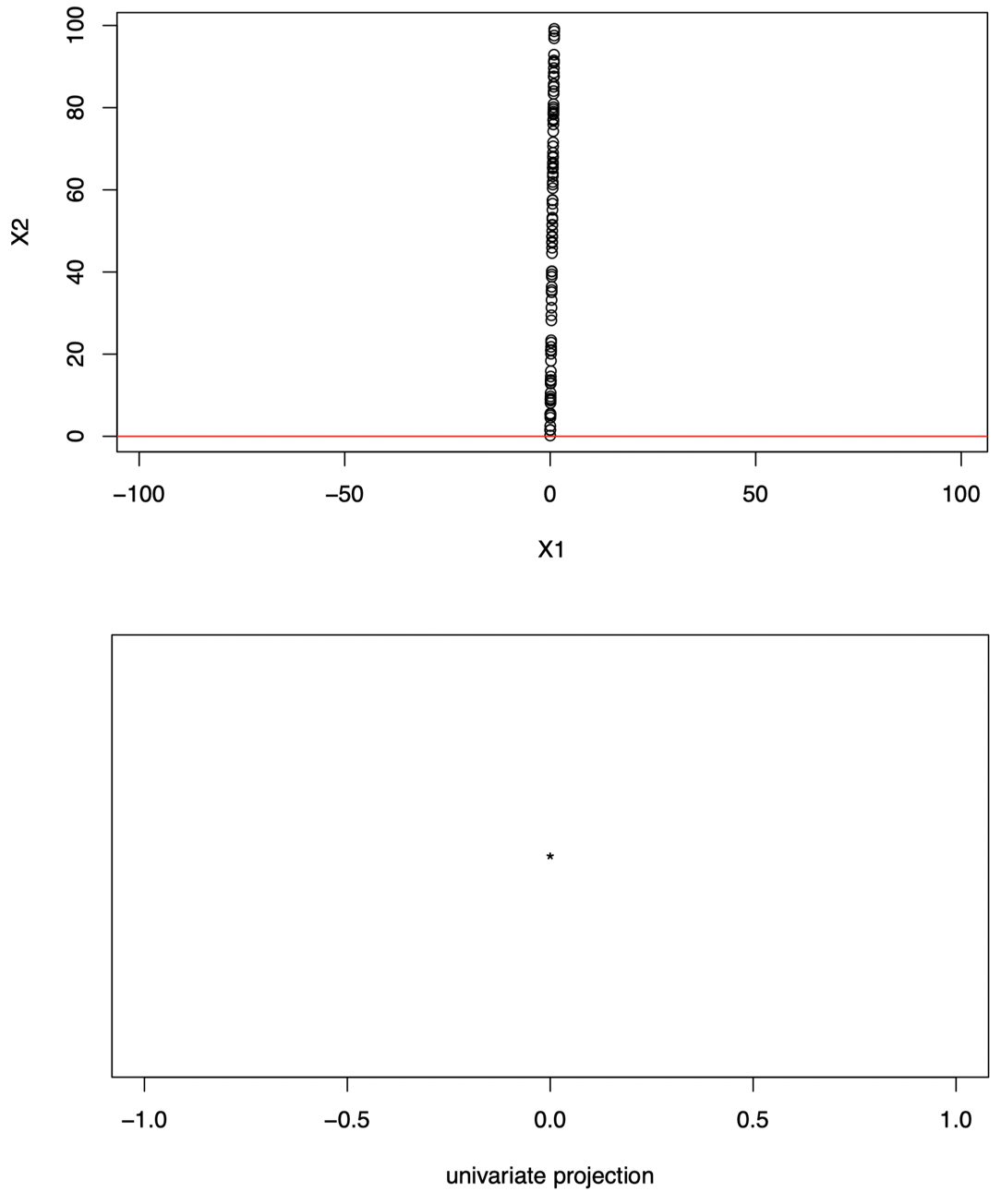
图 9：对于图中的原始二维数据，如果我们将其投影到图中的红色直线上，那么所有数据都投影到同一点上：投影的方差为零，我们无法从中获得任何信息。

回到之前的例子，我们将数据投影到了图 11 中的红色直线上：

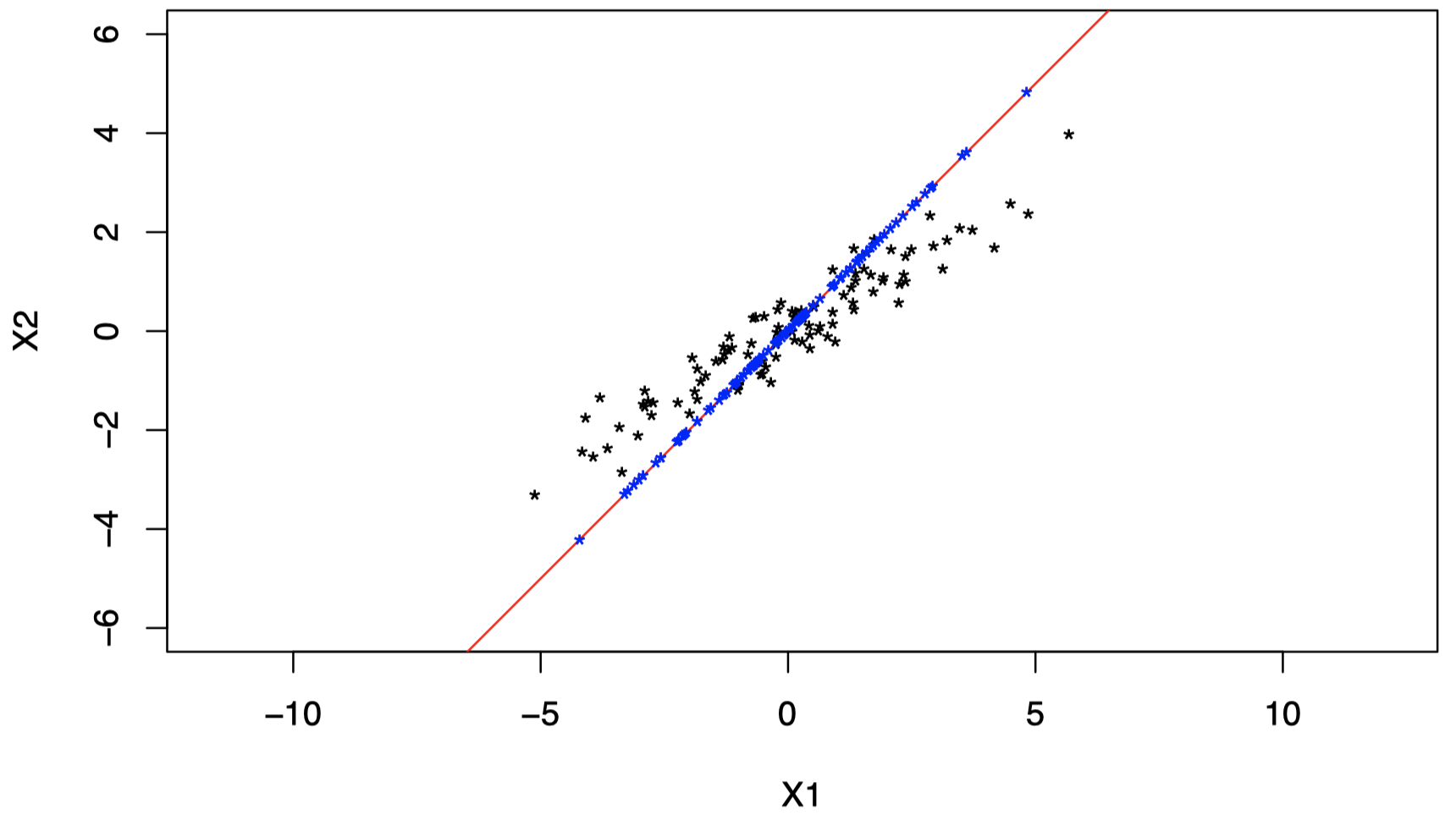
图 11：将原始二维数据投影到红色直线上。

但是，如果我们将数据投影在图 12 中的红色直线上，我们将保留更多信息：

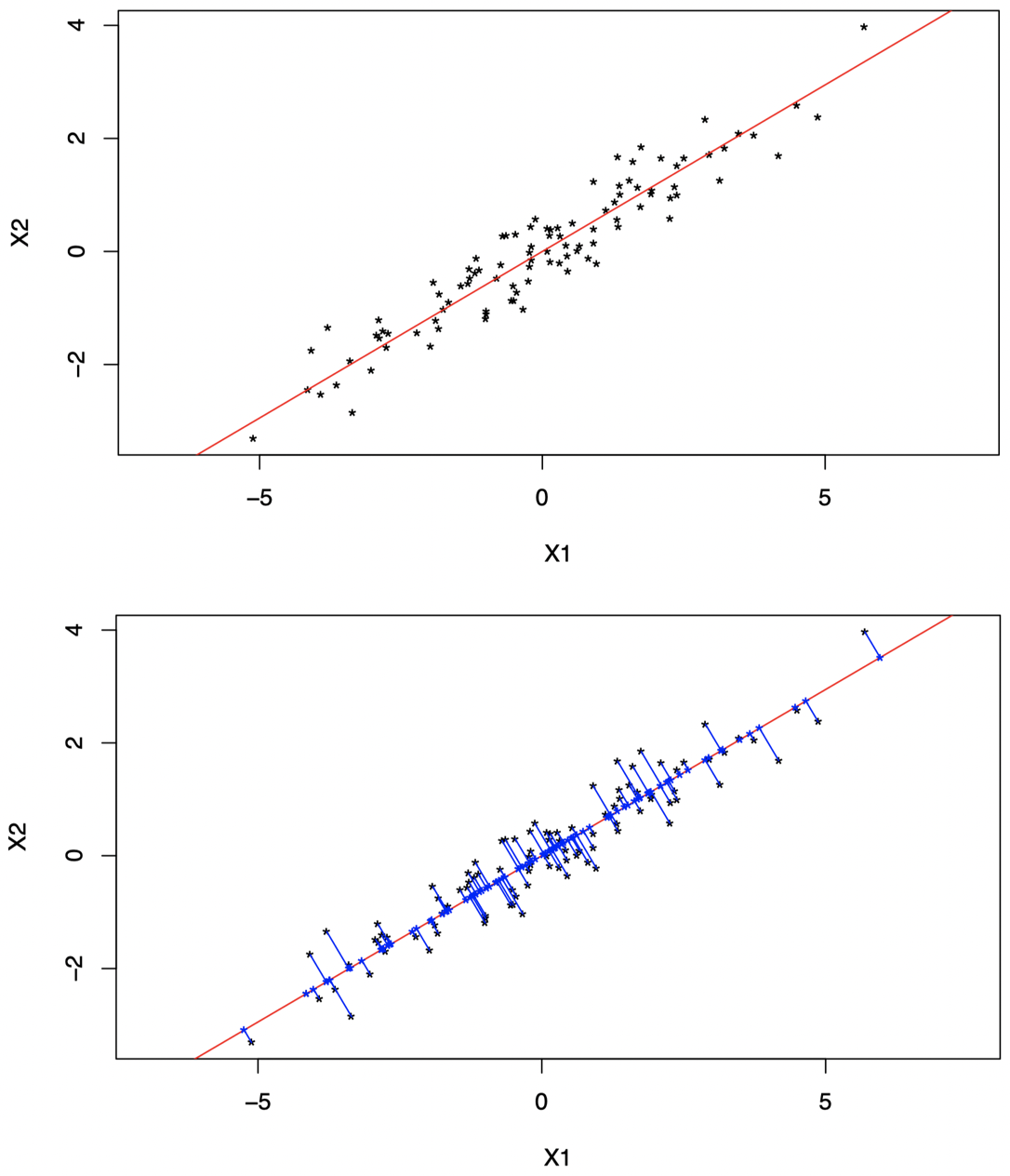
图 12：我们将数据投影到另一条直线上将保留更多信息：可以看到，在这条线上，投影数据要比之前在图 11 中的直线上更具可变性。

可以看到，与之前选择的投影直线相比，新的投影直线上的数据方差更大：

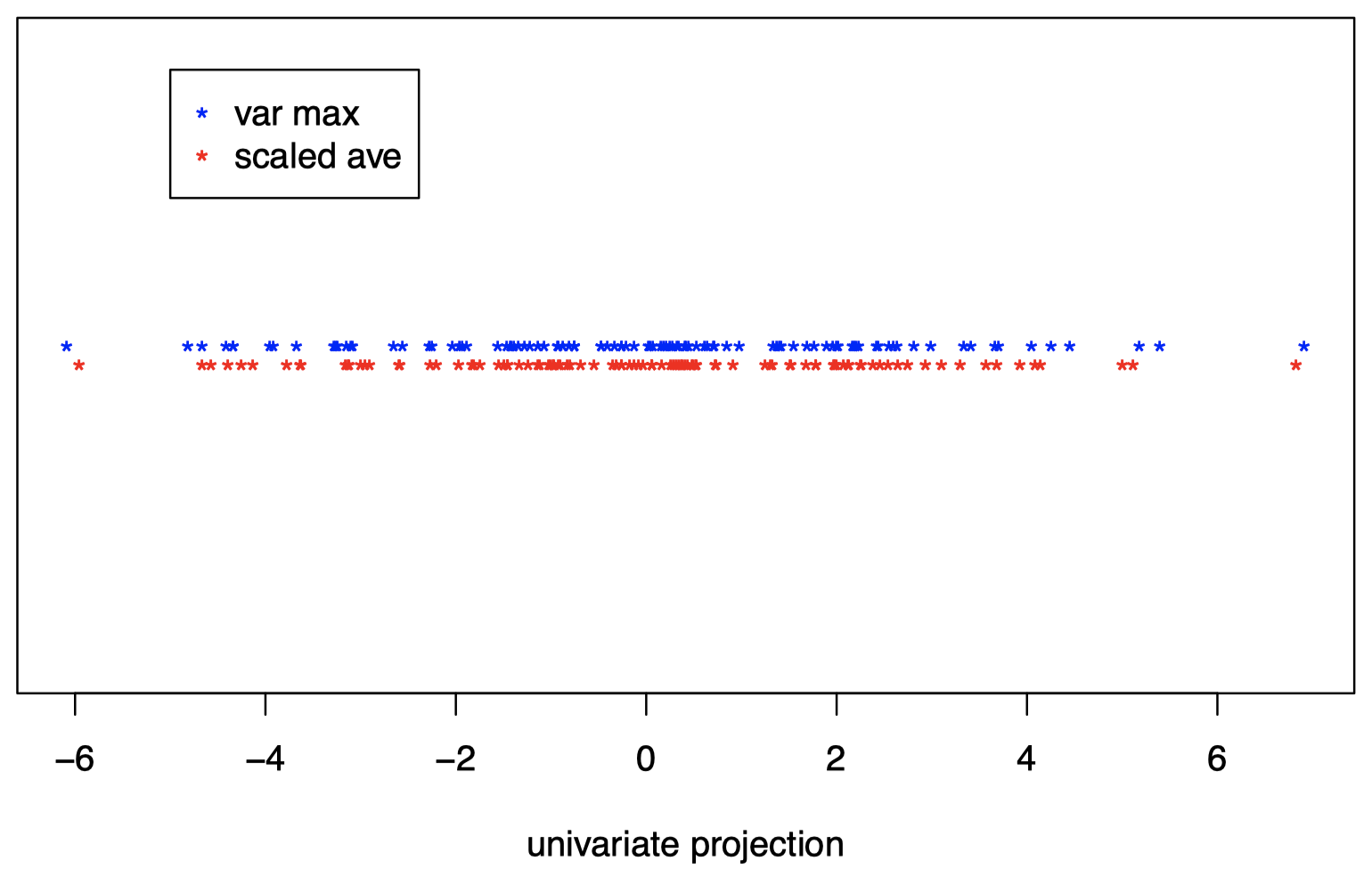
图 13：红色点为原始数据在之前直线上的投影，蓝色点为原始数据在之新的直线上的投影，可以看到蓝色数据点的方差更大，事实上，蓝色点对应的直线也是能够使投影数据方差最大化的方向。

2. 标准化的线性组合

通常，在 主成分分析 (Principal Component Analysis, PCA) 中，当我们将 $p$ 维的 $X_i$ 降维到一维的 $Y_i$ 时 ($i=1,\dots,n$)，其中 $X_i \sim \text{i.i.d.} \;(0,\Sigma)$，我们的目标是找到 一个关于 $X_i$ 的线性组合 $Y_i$，并且使得其方差 $\mathrm{Var}(Y_i)$ 尽可能大：

\[Y_{i1}=a_1 X_{i1} + \cdots + a_p X_{ip} = a^{\mathrm T} X_i\]

其中，$a=(a_1,\dots,a_p)^{\mathrm T}$，并且满足 \(\|a\|^2=\sum_{j=1}^{p}a_j^2 =1\)。

  • 这里，我们用 $Y_{i1}$ 代替 $Y_i$，因为我们将要投影的方向不止一个。
  • 对于 $a$ 的约束是一个缩放因子，可以在一定程度上简化我们的问题。

  • 令 $\gamma_1,\gamma_2,\dots,\gamma_p$ 表示协方差矩阵 $\Sigma$ 的 $p$ 个范数 $1$ 特征向量 (即 \(\|\gamma_j\|=1\))，它们分别对应以下特征值：

    \[\lambda_1 \ge \lambda_2 \ge \cdots \ge \lambda_p\]
  • 记住，$\gamma_j$ 的定义只取决于符号的变化，所以每个 $\gamma_j$ 都可以用 $-\gamma_j$ 来代替。

  • 可以证明，能够使投影数据方差 $\mathrm{Var}(Y_i)$ 最大化的 $a$ 为：

    \[a=\gamma_1\]

    即 最大特征值对应的特征向量。

  • 我们将以下变量称为 $X_i$ 的第一主成分：

    \[Y_{i1} = a_1 X_{i1}+\cdots + a_p X_{ip}=a^{\mathrm T}X_i = \gamma_1^{\mathrm T}X_i\]

  • 更一般地，如果 $X_i \sim \text{i.i.d.} \;(\mu,\Sigma)$，并且没有经过中心化处理，那么我们将以下变量称为 $X_i$ 的第一主成分：

    \[Y_{i1} = \gamma_1^{\mathrm T}\{X_i - E(X_i)\} = \gamma_1^{\mathrm T}(X_i - \mu)\]
  • 它是具有 最大方差 的 数据线性投影。
  • 在投影之前，我们总是先对数据进行中心化处理。

在 PCA 中，一旦我们找到了一单变量投影，如何添加第二个投影呢？

显然，我们不应该将数据只是简单地投影到一条任意的其他直线上，例如：

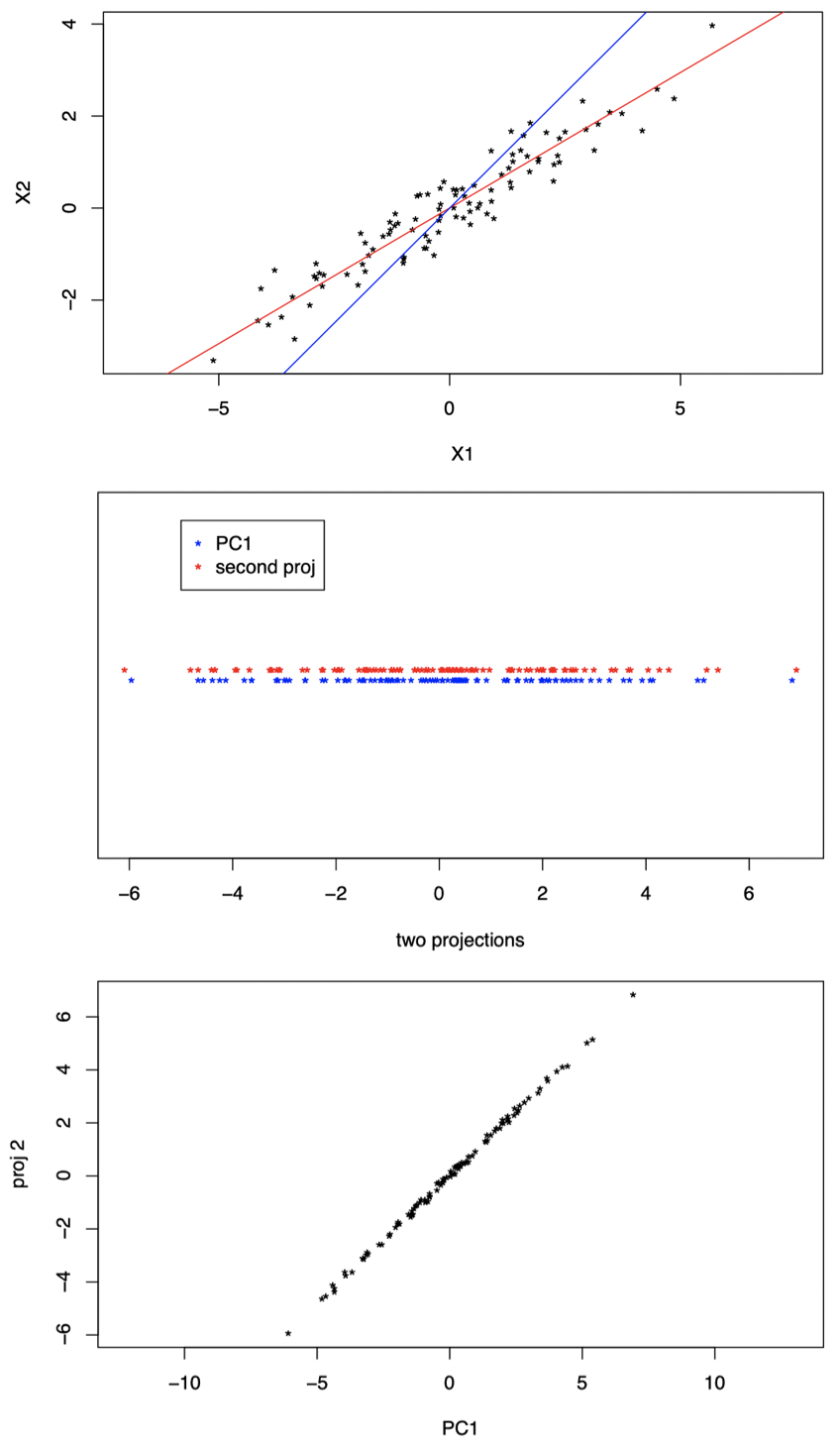
图 14：红色直线为第一主成分方向，蓝色直线为第二个投影方向。

可以看到，图 14 中的两个投影本质上是冗余的，我们并没有从第二个投影中获得关于数据的更多信息。

事实上，对于第二个投影方向，我们应该将数据投影到与第一主成分方向尽可能不同的一条直线上，以便从中学习到一些补充信息。那么应该怎样做呢？如图 15 所示，我们可以将数据投影到 垂直于 PC1 方向 的蓝色直线上，我们将通过此第二投影得到的变量称为 第二主成分。

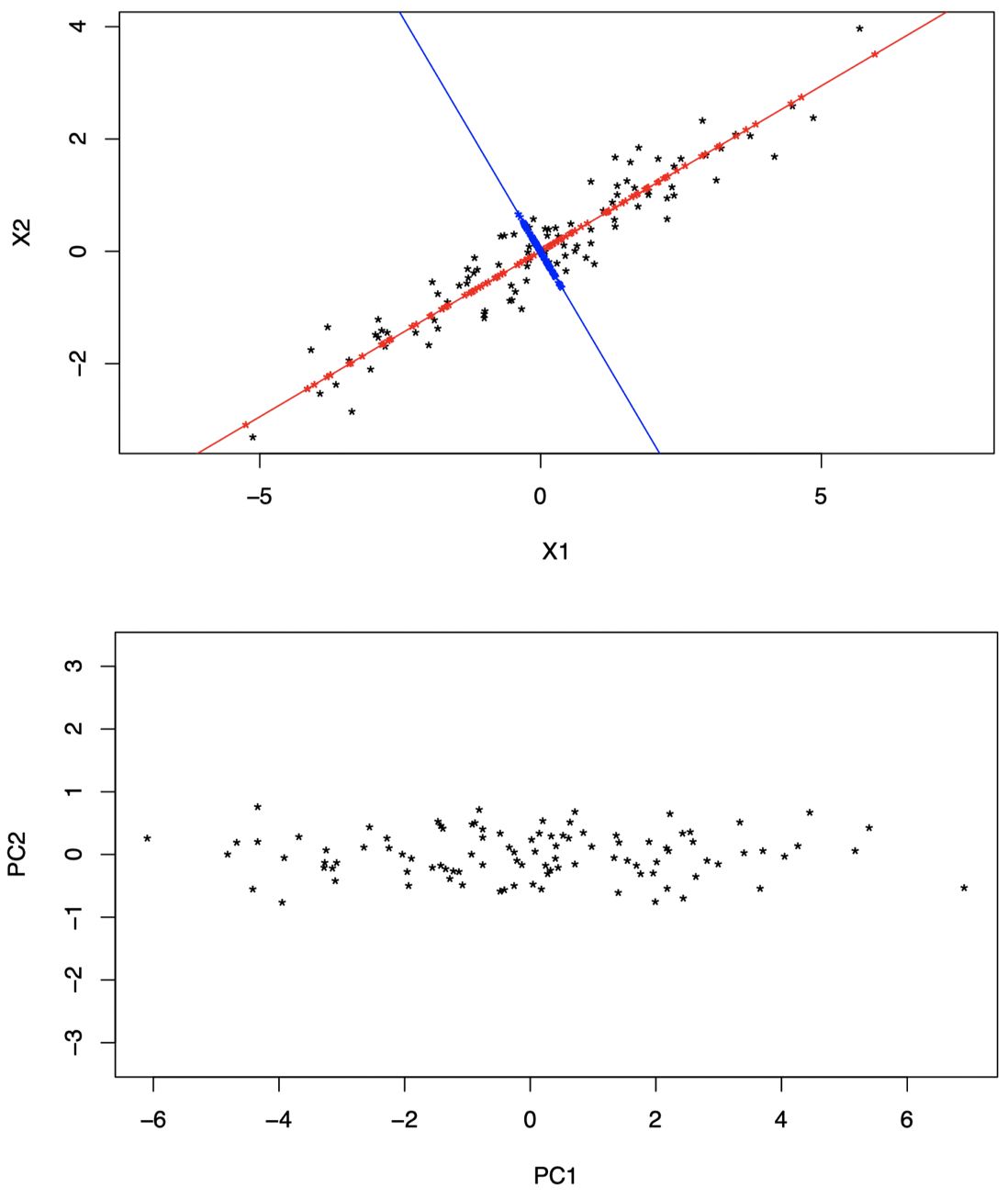
图 15：红色直线为第一主成分方向，蓝色直线为第二主成分方向。我们将原始数据分别投影到 PC1 和 PC2 方向上，并且旋转坐标轴以匹配这两个主成分方向。

更一般地，在 PCA 中，如果我们希望将 $p$ 维的 $X_i$ 降维到 $q \le p$ 维的 $Y_i$ ($i=1,\dots,n$)，其中 $X_i \sim \text{i.i.d.} \;(\mu,\Sigma)$，并且 $\gamma_j$ 和 $\lambda_j$ 按照与之前相同的定义 (即 \(\|\gamma_j\|=1\)，\(\lambda_1 \ge \lambda_2 \ge \cdots \ge \lambda_p\))。

  • 首先，我们可以将 $X_i$ 的 第一主成分 取为：

    \[Y_{i1} = \gamma_1^{\mathrm T}\{X_i - E(X_i)\} = \gamma_1^{\mathrm T}(X_i - \mu)\]

    其中，$\gamma_1$ 是协方差矩阵 $\Sigma$ 的最大特征值 $\lambda_1$ 对应的特征向量。

  • 然后，对于 $k=2,\dots,q$，我们将 $X_i$ 的 第 $q$ 个主成分 取为：

    \[Y_{ik} = \gamma_k^{\mathrm T}\{X_i - E(X_i)\} = \gamma_k^{\mathrm T}(X_i - \mu)\]

    其中，$\gamma_k$ 是协方差矩阵 $\Sigma$ 的第 $k$ 大的特征值 $\lambda_k$ 对应的特征向量。

  • 所有 $\gamma_j$ 都是范数 $1$ 的，并且彼此正交。因此，各投影方向也是彼此正交的。

  • 在矩阵表示下，令 $Y_i=(Y_{i1},\dots,Y_{ip})^{\mathrm T}$，我们有

    \[Y_i = \Gamma^{\mathrm T}(X_i - \mu)\]

  • 假如我们按照以上方式构造 $Y_{i1},\dots,Y_{ip}$，那么我们有

    \[\begin{align} &E(Y_{ij})=0, \; \text{for } j=1,\dots,p \\[2ex] &\mathrm{Var}(Y_{ij})=\lambda_j, \; \text{for } j=1,\dots,p \\[2ex] &\mathrm{Cov}(Y_{ik},Y_{ij})=0,\; k\ne j \\[2ex] &\mathrm{Var}(Y_{i1}) \ge \mathrm{Var}(Y_{i2}) \ge \cdots \ge \mathrm{Var}(Y_{ip}) \\[2ex] &\sum_{j=1}^{p} \mathrm{Var}(Y_{ij}) = \mathrm{tr}(\Sigma) \\[2ex] &\prod_{j=1}^{p} \mathrm{Var}(Y_{ij}) = | \Sigma | \end{align}\]

  • 可以证明，我们无法构造出一个方差比 $\lambda_1 = \mathrm{Var}(Y_{i1})$ 更大的线性组合：

    \[V_i = a^{\mathrm T} X_i\]

    其中，\(\|a\|=1\)。

  • 可以证明，如果我们构造了一个与 $X_i$ 的前 $k$ 个 PC 不相关的变量

    \[V_i = a^{\mathrm T} X_i\]

    其中，\(\|a\|=1\)。

    那么，通过将 $V_i$ 取为 $X_i$ 的第 $(k+1)$ 个主成分

    \[V_i = Y_{i(k+1)}\]

    可以使其方差最大化。

  • 根据这些特性，我们希望能够通过将原始数据投影到前几个 PC 上来收集尽可能多的关于原始数据的信息。
  • 请记住，我们的目标是将原始 $p$ 维数据投影到仅几个维度上，从而更轻松地进行可视化。

3. 主成分的应用

通常在实践中，我们并不知道 $\mu=E(X_i)$ 和 $\Sigma$，因此我们使用它们的经验对应项 $\overline X$ 和 $S$ 作为替代，即：

  • 首先，我们可以将 $X_i$ 的 第一主成分 取为：

    \[Y_{i1} = \gamma_1^{\mathrm T}(X_i - \overline X)\]

    其中，$\gamma_1$ 是样本协方差矩阵 $S$ 的最大特征值 $\lambda_1$ 对应的特征向量。

  • 然后，对于 $k=2,\dots,q$，我们将 $X_i$ 的 第 $q$ 个主成分 取为：

    \[Y_{ik} = \gamma_k^{\mathrm T}(X_i - \overline X)\]

    其中，$\gamma_k$ 是样本协方差矩阵 $S$ 的第 $k$ 大的特征值 $\lambda_k$ 对应的特征向量。

  • 在矩阵表示下，令

    \[Y_i = \underbrace{(Y_{i1},\dots, Y_{ip})^{\mathrm T}}_{p \times 1} \qquad \text{and} \qquad \mathcal Y = \underbrace{(Y_1,\dots,Y_n)^{\mathrm T}}_{n \times p}\]

    我们有

    \[\mathcal Y = (\mathcal X - 1_n \overline X^{\mathrm T})\Gamma\]

  • 一旦计算完 PC 后，我们就可以将它们绘制在图中以检查数据是否存在聚类，检查那些高影响的观测值 (离群值)，以及是否可以获得更多关于数据的认知。

  • 当我们在 PC 图中检测到某些东西时，我们还可以回到原始数据并尝试建立连接，并检查我们的解释是否正确。

例子：瑞士纸币数据

参考：Flury, B. and Riedwyl, H. (1988). Multivariate Statistics: A practical approach. London: Chapman & Hall, Tables 1.1 and 1.2, pp. 5–8.

数据包含的一系列变量是通过对 $200$ 张 $1000$ 面值的瑞士法郎进行测量得到的，其中 $100$ 张为真钞，剩下 $100$ 张为伪钞。可以通过在 R 包 mclust 中使用 data(banknote) 加载数据。

如前所述，测得的变量为：

  • $X_1$：钞票长度 (mm)
  • $X_2$：左边缘宽度 (mm)
  • $X_3$：右边缘宽度 (mm)
  • $X_4$：底部边距宽度 (mm)
  • $X_5$：顶部边距宽度 (mm)
  • $X_6$：对角线长度 (mm)

其中，前 $100$ 张为真钞，后 $100$ 张为伪钞。

图 16：瑞士纸币数据：可以看到，由于我们的原始数据只有 $6$ 个维度，我们仍然可以对数据进行一些可视化。

在 R 中，我们可以使用以下命令读取数据并生成散点图：

1
2
3
4

library(mclust)
data(banknote)
StatusX <- banknote[,1]
plot(banknote[,2:7])

Status 包含了一张纸币是真钞还是伪钞的相关信息，通过以下命令中心化数据并进行 PC 分析：

1
2
3

XCbank <- scale(banknote[,2:7], scale=FALSE)
PCX <- prcomp(XCbank, retx=T)
PCX

我们可以仔细观察一下两个 PC 上的钞票数据。R 中的特征值和特征向量通过以下形式给出：

1
2
3
4
5
6
7
8
9
10
11

Standard deviations (1, .., p=6):
[1] 1.7321388  0.9672748  0.4933697  0.4412015  0.2919107  0.1884534

Rotation (n x k) = (6 x 6):
            PC1     PC2    PC3     PC4     PC5     PC6
Length     0.044  -0.011  0.326  -0.562  -0.753   0.098
Left      -0.112  -0.071  0.259  -0.455   0.347  -0.767
Right     -0.139  -0.066  0.345  -0.415   0.535   0.632
Bottom    -0.768   0.563  0.218   0.186  -0.100  -0.022
Top       -0.202  -0.659  0.557   0.451  -0.102  -0.035
Diagonal   0.579   0.489  0.592   0.258   0.084  -0.046

特征向量是 旋转矩阵 (rotation matrix) 的列，特征值是 标准差 (standard deviations) 的平方。这里，我们将特征向量保留在 gamma 中，将特征值保留在 lambda 中：

1
2

gamma <- PCX$rotation
lambda <- PCX$sdevˆ2

让我们来看一下前两个 PC：可以看到，数据可以被很清晰地分为两组。

1
2

pX <- XCbank %*% gamma
plot(pX[,1], pX[,2], pch='*', xlab="PC1", ylab="PC2", asp=1)

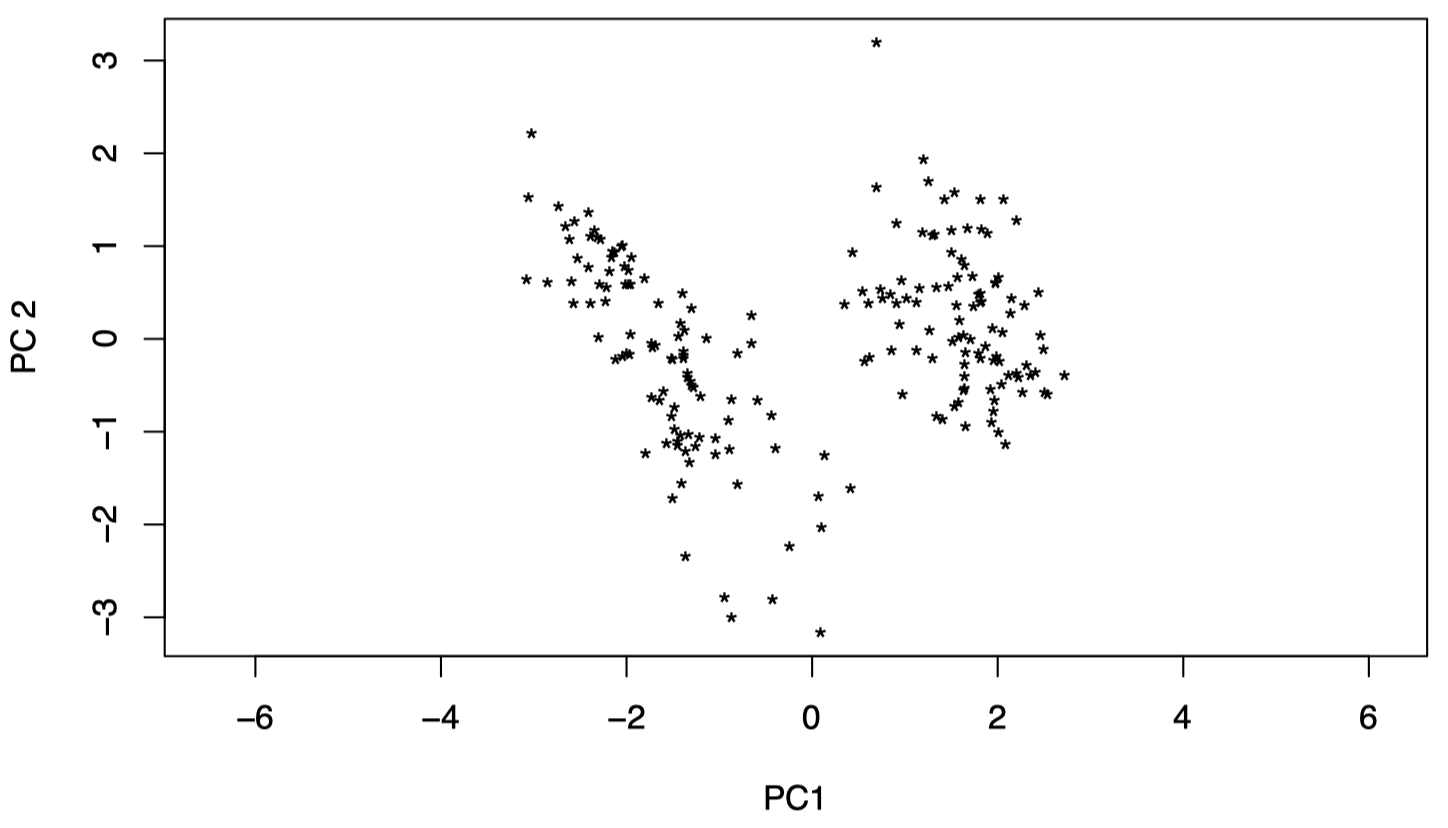
图 17：瑞士纸币数据：前两个 PC 数据，可以看到，数据可以被分为两组。

在 R 中，我们也可以用一种更简单的方式完成：将投影数据 $Y_i$ 保留在 Y 中。

1
2

Y <- PCX$x
plot(Y[,1], Y[,2], pch='*', xlab="PC1", ylab="PC2", asp=1)

图 18：瑞士纸币数据：与图 17 一样，图中显示了前两个 PC 数据。

实际上，上面的两个组分别对应真钞和假钞。因此，仅仅前两个 PC 就已经捕获了该信息。所以，我们并不需要保留全部 $6$ 个维度即可看到这点。

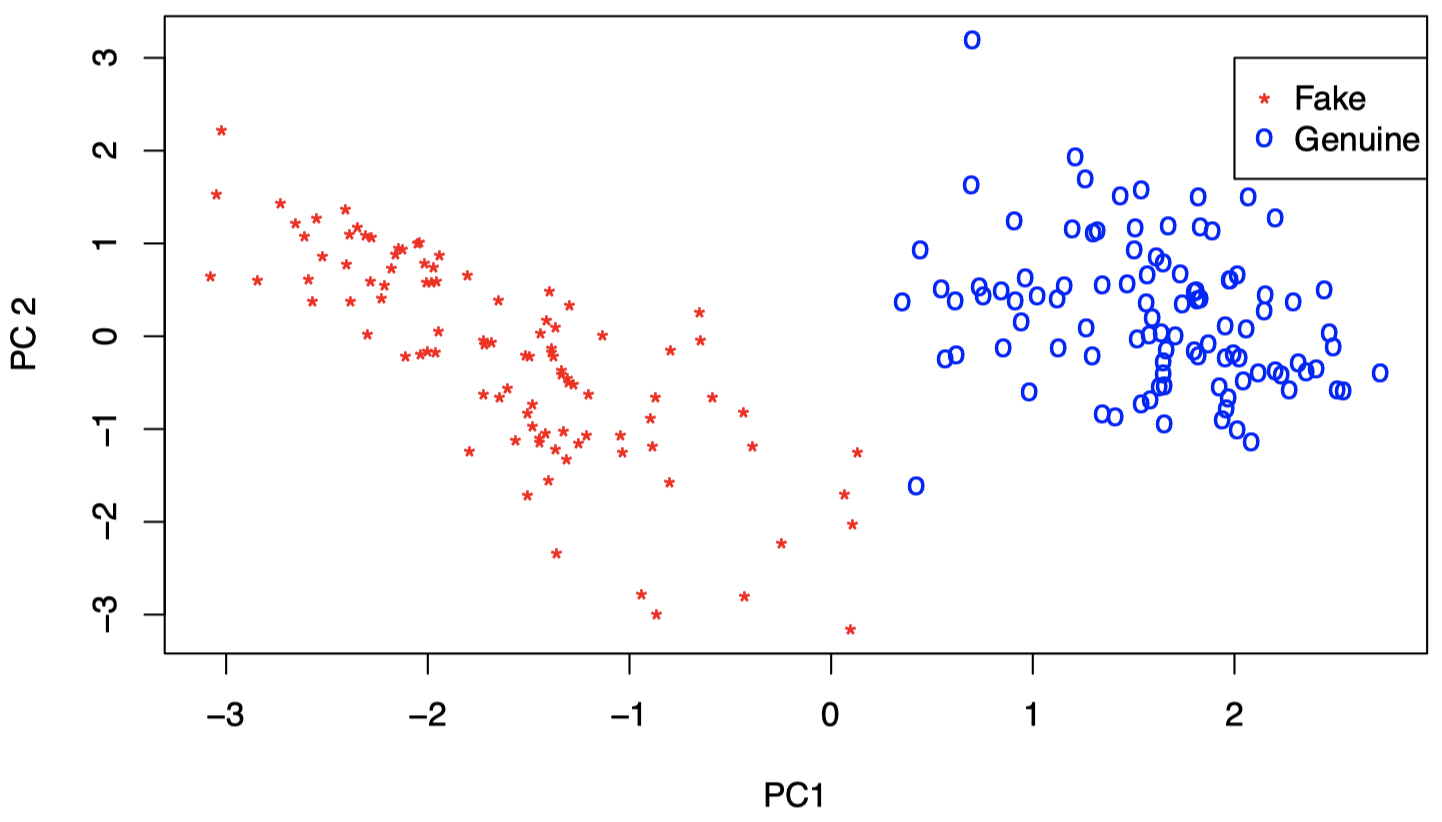
图 18：瑞士纸币数据：红色表示假钞，蓝色表示真钞。可以看到，仅仅依靠前两个 PC，我们已经能够将真钞和假钞区分开。

回顾前面 PCX 的输出结果：

1
2
3
4
5
6
7
8
9
10
11

Standard deviations (1, .., p=6):
[1] 1.7321388  0.9672748  0.4933697  0.4412015  0.2919107  0.1884534

Rotation (n x k) = (6 x 6):
            PC1     PC2    PC3     PC4     PC5     PC6
Length     0.044  -0.011  0.326  -0.562  -0.753   0.098
Left      -0.112  -0.071  0.259  -0.455   0.347  -0.767
Right     -0.139  -0.066  0.345  -0.415   0.535   0.632
Bottom    -0.768   0.563  0.218   0.186  -0.100  -0.022
Top       -0.202  -0.659  0.557   0.451  -0.102  -0.035
Diagonal   0.579   0.489  0.592   0.258   0.084  -0.046

这里，我们仅看前两个特征向量 (在 R 中被称为 PC1 和 PC2)，可以得到：

\[\begin{align} Y_{i1} &= 0.044X_{i1}− 0.112X_{i2}− 0.139X_{i3}− 0.768X_{i4}− 0.202X_{i5}+ 0.579X_{i6} \\[2ex] Y_{i2} &= −0.011X_{i1} − 0.071X_{i2} − 0.066X_{i3} + 0.563X_{i4} − 0.659X_{i5} + 0.489X_{i6} \end{align}\]

因此，我们知道：

  • 第一个 PC 大致是第 $6$ 个成分 (对角线的长度) 与第 $4$ 个成分 (底部边距宽度) 之差；
  • 第二个 PC 大致是第 $5$ 个成分 (顶部边距宽度) 与第 $6$ 和第 $4$ 个成分之和的差。

下节内容：主成分分析 (二)

知识共享许可协议本作品采用知识共享署名-非商业性使用-相同方式共享 4.0 国际许可协议进行许可。 欢迎转载，并请注明来自：YEY 的博客 同时保持文章内容的完整和以上声明信息！
CATALOG
    FEATURED TAGS
    随笔 课程笔记 统计机器学习 COMP90051 学习笔记 自然语言处理 COMP90042 PyTorch 人工智能伦理 COMP90087 数据科学多元统计学 MAST90138 AI 自动规划 COMP90054 数据分析 计算统计学与数据科学 MAST90083 高级数据库系统 COMP90050 统计建模 MAST90139 读书 📚 MySQL 学习索引 Hive 技术问题 Jekyll Workshop
    FRIENDS