Lecture 07 因子分析
参考教材:
- Hardle, W. and Simar, L (2015). Applied multivariate statistical analysis, 4th edition.
- Hastie, T. Tibshirani, R. and Friedman, J. (2009). The elements of statistical learning, 2nd edition
1. 正交因子模型
令 $X \sim (\mu, \Sigma)$ 为一个 $p$ 维的随机向量。在 PCA 中,我们知道,如果 $\Sigma$ 只有 $q< p$ 个非零特征值,那么我们可以将 $X$ 表示为
\[X-\mu =\Gamma_{(1)}Y_{(1)} \tag{1}\](之所以减去 $\mu$,是因为我们的计算是针对均值为零的 $X$)。
其中,
\[\Gamma_{(1)}=\underbrace{(\gamma_1,\dots,\gamma_q)}_{p \times q}\]并且
\[Y_{(1)}=\underbrace{(Y_1,\dots,Y_q)^{\mathrm T}}_{q \times 1}\]是主成分 (PCs) 的 $p$ 维向量 $Y=\Gamma^{\mathrm T} X$ 的前 $q$ 个分量。
回忆一下,$Y_{(1)}\sim (0, \Lambda_1)$,其中 $\Lambda_1=\text{diag}(\lambda_1,\dots,\lambda_q)$。
令 $Q=\Gamma_{(1)}\Lambda_{(1)}^{1/2}$ 和 $F=\Lambda_{(1)}^{-1/2}Y_{(1)}$,我们可以将式 $(1)$ 重写为
\[X=QF+\mu\]现在,我们有
\[\begin{align} \mathrm{E}(F) &= 0 \\[2ex] \mathrm{Var}(F) &= \Lambda_{(1)}^{-1/2}\mathrm{Var}(Y_{(1)})\Lambda_{(1)}^{-1/2}=I_q \\[2ex] \Sigma &= \mathrm{Var}(X)=Q\mathrm{Var}(F)Q^{\mathrm T} = QQ^{\mathrm T} = \sum_{j=1}^{q}\lambda_j \gamma_j \gamma_j^{\mathrm T} \end{align}\]在这种情况下,$X$ 可以完全由 $F=(F_1,\dots,F_q)^{\mathrm T}$ 中的 $q < p$ 个 不相关 因子的加权和确定。
-
注意,原始维度为 ${p \choose 2} + p = \frac{p(p+1)}{2}$ 的 $\mathrm{Var}(X)$ 可以由具有 $qp$ 项的载荷矩阵 $Q$ 的因子完全解释。
-
当 $q \ll p$ 时,$\frac{p(p+1)}{2}$ 的阶数约为 $O(p^2)$,而 $qp$ 的阶数约为 $O(p)$。 $\Rightarrow$ 我们实现了 降维。
-
$Q$ 的维数是一个微妙的问题,不仅仅是 $qp$。我们稍后会对此详细介绍。
但事情往往不会如此理想。
通常,在 正交因子模型 (orthogonal factor model) 中,我们假设以下数据生成机制:存在由 $q$ 个 公共因子 (common factors) 组成的随机向量 $F =(F_1,\dots,F_q)^{\mathrm T}$ 和 由 $p$ 个 特定因子 (specific factors) 组成的随机向量 $U =(U_1,\dots,U_p)$,使得
\[X=QF+U+\mu\]并且我们假定:
- $\mathrm{E}(F)=0$
- $\mathrm{Var}(F)=I_q$
- $\mathrm{E}(U)=0$
- $\mathrm{Cov}(U_i,U_j)=0 \quad \text{if} \quad i\ne j$
- $\mathrm{Cov}(F,U)=0$
$Q$ 是一个 $p\times q$ 的非随机矩阵,其分量称为 载荷 (loadings)。
特别地,我们定义 $\mathrm{Var}(U)\equiv \Psi \equiv \mathrm{diag}(\psi_1,\dots,\psi_p)$ 是一个对角矩阵。
现在,对于 $\Sigma := \mathrm{Var}(X)$,我们有
\[\Sigma = \mathrm{Var}(QF+U)=\mathrm{Var}(QF) + \mathrm{Var}(U)= QQ^{\mathrm T} + \Psi\]如果 $q \ll p$,是否实现了降维?是的,$Q$ 和 $\Psi$ 中总共只有 $qp + p$ 项,这要远少于 $p(p + 1)/ 2$。
从某种意义上看,$X$ 的 $p$ 个分量之间的相关性完全是通过载荷的因子来解释的,而 $U_i$ 会为每个分量添加一些特定的噪声。
- 历史:Spearman 将因子分析模型引入了心理学领域中的一些重要应用。(在其他一些统计学课程中,也被称为“ Spearman’s $\rho$”)
- 如果 $q = 1$,则 $F$ 为不可观测属性 (例如,智力等因素),而 $X_i$ 可能是在不同认知任务中获得的分数。
- 参见 Hardle 和 Simar 教材的第 363 页。
2. 解释因子
我们可以使用与 PCA 中类似的工具来解释这些因子。
我们可以依次用各分量表示模型
\[X=QF+U+\mu\]即,对于 $j=1,\dots,p$,
\[X_j = \sum_{\ell=1}^{q}q_{j\ell}F_{\ell} + U_j + \mu_j\]其中,$q_{j\ell}$ 是 $Q$ 中的第 $(j,\ell)$ 个元素。
回忆 $\mathrm{Cov}(U,F)=0$,$\mathrm{Var}(F)=I_q$,$\mathrm{Var}(U) = \mathrm{diag}(\psi_1,\dots,\psi_p)$,可以推断出
\[\mathrm{Var}(X_j)=\sum_{\ell=1}^{q}q_{j\ell}^2 + \psi_j\]其中,$\sum_{\ell=1}^{q}q_{j\ell}^2$ 被称为 公共方差 (communality variance),$\psi_j$ 则被称为 特定方差 (specific variance)。
然后,
\[\dfrac{\sum_{\ell=1}^{q}q_{j\ell}^2}{\mathrm{Var}(X_j)} \tag{2}\]是 $X_j$ 的方差中由 $q$ 个因子解释的部分所占的比例。其值越接近 $1$,则说明这 $q$ 个因子对 $X_j$ 的方差解释程度越好。
我们可以通过这些因子与 $X_j$ 之间的相关系数将二者联系起来。由于 $X=QF+U+\mu$,我们有
\[\mathrm{Cov}(X,F)=\mathrm{Cov}(QF+U,F)=\mathrm{Cov}(QF,F)=Q\mathrm{Cov}(F,F)=Q\]并且,由于 $\mathrm{Var}(X_j)=\sigma_{jj}$ 和 $\mathrm{Var}(F_j)=1$,可以推断出
\[\mathrm{Corr}(X,F)=D^{-1/2}Q\]其中,$D=\mathrm{diag}(\sigma_{11},\dots,\sigma_{pp})$。
就像我们在 PCA 中所做的一样,通过分析这些相关性,我们可以看到哪些 $X_j$ 与每个因子都高度相关,并由此推断出这些因子的一种解释。
3. 缩放数据
如果我们改变 $X_j$ 的测量尺度会怎样?假设我们使用 $Y = CX$ 来代替 $X$,其中 $C = \mathrm{diag}(c_1,\dots,c_p)$。回想一下
\[X=QF+U+\mu\]可以推断出
\[Y=Q_Y F+U_Y+\mu_Y\]其中,$U_Y=CU$,$\mathrm{Var}(U_Y)=\Psi_Y$,并且我们定义
\[Q_Y=CQ, \quad \Psi_Y=C\Psi C^{\mathrm T}, \quad \mu_Y=C\mu \tag{3}\]这种情况下,因子 $F$ 并没有改变,并且新模型仍然是一个正交因子模型:
- $\mathrm{E}(F)=0$
- $\mathrm{Var}(F)=I_q$
- $\mathrm{E}(U_Y)=0$
- $\mathrm{Cov}(U_{Y,i},U_{Y,j})=0 \quad \text{if} \quad i\ne j$
- $\mathrm{Cov}(F,U_Y)=0$
由于缩放不会影响 $F$,因此在许多应用中会使用经过缩放和中心化的数据来搜索载荷,即使用数据
\[Y=D^{-1/2}(X-\mu)\]其中,$D=\mathrm{diag}(\sigma_{11},\dots,\sigma_{pp})$。
也就是说,我们在以下模型中搜索 $Q_Y$ 和 $\Psi_Y$,
\[Y=Q_YF+U_Y\]在与以前相同的假设下:
- $\mathrm{E}(F)=0$
- $\mathrm{Var}(F)=I_q$
- $\mathrm{E}(U_Y)=0$
- $\mathrm{Cov}(U_{Y,i},U_{Y,j})=0 \quad \text{if} \quad i\ne j$
- $\mathrm{Cov}(F,U_Y)=0$
并且,$\mathrm{Var}(Y)=\mathrm{Corr}(Y)=Q_Y Q_Y^{\mathrm T} + \Psi_Y$。
令 $q_{Y,j\ell}$ 表示 $Q_Y$ 的第 $(j,\ell)$ 个元素,那么,对于 $j=1,\dots,p$,
\[\sum_{\ell=1}^{q}q_{Y,j\ell}^2 +\psi_{Y,j}=\mathrm{Var}(Y_j)=1\]如果公共方差 $\sum_{\ell=1}^{q}q_{Y,j\ell}^2$ 接近 $1$,则意味着第 $j$ 个变量 $X_j$ 可以很好地被前 $q$ 个因子所解释。
回忆一下,在 未缩放 的情况下,我们发现式 $(2)$,即
\[\dfrac{\sum_{\ell=1}^{q}q_{j\ell}^2}{\mathrm{Var}(X_j)}\]是 $X_j$ 的方差中由 $q$ 个因子解释的部分所占的比例。
由于 $q_{Y,j\ell}=q_{j\ell} / \sqrt{\mathrm{Var}(X_j)}$,因此
\[\sum_{\ell=1}^{q}q_{Y,j\ell}^2 = \sum_{\ell=1}^{q}q_{j\ell}^2 / \mathrm{Var}(X_j)\]实际上是 $X_j$ 的方差中由 $q$ 个因子解释的部分所占的比例。
为了解释这些因子,我们还可以计算相关系数矩阵
\[\mathrm{Corr}(Y,F)=\mathrm{Cov}(Y,F)=\mathrm{Cov}(Q_YF+U_Y,F)=Q_Y\]特别是,上面的 $\mathrm{Corr}$ 也是原始 $X$ 的 $\mathrm{Corr}$:
\[\mathrm{Corr}(X,F)=D^{-1/2}Q:= Q_Y=\mathrm{Corr}(Y,F)\]总而言之,使用缩放后的数据进行计算更容易,并且它们提供了相同的解释。
4. 载荷矩阵 $Q$ 的非唯一性
(注意:这是本节课程中最具挑战性的部分)
因子载荷的矩阵 $Q$ 是否唯一?不是,如果我们有因子模型
\[X=QF+U+\mu\]那么,对于任意 $q\times q$ 的正交矩阵 $G$,我们都有
\[X=QGG^{\mathrm T}F+U+\mu\]即
\[X=Q_G F_G+U+\mu\]其中,$Q_G=QG$,$F_G=G^{\mathrm T}F$。
这仍然是一个有效的因子模型:
- $\mathrm{E}(F_G)=0$
- $\mathrm{Var}(F_G)=G^{\mathrm T}G=I_q$
- $\mathrm{E}(U)=0$
- $\mathrm{Cov}(U_{i},U_{j})=0 \quad \text{if} \quad i\ne j$
- $\mathrm{Cov}(F_G,U)=G^{\mathrm T} \mathrm{Cov}(F,U)=0$
更重要的是,
\[\Sigma = QQ^{\mathrm T} +\Psi = Q_G Q_G^{\mathrm T} +\Psi\]- 从推断的角度来看,这是棘手的,因为我们无法从协方差 $\Sigma$ 中唯一地还原载荷矩阵 $Q$ ($Q$ 和 $\Psi$ 是模型的基本参数)。
- 从数值的角度来看,这种非唯一性同样是糟糕的,因为这会使得算法求解困难。
直观上,如果不对 $Q$ 施加限制,则 $Q$ 的可能解集至少应为维度 (或自由度) $\frac{q(q-1)}{2}$,因为这是所有 $q\times q$ 正交矩阵的集合的维度。
-
思考一下,当我们写下一个 $q\times q$ 正交矩阵时,有多少个 “自由度”?
-
任何这样的矩阵都有 $q^2$ 个元素,但是它需要满足这些代数约束:所有 $q$ 个列向量都需要具有单位长度,并且任何一对列向量之间的点积必须为零。总共有 $q+{q \choose 2}=\frac{q(q+1)}{2}$ 个约束,因此,自由度为 $q^2 - \frac{q(q+1)}{2}=\frac{q(q-1)}{2}$。
因此,通常需要施加 $\frac{q(q-1)}{2}$ 个约束以使 $Q$ 可以被确定下来。有很多不同的方法可以做到这点。
一种方法是将 $Q$ 限制为 “下三角形” 矩阵,即,对于所有 $j < \ell$,都有 $q_{j\ell}=0$。因此,这里恰好有 $\frac{q(q-1)}{2}$ 个零约束。
-
通常,将进一步限制所有对角线上的元素 $q_{jj}> 0 \quad (j=1,\dots,q)$,但这并没有真正降低自由度。(整个实数轴和半个实数轴都是维度为 $1$ 的对象)
-
上面的约束条件是由以下版本的 Cholesky 分解定理 引出的:对于秩为 $q\leq p$ 的 $p\times p$ 矩阵 $A$,可以找到唯一的 $p\times q$ 矩阵 $L =(l_{j\ell})$ 使得 $A = LL^{\mathrm T}$,并且 $L$ 是对角线元素大于零的下三角形矩阵,即:对于所有 $j=1,\dots,q$,都有 $l_{jj}> 0$;对于所有的 $j< \ell$,都有 $l_{j\ell} = 0$。
-
(对于我们的因子模型,上面讨论的 $q$ 秩矩阵 $A$ 即为 $QQ^{\mathrm T}$)
-
Hardle 和 Simar 在教材中介绍了其他一些施加约束的方法,但我发现某些贝叶斯统计学者使用的这些零约束更具指导意义。
总而言之,当我们为具有 $q$ 个因子的 $X1,\dots,X_p$ 定义一个因子分析模型时,我们通常需要额外一组 $\frac{q(q-1)}{2}$ 个约束,以使 $Q$ 和 $\Psi$ 可从协方差 $\Sigma$ 中识别出来。
因此,相对于协方差结构,一个因子模型的有效 “维度” (或自由度) 为
\[\underbrace{pq}_{Q \text{ 中元素的数量}} \quad + \quad \underbrace{p}_{\Psi \text{ 中对角线元素的数量}} \quad - \quad \underbrace{q(q-1)/2}_{\text{用于识别 } Q \text{ 的约束数量}}\]同时,在没有任何模型的情况下,$\Sigma$ 的维度为
\[\underbrace{p(p+1)/2}_{\text{对角线 } + \text{ 严格上三角部分}}\]因子建模的目标是降维。为了避免 “过度参数化 (over-parametrization)”,我们通常要求
\[p(p+1)/2 \ge pq + p - q(q-1)/2\]否则,在某些情况下,即使考虑了 $Q$ 的可识别性所需的 $q(q − 1)/2$ 个约束,也可能从相同的 $\Sigma$ 中得到无限多种可能的 $(Q,\Psi)$ 选择。
这意味着:对于变量数量 ($p$) 给定的观测 $X$,当我们为数据构建可识别 (唯一确定) 因子模型时,因子数量 ($q$) 存在上限。
最后注意:总而言之,即使对于非过度参数化的因子模型 (即具有与 $Q$ 相关的必要的 $q(q-1)/2$ 个约束),从最严格的意义上讲,仍然可能存在非唯一解。
-
例如,在前面的例子中,对 $q_{jj} > 0 \quad (j=1,\dots,q)$ 的 “进一步” 约束并非 $Q$ 的上三角中必要的 $q(q−1)/2$ 个零约束的一部分。假如没有这些正约束,如果存在某个特定的 $Q$ 满足 $\Sigma=QQ^{\mathrm T}+\Psi$,那么 $\tilde Q = -Q$ 同样满足 $\Sigma=\tilde Q \tilde Q^{\mathrm T}+\Psi$,也就是说,如果没有这些正约束,我们将无法识别 $Q$ 的正负号。
-
但是,这种不可识别性在本质上和之前讨论的非唯一性不同。它并没有真正增加解空间的维度 (或自由度)。
5. 正态性假设下的似然方法
根据数据估计 $(Q,\Psi)$:我们将通过假设 $F$ 和 $U$ 都是正态的(因此 $X$ 也是正态的)来聚焦 最大似然估计 (MLE) 方法。
因子模型实际上只是将协方差矩阵建模为 $\Sigma = \Sigma(Q,\Psi) = QQ^{\mathrm T} + \Psi$
对于一个包含 $n$ 个样本的数据集 $\mathcal X$,回忆一下,其 正态对数似然 (normal log likelihood) 为
\[l(\mathcal X; \mu,\Sigma)=-\dfrac{n}{2} \log |2\pi \Sigma| - \dfrac{1}{2}\sum_{i=1}^{n}(x_i - \mu)^{\mathrm T}\Sigma^{-1}(x_i - \mu)\]其中,$\overline x$ 是样本均值。
对于 $\mu$,其 MLE 估计总是 $\hat \mu = \overline x$,所以经过一些简单的代数之后,我们只需要最大化
\[\begin{align} l(\mathcal X; \hat \mu,\Sigma) &= -\dfrac{n}{2}\{\log |2\pi \Sigma| + \mathrm{tr}(\Sigma^{-1}S)\} \\[2ex] &= -\dfrac{n}{2}\{\log |2\pi (QQ^{\mathrm T} + \Psi)| + \mathrm{tr}((QQ^{\mathrm T} + \Psi)^{-1}S)\} \end{align}\]其中,$S$ 是无偏估计的样本协方差矩阵。这里,$l$ 是一个关于 $(Q,\Psi)$ 的函数,并且对于 $Q$ 施加了必要的约束以满足可识别性要求。
- 通常,这并非一个容易的数值问题;在 R 中,
factanal函数提供了相关实现。
我们还可以使用 似然比 (LR) 检验 来确定因子 $q$ 的数量 (在不会导致数据过度参数化的允许范围内),这可以通过 (对于每个允许的 $q$) 检验零假设完成:
\[H_0:q \text{ 是因子数量}\]对于一个给定的 $q$,其 LR 统计量为
\[-2\log \left(\dfrac{H_0 \text{ 下的最大似然}}{\text{没有模型的情况下的最大似然}}\right)=n\log \left(\dfrac{|\hat Q \hat Q^{\mathrm T} + \hat \Psi|}{|S|}\right) \tag{4}\]其中,$\hat Q$ 和 $\hat \Psi$ 是 MLE 估计量 (对于当前给定的 $q$ 而言)。
当 $H_0$ 为真时,LR 统计量具有近似卡方分布 $\chi^2_{\frac{1}{2}((p-q)^2-p-q)}$,可以用来校准模型拟合的 $\text{p}$-值。
- 在实践中,通常将式 $(4)$ 中最前面的 $n$ 替换为 $n − 1 −(2p + 4q + 5)/ 6$ 以改良 $\chi^2$ 逼近。
- 如果必须从中选择一个,我们将使用具有最大 $\text{p}$-值的模型。
- 有关更多详细信息,请参见 Hardle 和 Simar 教材中的第 369-370 页。
6. 旋转
人们经常做的一件有趣的事情是,在已经获得 $Q$ 的估计 $\hat Q$ 之后,对因子进行 方差最大旋转 (varimax rotation)。
令 $\hat Q^* = \hat Q G$,其中 $G$ 是需要确定的正交矩阵。我们选择 $G$,使得 $\hat Q^*$ 中每一列的估计平方载荷 \((\hat q_{j\ell}^*)^2\) 的方差之和能够最大化,也就是说,我们选择 $G$ 使得下式最大化:
\[\sum_{\ell=1}^{q}\left[\sum_{j=1}^{p}(\hat q_{j\ell}^*)^4 - \left \{ \sum_{j=1}^{p} (\hat q_{j\ell}^*)^2\right \}^2 \right]\]- 通常,从 $X_j$ 的角度出发,这种方式得到的因子更容易解释。某些组类的 $X_j$ 通常只与较少的几个因子相关。
- 这在 R 中的
factanal函数实现中是默认设置。
例子:来自《多变量分析》第 9 章
在工作面试中,分别根据 15 个变量对 48 个申请人进行了评判。变量包括
- 求职信的形式
- 外形
- 学术能力
- 好感度
- 自信心
- 清醒
- 诚实
- 销售技巧
- 经验
- 驱动力
- 野心
- 掌控力
- 潜力
- 加入意向
- 匹配度
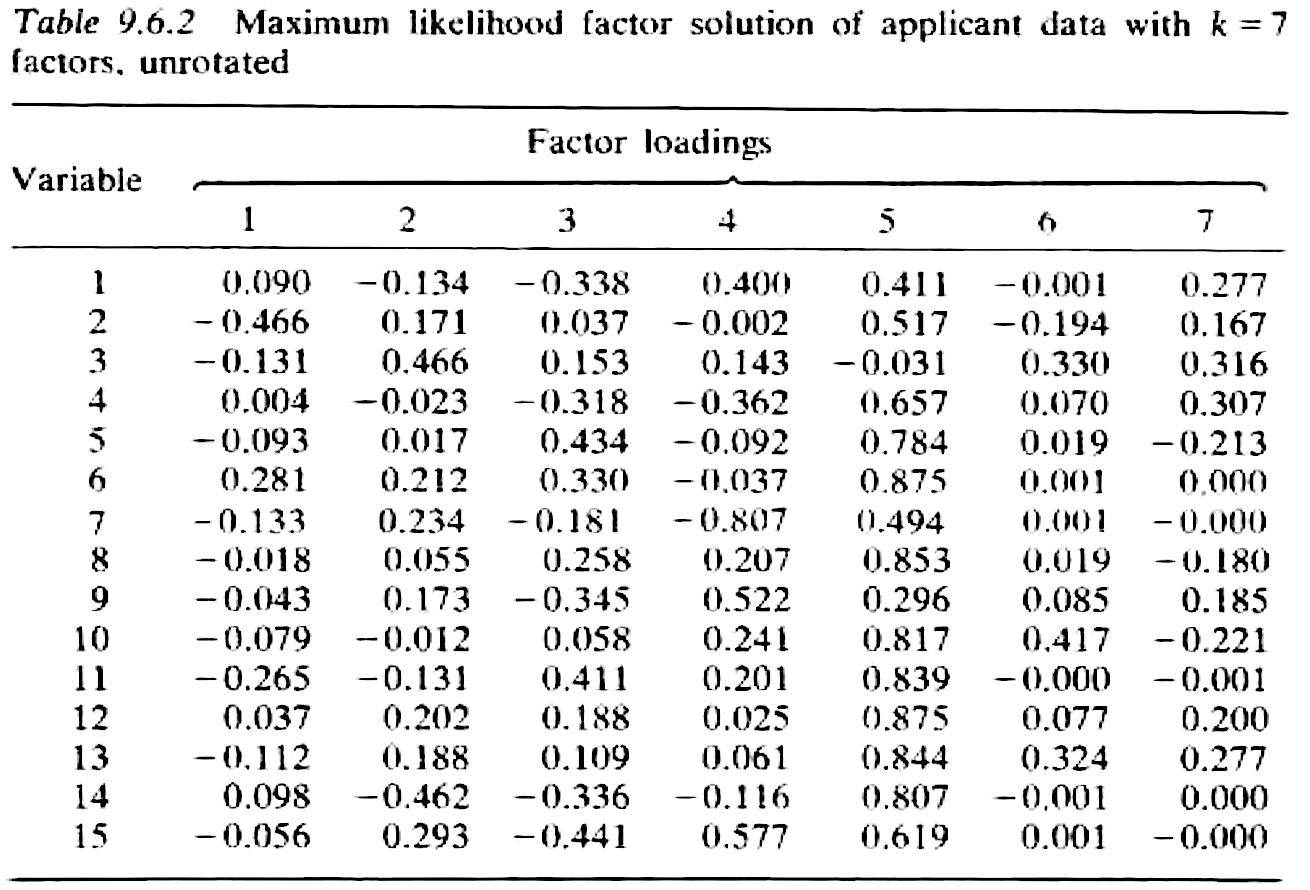
未经 varimax 旋转的因子载荷:
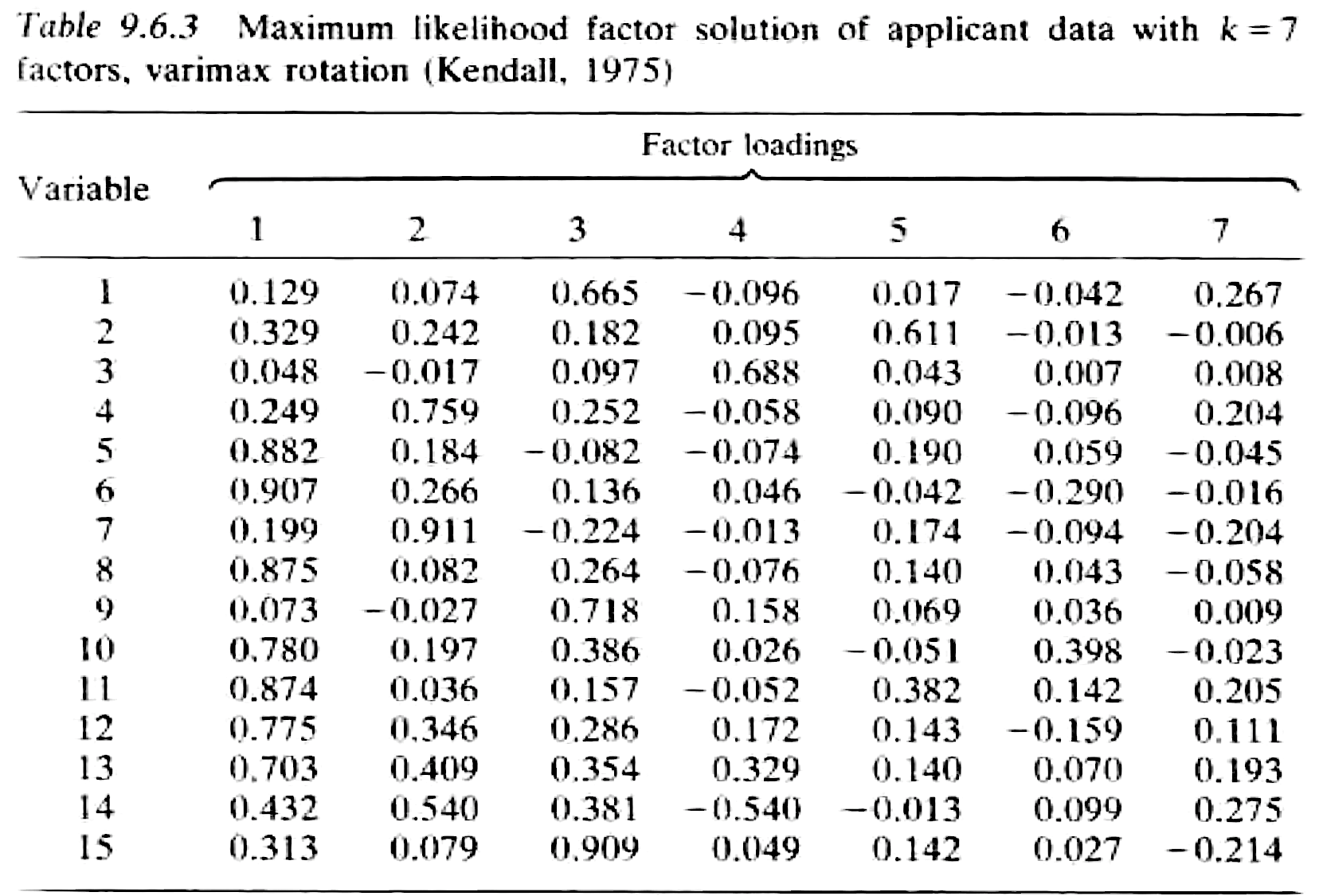
经过 varimax 旋转后的因子载荷:
解释:
- 通常,未经旋转的载荷在解释时比较困难 (在所有变量上的载荷都差不多),而旋转过的载荷解释时要更容易一些 (在某些特定变量上的载荷较大)。
- 第一个因子在变量 5、6、8、10、11、12 和 13 上载荷很大,并且可能代表着外向和推销员个性的人格。
- 因子 2 主要对变量 4 和 7 加权,表示好感度。
- 因子 3 主要对变量 1、9 和 15 加权,代表经验。
- 因子 4 和 5 各代表一个变量,分别为学术能力 3 和外表 2。
- 最后两个因子似乎不是特别重要。另外,变量 14 (加入意向) 似乎与其中几个因子相关。
7. 因子得分
与 PCA 不同,因子 $F_j$ 是隐变量并且不可计算,尽管有一些技术可以 “估计” 它们 (由于它们是随机变量,我们也可以说 “预测” 它们)。因子的预测值被称为 因子得分 (factor scores)。
在总体层面,我们的因子模型是
\[X=QF+U+\mu\]其中,$X\in \mathbb R^p$,$F\in \mathbb R^q$,$U\in \mathbb R^p$ 都是随机向量。
在样本 $X_1,\dots,X_n$ 层面,对于 $i=1,\dots,n$,我们记为
\[X_i=Q F_i + U_i + \mu\]其中,$X_i=(X_{i1},\dots,X_{ip})^{\mathrm T}$,$F_i=(F_{i1},\dots,F_{iq})^{\mathrm T}$,$U_i=(U_{i1},\dots,U_{ip})^{\mathrm T}$.
我们无法计算 $F_{ij}$,但是有些技术可以用来预测它们:对于每个 $i$,我们可以预测 (“估计”) 第 $j$ 个因子 $F_{ij}$。
我们不会在这里介绍详细过程,但请注意,预测变量 $\hat F_{ij}$ 不等于真正的不可观测的隐变量 $F_{ij}$。
8. 因子分析 vs. PCA
在 PCA 中,我们的目标是显式地找到 $X$ 的线性组合,而这正是我们构造 PC $Y_1,\dots,Y_p$ 的方式,并且它是模型无关的。
在因子分析中,因子无法直接计算,它们是隐变量。它们出现在对数据建模 (在协方差矩阵上) 之后。整个因子分析取决于我们假设的因子模型。如果模型是错误的,那么分析将是站不住脚的。
在因子分析中,因子并非原始变量的线性组合,它们是独立的因子,通常对应不同组类的变量可能代表的特征。实际上,在因子分析中,我们不是将 $F$ 视为 $X$ 的函数,而是将 $X$ 表示为 $F$ 的函数。
当我们想要提取某些无法直接测量的特征时,因子的这种隐变量属性会特别有用。例如:焦虑因子无法被真正测量,但它可能与其他一些可测量变量相关,例如出汗、考试成功、社交障碍等等。
在 PCA 中,前几个 PC 解释了数据中的大部分变化 (这正是我们构造 PC 的方式)。在因子分析中,$q$ 个因子通常是最容易解释的因子 (这正是我们构造因子的方式)。
有时,PCA 和因子分析可能会得出相似的结果,其原因是:如前所述,如果 $\Sigma$ 只有 $q < p$ 个非零特征值,那么我们可以使用前 $q$ 个 PC 来构建因子模型。
下节内容:线性和二次分类
本作品采用知识共享署名-非商业性使用-相同方式共享 4.0 国际许可协议进行许可。 欢迎转载,并请注明来自:YEY 的博客 同时保持文章内容的完整和以上声明信息!