Lecture 12 Q&A
参考教材:
- Gareth, J., Daniela, W., Trevor, H., & Robert, T. (2013). An intruduction to statistical learning: with applications in R. Spinger.
- Hastie, T., Tibshirani, R., & Friedman, J. (2009). The elements of statistical learning: data mining, inference, and prediction. Spinger Science & Business Media.
CH2 统计学习
Q1:高灵活度模型 vs. 低灵活度模型
(a) 样本数 $n$ 很大,预测变量数 $p$ 很小
高灵活度模型,因为样本数量足够大,而预测变量本身并不多,不会导致太高的模型复杂度,过拟合风险较低。
(b) 预测变量数 $p$ 很大,样本数 $n$ 很小
低灵活度模型,过多的预测变量会导致过于复杂的模型,加上观测数量不足,选择灵活模型很容易发生过拟合。
(c) 预测变量与响应之间的关系是高度非线性的
高灵活度模型,适用于高度非线性的情况,如果采用低灵活度模型,则容易发生欠拟合。
(d) 误差项的方差即 $\sigma^2 = \mathrm{Var}(\epsilon)$ 非常大
低灵活度模型,不可减小误差 $\mathrm{Var}(\epsilon)$ 很大说明测试错误率的 U 型曲线较早到达底部,因此,为了使得测试错误率尽可能低,应选择低灵活度模型。
Q3:绘制偏差平方、方差、测试误差、训练误差、不可减小误差的曲线并解释
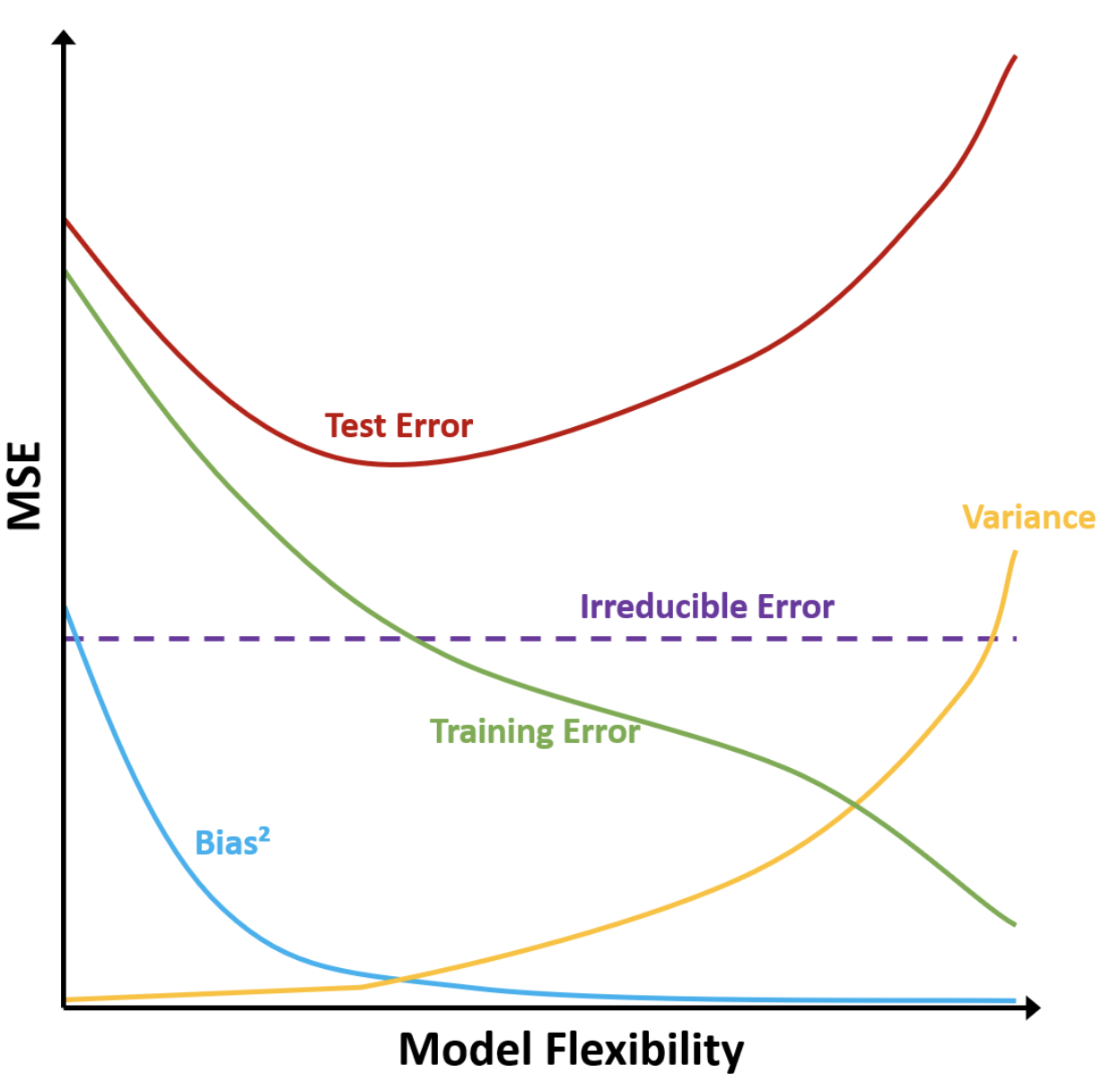
- 偏差:模型假设带来的误差。灵活度越高,模型假设越少,偏差越低。
- 方差:用不同训练集拟合模型时拟合值的变化。灵活度越高,模型越容易过拟合,方差越高。
- 不可减小误差:由未测量变量或者不可测量变化带来的系统噪声。是一个大于零的常数,与模型灵活度无关。无论选择怎样的模型去拟合真实函数,始终存在的一个误差下界。
- 训练误差:随模型灵活度增加而减小。过于灵活的模型可能会得到非常小的训练误差,存在过拟合风险。
- 测试误差:随模型灵活度增加,先减小后增大,最低点左边欠拟合,右边过拟合。
Q4:分类、回归、聚类例子各三个
(a) 分类的例子
- 申请学校 (University Application)
- 响应变量:1 (success) 或者 0 (fail)
- 预测变量:GPA, IELTS score, working experience
- 目标:prediction
- 糖尿病诊断 (Diabetes Diagnosis)
- 响应变量:1 (Positive) 或者 0 (negative)
- 预测变量:age, BMI, family medical history (yes or no)
- 目标:prediction
- 信用卡违约 (Credit Default)
- 响应变量:1 (Default) 或者 0 (not default)
- 预测变量:income, balance, student (yes or no)
- 目标:inference
(b) 回归的例子
- 个人收入 (Personal Salary)
- 响应变量:income
- 预测变量:age, gender, education
- 目标:inference
- 房价评估 (House Price)
- 响应变量:house price
- 预测变量:area, city, year, number of rooms
- 目标:prediction
- 广告销量 (Advertise Sales)
- 响应变量:sales
- 预测变量:advertisement budget on audio, neswpaper and TV
- 目标:prediction
(c) 聚类的例子
- 用户分组 (Group users)
- 特征变量:age, gender, education, income
- 目标:make different marketing strategies for different group users
- 产品分组 (Group products)
- 特征变量:size, weight, sweetness, grown area
- 目标:giving different price for apples in different groups
- 推荐系统 (Recommendation systems)
- 特征变量:age, gender, hobbies, browsing history
- 目标:recommend different types of movies to different users
Q5:高灵活度模型的优缺点,如何选择
- 高灵活度模型
- 优点:低偏差,假设少,捕获非线性,捕获复杂变量交互
- 缺点:高方差,过拟合风险,难以解释,需要调整,训练时间长
- 适用场景
- 高灵活度模型:存在非线性和交互效应、大量变量、大量数据、算力充足、主要关注预测
- 低灵活度模型:低灵活度模型假设基本满足 (例如线性、正态性等)、主要关注推断和可解释性
Q6:比较参数方法与非参数方法以及各自的优缺点
- 参数方法:基于模型估计的两阶段方法,首先对函数 $f$ 的形式给出假设,然后估计模型参数。
- 优点:将估计真实函数 $f$ 的问题简化为估计一组参数。
- 缺点:选定的模型与真实 $f$ 在形式上并非是一致,若差别过大会导致效果很差。如果选择灵活模型,则存在过拟合风险。
- 非参数方法:不需要对 $f$ 的形式进行假设。
- 优点:不限定 $f$ 的形式,可以在更大范围内选择更适合 $f$ 的形状。
- 缺点:由于没有简化为参数估计问题,需要大量观测数据 (远多于非参数方法) 以得到一个 $f$ 的准确估计。
Q7:用 KNN 方法在给定数据集上进行预测
贝叶斯决策边界非线性情况下,我们应当选择更小的 $K$。$K$ 越小,模型灵活度越高,得到的决策边界更接近真实情况。如果选择很大的 $K$,最终得到的决策边界会接近线性。
CH3 线性回归
Q2:KNN 分类与 KNN 回归之间的差异
- 相同点:两种方法都属于非参数方法,都考虑了目标观测附近的 $K$ 个最近邻样本。
- 不同点:
- KNN 分类:用于处理分类问题,响应变量为类别变量。它将 $K$ 个最近邻样本响应类别的多数投票作为分类结果。
- KNN 回归:用于处理回归问题,响应变量为数值变量。它将 $K$ 个最近邻样本的响应均值作为预测结果。
Q3:毕业起薪预测
(c) 判断真假:由于 GPA/IQ 交互项的系数很小表明二者之间不存在交互作用。
错误。线性回归中,交互项系数的绝对值大小和相关预测变量以及响应变量的测量尺度有关,并不能反映出交互项对于响应变量效应的重要性。如果我们需要检验某个回归系数的重要性,应当采用 $t$ 检验。
Q4:线性回归 vs. 多项式回归:训练/测试 RSS
(a) 假设真实函数满足线性关系,比较线性回归与多项式回归的训练 RSS
多项式回归的训练 RSS 更小,因为该模型灵活度更高,可以更好地拟合训练数据。
(b) 与 (a) 同样条件下,比较二者的测试 RSS
线性回归的测试 RSS 更小,因为真实函数满足线性关系,线性回归足以很好地拟合数据,而多项式回归由于高灵活度可能存在轻微的过拟合。
(c) 假设真实函数非线性,且非线性程度未知,比较线性回归与多项式回归的训练 RSS
如果真实函数具有很强的非线性,并且可以通过三次拟合很好地近似,那么多项式回归的训练 RSS 将明显低得多。如果真实函数非线性较弱或者无法通过三次函数很好地拟合,那么多项式回归的训练 RSS 可能会略低于线性回归。但不论哪种情况,多项式回归的训练 RSS 都会更低一些,因为其模型灵活度更高。
(d) 与 (c) 同样条件下,比较二者的测试 RSS
这取决于真实函数的非线性程度。如果真实函数非线性程度很高,这种情况下线性回归中的假设无法满足,这种情况下多项式回归的测试 RSS 可能更低一些。如果真实函数仅存在轻微的非线性,由于多项式回归的高灵活度导致模型方差较高,存在过拟合风险,而线性回归假设基本满足,这种情况下线性回归的 RSS 可能低一些。
CH4
CH5
CH6:线性模型选择与正则化
Q1:对比最优子集、前向选择、后向选择
(a) 含有 $k$ 个预测变量的模型中,哪种方法的训练 RSS 最小
通常最优子集会得到最小的训练 RSS (尽管前向、后向选择有一定机会得到相同的模型),因为它会检查所有可能的变量子集上的模型。
(a) 含有 $k$ 个预测变量的模型中,哪种方法的测试 RSS 最小
不清楚。三种算法都在测试集上使用交叉验证选择最终模型,我们无法判断哪种在测试集上的性能更好。
(c)
下节内容:非线性模型
本作品采用知识共享署名-非商业性使用-相同方式共享 4.0 国际许可协议进行许可。 欢迎转载,并请注明来自:YEY 的博客 同时保持文章内容的完整和以上声明信息!