Lecture 08 线性和二次分类
参考教材:
- Hardle, W. and Simar, L (2015). Applied multivariate statistical analysis, 4th edition.
- Hastie, T. Tibshirani, R. and Friedman, J. (2009). The elements of statistical learning, 2nd edition
1. 引言
在分类问题中,总体中我们感兴趣的个体来自一些不同的类别 (例如:$K$ 个类别)。
例如,$K=2$:健康;患病。
我们可以从观测到的 $(X_1,G_1),\dots, (X_n, G_n)$ 中获得训练样本,其中
- $G_i \in \{1,2,\dots,K\}$ 是第 $i$ 个观测样本的分组标签 (每个个体都刚好属于一个分组)。
- $X_i$ 是一个解释变量 (例如,年龄、血压等),或者,更常见的是由多个变量组成的一个向量 $X_i=(X_{i1},\dots, X_{ip})^{\mathrm T}$。
问题:假设现在又来了一个新的个体,我们只观测到了它的解释变量 $X=x=(x_1,\dots,x_p)^{\mathrm T}$,但是不知道它来自哪个分组。
目标:我们需要将这个新的个体分类到正确的分组之中 (即找到其所属的分组)。这等价于找到这个新个体的分组标签 $G\in \{1,\dots, K\}$。
我们应该怎么做?
2. 主要技术思想
主要思想:将该新值 $x$ 与训练样本 $X_i$ 进行比较。
如果 $x$ 与来自分组 $k$ 中的 $X_i$ 要比来自其他分组的样本更相似,那么我们就将这个新个体分到组 $k$。
那么如何确定 $x$ 与来自分组 $k$ 中的 $X_i$ 要比来自其他分组的样本 “更相似” 呢?
对于 $k=1,\dots, K$,使用训练数据来估计在给定 $X$ 等于 $x$ 的情况下,一个个体来自组 $k$ 的概率:
\[P(G=k\mid X=x)\]将其估计值表示为:
\[\hat P(G=k\mid X=x)\]然后,将这个新个体分类到组 $k$,如果
\[\hat P(G=k\mid X=x) > \max_{j=1,\dots,K,j\ne k} \hat P(G=j\mid X=x)\]存在许多不同的分类方法,但它们本质上都对应于估计上述概率的各种方式。
有两类主要方法:
- 回归估计技术
- 贝叶斯方法
首先介绍二分类情况下的方法,即 $K=2$(可以扩展到 $K > 2$ 个类的情况)。
在本章中:我们观测到 i.i.d. 的训练样本数据 $(X_i, G_i), i=1,\dots,n$。当我们不想突显样本这一概念时,可以用符号 $(X,G)$ 表示来自同一总体的一般个体。
3. 对于 $K=2$ 类的简单回归方法
假设所有个体都只来自 $K=2$ 个分组,那么我们可以将一个新个体分到组 $1$,如果
\[P(G=1\mid X=x) > P(G=2\mid X=x)\]在实践中:仅给定样本 $(X_1,G_1),\dots,(X_n, G_n)$,我们需要寻找 $P(G=k\mid X=x), k=1,2$ 的估计量。
主要思想:通过回归来估计 $P(G=k\mid X=x)$。
为此,我们需要根据 $G$ 定义一个新的变量。对于 $k=1,2$,令
\[Y_k=I\{G=k\}=\begin{cases}1 & \text{if } G=k \\[2ex] 0 & \text{otherwise}\end{cases}\]在样本级别,这意味着对于 $i=1,\dots,n$,我们定义
\[Y_{ik}=I\{G_i=k\}\]例如:假设我们观测到的训练样本大小为 $n=7$,其中 $G_i$ 为
\[(G_1,\dots,G_7)=(1,1,1,2,2,2,1)\]那么,对于 $i=1,\dots,n$ 和 $k=1,2$,$Y_{ik}$ 由下式给出:
\[\begin{align}(Y_{11},\dots,Y_{71}) &= (1,1,1,0,0,0,1) \\[2ex] (Y_{12},\dots,Y_{72}) &= (0,0,0,1,1,1,0)\end{align}\]如果我们定义回归曲线
\[m_k(x)=E(Y_k \mid X=x)\]那么,我们有
\[P(G=k\mid X=x)=E\left(I\{G=k\} \mid X=x\right)=m_k(x)\]我们可以使用标准回归估计技术来估计 $m_k$。
由于每个个体都必须属于两组之一,因此,对于所有 $x\in \mathbb R^p$,我们有
\[P(G=1\mid X=x) + P(G=2\mid X=x) = 1\]即,
\[m_2(x) = 1- m_1(x)\]因此,我们只需要估计 $m_1$ (然后 $m_2$ 可由上述关系推得)。
3.1 线性回归分类器
当我们使用线性回归分类器时,我们假设
\[m_1(x)=E(Y_1\mid X=x)=P(G=1\mid X=x) = \beta_0 + \beta^{\mathrm T}x\]使用 $\beta_0$ 和 $\beta$ 的 LS 估计量 (或者 PCR 或者 PLS;关于如何计算分类的 CV,请参见教材第 35 页) 来估计 $m_1$
\[\hat m_1(x) = \hat \beta_0 + \hat \beta^{\mathrm T} x\]可以推得 $\hat m_2=1-\hat m_1$。
将一个新的 $x$ 分类到组 $1$,如果
\[\hat m_1(x) > \hat m_2(x) \quad \Longleftrightarrow \quad \hat \beta_0 + \hat \beta^{\mathrm T} x > 1- \hat \beta_0 - \hat \beta^{\mathrm T} x \quad \Longleftrightarrow \quad \color{red}{\hat \beta_0 + \hat \beta^{\mathrm T} x > 1/2}\]否则,将 $x$ 分类到组 $2$。
注意:该方法依赖于线性回归模型的有效性,通常只是现实世界的一种近似。
例子:Golub 数据
Golub TR et al (1999), Molecular Classification of cancer: class Discovery and Class Prediction by gene expression monitoring, Science 286:531-7
- 两种类型的患者,对应于两种类型的白血病 (ALL 和 AML)。
- $X =(X_1, X_2)^{\mathrm T}$:两个已知的与白血病类型相关的基因表达。
根据估计的线性模型,我们可以得到
\[\begin{align} \hat m_1(x) &= 0.9231 + 0.2454 x_1− 0.4800 x_2 \\[2ex] \hat m_2(x) &= 0.07691 − 0.24542 x_1+ 0.47999 x_2 \approx 1 − \hat m_1(x) \end{align}\](其中,“$\approx$” 是由于数值误差)
区分/分类边界
分类边界是分到组 $1$ 的数据区域和分到组 $2$ 的数据区域之间的边界。它是通过求解以下方程式得到的
\[\hat m_1(x) - \hat m_2(x) = 0\]对于线性回归分类器而言,上式等价于
\[\hat m_1(x)=1/2\]在 Golub 数据的例子中,分类边界是通过求解下式得到的
\[0.9231 + 0.2454 x_1 − 0.4800 x_2 = 1/2\]可以将其用以下直线表示
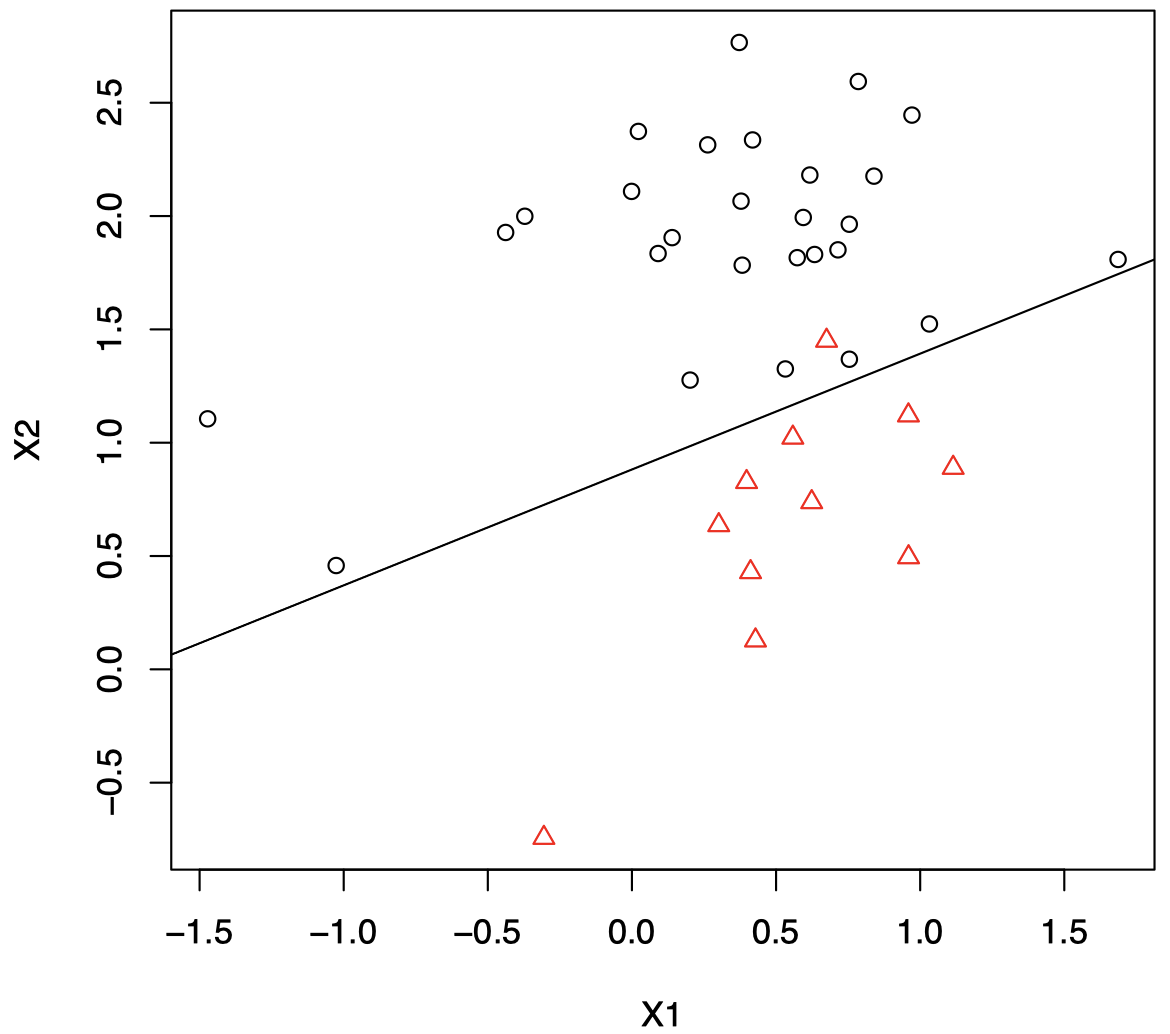
\[x_2 = \dfrac{0.9231 − 0.5}{0.4800} + \dfrac{0.2454}{0.4800} x_1 = 0.8815 + 0.5113 x_1\]我们将在该直线某一侧的数据分为一类,将直线另一侧的数据分为另一类。
下图中的直线代表分类边界。训练集的 $X_i$ 来自两个分组,由不同颜色/符号表示。如果一个新观测值落在该直线下方区域,则将其分类到红色三角组;否则将其分类到黑色圆圈组。
其他例子
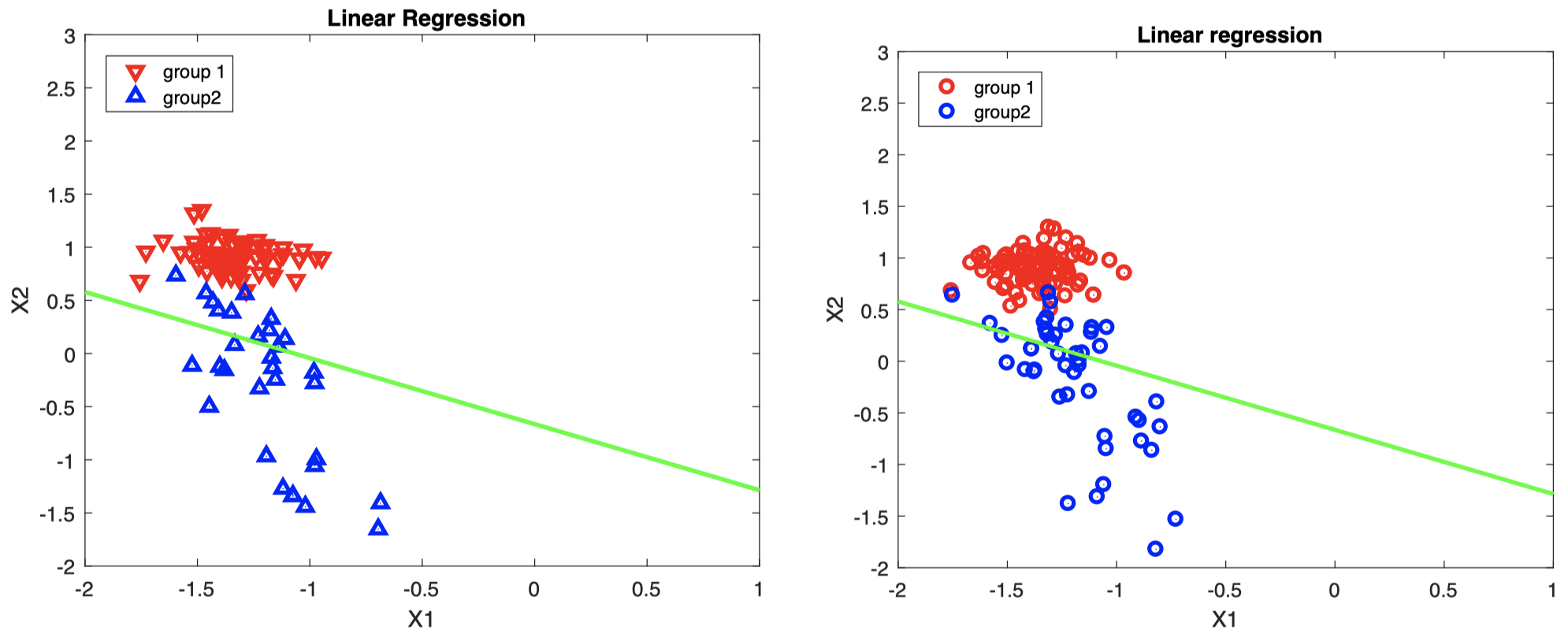
- 左图:训练集中的 $X_i$,不同分组用蓝色/红色表示。
- 右图:需要分类的新数据
这里只是一个例子。与现实生活不同,我们知道新数据的真实组类 (右图中的蓝色/红色):可以用来检查分类器的性能。
绿色直线表示根据训练集 $X_i$ 构造的决策边界:
\[\hat \beta_0 + \hat \beta_1 x_1 + \hat \beta_2 x_2 = 1/2\]如果新数据落在该直线上方,则将其分类到组 $1$;如果落在该直线下方,则将其分类到组 $2$ (可以发现,分类器也会犯一些错误:直线上方也有一些来自蓝色组的数据)。
3.2 逻辑回归分类器
线性回归分类器的问题:我们对于 $P(G = 1 \mid X = x)$ 的估计量 $\hat \beta_0 + \hat \beta ^{\mathrm T} x$ 无法保证落在 $0$ 到 $1$ 之间,但是这里我们是在估计一个概率。
建议:使用逻辑回归,即假设
\[m_1(x)=P(G=1\mid X=x)=E(Y_1\mid X=x) =\dfrac{\exp(\beta_0 + \beta^{\mathrm T}x)}{1+ \exp(\beta_0 + \beta^{\mathrm T}x)}\]使用根据以下训练数据得到的最大似然估计量 (MLE) $\hat \beta_0, \hat \beta$ 来估计 $\beta_0, \beta$
\[(X_1, Y_{11}),\dots,(X_n, Y_{n1})\](或者,可以根据需要将数据替换为其 PCA 或 PLS 成分,有关如何在分类中计算 CV,请参阅第教材第 35 页)。
注意:此方法依赖于逻辑模型假设,该假设通常只是现实世界的一种近似。
如前所述,$m_2 = 1- m_1$,即在此模型中:
\[\begin{align} m_1(x) &= P(G=1\mid X=x) = \dfrac{\exp(\beta_0 + \beta^{\mathrm T}x)}{1+ \exp(\beta_0 + \beta^{\mathrm T}x)} \\[2ex] m_2(x) &= P(G=2\mid X=x) = 1-m_1(x) = \dfrac{1}{1+ \exp(\beta_0 + \beta^{\mathrm T}x)} \end{align}\]将一个新的 $x$ 分类到组 $1$,如果
\[\hat m_1(x) > \hat m_2(x) \quad \Longleftrightarrow \quad \exp(\hat \beta_0 + \hat \beta^{\mathrm T}x) > 1 \quad \Longleftrightarrow \quad \color{red}{\hat \beta_0 + \hat \beta^{\mathrm T}x > 0}\]否则,将 $x$ 分类到组 $2$。
分类边界可以通过求解以下方程得到
\[\hat m_1(x) - \hat m_2(x) = 0 \quad \Longleftrightarrow \quad \exp(\hat \beta_0 + \hat \beta^{\mathrm T}x) = 1 \quad \Longleftrightarrow \quad \hat \beta_0 + \hat \beta^{\mathrm T}x = 0\]例子:Golub 数据
- 两种类型的患者,对应于两种类型的白血病 (ALL 和 AML)。
- $X =(X_1, X_2)^{\mathrm T}$:两个已知的与白血病类型相关的基因表达。
根据估计的逻辑回归模型,我们可以得到
\[\hat m_1(x)=\dfrac{\exp(0.9432 + 0.5487 x_1− 10.714 x_2)}{1+ \exp(0.9432 + 0.5487 x_1− 10.714 x_2)}\]在此示例中,分类边界可以通过求解下式得到
\[0.9432 + 0.5487 x_1 − 10.714 x_2 = 0\]可以将其用以下直线表示
\[x_2 = \dfrac{0.9432}{10.714} + \dfrac{0.5487}{10.714} x_1 = 0.08803435 + 0.05121337 x_1\]其他例子
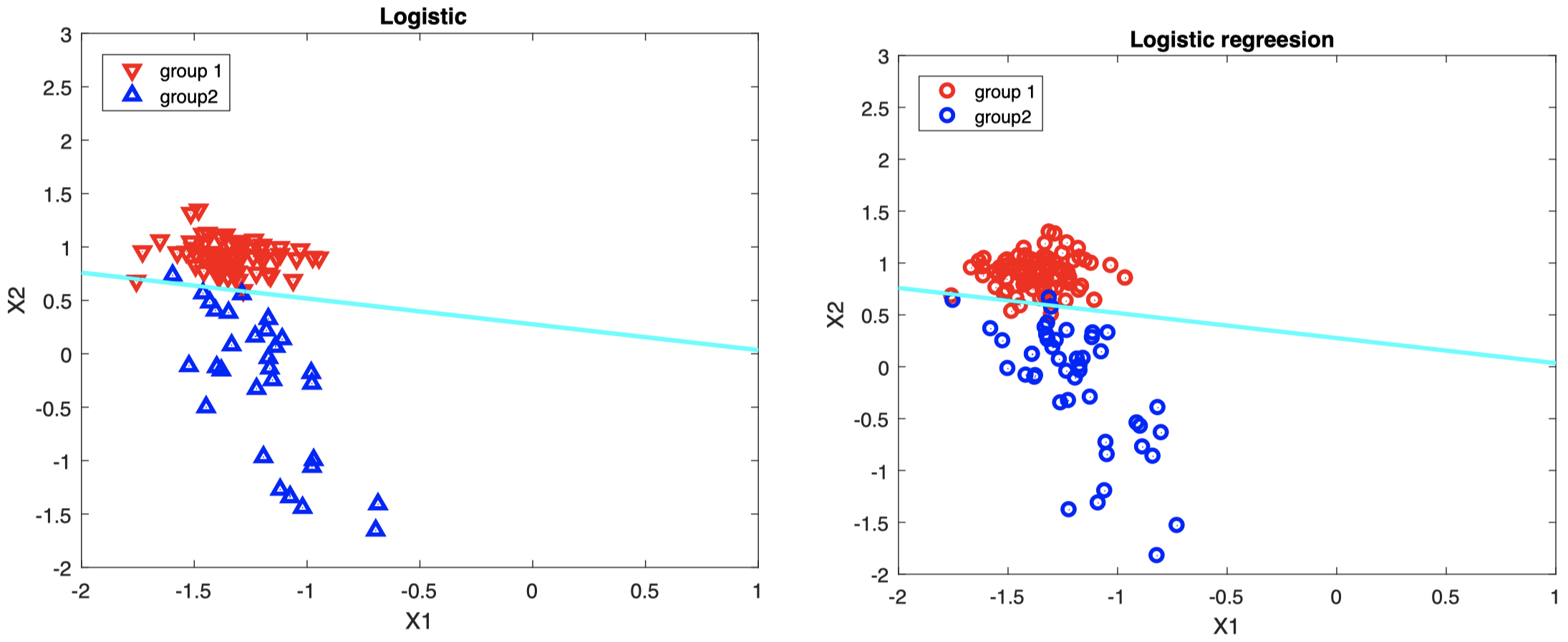
- 左图:训练集中的 $X_i$,不同分组用蓝色/红色表示。
- 右图:需要分类的新数据
这里只是一个例子。与现实生活不同,我们知道新数据的真实组类 (右图中的蓝色/红色):可以用来检查分类器的性能。
青色直线表示根据训练集 $X_i$ 构造的决策边界:
\[\hat \beta_0 + \hat \beta_1 x_1 + \hat \beta_2 x_2 = 0\]如果新数据落在该直线上方,则将其分类到组 $1$;如果落在该直线下方,则将其分类到组 $2$ (可以发现,分类器也会犯一些错误:直线上方也有一些来自蓝色组的数据)。
对比线性回归与逻辑回归
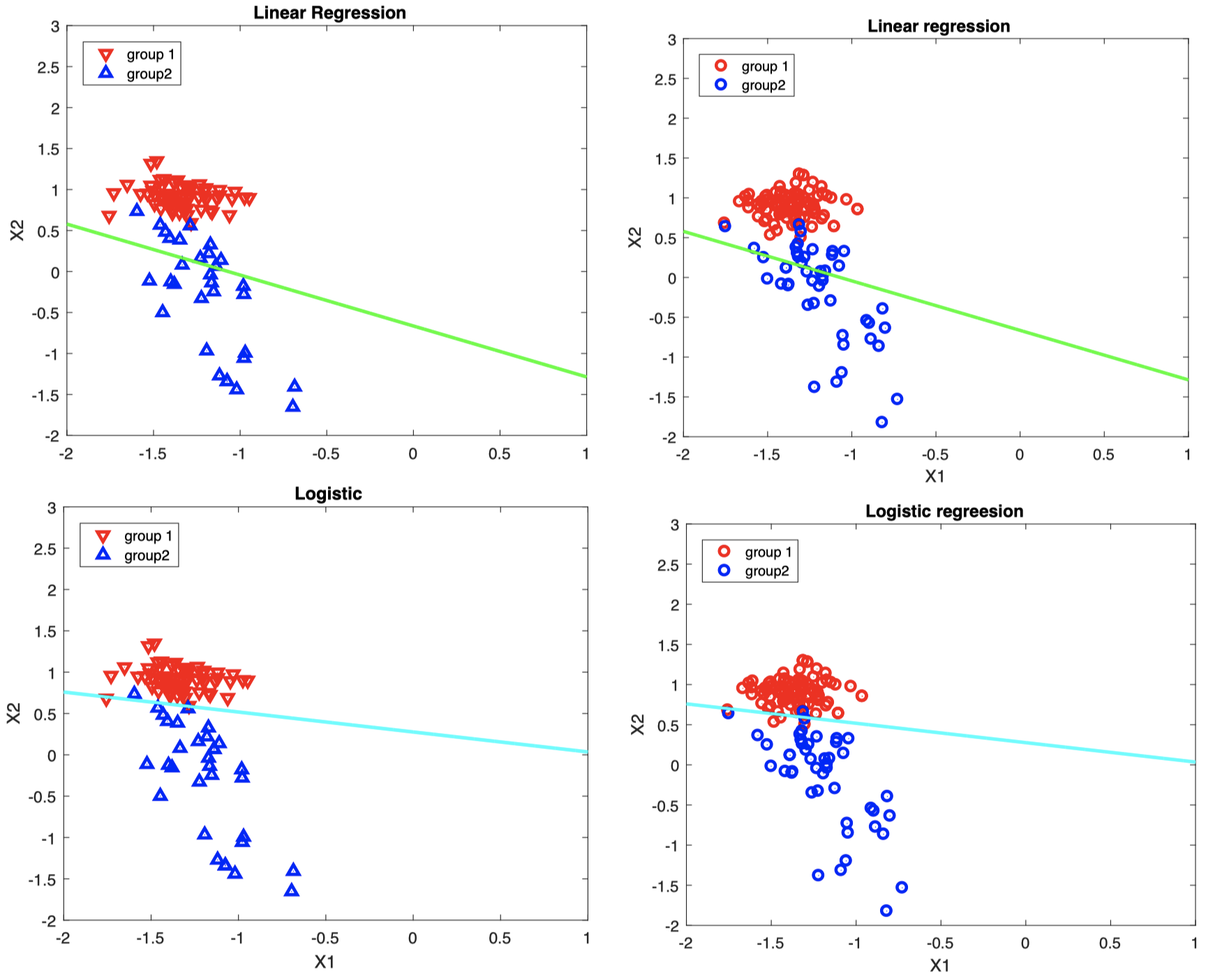
可以看到,逻辑回归的分类效果要优于线性回归。
4. 对于 $K=2$ 类的贝叶斯方法:线性和二次判别
另一种估计 $P(G=k\mid X=x)$ 的方法是利用贝叶斯定理。
利用贝叶斯定理,我们有
\[P(G=k\mid X=x) = \dfrac{P(X=x\mid G=k)\pi_k}{P(X=x)}\]其中,
\[\pi_k=P(G=k)\]需要估计训练数据集中的所有概率 $\pi_k$。
4.1 线性判别 (Linear Discriminant, LD)
对于 LD 方法,我们应用贝叶斯定理的前提是:假设 $P(X=x\mid G=k)$ 是多元正态分布 $N_p(\mu_k,\Sigma)$ 的概率密度函数。
回忆一下,$p$ 维正态分布 $N_p(\mu_k,\Sigma)$ 的概率密度函数被定义为
\[f_k(x)=(2\pi)^{-p/2} \{\mathrm{det}(\Sigma)\}^{-1/2} \exp \{-0.5(x-\mu_k)^{\mathrm T}\Sigma^{-1}(x-\mu_k)\}\]利用前面的贝叶斯定理,可以推得一个新的个体 $X=x$ 更有可能来自组 $1$,而不是组 $2$,当且仅当
\[\begin{align} & P(G=1\mid X=x) > P(G=2\mid X=x) \\[2ex] \Longleftrightarrow \quad & P(X=x\mid G=1)\pi_1 > P(X=x\mid G=2)\pi_2 \\[2ex] \Longleftrightarrow \quad & \exp \{-0.5(x-\mu_1)^{\mathrm T}\Sigma^{-1}(x-\mu_1)\} \pi_1 > \exp \{-0.5(x-\mu_2)^{\mathrm T}\Sigma^{-1}(x-\mu_2)\} \pi_2 \\[2ex] \Longleftrightarrow \quad & 2\log(\pi_1/ \pi_2) + 2x^{\mathrm T} \Sigma^{-1}(\mu_1-\mu_2) - \mu_1^{\mathrm T} \Sigma^{-1}\mu_1 +\mu_2^{\mathrm T} \Sigma^{-1}\mu_2 > 0 \end{align}\]如果上式条件满足,则将 $x$ 分类到组 $1$;否则将其分类到组 $2$。
这里,决策规则
\[2\log(\pi_1/ \pi_2) + 2x^{\mathrm T} \Sigma^{-1}(\mu_1-\mu_2) - \mu_1^{\mathrm T} \Sigma^{-1}\mu_1 +\mu_2^{\mathrm T} \Sigma^{-1}\mu_2 > 0\]是一个关于 $x$ 的线性函数,因此被称为线性判别。
注意:此方法依赖于正态性和方差齐性假设 (两个组的 $\Sigma$ 相同),而这些在实践中通常是无法满足的。因此,它只是提供了一种关于现实世界的近似。
在实践中,我们并不知道 $\pi_k, \mu_k, \Sigma$,但是我们可以利用训练集数据来估计它们:
\[\hat \pi_k = n_k / n\]其中,$n_k$ 为来自组 $k$ 的训练数据的数量。
注意:这里假设训练集数据中每个组的大小都代表了在总体中组的大小,但并非总是如此。如果我们不知道训练集中的组的大小是否具有代表性,那么采用上式计算出的 $\pi_k$ 可能存在错误估计的风险。
相反,在这种情况下,我们通常使用下式来估计 $\pi_k$:
\[\hat \pi_k = 1/K\](在这种情况下,对于 $K=2$,我们有 $\hat \pi_1=\hat \pi_2 = 1/2$)。
为了估计 $\mu_k$ 和 $\Sigma$,我们需要重新标记数据 $X_i$,以区分它们来自哪个组:令 $X_{i,k} \;(i=1,\dots,n_k)$ 表示所有来自组 $k$ 的 $X_i$。然后,我们有
\[\begin{align} \hat \mu_k &= \overline X_k = \dfrac{1}{n_k}\sum_{i=1}^{n_k}X_{i,k} \\[2ex] \hat \Sigma &= \dfrac{1}{n_1+n_2 -2}\sum_{k=1}^{2}\sum_{i=1}^{n_k}(X_{i,k}-\hat \mu_k)(X_{i,k}-\hat \mu_k)^{\mathrm T} \end{align}\]分类/决策边界可以通过求解下式得到:
\[\hat m_1(x) - \hat m_2(x)=0 \quad \Longleftrightarrow \quad 2\log(\hat \pi_1/ \hat \pi_2) + 2x^{\mathrm T} \hat \Sigma^{-1}(\hat \mu_1- \hat \mu_2) - \hat \mu_1^{\mathrm T} \hat \Sigma^{-1}\hat \mu_1 + \hat \mu_2^{\mathrm T}\hat \Sigma^{-1}\hat \mu_2 = 0\]例子:Golub 数据
- 两种类型的患者,对应于两种类型的白血病 (ALL 和 AML)。
- $X =(X_1, X_2)^{\mathrm T}$:两个已知的与白血病类型相关的基因表达。
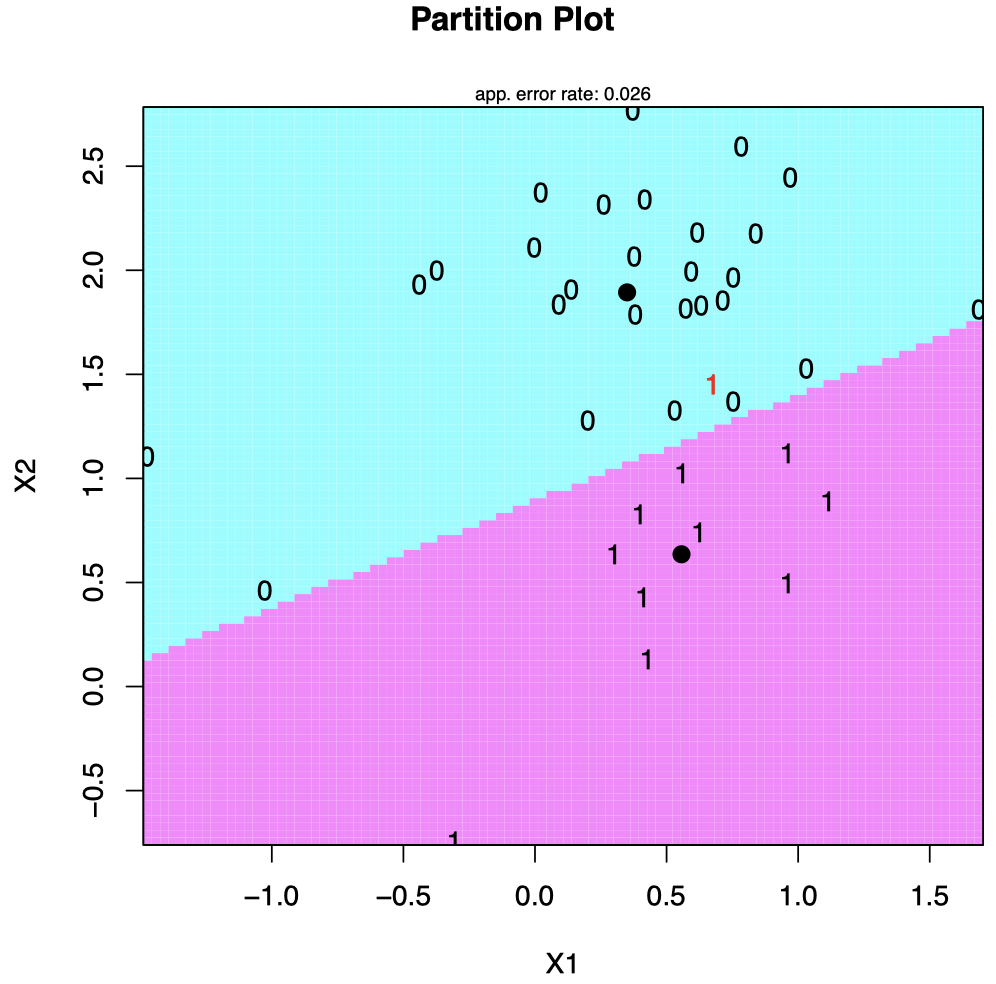
其他例子
- 左图:训练集中的 $X_i$,不同分组用蓝色/红色表示。
- 右图:需要分类的新数据
这里只是一个例子。与现实生活不同,我们知道新数据的真实组类 (右图中的蓝色/红色):可以用来检查分类器的性能。
洋红色直线表示根据训练集 $X_i$ 构造的决策边界:
\[2\log(\hat \pi_1/ \hat \pi_2) + 2x^{\mathrm T} \hat \Sigma^{-1}(\hat \mu_1- \hat \mu_2) - \hat \mu_1^{\mathrm T} \hat \Sigma^{-1}\hat \mu_1 + \hat \mu_2^{\mathrm T}\hat \Sigma^{-1}\hat \mu_2 = 0\]如果新数据落在该直线上方,则将其分类到组 $1$;如果落在该直线下方,则将其分类到组 $2$ (可以发现,分类器也会犯一些错误:直线上方也有一些来自蓝色组的数据)。

三种分类方法对比
如果我们令
\[\begin{align} \hat \beta_0 &= 2\log(\hat \pi_1 /\hat \pi_2) - \hat \mu_1^{\mathrm T} \hat \Sigma^{-1}\hat \mu_1 + \hat \mu_2^{\mathrm T}\hat \Sigma^{-1}\hat \mu_2 \\[2ex] \hat \beta &= 2 \hat \Sigma^{-1}(\hat \mu_1- \hat \mu_2) \end{align}\]那么 LD 可以写为:将 $x$ 分类到组 $1$,当且仅当
\[\hat \beta_0 + x^{\mathrm T}\hat \beta > 0\]对于线性回归,我们有:将 $x$ 分类到组 $1$,当且仅当
\[\hat \beta_0 + x^{\mathrm T}\hat \beta > 1/2\]对于逻辑回归,我们有:将 $x$ 分类到组 $1$,当且仅当
\[\hat \beta_0 + x^{\mathrm T}\hat \beta > 0\]这三种方法似乎看上去都一样,但是它们在构造 $\beta_0$ 和 $\beta$ 的方式上有差别。
在这三种情况下,决策/分类边界可以通过图形方式描述,即两个不同类别之间的一个线性分界:
-
LD:两个类别落在以下直线的两侧
\[\hat \beta_0 + x^{\mathrm T}\hat \beta = 0\] -
线性回归:两个类别落在以下直线的两侧
\[\hat \beta_0 + x^{\mathrm T}\hat \beta = 1/2\] -
逻辑回归:两个类别落在以下直线的两侧
\[\hat \beta_0 + x^{\mathrm T}\hat \beta = 0\]
所有这三种方法所依赖的模型假设都只是对于真实情况的近似。通常来说,逻辑回归要比其他两种方法的分类效果更好。
例子 1:线性可分数据
图中直线代表决策边界:绿色表示线性回归,青色表示逻辑回归,洋红色表示 LD。
- 左图:训练集中的 $X_i$ 与估计的线性决策边界。
- 右图:新数据将根据该线性决策边界进行分类。
右图中,来自不同组的新数据的真实类别分别用红/蓝两种颜色表示;如果数据点落在直线下方,我们将其分类到组 $2$,否则将其分类到组 $1$。

可以看到,逻辑回归 (青色直线) 的分类效果最好。
例子 2:线性不可分数据
图中直线代表决策边界:绿色表示线性回归,青色表示逻辑回归,洋红色表示 LD。
- 左图:训练集中的 $X_i$ 与估计的线性决策边界。
- 右图:新数据将根据该线性决策边界进行分类。
右图中,来自不同组的新数据的真实类别分别用红/蓝两种颜色表示;如果数据点落在直线上方,我们将其分类到组 $1$,否则将其分类到组 $2$。

可以看到,三种方法都无法很好地将两个类别区分开,因此对于某些数据集,线性方法并不总是有效的。
4.2 二次判别 (Quadratic Discriminant, QD)
与 LD 一样,对于 QD 方法,我们假设 $X \mid G =k$ 是一个 $p$ 维正态变量,但区别在于,这里我们假设对于 $k = 1$ 和 $k = 2$,它们的均值 $\mu$ 和协方差 $\Sigma$ 都不相同。而在 LD 中,两组的 $\Sigma$ 是相同的。
因此,在 QD 中,组 $k$ 中的 $X$ 的概率密度函数 $P(X=x \mid G=k)$ 为
\[f_k(x)=(2\pi)^{-p/2} \{\mathrm{det}(\Sigma_k)\}^{-1/2} \exp \{-0.5(x-\mu_k)^{\mathrm T}\Sigma_k^{-1}(x-\mu_k)\}\]这里,$x$ 更有可能来自组 $1$,而不是组 $2$,当且仅当
\[\begin{align} & P(G=1\mid X=x) > P(G=2\mid X=x) \\[2ex] \Longleftrightarrow \quad & P(X=x\mid G=1)\pi_1 > P(X=x\mid G=2)\pi_2 \\[2ex] \Longleftrightarrow \quad & \{\mathrm{det}(\Sigma_1)\}^{-1/2} \exp \{-0.5(x-\mu_1)^{\mathrm T}\Sigma_1^{-1}(x-\mu_1)\} \pi_1 \\ & \qquad > \{\mathrm{det}(\Sigma_2)\}^{-1/2} \exp \{-0.5(x-\mu_2)^{\mathrm T}\Sigma_2^{-1}(x-\mu_2)\} \pi_2 \\[2ex] \Longleftrightarrow \quad & -2\log(\pi_1) + \log \{\mathrm{det}(\Sigma_1)\} + (x-\mu_1)^{\mathrm T}\Sigma_1^{-1}(x-\mu_1) \\ & \qquad < -2\log(\pi_2) + \log \{\mathrm{det}(\Sigma_2)\} + (x-\mu_2)^{\mathrm T}\Sigma_2^{-1}(x-\mu_2) \end{align}\]这里,决策规则
\[\begin{align} \, & -2\log(\pi_1) + \log \{\mathrm{det}(\Sigma_1)\} + (x-\mu_1)^{\mathrm T}\Sigma_1^{-1}(x-\mu_1) \\ \, & \qquad < -2\log(\pi_2) + \log \{\mathrm{det}(\Sigma_2)\} + (x-\mu_2)^{\mathrm T}\Sigma_2^{-1}(x-\mu_2) \end{align}\]是一个关于 $x$ 的二次函数,因此被称为二次判别。
在实践中,我们通过下式估计未知的 $\mu_k$ 和 $\Sigma_k$
\[\begin{align} \hat \mu_k &= \overline X_k = \dfrac{1}{n_k}\sum_{i=1}^{n_k}X_{i,k} \\[2ex] \hat \Sigma_k &= \dfrac{1}{n_k -1}\sum_{i=1}^{n_k}(X_{i,k}-\hat \mu_k)(X_{i,k}-\hat \mu_k)^{\mathrm T} \end{align}\]如果我们知道样本中的组大小反映了总体中的组大小,则可以通过 $\hat \pi_k = n_k / n$ 来估计 $\pi_k$,其中,$n_k$ 为来自组 $k$ 的训练数据的数量。否则,我们将取 $\hat \pi_k = 1/K$。
QD 例子:Golub 数据
- 两种类型的患者,对应于两种类型的白血病 (ALL 和 AML)。
- $X =(X_1, X_2)^{\mathrm T}$:两个已知的与白血病类型相关的基因表达。
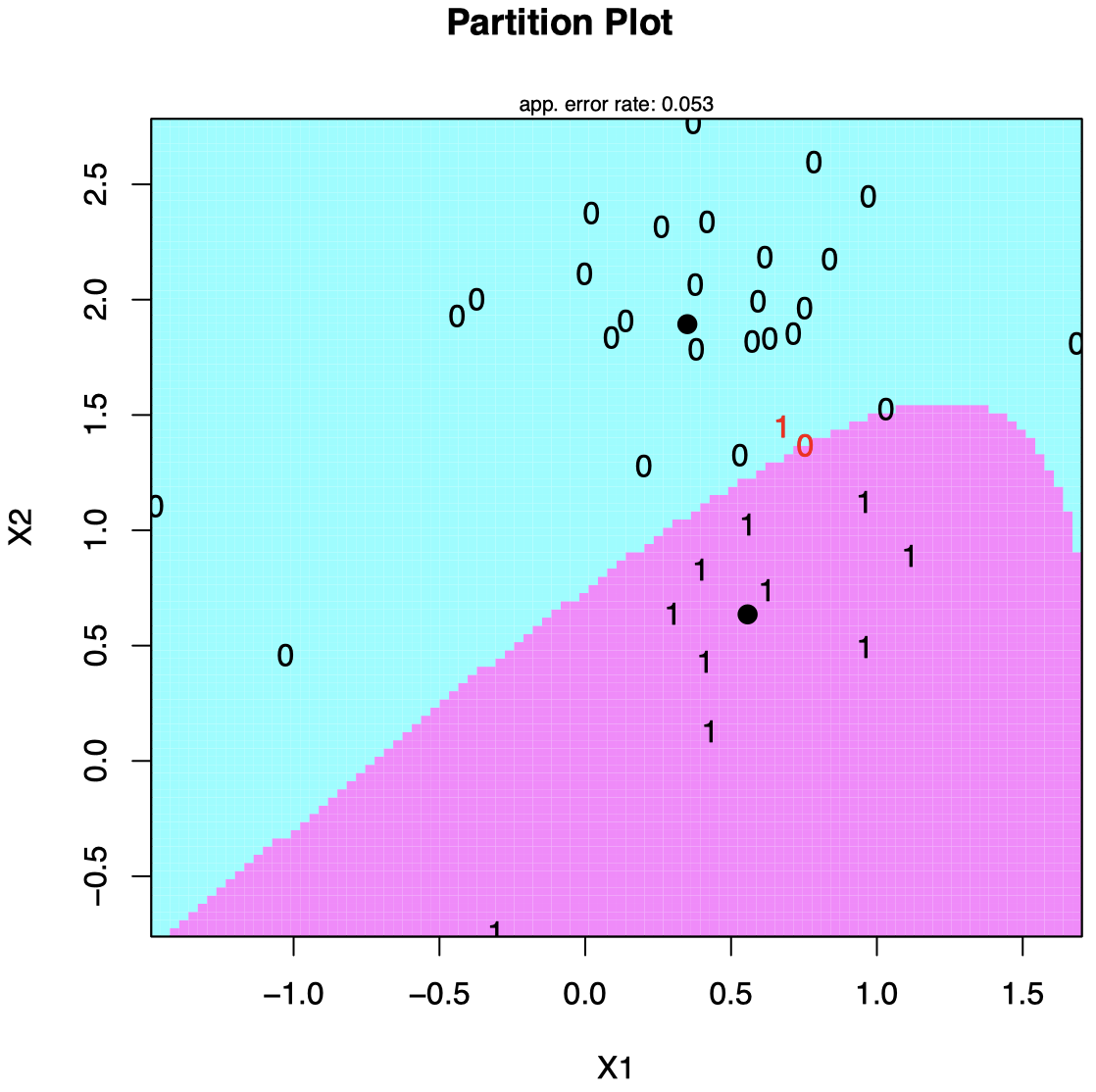
例子 1:线性可分数据
图中洋红色曲线表示根据训练集中的 $X_i$ 构造的二次决策边界。
- 左图:训练集中的 $X_i$ 与估计的二次决策边界。
- 右图:新数据将根据该二次决策边界进行分类。
右图中,来自不同组的新数据的真实类别分别用红/蓝两种颜色表示;如果数据点椭圆边界内,我们将其分类到组 $1$,否则将其分类到组 $2$。
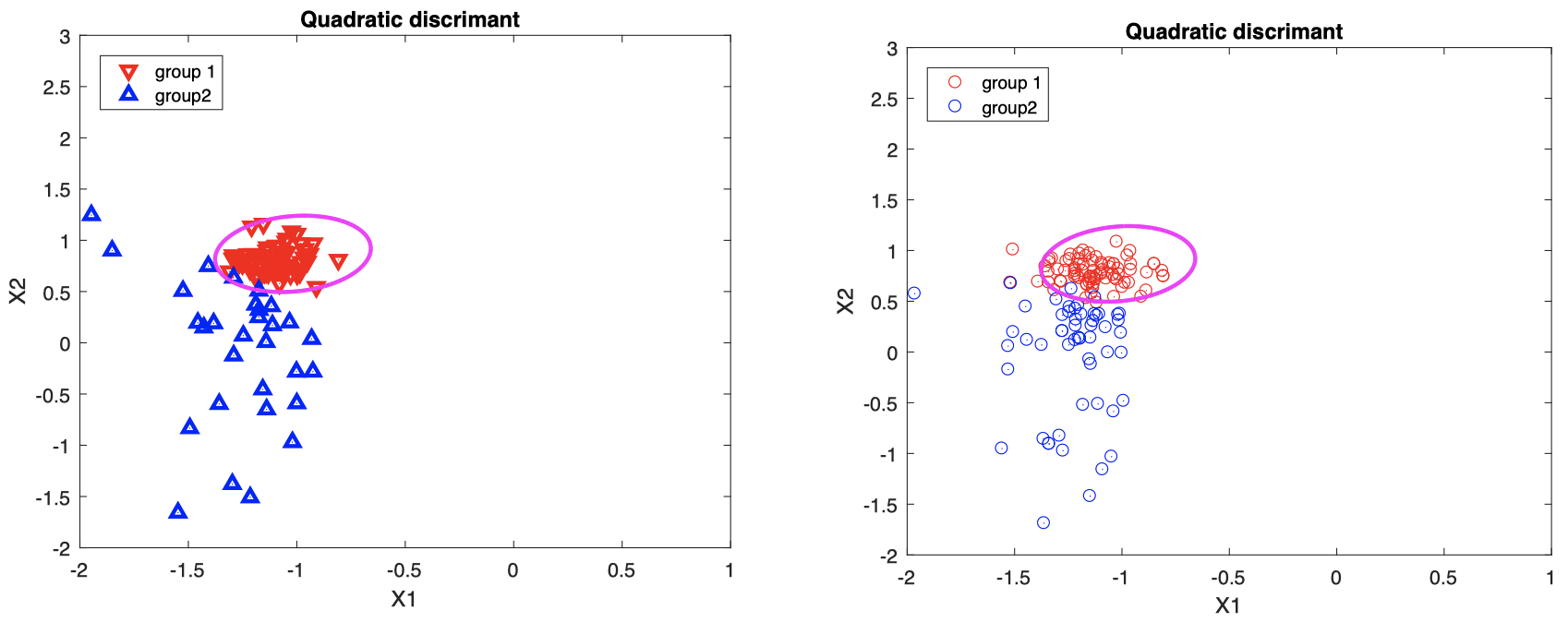
例子 2:线性不可分数据
图中洋红色曲线表示根据训练集中的 $X_i$ 构造的二次决策边界。
- 左图:训练集中的 $X_i$ 与估计的二次决策边界。
- 右图:新数据将根据该二次决策边界进行分类。
右图中,来自不同组的新数据的真实类别分别用红/蓝两种颜色表示;如果数据点椭圆边界内,我们将其分类到组 $1$,否则将其分类到组 $2$。

可以看到,对于线性不可分数据,二次判别的分类效果要优于前面三种线性方法。
4.3 QD vs LD、正则估计器、交叉验证
看起来 QD 方法比 LD 方法要好得多,那么为什么不总是使用它呢?
在 QD 方法中,我们需要估计 $K$ 个协方差矩阵 (这里我们主要研究 $K=2$ 的情况,但是可以推广到 $K > 2$ 的情况)。
如果 $p$ 很大,估计多个协方差矩阵意味着需要估计更多的参数。而当我们需要估计的参数过多时,可能会导致方法的精度降低,并且可能会使得决策 (分类) 结果不可靠。
某些版本的 QD 分析 (称为正则化 QD 分析) 会在 LD 和 QD 之间进行权衡,通过选择 $k$ 组协方差矩阵
\[\tilde \Sigma_k = \alpha \hat \Sigma_k + (1-\alpha) \hat \Sigma\]其中,$\alpha \in [0, 1]$ 可以通过 交叉验证 (cross-validation, CV) 进行选择。
当 $p$ 很大时,即使是 $\Sigma$ 也可能涉及太多参数。这种情况下,一种正则化的版本是在 $\Sigma$ 和一个常数方差 (对于 $X$ 的所有分量都相同) 之间进行权衡
\[\tilde \Sigma = \alpha \hat \Sigma + (1-\alpha) \hat \sigma^2 I_p\]其中,$\alpha \in [0, 1]$ 可以通过 CV 进行选择。
实现正则化的另一种方法是将数据 $X$ 替换为其 PCA 或 PLS 成分,然后通过 CV 选择需要保留的成分数量 $q$。
分类问题中的 CV 是什么?在这种情况下,我们会对 分类误差 进行估计。
什么是分类误差?令 $\hat G$ 为一个分类器,它将值为 $X$ 的个体分配给组 $\hat G$ (一个关于 $X$ 的函数);并且,令 $G$ 为该个体的真实分组。那么,该分类器的错误率为
\[\text{error} = P(\hat G\ne G) = P(\hat G \ne G \mid G=1)\pi_1 + P(\hat G \ne G \mid G=2)\pi_2\]当然,在实践中我们无法这样计算,因为我们并不知道 $G$ (这就是为什么我们要对其进行估计的原因)。
相反,我们使用分类误差的 CV 估计量。令 $G_1,\dots, G_n$ 表示训练集中 $n$ 个个体的真实组类,并假设尽管我们知道他们的真实组,但仍将其应用于分类器,并将它们分别分类为 $\hat G_1,\dots, \hat G_n$。然后,分类误差的 留一法 (leave-one-out) CV 估计量被定义为
\[CV= \dfrac{1}{n}\sum_{i=1}^{n}I(\hat G_i^{(-i)} \ne G_i)\]这里,$\hat G_i^{(-i)}$ 表示在不使用第 $i$ 个个体计算出分类器 $\hat G^{(-i)}$ 的情况下,$G_i$ (训练数据中第 $i$ 个个体的分类器) 的留一法估计量。例如,在 QD 方法中,我们使用除第 $i$ 个观测值外的所有观测值来估计 $\mu_k$ 和 $\Sigma_k$。
我们也可以使用 $B$-折 CV:
- 将数据随机分为大小相等的 $B$ 个块。
- 对于 $b=1,\dots,B$,我们在不使用第 $b$ 个数据块的情况下计算出分类器 $\hat G^{(-b)}$。
- 我们将 $\hat G^{(-b)}$ 应用于第 $b$ 个块中的所有数据:$\hat G^{(-b)}(X_i)$ 表示第 $i$ 个个体 (假定其落在第 $b$ 个块中) 的分类结果,并将其与 $G_i$ 进行比较。
- 对所有块进行求和。
换而言之,我们计算
\[CV=\dfrac{1}{n}\sum_{b=1}^{B}\sum_{i=1}^{n}I(\hat G_i^{(-b)} \ne G_i) \cdot I\{i\text{-th individual is in block } b\}\]这种方法的好处是我们将同样的分类器 $\hat G^{(-b)}$ 重复使用多次。
请注意,无论使用 “留一法” 还是 “$B$-折”,估计的 CV 分类误差都将通过分类器中涉及的调参实现隐式索引。
例如,如果使用教材第 33 页的正则化,则有 $CV = CV(\alpha)$。同样,如果使用 PCA/PLS,则有 $CV = CV(q)$。
我们最终选择的分类器将基于最小化 CV 估计值进行调参,例如:如果对于教材第 33 页的正则化方案,我们有
\[\hat \alpha =\mathop{\operatorname{arg\,min}}\limits_{\alpha \in [0, 1]}CV(\alpha)\]那么,基于该特定值 $\hat \alpha$,最后的 QD 分类器将具有 $\tilde \Sigma_k$。对于 PCA/PLS,我们也会类似地选择 $\hat q$。
5. 对于 $K > 2$ 类的简单回归方法
给定 i.i.d 数据:$(X_1,G_1),\dots,(X_n,G_n)$,其中,$G_i=1,2,\dots,K$ (类别标签)。
重新编码 $G_i$:对于 $k=1,\dots,K$,令
\[Y_{ik}=I\{G_i=k\}=\begin{cases}1 & \text{if } G_i=k \\[2ex] 0 & \text{otherwise}\end{cases}\]例如,如果有 $K=3$ 和 $n=5$,并且我们观测到
\[(G_1,G_2,G_3,G_4,G_5)=(2,3,1,1,2)\]那么,我们可以创建
\[\begin{pmatrix}Y_{11} \\ Y_{21} \\ Y_{31} \\ Y_{41} \\ Y_{51} \end{pmatrix}=\begin{pmatrix}0 \\ 0 \\ 1 \\ 1 \\ 0 \end{pmatrix},\quad \begin{pmatrix}Y_{12} \\ Y_{22} \\ Y_{32} \\ Y_{42} \\ Y_{52} \end{pmatrix}=\begin{pmatrix}1 \\ 0 \\ 0 \\ 0 \\ 1 \end{pmatrix},\quad \begin{pmatrix}Y_{13} \\ Y_{23} \\ Y_{33} \\ Y_{43} \\ Y_{53} \end{pmatrix}=\begin{pmatrix}0 \\ 1 \\ 0 \\ 0 \\ 0 \end{pmatrix}\]定义 $K$ 个回归曲线:对于 $k=1,\dots,K$,
\[m_k(x) = E(Y_k \mid X=x) = P(G=k\mid X=x)\]由于 $x$ 必须来自 $K$ 个分组中的某一个 (且仅一个),我们有
\[\sum_{k=1}^{K}m_k(x)=\sum_{k=1}^{K}P(G=k \mid X=x)=1\]因此,我们有
\[m_K(x) = 1- \sum_{j=1}^{K-1}m_j(x)\]我们只需要通过 $\hat m_1,\dots,\hat m_{K-1}$ 估计 $m_1,\dots,m_{K-1}$,并且取
\[\hat m_K(x)=1- \sum_{j=1}^{K-1}\hat m_j(x)\]将新的 $x$ 分类到具有最大 $\hat m_k(x)$ 的组。
5.1 对于 $K > 2$ 类的线性回归方法
重新编码数据:$(X_1, Y_{11},\dots,Y_{1K}),\dots,(X_n,Y_{n1},\dots,Y_{nK})$
定义 $K$ 个线性回归曲线:对于 $k=1,\dots,K$,
\[m_k(x) = E(Y_k\mid X=x)= \beta_{0k} + \beta_k^{\mathrm T}x = \beta_{0k} + \beta_{1k}x_1 + \cdots + \beta_{pk}x_p\]利用 LS、PLS、PCA 或者其他方法估计 $\beta_{jk}$。例如,对于标准 LS:
\[(\hat \beta_{0k},\hat \beta_{1k},\dots,\hat \beta_{pk})^{\mathrm T} = (\mathcal X^{\mathrm T}\mathcal X)^{-1}\mathcal X^{\mathrm T}Y_k\]其中,
\[\mathcal X=\begin{pmatrix}1 & X_{11} & \cdots & X_{1p} \\ \vdots & \vdots & & \vdots \\ 1 & X_{n1} & \cdots & X_{np}\end{pmatrix},\quad Y_k = \begin{pmatrix}Y_{1k} \\ \vdots \\ Y_{nk}\end{pmatrix}\]对于一个 $X$ 的值为 $x=(x_1,\dots,x_p)^{\mathrm T}$ 的新个体:
-
计算 $\hat m_1(x),\dots,\hat m_K(x)$,其中,对于 $k=1,\dots,K-1$,
\[\hat m_k(x)=\hat \beta_{0k} +\hat \beta_{1k}x_1 + \cdots + \hat \beta_{pk}x_p\]以及
\[\hat m_K(x) = 1- \sum_{j=1}^{K-1}\hat m_j(x)\] -
将该新个体分类到 $\hat m_1(x),\dots,\hat m_K(x)$ 中的最大值 $\hat G$:
\[\hat G = \mathop{\operatorname{arg\,max}}\limits_{k=1,\dots,K} \hat m_k(x)\]
5.2 对于 $K > 2$ 类的逻辑回归方法
在逻辑回归中,基于 $K = 2$ 的情况,似乎可以进一步假设:对于 $k = 1,\dots,K$,
\[m_k(x)=E(Y_k \mid X=x) = P(G=k \mid X=x) = \dfrac{\exp(\beta_{0k} + \beta_k^{\mathrm T}x)}{1 + \exp(\beta_{0k} + \beta_k^{\mathrm T}x)}\]然而,如前所述,我们必须满足 $m_1(x) + \cdots + m_K(x)=1$。
这可以通过使用以下略经修改的模型实现:对于 $k=1,\dots,K-1$,
\[m_k(x) = \dfrac{\exp(\beta_{0k} + \beta_k^{\mathrm T}x)}{1 + \sum_{\ell =1}^{K-1} \exp(\beta_{0\ell} + \beta_{\ell}^{\mathrm T}x)}\]然后,我们取
\[m_K(x) = 1- \sum_{k=1}^{K-1}m_k(x) = 1 - \dfrac{\sum_{k=1}^{K-1} \exp(\beta_{0k} + \beta_k^{\mathrm T}x)}{1 + \sum_{\ell =1}^{K-1} \exp(\beta_{0\ell} + \beta_{\ell}^{\mathrm T}x)} = \dfrac{1}{1 + \sum_{\ell =1}^{K-1} \exp(\beta_{0\ell} + \beta_{\ell}^{\mathrm T}x)}\]对于 $k=1, \dots, K-1$,使用最大似然估计量 $\hat \beta_{0k}$ 和 $\hat \beta_k$ 来估计 $\beta_{0k}$ 和 $\beta_k$ (同样,可以使用 PLS 成分代替),并推断出 $m_k$ 的估计量 $\hat m_k$。然后通过下式估计 $m_K(x)$
\[\hat m_K(x) = 1- \sum_{k=1}^{K-1}\hat m_k(x)\]将新个体分类到 $\hat m_1(x),\dots,\hat m_K(x)$ 中的最大值 $\hat G$:
\[\hat G = \mathop{\operatorname{arg\,max}}\limits_{k=1,\dots,K} \hat m_k(x)\]但是,实际上我们并不需要计算 $\hat m_k$,因此也不需要计算指数。其实,要找到最大值,我们可以在不同组之间进行两两比较。
我们可以计算
\[\begin{align} \log \dfrac{P(G=1\mid X=x)}{P(G=K \mid X=x)} &= \log \dfrac{m_1(x)}{m_K(x)} = \beta_{01} + \beta_1^{\mathrm T}x \\[2ex] \log \dfrac{P(G=2\mid X=x)}{P(G=K \mid X=x)} &= \log \dfrac{m_2(x)}{m_K(x)} = \beta_{02} + \beta_2^{\mathrm T}x \\[2ex] \vdots \\[2ex] \log \dfrac{P(G=K-1\mid X=x)}{P(G=K \mid X=x)} &= \log \dfrac{m_{K-1}(x)}{m_K(x)} = \beta_{0,K-1} + \beta_{K-1}^{\mathrm T}x \end{align}\]例如,假设 $K > 5$ 并且 $P(G=5 \mid X=x)$ 是最大值。然后我们将有
\[m_5(x) > m_K(x) \quad \Longleftrightarrow \quad \log \dfrac{m_5(x)}{m_K(x)} > 0\]并且,对于所有 $k\ne 5$,
\[m_k(x) < m_5(x) \quad \Longleftrightarrow \quad \dfrac{m_k(x)}{m_K(x)} < \dfrac{m_5(x)}{m_K(x)} \quad \Longleftrightarrow \quad \log \dfrac{m_k(x)}{m_K(x)} < \log \dfrac{m_5(x)}{m_K(x)}\]因此,我们可以仅根据这些对数比做出决策。
对于 $K = 2$ 的情况,这是一种线性方法。
5.3 对于 $K > 2$ 类的 LD 和 QD 方法
利用相同的思想,LD 和 QD 方法可以推广到 $K> 2$ 类的情况。
令 $\pi_1 = P(G=1),\dots,\pi_K = P(G=K)$。
-
LD:将一个新观测 $x$ 分类到能够最大化下式的组 $k$ 中
\[\delta_k(x) = x^{\mathrm T}\hat \Sigma^{-1} \hat \mu_k - \dfrac{1}{2}\hat \mu_k^{\mathrm T} \hat \Sigma^{-1} \hat \mu_k + \log \hat \pi_k\] -
QD:将一个新观测 $x$ 分类到能够最大化下式的组 $k$ 中
\[\delta_k(x) = \log(\hat \pi_k) - \dfrac{1}{2}\log\{\mathrm{det}(\hat \Sigma_k)\} - \dfrac{1}{2}(x-\hat \mu_k)^{\mathrm T} \hat \Sigma_k^{-1}(x-\hat \mu_k)\]
与在 $K = 2$ 组的情况下一样,为简单起见,我们重新标记数据 $X_i$,以区分它们来自哪个组:$X_{i,k}\;(i=1,\dots,n_k)$ 表示来自组 $k$ 的所有 $X_i$。
$\hat \pi_k = n_k/ n$ 是整个训练数据集中来自组 $k$ 的数据所占比例,
\[\begin{align} \hat \mu_k &= \overline X_k = \dfrac{1}{n_k} \sum_{i=1}^{n_k} X_{i,k} \\[2ex] \hat \Sigma_k &= \dfrac{1}{n_k-1} \sum_{i=1}^{n_k} (X_{i,k} - \hat \mu_k)(X_{i,k} - \hat \mu_k)^{\mathrm T} \\[2ex] \hat \Sigma &= \dfrac{1}{n_1 + \cdots + n_K - K} \sum_{k=1}^{K} \sum_{i=1}^{n_k} (X_{i,k} - \hat \mu_k)(X_{i,k} - \hat \mu_k)^{\mathrm T} \end{align}\]下节内容:分类和回归树 (CART)
本作品采用知识共享署名-非商业性使用-相同方式共享 4.0 国际许可协议进行许可。 欢迎转载,并请注明来自:YEY 的博客 同时保持文章内容的完整和以上声明信息!