Lecture 09 分类和回归树 (CART)

参考教材：

• Hardle, W. and Simar, L (2015). Applied multivariate statistical analysis, 4th edition.
• Hastie, T. Tibshirani, R. and Friedman, J. (2009). The elements of statistical learning, 2nd edition

1. 引言

前一章中的方法依赖于很强的 参数假设 (parametric assumptions) (线性模型、逻辑模型或正态性假设)。

当这些假设基本正确时，这些分类器可以很好地工作；但是当这些假设与真实情况相差很远时，这些分类器的性能可能会非常差。

回忆一下之前的例子：当分隔边界看上去并非线性时，线性分类器将无法很好地工作。

因此，我们需要一些对于强参数假设涉及较少的灵活模型。

这里，我们将介绍由 Leo Breiman 在 1980 年代普及的概念：回归树 (regression trees)。

2. 回归树

假设我们观察到一个 i.i.d. 样本 $(X_1,Y_1),\dots,(X_n,Y_n)$ 来自以下基础均值模型

\[E(Y_i \mid X_i=x) = m(x)\]

其中，$Y_i\in \mathbb R$ 和 $X_i=(X_{i1},\dots,X_{ip})^{\mathrm T} \in \mathbb R^p$ 是连续的。

在本节内容中，这种表示法可能会引起混淆。因此，我们将样本表示为

\[(\mathcal X_1,\mathcal Y_1),\dots,(\mathcal X_n,\mathcal Y_n)\]

其中，$\mathcal Y_i \in \mathbb R, \; \mathcal X_i=(\mathcal X_{i1},\dots,\mathcal X_{ip})^{\mathrm T}$。

当我们不想强调数据的样本依赖性时，我们使用符号 $(X,Y)$，其中，$(X,Y)$ 与 $(\mathcal X_i,\mathcal Y_i)$ 具有相同的分布。特别地，它也来自模型

\[E(Y\mid X=x) = m(x)\]

其中，$Y\in \mathbb R$ 和 $X=(X_1,\dots,X_p)^{\mathrm T} \in \mathbb R^p$ 是连续的。

因此，我们保留了符号 $\{X_1,\dots,X_p\}$ 以表示一般向量 $X$ 的 坐标 (coordinates)。

通常，均值函数 $m(\cdot)$ 在 特征空间 (feature space) (即 $X$ 的域，或者 $X$ 的所有可能值的 $\mathbb R^p$ 的子集) 上看上去可能非常不平滑。

但是，如果 $x_1$ 和 $x_2$ 是特征空间中两个距离很近的点，则很可能有 $m(x_1)\approx m(x_2)$。

回归树的主要思想：将特征空间 划分 (partition) 为不相交的区域 $R_1,R_2,\dots$，在每个区域 $R_i$ 上，我们用一个常数来近似 $m(x)$。

为了解决这个问题：考虑 $p=2$ 的情况。这里我们需要估计回归曲线

\[m(x) = E(Y \mid X = x)\]

其中，$Y\in \mathbb R$ 和 $X=(X_1,X_2)^{\mathrm T} \in \mathbb R^2$ 是连续的。

例如，我们构造了一系列关于类型的分区：

1. 首先，选择变量 $X_1$ 和一个实数 $t_1$。 然后，将特征空间中满足 $X_1 \le t_1$ 的所有点视为一个区域，将满足 $X_1 > t_1$ 的所有点视为另一个区域。这种二元拆分方法将产生两个区域，分别由 $\{X_1 \le t_1\}$ 和 $\{X_1 > t_1\}$ 描述。这里，我们将 $X_1$ 和 $t_1$ 分别称为该步的 分裂变量 (splitting variable) 和 分裂点 (split point)。

2. 接下来，在区域 $\{X_1 \le t_1\}$ 中，我们可以选择分裂变量 $X_2$ 和分裂点 $t_2$，并将 $\{X_1 \le t_1\}$ 进一步划分为两个子区域，分别由 $\{X_2 \le t_2\}$ 和 $\{X_2 > t_2\}$ 描述。

3. 对于第 1 步中的另一个区域 $\{X_1 > t_1\}$，我们可以再次选择 $X_1$ 作为分裂变量，以及一个分裂点 $t_3$，并类似地将该区域进一步划分为 $\{X_1 \le t_3\}$ 和 $\{X_1 > t_3\}$ 两个子区域。

4. 继续相同的过程……

(这里，我们没有讨论如何在每一步中选择分裂变量和分裂点……)

重复这种二元分区步骤几次后，我们会将特征空间划分为一些不相交的矩形区域，记为 $R_1,\dots,R_L$。

我们可以利用 $\{X_j \le t\}$ 和 $\{X_j > t\}$ 这种二元分区序列构造一棵树。经过多次划分后，停止分裂过程，并得到区域 $R_1,\dots,R_L$。这些划分和区域对应树中的分支和结点。$R_i$ 被称为终端结点/叶子。

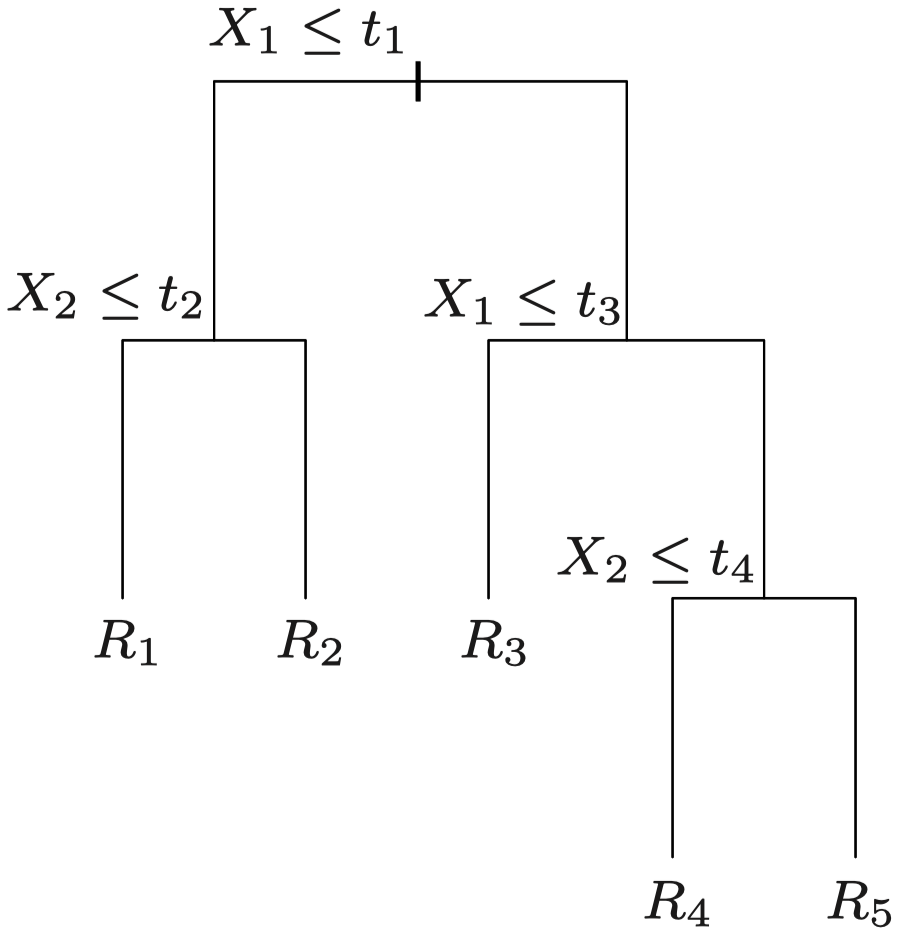
特征空间被划分为一系列矩形区域 $R_1,R_2,\dots$：

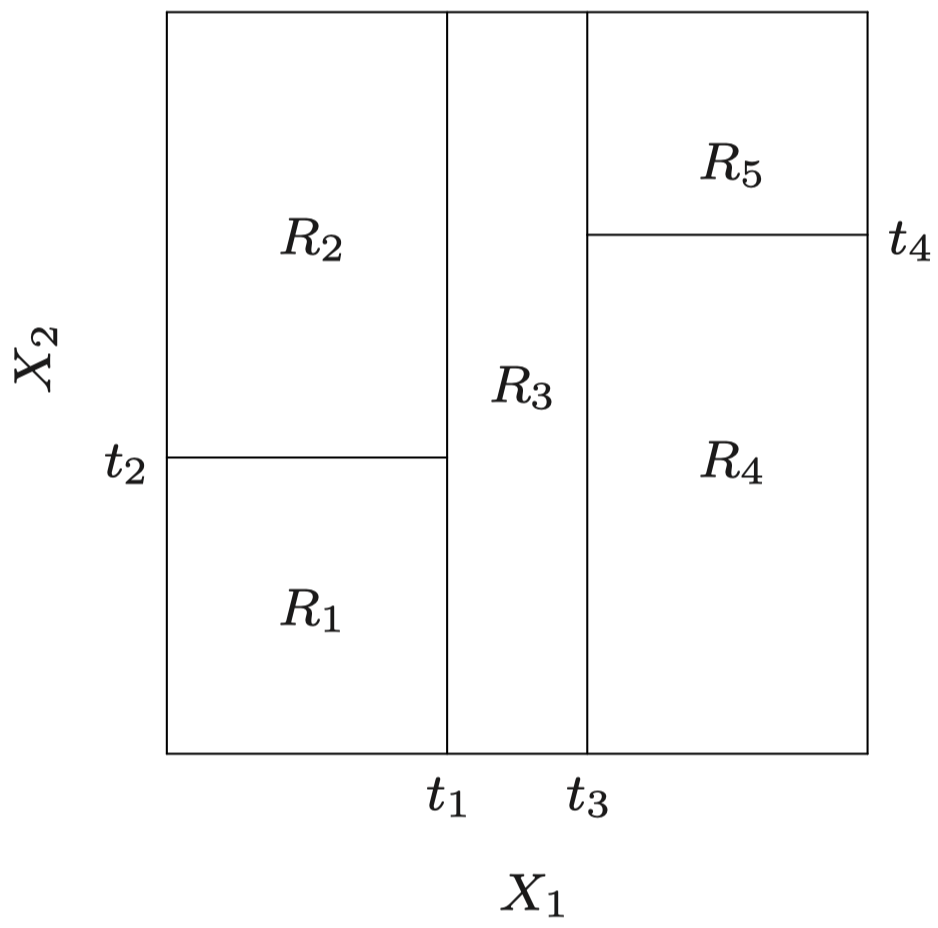
• 过程结束时得到的区域 $R_1,\dots,R_L$ 被称为树的 终端结点(terminal nodes) 或 叶子(leaves)。
• 树内部的 $\{X_1 \le 1\}$ 之类的划分被称为 内部结点 (internal nodes)。
• 连接结点的树的各段被称为树的 分支 (branches)。

一旦我们将空间划分为区域 $R_1,\dots,R_L$，在每个区域上，我们将用一个常数来近似回归曲线 $m$：

对于特征空间中的所有 $x$，

\[m(x)\approx \sum_{\ell=1}^{L}c_{\ell}I\{x \in R_{\ell}\}=\begin{cases}c_{\ell} & \text{if }x\in R_{\ell} \\[2ex] 0 & \text{otherwise}\end{cases}\]

区域 $R_1,R_2,\dots$ 上的分段常数近似如下：

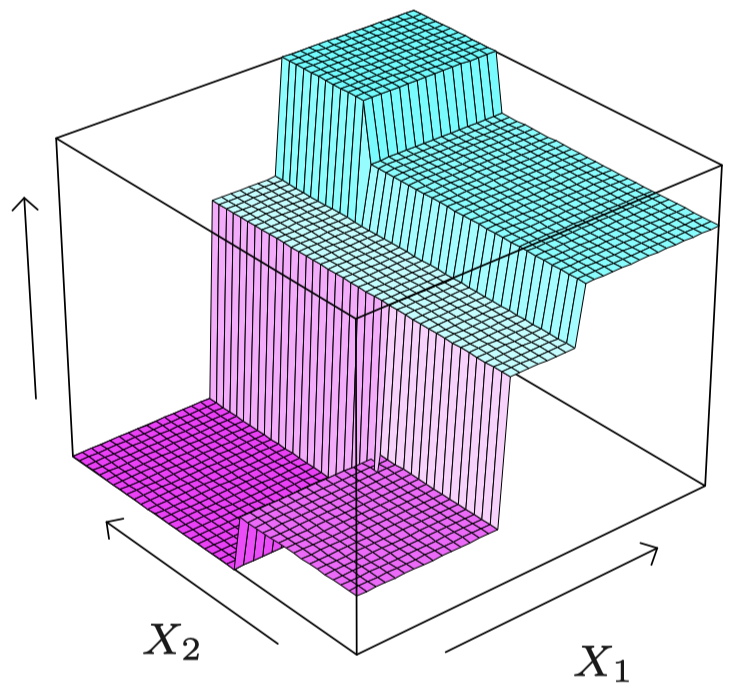
为什么这种方法很灵活？因为只要将特征空间划分为足够小的块，我们总是可以通过每个块上的常数来很好地近似回归曲线。

下面是 $p = 1$ 情况下的一个示例：这里，对特征空间进行分区意味着将 $X$ 的取值范围划分为不同的子区间。

• 在没有划分特征空间的情况下，我们无法用一个常数很好地近似 $m$ (暂时忽略 * 表示的数据点。想象一下，红线绘制为函数值 $m(x)$ 在整个区间上的平均值。这可以通过一个积分操作来完成）：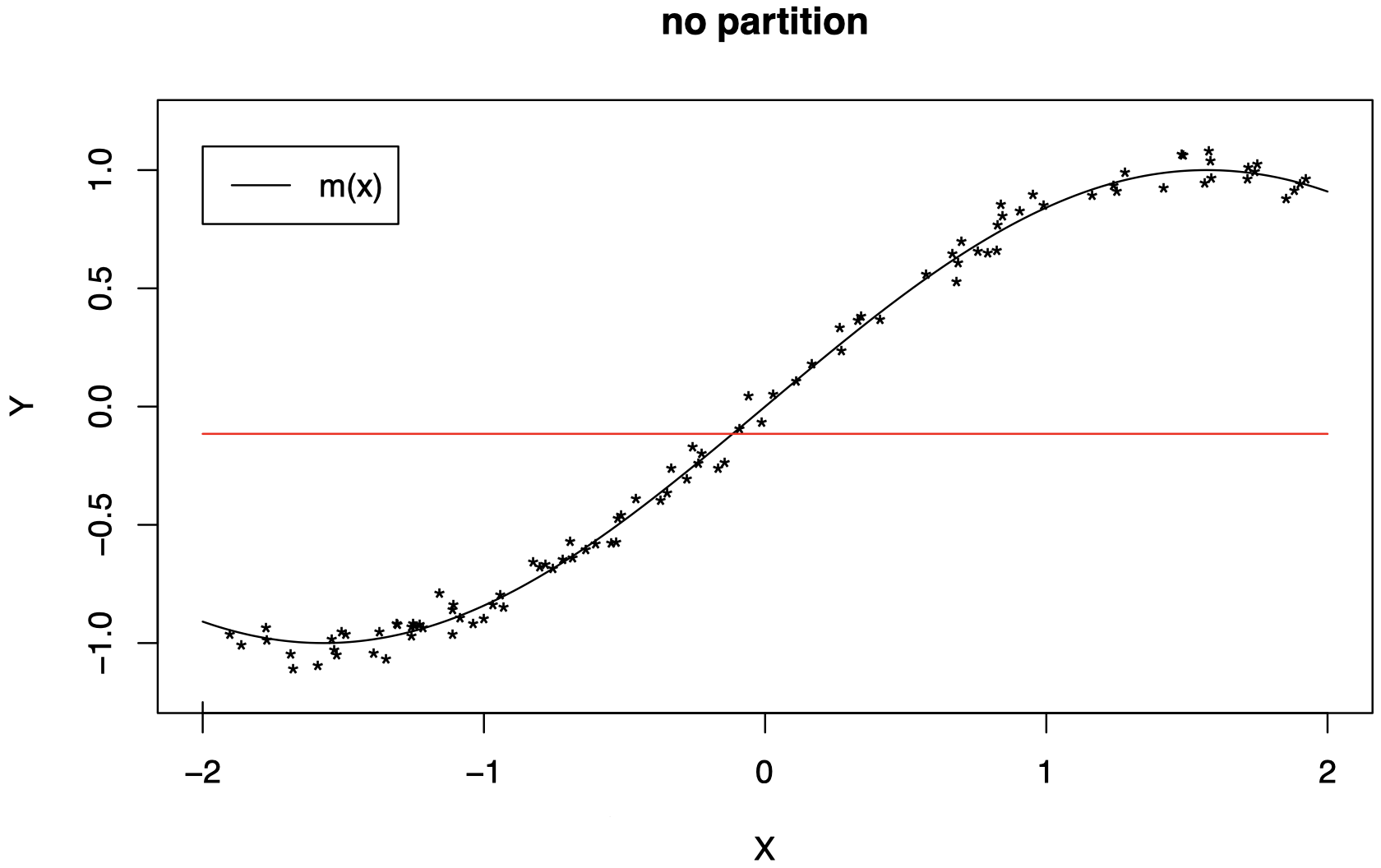

  

• 当我们划分为较小的区间时，效果明显更好了。(将每条红线的水平想象为 $m(x)$ 在红线所跨的区间上的平均值)：

  

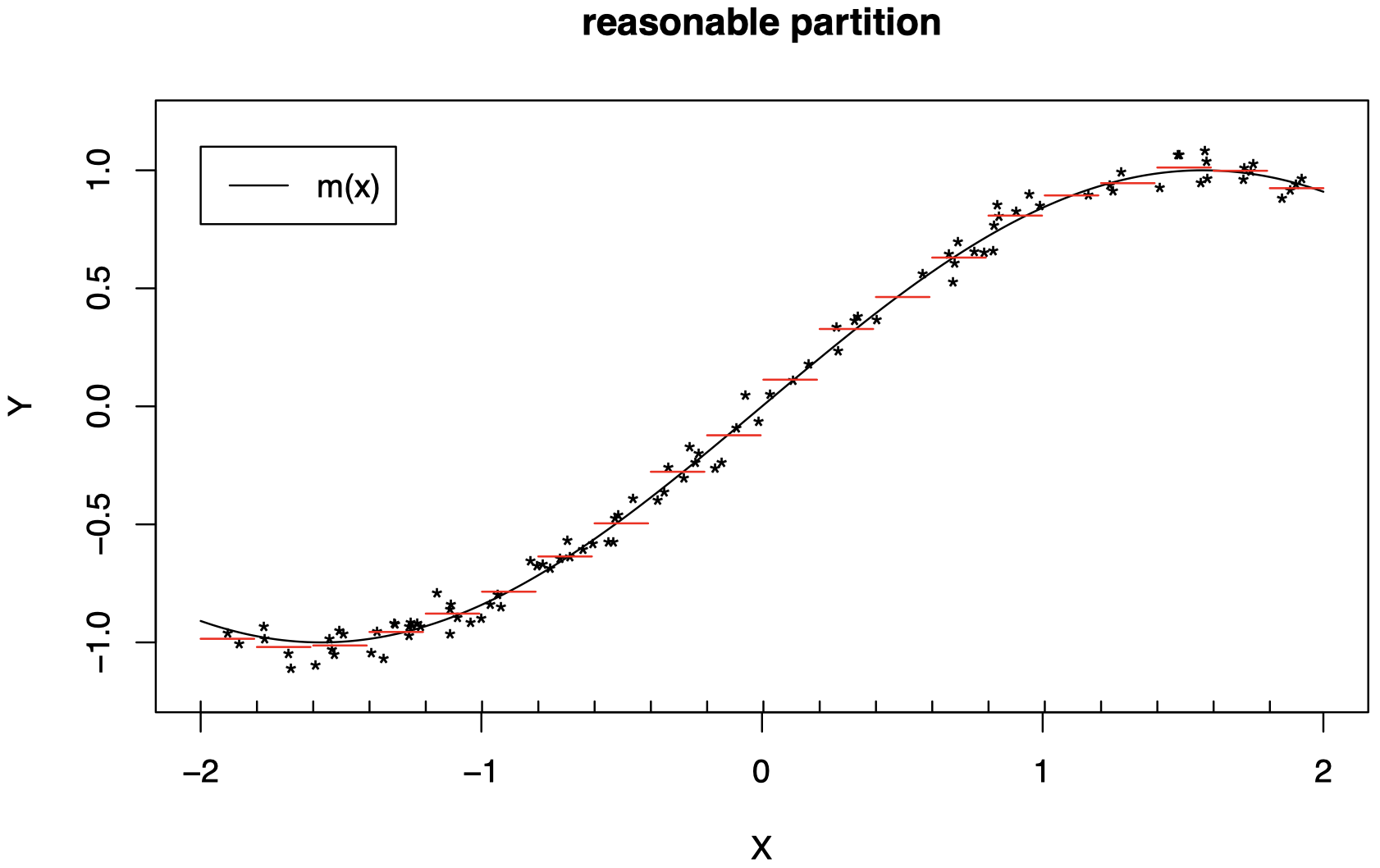
对特征空间的划分越细，常数 $c_1,c_2,c_3,\dots$ 在区域 $R_1,R_2,R_3,\dots$ 上对 $m$ 的近似就越好。

然而，这些只是理论上的：在实践中，我们仅观察到一组样本，因此，如果划分过于精细，将无法找到正确的常数。

那么，我们应该怎样从真实数据中选择常数 $c_1,c_2,\dots$ 呢？或者更一般地，当 $X$ 是一个 $p$ 维向量时，怎样拟合一棵回归树？

假设对于不同的 $j\in \{1,\dots,p\}$ 和 $t$ 值，我们使用一系列形式为 $\{X_j \le t\}$ 和 $\{X_j > t\}$ 的二元划分将特征空间划分为不相交的区域 $R_1,\dots,R_L$。

然后，对于 $\ell \in \{1,\dots,L\}$ 和 $x\in R_{\ell}$，我们通过下式来近似 $m(x)$

\[\hat m(x)=\hat c_{\ell}= \text{average}(\mathcal Y_i) \quad \text{s.t.} \quad \mathcal X_i \in R_{\ell}\]

因此，在每个区域 $R_{\ell}$ 上，我们取 $\mathcal X_i\in R_{\ell}$ 对应的 $\mathcal Y_i$ 的平均值。这与选择使下面的 RSS 最小化的 $c_1,\dots,c_L$ 是相同的

\[\sum_{i=1}^{n}\left[\mathcal Y_i - \sum_{\ell=1}^{L}c_{\ell}I\{\mathcal X_i \in R_{\ell}\}\right]^2 = \sum_{\ell=1}^{L}\sum_{\mathcal X_i \in R_{\ell}}(\mathcal Y_i - c_{\ell})^2\]

但是，我们如何确定树的骨架？换而言之，我们如何选择连续的划分？

回忆 $X=(X_1,\dots,X_p)^{\mathrm T}$，并且一个划分是基于 $X$ 的一个分量 $X_j$。

理想情况下，我们希望找到能够最小化 RSS 的树，但是这在 计算上不可行。

为什么？因为这将涉及比较 所有可能的划分序列 $\{X_j \le t\}$ 和 $\{X_j > t\}$，对于所有的 $j=1,\dots,p$ 和 $X_j$ 所能取得的所有 $t$ 值。

实际上，对于 $X_j$ 的划分，我们只需要考虑 $t$ 在 $\mathcal X_{1j},\dots,\mathcal X_{nj}$ 上的值。为什么？因为一个划分会将观测数据分为两部分。仅当 $t$ 等于观测数据之一时，这些分区才会发生改变。

但是考虑所有分区仍然非常耗时。

因此，我们选择 逐渐生成一棵树，并在每一步中构造使 RSS 最小化的划分：

1. 从全部数据开始，并考虑第一次划分的所有可能方式，即考虑将数据分为两个区域的所有划分

   \[R_1(j,t)=\{\mathcal X_i \quad \text{s.t.} \quad \mathcal X_{ij}\le t\},\quad R_2(j,t)=\{\mathcal X_i \quad \text{s.t.} \quad \mathcal X_{ij} > t\}\]

   对于所有的 $j=1,\dots,p$ 和 $\mathcal X_{ij}$ 所能取得的所有 $t$ 值。

   如前所述，我们只需要考虑 $t\in \{\mathcal X_{1j},\dots,\mathcal X_{nj}\}$。

2. 在所有 $j$ 和 $t$ 上，选择能够最小化 RSS 的 分裂变量 $j$ 和 分裂点 $t$：

   \[\min_{c_1} \sum_{\mathcal X_i\in R_1(j,t)} (\mathcal Y_i-c_1)^2 + \min_{c_2} \sum_{\mathcal X_i\in R_2(j,t)} (\mathcal Y_i-c_2)^2\]

   如前所述，这等价于在所有 $j$ 和 $t$ 上，最小化

   \[\sum_{\mathcal X_i\in R_1(j,t)} (\mathcal Y_i- \hat c_1)^2 + \sum_{\mathcal X_i\in R_2(j,t)} (\mathcal Y_i- \hat c_2)^2\]

   其中，

   \[\hat c_{\ell} = \text{average}(\mathcal Y_i) \quad \text{s.t.}\quad \mathcal X_i \in R_{\ell}(j,t)\]

3. 一旦找到了上面定义的最佳 $j$ 和 $t$，我们就确定了第一个划分。它创建了 $R_1(j,t)$ 和 $R_2(j,t)$ 两个数据区域。

4. 然后，在这两个区域中的每一个上，我们 重复相同的过程：

   • 考虑在所有 $j$ 和 $t$ 上，$R_1$ 的所有可能划分，并找到能够最小化 RSS 的 $j$ 和 $t$。
   • 然后考虑在所有 $j$ 和 $t$ 上，$R_2$ 的所有可能划分，并找到能够最小化 RSS 的 $j$ 和 $t$。
   • 这样，我们总共确定了 4 个区域 (之前的每个区域都已被划分为两部分)。

   同样，在这里，当根据 $X_j$ 将 $R_{\ell}$ 划分为两部分时，我们只需要考虑 $t$ 在 $\mathcal X_{ij}$ 上的值，其中 $\mathcal X_i\in R_{\ell}$。

5. 注意：每个 $R_{\ell}$ 都有自己的分裂变量 $X_j$ 和分裂点 $t$。

6. 我们在前一步中创建的 每个新区域上 继续重复这种划分过程，直到我们决定让树停止生长。

这是 “贪心算法” 的一个示例：我们在每个阶段做出局部最优决策。

我们什么时候应该停止这种划分过程？ 或者说，我们应该让树生长到多大？

• 我们不能任意决定。
• 例如，树的大小应取决于样本大小 $n$。
• 小样本：对特征空间进行粗略划分 (较小的 $L$)。
• 随着样本数量的增加：对特征空间进行更精细的划分 (较大的 $L$)。

当 $p=1$ 时的示例：

• 使用过于粗略的分区 ($L$ 太小) 将无法很好地工作：我们没有捕获到曲线 $m$ 的重要结构 (此处我们将红线水平视为在相应区间内计算得到的数据的平均值)。

  

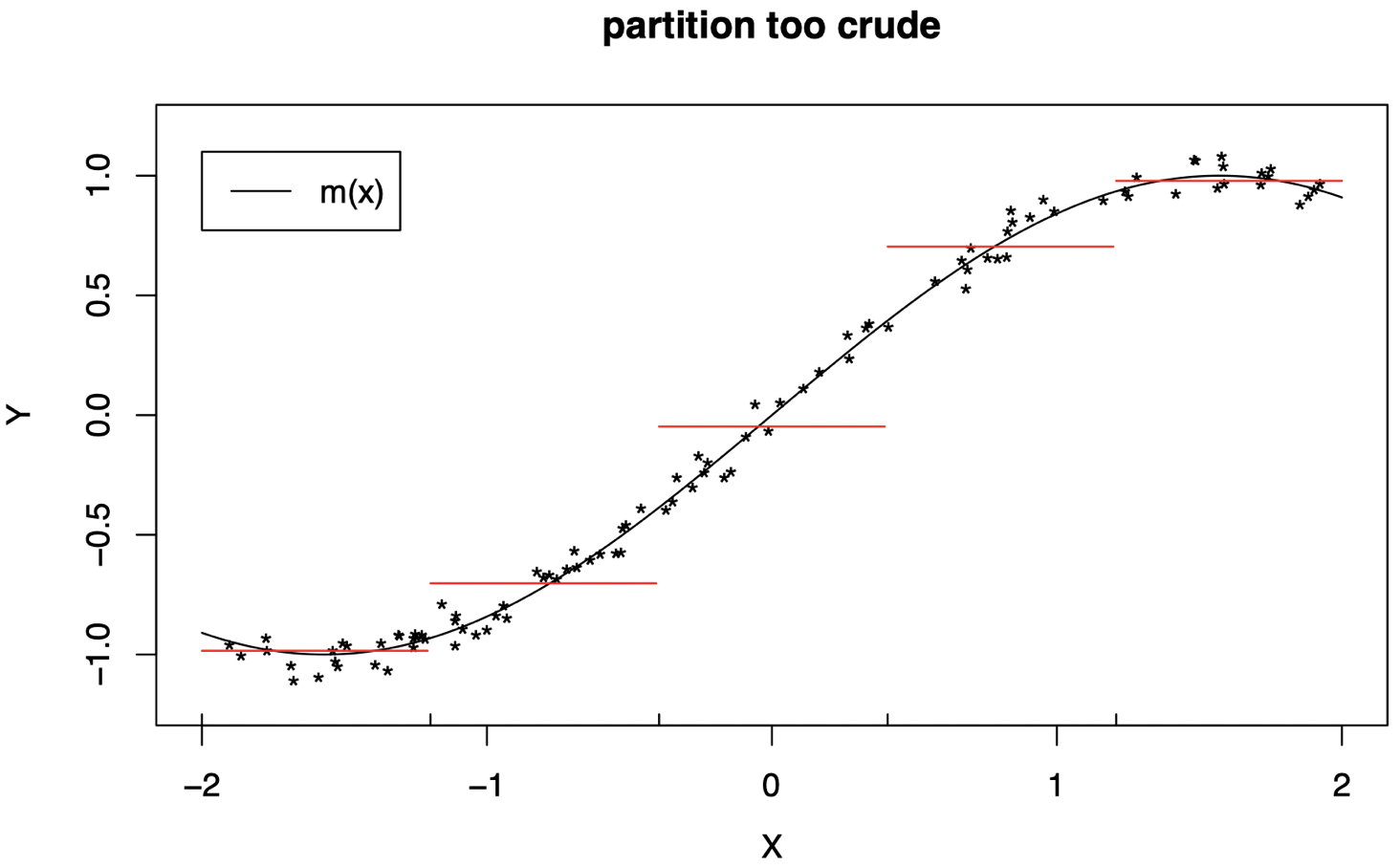
• 使用过于精细的分区 ($L$ 太大) 同样无法很好地工作：我们对数据进行了过拟合，并且某些区间中没有数据，因此无法计算一个常数来拟合这些区间 (回忆一下，$\hat c_{\ell}$ 是每个区域中的 $\mathcal Y_i$ 的平均值。同样地，我们将红线水平视为根据该区间内的数据计算得到的平均值)。

  

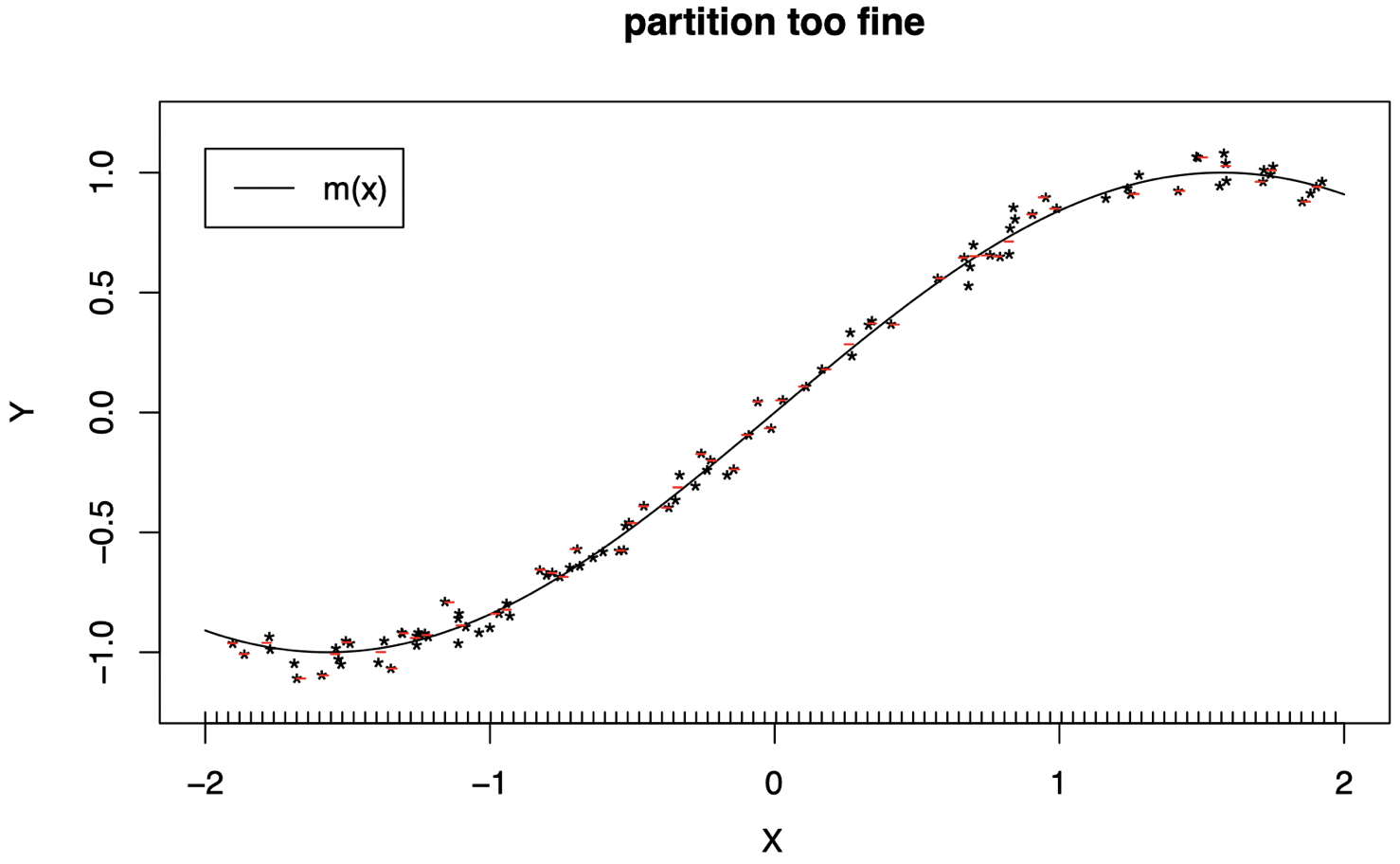
• 我们需要选择正确的分区级别，才能很好地工作。

  

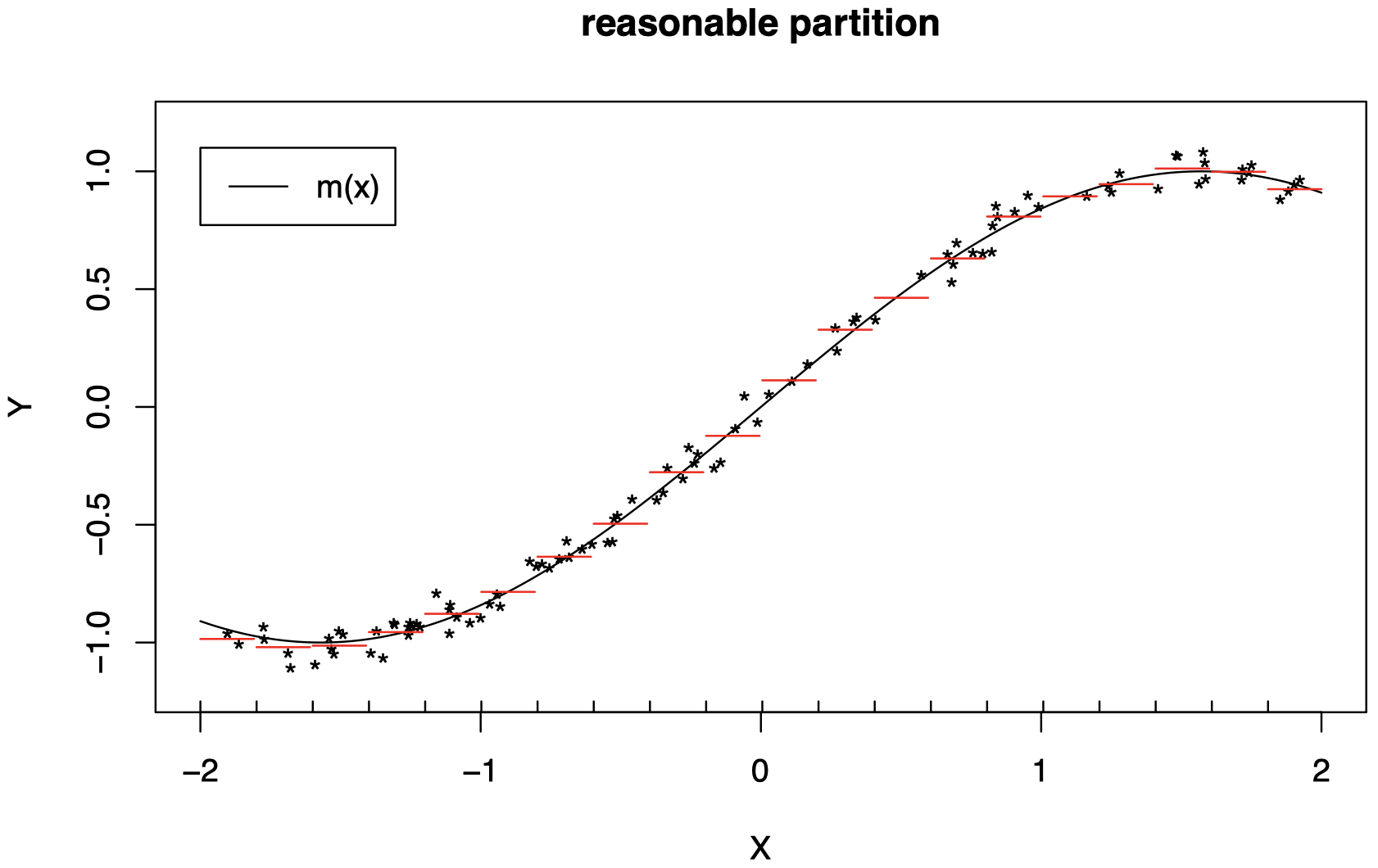
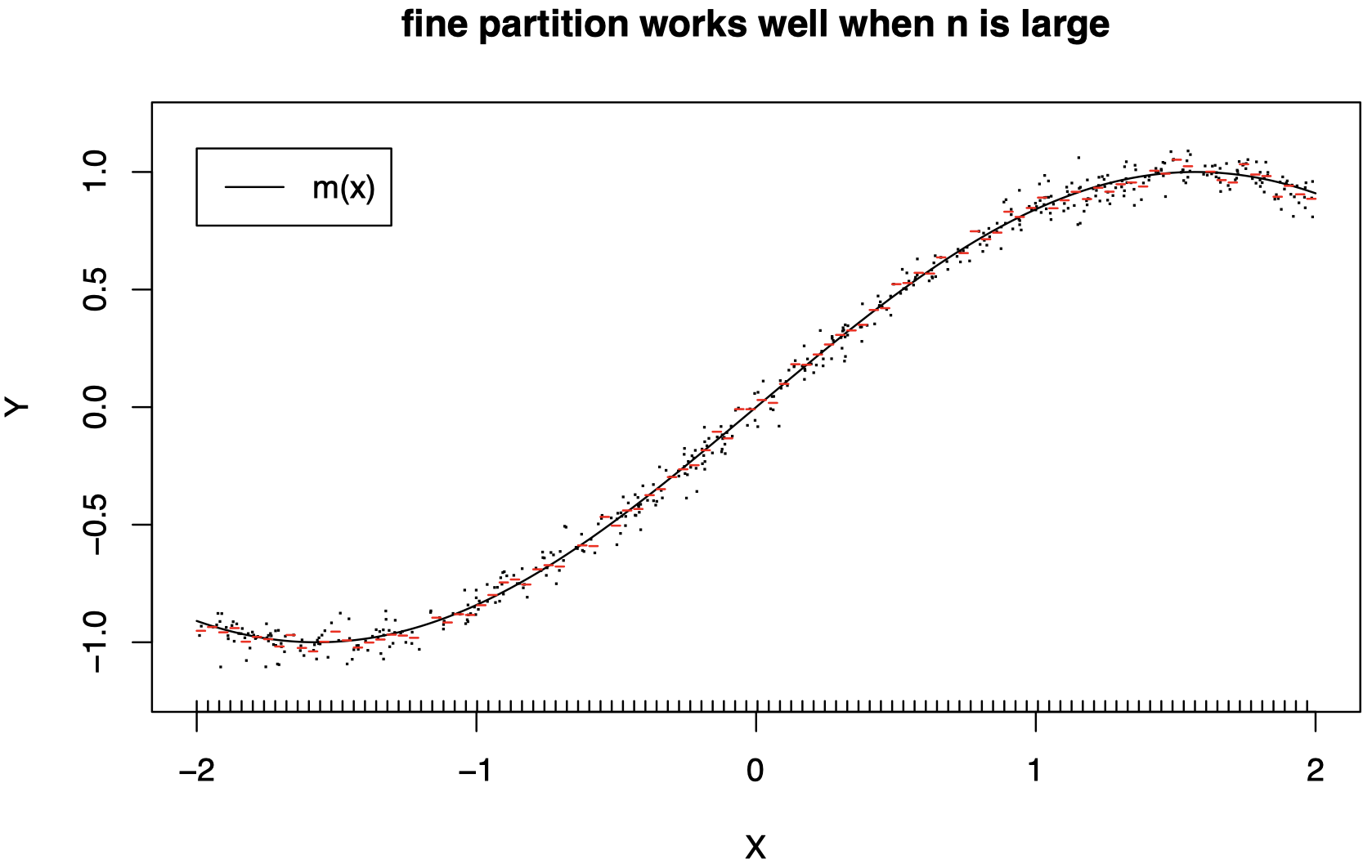
• 随着 $n$ 的增加，分区应该变得更加精细 ($L$ 应该增加)。

  

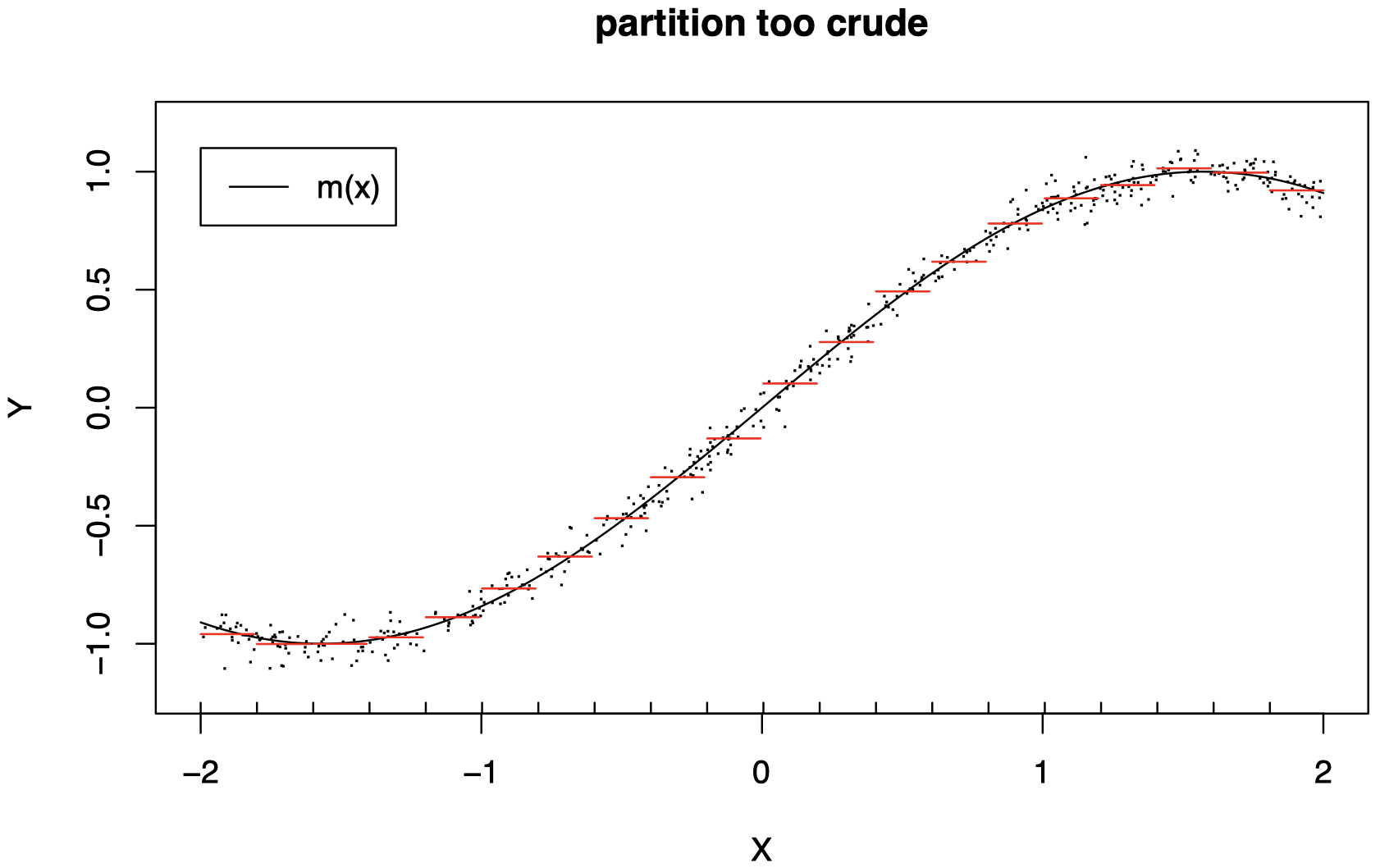
• 当 $n$ 较大时，精细的分区 (较大的 $L$) 可以很好地工作，因为在小区域上，我们现在有更多数据可以用来拟合常数。

  

确定树的大小

回到一般的树 ($X\in \mathbb R^p$)：太大的树会对数据过拟合，而太小的树将无法捕获 $m$ 的足够结构。

树的大小 ($L$)：一个调整参数，用于控制模型复杂度。

树的大小应适应数据 (回顾前面 $p = 1$ 的示例)。

回想一下，理想情况下，我们将比较所有可能的划分序列，但相应地，我们会顺序生长一棵树。

一种策略：仅当一个划分能够使 RSS 的减少量超过某个阈值的情况下，才在两个区域中执行该划分，其中

\[\mathrm{RSS}=\sum_{i=1}^{n}\{\mathcal Y_i-\hat m(\mathcal X_i)\}^2\]

并且，对于 $x\in \mathbb R^p$，

\[\hat m(x) = \sum_{\ell =1}^{L}\hat c_{\ell}I\{x\in R_{\ell}\}\]

但是，可能会发生这样的情况：某一次划分毫无价值，而接下来的一次划分可能会非常有用，因此这种策略过于短视了。

首选策略：生成一棵很大的树 (比我们实际需要的更大)，直到每个区域仅包含一个预定义的很小数量的观测数据 (例如：5 个)，将此树称为 $T_0$。然后，采用下面的 “成本复杂度” 修剪方法对 $T_0$ 进行 “修剪” (移除一些无用分支，并合并相应的区域，即折叠一些内部结点)，如下所示：

成本复杂度修剪 (Cost Complexity Pruning)

令 $T \subset T_0$ 为可通过修剪 $T_0$ 得到的任何树 (即，通过折叠一定数量的内部结点得到 $T$)。我们通过计算 $T$ 的叶子数来衡量 $T$ 的大小，记为 $|T|$。

对于第 $\ell$ 层，令

\[N_{\ell} = \text{number of observed } \mathcal X_i \in R_{\ell}\]

回忆一下，在一个区间 $R_{\ell}$ 内 (即对于 $x\in R_{\ell}$)，我们通过下式估计 $m(x)$

\[\hat m(x)=\hat c_{\ell} =\dfrac{1}{N_{\ell}}\sum_{\mathcal X_i\in R_{\ell}}\mathcal Y_i\]

对于一棵树 $T$，将区域 $R_{\ell}$ 中的 RSS 除以 $N_{\ell}$，表示为

\[Q_{\ell}(T)=\dfrac{1}{N_{\ell}}\sum_{\mathcal X_i\in R_{\ell}}(\mathcal Y_i-\hat c_{\ell})^2\]

成本复杂度标准定义为

\[C_{\alpha}(T)=\sum_{\ell=1}^{|T|}N_{\ell}Q_{\ell}(T) + \alpha |T|\]

其中，$\alpha \ge 0$ 是一个调整参数，用于控制树大小 $|T|$ 和数据拟合优度 $\sum_{\ell=1}^{|T|}N_{\ell}Q_{\ell}(T)$ 之间的权衡。

• $\alpha$ 很大：对树的大小 $|T|$ 施加一个较大的惩罚 $\Longrightarrow$ 最小化 $C_{\alpha}(T)$ 的树将较小 (我们将合并很多区域)。

• $\alpha$ 很小：对树的大小 $|T|$ 施加一个较小的惩罚 $\Longrightarrow$ 最小化 $C_{\alpha}(T)$ 的树将较大 (我们将合并很少区域)。

• $\alpha=0$ 的极端情况：不对树的大小施加任何惩罚 $\Longrightarrow$ 最小化 $C_{\alpha}(T)$ 的树为 $T_0$。很明显，一棵较大的树的 RSS 不会大于其子树的 RSS。

可以证明，对于每个 $\alpha$，都存在一个唯一最小子树 $T_{\alpha} \subset T_0$，使得 $C_{\alpha}(T)$ 最小化。

为了找到 $T_{\alpha}$，我们使用下面的 最弱连接修剪 (weakest link pruning) 方法：

1. 折叠结点 (对一个结点产生的两个叶子/区域进行合并)，使得 $\sum_{\ell=1}^{|T|}N_{\ell}Q_{\ell}(T)$ 的增加量最小。

2. 重复此过程，直到没有可以合并的区域为止 (单叶树)。

3. 然后，对于上面过程中生成的有限的子树序列中的所有树 $T$，计算 $C_{\alpha}(T)$。

4. 可以证明，在上面的子树序列中，$T_{\alpha}$ 将是能够最小化 $C_{\alpha}(T)$ 的树。

$\alpha$ 可以通过交叉验证进行选择 (有关分类的 CV，请参见上一章内容)。

3. 分类树

当我们将树用于分类时 (当 $Y$ 取值为 $\{1,\dots,K\}$ 中的类别值时)，我们不会按照相同的方式去构造或拟合它们。

RSS 并不适用于构建分类树：我们的目标不是构建一个良好的回归估计器，而是执行良好的分类。

在分类问题中，我们观测到训练数据 $(\mathcal X_i,G_i) \; (i=1,\dots,n)$，其中 $G_i\in \{1,\dots,K\}$ 是第 $i$ 个个体的类标签。

假设我们已经将特征空间划分为区域 $R_1,\dots,R_L$。我们将通过下式估计一个新个体 $X$ 的类标签 $G$：

\[\hat G = \hat G(X)=\sum_{\ell=1}^{L}\hat c_{\ell}I\{X\in R_{\ell}\}=\begin{cases}\hat c_1 & \text{if } X\in R_1 \\ \vdots \\ \hat c_L & \text{if } X\in R_L\end{cases}\]

其中，$\hat c_{\ell}$ 是区域 $R_{\ell}$ 的预测类。

如何计算区域 $R_{\ell}$ 的预测类 $\hat c_{\ell}$？

• 在一个区域 $R_{\ell}$ 中，对于每个类标签 $k=1,\dots,K$，我们计算训练数据中 $G_i=k$ 的数据所占比例 $\hat p_{\ell k}$：

  \[\hat p_{\ell k}=\dfrac{1}{N_{\ell}}\sum_{i \text{ s.t. }\mathcal X_i\in R_{\ell}}I\{G_i = k\}\]

  其中，$N_{\ell}$ 是区域 $R_{\ell}$ 中的训练数据量。

• 我们将区域 $R_{\ell}$ 中的预测类 $\hat c_{\ell}$ 取为

  \[\hat c_{\ell}=\mathop{\operatorname{arg\,max}}\limits_{k=1,\dots,K}\hat p_{\ell k}\]

  即我们采用区域 $R_{\ell}$ 的训练数据中最常见的类作为该区域的预测类。

为了选择分划分以及修剪树，我们必须采用更适合分类问题的标准来代替 RSS。

也就是说，我们会采用其他准则来代替之前回归树中的 $Q_{\ell}$，例如：误分类误差、基尼系数、交叉熵/偏差。

• 误分类误差 (Misclassification error)：

  \[Q_{\ell}(T) = \dfrac{1}{N_{\ell}} \sum_{i \text{ s.t. }\mathcal X_i \in R_{\ell}}I\{G_i \ne \hat c_{\ell}\}=1-\hat p_{\ell \hat c_{\ell}}\]

• 基尼系数 (Gini index)：

  \[Q_{\ell}(T) = \sum_{k \ne k'}\hat p_{\ell k} \hat p_{\ell k'}=\sum_{k=1}^{K}\hat p_{\ell k}(1- \hat p_{\ell k})\]

• 交叉熵/偏差 (Cross-entropy/deviance)：

  \[Q_{\ell}(T) = - \sum_{k=1}^{K}\hat p_{\ell k} \log \hat p_{\ell k}\]

在 $K=2$ 的情况下，对比三种标准。每个指标都是一个关于 $p=p_{\ell 2}$ 的函数：

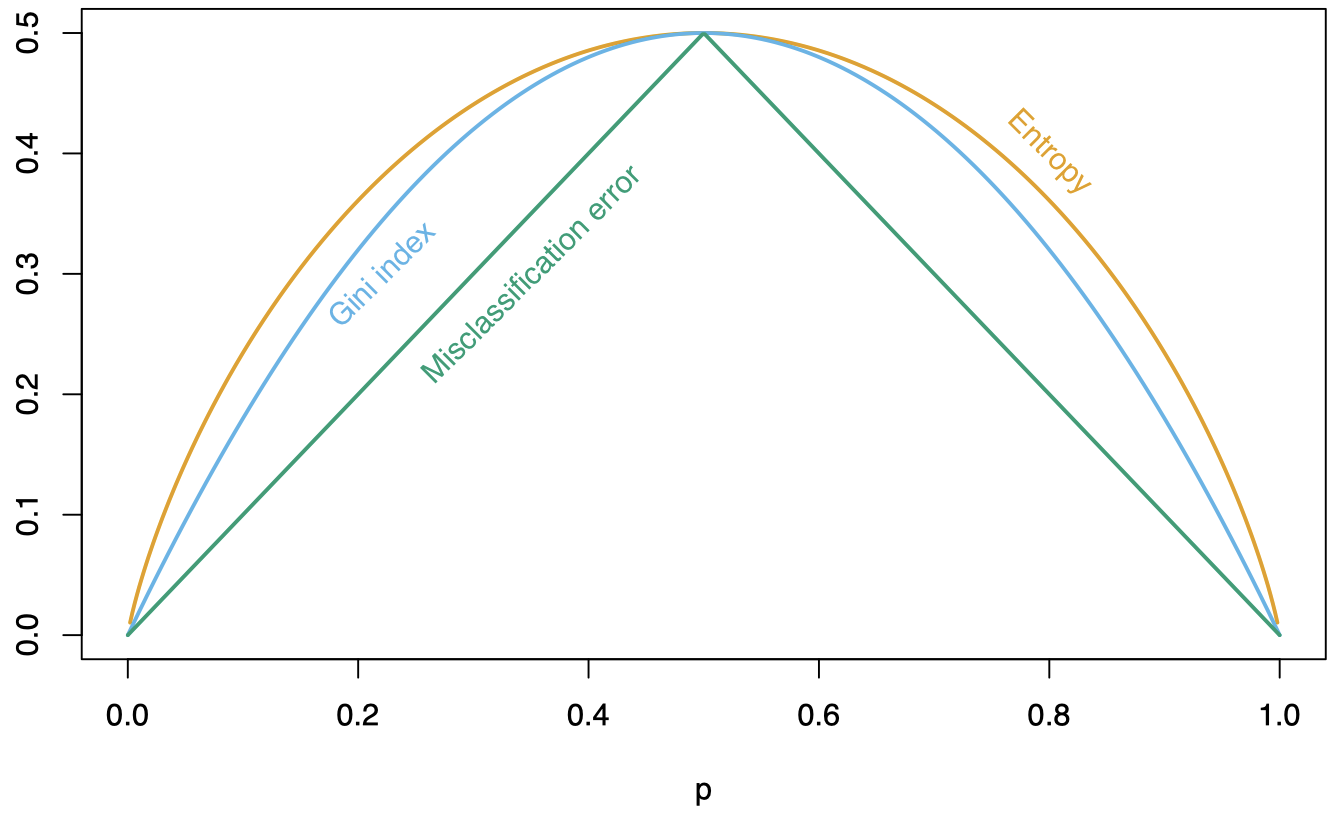
以上这些都是用于生成树的标准。其中，交叉熵和基尼系数是 可微的 (differentiable) $\Longrightarrow$ 更适合数值优化。

在分类问题中如何生成树？

1. 从全部数据开始，并考虑将数据分为两个区域的所有可能的划分方式

   \[R_1(j,t)=\{\mathcal X_i \quad \text{s.t.} \quad \mathcal X_{ij}\le t\},\quad R_2(j,t)=\{\mathcal X_i \quad \text{s.t.} \quad \mathcal X_{ij} > t\}\]

   对于所有的 $j=1,\dots,p$ 和 $\mathcal X_{j}$ 在训练样本上所能取得的所有 $t$ 值，即 $t\in \{\mathcal X_{1j},\dots,\mathcal X_{nj}\}$。

2. 创建第一棵树 $T$，它包含两个区域 $R_1$ 和 $R_2$。在所有可能的 $j$ 和 $t$ 上，选择分裂变量 $X_j$ 和分裂点 $t$，以最小化

   \[\sum_{\ell=1}^{2}N_{\ell}Q_{\ell}\]

   其中，$Q_{\ell}$ 可以是交叉熵或者基尼系数。

3. 一旦找到上面定义的最佳 $j$ 和 $t$，我们就确定了第一个划分。它创建了两个数据区域 $R_1(j,t)$ 和 $R_2(j,t)$。

4. 然后，在这两个区域中的每一个上，我们重复相同的过程：

   • 考虑在所有 $j$ 和 $t$ 上，$R_1$ 的所有可能划分，记为 $R_1’$ 和 $R_2’$，并找到能够最小化下式的 $j$ 和 $t$。

     \[\sum_{\ell=1}^{2}N_{\ell}Q_{\ell}\]

     其中，$Q_1$ 和 $Q_2$ 可以是交叉熵或基尼系数，分别应用于区域 $R_1’$ 和 $R_2’$。

   • 然后考虑在所有 $j$ 和 $t$ 上，$R_2$ 的所有可能划分，记为 $R_3’$ 和 $R_4’$，并找到能够最小化下式的 $j$ 和 $t$。

     \[\sum_{\ell=3}^{4}N_{\ell}Q_{\ell}\]

     其中，$Q_3$ 和 $Q_4$ 可以是交叉熵或基尼系数，分别应用于区域 $R_3’$ 和 $R_4’$。

   • 这样，我们总共确定了 4 个区域 (之前的每个区域都已被划分为两部分)。

   同样，在这里，当根据 $X_j$ 将 $R_{\ell}$ 划分为两部分时，我们只需要考虑 $t$ 在 $\mathcal X_{ij}$ 上的值，其中 $\mathcal X_i\in R_{\ell}$。

5. 我们在前一步中创建的每个新区域上继续重复这种划分过程，直到我们决定让树停止生长。

接下来，对于分类问题，我们应当如何修剪我们的树呢？回忆一下，在之前的回归树中，我们首先使用上述过程生成一棵很大的树 $T_0$，使得每个区域仅包含预定义的很少数目的观测数据 (例如：5 个)。

这里，成本复杂度标准定义为

\[C_{\alpha}(T)=\sum_{\ell=1}^{|T|}N_{\ell}Q_{\ell}(T) + \alpha |T|\]

在这种情况下，为了修剪树，我们可以将 $Q_{\ell}$ 设为之前定义的三个标准中的任何一个，而最常用的是误分类率。

为了找到 $T_{\alpha}$，我们可以使用最弱连接修剪方法，就像之前在回归树中那样。

$\alpha$ 可以通过交叉验证进行选择。

4. 例子：垃圾邮件数据 (Spam Data)

• 垃圾邮件数据：来自 $4602$ 封电子邮件的信息。
• 目标：预测一封电子邮件是垃圾邮件还是正常邮件。

在此示例中，邮件的真实类别 (email 或 spam) 是可获取的。

我们还知道这些邮件中最常见的 $57$ 个单词和标点符号出现的相对频率：

表 1：电子邮件信息中指定的单词或字符的平均百分比。这里选取显示 spam 和 email 之间差别最大的单词和字符。

这里，我们基于 偏差 (deviance) 来生成树，并基于 误分类率 (misclassification rate) 来修剪树。

在来自区间 $[0, 180]$ 的 $\alpha$ 值的网格上计算 10-折 $CV(\alpha)$。对于每个 $\alpha$，将 $CV(\alpha)$ 绘制为关于参数为 $\alpha$ 的树的大小 $|T_{\alpha}|$ 的函数 (回想一下，随着 $\alpha$ 的减少，树的大小会增加)。并与真实的误分类错误率进行比较。

当 $|T_{\alpha}|=17$ (终端结点/叶子数) 时，$CV$ 最小。

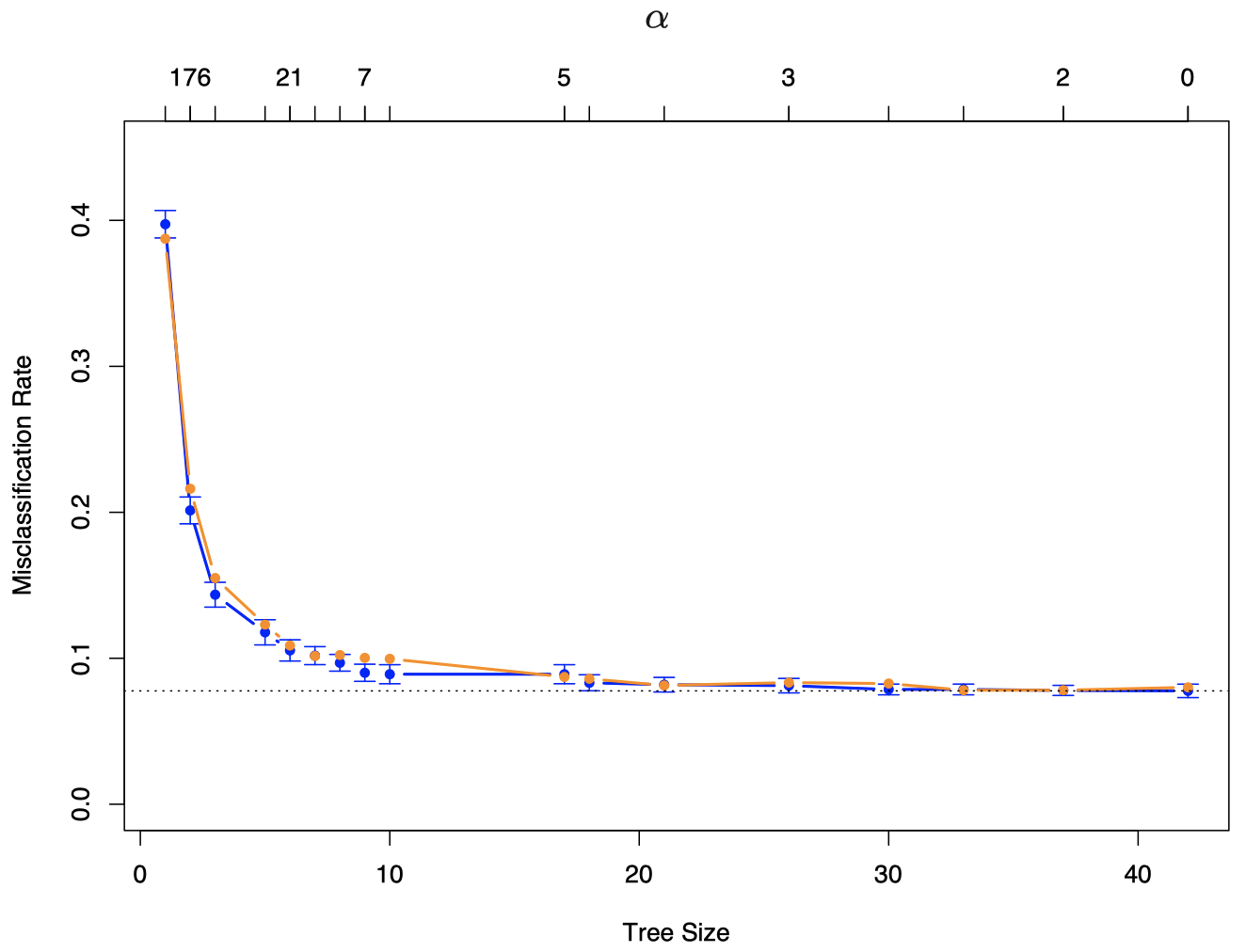
图 1：垃圾邮件例子的结果。蓝色曲线是误分类率的 10-折交叉验证估计，误分类率是关于树的大小的函数，带有标准误差条。最小值出现在大小约为 17 个终端结点的树上 (使用 “一个标准误” 规则)。 橙色曲线是测试误差，它与 CV 误差非常接近。交叉验证由 $\alpha$ 值索引 (见图上方坐标)。图底部的树的大小 $|\alpha|$ 是指由 $\alpha$ 索引的原始树的大小。

在此示例中，我们知道邮件的真实类别 (email 或 spam)，因此我们可以计算出有多少垃圾邮件和正常邮件被正确或错误地分类：

表 2：垃圾邮件数据：具有 17 个结点 (由交叉验证选择) 的树在测试数据上的混淆矩阵。总体错误率为 $9.3\%$

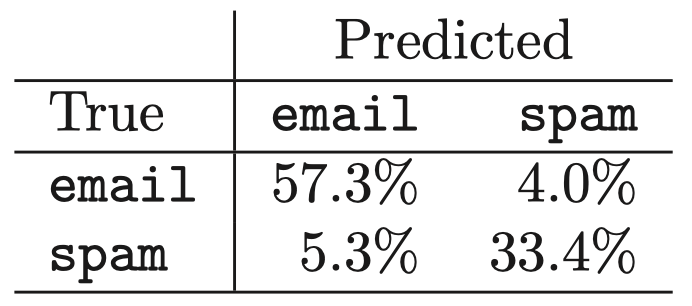
可以看到，$57.3\%$ 的正常邮件被正确分类到 email，以及 $33.4\%$ 的垃圾邮件被正确分类到 spam。其余邮件的分类结果是错误的，但总的来说，这里的错误率相当低。

在实践中，与将垃圾邮件分类为 email 相比，将正常邮件分类为 spam 更让人无法接受。为此，我们可以对分类器进行修改：对于误分类，给予正常邮件比垃圾邮件更高的权重。如有兴趣，请参阅相关文献。

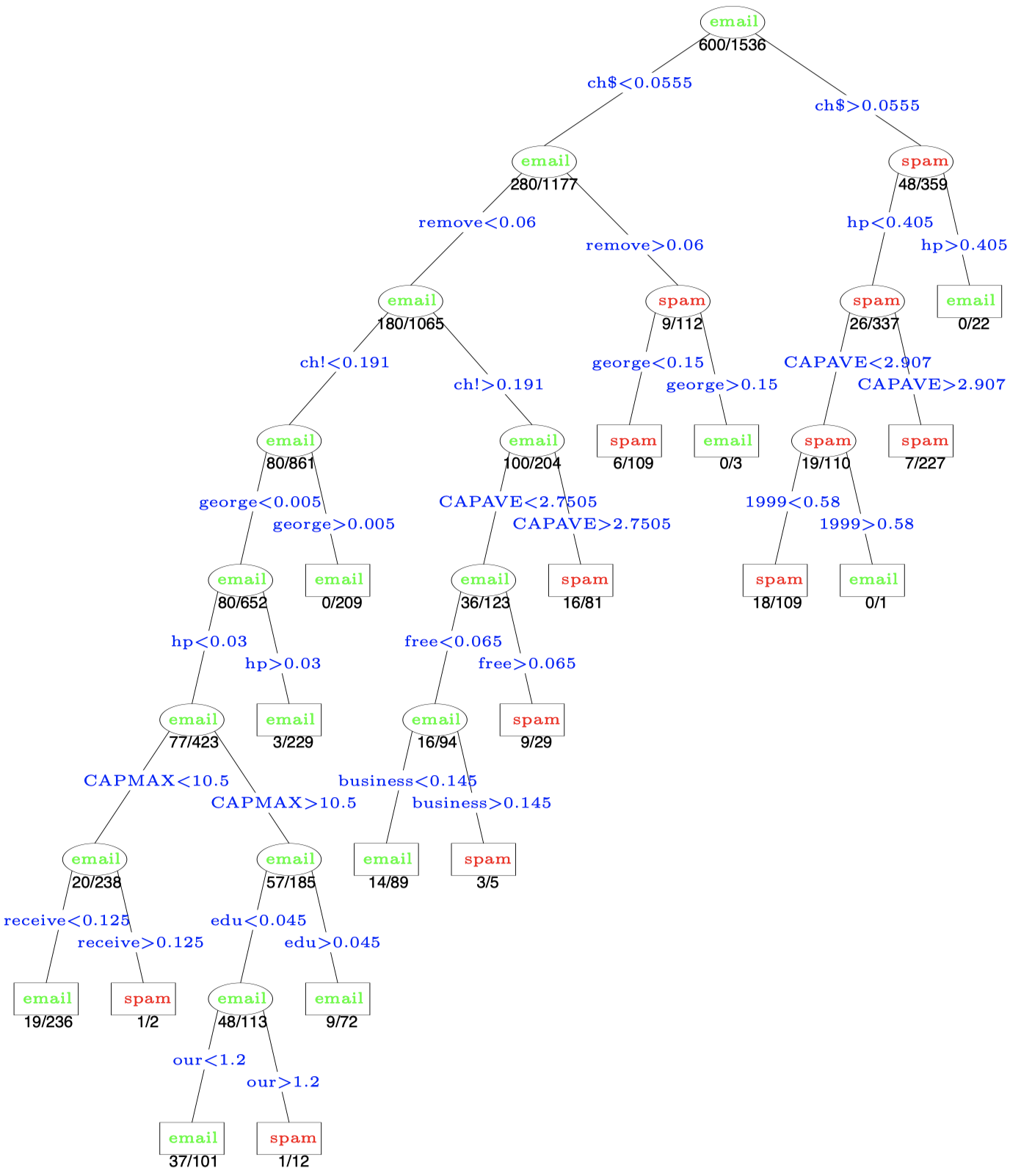
图 2：垃圾邮件例子的剪枝树。分裂变量在分支上显示为蓝色，分类则显示在每个结点上。终端结点下面的数字表示测试数据上的误分类率。

下节内容：Bagging 和随机森林

本作品采用知识共享署名-非商业性使用-相同方式共享 4.0 国际许可协议进行许可。 欢迎转载，并请注明来自：YEY 的博客 同时保持文章内容的完整和以上声明信息！

---

• Previous
  数据科学多元统计学 08：线性和二次分类
• Next
  数据科学多元统计学 10：Bagging 和随机森林

---