Lecture 10 Bagging 和随机森林
参考教材:
- Hardle, W. and Simar, L (2015). Applied multivariate statistical analysis, 4th edition.
- Hastie, T. Tibshirani, R. and Friedman, J. (2009). The elements of statistical learning, 2nd edition
1. Bagging 分类树
树模型具有 高方差。相似的样本可能会生成截然不同的树,尤其是在各个分量 ($X_j$) 相关性很高的情况下。这会导致预测结果不稳定。
从更高的层面来看,这是由于在顶部划分过程中产生的错误会向下传播到其下方的所有划分中。
Bagging 是一种降低方差的方法:与仅生成一棵树相比,我们将基于数据生成许多 (例如:$B$ 棵) 深树。然后,我们以某种方式聚合 (或 “装袋”) 这 $B$ 棵树。
深树的偏差很低,但方差很高。对它们进行聚合可以解决方差的问题。(直觉上:随机变量的平均值通常具有较小的方差,而聚合可以达到类似的效果)。
Bootstrapping:根据原始训练数据 $(\mathcal X_1,G_1),\dots,(\mathcal X_n,G_n)$ 创建 $B$ 个人工 bootstrap 样本。每个 bootstrap 样本都是通过有放回随机抽样得到的 $n$ 个数据对 $(\mathcal X_i, G_i)$ 生成的。
(注意:我们是对整个数据对 $(\mathcal X_i, G_i)$,而不是分别对 $\mathcal X_i$ 和 $G_i$,进行重抽样。有放回意味着我们可以在多次抽样中得到相同的数据对:这 $n$ 个 bootstrap 数据对中的每一个都是从训练样本中的 $n$ 个原始数据对中选取的)。
对于 $b=1,\dots,B$,我们将第 $b$ 个 bootstrap 样本记为
\[(\mathcal X_{b,1}^*, G_{b,1}^*),\dots,(\mathcal X_{b,n}^*, G_{b,n}^*)\]对于每个 bootstrap 样本,按照以下方法计算一棵分类树:对于 $b=1,\dots,B$,第 $b$ 个 bootstrap 样本的树的结果为
\[\hat G_b = \hat G_b(x) = \sum_{\ell=1}^{L}\hat c_{b,\ell}^{*} I\{x\in R_{b,\ell}^{*}\}=\begin{cases}\hat c_{b,1}^* & \text{if }x\in R_{b,1}^* \\ \vdots \\ \hat c_{b,L}^* & \text{if }x\in R_{b,L}^*\end{cases}\]其中,$\hat c_{b,\ell}^{*}$ 是区域 $R_{b,\ell}^{*}$ 的预测类。
然后,以下列方式之一聚合这 $B$ 棵树并生成一个新的单一结果 $\hat G_{bag}$:
-
共识/多数投票 (Consensus/Majority voting):对特征空间中的所有 $x$,令 $p_1(x),\dots,p_K(x)$ 分别为这 $B$ 棵树中将 $x$ 分类到组 $1,\dots,$ 组 $K$ 的树所占比例。然后,我们有
\[\hat G_{bag}(x)=\mathop{\operatorname{arg\,max}}\limits_k p_k(x)\](我们取占比最高的类作为聚合后的结果类)
-
平均类别占比 (Average the class proportions):对于这 $B$ 棵树中的每一棵树的分类占比进行平均。这里,对于第 $b$ 棵树,如果 $x\in R_{b,\ell}^{*}$,对于 $k=1,\dots,K$,计算
\[\hat p_{b,k}^*(x)=\dfrac{1}{N_{b,\ell}^*}\sum_{i \text{ s.t. }\mathcal X_{b,i}^* \in R_{b,\ell}^*} I\{G_{b,i}^* = k\}\]其中,$N_{b,\ell}^{*}$ 是区域 $R_{b,\ell}^{*}$ 中的 bootstrap 样本 $\mathcal X_{b,i}^{*}$ 的数量。
然后,我们取
\[\hat p_{k}^*(x)=\dfrac{1}{B} \sum_{b=1}^{B}\hat p_{b,k}^*(x)\]并且将 $x$ 分类到能够最大化 $\hat p_k^{*}$ 的类。
通常来说,上面第二种方法的效果更好 (方差更低),特别是对于 $B$ 很小的情况;另外,它还可以为类的概率提供一个良好的估计。
使用 “bagging” 方法的代价是什么?我们牺牲了 可解释性 (interpretability):从 $B$ 棵树中获得的决策规则本身并不是一棵树。(一棵树被认为是 “可解释的” 对象;可以通过视觉表示)
例子:具有模拟数据的树
假设原始数据具有两个类 ($1$ 和 $2$),以及 $p=5$ 个特征 $X_1,\dots,X_5$,每个特征都服从标准正态分布,并且每对特征之间的相关系数都是 $0.95$。响应 $Y$ 完全由 $X_1$ 确定:
\[P(Y=1\mid x_1\le 0.5)=0.2 \quad \text{and} \quad P(Y=1\mid x_1 > 0.5)=0.8\]我们的训练样本大小为 $N=30$,并且我们创建了 $B=200$ 个 bootstrap 样本。
另外,大小为 $2000$ 的测试样本也从相同的总体中产生。
我们为训练样本和 $200$ 个 bootstrap 样本中的每一个拟合分类树,并且没有使用剪枝。图 1 显示了原始树和 11 个 bootstrap 树。注意,这些树是各不相同的,它们都有各自的分裂特征和分裂点。

图 1:模拟数据集上的 bagging 树。左上角是原始树,其余 11 棵树基于 bootstrap 样本生成的。每棵树的顶部都有关于分裂特征和分裂点的注释。
可以看到,这些树看上去都各不相同。原始树的变化很大,因为 5 个 $X_j$ 变量是高度相关的 (因此,样本中的一个微小变化可能会生成非常不同的树)。另外,这里没有使用剪枝。
图 2 显示了原始树和 bagging 树的测试误差。在这个例子中,由于预测变量之间的相关性,这些树具有较高的方差, 而 bagging 方法成功平滑了这种方差,并因此降低了测试误差。

图 2:图 1 中 bagging 例子的误差曲线。这里显示的是原始树与 bagging 树的测试误差,它是关于 bootstrap 样本数的一个函数。橙色点对应共识投票方法,而绿色点对应概率平均方法。
2. 随机森林分类
Bagging 的缺点:生成的 $B$ 棵树之间不是相互独立的。这会削弱聚合的方差减小效应。
直觉上:如果 $B$ 个变量来自相同分布,其方差为 $\sigma^2$ 且每对变量之间相关系数为 $\rho$,那么,这 $B$ 个变量的平均值的方差为
\[\rho \sigma^2 + (1-\rho)\sigma^2/B\]其中,第一项 $\rho \sigma^2$ 不会随着 $B$ 的增长而缩小。
随机森林 (Random forests, RF):通过特定方式生成 bootstrap 树来减少 $B$ 棵树之间的相关性。
当生成 boostrap 树时,在每次分裂之前,随机选择 $m (\le p)$ 个 $X_j$ 作为分裂的候选对象 (而不是将全部 $p$ 个 $X_j$ 都视为候选对象)。
通常,$m =\sqrt p$ (R 中的函数 randomForest() 的默认设置),但由于它是一个调整参数,因此我们可能希望能够自适应地选择其值。
对于 randomForest(),每个终端结点的默认大小为 $1$ (尽可能生成最大的树)。
$B$ 不是调整参数。随着 $B$ 的增加,RF 变得更加稳定,但是当 $B$ 增加到一定程度后,继续增加带来的收益将非常小。只需将 $B$ 取一个较大的值 (例如,计算上可行的值) 即可。另外,我们后面还将提到可能出现的 袋外 (out-of-bag, OOB) 误差。
随机森林算法:

回顾上节课中的垃圾邮件分类的例子。这里,我们采用随机森林进行分类。可以看到,相比 bagging 方法,随机森林在分类效果上有显著提升。在随机森林中,我们需要生成足够数量的树,但也并非越多越好。
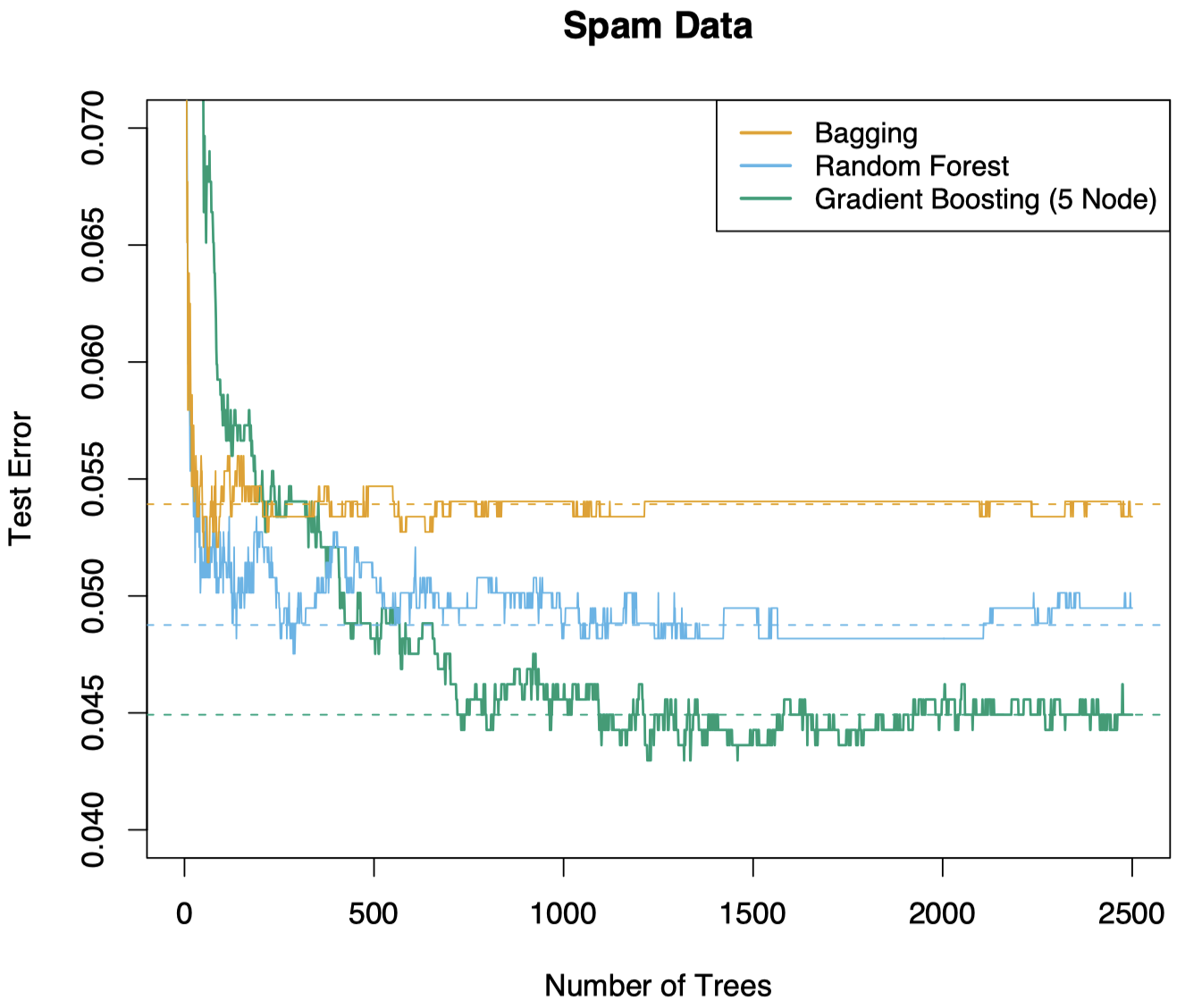
图 3:Bagging、随机森林、梯度 boosting 方法分别应用于垃圾邮件数据。对于 boosting,使用了 5-结点树,并通过 10-折交叉验证选择树的数量 (2500 棵树)。图中的每 “步” 都对应于 (在一个大小为 1536 的测试集上) 的一个错误分类导致的变化。
2.1 袋外数据 (Out-of-bag/OOB Data)
对于 RF,我们不需要使用交叉验证来选择 $m$。相反,我们可以使用 袋外 (OOB) 采样。
OOB:对于训练数据中的每个 $(\mathcal X_i,G_i)$,仅使用那些在生成过程中没有涉及 $(\mathcal X_i,G_i)$ 的 bootstrap 树来构造其 RF 分类器。并将分类结果记为 $\hat G_i$。
我们可以使用 OOB 误分类误差:
\[\dfrac{1}{n}\sum_{i=1}^{n}I\{\hat G_i \ne G_i\}\]它可以动态地实现一些 CV,而且计算速度更快。
还是回到前面的垃圾邮件的例子。可以看到,OOB 误差与测试误差很接近。我们可以在 OOB 误差曲线中较为平稳的地方选取 $B$ 值。
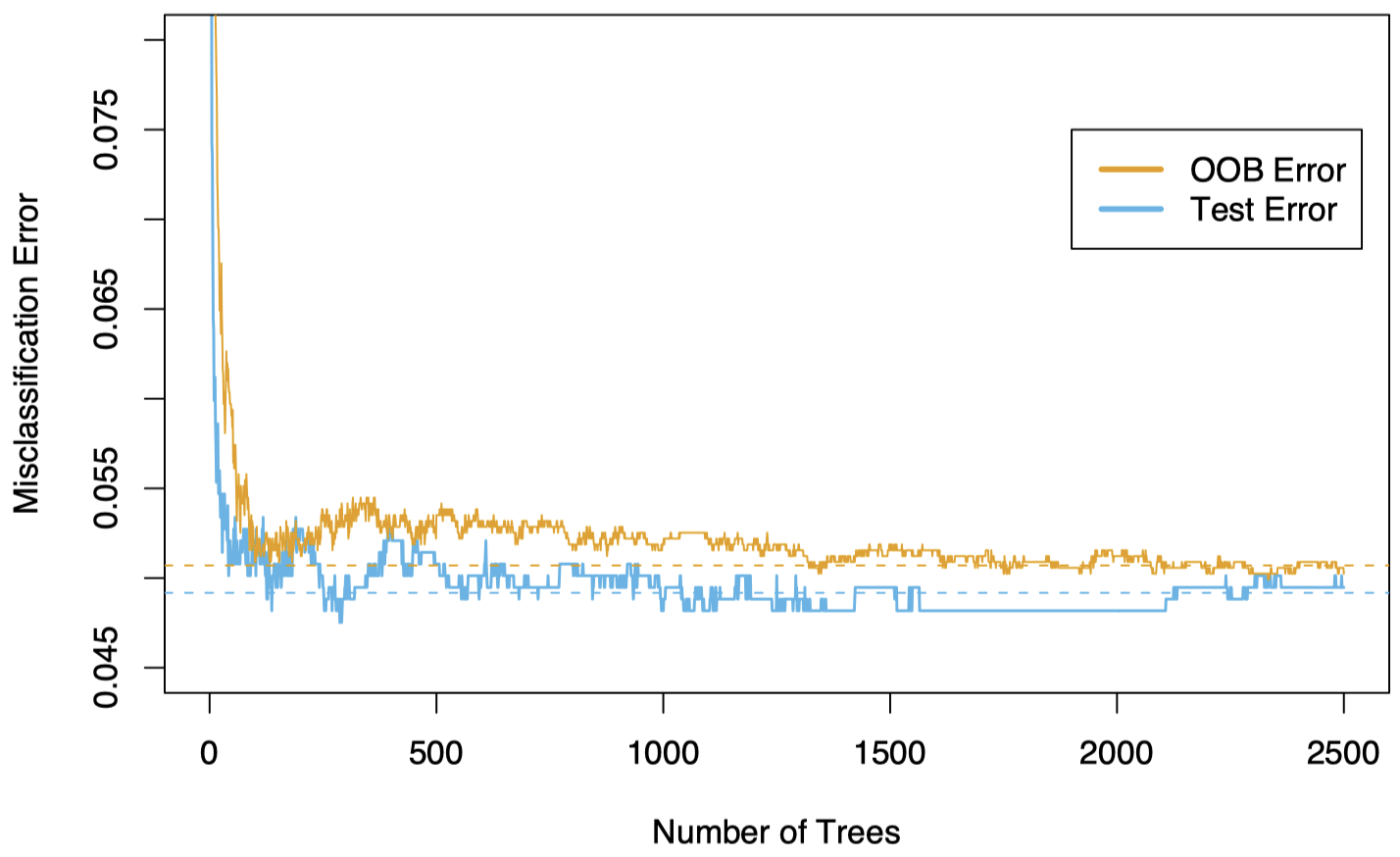
图 4:在 spam 训练数据上计算 OOB 误差,并与在测试集上计算的测试误差进行比较。
2.2 变量重要性
对于分类问题,并非所有的 $X$ 变量都具有相同的重要性。我们可以计算出每个变量 $X_j$ 的重要性的度量。
回想一下,在构造树的每个阶段,分裂变量有助于在某种程度上降低总的 “风险” 量 $\sum N_{l}Q_{l}$,即不纯度的加权和。
特别是当我们有 $L$ 个区域,当前风险为 $\sum_{l=1}^{L}N_{l}’Q_{l}’$,并且需要将其中某个区域一分为二,从而创建 $L+1$ 个区域 $R_1,\dots,R_{L+1}$ 时,我们选择一个分裂变量和分裂点以最小化新的风险
\[\sum_{\ell=1}^{L+1}N_{\ell}Q_{\ell}\]它要比之前的风险 $\sum_{l=1}^{L}N_{l}’Q_{l}’$ 更小。(当引入一个划分时,风险会减小;这与我们上节课中展示的基尼系数和交叉熵曲线的凹度有关)
假设在最终创建的树的第 $t$ 个内部结点上,我们使用分裂变量 $X_{v(t)}$ 分割了一个区域。例如,如果第 $t$ 个内部结点是按照 $\{X_2 < 5.1 \}$ 和 $\{X_2 \ge 5.1\}$ 划分的,那么 $v(t) = 2$。
令 $\widehat{\text{impr}}_t$ 表示通过引入这种分割获得的风险 $\sum N_lQ_l$ 的减少量,一种用于衡量 $X_j$ 的重要性的标准是:
\[\mathcal I_j(T) = \sum_t \widehat{\text{impr}}_t \cdot I\{v(t)=j\}\]其中,求和式是在最终树中的所有内部结点上。其值越大,说明变量 $j$ 越重要。
在 RF 中我们有 $B$ 棵树,记为 $T_1,\dots,T_B$。对于第 $j$ 个变量 $X_j$,计算其重要性的一种方式是对于 $b=1,\dots,B$,分别计算 $\mathcal I_j(T_b)$。然后取平均值:
\[\dfrac{1}{B}\sum_{b=1}^{B} \mathcal I_j(T_b)\]当 $Q_l$ 是基尼系数度量时,这种重要性度量被称为 基尼重要性 (Gini importance)。
另一种衡量某个变量重要性的方法是:使用 OOB。当第 $b$ 棵树生成后,我们将得到的分类器应用于 OOB 数据 (即生成第 $b$ 棵树时没有用到的数据) 上。我们计算通过该方法得到的预测准确率 (被正确分类的 OOB 数据的数量)。
然后,为了计算第 $j$ 个变量 $X_j$ 的重要性,我们来看一下如果改变 OOB 数据中第 $j$ 个变量的值会发生什么。如何改变这些值?我们在 OOB 样本中对 $X_j$ 的值进行随机重新排列。如果 $X_j$ 很重要,那么改变 $X_j$ 的值会对分类效果产生不利影响。
$\Longrightarrow$ 对由于重新排列 OOB 数据中 $X_j$ 值而导致的预测准确率的减少量进行计算。然后对这 $B$ 棵树上的准确率的减少量取平均值。这就是我们衡量 $X_j$ 的重要性的方法。
另外,可能还采取了一些归一化操作,具体取决于不同的软件包实现 (如果感兴趣,请参阅文献)。在任何情况下,我们都会得到一些可以相互比较的值 (标度不是重点,关键在于相对重要性)。通常,最大的数值对应最重要的变量。
关于上面提到的两种衡量变量重要性的方法,并没有清楚证据表明哪一种更好,两者都值得一试。
图 5 通过基尼系数和 OOB 随机排列两种方式衡量了之前的垃圾邮件数据集中各个变量的重要性。其中,所有的变量重要性度量值都已经除以了其最大值 (最重要的变量的值),以保证重要性的值落在 $0$ 到 $100\%$ 之间。但并非总是如此,具体取决于我们的使用惯例。可以看到,!、$ 和 remove 这三个特征对于区分垃圾邮件和正常邮件最重要。
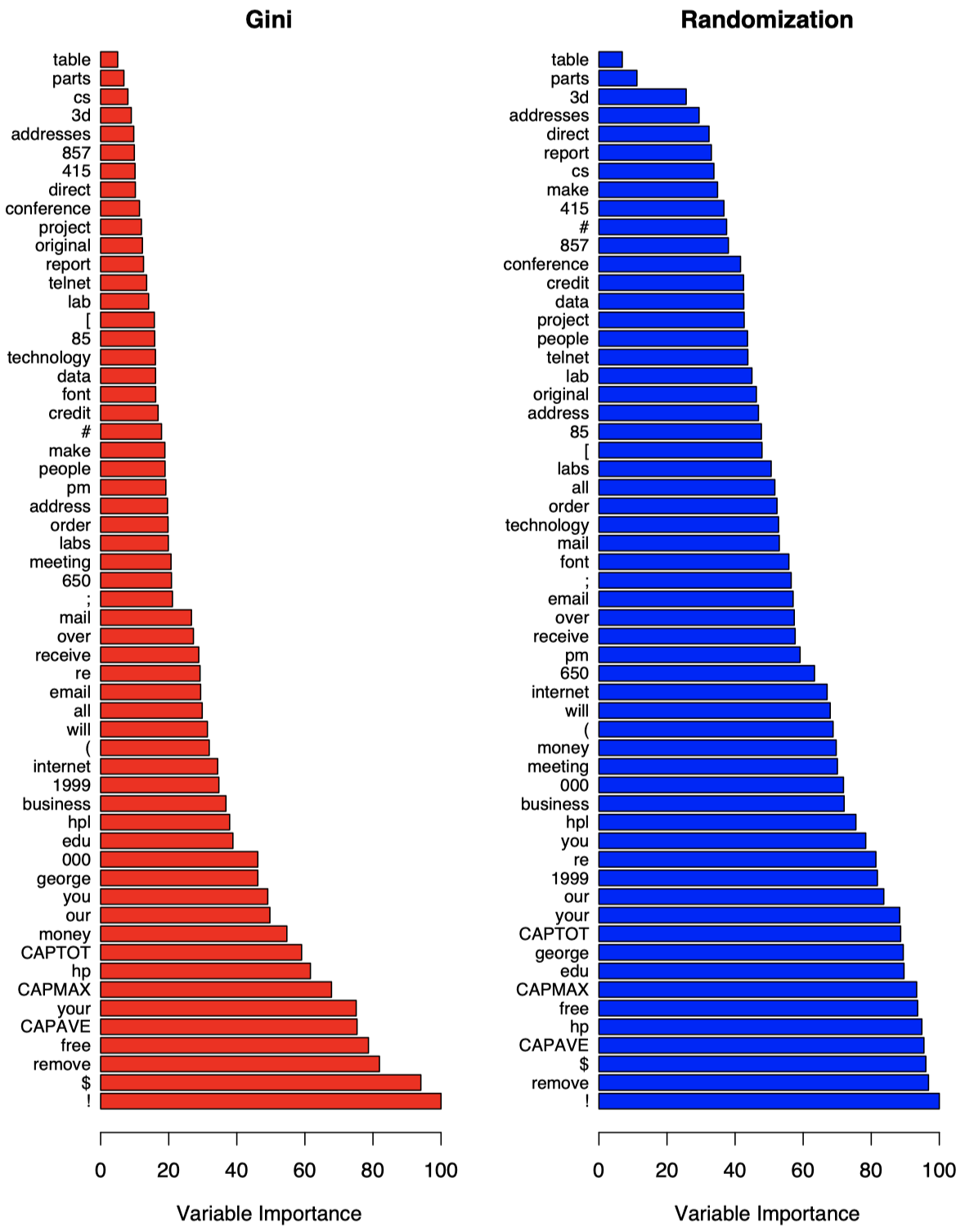
图 5:在 spam 数据上生成的随机森林分类器的变量重要性。左图是基于基尼分裂系数计算出的变量重要性。右图是使用 OOB 随机化计算出的变量重要性,可以看到这种方式下,这些不同变量的重要性倾向于更均匀地分布。
2.3 关于 RF 性能的一些结论
对于分类问题,并非所有的 $X_j$ 都是重要的,其中有些变量并不能帮助区分不同类别的个体。
一棵树会根据某些 $X_j$ (希望是重要的) 来划分区域。
当变量数量 $p$ 很大,并且其中只有一小部分与分类相关时,如果 $m$ 太小,那么 RF 的性能会很差,因为我们只有很小的几率能够选择到那些重要变量进行分裂。
这种情况下,我们需要选择足够大的 $m$。根据数据来选择 $m$ (例如:使用 OOB 版本的 CV) 可能会有所帮助。
相比之下,通常可以选择生成最大的树 (而不是通过 OOB 选择结点大小,这将耗费更多时间)。
3. 一般分类问题常用的 R 命令和注释
3.1 随机森林
要在 R 中计算一个随机森林,可以使用软件包 randomForest。
其中,函数 randomForest() 要求指定模型方程参数 formula (例如:G ~ ···),以及使用的数据集 data。这表示变量 $G$ 包含了数据的分类,而数据集中的所有其他变量都是 $X_j$。如果我们只想使用其中的某些变量,则需要在 data 参数中指定清楚。
注意:需要对变量 $G$ 进行因子化,以确保我们计算出的是一个分类树,而非回归树。
- 对于分类树中的 $m$ 参数 (
mtry),该软件包将默认使用 $m=\sqrt{p}$。 - 通常,不需要改变终端结点的默认数量。
- 可以通过参数
ntree选择树的数量。 - 可以要求对变量重要性的度量进行计算,并且还可以使用该包的内置函数来绘制这些度量。
- 使用
predict来为新个体预测分类。 predict(yourtree)(yourtree是已构建的树) 将计算 $i=1,\dots,n$ 的 OOB 预测类 $\hat G_i$。
3.2 PLS
我们还可以使用 R 软件包 PLS 中的 plsr() 函数计算 PLS 成分。
回忆一下之前 PLS 的内容,为了计算一个变量 $X\in \mathbb R^p$ 的 PLS 成分 $T\in \mathbb R^p$,我们取
\[T=\Phi^{\mathrm T}X\]对于某个特定矩阵 $\Phi^{\mathrm T}$。该矩阵是 plsr() 的输出之一 (投影矩阵)。
$T$ 是 scores() 函数输出的。但请注意,这些得分是在经过中心化的 $X$ 上计算得到的,因此,如果我们想将它们和新数据结合在一起,那么需要先对新数据进行中心化,否则会出问题。为了确保对新数据进行正确处理,可以将 plsr() 计算出的训练数据的得分和我们直接手动计算的训练数据的得分进行对比,二者应该是相同的。
3.3 使用 PCA 或 PLS 交叉验证
问题:当我们基于 PLS 或 PCA 变量,对回归或分类进行 CV 时,是否需要重新计算 PLS 或 PCA 的投影矩阵 ($\Gamma$ 或 $\Phi$)?
答案:通常可以避免在完整样本上计算 $\Gamma$ 和 $\Phi$,而只对我们拟合的回归/分类模型的参数进行 CV。
下节内容:聚类分析
本作品采用知识共享署名-非商业性使用-相同方式共享 4.0 国际许可协议进行许可。 欢迎转载,并请注明来自:YEY 的博客 同时保持文章内容的完整和以上声明信息!