Lecture 11 聚类分析

参考教材：

• Hardle, W. and Simar, L (2015). Applied multivariate statistical analysis, 4th edition.
• Hastie, T. Tibshirani, R. and Friedman, J. (2009). The elements of statistical learning, 2nd edition

1. 引言

分类 (有监督的学习问题)：将观察结果分类为我们事先知道的不同分组；我们有来自每个分组的训练数据。

聚类分析 (无监督学习问题)：我们怀疑数据可能来自多个组，我们希望统计技术可以帮助我们识别出这些分组，并将个体分配给这些不同的分组。聚类分析 (cluster analysis) 是一种描述性统计工具。

目标：将数据集中的个体分组到被称为 簇 (clusters) 的子集中，使得每个簇内的个体之间的关系比分配给不同簇的个体之间的关系更紧密。同一个簇内的个体彼此 相似。这个概念取决于相似性的定义。不同的 相似性度量 (measures of similarity) 可能导致不同的聚类结果。

层次聚类 (Hierarchical clustering)：有时我们也可以将簇按照某种自然层次排列：首先将所有个体分组为少数几个很大的簇，然后再将这些簇本身分为更小的簇。这种操作可以重复多次。

总而言之，聚类分析是从多元数据对象中建立组 (类) 的一套工具，其目的在于在异质大样本中构建同质的组别。同一组别内的个体之间应当越同质越好，不同组别的个体之间的差别则应越大越好。聚类分析可以分为以下两个基本步骤：

1. 邻近度 (Proximity) 度量的选择

   我们检验每一对观测值 (对象) 取值的相似性。一个相似性 (邻近度) 的度量定义为对象间的 “接近” 程度，它们越接近，就越同质。

2. 组别构建算法的选择

   基于邻近度的度量，被分配到各组的对象之间的应当差别很大，而分配到同一组的观测值则应尽可能接近。

2. 邻近度矩阵

大多数聚类算法都将 相异度矩阵 (dissimilarity matrix) 作为输入。

这类数据可以用一个 $n\times n$ 的矩阵 $D$ 表示，其中 $D_{ij},\; i,j=1,\dots,n$ 是第 $i$ 个个体和第 $j$ 个个体之间的 相异性 (dissimilarity) 度量。$D_{ij}$ 是 相异度矩阵 $D$ 的第 $(i,j)$ 个的元素。大多数算法假设该矩阵具有非负元素，并且对角线元素为零：$D_{ii}=0,\; i=1,\dots,n$。

大多数算法还假设输入为 对称 (symmetric) 相异度矩阵。因此，如果原始的 $D$ 不对称，则必须将其替换为 $(D+D^{\mathrm T})/2$。

如果收到的数据是 相似度 (similarities) 而不是相异度的形式，我们通常会应用单调递减函数将其转变为相异度。

我们也可以将相异度视为一个函数，例如

\[\mathcal D: \mathbb R^p \times \mathbb R^p \to \mathbb R^+\]

它衡量了两个个体之间的相异度。具体来说，我们可以记为 $D_{ij}=\mathcal D(\mathcal X_i,\mathcal X_j)$。这里的 $\mathcal D$ 可以是二者的距离，也可是其他度量形式。

回忆一下，$\mathcal D: \mathbb R^p \times \mathbb R^p \to \mathbb R^+$ 是一个距离，当且仅当：

\[\begin{align} &\forall a,b \in \mathbb R^p: \quad \mathcal D(a,b)= \mathcal D(b,a) \\[2ex] &\forall a,b \in \mathbb R^p: \quad \mathcal D(a,b)= 0 \quad \Longleftrightarrow \quad a=b \\[2ex] &\forall a,b,c \in \mathbb R^p: \quad \mathcal D(a,c) \le \mathcal D(a,b) + \mathcal D(b,c) \end{align}\]

如果 $\mathcal D$ 不是真实距离，则不能将基于真实距离的聚类算法应用于矩阵 $D$。

3. 基于属性的相异度

通常，对于 $n$ 个个体中的每一个，我们都可以观测到它的 $p$ 个变量 (或属性) $X_1,\dots,X_p$。然后，对于 $i = 1,\dots,n$，我们可以观测到向量 $\mathcal X_i =(\mathcal X_{i1},\dots,\mathcal X_{ip})^{\mathrm T}$。

通常，我们将为每个 $X_j$ 定义一个关于个体 $i$ 和 $k$ 之间的相异性度量 $d(\mathcal X_{ij},\mathcal X_{kj})$，并以此创建相异性矩阵。一种简单的方法是将

\[D_{ik} = \mathcal D(\mathcal X_i,\mathcal X_k) = \sum_{j=1}^{p}d(\mathcal X_{ij},\mathcal X_{kj})\]

作为相异度矩阵 $D$ 的第 $(i,k)$ 个元素。

当 $\mathcal X_i$ 是 定量的 (quantitative) 时，通常会取

\[d(\mathcal X_{ij},\mathcal X_{kj}) = (\mathcal X_{ij} - \mathcal X_{kj})^2\]

根据数据性质的不同，我们需要用不同方法来定义 $d()$：

• 定量变量 (Quantitative variables)：

  • $X_1,\dots,X_p$ 形式为连续的实值数字。

  • 对于两个实数 $x$ 和 $y$ 通常采用以下形式

    \[d(x,y) = \ell (|x - y|)\]

    其中，$\ell$ 是一个递增函数，$\| \cdot \|$ 表示绝对值。

  • 平方差：

    \[\ell(|x-y|) = (x-y)^2\]

  • 绝对差：

    \[\ell(|x-y|) = |x-y|\]

  注意：与绝对差相比，平方差会使较小的差异变得更小，较大的差异变得更大 $\quad \Longrightarrow \quad$ 更加强调较大的差异。

  • 另一种可能性：通过 “相关系数” 测量第 $i$ 个和第 $k$ 个个体之间的相似度

    \[\rho (\mathcal X_i,\mathcal X_k) = \dfrac{\sum_{j=1}^{p}(\mathcal X_{ij} - \overline{\mathcal X}_i)(\mathcal X_{kj} - \overline{\mathcal X}_k)}{\sqrt{\sum_{j=1}^{p}(\mathcal X_{ij} - \overline{\mathcal X}_i)^2 \sum_{j=1}^{p}(\mathcal X_{kj} - \overline{\mathcal X}_k)^2}}\]

    其中，

    \[\overline{\mathcal X}_i = \sum_{j=1}^{p} \mathcal X_{ij}/p\]

    注意：与通常的相关系数不同，这里涉及在个体上的求和计算。实际上这已经超越了分量的概念 $\quad \Longrightarrow \quad$ 我们现在计算的是两个个体而不是两个变量之间的相关系数。

  • 这仅在某些特定情况下有用，但通常可能毫无意义 (如有兴趣，请参阅文献)。

  • 假设我们处于有意义的情况下，我们可以根据相似度 $\rho(\mathcal X_i,\mathcal X_k)$ 来定义相异度，例如，

    \[D_{ik} = \mathcal D(\mathcal X_i,\mathcal X_k) = 1- \rho(\mathcal X_i,\mathcal X_k)\]

    (这将始终在 $0$ 到 $2$ 之间，并且 $D_{ii}=0$)。

  • 如果观测值是预先标准化的，即在计算任何东西之前，我们先将每个 $\mathcal X_i$ 替换为

    \[S^{-1/2}(\mathcal X_i - \overline{\mathcal X})\]

    然后，这等价于使用 $\ell (|x - y|) = (x-y)^2$；事实上，我们可以证明

    \[\sum_{j=1}^{p}(\mathcal X_{ij} - \mathcal X_{kj})^2 = \textit{constant} \cdot \{1- \rho(\mathcal X_i,\mathcal X_k)\}\]

    相关证明请参阅 这里。

  
  

• 分类/名义变量 (Categorical/nominal variables)：

  • 变量具有不同的类别 (可以取几个不同的值)，但是这些类别值之间没有顺序 (或偏好) 概念。
  • 例如：某个变量可能取值为黑色、橙色、蓝色、绿色。
  • 在这种情况下，我们必须定义​​一种方法来衡量任意两对值之间的差异程度。由于变量本身不包含数字，因此我们必须自己设计出这种度量。
  • 有一些专门为分类变量设计的相关技术。如有兴趣，请参阅文献。

  
  

• 有序变量 (Ordinal variables)：

  • 变量的值可以是定量的或者分类的，但是即使它们是分类的，不同值之间也存在某种顺序关系。
  • 例如：学术成绩 (A、B、C、D、F-不及格)，偏好程度 (无法忍受、不喜欢、一般、喜欢、狂热)，排名数据 (当我们根据某种偏好对数据进行排名时，可能会得到排名 1、2、3 等)。

  • 假设有序数据可以取 $M$ 个不同的值。为了计算相异性度量，通常会将 $M$ 值替换为

    \[\dfrac{i-1/2}{M} \, , \;\; i=1,\dots,M\]

    其中，$i=1,\dots,M$ 对应于原始 $M$ 值的顺序 (例如：顺序为 $1=$ 优选，$2 =$ 第二优选，依此类推)。然后，我们可以将其视为定量变量对待。

4. 目标 (观测) 相异度

除了

\[D_{ik} = \mathcal D(\mathcal X_i,\mathcal X_k) = \sum_{j=1}^{p}d(\mathcal X_{ij},\mathcal X_{kj})\]

之外，我们可能还希望得到一个加权版本，即

\[D_{ik} = \mathcal D(\mathcal X_i,\mathcal X_k) = \sum_{j=1}^{p} w_j d(\mathcal X_{ij},\mathcal X_{kj})\]

其中，$w_j$ 是一些正的权重，具体取决于上下文。

如果我们认为某些分量对于聚类更为重要，那么我们可以给予它们更高的权重，但这取决于主观方面的考虑。

注意：对每个分量赋予相同的权重 ($w_j=1$) 并不一定 意味着所有变量在聚类中都具有相同的重要性。

例如：如果 $d(x,y)=(x-y)^2$，那么

\[D_{ik} = \mathcal D(\mathcal X_i,\mathcal X_k) = \sum_{j=1}^{p} (\mathcal X_{ij},\mathcal X_{kj})^2\]

然后，方差较大的分量对相异性度量的贡献会更大一些。这并不是因为它们对于聚类更重要，而是因为它们的标度更大，也就是说，它们给 $D_{ik}$ 赋予更高权重是由人为因素导致的。

在这种情况下，为了使所有变量具有同等重要性，我们可以取

\[w_j = 1/ \hat s_{jj}\]

其中，$\hat s_{jj}$ 是根据 $n$ 个观测值计算出的 $X_j$ 的方差的经验估计量。

更一般地，当我们使用度量 $d$ 来计算 $D_{ik}$ 时，赋予一个权重

\[w_j = 1/ \overline d_j\]

其中，

\[\overline d_j =\dfrac{1}{n^2}\sum_{i=1}^{n}\sum_{k=1}^{n} d(\mathcal X_{ij},\mathcal X_{kj})\]

通常会导致在计算相异度时，每个分量具有相同的影响力。

但是，也许对每个分量分配相等的权重并不是一个好主意：我们也许应该为某些分量分配更多的权重，因为它们可能与聚类更加相关。

下面是来自教材 Hastie et al. (2017) 中第 506 页的一个例子：将 $K\text{-means}$ 算法分别应用于非标准化数据 (左图) 和标准化数据 (右图)，将数据聚类为 $2$ 个分组：在这个例子中，数据标准化会导致簇之间的可区分度降低。

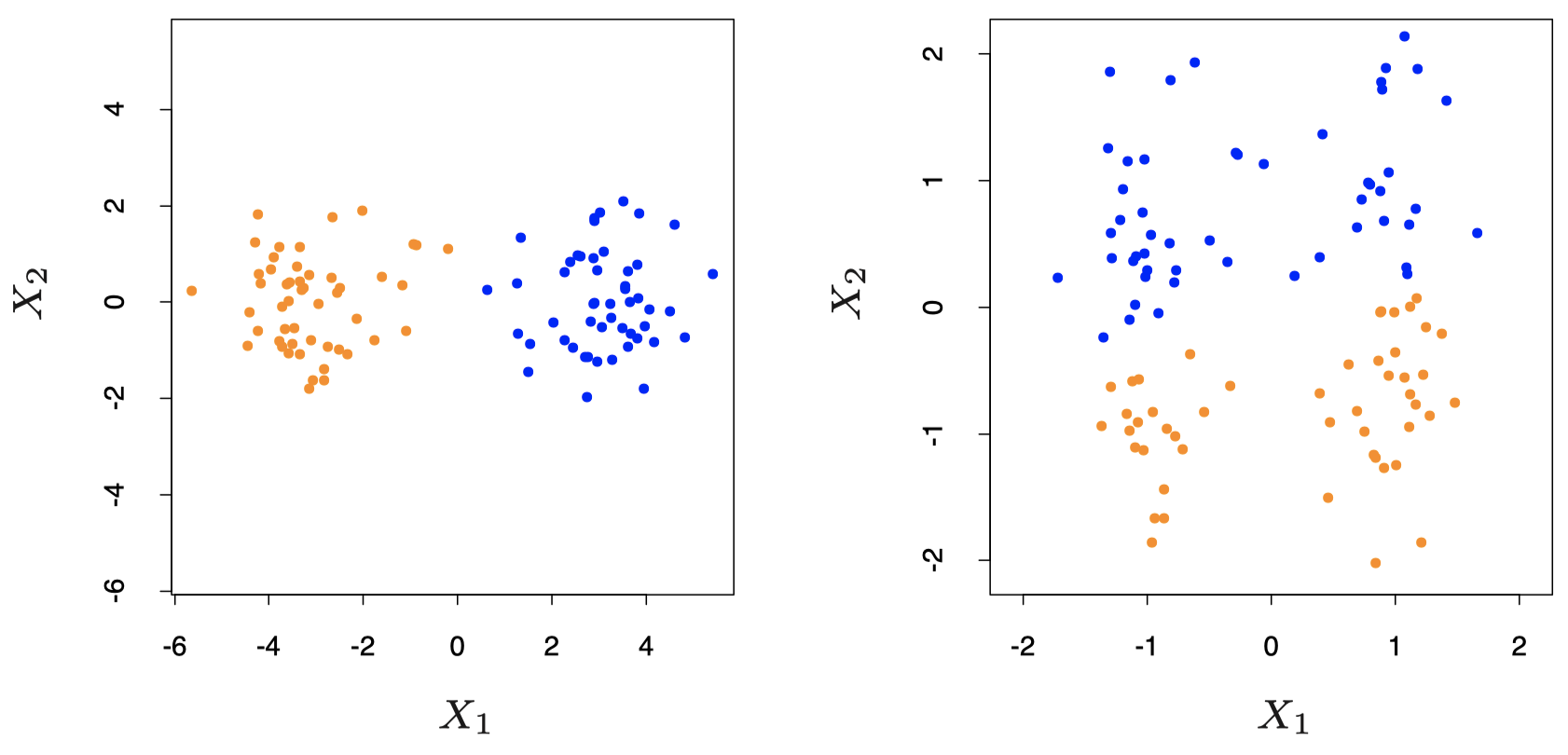
图 1：模拟数据的例子。左图：将 $K\text{-means}$ 聚类 ($K = 2$) 应用于原始数据。两种不同颜色表示分到不同簇的成员。右图：在聚类之前先对特征进行标准化，这等效于使用特征权重 $1/[2\cdot \mathrm{Var}(X_j)]$。可以看到，标准化使两个完全分开的组之间的边界变得模糊。请注意，两张图在水平和垂直轴上使用的单位都是相同的。

问题在于，因为我们处于无监督问题下，所以我们无法知道哪些分量对于聚类最重要：事实上，我们并不清楚我们要寻找的是怎样的结果，并且也没有任何训练数据可以指导我们。

由于每个问题都不相同，我们需要仔细审视我们的问题，以决定如何对分量进行加权。这对于任何聚类算法的成功至关重要。

5. 聚类算法

聚类算法可以分为三种不同的类型：

• 组合算法 (Combinatorial algorithms)：直接在观测数据上进行处理，并不直接参考任何潜在的概率模型。
• 混合建模 (Mixture modeling)：假设数据是来自由某个概率密度函数描述的总体的 i.i.d 样本。该密度函数是各个分量密度函数的一个混合，其中，每个分量密度函数描述了一个簇。
• 模式发现者/凸点搜索 (Mode seekers/Bump hunters)：从非参数角度出发，试图直接估计概率密度函数的不同模式。然后，最接近每种模式的观测值将定义各个簇。

6. 组合算法

组合算法是目前最流行的聚类算法，它将 $n$ 个要聚类的个体中的每一个都分配到一个组或一个簇中，而不考虑描述数据的概率模型。

每个观测值/个体用整数 \(i\in \{1,\dots,n\}\) 唯一标记。

开始之前，我们需要先确定簇 $K$ 的数量。

每个个体都被分配到一个且仅一个簇。我们用符号 $\mathcal C$ 表示 编码器 (encoder) 函数 (或者 聚类器 (clusterer))，它将个体划分为簇 $\mathcal C_1,\dots,\mathcal C_K$，并且我们用 $k = \mathcal C(i)$ 表示将个体 $i$ 分配给簇 \(k\in \{1,\dots,K\}\)。

我们通过最小化一个能够表征聚类未达标程度的损失函数来确定编码器映射 $\mathcal C()$。

一个自然的损失函数可能是

\[W(\mathcal C) = \sum_{k=1}^{K}\sum_{\mathcal C(i)=k}\sum_{\mathcal C(i')=k}D_{ii'}\]

尽管我们更倾向于使用

\[W(\mathcal C) = \dfrac{1}{2}\sum_{k=1}^{K} \dfrac{1}{n_k}\sum_{\mathcal C(i)=k}\sum_{\mathcal C(i')=k}D_{ii'}\]

其中，

\[n_k = \sum_{i=1}^{n}I\{\mathcal C(i)=k\}\]

是簇 $k$ 中的个体数量。

我们将上面的损失函数 $W(\mathcal C)$ 称为 簇内变化 (within-cluster variation)，因为它测量了一个给定簇内各个个体之间相异度的平均总和，然后对所有簇进行求和。如果簇内个体之间相似度较高，则 $W(\mathcal C)$ 趋向于较小的值，即对于 $\mathcal C(i)=\mathcal C(i’)$ 的情况，$D_{ii’}$ 较小。

我们将根据每个簇的大小进行重新缩放，否则损失函数可能会被非常大的簇所主导。

注意：ELS 中使用的簇内变化不会根据簇大小进行调整；这与 ISLR 中是一样的。

ISLR：An introduction to Statistical Learning with Applications in R by James, G, Witten, D, Hastie, T and Tibshirani, R.

对于将 $n$ 个数据点分给 $K$ 个簇，我们通常无法考虑其所有可能的分配 $\mathcal C$，除非数据集确实非常小。

根据 Jain and Dubes (1988)，所有可能的不同分配的数量为：

\[S(n,K) = \dfrac{1}{K!}\sum_{k=1}^{K}(-1)^{K-k} {K \choose k} k^n\]

例如，$S(10,4)= 34105$ 还不算太大。但是 $S(19,4)\approx 10^{10}$，而大多数聚类问题涉及的数据集通常比 $n = 19$ 还要大得多。

因此，我们不得不依靠 “贪婪” 迭代算法，这与我们之前在训练回归树的过程中用到的贪婪方法类似。

• 我们从个体的初始划分开始，通常是通过将个体随机分配给 $K$ 个簇来选择的。
• 然后在每次迭代中，我们尝试改善划分：更改簇的分配，使得要优化标准的值 (例如 $W(\mathcal C)$) 在前一轮的基础上有所改善。
• 当算法不再能够改善我们的标准时，则停止迭代，并将当前划分作为解决方案。

这种类型的算法仅考虑将个体划分为 $K$ 个簇的所有可能划分中的一小部分。通常，它将收敛到局部最优，与全局最优相比，局部最优可能会处于次优状态。

7. $K\text{-means}$ 算法

$K\text{-means}$ 算法是一种主流的迭代下降聚类方法。它专用于所有变量类型都是定量的情况，并采用平方欧式距离作为相异度：

\[D_{ii'} = \mathcal D(\mathcal X_i, \mathcal X_{i'}) = \|\mathcal X_i - \mathcal X_{i'}\|^2 = \sum_{j=1}^{p} d(\mathcal X_{ij},\mathcal X_{i'j}) = \sum_{j=1}^{p}(\mathcal X_{ij} - \mathcal X_{i'j})^2\]

其中，$\mathcal X_i \in \mathbb R^p\;\; (i=1,\dots,n)$ 是定量变量。

(如前所述，我们可以在使用聚类算法之前先对 $\mathcal X_{ij}$ 进行重新缩放)。

目标：将 $n$ 个个体分配到 $K$ 个簇中，使得下式最小化

\[W(\mathcal C) = \dfrac{1}{2}\sum_{k=1}^{K} \dfrac{1}{n_k}\sum_{\mathcal C(i)=k}\sum_{\mathcal C(i')=k} \|\mathcal X_i - \mathcal X_{i'}\|^2 = \sum_{k=1}^{K} \sum_{\mathcal C(i)=k} \|\mathcal X_i - \overline{\mathcal X}_k\|^2\]

其中，$\overline{\mathcal X}_k = (\overline{\mathcal X}_{k1},\dots,\overline{\mathcal X}_{kp})^{\mathrm T}$ 表示分配给簇 $k$ 的 $\mathcal X_i$ 的均值向量。

这等价于：寻找使簇内方差最小化的划分。(创建紧密环绕在均值附近的簇)

注意：我们总是有 $m$ 个观测值 $Y_1,\dots,Y_m$ 经验均值 $\overline Y$ 使得

\[\overline Y =\mathop{\operatorname{arg\,min}}\limits_c \sum_{i=1}^{m}\|Y_i - c\|^2\]

寻找使得下式最小化的 $\mathcal C$

\[W(\mathcal C) = \sum_{k=1}^{K} \sum_{\mathcal C(i)=k} \|\mathcal X_i - \overline{\mathcal X}_k\|^2\]

等价于寻找 $\mathcal C$ 和常数 $c_1,\dots,c_K$，使得下式在 $\mathcal C$ 和常数 $c_1,\dots,c_K$ 上最小化

\[\sum_{k=1}^{K} \sum_{\mathcal C(i)=k} \|\mathcal X_i - c_k\|^2 \tag{1}\label{eq1}\]

$K\text{-means}$ 算法：一种 迭代下降 (iterative descent) 算法，通过交替在 $\mathcal C$ 上最小化与在 $c_1,\dots,c_K$ 上最小化的方式进行迭代，从而找到最优解的一个近似。

其工作方式如下：

1. 首先，将个体初始聚类到 $K$ 个簇 $\mathcal C_1^1,\dots,\mathcal C_K^1$ 中，并且令 $\mathcal C^1$ 表示将每个个体分配给这些簇之一所对应的编码器。

2. 对于 $\ell = 1,2,\dots$ (重复直到算法停止)：
   (a) 对于编码器 $\mathcal C^{\ell}$，对 $k=1,\dots,K$，令 $\overline{\mathcal X}_{k}^{\ell}$ 表示簇 $\mathcal C_{k}^{\ell}$ 内的所有个体 $\mathcal X_i$ 的当前均值。

   (b) 找到一个新的聚类器 $\mathcal C^{\ell +1}$，使得对于 $i=1,\dots,n$，

   \[\mathcal C^{\ell +1}(i) = \mathop{\operatorname{arg\,min}}\limits_{k=1,\dots,K} \|\mathcal X_i - \overline{\mathcal X}_k^{\ell}\|^2\]

   $\quad \; \mathcal C^{\ell +1}$ 将 $n$ 个个体分配给 $K$ 个簇，记为

   \[\mathcal C_1^{\ell +1},\dots,\mathcal C_K^{\ell +1}\]

说明：

• 数据的初始聚类是通过将 $n$ 个个体随机分配给相同大小的 $K$ 个聚类进行的；如果 $n$ 不是 $K$ 的整数倍，则保证各簇大小大致相同即可。

• 步骤 (a)：当 $\mathcal C=\mathcal C^{\ell}$ 时，在 $c_1,\dots,c_K$ 上最小化式 $(\ref{eq1})$，我们将得到 $c_k = \overline{\mathcal X}_k^{\ell}$。

• 步骤 (b)：当 $c_k = \overline{\mathcal X}_k^{\ell}$ 时，在 $\mathcal C$ 上最小化式 $(\ref{eq1})$，为了找到步骤 (b) 中的 $\mathcal C^{\ell+1}$，对于 $i = 1,\dots,n$，它将第 $i$ 个个体重新分配给在上一步中得到的均值 $\overline{\mathcal X}_k^{\ell}$ 最接近 $\mathcal X_i$ 的簇 $k$。

例子 1：随机二维数据集上应用 $K\text{-means}$ 聚类 ($K=3$)

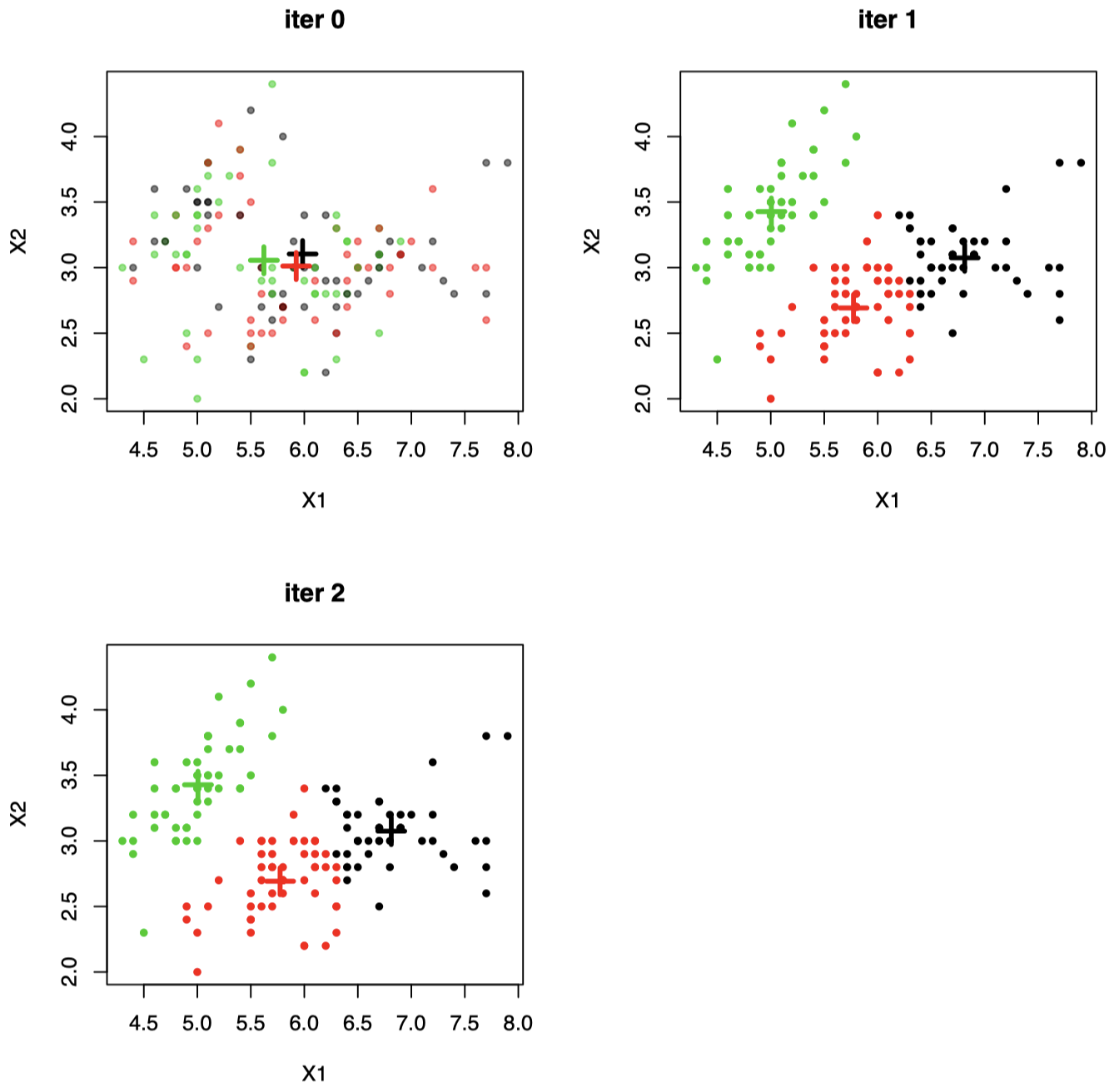
图 2：当 $\mathcal X_i \in \mathbb R^2$ 时，随机初始聚类的示例：仅经过 $2$ 次迭代即可收敛。图中 “$+$” 代表聚类中心。每个数据点都会移动到中心最接近的簇。

例子 2：Iris 数据集上应用 $K\text{-means}$ 聚类 ($K=3$)

Iris 数据集可以天然分为三类 (鸢尾花类型)：可以看到，$K\text{-means}$ 算法发现了这些不同类型。这里，我们使用全部 $4$ 个 $X_j \;(X_i \in \mathbb R^4)$ 进行聚类，但是每次绘制一个 $2$ 维图。

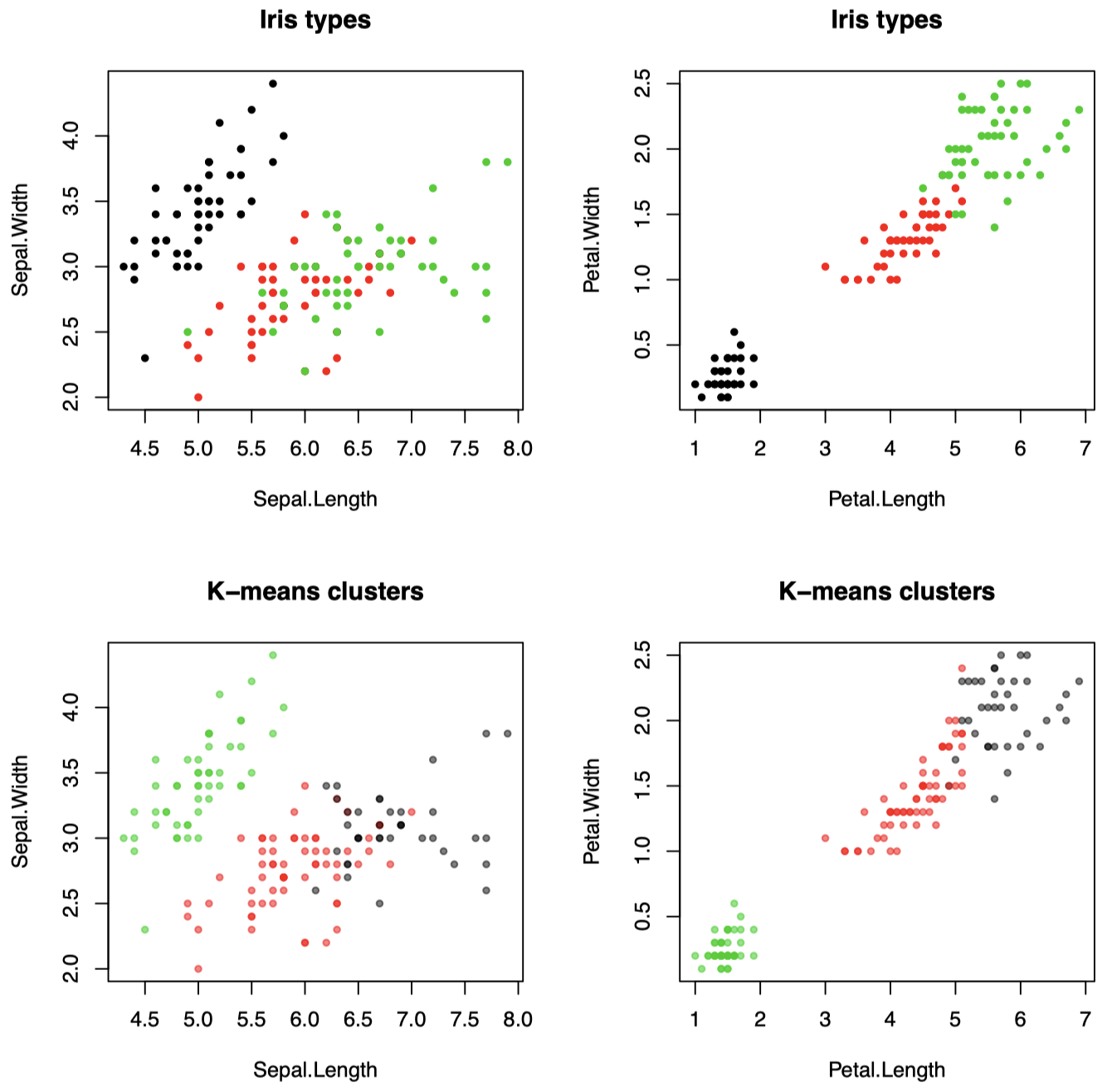
图 3：Iris 数据集上应用 $K\text{-means}$ 聚类 ($K=3$)，使用全部 $4$ 个 $X_j \;(X_i \in \mathbb R^4)$ 进行聚类，每次绘制一个 $2$ 维图。

为了查看每个 $\mathcal X_i$ 都已经距离其簇均值最接近，则意味着我们需要同时对这 $4$ 个维度进行可视化。如果我们仅查看 $2$ 个维度，则每个点不一定是最接近其簇的 $2$ 维均值：如果 $x,\mu_1,\dots,\mu_K \in \mathbb R^4$，并且对于一个向量 $v\in \mathbb R^4$，我们令 $\tilde v$ 表示其前两个分量，然后

\[\require{cancel} \mu_{\ell} = \mathop{\operatorname{arg\,min}}\limits_{k} \|x - \mu_k\|^2 \quad \cancel{\Longrightarrow} \quad \tilde \mu_{\ell} = \mathop{\operatorname{arg\,min}}\limits_{k} \| \tilde x - \tilde \mu_k\|^2\]

这是一个简单的示例，因为数据来自 $3$ 个分隔良好的组，并且我们也知道我们希望得到 $3$ 个分组。但是，实际情况并非总是如此，在真正的聚类问题中我们应该如何选择 $K$？

迭代的 $K\text{-means}$ 算法最终将会收敛，因为在每一步中的式 $(\ref{eq1})$ 标准的值都会减小。但是，它通常会收敛到式 $(\ref{eq1})$ 的局部最小值，它通常找不到全局最优解。

由于该过程取决于随机初始聚类器 $\mathcal C^1$，通常我们可以使用几个不同的随机起始点多次重复该过程，并且在收敛后采用具有式 $(\ref{eq1})$ 最小值的聚类方案。

8. $K\text{- medoids}$ 算法

如前所述，平方欧几里得距离高度强调很大的值，这将使得聚类算法对于离群值不具有鲁棒性。我们可以用更加通用的相异性度量代替。

$K\text{- medoids}$ 算法有以下两种泛化方式：

• 它使用更加通用的相异性度量。
• 它使用更加通用的中心点来代替每个簇均值，该中心点是该簇内的一个实际数据点。

对于 $K\text{- medoids}$，我们需要的只是一个 $n\times n$ 的相异度矩阵 $D$，目的是最小化之前讨论过的更加通用的损失函数：

\[W(\mathcal C) = \dfrac{1}{2}\sum_{k=1}^{K} \dfrac{1}{n_k}\sum_{\mathcal C(i)=k}\sum_{\mathcal C(i')=k}D_{ii'}\]

该算法工作流程如下：

1. 首先，将个体初始聚类到 $K$ 个簇 $\mathcal C_1^1,\dots,\mathcal C_K^1$ 中，并且令 $\mathcal C^1$ 表示将每个个体分配给这些簇之一所对应的编码器。

2. 对于 $\ell = 1,2,\dots$ (只要标准发生变化就继续迭代)：
   (a) 对于编码器 $\mathcal C^{\ell}$，对 $k=1,\dots,K$，找到

   \[i_k^{\ell} = \mathop{\operatorname{arg\,min}}\limits_{\{i:\, \mathcal C(i)=k\}} \sum_{\mathcal C(i')=k} D_{ii'}\]

   $\quad \;$并且将第 $i_k^{\ell}$ 个个体选为簇 $k$ 的中心个体。

   (b) 找到一个新的聚类器 $\mathcal C^{\ell +1}$，使得对于 $i=1,\dots,n$，

   \[\mathcal C^{\ell +1}(i) = \mathop{\operatorname{arg\,min}}\limits_{k=1,\dots,K} D_{i i_k^{\ell}}\]

   $\quad \; \mathcal C^{\ell +1}$ 会将我们的数据重新分配给 $K$ 个新的簇。

说明：

• 步骤 (a)：找到总体上与簇 $k$ 中所有点距离最近的个体 $i_k^{\ell}$，并将其将作为该簇的中心点。
• 步骤 (b)：创建一个新的划分，将每个个体重新分配给其最接近的中心观测点 $i_k^{\ell}$ 所在的簇。
• 通常，$K\text{- medoids}$ 算法要比 $K\text{- means}$ 算法的时间开销高得多，因为寻找每个中心点的过程涉及 $O(n_k^2)$ 次计算。
• 注意：对于 $K\text{- medoids}$ 算法，上面我们的表述是 “只要标准发生变化就继续迭代”，而没有像教材 ESL 中描述的 “直到分配不再变化即停止”。与 $K\text{- means}$ 不同，我不认为这里可以保证标准值每次迭代都会下降，具体请参阅 Wiki 页面上有关 Voronoi 迭代方法的说明。

例子：ESL 第 517 页的示例，源自 Kaufman and Rousseeuw (1990)

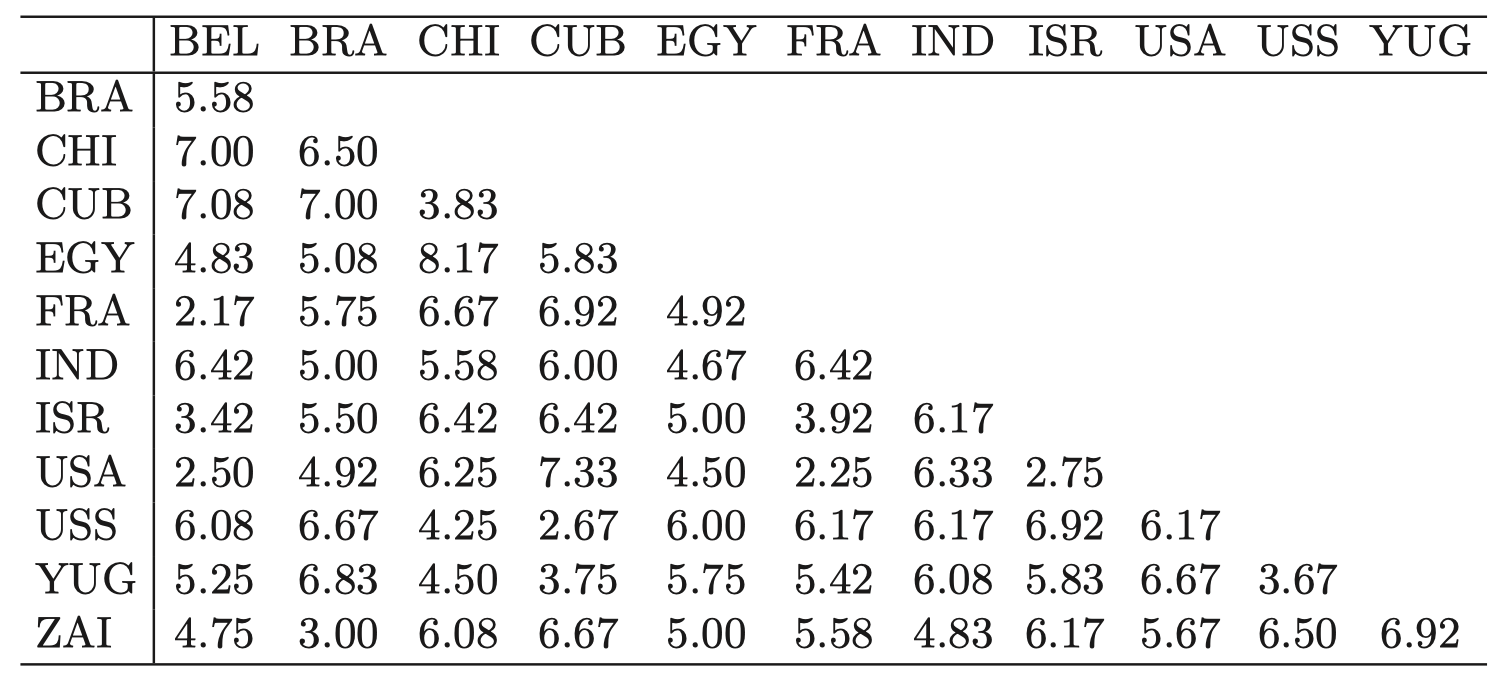
一群政治学专业的学生要求为 $12$ 个国家 (当时存在的国家) 提供成对的相异性度量：比利时 (BEL)、巴西 (BRA)、智利 (CHI)、古巴 (CUB)、埃及 (EGY)、法国 (FRA)、印度 (IND)、以色列 (ISR)、美国 (USA)、苏维埃社会主义共和国联盟 (USS)、南斯拉夫 (YUG) 和扎伊尔 (ZAI)。

通过对学生们给出的相异度取平均值，创建一个 $12\times12$ 的相异度矩阵 $D$，得到下表。全零对角线在这里没有显示。

表 1：政治学调查的数据：表中的值是根据发给政治学专业学生的问卷调查得出的国家/地区的平均成对相异度。

我们在相异度矩阵 $D$ 上应用 $3\text{-medoids}$ 算法，得到下面的聚类结果：

图 4：政治学调查的数据：在相异度矩阵 $D$ 上应用 $3\text{-medoids}$ 算法。使用 多维缩放 (multidimensional scaling) 得到关于结果簇的二维表示。

9. 如何选择 $K$

在应用 $K\text{-means}$ 或者 $K\text{-medoids}$ 算法之前，我们必须先确定簇的数量 $K$。对于大多数问题，这通常需要根据实际数据进行估算，除非某些特定应用已经给出了 $K$ 的自然值建议。

一种启发式方法：对范围 \(\{1,\dots,K_{\max}\}\) 的 $K$ 执行聚类，这将生成一系列簇内变化值 $W_1,\dots,W_{\max}$，通常将随着 $K$ 的增加而逐渐减小。

从直觉上看，如果在数据之下存在一个 “真实” 的簇数量 $K^*$，我们期望

\[\{W_K - W_{K+1} \mid K < K^*\} \gg \{W_K - W_{K+1} \mid K \ge K^* \}\]

如果将 $W_K$ 绘制为一个关于 $K$ 的函数，我们可以期望在真实值 $K^*$ 附近将出现 “扭结 (kink)”。

10. 层次聚类

应用 $K\text{-means}$ 或者 $K\text{-medoids}$ 算法的结果取决于预先定义的簇的数量以及初始划分设定。相比之下，层次聚类 (hierarchical clustering) 方法对这些没有要求。作为替代，我们将生成一个层次结构表示，通过合并下一个较低级别的簇来生成较高层次结构的簇，这需要一个不同组之间的相异性度量。

层次聚类通常可以分为两种基本策略：凝聚法 (agglomerative) 和 分裂法 (divisive)。

• 凝聚法 (自底向上)：
  • 从 $n$ 个组开始 (每个组包含 $1$ 个个体)。
  • 在每个层级上，递归合并一对簇以形成一个更大的簇 $\quad \Longrightarrow \quad$ 在下一个更高层级上减少一个簇。
  • 选择合并的簇对是使得组间相异度最小化的簇对。
• 分裂法 (自顶向下)：
  • 初始时，所有数据都在一个组内。
  • 在每个层级上将一个现有的簇递归地分成两部分。
  • 选择拆分的组是使得生成的两个新组之间相异度最大化的组。

这两种算法在层次结构中都具有 $n-1$ 个层级。完整的层次结构表示这种分组/拆分的有序序列。

至于在哪个层级上代表数据 “自然的” 聚类则由用户决定。这实际上等同于一般聚类算法如 $K\text{- means}$ 选择 $K$。有一些自动技术可以做到这点，但是它们通常需要手动进行微调，并且不一定 “做得很好”。

通常，用户会选择看上去对他们的特定问题最有用/最有趣的 $K$ 值。

上面两种方法都可以用一棵有根的二叉树来表示：

• 树的结点 $\quad \Longleftarrow \quad$ 组
• 根结点 $\quad \Longleftarrow \quad$ 完整数据
• 终端结点 $\quad \Longleftarrow \quad$ 各观测值
• 每个非终端结点都有两个子结点。对于分裂法，这两个子结点代表由父结点拆分产生的两个组；对于凝聚法，子结点表示被合并为父结点的两个组。

单调性 (Monotonicity property)：大多数凝聚法和某些分裂法 (当我们将自底向上视为一系列合并时)，合并后的簇之间的相异度会随着层级的增加而增加：每次我们合并两个簇时，它们之间的相异度要比在之前层级上合并两个簇时的相异度更大。

当上述单调性能够满足时，该二叉树可以绘制为一个 dendogram 图，其中每个结点的高度 (从最底部算起) 与两个子结点之间的相异度成比例。终端结点的高度为零 (因为它们没有子结点)。

例子：人体肿瘤微阵列数据上应用层次聚类

数据：$p=6820, n=64$。每个 $i=1,\dots,n$ 代表某种类型的癌症肿瘤样品 (乳腺，肾等)。每个 $j = 1,\dots,p$ 是根据 DNA 芯片实验测得的给定基因 $j$ 的表达水平。

目标：查看基于基因表达水平的聚类是否可以形成不同癌症类型的分组。

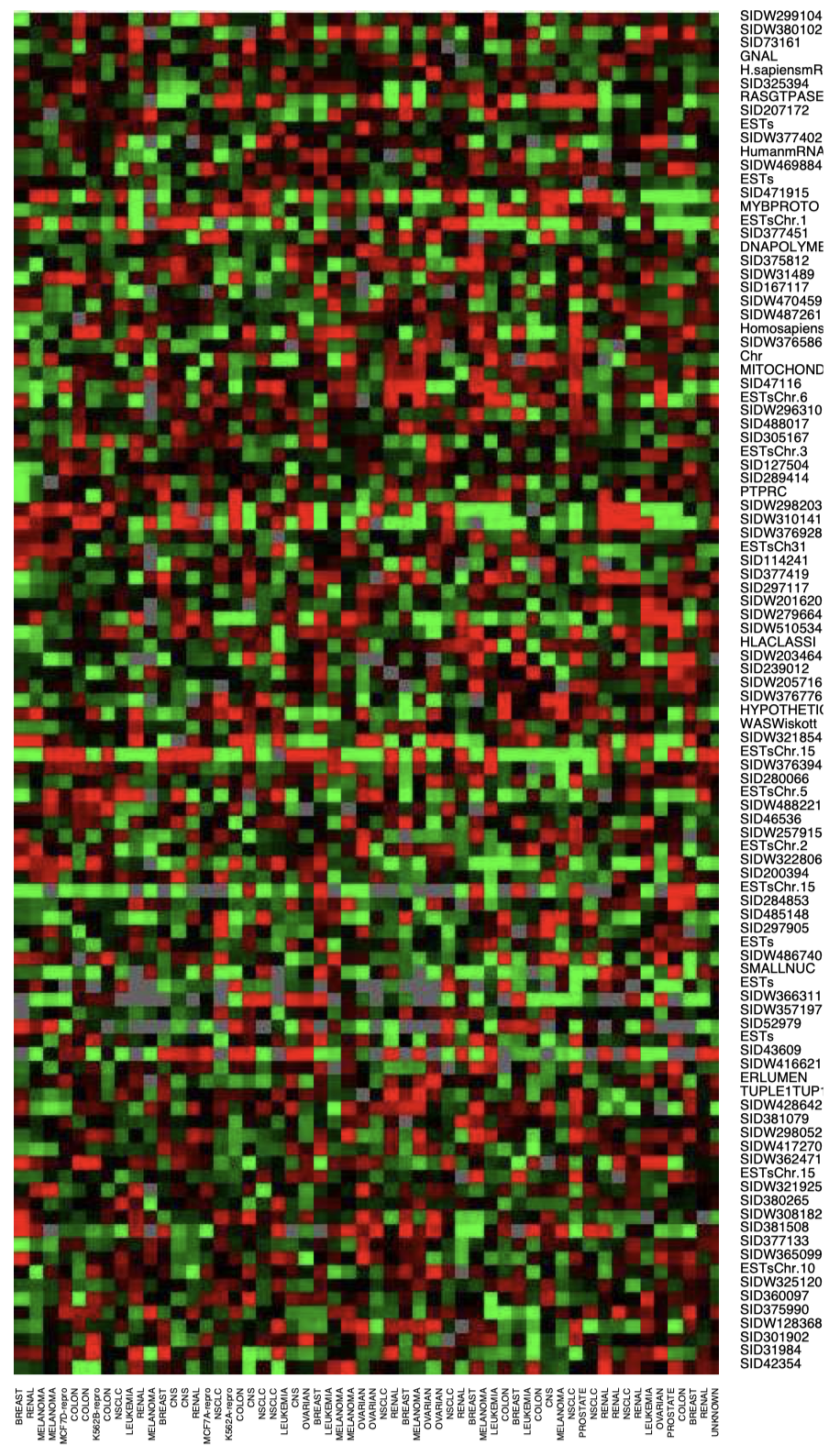
图 5：DNA 微阵列数据：$6830$ 个基因 (行) 和 $64$ 个样本 (列) 的表达矩阵，用于人类肿瘤数据。这里仅显示了基于 $100$ 行随机样本的热力图，范围从鲜绿色 (负，表达不足) 到鲜红色 (正，表达过度)，灰色表示缺失值。行和列以随机选择的顺序显示。

Dendogram 图的例子：

图 6：人类肿瘤微阵列数据，通过采用平均连接的凝聚法层次聚类生成的 dendogram 图。

(严格来说，我认为它们应该将所有终端结点一直延伸到底部)。

10.1 凝聚聚类

凝聚聚类算法过程如下：

• 初始时，每个观测都代表一个单例簇。
• 对于 $n-1$ 步中的每一步，我们将两个最不相似的簇合并为一个簇，同时在下一个更高层级上减少一个簇。
• 我们需要选择两个簇之间的相异性度量。
• 令 $G$ 和 $H$ 分别代表两个簇。$G$ 和 $H$ 之间的相异度 $d(G,H)$ 是根据一系列成对的观测相异度 $D_{ii’}$ 计算得到的，其中 $i$ 在簇 $G$ 内，$i’$ 在簇 $H$ 内。

• 有很多不同方法可以衡量这种簇间相异度：

  • 单连接凝聚聚类 (Single linkage agglomerative clustering, SL)：将最小成对相异度作为组间相异度：

    \[d(H,G) = \min \limits_{i\in G, i' \in H} D_{ii'}\]

    (也被称为最近邻技术)

  • 全连接凝聚聚类 (Complete linkage agglomerative clustering, CL)：将最大成对相异度作为组间相异度：

    \[d(H,G) = \max \limits_{i\in G, i' \in H} D_{ii'}\]

    (也被称为最远邻技术)

  • 组平均凝聚聚类 (Group average agglomerative clustering, GA)：使用组间平均相异度：

    \[d(H,G) = \dfrac{1}{n_H}\dfrac{1}{n_G} \sum_{i\in G, i' \in H} D_{ii'}\]

    其中，$n_H$ 和 $n_G$ 分别为 $H$ 和 $G$ 中的观测数量。

• 如果数据相异度 $D_{ii’}$ 表现出很强的聚类趋势，并且每个簇中的观测值都聚集在中心附近，并且与其他簇分隔良好，那么上面三种不同的簇间相异度计算方法会得到相似的结果。否则，它们会产生完全不同的结果。

• 在人体肿瘤微阵列数据上分别应用上面 $3$ 种不同的簇间相异度计算方法得到的 dendogram 图：

  

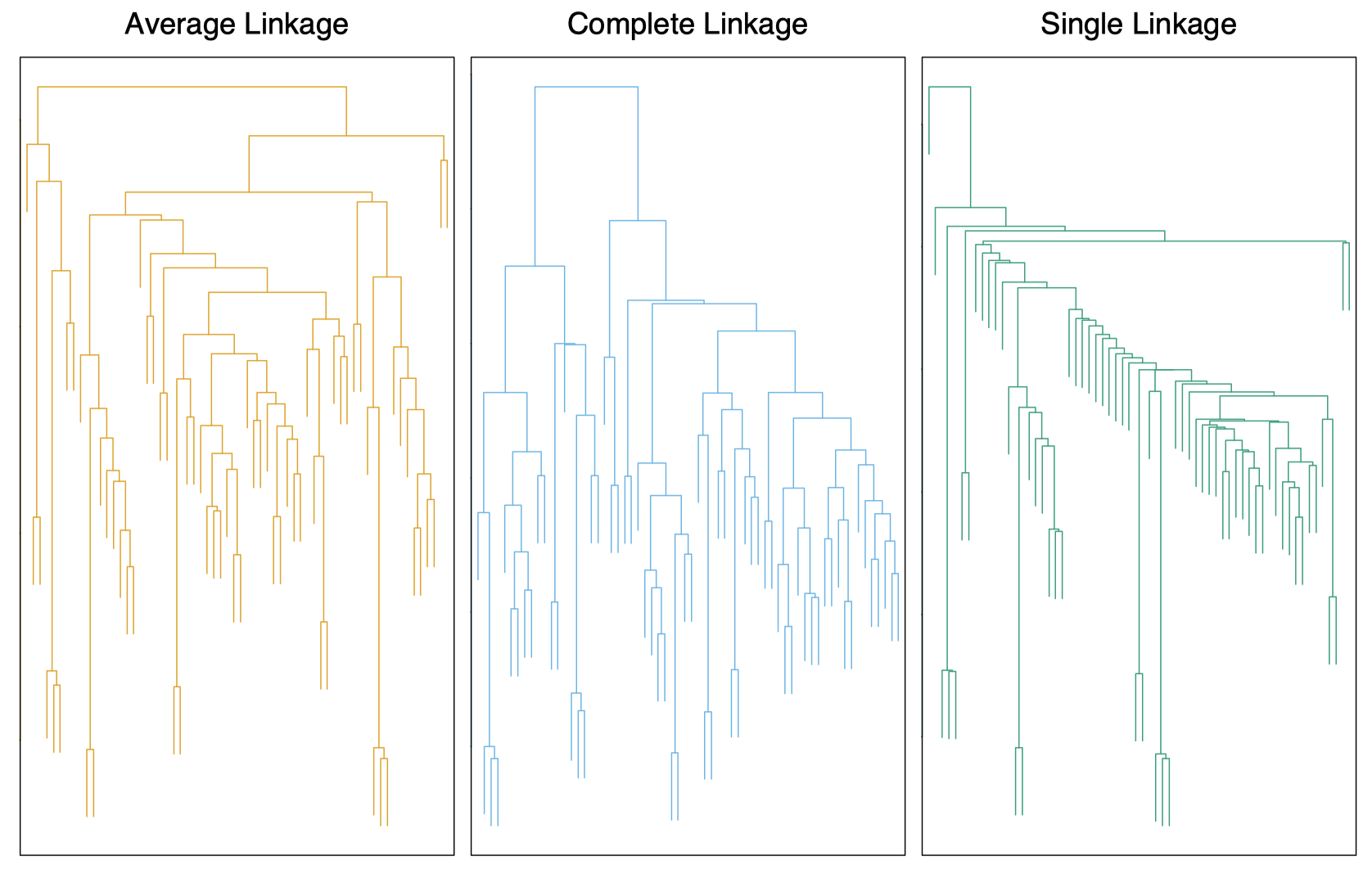
  图 7：人类肿瘤微阵列数据，通过 $3$ 种不同的簇间相异度计算方法得到的 dendogram 图。左图：平均连接。中图：全连接。右图：单连接。

10.2 分裂聚类

分裂聚类算法以全部数据作为一个簇开始，并且以自顶向下的方式进行，在每次迭代中将现有的一个簇分为两个子簇。可以通过递归应用 $K = 2$ 的 $K\text{-means}$ 或 $K\text{-medoids}$ 来实现。但是这种方法可能无法满足 dendogram 图表示所要求的单调性。

Macnaughton Smith 等人 (1965) 提出了一种避免这些问题的方法：

• 初始时，将所有观测个体放入一个单独的簇 $G$ 中。
• 然后，选择与其他所有个体的平均相异度最大的那个个体，并将这个个体作为第二个簇 $H$ 中的第一个成员。
• 在每个后继步中，对于 $G$ 中的每个个体，计算其到 $H$ 中的各个个体的平均距离，并减去它到 $G$ 中其余个体的平均距离，然后选择结果最大的那个个体并将其转移到簇 $H$ 中。
• 该过程一直持续进行，直到相应差值的平均值变为负数，即 $G$ 中不再有任何这样的观测：它在平均意义上更接近于 $H$ 中的个体而不是 $G$ 中的其他个体。

其结果是将原始的簇分为了两个子簇：转移到 $H$ 的个体，以及其余留在 $G$ 中的个体。这两个簇代表了层次结构的第二层级。

每个后继层级都可以通过将上述拆分过程应用于前一层级的簇之一得到。

持续该递归拆分过程，直到所有簇要么成为单例 (只包含一个观测)，要么每个簇内的所有成员与其它簇之间的相异度为零。

当然，还有一些其他版本的分裂聚类算法 (如有兴趣，请参阅 ESL 中的参考文献)。

本作品采用知识共享署名-非商业性使用-相同方式共享 4.0 国际许可协议进行许可。 欢迎转载，并请注明来自：YEY 的博客 同时保持文章内容的完整和以上声明信息！

---

• Previous
  数据科学多元统计学 10：Bagging 和随机森林
• Next
  PyTorch 01：PyTorch 简介与安装

---