Lecture 18 优化器 (二)

上节课我们学习了 PyTorch 中优化器的主要属性和基本方法。我们知道优化器的主要作用是管理并更新我们的参数，并且在更新时会利用到参数的梯度信息，然后采用一定的更新策略来更新我们的参数。本节课我们将学习一些最常用的更新策略，例如随机梯度下降法等。

1. 学习率

梯度下降中的参数更新过程：

\[w_{i+1} = w_i - g(w_i)\]

其中，$g(w_i)$ 表示 $w_i$ 的梯度。

下面我们通过一个例子来观察梯度下降的过程以及可能存在的问题：

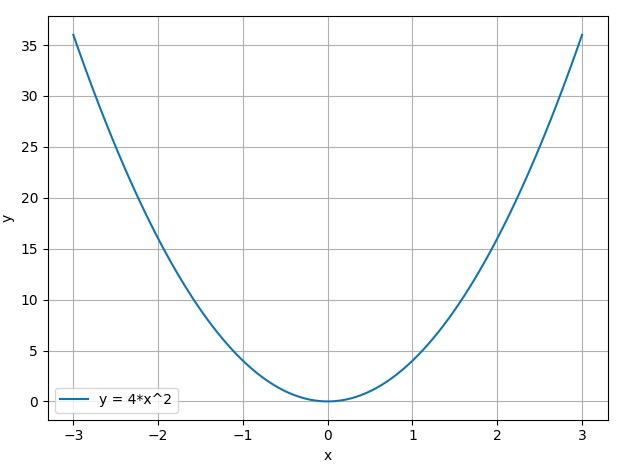
假设我们现在有一个函数：

\[y=f(x) = 4x^2\]

假设我们的起始点为 $x_0=2$，现在我们采用梯度下降法更新函数值 $y$ 使其达到其极小值点 $x=0$。首先我们求取 $y$ 的导函数：

\[y' = f'(x) = 8x\]

我们从起始点 $x_0=2$ 开始沿负梯度方向更新 $y$ 值：

$x_0 = 2, \; y_0 = 16,\; f’(x_0) = 16$

$x_1 = x_0 - f’(x_0) = 2 -16 = -14$
$x_1 = -14, \; y_1 = 784,\; f’(x_1) = -112$

$x_2 = x_1 - f’(x_1) = -14 + 112 = 98,\; y_2 = 38416$
……

我们发现，$y$ 值不但没有减小，反而越来越大了。这是什么原因导致的呢？下面我们先通过代码来演示这一过程，然后再分析导致该问题的原因。

首先，我们先绘制出函数曲线：

import torch
import numpy as np
import matplotlib.pyplot as plt

torch.manual_seed(1)

def func(x_t):
    """
    y = (2x)^2 = 4*x^2      dy/dx = 8x
    """
    return torch.pow(2*x_t, 2)

# init
x = torch.tensor([2.], requires_grad=True)

# plot data
x_t = torch.linspace(-3, 3, 100)
y = func(x_t)
plt.plot(x_t.numpy(), y.numpy(), label="y = 4*x^2")
plt.grid()
plt.xlabel("x")
plt.ylabel("y")
plt.legend()
plt.show()

输出结果：

下面我们通过代码来演示一下前面例子中的梯度下降过程：

iter_rec, loss_rec, x_rec = list(), list(), list()

lr = 1.
max_iteration = 4

for i in range(max_iteration):
    y = func(x)
    y.backward()

    print("Iter:{}, X:{:8}, X.grad:{:8}, loss:{:10}".format(
        i, x.detach().numpy()[0], x.grad.detach().numpy()[0], y.item()))

    x_rec.append(x.item())

    x.data.sub_(lr * x.grad)    # x -= x.grad  数学表达式意义:  x = x - x.grad
    x.grad.zero_()

    iter_rec.append(i)
    loss_rec.append(y)

plt.subplot(121).plot(iter_rec, loss_rec, '-ro')
plt.xlabel("Iteration")
plt.ylabel("Loss value")

x_t = torch.linspace(-3, 3, 100)
y = func(x_t)
plt.subplot(122).plot(x_t.numpy(), y.numpy(), label="y = 4*x^2")
plt.grid()
y_rec = [func(torch.tensor(i)).item() for i in x_rec]
plt.subplot(122).plot(x_rec, y_rec, '-ro')
plt.legend()
plt.show()

输出结果：

Iter:0, X:     2.0, X.grad:    16.0, loss:      16.0
Iter:1, X:   -14.0, X.grad:  -112.0, loss:     784.0
Iter:2, X:    98.0, X.grad:   784.0, loss:   38416.0
Iter:3, X:  -686.0, X.grad: -5488.0, loss: 1882384.0

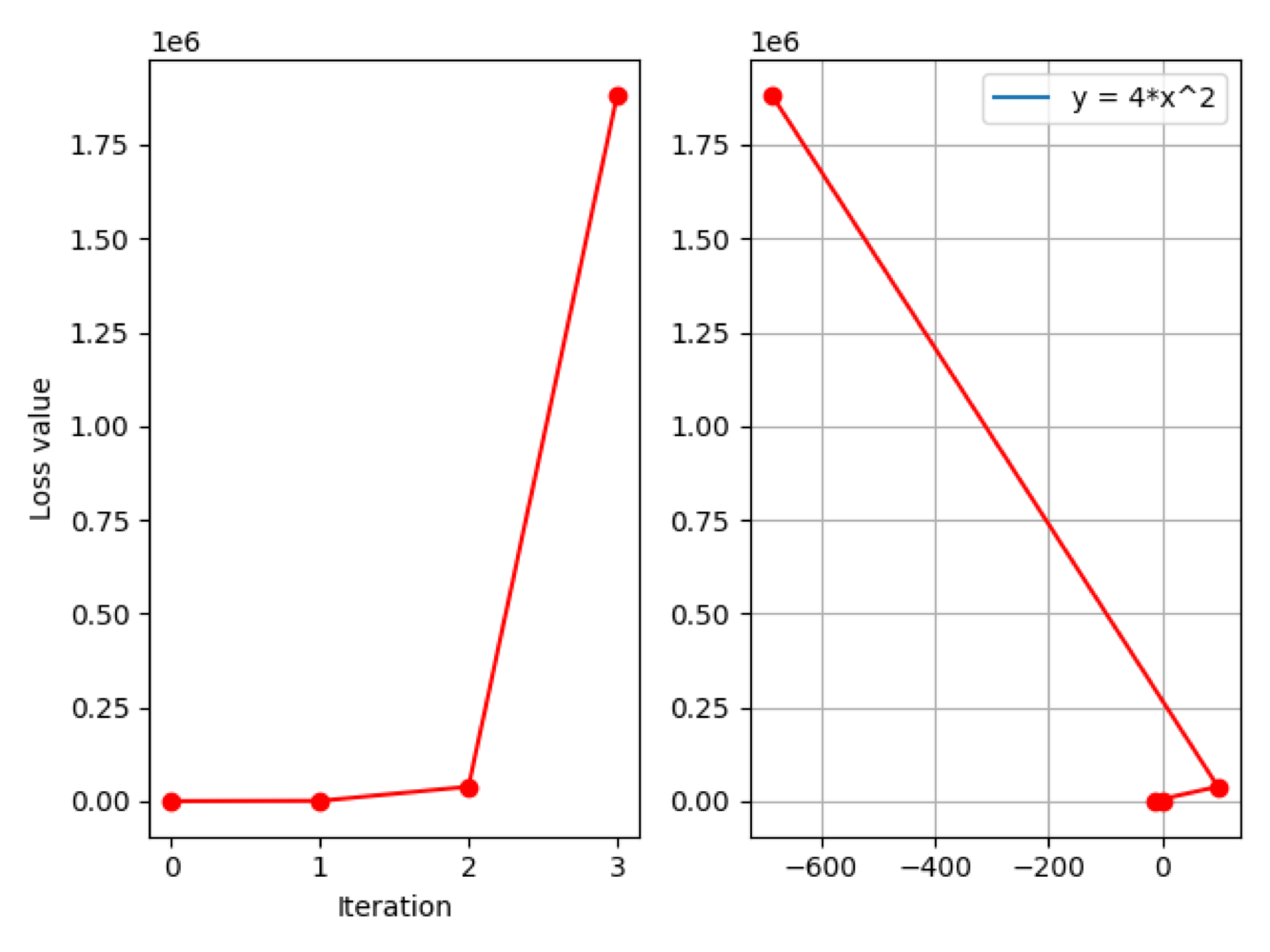
左边是 loss 曲线图，横轴是迭代次数，纵轴是 loss 值；右边是函数曲线图，由于尺度过大这里暂时看不出来函数形状。

从打印信息可以看到，在第 0 次迭代时，$x$ 的初始值为 $2$，对应梯度为 $16$，loss 值也是 $16$。随着迭代次数的增加，我们发现 loss 值激增到 $1882384$。所以，$y$ 并没有减小，反而是激增的，而梯度也达到了 $10^3$ 数量级，所以存在梯度爆炸的问题。

回到前面的梯度更新公式：

\[w_{i+1} = w_i - g(w_i)\]

这里可能存在一个问题，我们目前是直接减去梯度项 $g(w_i)$，而这里减去的梯度项可能由于其尺度过大从而导致参数项越来越大，从而导致函数值无法降低。因此，通常我们会在梯度项前面乘以一个系数，用于缩减尺度：

\[w_{i+1} = w_i - \mathrm{LR}\cdot g(w_i)\]

这里，我们将系数 $\mathrm{LR}$ 称为 学习率 (learning rate)，它被用来控制更新的步伐。

下面我们在代码中调整学习率，观察函数值的变化：

$\mathrm{LR} = 0.5$

lr = 0.5

输出结果：

Iter:0, X:     2.0, X.grad:    16.0, loss:      16.0
Iter:1, X:    -6.0, X.grad:   -48.0, loss:     144.0
Iter:2, X:    18.0, X.grad:   144.0, loss:    1296.0
Iter:3, X:   -54.0, X.grad:  -432.0, loss:   11664.0

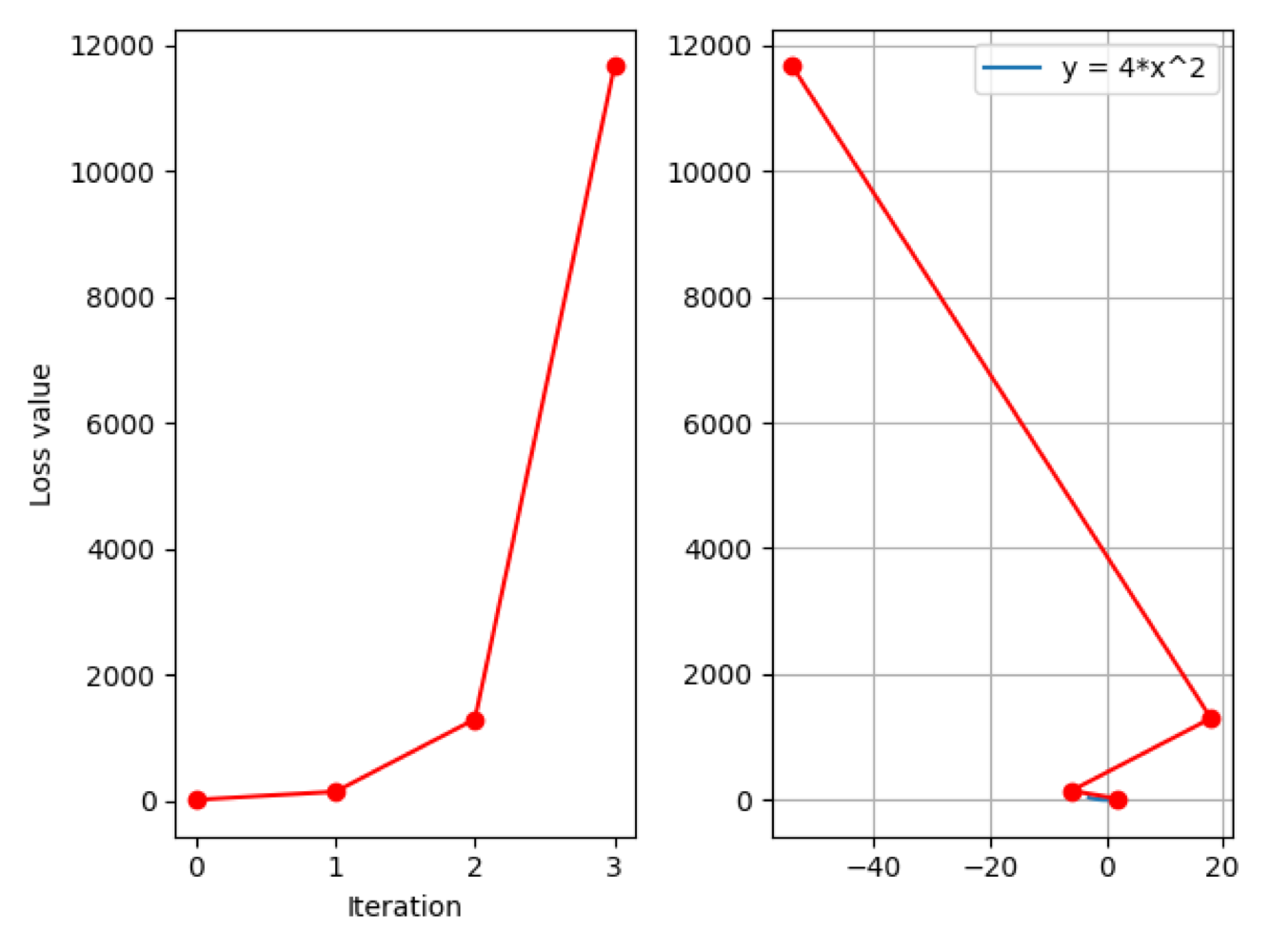
可以看到，loss 值仍然呈激增趋势，但是情况有所缓解，尺度比之前小了很多。

$\mathrm{LR} = 0.2$

lr = 0.2

输出结果：

Iter:0, X:     2.0, X.grad:    16.0, loss:      16.0
Iter:1, X:-1.2000000476837158, X.grad:-9.600000381469727, loss:5.760000228881836
Iter:2, X:0.7200000286102295, X.grad:5.760000228881836, loss:2.0736000537872314
Iter:3, X:-0.4320000410079956, X.grad:-3.456000328063965, loss:0.7464961409568787

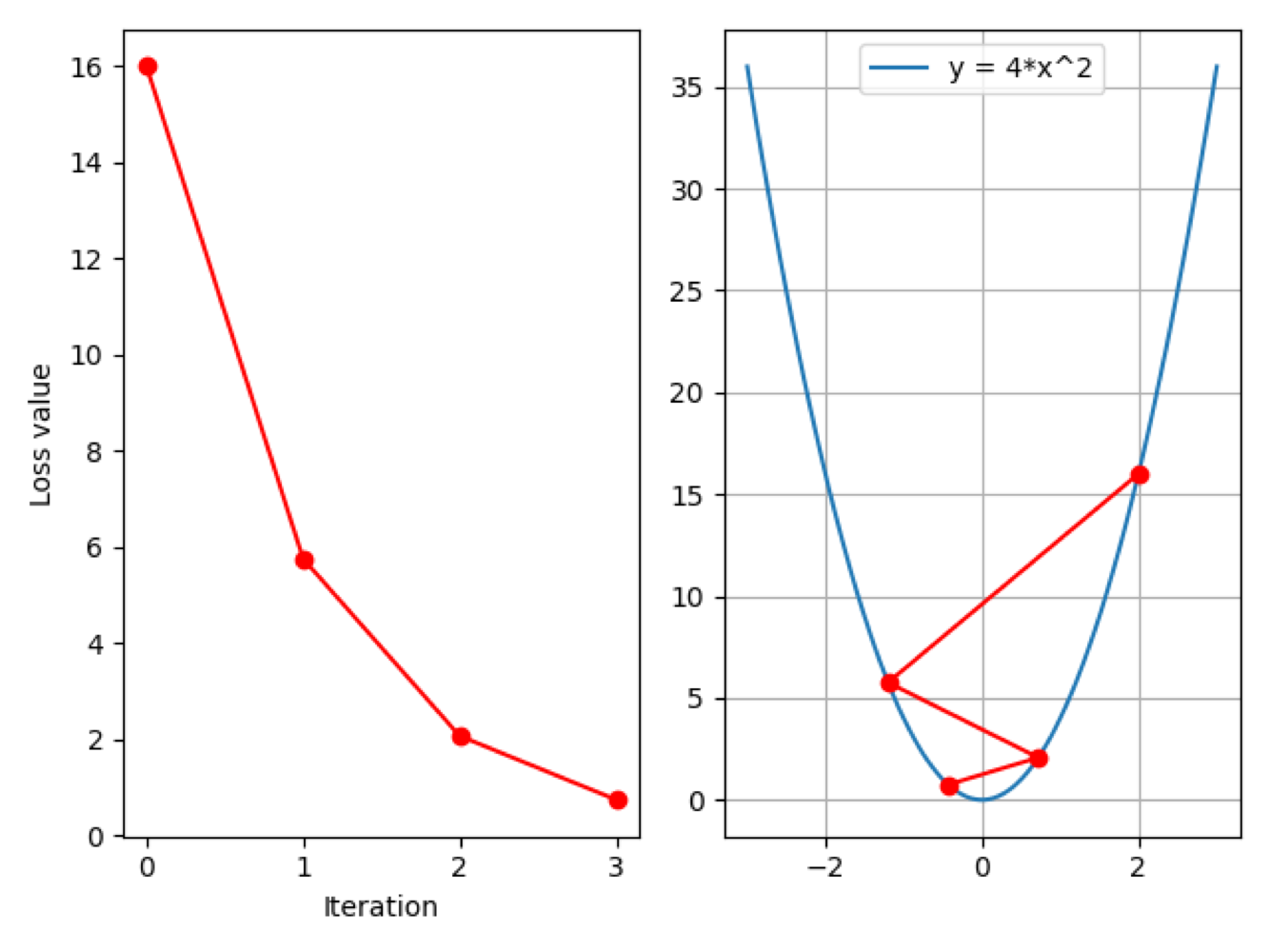
可以看到，现在 loss 值呈下降趋势，同时右图也可以看到正常的函数图像了。当前学习率为 $0.2$，从右图可以看到：初始点为 $x=2$，loss 值为 $16$；经过一步更新后来到点 $x = -1.2$，此时 loss 值为 $5.76$；然后再次迭代后来到 $x=0.72$，loss 值为 $2.07$；第三次迭代后，$x = -0.43$，loss 值为 $0.75$。

现在我们将增加迭代次数增加到 $20$ 次，来观察函数是否能够到达极小值点 $x=0$ 附近：

max_iteration = 20

输出结果：

Iter:0, X:     2.0, X.grad:    16.0, loss:      16.0
Iter:1, X:-1.2000000476837158, X.grad:-9.600000381469727, loss:5.760000228881836
Iter:2, X:0.7200000286102295, X.grad:5.760000228881836, loss:2.0736000537872314
Iter:3, X:-0.4320000410079956, X.grad:-3.456000328063965, loss:0.7464961409568787
Iter:4, X:0.2592000365257263, X.grad:2.0736002922058105, loss:0.26873862743377686
Iter:5, X:-0.1555200219154358, X.grad:-1.2441601753234863, loss:0.09674590826034546
Iter:6, X:0.09331201016902924, X.grad:0.7464960813522339, loss:0.03482852503657341
Iter:7, X:-0.05598720908164978, X.grad:-0.44789767265319824, loss:0.012538270093500614
Iter:8, X:0.03359232842922211, X.grad:0.26873862743377686, loss:0.004513778258115053
Iter:9, X:-0.020155396312475204, X.grad:-0.16124317049980164, loss:0.0016249599866569042
Iter:10, X:0.012093238532543182, X.grad:0.09674590826034546, loss:0.0005849856534041464
Iter:11, X:-0.007255943492054939, X.grad:-0.058047547936439514, loss:0.000210594866075553
Iter:12, X:0.0043535660952329636, X.grad:0.03482852876186371, loss:7.581415411550552e-05
Iter:13, X:-0.0026121395640075207, X.grad:-0.020897116512060165, loss:2.729309198912233e-05
Iter:14, X:0.001567283645272255, X.grad:0.01253826916217804, loss:9.825512279348914e-06
Iter:15, X:-0.0009403701405972242, X.grad:-0.007522961124777794, loss:3.537184056767728e-06
Iter:16, X:0.0005642221076413989, X.grad:0.004513776861131191, loss:1.2733863741232199e-06
Iter:17, X:-0.00033853325294330716, X.grad:-0.0027082660235464573, loss:4.584190662626497e-07
Iter:18, X:0.00020311994012445211, X.grad:0.001624959520995617, loss:1.6503084054875217e-07
Iter:19, X:-0.00012187196989543736, X.grad:-0.0009749757591634989, loss:5.941110714502429e-08

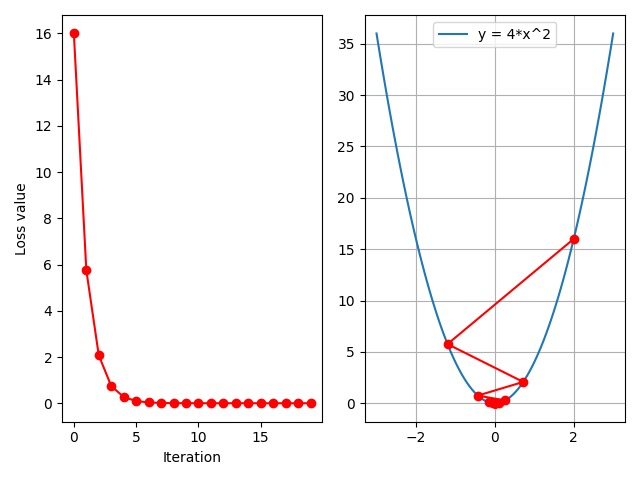
可以看到，在迭代 $5$ 到 $7$ 次之后，左图中的 loss 曲线已经趋近于零了，即已经达到收敛，同时右图可以看到最后几次迭代都在极小值点附近来回振动，这说明我们的学习率是比较合理的。

$\mathrm{LR} = 0.1$

那么，是否还存在更好的学习率呢？我们尝试将学习率调整到 $0.1$，观察函数值的变化：

lr = 0.1

输出结果：

Iter:0, X:     2.0, X.grad:    16.0, loss:      16.0
Iter:1, X:0.3999999761581421, X.grad:3.1999998092651367, loss:0.6399999260902405
Iter:2, X:0.07999998331069946, X.grad:0.6399998664855957, loss:0.025599990040063858
Iter:3, X:0.015999995172023773, X.grad:0.12799996137619019, loss:0.0010239994153380394
Iter:4, X:0.0031999992206692696, X.grad:0.025599993765354156, loss:4.0959981561172754e-05
Iter:5, X:0.0006399997510015965, X.grad:0.005119998008012772, loss:1.6383987713197712e-06
Iter:6, X:0.00012799992691725492, X.grad:0.0010239994153380394, loss:6.553592868385749e-08
Iter:7, X:2.5599983928259462e-05, X.grad:0.0002047998714260757, loss:2.621436623329032e-09
Iter:8, X:5.1199967856518924e-06, X.grad:4.095997428521514e-05, loss:1.0485746992916489e-10
Iter:9, X:1.0239991752314381e-06, X.grad:8.191993401851505e-06, loss:4.194297253262702e-12
Iter:10, X:2.047998464149714e-07, X.grad:1.6383987713197712e-06, loss:1.6777191073034936e-13
Iter:11, X:4.095996075648145e-08, X.grad:3.276796860518516e-07, loss:6.710873481539318e-15
Iter:12, X:8.191992861839026e-09, X.grad:6.553594289471221e-08, loss:2.6843498478959363e-16
Iter:13, X:1.6383983059142793e-09, X.grad:1.3107186447314234e-08, loss:1.0737395785076275e-17
Iter:14, X:3.2767966118285585e-10, X.grad:2.621437289462847e-09, loss:4.294958520825663e-19
Iter:15, X:6.55359377876863e-11, X.grad:5.242875023014903e-10, loss:1.7179836926736008e-20
Iter:16, X:1.3107185475869088e-11, X.grad:1.048574838069527e-10, loss:6.871932690625968e-22
Iter:17, X:2.62143692170147e-12, X.grad:2.097149537361176e-11, loss:2.748772571379408e-23
Iter:18, X:5.242874277083809e-13, X.grad:4.194299421667047e-12, loss:1.0995092021011623e-24
Iter:19, X:1.0485747469965445e-13, X.grad:8.388597975972356e-13, loss:4.398036056521599e-26

可以看到，当学习率调整为 $0.1$ 时，loss 曲线也可以快速收敛。

$\mathrm{LR} = 0.125$

那么，有没有能够使得收敛速度更快的学习率呢？我们尝试将学习率设置为 $0.125$：

lr = 0.125

输出结果：

Iter:0, X:     2.0, X.grad:    16.0, loss:      16.0
Iter:1, X:     0.0, X.grad:     0.0, loss:       0.0
Iter:2, X:     0.0, X.grad:     0.0, loss:       0.0
Iter:3, X:     0.0, X.grad:     0.0, loss:       0.0
Iter:4, X:     0.0, X.grad:     0.0, loss:       0.0
Iter:5, X:     0.0, X.grad:     0.0, loss:       0.0
Iter:6, X:     0.0, X.grad:     0.0, loss:       0.0
Iter:7, X:     0.0, X.grad:     0.0, loss:       0.0
Iter:8, X:     0.0, X.grad:     0.0, loss:       0.0
Iter:9, X:     0.0, X.grad:     0.0, loss:       0.0
Iter:10, X:     0.0, X.grad:     0.0, loss:       0.0
Iter:11, X:     0.0, X.grad:     0.0, loss:       0.0
Iter:12, X:     0.0, X.grad:     0.0, loss:       0.0
Iter:13, X:     0.0, X.grad:     0.0, loss:       0.0
Iter:14, X:     0.0, X.grad:     0.0, loss:       0.0
Iter:15, X:     0.0, X.grad:     0.0, loss:       0.0
Iter:16, X:     0.0, X.grad:     0.0, loss:       0.0
Iter:17, X:     0.0, X.grad:     0.0, loss:       0.0
Iter:18, X:     0.0, X.grad:     0.0, loss:       0.0
Iter:19, X:     0.0, X.grad:     0.0, loss:       0.0

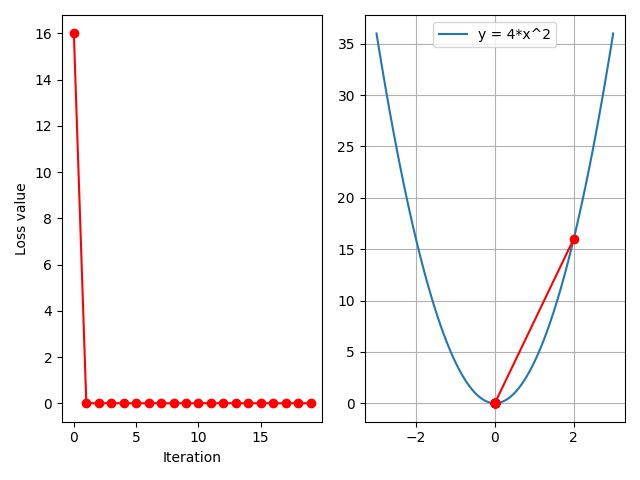
可以看到，当学习率为 $0.125$ 时，仅经过一次迭代，loss 值就已经达到收敛。那么，这个 $0.125$ 是如何得到的呢？如果我们不知道函数表达式，我们是没办法直接计算出最佳学习率的。所以，通常我们会尝试性地设置一系列的学习率，以找到最佳学习率。下面我们来观察设置多个学习率时的 loss 变化情况。

设置多个学习率

我们在 $0.01$ 到 $0.5$ 之间线性地设置 10 个学习率：

iteration = 100
num_lr = 10
lr_min, lr_max = 0.01, 0.5

lr_list = np.linspace(lr_min, lr_max, num=num_lr).tolist()
loss_rec = [[] for l in range(len(lr_list))]
iter_rec = list()

for i, lr in enumerate(lr_list):
    x = torch.tensor([2.], requires_grad=True)
    for iter in range(iteration):

        y = func(x)
        y.backward()
        x.data.sub_(lr * x.grad)  # x.data -= x.grad
        x.grad.zero_()

        loss_rec[i].append(y.item())

for i, loss_r in enumerate(loss_rec):
    plt.plot(range(len(loss_r)), loss_r, label="LR: {}".format(lr_list[i]))
plt.legend()
plt.xlabel('Iterations')
plt.ylabel('Loss value')
plt.show()

输出结果：

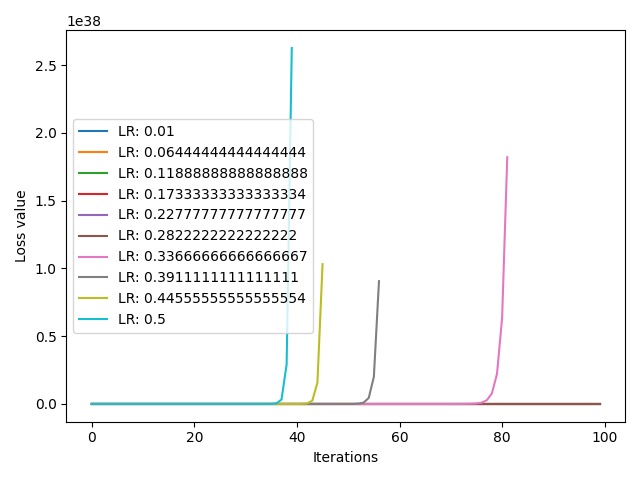
我们得到了 10 个不同的 loss 曲线，横轴表示迭代次数，纵轴表示 loss 值。可以看到，loss 值的尺度是 $10^{38}$，这是一个非常大的数字，不是我们所希望的。可以看到，从 $0.5$ 到 $0.337$ 这 4 条曲线都存在激增趋势。这表明我们的学习率上限设置得过大了，导致了 loss 激增和梯度爆炸。现在，我们将学习率上限改为 $0.3$，观察一下 loss 曲线的变化情况：

lr_min, lr_max = 0.01, 0.3

输出结果：

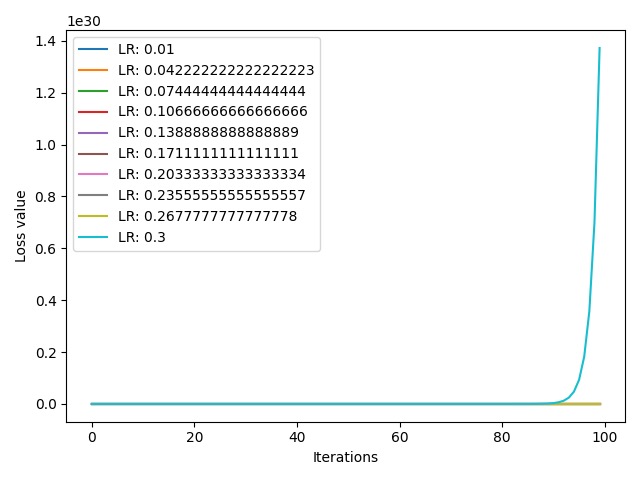
可以看到，在学习率取到最大值 $0.3$ 时，loss 值尺度为 $10^{30}$，相比之前 $10^{38}$ 有所下降，但是 loss 值仍然存在激增现象。下面我们将学习率上限改为 $0.2$，观察一下 loss 曲线的变化情况：

lr_min, lr_max = 0.01, 0.2

输出结果：

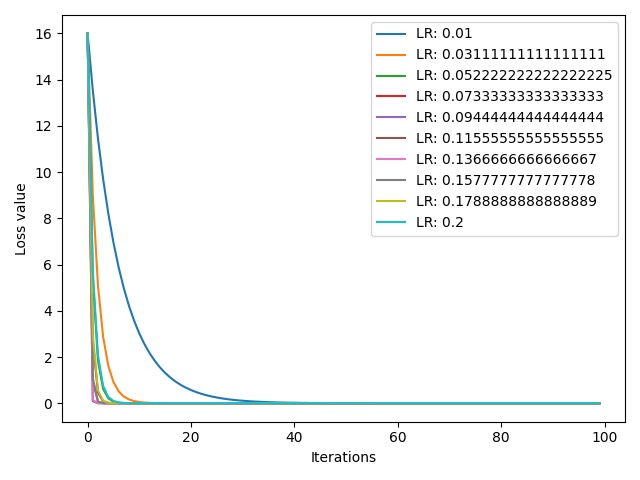
可以看到，现在的 10 条曲线都呈现下降趋势，这正是我们所期望的。最右边的蓝色曲线对应最小学习率 $0.01$，其收敛速度也是最慢的，大约为 30 次。右数第二条橙色曲线对应第二小的学习率 $0.03$，其收敛速度也是第二慢的。那么，是否学习率越大，收敛越快呢？我们看到，收敛最快的曲线并不是最大学习率 $0.2$ 对应的青色曲线，而是学习率 $0.136$ 对应的粉色曲线。回忆一下，前面我们提到的最佳学习率 $0.125$，这些学习率中与其距离最近的正是 $0.136$。因此，当学习率距离最优学习率最近时，收敛速度最快。但是，我们没有上帝视角，无法提前知道最优学习率，所以我们通常会设置诸如 $0.01$ 这样非常小的学习率，以达到收敛效果，其代价就是收敛速度可能会较慢。

综上所述，设置学习率时不能过大，否则将导致 loss 值激增，并且引发梯度爆炸；同时也不能过小，否则会导致收敛速度过慢，时间成本增加。通过将学习率设置为 $0.01$ 这样较小的值，就可以使得我们的 loss 值逐渐下降直到收敛。

2. 动量

Momentum (动量/冲量)：结合当前梯度与上一次更新信息，用于当前更新。

指数加权更新：求取当前时刻的平均值，常用于时间序列分析。对于那些距离当前时刻越近的参数值，它们的参考性越大，所占的权重也越大，而权重随时间间隔的增大呈指数下降。

\[v_t = \beta \cdot v_{t-1} + (1-\beta) \cdot \theta_t\]

其中，$v_t$ 是当前时刻的平均值，$v_{t-1}$ 是前一个时刻的平均值，$\theta_t$ 是当前时刻的参数值，$\beta$ 是权重参数。

例子：

数据集为连续多天的温度值：

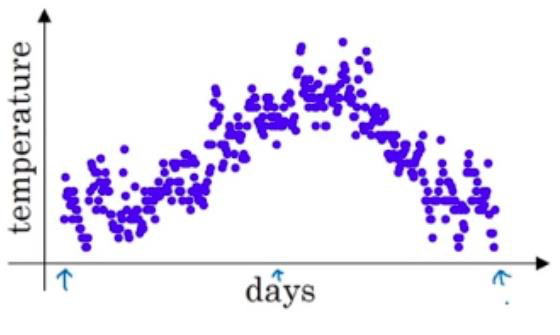
假设现在我们要求取第 100 天的温度平均值：

\[\begin{aligned} v_{100} &= \beta \cdot v_{99} + (1-\beta) \cdot \theta_{100} \\[2ex] &= (1-\beta) \cdot \theta_{100} + \beta \cdot (\beta \cdot v_{98} + (1-\beta) \cdot \theta_{99}) \\[2ex] &= (1-\beta) \cdot \theta_{100} + (1-\beta) \cdot \beta \cdot \theta_{99} + \beta^2 \cdot v_{98} \\[2ex] &= (1-\beta) \cdot \theta_{100} + (1-\beta) \cdot \beta \cdot \theta_{99} + (1-\beta) \cdot \beta^2 \cdot \theta_{98} + \beta^3 \cdot v_{97} \\[2ex] &= \cdots \\[2ex] &= \sum_{i=0}^{100} (1-\beta) \cdot \beta^i \cdot \theta_{n-i} \end{aligned}\]

代码示例：

import torch
import numpy as np
import torch.optim as optim
import matplotlib.pyplot as plt

torch.manual_seed(1)


def exp_w_func(beta, time_list):
    return [(1 - beta) * np.power(beta, exp) for exp in time_list]


beta = 0.9
num_point = 100
time_list = np.arange(num_point).tolist()

weights = exp_w_func(beta, time_list)    # 指数权重

plt.plot(time_list, weights, '-ro', label="Beta: {}\ny = B^t * (1-B)".format(beta))
plt.xlabel("time")
plt.ylabel("weight")
plt.legend()
plt.title("exponentially weighted average")
plt.show()

print(np.sum(weights))

输出结果：

0.9999734386011124

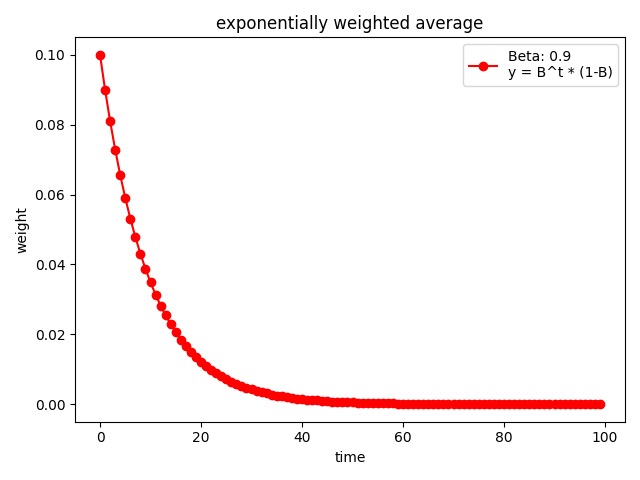
可以看到，权重随时间间隔的增加呈指数下降。下面我们尝试调整超参数 $\beta$ 的值，来观察一下权重的变化：

# 多个权重曲线
beta_list = [0.98, 0.95, 0.9, 0.8]
w_list = [exp_w_func(beta, time_list) for beta in beta_list]

for i, w in enumerate(w_list):
    plt.plot(time_list, w, label="Beta: {}".format(beta_list[i]))
    plt.xlabel("time")
    plt.ylabel("weight")

plt.legend()
plt.show()

输出结果：

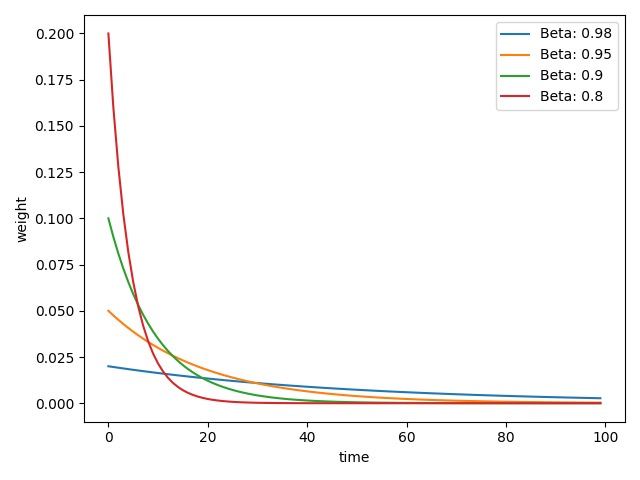
可以看到，随着权重参数 $\beta$ 的增大，权重曲线逐渐变得平缓。我们可以将其理解为某种记忆周期，$\beta$ 值越小，其记忆周期越短，对于较长时间间隔参数的关注越少。通常我们将 $\beta$ 设置为 $0.9$，即权重曲线将更加关注距离当前时间 $1/(1-\beta) = 10$ 天以内的数据。

我们已经了解了指数加权平均中的权重参数 $\beta$，在梯度下降中它对应的就是 momentum 系数。

梯度下降：

\[w_{i+1} = w_i - \mathrm{LR} \cdot g(w_i)\]

PyTorch 中的更新公式：

\[v_i = m \cdot v_{i-1} + g(w_i)\] \[w_{i+1} = w_i - \mathrm{LR} \cdot v_i\]

其中，$w_{i+1}$ 是第 $i+1$ 次更新的参数，$\mathrm{LR}$ 是学习率，$g(w_i)$ 是 $w_i$ 的梯度，$v_i$ 是更新量，$m$ 是 momentum 系数。

例如：

\[\begin{aligned} v_{100} &= m \cdot v_{99} + g(w_{100}) \\[2ex] &= g(w_{100}) + m \cdot (m \cdot v_{98} + g(w_{99})) \\[2ex] &= g(w_{100}) + m \cdot g(w_{99}) + m^2 \cdot v_{98} \\[2ex] &= g(w_{100}) + m \cdot g(w_{99}) + m^2 \cdot g(w_{98}) + m^3 \cdot v_{97} \\[2ex] &= \cdots \end{aligned}\]

可以看到，momentum 系数的作用就是当前更新不仅考虑了当前的梯度信息，同时也考虑了之前几次的梯度信息。由于 momentum 系数取值在 $[0,1]$，所以时间间隔越长的梯度信息所占权重越低。

代码示例：

下面我们设置两个学习率，在都不加上 momentum 系数的情况下，对比两者的权重曲线：

def func(x):
    return torch.pow(2*x, 2)    # y = (2x)^2 = 4*x^2        dy/dx = 8x

iteration = 100

m = 0.    # Momentum 系数
lr_list = [0.01, 0.03]    # 学习率

momentum_list = list()
loss_rec = [[] for l in range(len(lr_list))]
iter_rec = list()

for i, lr in enumerate(lr_list):
    x = torch.tensor([2.], requires_grad=True)

    momentum = 0. if lr == 0.03 else m
    momentum_list.append(momentum)

    optimizer = optim.SGD([x], lr=lr, momentum=momentum)

    for iter in range(iteration):

        y = func(x)
        y.backward()

        optimizer.step()
        optimizer.zero_grad()

        loss_rec[i].append(y.item())

for i, loss_r in enumerate(loss_rec):
    plt.plot(range(len(loss_r)), loss_r, label="LR: {} M:{}".format(lr_list[i], momentum_list[i]))

plt.legend()
plt.xlabel('Iterations')
plt.ylabel('Loss value')
plt.show()

输出结果：

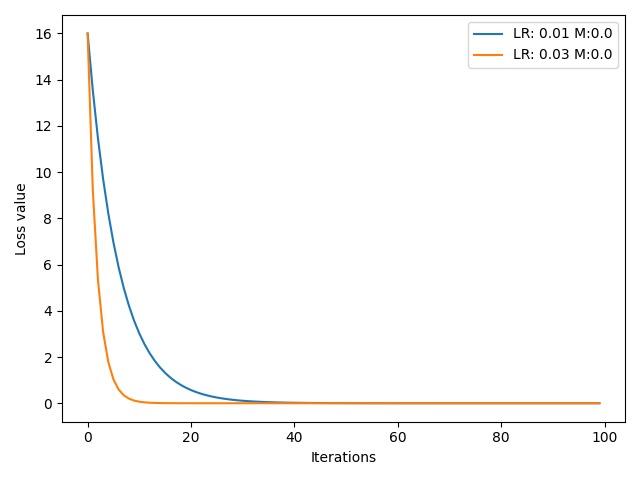
可以看到，学习率为 $0.03$ 的橙色曲线要比学习率为 $0.01$ 的蓝色曲线的收敛速度更快。下面我们为较小的学习率 $0.01$ 增加一个 momentum 系数，与不加 momentum 系数的学习率 $0.03$ 对比：

m = 0.9    # 为学习率 0.01 增加一个 momentum 系数 0.9

输出结果：

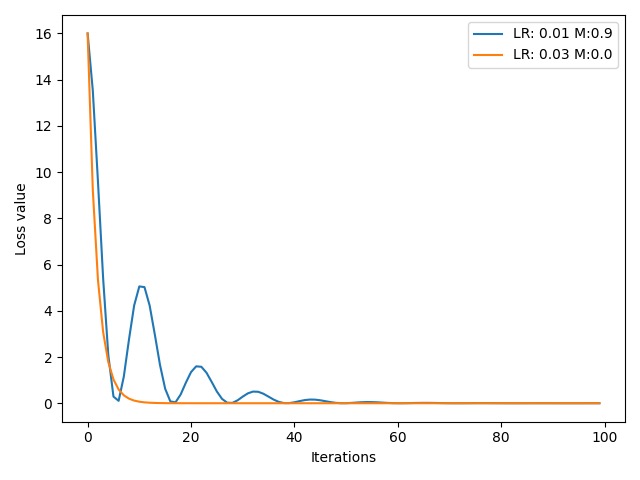
可以看到，在增加了一个 momentum 系数 $0.9$ 后，学习率 $0.01$ 对应的蓝色曲线要比学习率为 $0.03$ 但是没有增加 momentum 系数的橙色曲线更快到达最低点。另外，蓝色曲线前期呈现震荡趋势，这是由于我们的momentum 系数设置过大，虽然我们当前梯度很小，但是之前的梯度很大，导致在到达极小值后受到前几个时刻的梯度信息的影响而反弹，如此往复震荡。我们可以尝试修改 momentum 系数的值：

m = 0.63    # 为学习率 0.01 增加一个 momentum 系数 0.63

输出结果：

可以看到，通过合理地设置 momentum 系数，结合之前的梯度信息，我们可以让 loss 曲线更快收敛到极小值点。不过大部分情况下，我们通常会将 momentum 系数设置为 $0.9$。

3. PyTorch 中的常用优化器

`optim.SGD`

功能：随机梯度下降。

optim.SGD(
    params,
    lr=<object object>,
    momentum=0,
    dampening=0,
    weight_decay=0,
    nesterov=False
)

主要参数：

params：管理的参数组。
lr：初始学习率。
momentum：动量系数 $\beta$。
weight_decay：L2 正则化系数。
nesterov：是否采用 NAG。

NAG 参考文献：On the importance of initialization and momentum in deep learning

PyTorch 中的 10 种常用优化器：

optim.SGD：随机梯度下降法。
optim.Adagrad：自适应学习率梯度下降法。
optim.RMSprop：Adagrad 的改进。
optim.Adadelta：Adagrad 的改进。
optim.Adam：RMSprop 结合 Momentum。
optim.Adamax：Adam 增加学习率上限。
optim.SparseAdam：稀疏版的 Adam。
optim.ASGD：随机平均梯度下降。
optim.Rprop：弹性反向传播。
optim.LBFGS：BFGS 的改进。

参考文献：

optim.SGD：On the importance of initialization and momentum in deep learning
optim.Adagrad：Adaptive subgradient methods for online learning and stochastic optimization
optim.RMSprop：RMSProp
optim.Adadelta：ADADELTA: An Adaptive Learning Rate Method
optim.Adam：Adam: A Method for Stochastic Optimization
optim.Adamax：Adam: A Method for Stochastic Optimization
optim.SparseAdam：稀疏版的 Adam。
optim.ASGD：Accelerating Stochastic Gradient Descent using Predictive Variance Reduction
optim.Rprop：RPROP-A Fast Adaptive Learning Algorithm
optim.LBFGS：BDGS 的改进。

4. 总结

本节课中，我们学习了优化器 Optimizer 中的两个主要参数：学习率和 momentum。下节课中，我们将学习关于学习率的调整策略。

下节内容：学习率调整策略

本作品采用知识共享署名-非商业性使用-相同方式共享 4.0 国际许可协议进行许可。欢迎转载，并请注明来自：YEY 的博客同时保持文章内容的完整和以上声明信息！

PyTorch 18：优化器 (二)

PyTorch 学习笔记

Lecture 18 优化器 (二)

1. 学习率

$\mathrm{LR} = 0.5$

$\mathrm{LR} = 0.2$

$\mathrm{LR} = 0.1$

$\mathrm{LR} = 0.125$

设置多个学习率

2. 动量

3. PyTorch 中的常用优化器

`optim.SGD`

4. 总结

CATALOG

FEATURED TAGS

FRIENDS