Lecture 12 集成学习
主要内容
- 集成学习:对冲你的赌注
- Bagging 和随机森林
- Boosting
- Stacking
1. 集成学习
集成学习:对冲你的赌注
1.1 为什么是 “一个正确” 的模型?
- 到目前为止,我们已经讨论了各个模型,并在孤立 / 竞争中考虑了每个模型
- 我们知道如何评估每个模型的性能(通过准确率、F-measure 等),这使我们能够给一个数据集从 总体上 选择出最优的模型
- 但 总体上 并没有隐含着每个样本的表现
- 总体上最优的模型:在某些实例上可能会出错
- 总体上最差的模型:在某些实例上可能会更好
- 集成 让我们可以综合使用多个模型
1.2 专家小组
- 考虑一个由 3 位专家组成的小组,他们 各自独立地 做出分类决策。每个专家决策出错的概率都是 0.3。共识决策由 多数投票 产生。
思考:共识决策出错的概率是多少?
在共识决策下,出错可能有两种情况:
a. 3 位专家都出错了
b. 2 位专家出错了导致最终投票得出错误答案
所以,将两种情况的概率相加即可:$0.3^3+3\times 0.3^2\times (1-0.3)=0.216$
- 设定:错误之间互相独立,每一个的概率都是 $p$
-
$n$ 个专家各自决策产生的 错误的数量 服从 二项分布 $\color{red}{\text{Binom}(n,p)}$
\[\Pr(k)=\begin{pmatrix}n \\ k\end{pmatrix}p^k(1-p)^{n-k}\] -
当 至少 $\color{red}{\lceil n/2 \rceil}$ 的专家出错(对于 $n$ 为奇数的情况)时,多数投票将会出错
\[\Pr(panel\, error)=\sum_{k=\lceil n/2 \rceil}^{n}\begin{pmatrix}n \\ k\end{pmatrix}p^k(1-p)^{n-k}\]

1.3 组合模型
- 模型组合(又称 集成学习)根据给定的训练集构造一个基模型(又称 基学习器)的集合,并将输出结果聚合到一个单独的元模型中(集成)
- 分类问题采用(加权)多数投票
- 回归问题采用(加权)平均
- 更一般地:元模型 $=f($基模型$)$
-
回忆 偏差-方差权衡:
\[\Bbb E\left[ l\left(y,\hat f(\boldsymbol x_0)\right) \right]=\left(\Bbb E[y]-\Bbb[\hat f]\right)^2+Var[\hat f]+Var[y]\] \[\text{test error}=(\text{bias})^2+\text{variance}+\text{irreducible error}\] -
对 $k$ 个 独立同分布 的预测进行平均可以减小方差:
\[\color{red}{Var\left[\hat f_{avg}\right]=\dfrac{1}{k}Var\left[\hat f\right]}\]
2. Bagging
Bootstrap aggregating —— Breiman’94
2.1 Bagging 方法
- 方法: 通过有放回抽样构建 “近似独立” 的数据集
- 生成 $k$ 个数据集,每个数据集都包含从 $n$ 条训练数据中通过有放回抽样得到的 $n$ 个样本 —— Bootstrap 采样
- 在每个生成的数据集上构建基分类器
- 通过投票 / 平均对预测结果进行聚合
2.2 Bagging:采样例子
- 原始训练数据集:
\(\{0,1,2,3,4,5,6,7,8,9\}\) - Bootstrap 采样:
\(\{7,2,6,7,5,4,8,8,1,0\}\) —— 未采样 $3,9$
\(\{1,3,8,0,3,5,8,0,1,9\}\) —— 未采样 $2,4,6,7$
\(\{2,9,4,2,7,9,3,0,1,0\}\) —— 未采样 $3,5,6,8$
2.3 回忆决策树
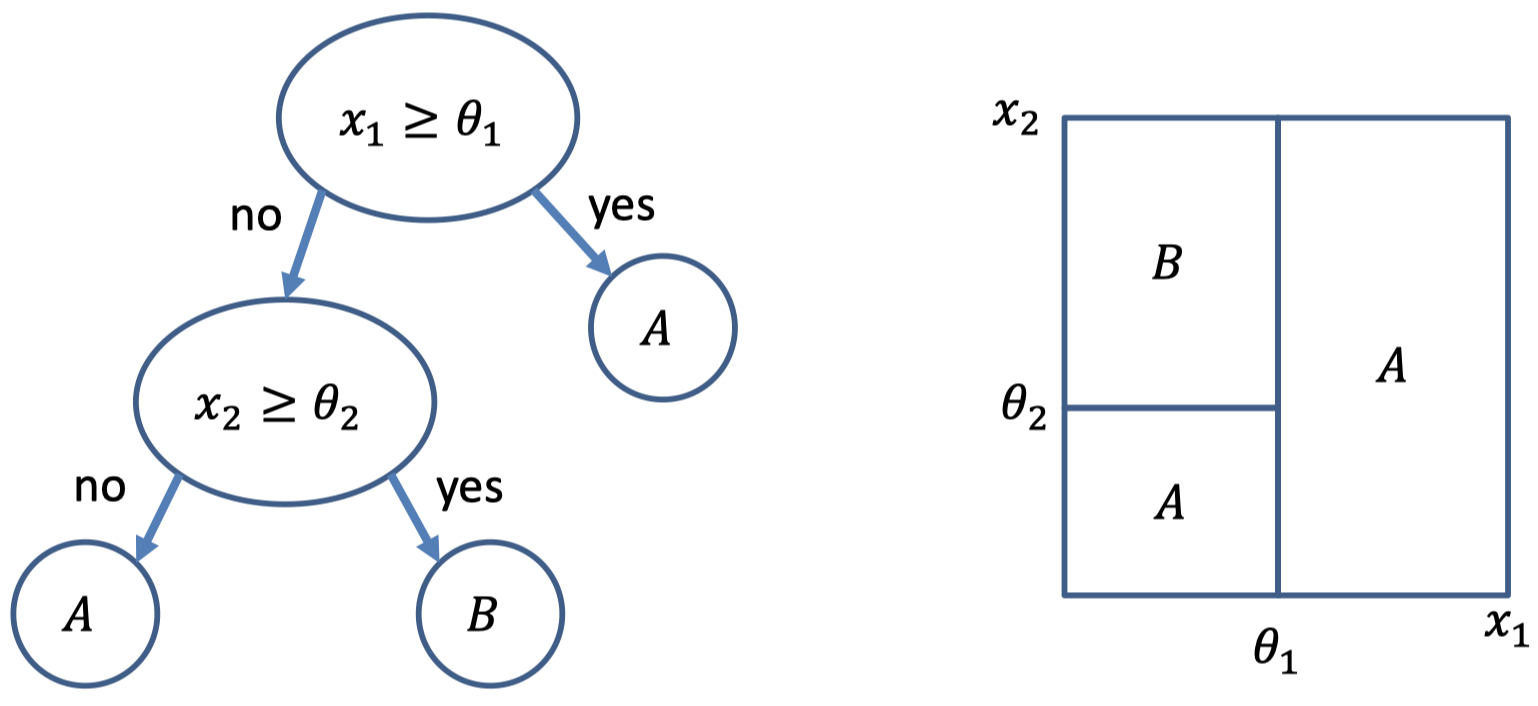
- 训练标准:每个最终分区的纯度
- 优化:启发式贪婪迭代方法
- 模型复杂度由树的深度定义
- 深树:非常适合特定数据 $\rightarrow$ 高方差,低偏差
- 浅树:粗略近似 $\rightarrow$ 低方差,高偏差
2.4 Bagging 的例子:随机森林
- Just bagged trees
- 算法描述:
参数:树的数量 $k$,特征数量 $l\le m$
1.$\,$初始化一个空的森林
2.$\,$对于 $c$ 从 $1$ 到 $k$:
$\qquad$ a. 从训练数据创建新的 Bootstrap 采样
$\qquad$ b. 从 $m$ 个特征中随机选择出包含 $l$ 个特征的子集
$\qquad$ c. 用这 $l$ 个特征在 Bootstrap 样本上训练决策树
$\qquad$ d. 将树添加进森林里
3.$\,$通过多数投票或者平均来作出预测 - 在许多实际设定下效果非常好
2.5 利用未采样数据
- 在每轮中,一个特定的训练样本有 $\left(1-\dfrac{1}{n}\right)$ 的概率不被选中
- 因此,在经过 $n$ 轮后最终没有被采样到的概率为 $\left(1-\dfrac{1}{n}\right)^n$
- 对于 $n$ 很大的情况,这一概率近似为 $e^{-1}\approx 0.368$
- 平均情况下,每轮 Bootstrap 采样只包含了 $63.2\%$ 的数据
- 可以将其用于对集成的独立误差估计
- 像交叉验证一样安全,但是子样本重叠
- 在每个 $36.8\%$ 的未采样样本上对每个基学习器进行评估
- 平均这些评估 $\rightarrow$ 集成评估
2.6 Bagging:总结
- 基于采样和投票的简单方法
- 各个基学习器有可能进行并行计算
- 能够高效处理带噪声的数据集
- 性能通常比(简单的)基分类器要好得多,永远不会太差
- 通过减小方差来提升不稳定的分类器
3. Boosting
3.1 Boosting 方法
- 直觉: 将基分类器的注意力集中在 “难以分类” 的样本上
- 方法: 迭代地改变样本的分布以反映分类器在上一次迭代中的性能
- 初始时,每个训练样本有 $\dfrac{1}{n}$ 的概率包含在采样中
- 经过 $k$ 轮迭代后,训练一个分类器,并根据分类器对每个实例分类的能力来更新每个实例的权重
- 通过加权投票来组合基分类器
3.2 Boodting:采样例子
- 原始训练数据集:
\(\{0,1,2,3,4,5,6,7,8,9\}\) - Boosting 采样:
第 1 轮迭代:\(\{7,\color{red}{2},6,7,5,4,8,8,1,0\}\)
假设样本 $2$ 被错误分类
第 2 轮迭代:\(\{1,3,8,\color{red}{2},3,5,\color{red}{2},0,1,9\}\)
假设样本 $2$ 依旧被错误分类
第 3 轮迭代:\(\{\color{red}{2},9,\color{red}{2,2},7,9,3,\color{red}{2},1,0\}\)
3.3 Boosting 的例子:AdaBoost
- 算法描述:
1.$\,$初始样本分布 $P_1(i)=1/n,\;i=1,…,n$
2.$\,$对于 $c$ 从 $1$ 到 $k$:
$\qquad$ a. 在从 $P_c$ 有放回抽样得到的样本上训练基分类器 $A_c$
$\qquad$ b. 为每个分类器的错误率 $\varepsilon_c$ 设定置信度 $\alpha_c=\dfrac{1}{2}\ln \dfrac{1-\varepsilon_c}{\varepsilon_c}$
$\qquad$ c. 更新样本分布以归一化:
$\qquad\quad$ \(P_{c+1}(i)\propto P_c(i)\times \begin{cases}\exp(-\alpha_c), & \text{if } A_c(i)=y_i \\ \exp(\alpha_c), & \text{otherwise}\end{cases}\)
3.$\,$根据置信度加权的多数投票进行分类:
$\quad \mathop{\operatorname{arg\,max}} \limits_y \sum_{c=1}^{k}\alpha_t \delta \left(A_c(\boldsymbol x)=y\right)$
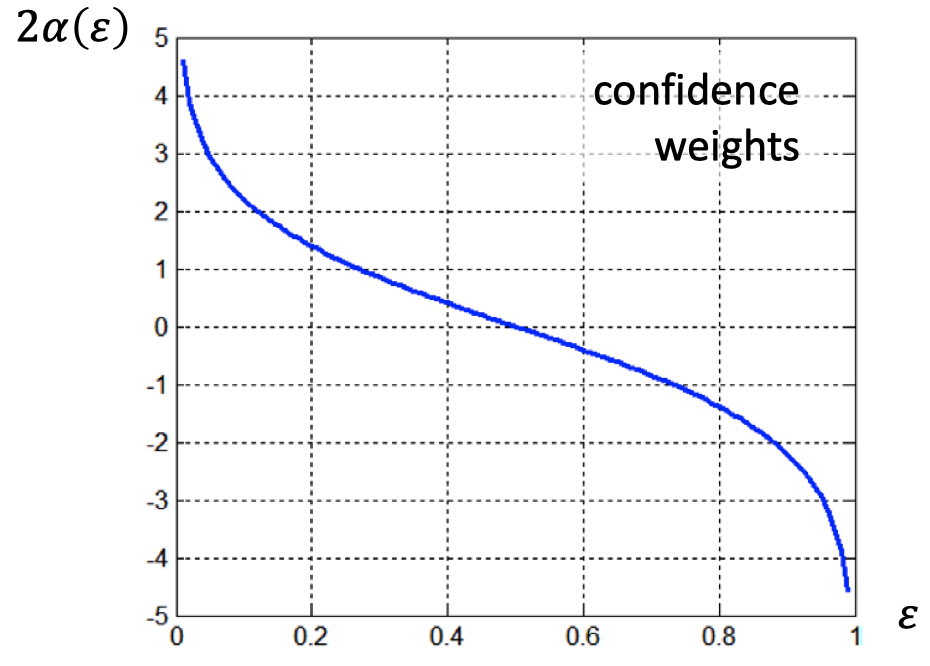
- 技术上:每当 $\varepsilon_c>0.5$ 时,就对样本分布进行重新初始化
- 基学习器:通常是决策桩或者决策树,任何 “弱” 分类器
- 决策桩是只有一个分裂节点的决策树
3.4 Boosting:总结
- 基于迭代采样和加权投票的方法
- 计算上的开销比 Bagging 更大
- 该方法以训练数据上的误差边界的形式保证了性能
- 在实际应用中,Boosting 可能导致过拟合
| Bagging | Boosting |
|---|---|
| 并行采样 | 迭代采样 |
| 最小化方差 | 关注 “困难” 样本 |
| 简单投票 | 加权投票 |
| 分类或者回归 | 分类或者回归 |
| 不容易过拟合 | 容易过拟合(除非基学习器很简单) |
4. Stacking
4.1 Stacking 方法
- 直觉: 能够对一系列具有不同偏差的算法进行误差 “平滑”
- 方法: 在基学习器的输出上训练一个元模型
- 利用交叉验证训练基学习器和元学习器
- 简单的元分类器:Logistic 回归
- 对于 Bagging 和 Boosting 的泛化(这里的 “泛化” 是针对模型而言,而非学习器)
4.2 Stacking:总结
- 将其对比 ANN 和基扩展
- 该方法在数学上很简单,但是计算上开销很大
- 能够将各种各样的不同性能的分类器组合起来
- 如果能够合理谨慎地应用,Stacking 可以在性能上达到或者超过最好的基分类器
总结
- 集成学习
- Bagging 和随机森林
- Boosting
- Stacking
下节内容:多臂老虎机问题
本作品采用知识共享署名-非商业性使用-相同方式共享 4.0 国际许可协议进行许可。 欢迎转载,并请注明来自:YEY 的博客 同时保持文章内容的完整和以上声明信息!