Lecture 13 多臂老虎机
主要内容
- 随机多臂老虎机
- “我们学会采取行动的地方;我们仅仅接受奖励形式的间接监督;并且我们只观测行动带来的奖励。” —— 这是一个关于如何权衡 探索-利用(Exploration-Exploitation) 最简单的设定
- 不确定性下的顺序决策
- $(\varepsilon)$-Greedy 算法
- UCB 算法
1. 多臂老虎机
1.1 多臂老虎机问题(MAB)

问题描述:
赌场内,有一名赌徒想要去摇 老虎机(bandit),他面前有一排机器,每台机器都拥有一个 臂(arm),而且每台机器看上去都一样。每次投一枚游戏币就能获得一次 摇臂(play) 的机会,而且每个臂摇下都有可能吐出一枚硬币,即 奖励(rewards) —— 但是,每台老虎机吐出硬币的概率分布是未知的。作为赌徒,自然希望自己的 累积收益的期望(expected cumulative reward)最大化(假如一共有 $n$ 次摇臂的机会),那么,请问这名赌徒应该采取怎样的行动?
—— 这就是 多臂老虎机问题(Multi-armed bandit, MAB)
1.2 探索(Exploration)vs. 利用(Exploitation)
- 多臂老虎机问题(MAB)
- 关于平衡探索(Exploration)和利用(Exploitation)的最简单的设定
- 与强化学习同属一类机器学习任务家族
- 一些应用场景
- 在线广告
- 投资组合选择
- 数据库中的缓存
- 游戏中的随机搜索(例如,AlphaGo)
- 自适应 A / B 测试
- …
1.3 随机 MAB 设定
- 可能采取的 行动(action) \(\{1,...,k\}\) 称为 “臂(arms)”
- 臂(arm)$i$ 具有在有界 奖励(rewards) 上的分布 $P_i$,其期望为 $u_i$
- 在 $t=1…T$ 轮:
- 摇臂行为(play) \(i_t\in \{1,...,k\}\)(可能是随机的)
- 得到奖励 $X_{i_t}(t)\sim P_{i_t}$
- 目标:最小化累积 遗憾(regret)
- \(u^*T-\sum_{t=1}^{T}E\left[X_{i_t}(t) \right]\) $\qquad$其中,\(u^*=\max \limits_i u_i\)
第一部分为 在预先知道每台机器奖励概率分布的情况(上帝视角)下的累积奖励的期望
第二部分为 实际摇完老虎机后的累积奖励的期望 - 直觉上,我们应该制定一个简单但是包含未来知识的规则
- \(u^*T-\sum_{t=1}^{T}E\left[X_{i_t}(t) \right]\) $\qquad$其中,\(u^*=\max \limits_i u_i\)
2. Greedy 和 $\varepsilon$-Greedy 算法
2.1 Greedy 算法
- 在第 $t$ 轮:
-
将每个臂(arm)$i$ 观测到的平均奖励(average reward)作为 估计值
\[Q_{t-1}(i)=\begin{cases}\dfrac{\sum_{s=1}^{t-1}X_i(s)1[i_s=i]}{\sum_{s=1}^{t-1}1[i_s=i]}, & \text{if }\sum_{s=1}^{t-1}1[i_s=i]>0 \\ Q_0 , & \text{otherwise}\end{cases}\]在某个臂(arm)$i$ 被第一次摇到之前,其估计值都设为初始常数 $Q_0(i)=Q_0$
也就是说,在经过 $(t-1)$ 轮后,如果臂 $i$ 被摇动过了,那么将之前 $(t-1)$ 轮的平均奖励作为这台机器的在第 $t$ 轮奖励的估计值;否则,将初始值 $Q_0(i)=Q_0$ 作为估计值。
-
利用(exploit)
\[i_t\in \mathop{\operatorname{arg\,max}}\limits_{1\le i\le k}Q_{t-1}(i)\]选择摇臂(play): 在第 $t$ 轮,从目前为止奖励估计值最大(即经过之前 $(t-1)$ 轮后平均奖励最大)的臂 $i$ 的 集合(因为具有最大奖励估计值的臂可能不止一个)中选择一个作为本轮摇臂。
-
随机平局决胜机制: 因为具有最大奖励估计值的臂是一个集合,因此,我们随机地从中选择一个作为本轮要摇的臂即可。
-
思考: 初始值 $Q_0$ 的设定应当如何选择?会有什么影响?
2.2 $\varepsilon$-Greedy 算法
- 在第 $t$ 轮:
-
将每个臂 $i$ 观测到的平均奖励作为 估计值
\[Q_{t-1}(i)=\begin{cases}\dfrac{\sum_{s=1}^{t-1}X_i(s)1[i_s=i]}{\sum_{s=1}^{t-1}1[i_s=i]}, & \text{if }\sum_{s=1}^{t-1}1[i_s=i]>0 \\ Q_0 , & \text{otherwise}\end{cases}\]在某个臂(arm)$i$ 被第一次摇到之前,其估计值都设为初始常数 $Q_0(i)=Q_0$
-
可能 利用(exploit),可能 探索(explore)
\[i_t\sim \begin{cases}i_t\in \mathop{\operatorname{arg\,max}}\limits_{1\le i\le k}Q_{t-1}(i), & \text{w.p.}\quad 1-\varepsilon \\ \text{Unif}(\{1,...,k\}), & \text{w.p.}\quad \varepsilon\end{cases}\]选择摇臂(play): 在第 $t$ 轮,以 $(1-\varepsilon)$ 的概率 从目前为止奖励估计值最大的臂 $i$ 的 集合 中选择一个作为本轮摇臂;以 $\varepsilon$ 的概率 从所有臂的集合 \(\{1,...,k\}\) 中按照等概率随机选取一个作为本轮摇臂。
-
随机平局决胜机制
-
- 超参数 $\varepsilon$ 控制 探索(Exploration)vs. 利用(Exploitation)
2.3 $\varepsilon$-Greedy 算法评估

- 10 个摇臂的老虎机
- 奖励 $P_i=\text{Normal}(\mu_i,1)$,其中 $\mu_i \sim \text{Normal}(0,1)$
- 一场游戏摇 300 轮
- 重复 1000 场游戏,绘制每轮的平均奖励图
增加轮数

- Greedy 算法上升更快,但最终在一个较低的奖励值趋于平稳
- $\varepsilon$-Greedy 算法 通过探索(exploration)使得长期表现更好
- 0.01-Greedy(很少的探索过程)初始时上升较慢,但是最终的平均奖励值要高于 0.1-Greedy(在经过足够的探索后才开始利用)
乐观的初始化可以提升 Greedy 算法的表现
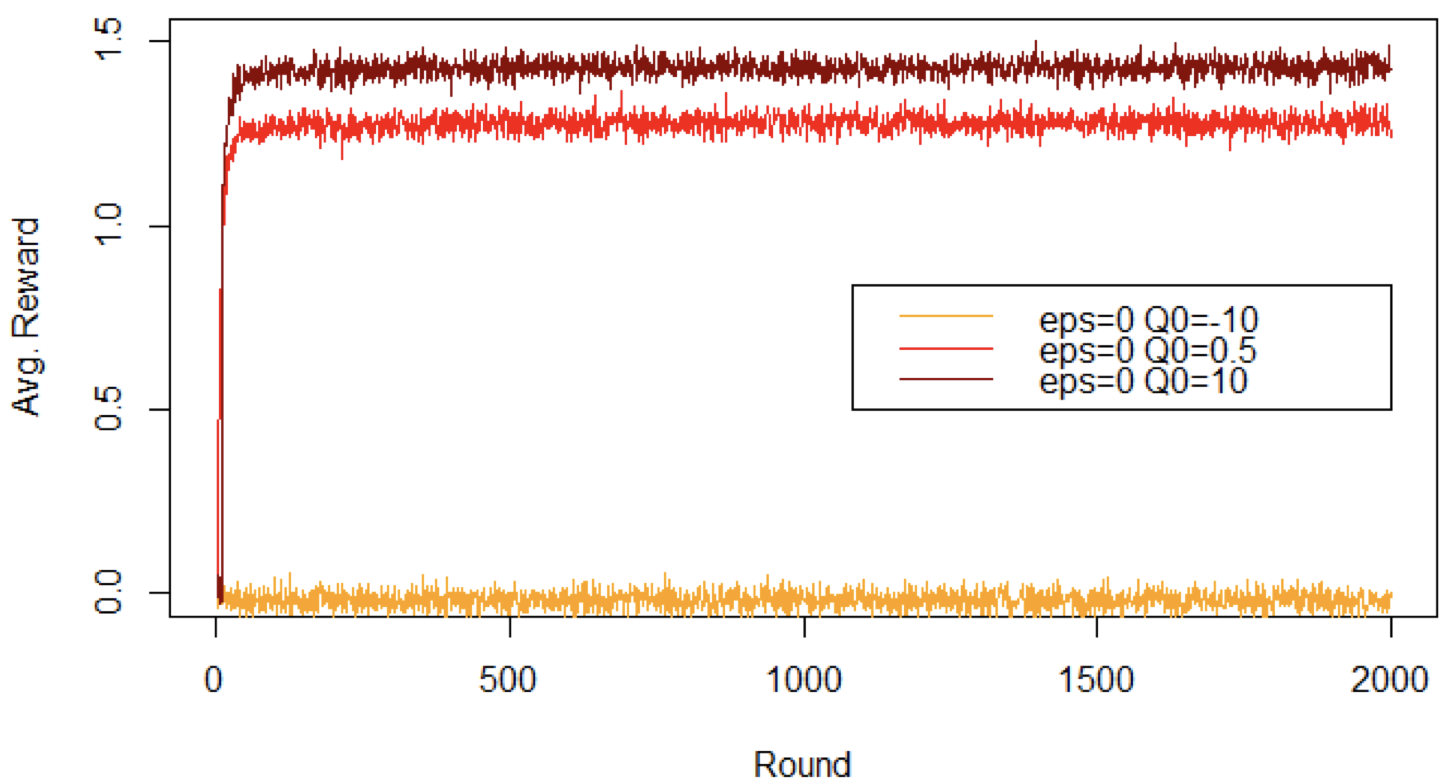
- 悲观主义:初始化的 $Q$ 值低于可观测到的奖励 $\rightarrow$ 只尝试一个摇臂
- 乐观主义:初始化的 $Q$ 值高于可观测到的奖励 $\rightarrow$ 保证每个摇臂都尝试一次
- 中间立场初始化的 $Q$ 值 $\rightarrow$ 每个摇臂最多探索一次
但是,单纯的 Greedy 算法永远不会对一个摇臂探索超过一次
$\varepsilon$-Greedy 算法的局限
- 虽然我们可以通过乐观的初始化和减小 $\varepsilon$ 来提升基本的 Greedy 算法,但还是存在一些问题…
- 在 Greedy 算法中,探索(Exploration) 和 利用(exploitation) 这两部分太过于割裂
- 探索过程 完全无视了 有潜力的臂
- 初始化技巧 仅仅对于 “冷启动” 有帮助
- 利用过程 对估计值的 置信度 视而不见
- 在实践中,这些局限是很严重的
3. UCB 算法
3.1 $Q$ 估计值的(上)置信区间
- 定理:霍夫丁不等式(Hoeffding’s inequality)
- 令 $X_1,…,X_n$ 为独立同分布的随机变量,并且 $X_i \in [0,1]$,均值为 $\mu$,它们的样本均值则由 $\overline{X_n}$ 表示
-
对于任何 $\varepsilon \in (0,1)$,至少有 $(1-\varepsilon)$ 的概率使得
\[\mu \le \overline{X_n}+\sqrt{\dfrac{\log(1/\varepsilon)}{2n}}\]
- 应用到 $Q_{t-1}(i)$ 的估计(同样存在独立同分布和均值的场景)
- 经过 $(t-1)$ 轮,臂 $i$ 一共被摇过的次数为 $n=N_{t-1}(i)=\sum_{s=1}^{t-1}1[i_s=i]$
- 然后,$\overline{X_n}=Q_{t-1}(i)$
- 临界水平 $\varepsilon=1/t$(Lai & Robbins, 1985),取 $\color{red}{\varepsilon=1/t^4}$
3.2 置信区间上界(UCB)算法
- 在第 $t$ 轮:
-
将每个臂 $i$ 观测到的平均奖励作为 估计值
\[Q_{t-1}(i)=\begin{cases}\hat \mu_{t-1}(i)+\sqrt{\dfrac{2\log(t)}{N_{t-1}(i)}}, & \text{if }\sum_{s=1}^{t-1}1[i_s=i]>0 \\ Q_0 , & \text{otherwise}\end{cases}\]在某个臂(arm)$i$ 被第一次摇到之前,其估计值都设为初始常数 $Q_0(i)=Q_0$;
其中,$N_{t-1}(i)=\sum_{s=1}^{t-1}1[i_s=i]\qquad \hat \mu_{t-1}(i)=\dfrac{\sum_{s=1}^{t-1}X_i(s)1[i_s=i]}{\sum_{s=1}^{t-1}1[i_s=i]}$ -
“乐观面对不确定性”
\[i_t\in \mathop{\operatorname{arg\,max}}\limits_{1\le i\le k}Q_{t-1}(i)\]选择摇臂(play): 在第 $t$ 轮,从目前为止奖励估计值最大的臂 $i$ 的 集合 中选择一个作为本轮摇臂。
-
随机平局决胜机制
-
- 克服了 $\varepsilon$-Greedy 算法的一些局限
- 可能在某个坏的臂 “暂停” 一段时间,但最终会找到最优的臂
3.3 UCB 算法评估
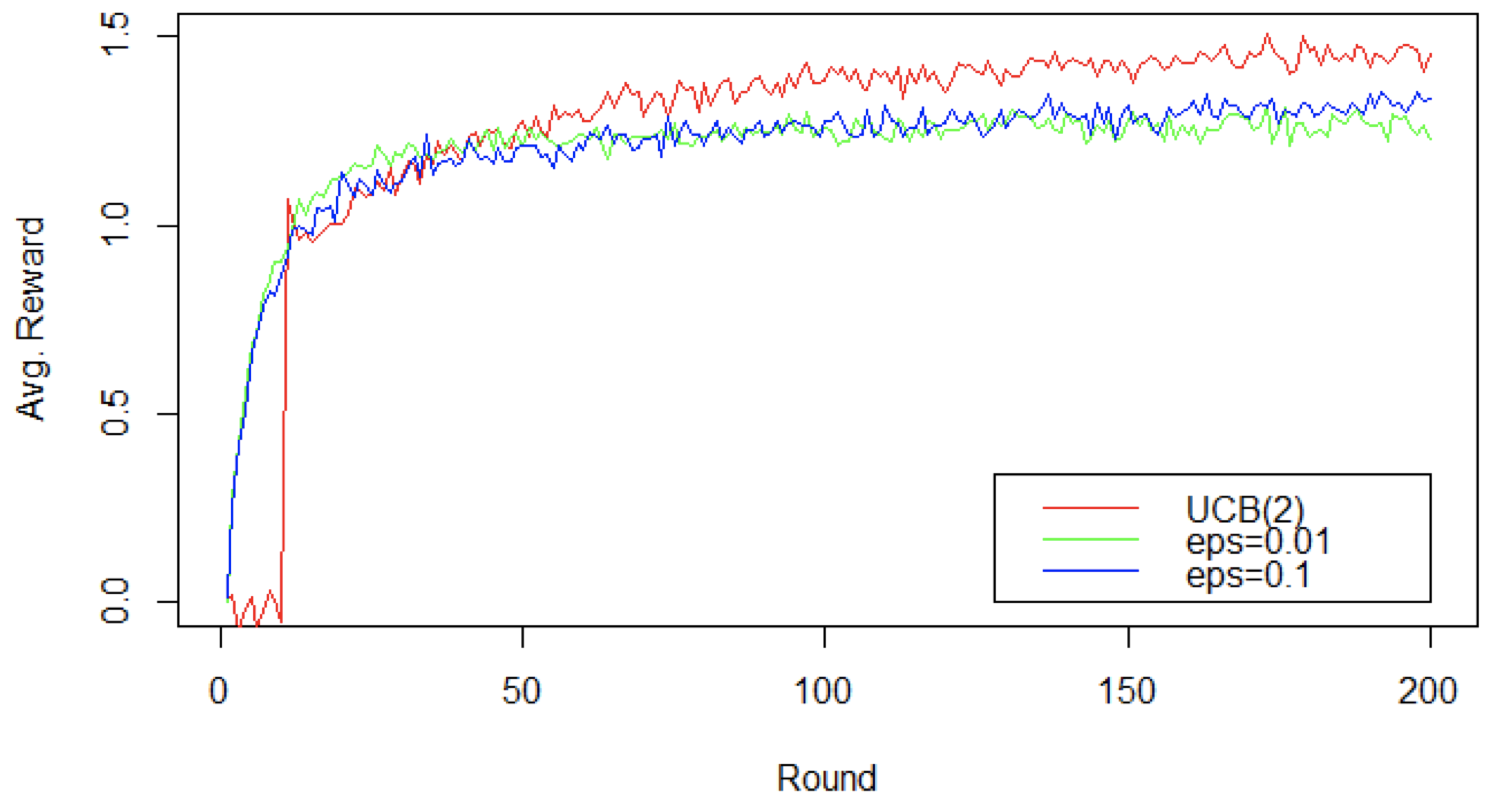
- UCB 算法快速超过了 $\varepsilon$-Greedy 算法
增加轮数:平均奖励比较
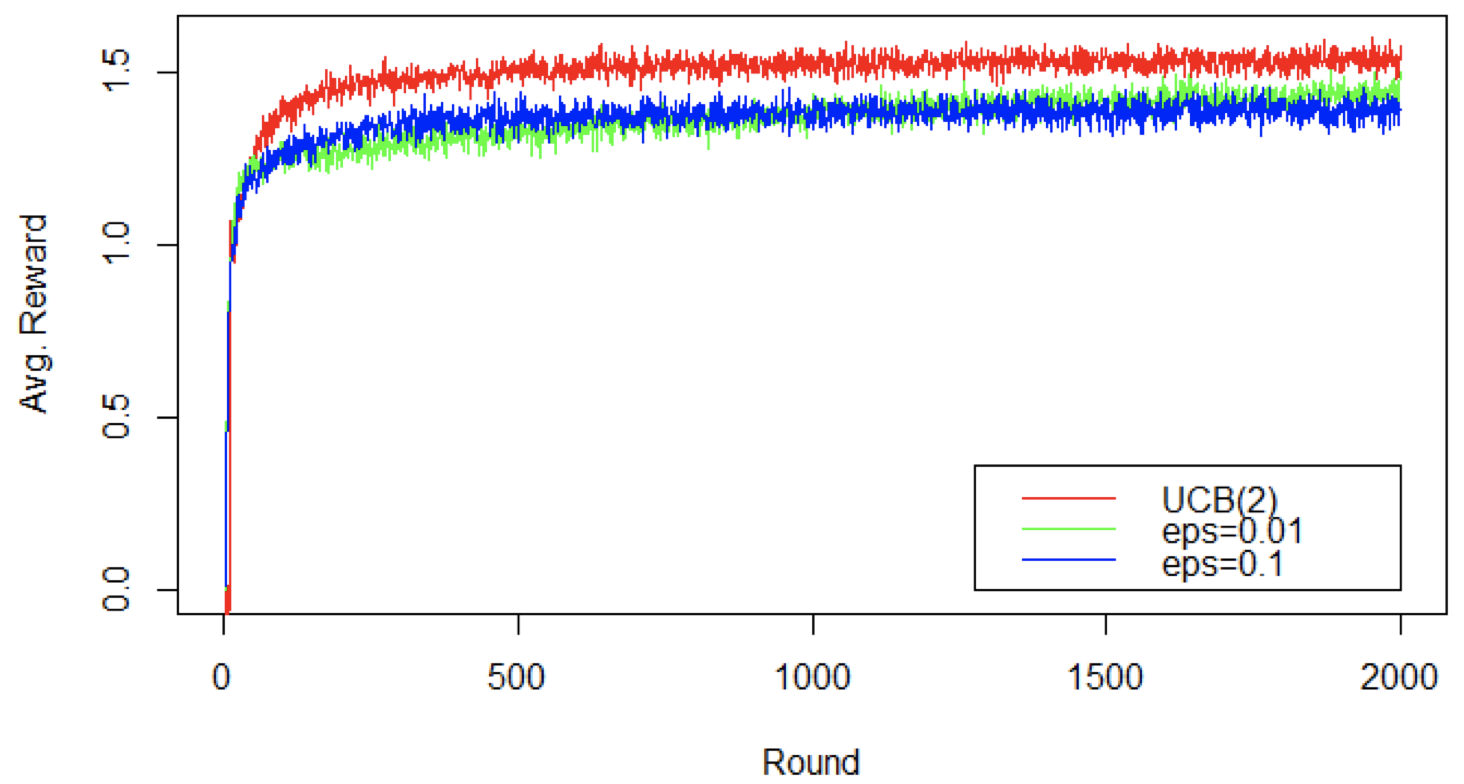
- 在一段时间内,UCB 算法的平均奖励持续超过 $\varepsilon$-Greedy 算法
增加轮数:平均累积奖励比较
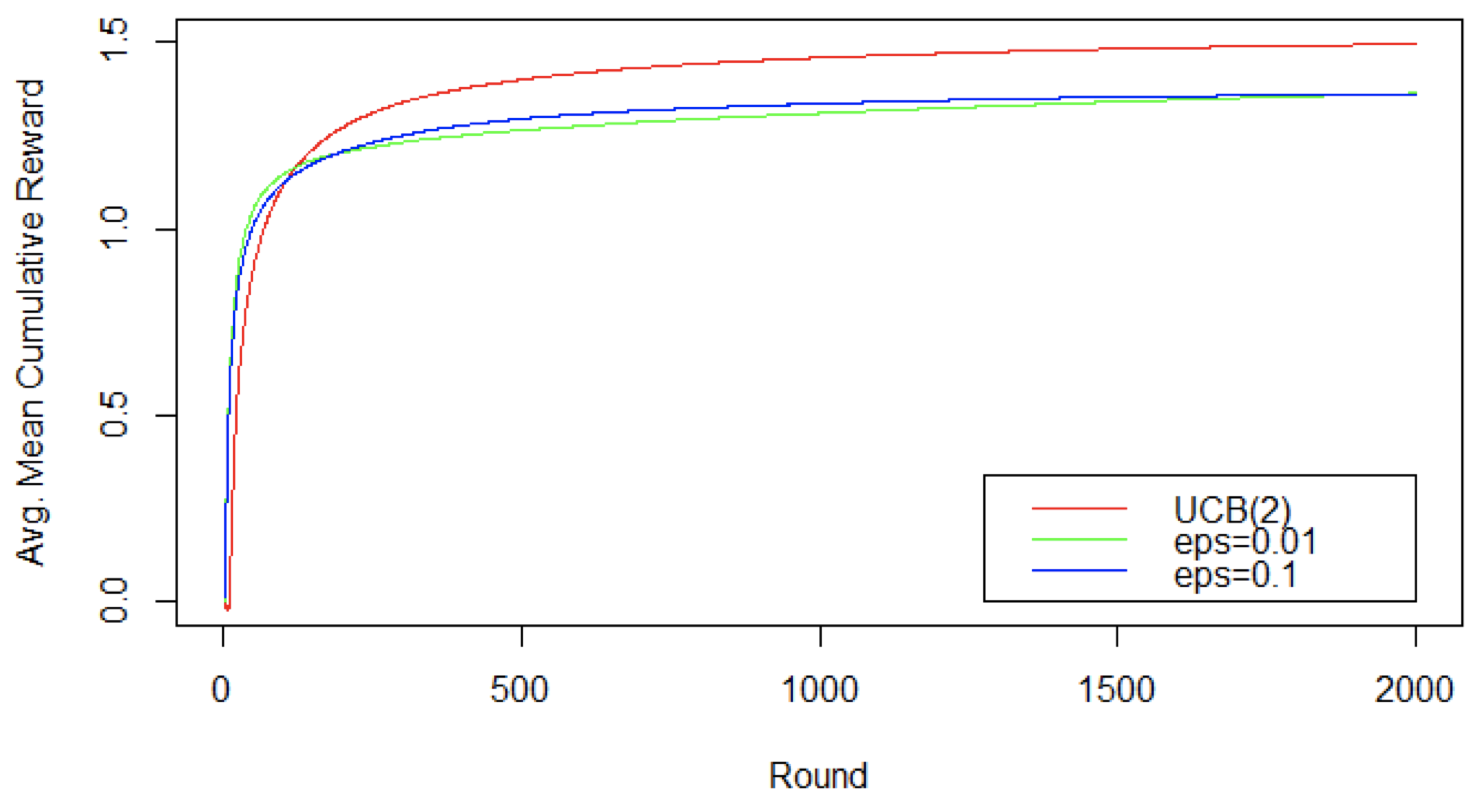
- 当我们观察平均累积奖励时,UCB 算法的优势更明显
3.4 UCB 注意事项
- 理论 遗憾边界(regret bounds) 最高可达乘常数
- 像 $O(\log t)$ 一样增长,即平均遗憾(averaged regret)趋近于零
-
探索超参数(exploration hyperparam)$\color{red}{\rho>0}$ 可调,不一定要为 “$2$”
\[Q_{t-1}(i)=\begin{cases}\hat \mu_{t-1}(i)+\sqrt{\dfrac{\color{red}{\rho}\log(t)}{N_{t-1}(i)}}, & \text{if }\sum_{s=1}^{t-1}1[i_s=i]>0 \\ Q_0 , & \text{otherwise}\end{cases}\]- 可以针对不同 $\varepsilon$ 比率的 Greedy 算法进行对比,并且遗憾边界可以在 $[0,1]$ 之外
- UCB 算法有很多变体,例如:不同的置信边界
- UCB 是在 AlphaGo 中所使用的 蒙特卡洛树搜索 的基础
4. MAB vs. 强化学习
- 上下文老虎机(Contextual bandits) 引入了 状态(state)
- 但没有将 行动(actions) 建模为导致 状态转移(state transitions) 的原因
- 新的状态以 “某种方式” 到达
- 强化学习 也具有很多 轮(rounds) 的 状态(states)、行动(actions) 和 奖励(rewards)
- 但是 (状态,行动) 决定了 下一个状态
- 例如,下围棋,移动一个机器人,物流规划
- 欲了解更多有关规划的内容,请参考课程: COMP90054 人工智能的自治规划
- 强化学习和上下文老虎机算法都通过 回归(regression) 学习 价值函数(value function),但是由于存在状态转移,强化学习将预期的奖励 “推向” 未来
总结
- 随机多臂老虎机
- 不确定性下的顺序决策
- 最简单的 “探索-vs-利用” 的设定
- $(\varepsilon)$-Greedy,UCB 算法
- 很多应用和变体:
- 对抗 MAB:奖励不是随机的,而是任何东西
- 上下文 MAB:行动基于上下文特征向量
- 强化学习:更加通用的设定
下节内容:贝叶斯回归
本作品采用知识共享署名-非商业性使用-相同方式共享 4.0 国际许可协议进行许可。 欢迎转载,并请注明来自:YEY 的博客 同时保持文章内容的完整和以上声明信息!