统计机器学习 COMP90051 课程笔记

统计机器学习 14：贝叶斯回归

墨尔本大学 COMP90051 课程笔记

Posted by YEY on November 19, 2019

Lecture 14 贝叶斯回归

主要内容

  • 点估计没有捕捉到的不确定性
  • 贝叶斯方法保留了不确定性
  • 顺序贝叶斯更新
  • 共轭先验（Normal-Normal）
  • 利用后验在测试集上进行贝叶斯预测

1. 回顾贝叶斯

1.1 训练 = 优化？

学习与推断阶段：

  • 对于分类问题：

    • 建模（以 Logistic 回归为例）

      \[p(y|\boldsymbol x)=\text{sigmoid}(\boldsymbol x'\boldsymbol w)\]

    • 参数拟合数据

      \[\hat{\boldsymbol w}=\mathop{\operatorname{arg\,max}}\limits_{\boldsymbol w}p(\boldsymbol y|\boldsymbol X,\boldsymbol w)p(\boldsymbol w)\]

    • 进行预测

      \[p(y_*|\boldsymbol x_*)=\text{sigmoid}(\boldsymbol x_*'\hat{\boldsymbol w})\]
  • 对于回归问题：

    • 建模

      \[p(y|\boldsymbol x)=\text{Normal}(\boldsymbol x'\boldsymbol w;\sigma^2)\]

    • 参数拟合数据

      \[\hat{\boldsymbol w}=\mathop{\operatorname{arg\,max}}\limits_{\boldsymbol w}p(\boldsymbol y|\boldsymbol X,\boldsymbol w)p(\boldsymbol w)\]

    • 进行预测

      \[E[y_* ]=\boldsymbol x_*'\hat{\boldsymbol w}\]

\(\hat{\boldsymbol w}\) 对应于 “点估计”

1.2 贝叶斯替代

\(\hat{\boldsymbol w}\) 并没有什么特别之处……如果我们不只是使用参数的一个估计值呢？

  • 对于分类问题：

    • 建模

      \[p(y|\boldsymbol x)=\text{sigmoid}(\boldsymbol x'\boldsymbol w)\]

    • 考虑那些可以比较好地拟合数据的 可能的参数空间

      \[p(\boldsymbol w|\boldsymbol X,\boldsymbol y)\]

    • 进行 “期望的” 预测

      \[p(y_*|\boldsymbol x_*)=E_{p(\boldsymbol w|\boldsymbol X,\boldsymbol y)}\left[\text{sigmoid}(\boldsymbol x_*'\boldsymbol w)\right]\]
  • 对于回归问题：

    • 建模

      \[p(y|\boldsymbol x)=\text{Normal}(\boldsymbol x'\boldsymbol w;\sigma^2)\]

    • 考虑那些可以比较好地拟合数据的 可能的参数空间

      \[p(\boldsymbol w|\boldsymbol X,\boldsymbol y)\]

    • 进行 “期望的” 预测

      \[p(y_*|\boldsymbol x_*)=E_{p(\boldsymbol w|\boldsymbol X,\boldsymbol y)}\left[\text{Normal}(\boldsymbol x_*'\boldsymbol w;\sigma^2)\right]\]

2. 不确定性

如果用于训练的数据集很小，我们很少会完全信任任何从中学习到的模型。我们能否量化这种不确定性，并将其用于预测呢？

2.1 重新审视回归问题

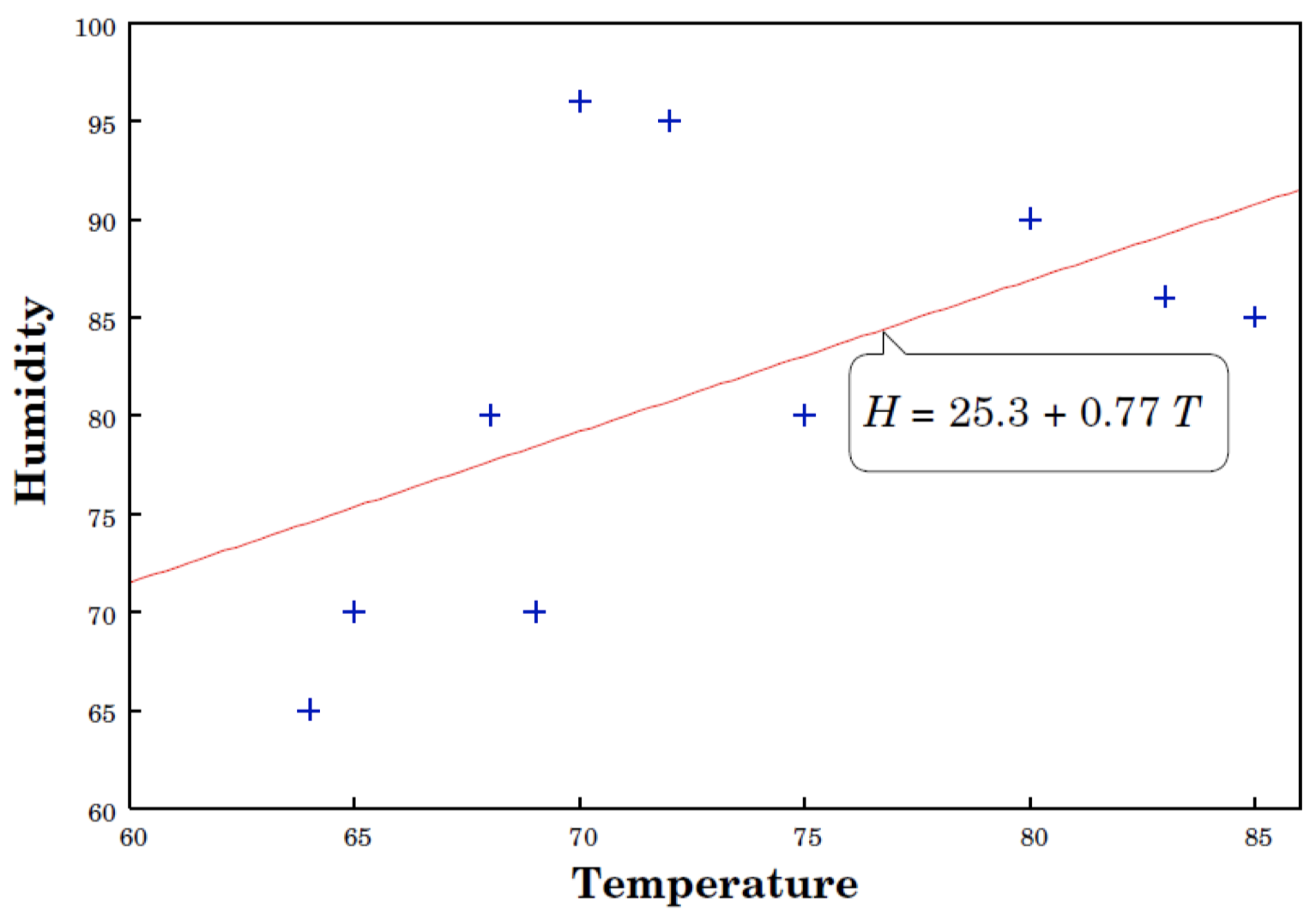
线性回归： $y=w_0+w_1x$
这里，$y=$ humidity（湿度），$x=$ temperature（温度）

  • 从数据中学习模型

    • 通过选择权重来最小化误差残差

      \[\hat{\boldsymbol w}=(\boldsymbol X'\boldsymbol X)^{-1}\boldsymbol X'\boldsymbol y\]
  • 但是我们对于得到的 $\hat{\boldsymbol w}$ 和预测值有多大的信心？

2.2 我们应该相信点估计 $\hat{\boldsymbol w}$ 吗？

  • 我们的学习算法有多稳定？

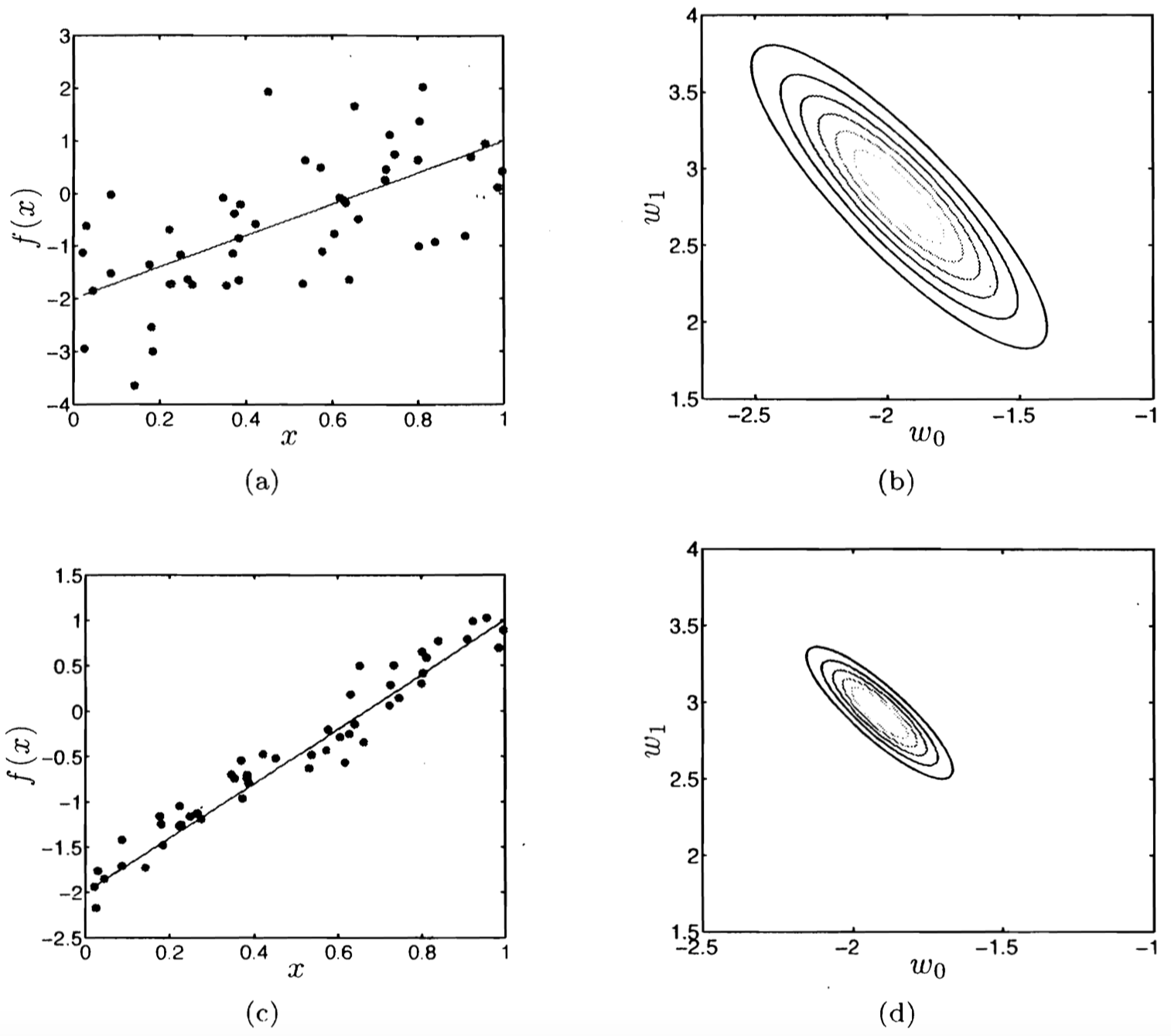
    两个具有不同噪声水平的数据集以及它们各自对应的似然函数
    Source: A First Course in Machine Learning (p.81) by Rogers & Girolami


    • $\hat{\boldsymbol w}$ 对于噪声高度敏感
    • 参数估计的不确定性有多少？
    • 如果目标参数的 负对数似然（Negative Log Likelihood, NLL） 的在峰值处越高且窄，说明我们掌握的信息量越大
  • 形式化为 费雪信息矩阵（Fisher Information Matrix）
    • $E[ 2^{nd} \text{ deriv of NLL}]$
      $\cal I$ $=\dfrac{1}{\sigma^2}\boldsymbol X’\boldsymbol X$
  • 衡量关于 $\hat{\boldsymbol w}$ 的目标函数的曲率

3. 贝叶斯视角

保留所有的未知因素（例如：参数的不确定性）并对它们进行建模，并且在进行统计推断时利用这些信息。

3.1 一个贝叶斯人的视角

  • 我们有理由认为 所有的 参数对于数据而言都是常数吗？
    • 对于训练数据拟合更好的权重的概率应该大于其他权重的概率
    • 利用所有可能的权重进行预测，乘以各自的概率作为缩放系数
  • 这就是 贝叶斯推断 背后的思想

3.2 参数的不确定性

  • 目标函数有很多合理的解
    • 为什么只选择其中的某一个呢？
  • 考虑 所有 可能的参数值背后的原因
    • 乘以它们的 后验概率 作为加权项
  • 更具鲁棒性的预测
    • 可以更好地避免过拟合，尤其是对于小的训练集而言
    • 可以得到表达能力更强的模型类别（例如：贝叶斯 Logistic 回归是非线性模型）

3.3 频率学家 vs. 贝叶斯人的 “分歧”

  • 频率学家： 使用 点估计、正则化、p值 … 进行学习
    • 简单的假设背后是复杂的理论支撑
    • 大部分算法都比较简单，非常偏实用的机器学习研究
  • 贝叶斯人： 保留 不确定性，在进行统计推断时对未知因素进行 边缘化（求和）
    • 一些理论
    • 算法通常更加复杂，但并非总是如此
    • 通常（并非绝对）在计算上开销更高

4. 贝叶斯回归

将贝叶斯推断应用于线性回归，对于 $\boldsymbol w$ 使用正态先验

4.1 再谈线性回归

  • 回忆线性回归的概率公式

    \[y\sim \text{Normal}(\boldsymbol x'\boldsymbol w, \sigma^2)\] \[\boldsymbol w\sim \text{Normal}(\boldsymbol 0,\gamma^2 \boldsymbol I_D)\]

    其中，$\boldsymbol I_D$ 是 $D\times D$ 的单位矩阵

  • 贝叶斯规则

    \[p(\boldsymbol w|\boldsymbol X,\boldsymbol y)=\dfrac{p(\boldsymbol y|\boldsymbol X,\boldsymbol w)p(\boldsymbol w)}{p(\boldsymbol y|\boldsymbol X)}\]

    这里，我们假设 $\boldsymbol w$ 与 $\boldsymbol X$ 之间互相独立：
    \(p(\boldsymbol w|\boldsymbol X,\boldsymbol y) = \dfrac{p(\boldsymbol w,\boldsymbol X,\boldsymbol y)}{p(\boldsymbol X,\boldsymbol y)} =\dfrac{p(\boldsymbol y|\boldsymbol X,\boldsymbol w)p(\boldsymbol X,\boldsymbol w)}{p(\boldsymbol y|\boldsymbol X)p(\boldsymbol X)} =\dfrac{p(\boldsymbol y|\boldsymbol X,\boldsymbol w)p(\boldsymbol X)p(\boldsymbol w)}{p(\boldsymbol y|\boldsymbol X)p(\boldsymbol X)} =\dfrac{p(\boldsymbol y|\boldsymbol X,\boldsymbol w)p(\boldsymbol w)}{p(\boldsymbol y|\boldsymbol X)}\)


    \[\max \limits_{\boldsymbol w}p(\boldsymbol w|\boldsymbol X,\boldsymbol y)=\max \limits_{\boldsymbol w}p(\boldsymbol y|\boldsymbol X,\boldsymbol w)p(\boldsymbol w)\]

    这里，我们采用点估计避免计算边缘似然项。

  • 导致目标函数惩罚化（岭回归）

4.2 贝叶斯线性回归

  • 回退一步，考虑完全后验

    \[\begin{align} p(\boldsymbol w|\boldsymbol X,\boldsymbol y,\sigma^2) &= \dfrac{p(\boldsymbol y|\boldsymbol X,\boldsymbol w,\sigma^2)p(\boldsymbol w)}{p(\boldsymbol y|\boldsymbol X,\sigma^2)} \\ &= \dfrac{p(\boldsymbol y|\boldsymbol X,\boldsymbol w,\sigma^2)p(\boldsymbol w)}{\int \color{red}{\underbrace{\color{black}{p(\boldsymbol y|\boldsymbol X,\boldsymbol w,\sigma^2)p(\boldsymbol w)}}_{p(\boldsymbol y,\boldsymbol w|\boldsymbol X,\sigma^2)}} \text{ d} \boldsymbol w} \end{align}\]

    这里，我们假设噪声的方差已知。

  • 我们可以计算分母（边缘似然 或者 证据）吗？
    • 如果是这样，我们可以使用完全后验，而非仅仅是它的众数
  • 我们有两个正态分布
    • 正态似然 $\times$ 正态先验
  • 它们的乘积也是一个正态分布
    • 共轭先验： 当似然函数和先验的乘积结果的分布与先验分布相同时（即后验分布与先验分布属于同类），则先验分布与后验分布被称为 共轭分布，而先验分布被称为似然函数的 共轭先验。
      例如，高斯分布家族在高斯似然函数下与其自身共轭(自共轭)。
    • 利用正态分布的归一化常数可以很容易地计算出 证据（边缘似然）
  • 后验的闭合解（Closed Form Solution）
\[\begin{align} p(\boldsymbol w|\boldsymbol X,\boldsymbol y,\sigma^2) &\propto \text{Normal}(\boldsymbol w|\boldsymbol 0,\gamma^2\boldsymbol I_D)\text{Normal}(\boldsymbol y|\boldsymbol {Xw},\sigma^2\boldsymbol I_N) \\ &\propto \text{Normal}(\boldsymbol w|\boldsymbol w_N,\boldsymbol V_N) \end{align}\]

其中，$\boldsymbol w_N=\dfrac{1}{\sigma^2}\boldsymbol V_N\boldsymbol X’\boldsymbol y \;,\quad \boldsymbol V_N=\sigma^2(\boldsymbol X’\boldsymbol X+\dfrac{\sigma^2}{\gamma^2}\boldsymbol I_D)^{-1}$

注意： 之前的均值（和众数）都是 MAP 的解。

我们可以通过两个正态分布的乘积来验证：将指数部分合并在一起，并对常系数部分 “完成平方” 来表示为常系数的平方乘以一个指数部分（即正态分布）。

回顾之前 Lecture 02 的 3.2 节 中提到的例子：

  • 我们对 $X\mid\theta$ 建模为 $\text{N}(\theta,1)$，先验为 $N(0,1)$

  • 假设我们观测到 $X=1$，然后更新先验

    \[\begin{align} P(\theta|X=1) &= \dfrac{P(X=1| \theta)P(\theta)}{P(X=1)} \quad\quad\color{purple}{\text{目标是将后验转换为已知分布形式。指数的二次方一定为正态}}\\ &\propto P(X=1| \theta)P(\theta) \\ &=\left[\color{purple}{\dfrac{1}{\sqrt{2\pi}}}\exp\left(-\dfrac{(1-\theta)^2}{2}\right)\right]\left[\color{purple}{\dfrac{1}{\sqrt{2\pi}}}\exp\left(-\frac{\theta^2}{2}\right)\right] \quad\quad\color{purple}{\text{丢弃关于 }\theta\text{ 的常数项}}\\ &\propto \exp\left(-\dfrac{(1-\theta)^2+\theta^2}{2}\right) \quad\quad\color{purple}{\text{合并指数项}}\\ &= \exp\left(-\dfrac{2\theta^2-2\theta+1}{2}\right) \\ &= \exp\left(-\dfrac{\theta^2-\theta+\frac{1}{2}}{2\times \color{purple}{\frac{1}{2}}}\right) \quad\quad\color{purple}{\text{将分子项中 }\theta^2\text{ 的系数移到分母上}}\\ &= \exp\left(-\dfrac{\theta^2-\theta+\color{purple}{\frac{1}{4}}}{2\times \frac{1}{2}}\right) \cdot \color{purple}{\exp\left(-\dfrac{\frac{1}{4}}{2\times \frac{1}{2}}\right)} \quad\quad\color{purple}{\text{将分子项凑成平方形式：移除多余的常数项}}\\ &\propto \exp\left(-\dfrac{\theta^2-\theta+\frac{1}{4}}{2\times \frac{1}{2}}\right)\\ &= \exp\left(-\dfrac{(\theta-\frac{1}{2})^2}{2\times \frac{1}{2}}\right) \quad\quad\color{purple}{\text{因式分解}}\\ &\propto N(0.5,0.5) \quad\quad\quad\color{purple}{\text{发现为（非标准）正态分布}} \end{align}\]

    注意：允许将常量提到前面，并通过归一化 “忽略”

4.3 贝叶斯线性回归例子

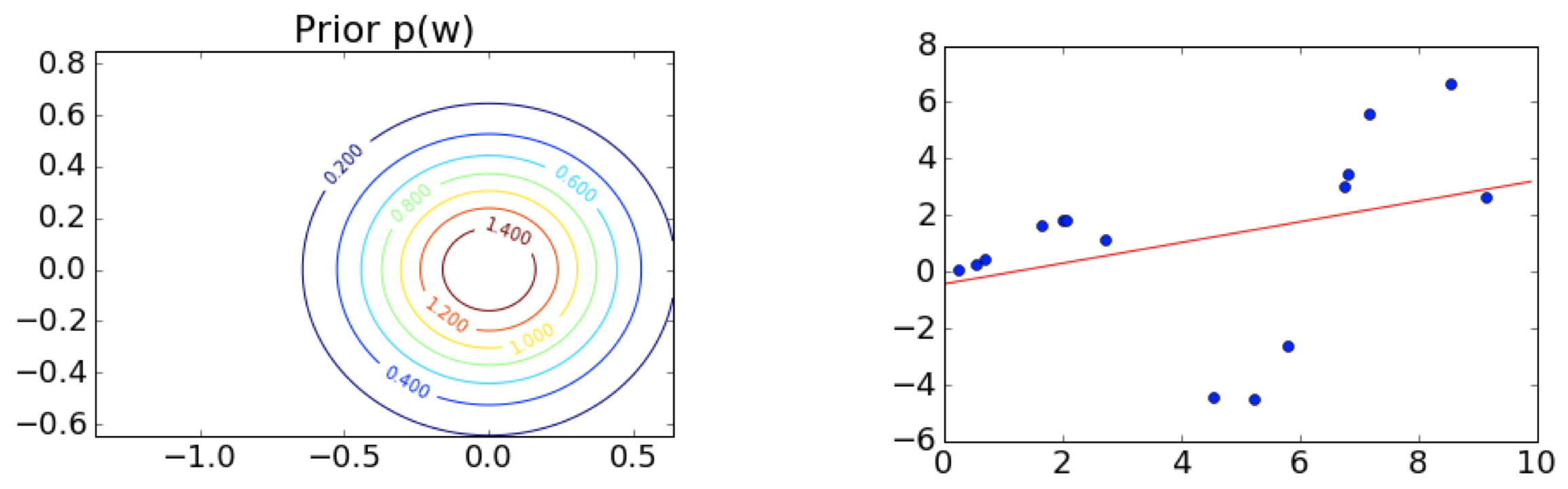
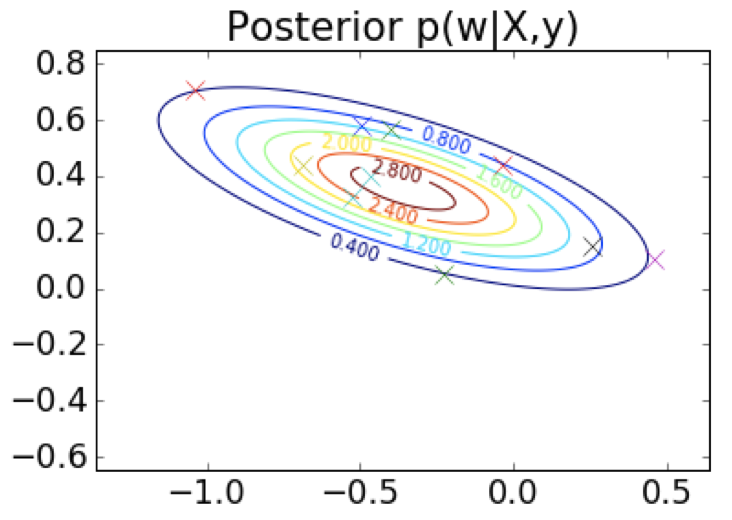
第 1 步：选择先验，这里是中心在原点 (0,0) 附近的球形 $\qquad \qquad \qquad \;$ 第 2 步：观测训练数据

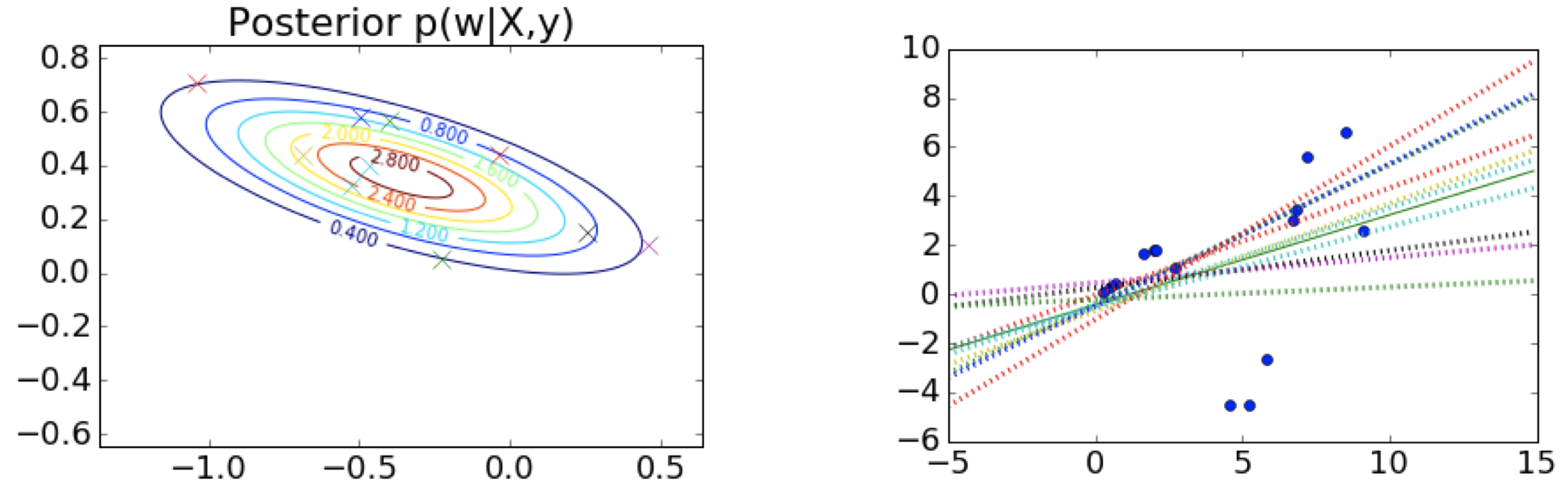
$\;\;$ 第 3 步：根据先验和似然函数，写出后验的形式 $\qquad \qquad \qquad \quad\;\;$ 第 4 步：从后验中采样

4.4 顺序贝叶斯更新

  • 可以为给定的数据集构建 \(p(\boldsymbol w|\boldsymbol X,\boldsymbol y,\sigma^2)\)

  • 如果我们观察到越来越多的数据会发生什么？

    1. 从先验 $p(\boldsymbol w)$ 开始
    2. 观测新的带标签的数据点
    3. 计算后验 \(p(\boldsymbol w|\boldsymbol X,\boldsymbol y,\sigma^2)\)
    4. 将得到的后验视为当前的先验，然后再从第 2 步开始重复这个过程

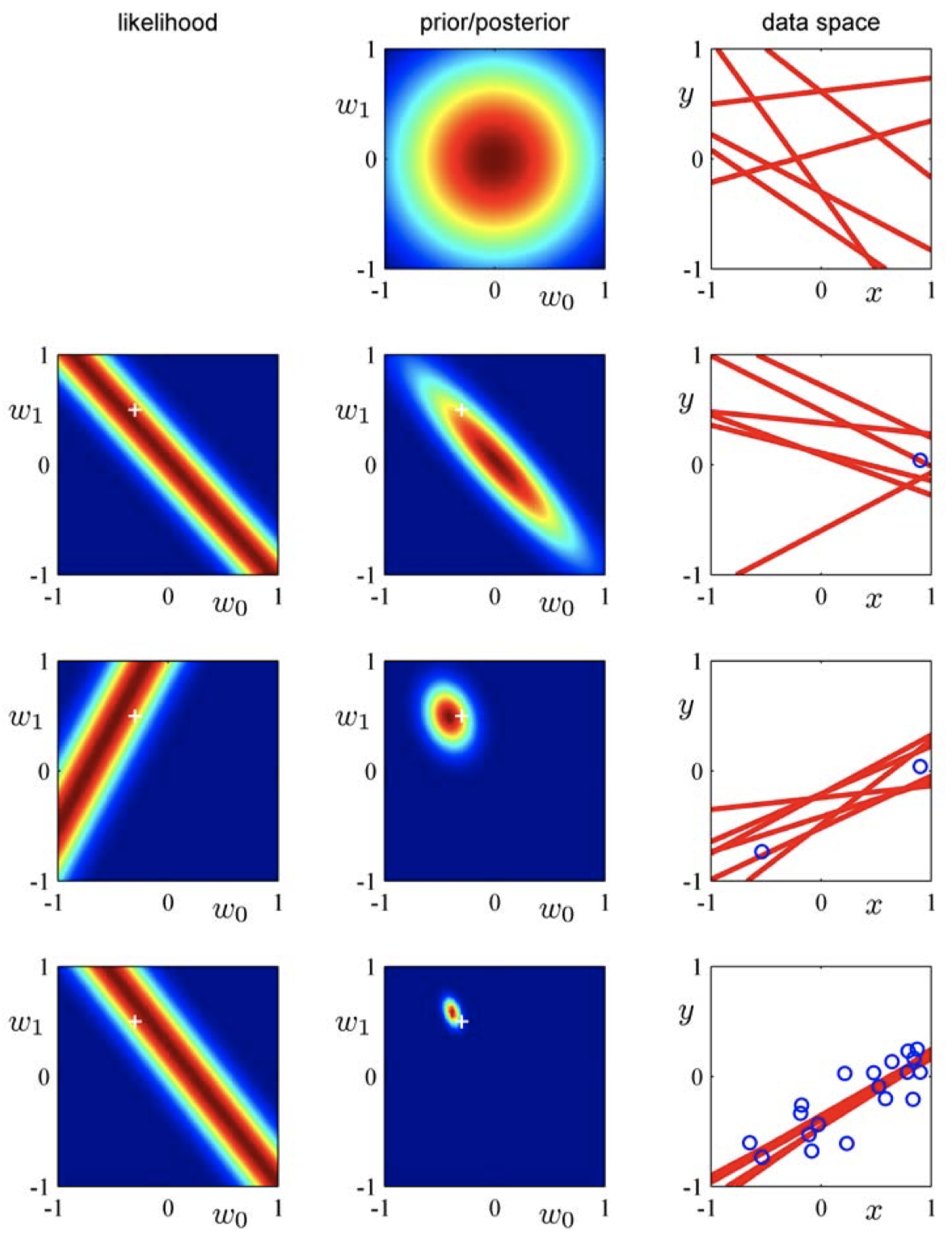
一个简单线性模型 $\,y(x,\boldsymbol w)=w_0+w_1x\,$ 使用顺序贝叶斯学习的例子
Source: Pattern Recognition and Machine Learning (p.155) by Bishop

  • 初始时，我们掌握的信息量很少，存在很多可能的回归直线
  • 似然函数约束了可能存在的权重，使得回归直线靠近数据点
  • 随着更多数据的引入，后验变得更加精确 / 达到峰值
  • 接近质心

4.5 训练阶段

$\,$1. 决定模型的数学表示和先验
$\,$2. 计算参数的后验 \(p(\boldsymbol w|\boldsymbol X,\boldsymbol y)\)

$\qquad \;$ MAP $\qquad \qquad \qquad \qquad$ approx.Bayes $\qquad \qquad \qquad$ exact Bayes

$\,$3. 寻找 $\boldsymbol w$ 的众数 $\qquad \quad \,$ 3. 采用很多 $\boldsymbol w$ $\qquad \qquad \qquad \quad\,$ 3. 使用所有的 $\boldsymbol w$
$\,$4. 在测试集上进行预测 $\quad\;$ 4. 在测试集上进行 集成 平均预测 $\quad$ 4. 在测试集上进行 期望 预测

4.6 利用不确定的 $\boldsymbol w$ 进行预测

  • 可以利用简单的回归曲线进行预测
    • 采样 $S$ 个参数 \(\boldsymbol w^{(s)}\)，其中 \(s\in\{1,...,S\}\)
    • 对于每一个样本参数 \(\boldsymbol w^{(s)}\)，在测试集数据点 \(\boldsymbol x_*\) 上计算预测值 \(y_*^{(s)}\)
    • 计算这些预测值的均值（和方差）
    • 这个过程被称为 蒙特卡洛积分
  • 对于贝叶斯回归存在一个更简单的解

    • 积分可以被解析计算

      \[p(\hat y_*|\boldsymbol X,\boldsymbol y,\boldsymbol x_*,\sigma^2)=\int p(\boldsymbol w|\boldsymbol X,\boldsymbol y,\sigma^2)p(y_*|\boldsymbol x_*,\boldsymbol w,\sigma^2)\,\text{d}\boldsymbol w\]

  • 高斯分布的良好性质意味着积分是易于处理的

    \[\begin{align} p(\hat y_*|\boldsymbol X,\boldsymbol y,\boldsymbol x_*,\sigma^2) &= \int p(\boldsymbol w|\boldsymbol X,\boldsymbol y,\sigma^2)p(y_*|\boldsymbol x_*,\boldsymbol w,\sigma^2)\,\text{d}\boldsymbol w \\ &= \int \text{Normal}(\boldsymbol w|\boldsymbol w_N,\;\boldsymbol V_N) \text{Normal}(y_*|\boldsymbol x_*'\boldsymbol w,\;\sigma^2)\,\text{d}\boldsymbol w\\ &=\text{Normal}\left(y_*|\boldsymbol x_*'\boldsymbol w_N,\;\sigma_N^2(\boldsymbol x_*)\right) \end{align}\]

    其中，

    \[\sigma_N^2(\boldsymbol x_*)=\sigma^2+\boldsymbol x_*'\boldsymbol V_N\boldsymbol x_*\]
    • 基于训练数据 $\boldsymbol x_*$ 匹配的加性方差
    • 比较 MLE / MAP 估计（它们的方差均为一个固定的常数）

    （当进行贝叶斯线性回归拟合时，$\boldsymbol w_N$ 和 $\boldsymbol V_N$ 在后验中定义）

4.7 贝叶斯预测例子

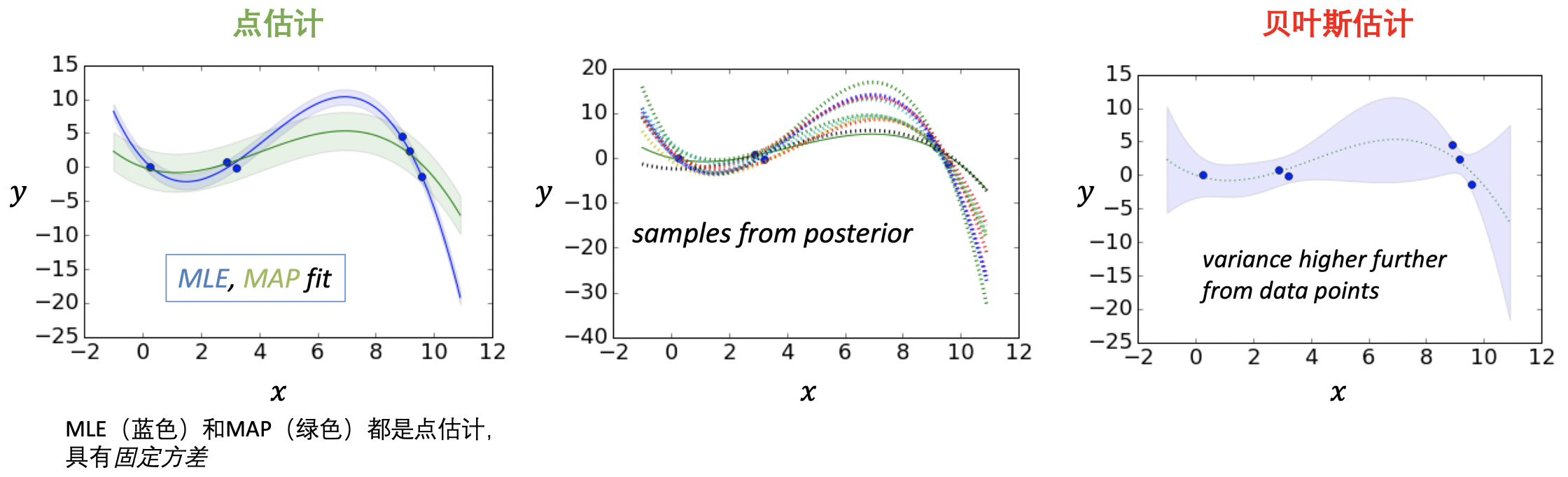
数据：$y=x \sin(x)\qquad$ 模型：三阶立方

4.8 说明

  • 假设
    • 数据噪声参数已知，$\sigma^2$
    • 数据来源于模型分布
  • 在现实设定中，$\sigma^2$ 是未知的
    • 具有自己的共轭先验
      Normal likelihood（正态似然）$\times$ InverseGamma prior（逆伽马先验）
      结果为 InverseGamma posterior（逆伽马后验）
    • 闭合形式的预测分布，具有 student-T likelihood（学生-T 似然）

总结

  • 点估计（MLE，MAP）没有捕捉到的不确定性
  • 贝叶斯方法保留了不确定性
    • 关注预测而非参数
    • 选择参数空间上的先验，然后对后验建模
  • 新的概念：
    • 顺序贝叶斯更新
    • 共轭先验（Normal-Normal）
  • 利用后验在测试集上进行贝叶斯预测

下节内容：贝叶斯分类

知识共享许可协议本作品采用知识共享署名-非商业性使用-相同方式共享 4.0 国际许可协议进行许可。 欢迎转载，并请注明来自：YEY 的博客 同时保持文章内容的完整和以上声明信息！
CATALOG
    FEATURED TAGS
    随笔 课程笔记 统计机器学习 COMP90051 学习笔记 自然语言处理 COMP90042 PyTorch 人工智能伦理 COMP90087 数据科学多元统计学 MAST90138 AI 自动规划 COMP90054 数据分析 计算统计学与数据科学 MAST90083 高级数据库系统 COMP90050 统计建模 MAST90139 读书 📚 MySQL 学习索引 Hive 技术问题 Jekyll Workshop
    FRIENDS