Lecture 15 贝叶斯分类
主要内容
- 离散设定下的贝叶斯思想
- Beta-Binomial 共轭
- 贝叶斯分类
- 非共轭的渐进必要性
1. 离散设定下的贝叶斯思想
1.1 如何将贝叶斯观点应用于离散数据?
- 优先考虑 生成 输入的 生成式模型
-
对比 判别式模型,其将输入作为 条件
生成式模型 判别式模型 对输入 $\boldsymbol x$ 和标签 $y$ 的联合分布 $p(\boldsymbol x,y)$进行建模,并通过贝叶斯规则来计算 $p(y\mid \boldsymbol x)$,然后选择最可能的标签 $y$ 进行预测 直接对后验条件概率 $p(y\mid \boldsymbol x)$ 建模,或者从输入 $\boldsymbol x$ 学习一个直接映射到类别的标签 $y$ 例如:朴素贝叶斯 例如:Logistic 回归
-
- 为了便于理解,我们从最基础的设定开始
- 抛 $n$ 次硬币,其中有 $k$ 次正面朝上
- 只有 $\boldsymbol x$(结果的序列),没有 “类别” $y$
- 在离散数据上应用 生成式模型
1.2 离散共轭先验:Beta-Binomial
- 离散空间也存在共轭先验
- 考虑抛 $n$ 次硬币,其中有 $k$ 次正面朝上
- 令单次抛掷正面朝上的概率为 $p(Head)=q$(伯努利分布)
- 推断问题为:硬币是否是公正的(即 $q \approx 0.5$)?
-
多次尝试,利用 二项式分布
\[p(k|n,q)= {n\choose k}q^k(1-q)^{n-k}\]-
以及它的共轭先验 Beta 分布
\[\begin{align} p(q) &= \text{Beta}(q;\alpha,\beta) \\ &= \dfrac{\gamma(\alpha+\beta)}{\gamma(\alpha)\gamma(\beta)}q^{\alpha-1}(1-q)^{\beta-1} \end{align}\]
-
1.3 Beta 分布
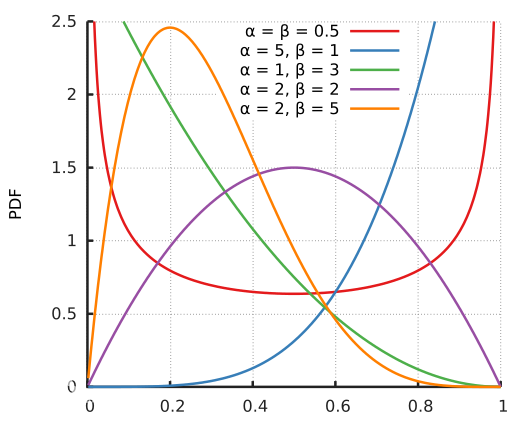
1.4 Beta-Binomial 共轭
-
二项式(Binomial)分布
\[p(k|n,q)= {n\choose k}q^k(1-q)^{n-k}\] -
Beta 分布
\[\begin{align} p(q) &= \text{Beta}(q;\alpha,\beta) \\ &= \color{red}{\dfrac{\gamma(\alpha+\beta)}{\gamma(\alpha)\gamma(\beta)}}q^{\alpha-1}(1-q)^{\beta-1} \qquad \color{red}{\text{很好,现在我们知道了 Beta 分布的归一化算子}} \end{align}\] -
证明二者共轭:
\[\begin{eqnarray} \color{green}{\text{贝叶斯后验} \qquad p(q|k,n)}\; &{\color{purple}\propto}& p(k|n,q)p(q) \\ &{\color{purple}\propto}& q^k(1-q)^{n-k}q^{\alpha-1}(1-q)^{\beta-1} \\ &{\color{black}=}& q^{k+\alpha-1}(1-q)^{n-k+\beta-1} \\ &{\color{purple}\propto}& \color{red}{\text{Beta}}(q;k+\alpha,n-k+\beta) \qquad \color{purple}{\text{技巧:忽略常数项因子(归一化算子)}} \end{eqnarray}\]
1.5 归一化的唯一性
- 我们多次用到了一种技巧: 当一个非规范分布(unnormalized distribution)和某一已知分布成比例时,我们可以认为其就是该分布。
- 如果 $f(\theta) \propto g(\theta)$,其中 $g$ 为某一已知分布,那么 $\dfrac{f(\theta)}{\int_{\boldsymbol \Theta} f(\theta)\,\text{d}\theta}=g(\theta)$
-
证明: $f(\theta) \propto g(\theta)$ 意味着
\[f(\theta) = C\cdot g(\theta) \tag{1}\] \[\int_{\boldsymbol \Theta} f(\theta)\,\text{d}\theta = C\cdot \int_{\boldsymbol \Theta} g(\theta)\,\text{d}\theta = C \tag{2}\]将 $(1)$ 和 $(2)$ 的等号两边的对应项相除,即可得到
\[\dfrac{f(\theta)}{\int_{\boldsymbol \Theta} f(\theta)\,\text{d}\theta}=g(\theta)\]
1.6 拉普拉斯的日出问题
每天清晨,你都观察到太阳升起。仅基于这一事实,明天太阳会升起的概率是多少?

- 利用 Beta-Binomial 共轭,其中 $q$ 为太阳早上升起的概率 $\Pr($ “太阳早上升起” $)$
- 后验 \(p(q|k.n)=\text{Beta}(q;k+\alpha,n-k+\beta)\)
- $n=k=$ 观察者的年龄(按天数计算)
- 令 $\alpha=\beta=1$(等同于均匀分布先验)
-
基于上面这些假设,可以得到后验
\[p(q|k)=\text{Beta}(q;\color{purple}{k+1},\color{purple}{1}) \qquad \color{purple}{\text{“自然地”计算太阳升起 / 没有升起的天数}}\]所以,明天早上太阳升起的概率的期望为
\[E_{p(q|k)}[q]=\dfrac{k+1}{k+2}\qquad\qquad\]
考虑观察者的年龄:
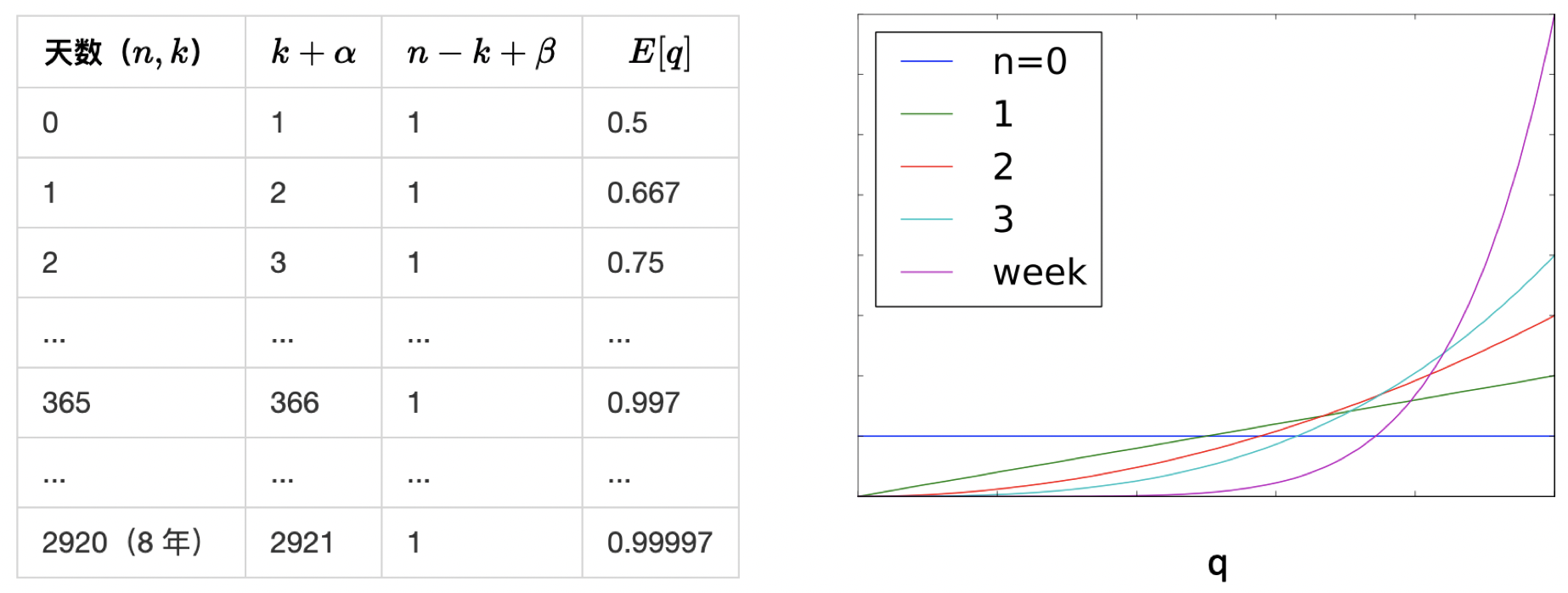
随着数据的增加,先验的影响逐渐减小,但永远不会消失。
1.7 常见的共轭先验

2. 贝叶斯 Logistic 回归
判别式分类器,将输入作为条件对后验建模。在这样的设定下,我们应该如何进行贝叶斯推断?
2.1 再看 Logistic 回归
- 与回归问题相比,同样存在类似的参数不确定性问题
- 尽管内置了预测不确定性对输出建模
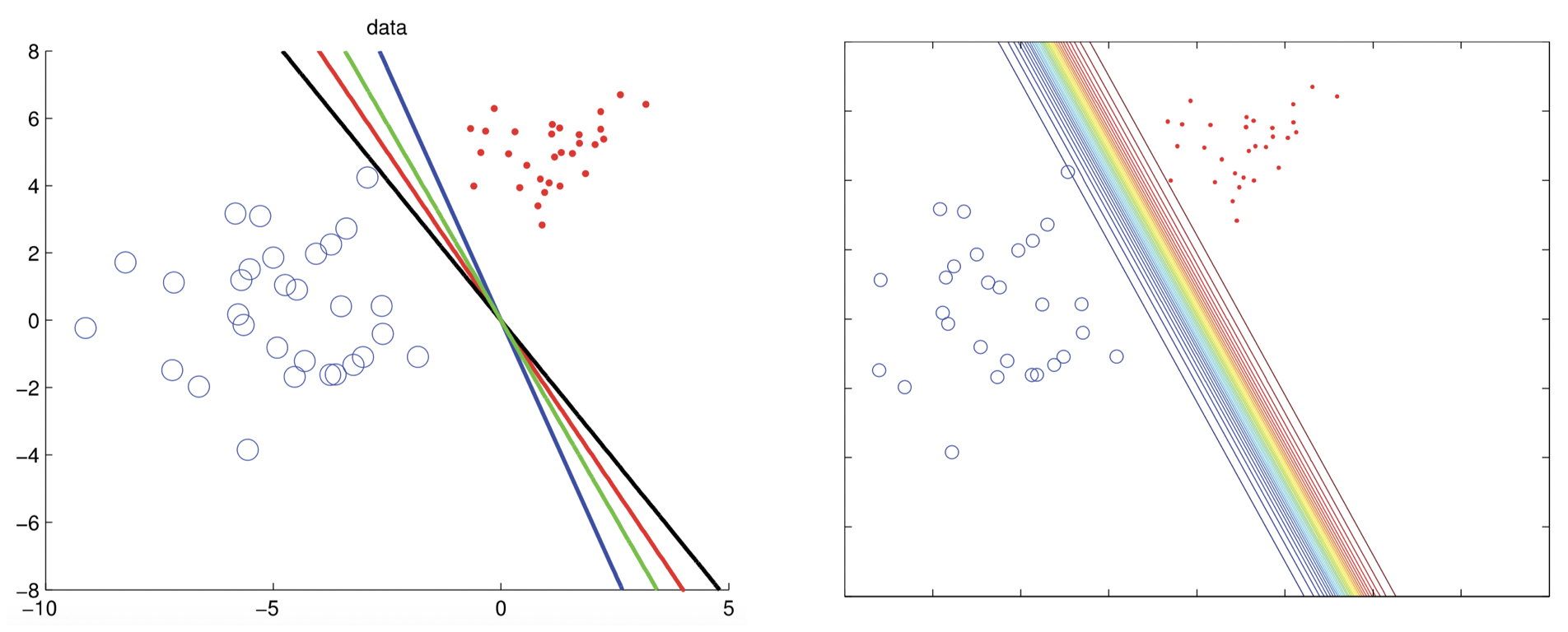
2.2 共轭不存在的情况
- 我们可以利用共轭先验吗?例如:
- 生成二分类模型(generative binary models)的 Beta-Binomial 共轭
- 多分类模型的 Dirichlet-Multinomial 共轭(类似的公式)
-
模型是 判别式的,Logistic 回归的参数由 sigmoid 函数定义(或者,对于多分类模型,参数由 softmax 函数定义;类似的问题和类似的解)
\[p(y|q,\boldsymbol x)=q^y(1-q)^{1-y}\] \[q=\sigma(\boldsymbol x'\boldsymbol w)\]- 需要 $\boldsymbol w$ 的先验,而不是 $q$
- 没有已知的共轭先验,所以使用高斯先验
2.3 近似
-
归一化常数没有已知的解
\[\begin{align} p(\boldsymbol w|\boldsymbol X,\boldsymbol y) &\propto p(\boldsymbol w)p(\boldsymbol y|\boldsymbol X,\boldsymbol w) \\ &= \text{Normal}(\boldsymbol 0,\sigma^2 \boldsymbol I)\prod_{i=1}^{n}\sigma(\boldsymbol x_i'\boldsymbol w)^{y_i}\left(1-\sigma(\boldsymbol x_i'\boldsymbol w)\right)^{1-y_i} \end{align}\] -
通过近似求解
拉普拉斯近似:- 假定众数的后验服从渐进正态
- 可以计算归一化常数、抽样等

Source: Machine Learning A Probabilistic Perspective, MLAPP (p.258) by Murphy
总结
- 离散设定下的贝叶斯思想
- Beta-Binomial 共轭
- 贝叶斯分类
- 非共轭的渐进必要性
下节内容:概率图模型
本作品采用知识共享署名-非商业性使用-相同方式共享 4.0 国际许可协议进行许可。 欢迎转载,并请注明来自:YEY 的博客 同时保持文章内容的完整和以上声明信息!