统计机器学习 COMP90051 课程笔记

统计机器学习 16：概率图模型

墨尔本大学 COMP90051 课程笔记

Posted by YEY on November 21, 2019

Lecture 16 概率图模型

主要内容

  • 联合分布的表示
  • 条件 / 边缘独立
    • 有向 vs 无向

1. 概率图模型

图论与概率论的结合，贝叶斯统计学习的首选工具。我们将从简单的离散情况出发，再延伸到连续情况。

1.1 实际意义驱动

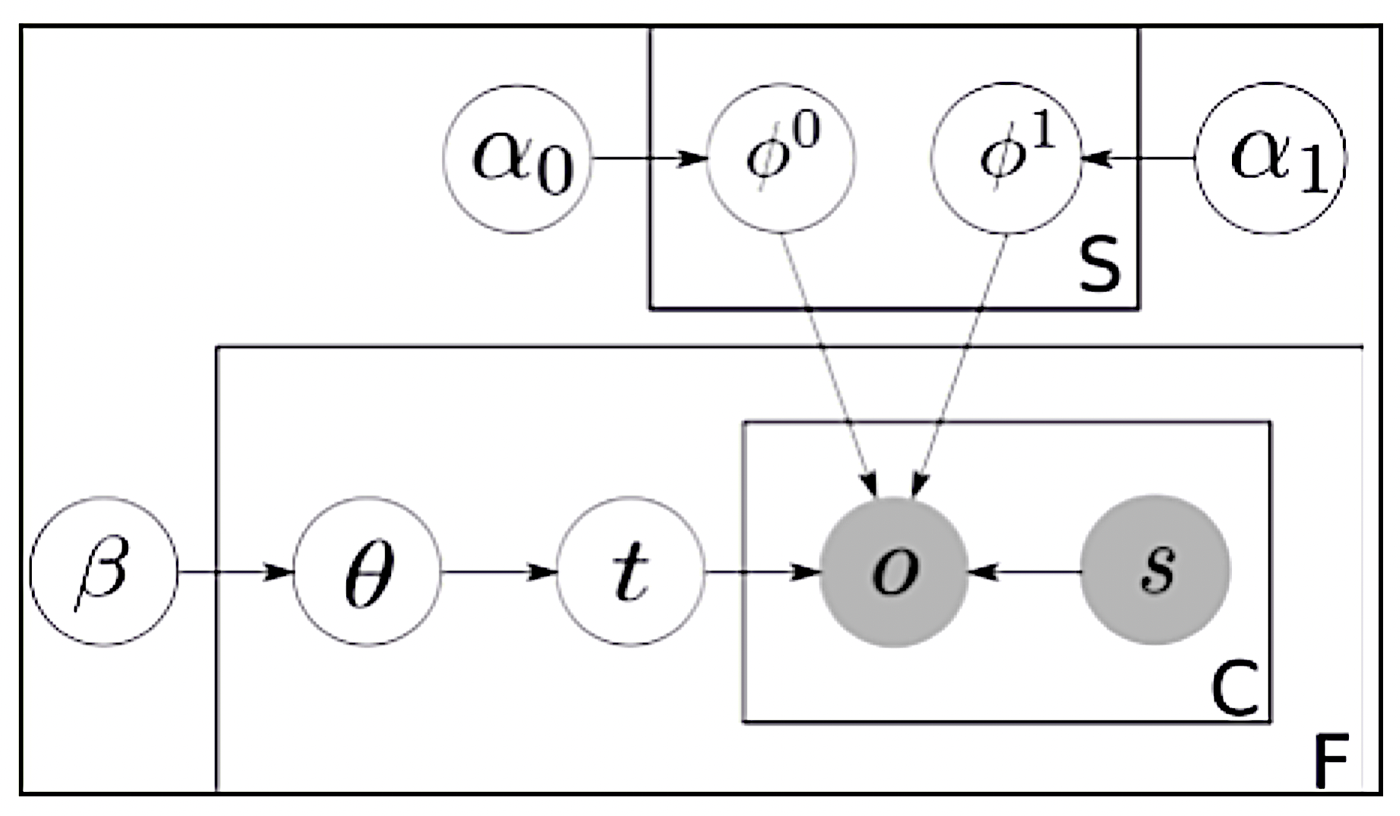
很多应用

  • 进化树
  • 谱分析、关联分析
  • 错误控制代码
  • 语音识别
  • 文档主题模型
  • 概率解析
  • 图像分割
  • …

发现的算法

  • HMM
  • 卡尔曼滤波器
  • 混合模型
  • LDA
  • MRF
  • CRF
  • Logistic 回归、线性回归
  • …

1.2 比较方式驱动

贝叶斯统计学习

  • 对 $\boldsymbol X, \boldsymbol y$ 和参数随机变量的联合分布进行建模
    • “先验”：参数边缘化
  • 训练：利用观测数据，将先验更新为后验
  • 预测：输出后验，或者后验的某个函数（MAP）

概率图模型（PGM），又称 “贝叶斯网络”

  • 高效的联合表示
    • 显式表示独立性
    • 容易在表达性和数据需求之间做出权衡
    • 易于从业者建模
    • 拟合参数、计算边缘和后验的算法

1.3 一切始于联合分布

  • 所有离散随机变量的联合分布都可以用表格表示
  • 随着随机变量数量的增加，表格行数呈指数上升
  • 例子：真值表
    • $m$ 个布尔随机变量需要 $(2^m-1)$ 行
    • 表格为每行分配概率

1.4 好处：我们可以基于联合分布做些什么？

  • 根据随机变量的联合分布进行 概率推断
    • 计算任何涉及这些随机变量的其他分布
  • 模式：已有联合分布，希望得到一个分布
    利用：贝叶斯规则 + 边缘化
  • 例子：朴素贝叶斯分类器
    • 预测实例 $\boldsymbol x$ 的类别 $y$，通过最大化
    \[\Pr(Y=y|\boldsymbol X=\boldsymbol x)=\dfrac{\color{steelblue}{\Pr(Y=y,\boldsymbol X=\boldsymbol x)}}{\color{steelblue}{\Pr(\boldsymbol X=\boldsymbol x)}}=\dfrac{\Pr(Y=y,\boldsymbol X=\boldsymbol x)}{\color{red}{\sum_y \Pr(\boldsymbol X=\boldsymbol x,Y=y)}}\]

    回忆：连续分布（在参数上）的积分与离散分布的求和等价（均称为边缘化）

1.5 坏处和丑陋：表格会变得非常大

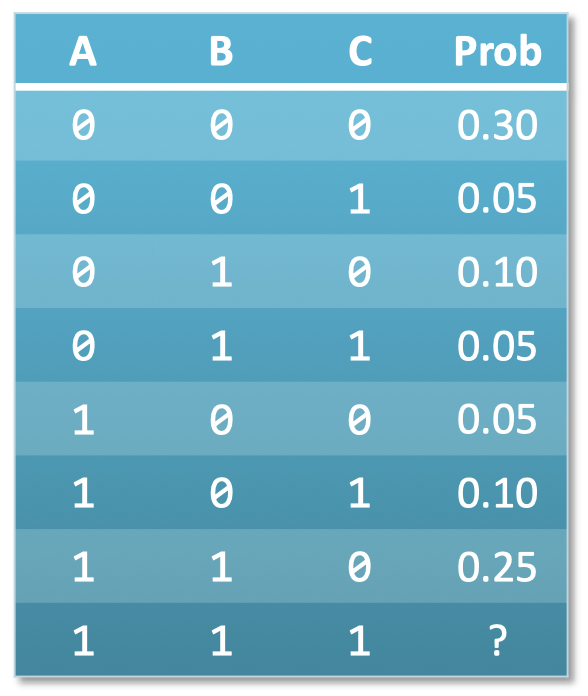
  • 坏处： 计算复杂度
    • 表格行数随着随机变量的增加呈指数增长
    • 因此 $\to$ 边缘化的空间和时间不足
  • 丑陋： 模型复杂度
    • 太过灵活
    • 太多参数需要拟合
      $\to$ 需要大量数据，否则会过拟合
  • 对抗手段：假设独立

1.6 例子：你迟到了

  • 对一个喜欢迟到的老师进行建模，使用布尔随机变量
    • $\color{red}{T}$：班级教学老师是 Ben
    • $\color{steelblue}{S}$：大晴天（否则为坏天气）
    • $\color{purple}{L}$：老师迟到了（否则为准时到达）
  • 假设：Ben 有时会因为坏天气而迟到，Ben 比其他教师更容易迟到

    • $\Pr(\color{steelblue}{S}|\color{red}{T})=\Pr(\color{steelblue}{S})$

      $\Pr(\color{steelblue}{S})=0.3$

      $\Pr(\color{red}{T})=0.6$

  • 迟到不独立于天气和老师
    • 需要考虑 $\Pr(\color{purple}{L}| \color{red}{T=t},\color{steelblue}{S=s})$ 的所有组合
  • 只需要 6 个参数

1.7 独立性

  • 独立性假设
    • 随机变量之间是否满足独立性，可以根据领域专业知识做出合理判断
    • 允许我们通过直接因式分解来计算联合概率 $\to$ 模型易处理的关键

1.8 联合分布因式分解

  • 链式法则： 对于任意顺序的随机变量总是可以因式分解为

    \[\Pr(X_1,X_2,...,X_k)=\prod_{i=1}^{k}\Pr(X_i|X_{i+1},...,X_k)\]
  • 模型的独立性假设对应于
    • 消除因子中的条件随机变量
    • 无条件独立 的例子：$\Pr(X_1|X_2)=\Pr(X_1)$
    • 条件独立 的例子：$\Pr(X_1|X_2,X_3)=\Pr(X_1|X_2)$
  • 例子：独立随机变量 $\Pr(X_1,…,X_k)=\prod_{i=1}^{k}\Pr(X_i)$
  • 更简单的因式分解可以：加速推断过程，以及 防止过拟合

1.9 有向 PGM

  • 节点 表示 随机变量
  • 边（无环的）表示 条件独立
    • 节点表： $\Pr(child \mid parents)$
    • 子节点（$child$）直接取决于 父母节点（$parents$）

  • 联合因式分解

    \[\Pr(X_1,X_2,...,X_k)=\prod_{i=1}^{k}\Pr(X_i|X_j \in parents(X_i))\]

迟到教师的例子

1.10 例子：核电站

  • 核心温度 $\to$ 温度表 $\to$ 警报
  • 监控故障中的模型不确定性
    • GRL：gauge reads low（温度表显示低数值）
    • CTL: core temperature low（核心温度低）
    • FG: faulty gauge（温度表故障）
    • FA: faulty alarm（警报故障）
    • AS: alarm sounds（警报响起）

  • PGM 解决问题

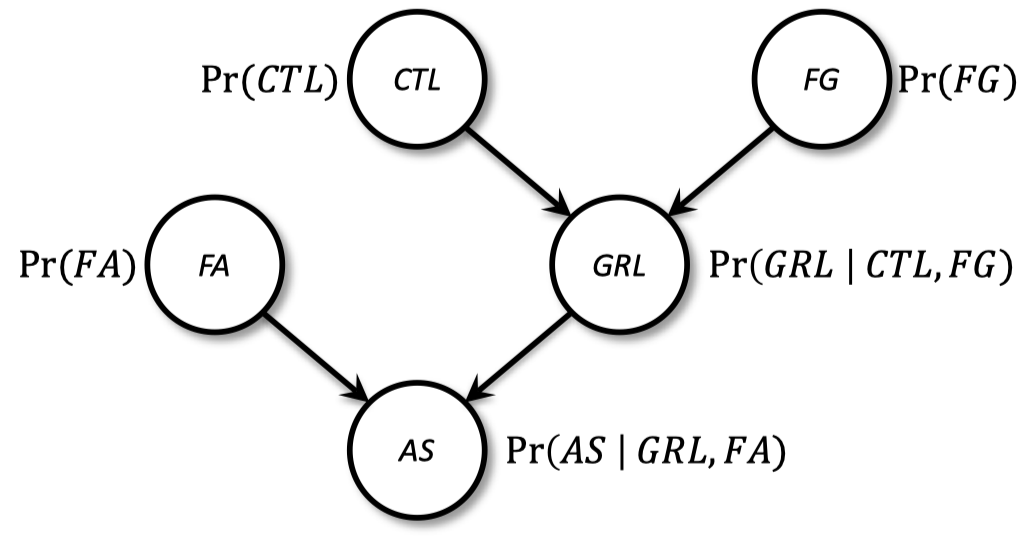
    联合概率 $\Pr(CTL,FG,FA,GRL,AS)$ 由下式给出：

    \[\Pr(AS|FA,GRL) \Pr(FA) \Pr(GRL|CTL,FG) \Pr(CTL) \Pr(FG)\]

1.11 朴素贝叶斯

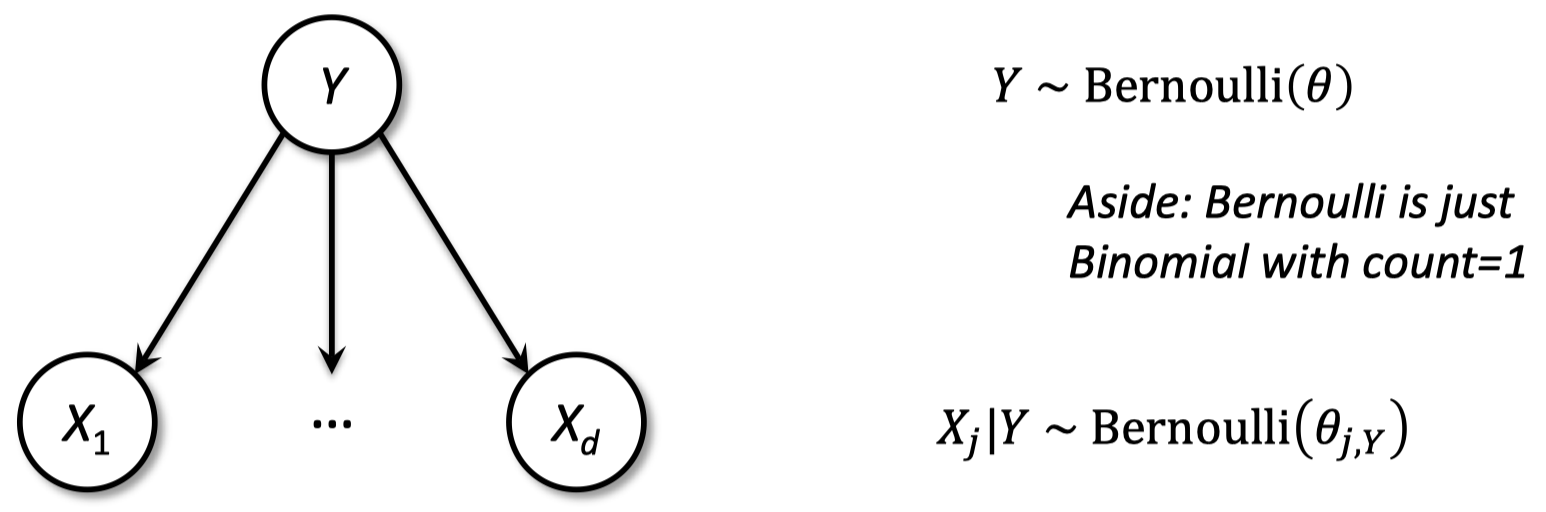
\[\begin{align} \Pr(Y,X_1,...,X_d) &= \Pr(X_d,...,X_1,Y) \\ &= \Pr(X_1|Y)\Pr(X_2|X_1,Y) ... \Pr(X_d|X_1,...,X_{d-1},Y) \Pr(Y) \\ &= \Pr(X_1|Y) \Pr(X_2|Y) ... \Pr(X_d|Y) \Pr(Y) \end{align}\]

预测：基于最大化 $\Pr(Y|X_1,…,X_d)$ 预测标签

重复的简记：盘子表示（Plate notation）

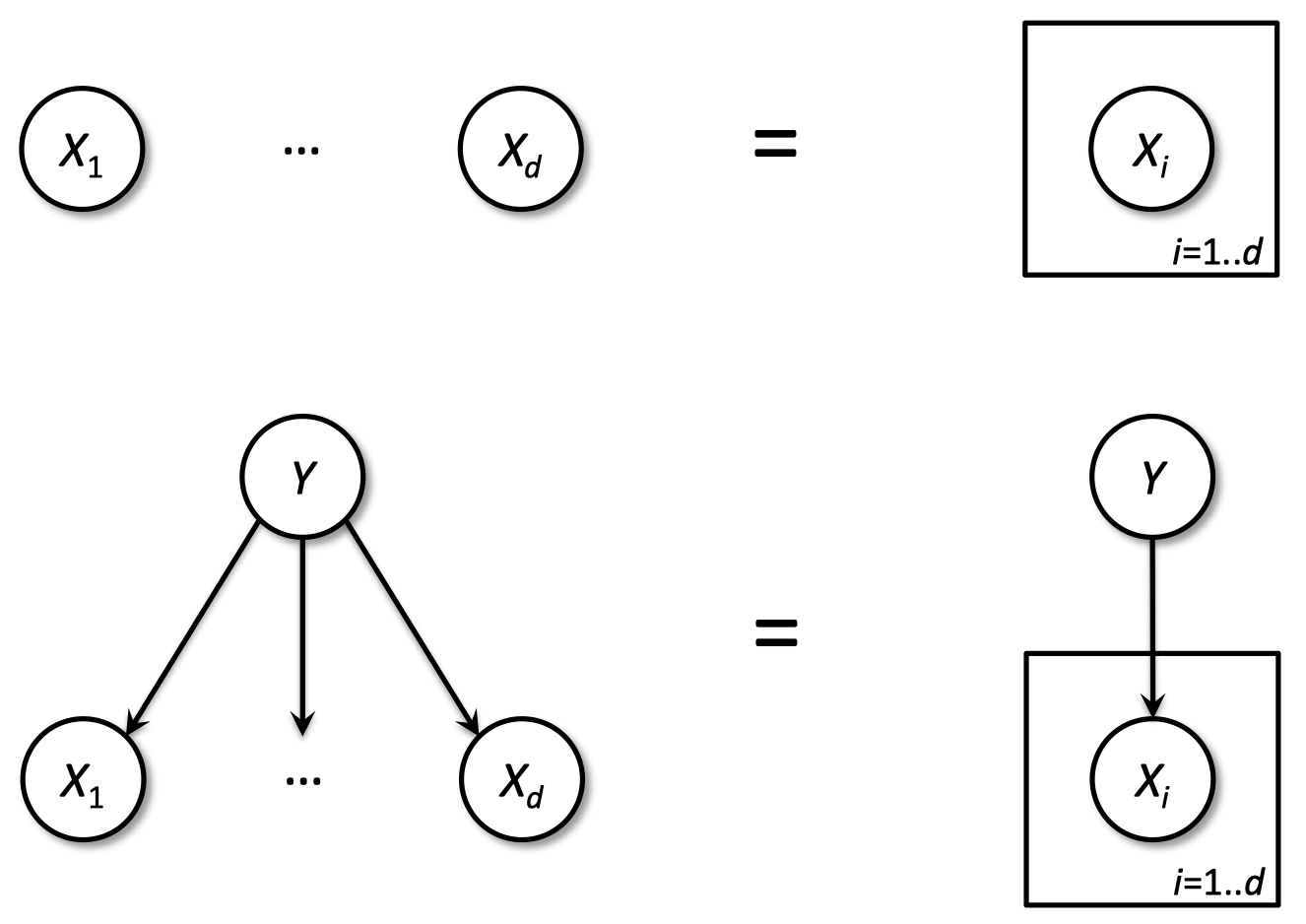
1.12 PGM 频率学家或者贝叶斯人

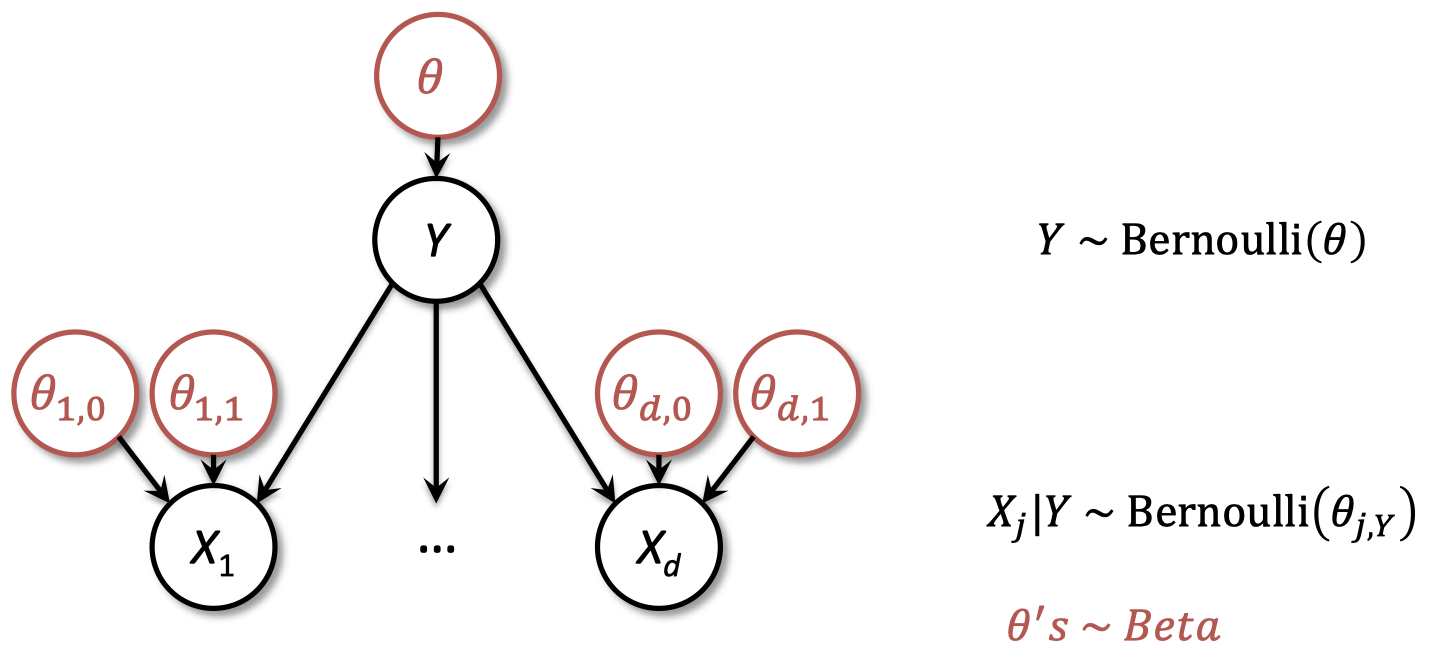
  • PGM 表示联合概率，这是贝叶斯学派的中心

  • 贝叶斯在此基础上：为每个参数添加节点，以及参数先验的表格

2. 无向 PGM

PGM 的无向变体，通过变量的任意正值函数进行参数化，并进行全局归一化。又称为 “马尔可夫随机场”。

2.1 无向 vs 有向

无向 PGM（Undirected PGM, U-PGM）

  • 图
    • 边是无向的
  • 概率
    • 每个节点都是一个随机变量
    • 每个 clique $C$ 都有 “因子（factor）”：$\psi_C(X_j:j\in C)\ge 0$
    • 联合概率 $\propto$ 因子的乘积

有向 PGM（Directed PGM, D-PGM）

  • 图
    • 边是有向的
  • 概率
    • 每个节点都是一个随机变量
    • 每个节点都有条件概率：$\Pr\left(X_i|X_j \in parents(X_i)\right)$
    • 联合概率 $=$ 条件概率的乘积

关键区别：归一化

2.2 无向 PGM 公式

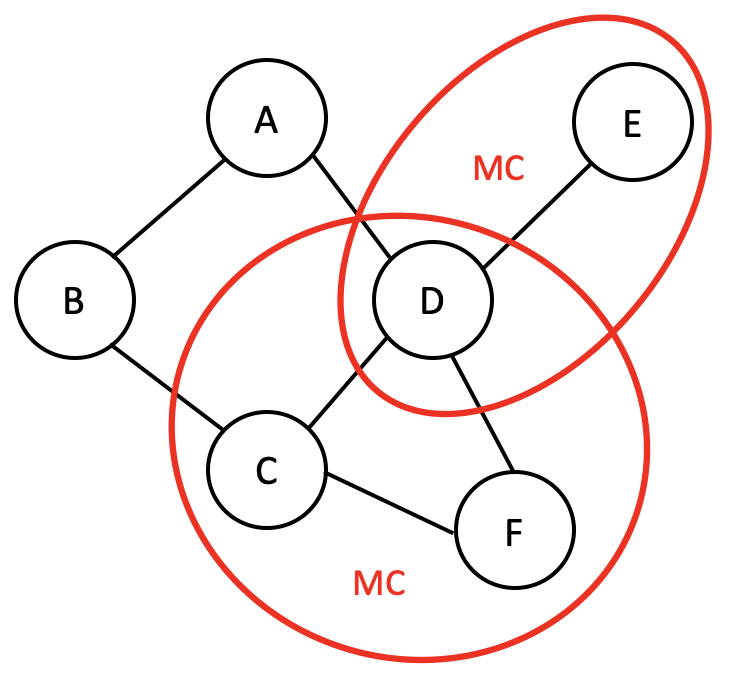
  • Clique： 一个 全连接 节点的集合
    • 全连接的意思是集合中的各点之间两两相连，例如：A-D, C-D, C-D-F。
  • Maximal clique： 图中 最大的 cliques
    • 注意：这里最大 cliques 不是指节点数量最多，而是说不能再加入新的节点了，所以， C-D 不是, 因为还有 C-D-F。
    • 此外，D-E 也是，因为再往这个集合之中添加任何节点，都不能满足各节点两两相连从而构成一个 clique 了。

  • 联合概率由下式定义

    \[\Pr(a,b,c,d,e,f)=\dfrac{1}{Z}\psi_1(a,b)\,\psi_2(b,c)\,\psi_3(a,d)\,\psi_4(d,c,f)\,\psi_5(d,e)\]

    • 其中，$\psi$ 是一个正值函数，$Z$ 是归一化 “分区” 函数

      \[Z=\sum \limits_{a,b,c,d,e,f}\psi_1(a,b)\,\psi_2(b,c)\,\psi_3(a,d)\,\psi_4(d,c,f)\,\psi_5(d,e)\]

2.3 有向到无向

  • 有向 PGM 公式为

    \[P(X_1,X_2,...,X_k)=\prod_{i=1}^{k}\Pr(X_i|X_{\pi_i})\]

    其中，$\boldsymbol \pi$ 是父母节点的索引。

  • 等价于无向 PGM，其中

    • 每个条件概率项都包含在一个因子函数（factor function）$\psi_c$ 里面
    • Clique 结构连接着 变量的群体，即 \(\{\{X_i\}\cup X_{\pi_i}, \forall i\}\)
    • 归一化项可以忽略，$Z=1$

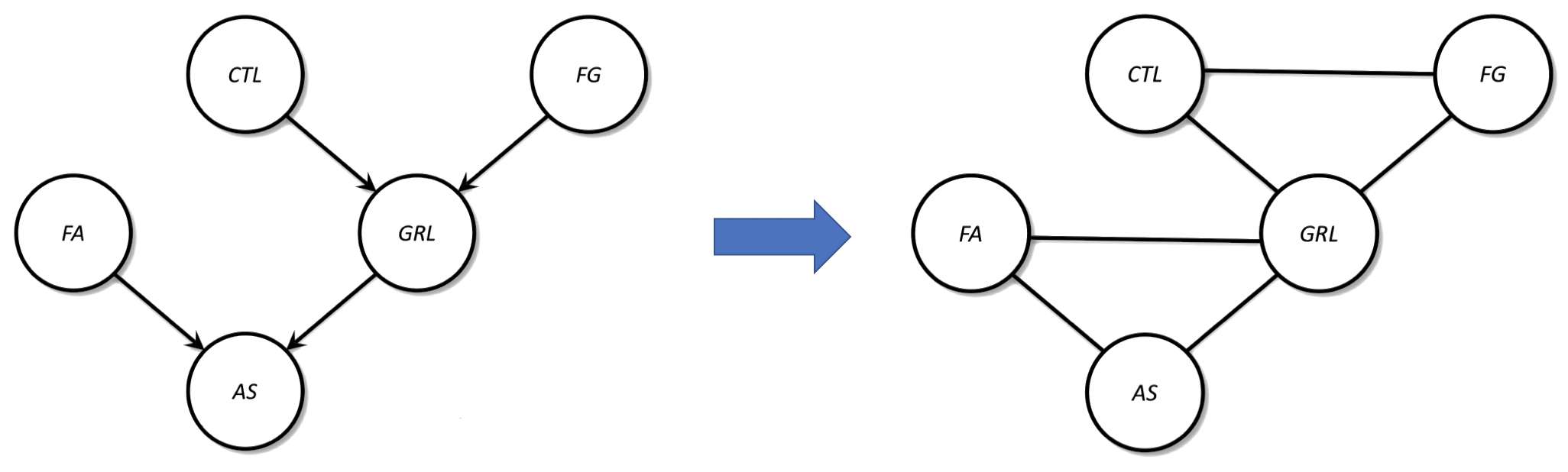
有向 PGM 转为无向 PGM 的步骤：

  1. 复制节点
  2. 复制边，移除方向
  3. “伦理化” 父母节点

2.4 为什么需要 U-PGM？

  • 优点
    • D-PGM 的泛化
    • 建模方法更简单，不需要每个因子（factor）归一化
    • 通用的推断算法使用 U-PGM 表示（同时支持两种 PGM）
  • 缺点
    • ($\,$稍微$\,$) 较弱的独立性
    • 计算全局归一化项（$Z$）通常比较困难（但对于链 / 树则易于处理，例如，CRF）

3. PGM 例子

隐马尔可夫模型（HMM）；格子马尔可夫随机场（MRF）；条件随机场（CRF）

3.1 HMM 和卡尔曼滤波器

  • 顺序观测的 输出 来自隐藏 状态

    $A=\{a_{ij}\}$ $\qquad$ 转移概率矩阵；$\forall i: \sum_j a_{ij}=1$

    $B=\{b_i(o_k)\}$ $\qquad$ 输出概率矩阵；$\forall i: \sum_k b_i(o_k)=1$

    $\Pi =\{\pi_i\}$ $\qquad$ 初始状态分布；$\sum_i \pi_i=1$

  • 卡尔曼滤波器 也是一样，具有连续高斯随机变量

  • CRF 模型与之类似，只不过是无向的

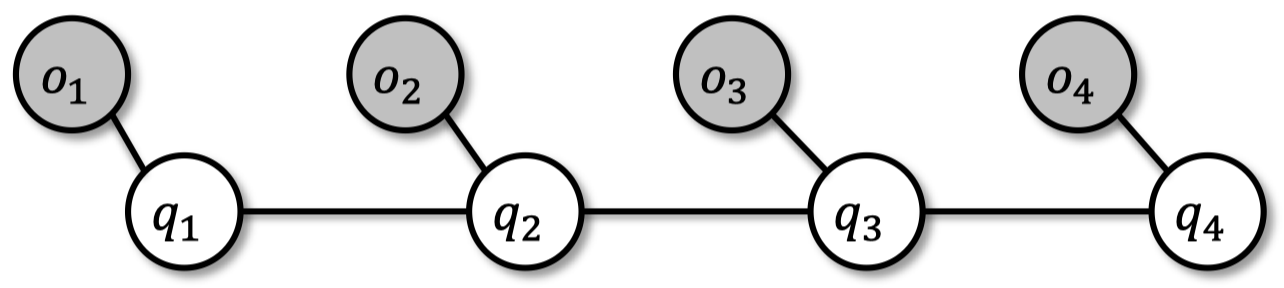
3.2 HMM 应用

  • NLP - 部分语音标记：给定句子中的词，推断语音中的隐藏部分

    “I love Machine Learning” $\to$ noun, verb, noun, noun

  • 语音识别：给定波形，确定音素

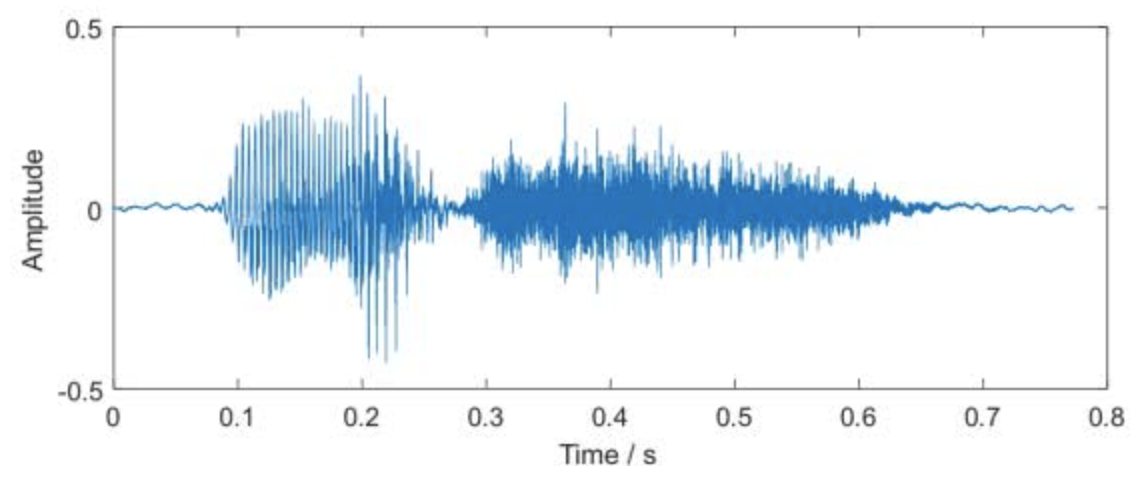
  • 生物序列：分类、搜索、比对
  • 计算机视觉：识别视频中行走的物体，进行追踪

3.3 HMM 基本任务

HMM 任务 PGM 任务
估计： 给定一个 HMM 均值 $\mu$ 和观测序列 $O$，求解似然函数 $\Pr(O \mid \mu)$ 概率推断
解码： 给定一个 HMM 均值 $\mu$ 和观测序列 $O$，求解最可能的隐藏状态序列 $Q$ MAP 点估计
学习： 给定一个观测序列 $O$ 和状态集合，学习参数 $A, B, \Pi$ 统计推断

3.4 计算机视觉中的像素标签任务

  • 语义标注

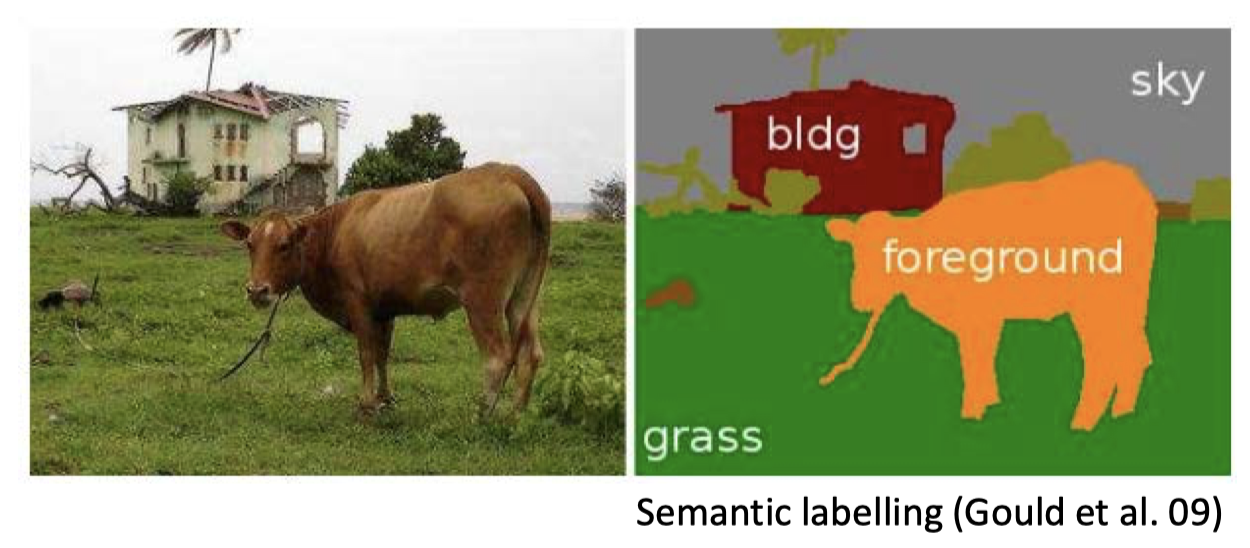
  • 交互式图形-场地分割

  • 图像去噪

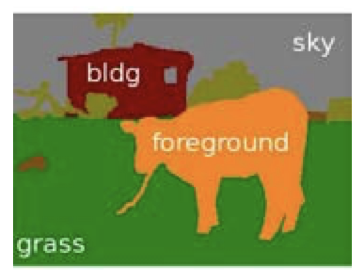
3.5 这些任务的共同点是什么？

  • 隐藏状态表示图像的语义
    • 语义标注：牛 vs. 树 vs. 草地 vs. 天空 vs. 房子
    • 前后分割：图形 vs. 场地
    • 去噪：清理像素
  • 图片的像素
    • 是我们从隐藏状态中观测到的东西

  • 想起 HMM 了吗？

3.6 一个隐藏的方格马尔可夫随机场

  • 隐藏状态：方格模型

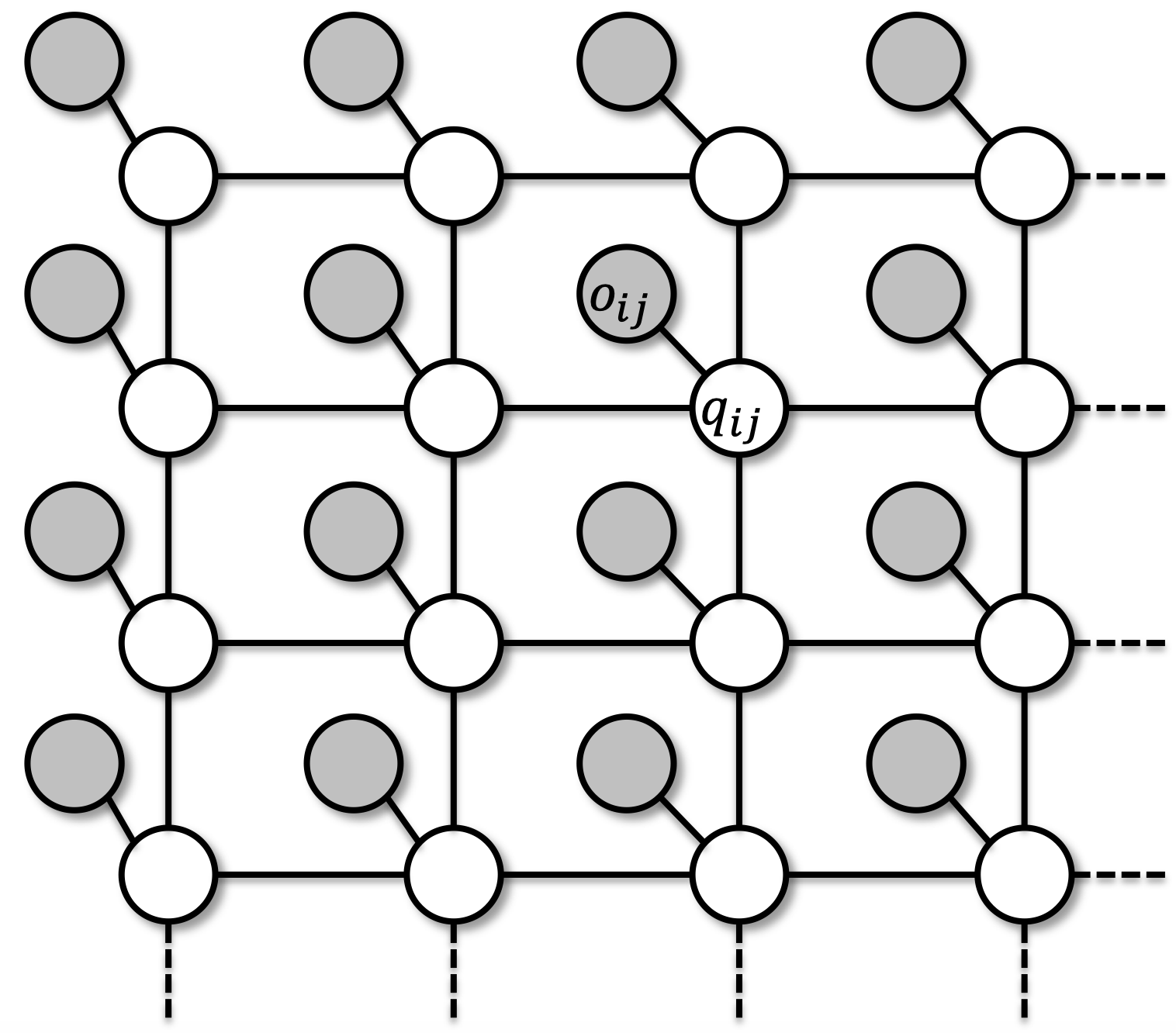
    • 两个类别状态为布尔的

    • 多个类别状态为离散的

    • 去噪任务则为连续的

  • 像素：观测到的输出

    • 连续的，例如：正态

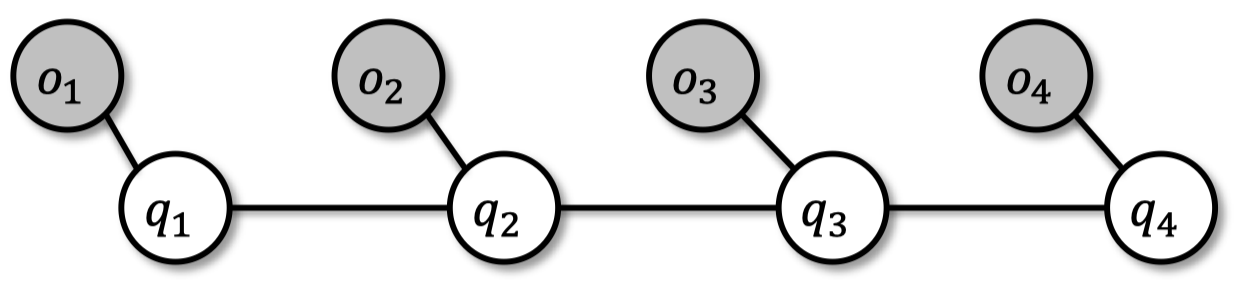
3.7 应用于序列：CRF

  • 条件随机场：同样的模型应用于序列
    • 观测到的输出为单词、语音、氨基酸等
    • 状态是标签：词性、音素、序列
  • CRF 是判别式模型，对 $\Pr(Q|O)$ 建模
    • 对比 HMM 是生成式模型，对 $\Pr(Q,O)$ 建模

    • 无向 PGM 更通用，表达性更强

总结

  • 概率图模型
    • 动机：应用，统一算法
    • 动机：贝叶斯理论的理想工具
    • 独立性降低了计算 / 模型复杂度
    • PGM：联合概率因式分解的简洁表示
    • U-PGM
  • PGM 的例子与应用

下节内容：PGM 的概率推断和统计推断

知识共享许可协议本作品采用知识共享署名-非商业性使用-相同方式共享 4.0 国际许可协议进行许可。 欢迎转载，并请注明来自：YEY 的博客 同时保持文章内容的完整和以上声明信息！
CATALOG
    FEATURED TAGS
    随笔 课程笔记 统计机器学习 COMP90051 学习笔记 自然语言处理 COMP90042 PyTorch 人工智能伦理 COMP90087 数据科学多元统计学 MAST90138 AI 自动规划 COMP90054 数据分析 计算统计学与数据科学 MAST90083 高级数据库系统 COMP90050 统计建模 MAST90139 读书 📚 MySQL 学习索引 Hive 技术问题 Jekyll Workshop
    FRIENDS