Lecture 18 高斯混合模型和 EM 算法
主要内容
- 无监督学习
- 问题的多样性
- 高斯混合模型(GMM)
- 一种用于聚类的概率方法
- GMM 模型
- GMM 聚类作为一个优化问题
- 期望最大化(EM)算法
1. 无监督学习
机器学习中的一个大的分支,关注在标签缺失的数据上学习其结构
1.1 在此之前:监督学习
- 监督学习:总体目标是根据数据做出预测
- 为此,我们学习了诸如:随机森林、ANN 和 SVM 等算法
- 我们有实例 $\boldsymbol x_i\in \boldsymbol R^m\;(i=1,…,n)$,以及对应的标签 $y_i$ 作为输入,目标是预测新的实例的标签。
- 可以看作是一个函数逼近问题,但请注意:泛化能力很关键
- 老虎机:部分监督的设定
1.2 现在:无监督学习
- 接下来我们将介绍无监督学习方法
- 在无监督学习中,没有所谓叫做 “标签” 的专门变量
- 相应地,我们只有一个数据点的集合 $\boldsymbol x_i\in \boldsymbol R^m\;(i=1,…,n)$
- 无监督学习的目的是 探索数据的结构(模式、规律等)
- “探索数据结构” 的目的是模糊的
1.3 无监督学习任务
- 无监督学习包括很多不同类别的任务:
- 聚类
- 降维
- 概率模型的参数学习
- 相关应用:
- 市场篮子分析。例如,使用超市的交易日志查找经常被一起购买的商品
- 离群值检测。例如,发现潜在的信用卡交易欺诈
- 经常用于(有监督)机器学习 pipeline 中的无监督任务
1.4 回顾:k-means 聚类
k-means 算法描述:
1.$\,$初始化: 随机选择 $k$ 个集群 中心
2.$\,$更新:
$\qquad$a. 分配数据点 到最近的集群中心
$\qquad$b. 在当前的分配下,重新计算集群中心
3.$\,$终止: 如果集群中心没有发生变化,那么 算法停止
4.$\,$返回 步骤 2
选择典型的 $L_2$ 范数来表示距离。
K-means 仍然是最受欢迎的数据挖掘算法之一。

- 需要预先指定集群数 $k$
- 使用欧几里得距离衡量 “差异性”
- 寻找 “球形” 集群
- 迭代优化过程
2. 高斯混合模型(GMM)
从概率的视角看聚类算法
2.1 对数据聚类中的不确定性建模
- k-means 聚类将每个数据点都精确地分配到某一个集群
- 类似于 k-means,一个概率的混合模型同样需要预先指定集群数 $k$
- 不同于 k-means,概率模型让我们得以表达有关每个数据点 来源的不确定性
- 每个数据点来自集群 $c$ 的概率为 $w_c$,其中 $c=1,…,k$
- 也就是说,每个数据点仍然只来自某个特定的集群(又称 “组分”),但是我们不确定来自哪一个
- 接下来
- 将各个组分建模为高斯分布
- 拟合过程展示了一般的期望最大化(EM)算法
2.2 聚类:概率模型
数据点 $\boldsymbol x_i$ 是来自 $K$ 个分布(或者说 “组分”)的混合的独立同分布(i.i.d.)样本
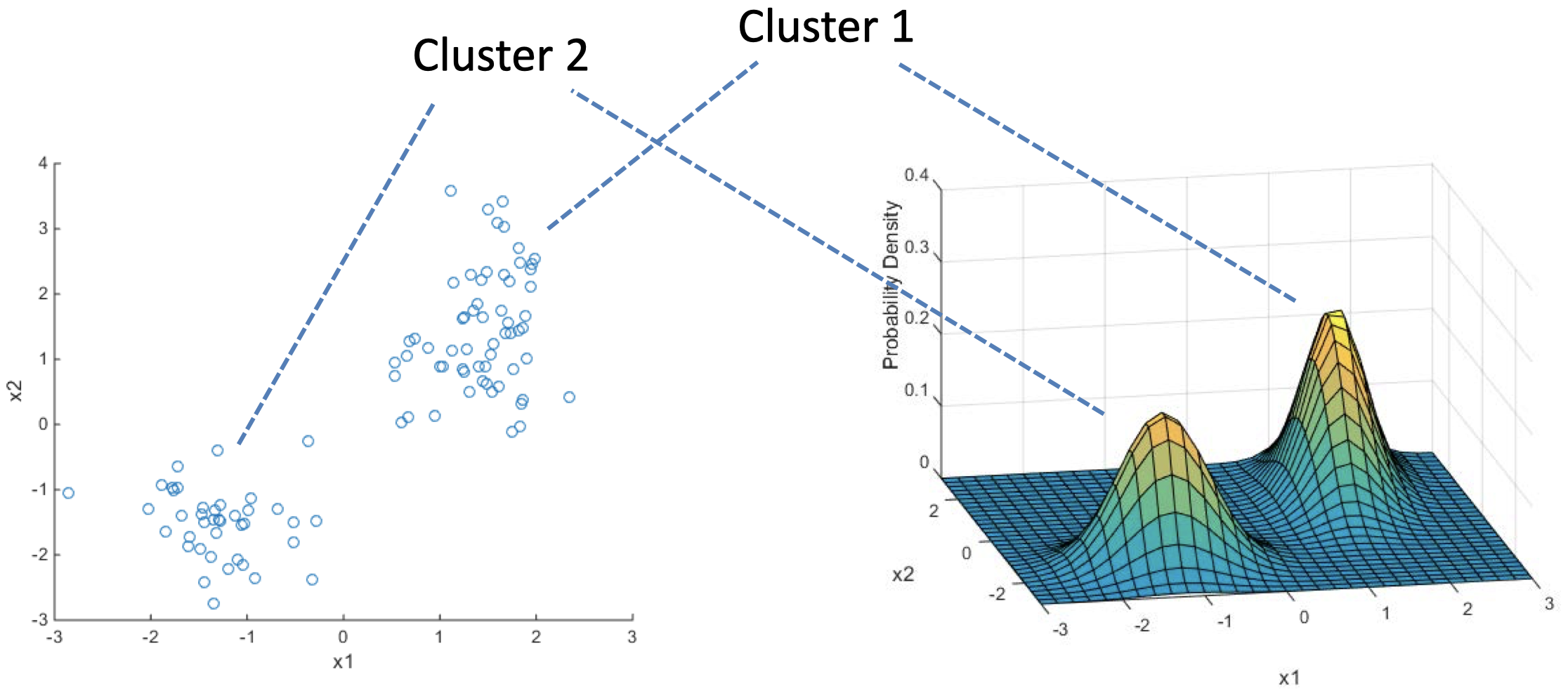
原则上,我们可以将 组分 假设为任何分布,但是,正态分布是一种常见的建模选择 $\to$ 高斯混合模型(Gaussian Mixture Model, GMM)
2.3 正态(又称 “高斯”)分布
-
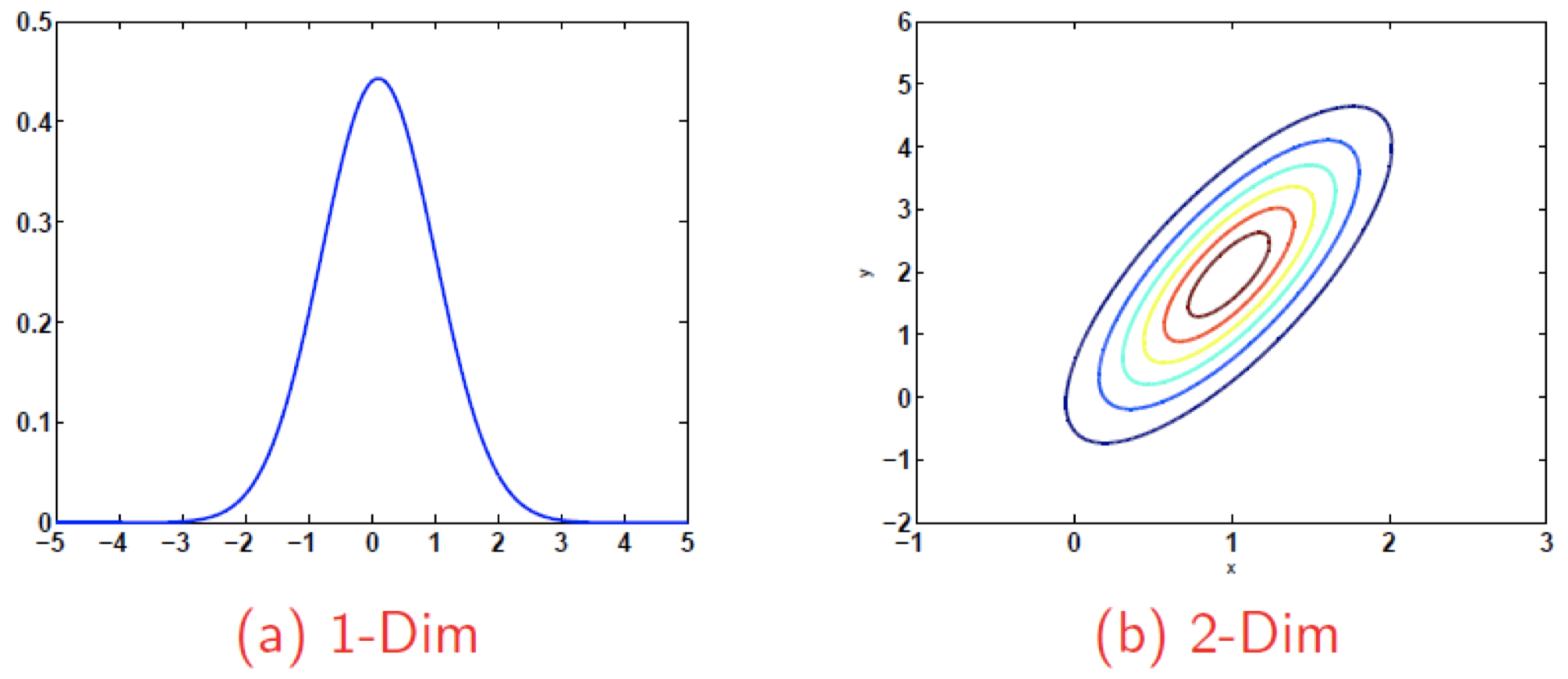
回忆 $1$-维 高斯分布:
\[\mathcal N(x|\mu,\sigma)\equiv \dfrac{1}{\sqrt{2\pi \sigma^2}}\exp \left(-\dfrac{(x-\mu)^2}{2\sigma^2}\right)\] -
然后,一个 $d$-维 高斯分布为:
\[\mathcal N(\boldsymbol x|\boldsymbol{\mu},\mathbf{\Sigma})\equiv (2\pi)^{-\frac{d}{2}}|\mathbf{\Sigma}|^{-\frac{1}{2}}\exp \left(-\dfrac{1}{2}(\boldsymbol x-\boldsymbol \mu)^T \mathbf{\Sigma}^{-1}(\boldsymbol x-\boldsymbol \mu)\right)\]- $\mathbf{\Sigma}$ 是 协方差矩阵,是一个 PSD(半正定)对称 $d\times d$ 矩阵
- $|\mathbf{\Sigma}|$ 表示行列式
- 不需要记住完整的公式
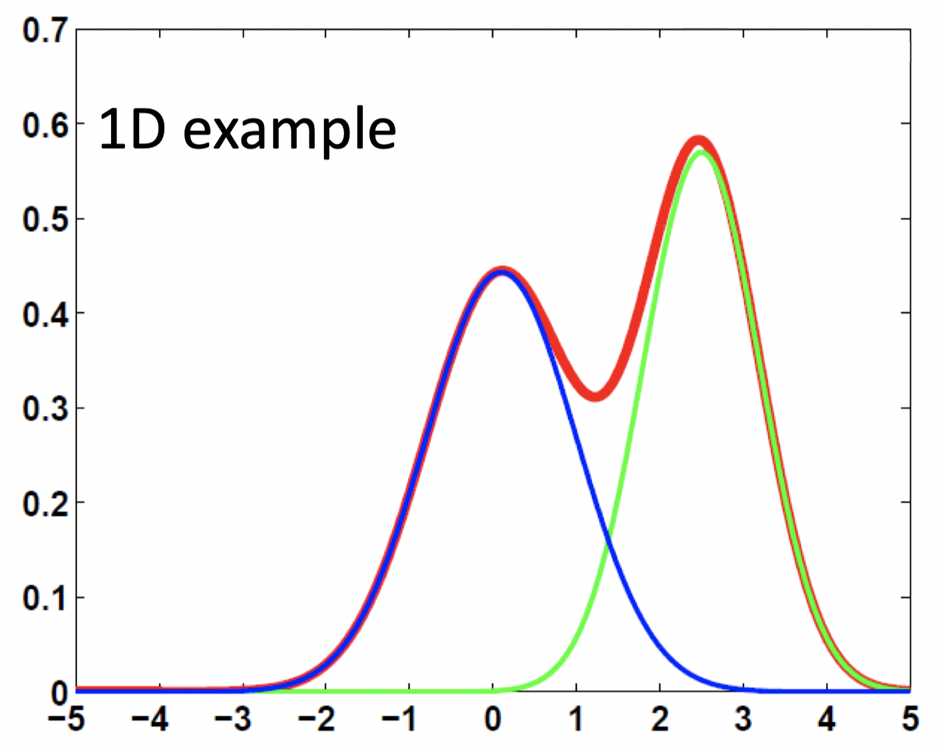
2.4 高斯混合模型(GMM)
-
高斯混合分布(对于单个数据点):
\[p(\boldsymbol x)\equiv \sum_{j=1}^{k}w_j \mathcal N(\boldsymbol x|\boldsymbol{\mu}_j,\mathbf{\Sigma}_j)\equiv \sum_{j=1}^{k}p(\boldsymbol C_j)p(\boldsymbol x|\boldsymbol C_j)\] - \(p(\boldsymbol x|\boldsymbol C_j)\equiv \mathcal N(\boldsymbol x|\boldsymbol{\mu}_j,\mathbf{\Sigma}_j)\) 是类别 $j$ 的类别 / 组分条件密度(建模为高斯分布)
- 这里,$p(\boldsymbol C_j)\ge 0$,并且 $\sum_{j=1}^{k}p(\boldsymbol C_j)=1$
- 模型的参数为 $p(\boldsymbol C_j),\boldsymbol \mu_j,\mathbf{\Sigma}_j$,其中 $j=1,…,k$
思考: 考虑一个 3D 数据的 GMM 模型,该模型包含 5 个组分。请问该模型有多少个独立的 标量参数?
请注意,这里要求独立的标量参数。
对于某个集群 \(\boldsymbol C_j\;(j=1,...,5)\) 而言:
首先,3D 数据的协方差矩阵 \(\mathbf{\Sigma}_j\) 是一个 \(3\times 3\) 的对称矩阵,所以有 6 个(对角线 + 某一侧的元素)不同的标量参数;
然后,均值 \(\boldsymbol{\mu}_j\) 是一个 \(3 \times 1\) 的向量,所以有 3 个不同的标量参数;
最后,每个集群 \(\boldsymbol C_j\;(j=1,...,5)\) 对应一个权重参数 $w_j$(即该集群对应的概率),但是由于存在归一化约束 \(\sum_{j=1}^{5}w_j=1\),所以,权重的独立标量个数为 4 个(最后一个权重可以用 1 减去其余权重之和表示);
因此,该模型独立的标量参数的个数为 \(6 \times 5+3\times 5+1\times 4=49\)
2.5 聚类的模型估计
- 给定一组数据点,我们假设数据点是由 GMM 生成的
- 我们数据集中的每个点来源于第 $j$ 个正态分布组分的概率为 $w_j=p(\boldsymbol C_j)$
- 现在,聚类等同于寻找 “最佳解释” 观测数据的 GMM 参数
- 利用之前学过的 MLE 方法寻找能够最大化 $p(\boldsymbol x_1,…,\boldsymbol x_n)$ 的参数
2.6 拟合 GMM
-
建模假设数据点之间互相独立,目标是找到 $p(\boldsymbol C_j),\boldsymbol \mu_j,\mathbf \Sigma_j\;(j=1,…,k)$,使得最大化
\[p(\boldsymbol x_1,...,\boldsymbol x_n)=\prod_{i=1}^{n}\sum_{j=1}^{k}p(\boldsymbol C_j)p(\boldsymbol x_i|\boldsymbol C_j)\]其中, \(p(\boldsymbol x|\boldsymbol C_j)\equiv \mathcal N(\boldsymbol x|\boldsymbol \mu_j,\mathbf \Sigma_j)\)
我们可以对其解析求解吗?
-
我们很难直接对原式求导,可以利用常见的 取对数技巧
\[\log p(\boldsymbol x_1,...,\boldsymbol x_n)=\sum_{i=1}^{n}\log \left(\sum_{j=1}^{k}p(\boldsymbol C_j)p(\boldsymbol x_i|\boldsymbol C_j)\right)\]$\to$ 期望最大化(EM)
3. 期望最大化(EM)算法
3.1 EM 的动机
- 考虑一个参数概率模型 $p(\boldsymbol X|\boldsymbol{\theta})$,其中 $\boldsymbol X$ 表示数据,$\boldsymbol{\theta}$ 表示一个参数向量
- 根据 MLE,我们需要最大化关于 $\boldsymbol{\theta}$ 的函数 $p(\boldsymbol X|\boldsymbol{\theta})$
- 等价于最大化 $\log p(\boldsymbol X|\boldsymbol{\theta})$
- 然而,存在一些问题:
- 有时我们 没有观测到 其中一些计算对数似然所需的变量
例如:我们并不能预先知道 GMM 集群归属 - 有时对数似然的形式处理起来不方便
例如:对一个 GMM 对数似然求导,会得到一个很麻烦的等式
- 有时我们 没有观测到 其中一些计算对数似然所需的变量
3.2 MLE vs EM
- MLE 是频率学家的做法,其建议在给定数据集的情况下,我们应该使用的 “最佳” 参数是使数据概率最大化的参数
- MLE 是一种正式提出问题的方法
- EM 是一种算法
- EM 是一种用来解决 MLE 所提出的问题的方法
- 尤其是存在未观测到的隐变量时,EM 算法非常便捷
- MLE 可以通过其他方法求解,例如:梯度下降(但是梯度下降并不总是最便捷的方法)
3.3 期望最大化(EM)算法
EM 算法描述:
1.$\,$初始化步骤:
$\qquad$初始化 $K$ 个集群:$\boldsymbol C_1,…,\boldsymbol C_K$
$\qquad$对于每个集群 $j$,都有参数 $(\boldsymbol \mu_j,\mathbf \Sigma_j)$ 和 $p(\boldsymbol C_j)$
2.$\,$迭代步骤:
$\qquad$a. 估计每个数据点的所属集群 $p(\boldsymbol C_j|\boldsymbol x_i)$ $\qquad \color{blue}{\Longrightarrow} \qquad$ 期望
$\qquad$b. 重新估计每个集群 $j$ 的参数 $(\boldsymbol \mu_j,\mathbf \Sigma_j)$ 和 $p(\boldsymbol C_j)$ $\qquad \color{blue}{\Longrightarrow} \qquad$ 最大化
3.4 将 EM 算法用于 GMM 和泛化
- EM 是一种通用方法,不仅仅局限于 GMM
- 目的:在存在 隐变量 $\boldsymbol Z$ 的情况下,实现 MLE
- GMM 中的变量和参数分别是什么?
- 变量: 点的位置 $\boldsymbol X$ 和集群分配 $\boldsymbol Z$
令 $z_i$ 表示每个数据点 $\boldsymbol x_i$ 的真实集群归属,在 $\boldsymbol z$ 已知的情况下,计算似然函数很简单 - 参数: $\boldsymbol \theta$ 表示集群的位置与大小
- 变量: 点的位置 $\boldsymbol X$ 和集群分配 $\boldsymbol Z$
- EM 算法到底做了什么?
- 在对数似然的下界上的 坐标上升法
- M 步骤:在模型参数 $\boldsymbol \theta$ 中的上升
- E 步骤:在边缘化似然 $p(\boldsymbol Z)$ 中的上升
- 每一步都朝着 局部 最优方向移动
- 可能中途会卡住,可能需要 随机重启
- 在对数似然的下界上的 坐标上升法
3.5 所需工具:Jensen 不等式
-
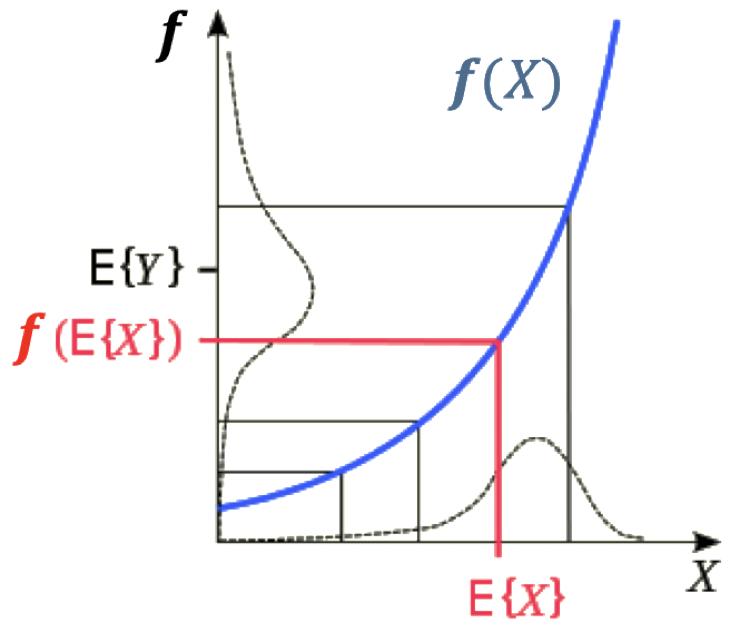
比较将平均函数作用在一个凸函数前后的影响:
\[f\left(Average(\boldsymbol x)\right)\le Average\left(f(\boldsymbol x)\right)\] - 例子:
- 令 $f$ 为某个凸函数,例如 $f(x)=x^2$
- 考虑 $\boldsymbol x=[1,2,3,4,5]’$,那么 $f(\boldsymbol x)=[1,4,9,16,25]’$
- 输入的平均值为 $Average(\boldsymbol x)=3$
- $f\left(Average(\boldsymbol x)\right)=9$
- 输出的平均值为 $Average\left(f(\boldsymbol x)\right)=12.4$
- 证明来自凸度的定义
- 归纳证明
- 一般表述:
- 如果 $\boldsymbol X$ 是一个随机变量,$f$ 是一个凸函数
- 那么,$\color{red}{f\left(\mathbb{E}[\boldsymbol X] \right)\le \mathbb{E}\left[f(\boldsymbol X)\right]}$
3.6 利用隐变量
我们希望最大化 $\log p(\boldsymbol X|\boldsymbol \theta)$,我们没有观测到 $\boldsymbol Z$(这里为离散),但我们仍然可以引入它。
3.7 最大化下界
- $\,$ \(\log p(\boldsymbol X|\boldsymbol \theta)\ge \mathbb{E}_{\boldsymbol Z}\left[ \log p(\boldsymbol X,\boldsymbol Z|\boldsymbol \theta) \right] - \mathbb{E}_{\boldsymbol Z}\left[ \log p(\boldsymbol Z)\right]\\\)
- 不等式右边的部分(Right Hand Side, RHS)是原始对数似然的一个 下界
- 这对于任何 $\boldsymbol \theta$ 和任何非零 $p(\boldsymbol Z)$ 都满足
- 直觉上,我们希望将下界尽可能往上推进
- 这个下界是一个关于 两个 “变量” $\boldsymbol \theta$ 和 $p(\boldsymbol Z)$ 的函数。我们希望最大化 RHS(不等式右边的部分),将其视为关于这两个 “变量” 的一个函数。
- 同时对两个 “变量” 进行优化是非常困难的,因此,EM 算法采用了一种迭代过程
- EM 本质上是 坐标上升:
- 固定 $\boldsymbol \theta$,优化关于 $p(\boldsymbol Z)$ 的下界函数
- 固定 $p(\boldsymbol Z)$,优化 $\boldsymbol \theta$
- EM 算法的方便之处在于:
- 对于任何点 $\boldsymbol \theta^*$,可以证明设定 $p(\boldsymbol Z)=p(\boldsymbol Z|\boldsymbol X,\boldsymbol \theta^*)$ 使得下界更紧(关于这点,我们将在后面给出简略证明)
- 对于任何 $p(\boldsymbol Z)$,不等式右边第二项与 $\boldsymbol \theta$ 无关
- 当 $p(\boldsymbol Z)=p(\boldsymbol Z|\boldsymbol X,\boldsymbol \theta^*)$ 时,不等式右边第一项可以视为一个关于 $\boldsymbol \theta$ 的函数,通常情况下,我们可以得到使得该函数最大化的 $\boldsymbol \theta$ 的闭合解
- 如果不能,那么我们可能不会采用 EM 算法
3.8 示例
\[\log p(\boldsymbol X|\boldsymbol \theta)\ge \underbrace{\mathbb{E}_{\boldsymbol Z}\left[ \log p(\boldsymbol X,\boldsymbol Z|\boldsymbol \theta) \right] - \mathbb{E}_{\boldsymbol Z}\left[ \log p(\boldsymbol Z)\right]}_{\equiv \,G\left(\boldsymbol \theta,\,p(\boldsymbol Z)\right)}\\\]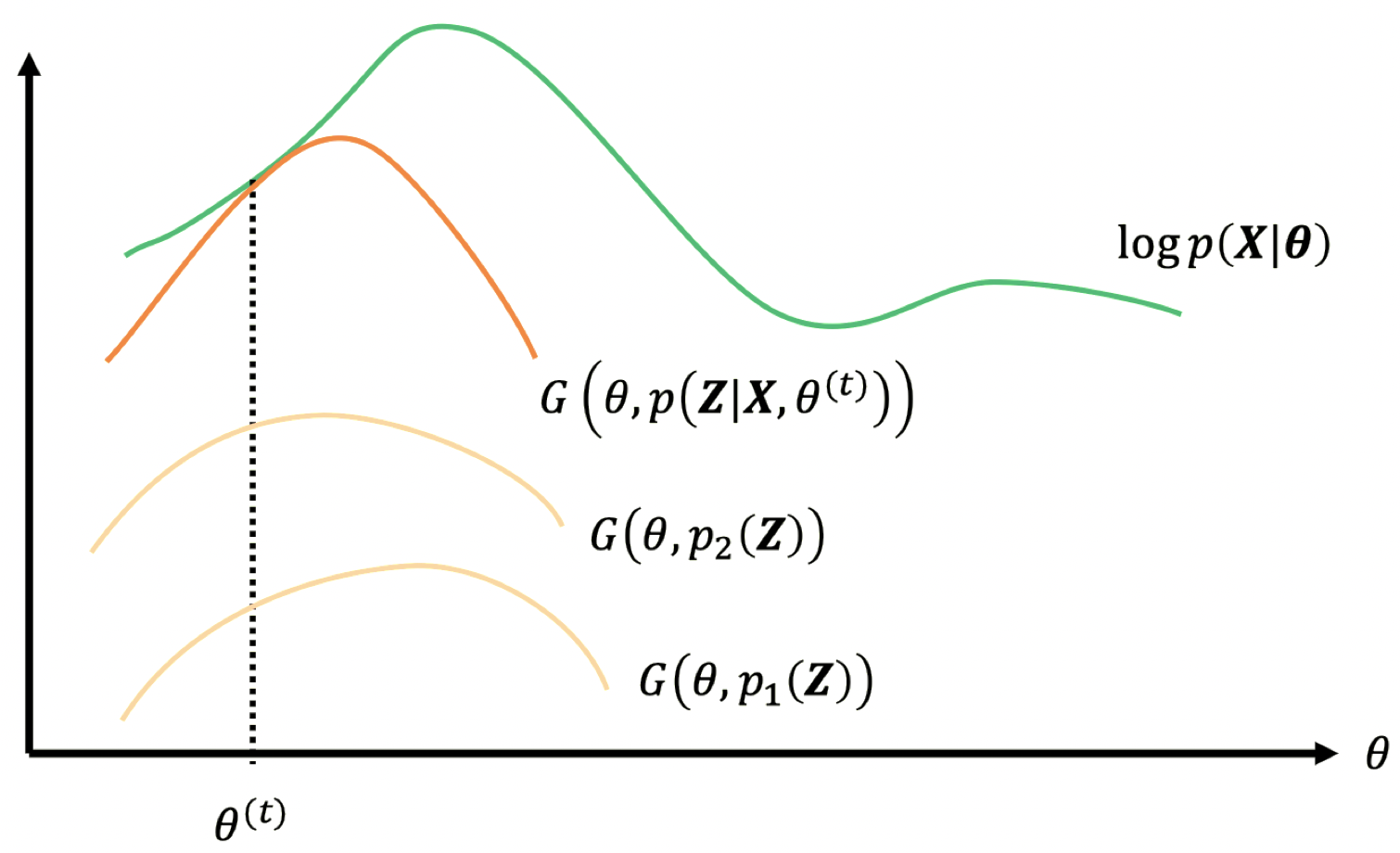
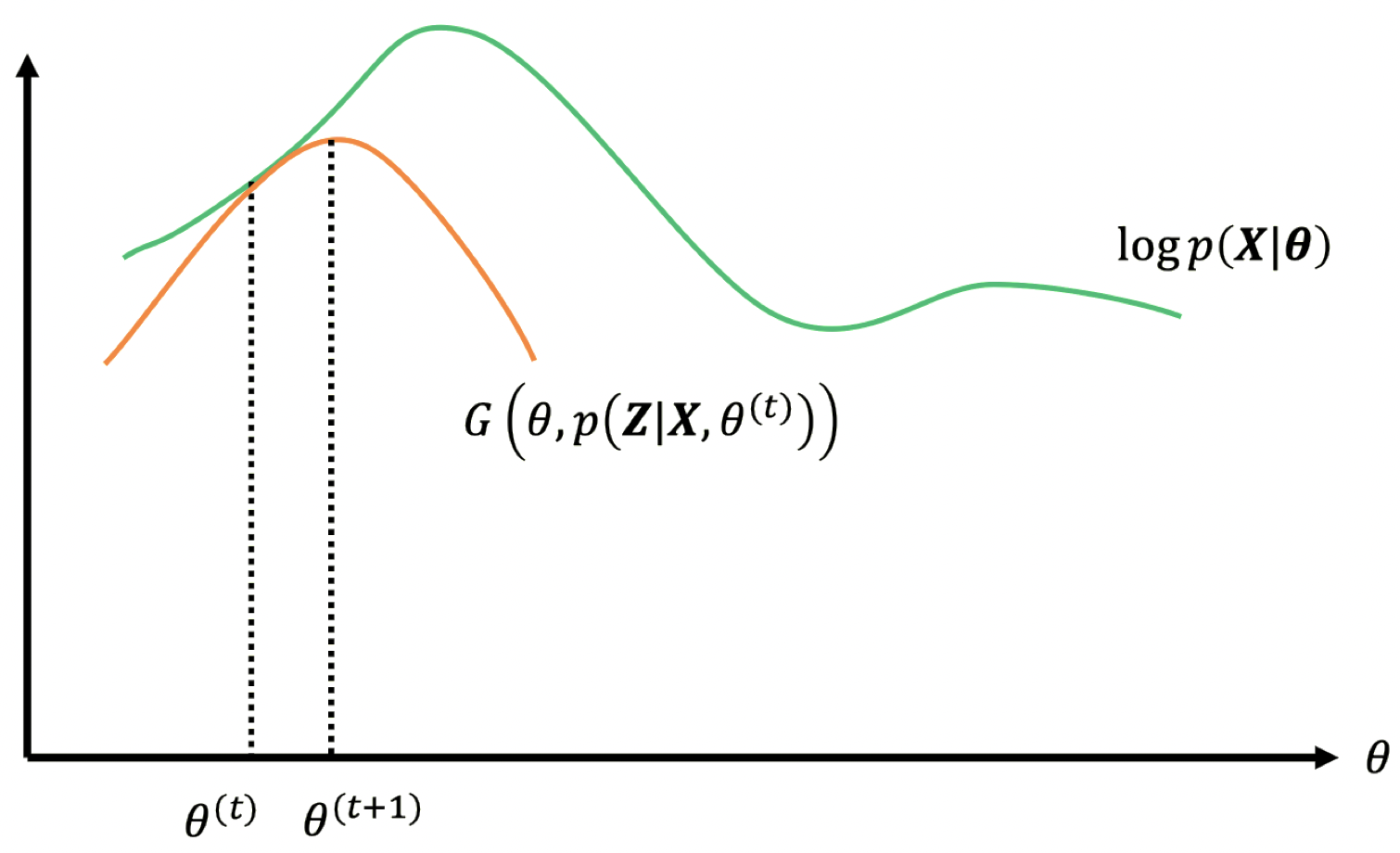
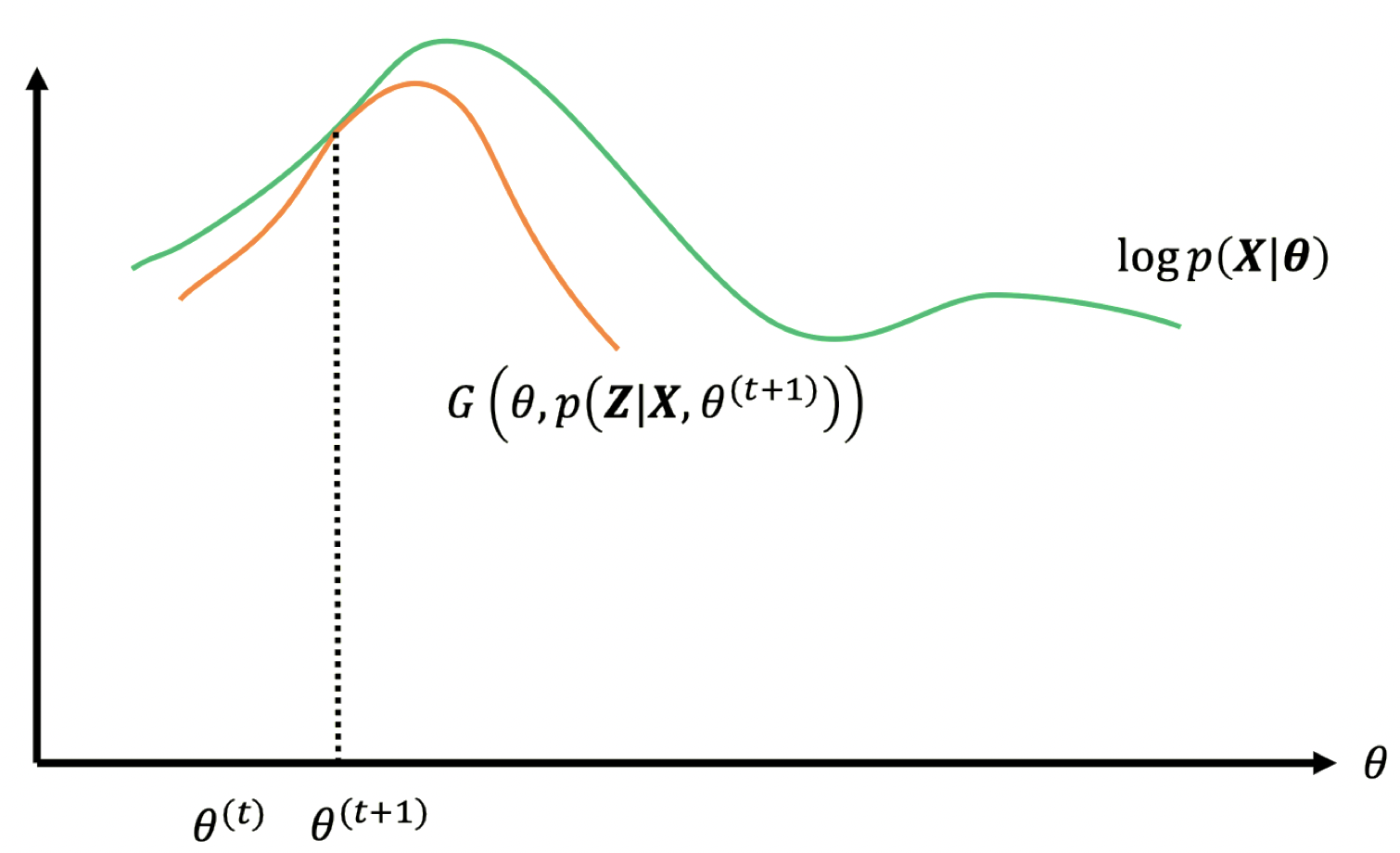
3.9 EM 作为迭代优化
EM 算法描述:
1.$\,$初始化: 选择(随机)初始值 $\boldsymbol \theta^{(1)}$
2.$\,$更新:
$\qquad$a. E 步骤:计算 $Q\left(\boldsymbol \theta,\boldsymbol \theta^{(t)}\right)\equiv \mathbb E_{\boldsymbol Z|\boldsymbol X,\boldsymbol \theta^{(t)}}\left[\log p(\boldsymbol X,\boldsymbol Z| \boldsymbol \theta)\right]$
$\qquad$b. M 步骤:$\boldsymbol \theta^{(t+1)}=\mathop{\operatorname{arg\,max}}\limits_{\boldsymbol \theta}Q\left(\boldsymbol \theta,\boldsymbol \theta^{(t)}\right)$
3.$\,$终止: 如果没有变化,那么 算法停止
4.$\,$返回 步骤 2
该算法最终将会停止(收敛),但最终得到的估计值可能只是一个局部最大值
3.10 设定一个紧的下界
现在,我们将证明之前 “3.7 最大化下界” 中提到的:
对于任何点 $\boldsymbol \theta^*$,可以证明设定 $p(\boldsymbol Z)=p(\boldsymbol Z|\boldsymbol X,\boldsymbol \theta^*)$ 使得下界更紧
回顾之前“3.6 利用隐变量” 中的推导过程:
\[\begin{align} \color{steelblue}{\fbox{$\color{black}{\log p(\boldsymbol X|\boldsymbol \theta)}$}} &= \log \sum_{\boldsymbol Z}p(\boldsymbol X,\boldsymbol Z|\boldsymbol \theta)\\ &= \log \sum_{\boldsymbol Z}\left(p(\boldsymbol X,\boldsymbol Z|\boldsymbol \theta)\cdot \dfrac{p(\boldsymbol Z)}{p(\boldsymbol Z)} \right)\\ &= \log \sum_{\boldsymbol Z}\left(p(\boldsymbol Z)\cdot \dfrac{p(\boldsymbol X,\boldsymbol Z|\boldsymbol \theta)}{p(\boldsymbol Z)} \right)\\ &= \log \mathbb{E}_{\boldsymbol Z}\left[\dfrac{p(\boldsymbol X,\boldsymbol Z|\boldsymbol \theta)}{p(\boldsymbol Z)}\right]\\ &\color{steelblue}{\fbox{$\color{black}{\ge \mathbb{E}_{\boldsymbol Z}\left[ \log \dfrac{p(\boldsymbol X,\boldsymbol Z|\boldsymbol \theta)}{p(\boldsymbol Z)}\right]}$}}\\ &= \mathbb{E}_{\boldsymbol Z}\left[ \log p(\boldsymbol X,\boldsymbol Z|\boldsymbol \theta) \right] - \mathbb{E}_{\boldsymbol Z}\left[ \log p(\boldsymbol Z)\right] \end{align}\]我们将最终结果回退一步:
\[\begin{align} \log p(\boldsymbol X|\boldsymbol \theta) &\ge \mathbb{E}_{\boldsymbol Z}\left[ \log \dfrac{p(\boldsymbol X,\boldsymbol Z|\boldsymbol \theta)}{p(\boldsymbol Z)}\right]\\ &= \mathbb{E}_{\boldsymbol Z}\left[ \log \dfrac{p(\boldsymbol Z|\boldsymbol X,\boldsymbol \theta)p(\boldsymbol X|\boldsymbol \theta)}{p(\boldsymbol Z)}\right] \qquad \color{steelblue}{\leftarrow \,概率的链式法则}\\ &= \mathbb{E}_{\boldsymbol Z}\left[ \log \dfrac{p(\boldsymbol Z|\boldsymbol X,\boldsymbol \theta)}{p(\boldsymbol Z)}+\log p(\boldsymbol X|\boldsymbol \theta)\right]\\ &= \mathbb{E}_{\boldsymbol Z}\left[ \log \dfrac{p(\boldsymbol Z|\boldsymbol X,\boldsymbol \theta)}{p(\boldsymbol Z)}\right] + \mathbb{E}_{\boldsymbol Z}\left[\log p(\boldsymbol X|\boldsymbol \theta)\right] \qquad \color{steelblue}{\leftarrow \, \mathbb{E}[.]\,的线性性质}\\ &= \mathbb{E}_{\boldsymbol Z}\left[ \log \dfrac{p(\boldsymbol Z|\boldsymbol X,\boldsymbol \theta)}{p(\boldsymbol Z)}\right] + \log p(\boldsymbol X|\boldsymbol \theta) \qquad \color{steelblue}{\leftarrow \, 常数的\,\mathbb{E}[.]\,是其本身}\\ \end{align}\]最后,我们得到:
\[\color{steelblue}{\overbrace{\color{black}{\log p(\boldsymbol X|\boldsymbol \theta)}}^{最终目标:最大化}} \ge\, \color{steelblue}{\overbrace{\color{orange}{\underbrace{\color{black}{\mathbb{E}_{\boldsymbol Z}\left[ \log \dfrac{p(\boldsymbol Z|\boldsymbol X,\boldsymbol \theta)}{p(\boldsymbol Z)}\right]}}_{首先,注意到该项\,\le\,0 \\该项也称为\,p(\boldsymbol Z)\,和\, p(\boldsymbol Z|\boldsymbol X,\boldsymbol \theta)\,之间的\\负的 \text{ KL (Kullback-Leibler) } 散度}} \color{black}{+ \log p(\boldsymbol X|\boldsymbol \theta)}}^{我们希望最大化的下界}}\]其次,注意到如果 $p(\boldsymbol Z)=p(\boldsymbol Z|\boldsymbol X,\boldsymbol \theta)$,那么
\[\mathbb{E}_{p(\boldsymbol Z|\boldsymbol X,\boldsymbol \theta)}\left[\log \dfrac{p(\boldsymbol Z|\boldsymbol X,\boldsymbol \theta)}{p(\boldsymbol Z|\boldsymbol X,\boldsymbol \theta)}\right]=\mathbb{E}_{p(\boldsymbol Z|\boldsymbol X,\boldsymbol \theta)}[\log 1]=0\]对于任何 $\boldsymbol \theta^*$,设定 $p(\boldsymbol Z)=p(\boldsymbol Z|\boldsymbol X,\boldsymbol \theta^*)$ 通过在 $\log p(\boldsymbol X| \boldsymbol \theta^{*})$ 上最大化下界,使得其更紧
4. 高斯混合模型的参数估计
EM 算法的一个经典应用
4.1 GMM 的隐变量
- 令 $z_1,…,z_n$ 表示对应数据点 $\boldsymbol x_1,…,\boldsymbol x_n$ 的 真实来源。每个 $z_i$ 都是一个取值在 $1,…,k$ 之间的离散变量,其中,$k$ 是集群的数量
-
现在,对比原始对数似然
\[\log p(\boldsymbol x_1,...,\boldsymbol x_n)=\sum_{i=1}^{n}\log \left(\sum_{c=1}^{k}w_c \mathcal N(\boldsymbol x_i|\boldsymbol \mu_c,\mathbf \Sigma_c)\right)\] -
根据 完全对数似然(如果我们知道 $\boldsymbol z$)
\[\log p(\boldsymbol x_1,...,\boldsymbol x_n,\boldsymbol z)=\sum_{i=1}^{n}\log \left(w_{z_i} \mathcal N(\boldsymbol x_i|\boldsymbol \mu_{z_i},\mathbf \Sigma_{z_i})\right)\] - 回忆一下,对一个正态密度函数取对数,可以得到一个 容易处理 的表达式
4.2 处理关于 $\boldsymbol z$ 的不确定性
- 我们无法计算完全对数似然,因为我们不知道 $\boldsymbol z$
- EM 算法处理这种不确定性的方法是:将 $\log p(\boldsymbol X,\boldsymbol z|\boldsymbol \theta)$ 用其期望 $\mathbb{E}_{\boldsymbol z|\boldsymbol X,\boldsymbol \theta^{(t)}}\left[\log p(\boldsymbol X,\boldsymbol z|\boldsymbol \theta)\right]$ 来替代
- 这反过来需要给定当前参数估计的 $\color{red}{p\left(\boldsymbol z|\boldsymbol X,\boldsymbol \theta^{(t)}\right)}$ 的分布
- 假设 $z_i$ 成对独立,我们需要得到 $p\left(z_i=c|\boldsymbol x_i,\boldsymbol \theta^{(t)}\right)$
-
例如:假设 $\boldsymbol x_i=(-2,-2)$,请问这个数据点来自集群 1 的概率是多少?
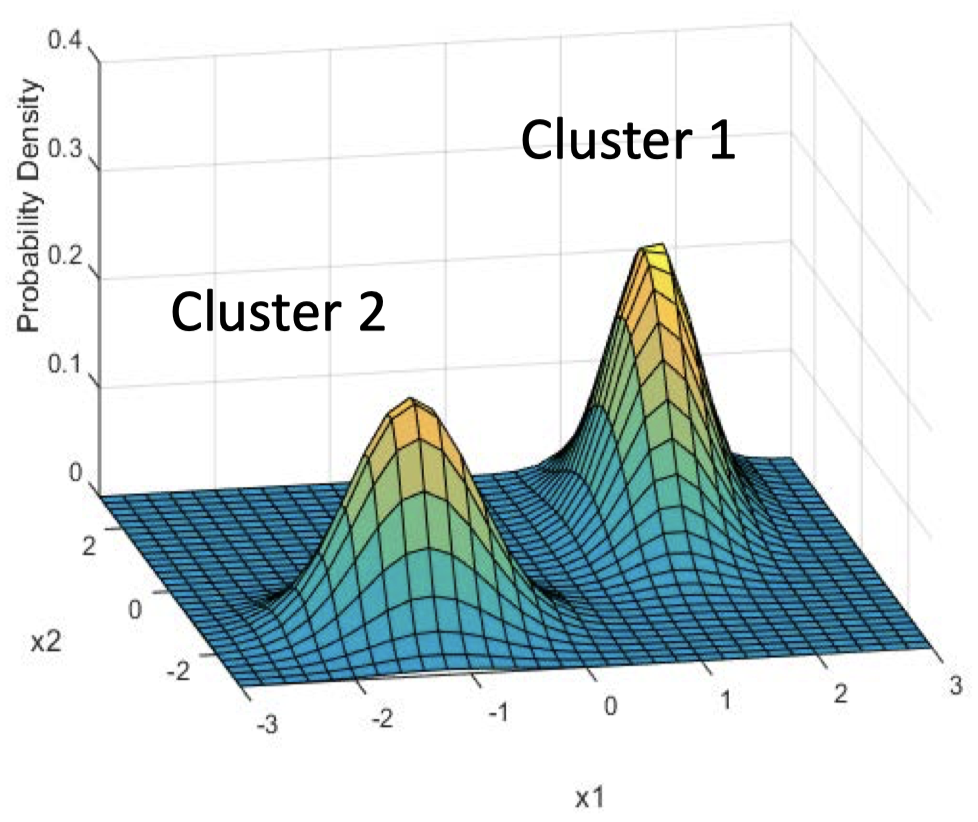
-
设隐变量 $\boldsymbol Z$ 为真实来自的集群,根据贝叶斯规则,其满足
\[p\left(z_i=c|\boldsymbol x_i,\boldsymbol \theta^{(t)}\right)=\dfrac{w_c \mathcal N(\boldsymbol x_i|\boldsymbol \mu_c,\mathbf \Sigma_c)}{\sum_{l=1}^{k}w_l \mathcal N(\boldsymbol x_i|\boldsymbol \mu_l,\mathbf \Sigma_l)}\] -
这个概率称为集群 $c$ 对数据点 $i$ 承担的 “责任”
\[r_{ic}\equiv p\left(z_i=c|\boldsymbol x_i,\boldsymbol \theta^{(t)}\right)\]
4.3 GMM 的 E 步骤(期望)
为了简化表示,我们将 $\boldsymbol x_1,…,\boldsymbol x_n$ 记为 $\boldsymbol X$
\[\begin{align} Q\left(\boldsymbol \theta,\boldsymbol \theta^{(t)}\right) &\equiv \mathbb{E}_{\boldsymbol z|\boldsymbol X,\boldsymbol \theta^{(t)}}\left[\log p(\boldsymbol X,\boldsymbol z|\boldsymbol \theta)\right]\\\\ &= \sum_{\boldsymbol z}p\left(\boldsymbol z|\boldsymbol X,\boldsymbol \theta^{(t)}\right) \log p(\boldsymbol X,\boldsymbol z|\boldsymbol \theta)\\ &= \sum_{\boldsymbol z}p\left(\boldsymbol z|\boldsymbol X,\boldsymbol \theta^{(t)}\right) \sum_{i=1}^{n}\log w_{z_i}\mathcal N(\boldsymbol x_i|\boldsymbol \mu_{z_i},\mathbf \Sigma_{z_i})\\ &= \sum_{i=1}^{n}\sum_{\boldsymbol z}p\left(\boldsymbol z|\boldsymbol X,\boldsymbol \theta^{(t)}\right) \log w_{z_i}\mathcal N(\boldsymbol x_i|\boldsymbol \mu_{z_i},\mathbf \Sigma_{z_i})\\ &= \sum_{i=1}^{n}\sum_{c=1}^{k}r_{ic}\log w_{z_i}\mathcal N(\boldsymbol x_i|\boldsymbol \mu_{z_i},\mathbf \Sigma_{z_i})\\ &= \sum_{i=1}^{n}\sum_{c=1}^{k}r_{ic}\log w_{z_i} + \sum_{i=1}^{n}\sum_{c=1}^{k}r_{ic}\log \mathcal N(\boldsymbol x_i|\boldsymbol \mu_{z_i},\mathbf \Sigma_{z_i}) \end{align}\]4.4 GMM 的 M 步骤(最大化)
-
在 M(最大化)步骤中,将 $Q\left(\boldsymbol \theta,\boldsymbol \theta^{(t)}\right)$ 对每个参数取其对应的偏导数,并且将这些偏导数设为零,从而得到新的参数估计
\[w_c^{(t+1)}=\dfrac{1}{n}\sum_{i=1}^{n}r_{ic}\] \[\boldsymbol \mu_c^{(t+1)}=\dfrac{\sum_{i=1}^{n}r_{ic}\boldsymbol x_i}{r_c}\]这里,$r_c \equiv \sum_{i=1}^{n}r_{ic}$
\[\mathbf \Sigma_c^{(t+1)}=\dfrac{\sum_{i=1}^{n}r_{ik}\boldsymbol x_i\boldsymbol x_i'}{r_k}-\boldsymbol \mu_c^{(t)}\left(\boldsymbol \mu_c^{(t)}\right)'\]注意,这些是在第 $(t+1)$ 步的估计
4.5 拟合高斯混合模型的例子
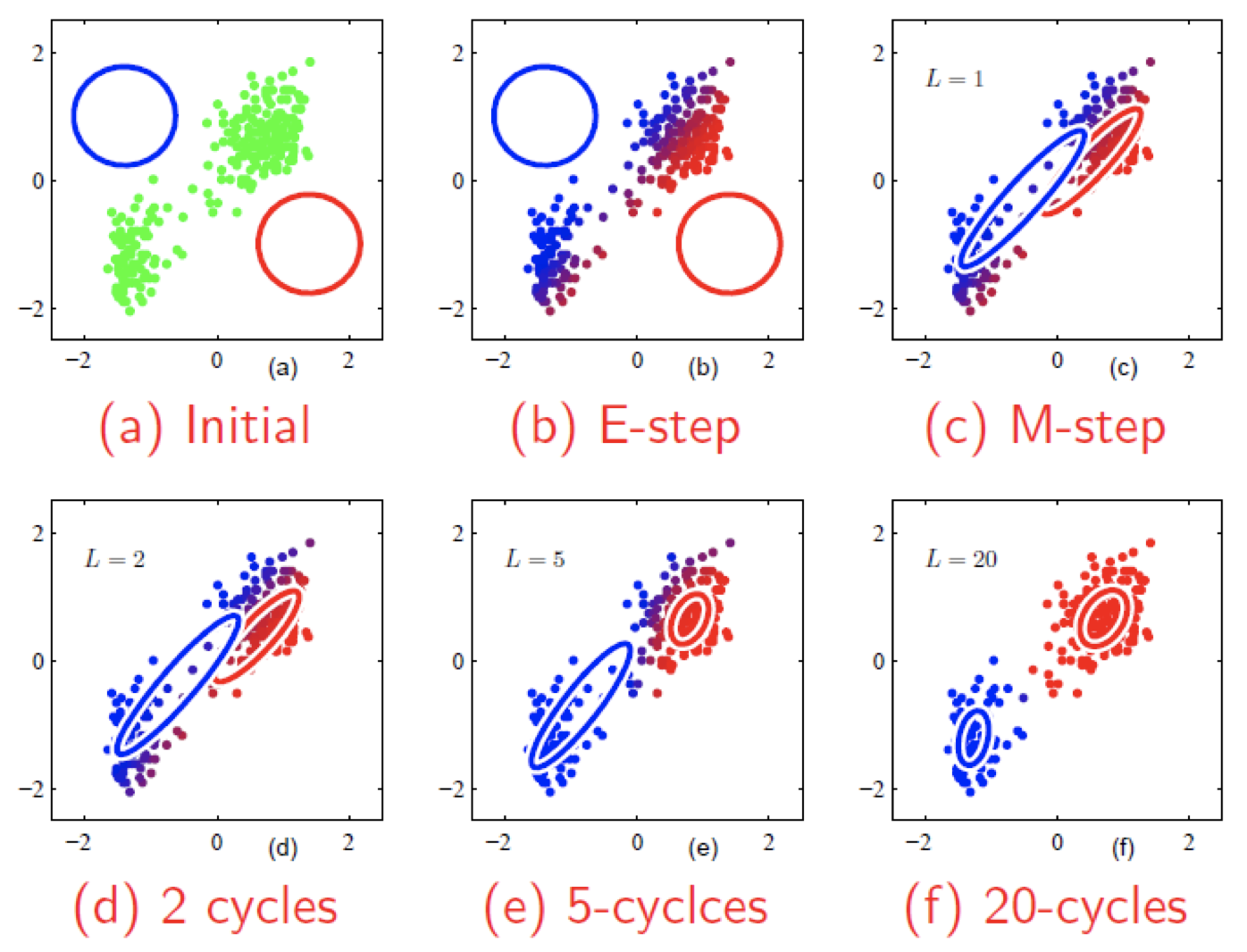
4.6 K-means 相当于在一个带约束的 GMM 上使用 EM
- 考虑一个 GMM 模型,其中所有的组分都有相同的固定概率 $w_c=1 / k$,并且每个高斯分布都具有相同的固定的协方差矩阵 $\mathbf \Sigma_c=\sigma^2 \boldsymbol I$,其中 $\boldsymbol I$ 是单位矩阵
- 在这样一个模型中,只有组分的中心 $\boldsymbol \mu_c$ 需要被估计
- 接下来,近似一个概率集群的 “责任” $r_{ic}=p\left(z_i=c|\boldsymbol x_i,\boldsymbol \mu_c^{(t)}\right)$,其中,如果 $\boldsymbol \mu_c^{(t)}$ 是距离数据点 $\boldsymbol x_i$ 最近的集群中心,那么我们规定 $r_{ic}=1$,否则,$r_{ic}=0$
- 上面的公式相当于是一个 E 步骤,其中 $\boldsymbol \mu_c$ 应该被设定为被分配到集群 $c$ 的数据点的中心
- 换而言之,k-means 算法可以视为用于带约束的 GMM 模型的一种 EM算法
总结
- 无监督学习
- 问题的多样性
- 高斯混合模型(GMM)
- 一种聚类的概率方法
- GMM 模型
- GMM 聚类作为一个优化问题
- 期望最大化(EM)算法
下节内容:降维
本作品采用知识共享署名-非商业性使用-相同方式共享 4.0 国际许可协议进行许可。 欢迎转载,并请注明来自:YEY 的博客 同时保持文章内容的完整和以上声明信息!