Lecture 19 降维
主要内容
- 主成成分分析(PCA)
- 线性降维方法
- 对角化协方差矩阵
- 核化 PCA
1. 关于降维
1.1 数据的真实维度?
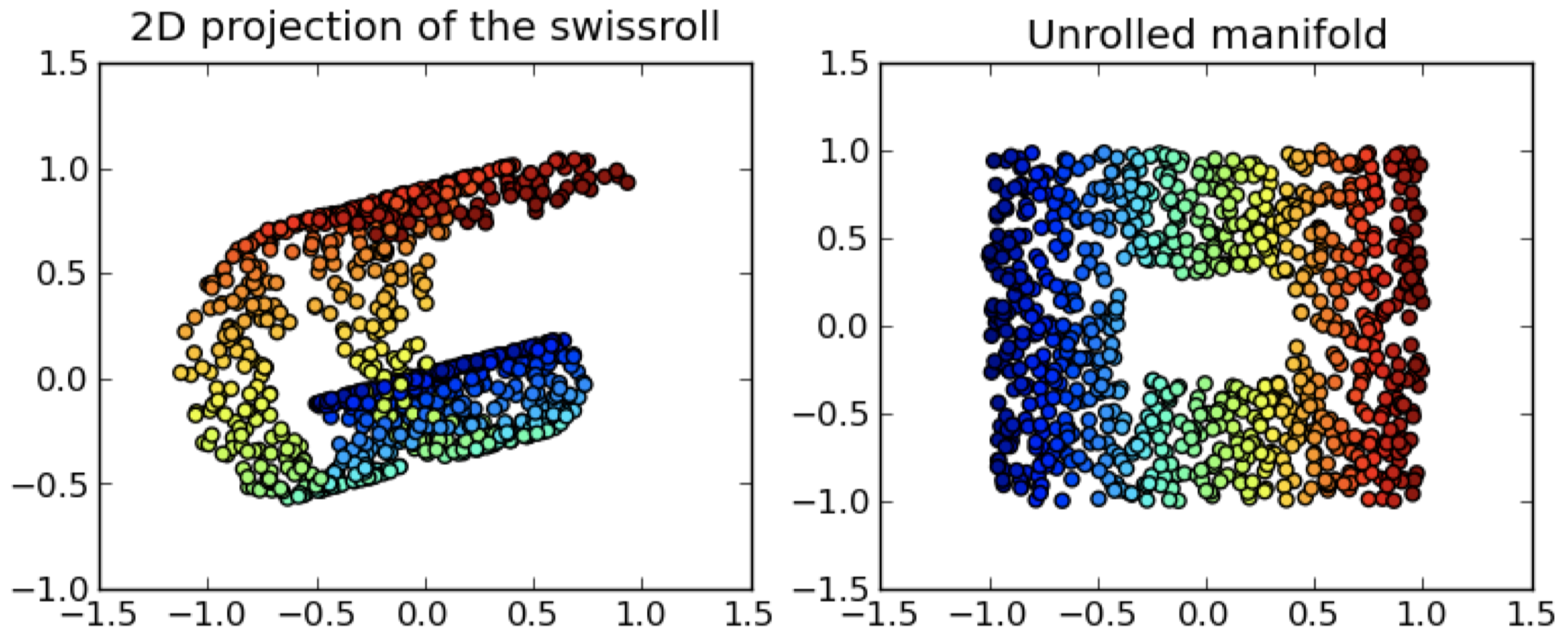
1.2 降维
- 之前我们介绍了无监督学习中的一类常见任务:聚类
- 降维 是指使用 较少数量的变量(维度)来表示数据,同时保留数据中我们 “感兴趣的” 结构
- 通过降维,我们可以达到以下目的:
- 可视化(例如,将高维数据映射到 2D)
- 提高 pipeline 中的 计算效率
- 提升 pipeline 中的数据压缩或者 统计效率
1.3 探索数据结构
- 一般而言,降维会导致信息丢失
- 诀窍是确保大部分我们 “感兴趣的” 信息被保留下来,而丢失的大部分都属于噪声
- 这通常是可能的,因为相比那些记录的变量,真实数据具有的 内在维度可能要少得多
- 例子: GPS 坐标是 3D 的,而平坦道路上的汽车定位实际是在 2D 流形上的
2. 主成成分分析(PCA)
寻找一种数据的旋转方式使得(新)变量之间的协方差最小化
2.1 主成成分分析
- 主成成分分析(PCA)是普遍用于降维和数据分析的一种常用方法
- 给定一个数据集 $\boldsymbol x_1,…,\boldsymbol x_n$,其中 $\boldsymbol x_i\in \boldsymbol R^m$,PCA 的目标是找到一个新的坐标系,使得大部分方差都集中在第一个坐标轴上,然后剩下的大部分方差都集中在第二个坐标轴上,以此类推
- 然后,降维是基于 丢弃坐标 实现的,我们仅保留前 $l$ 个坐标,丢弃后面的其余坐标($l< m$)
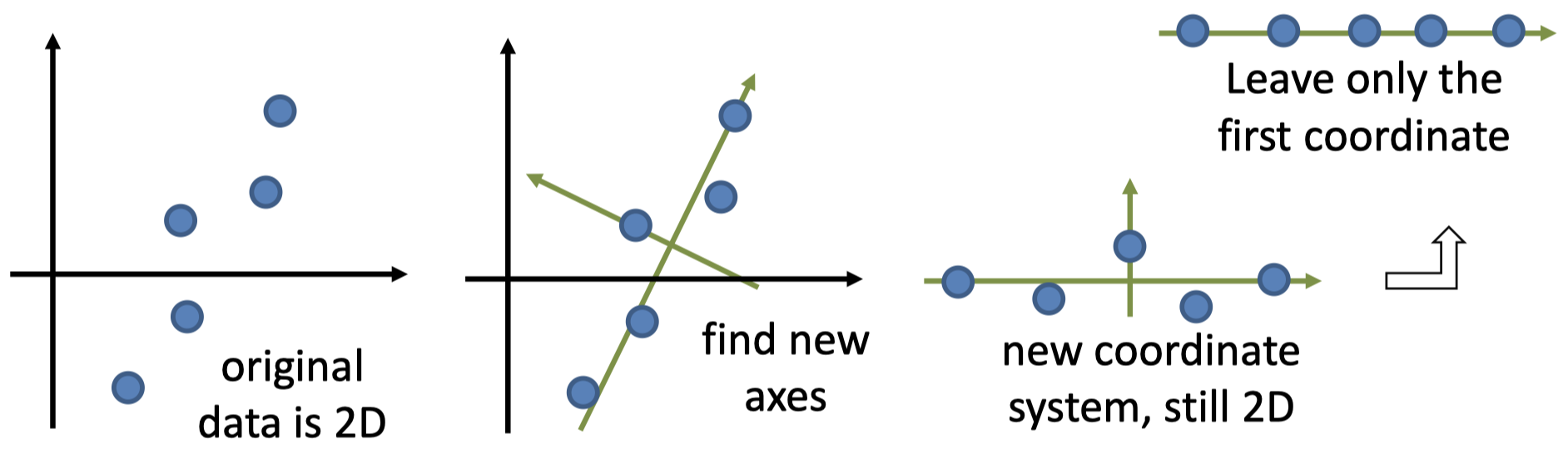
2.2 朴素 PCA 算法
朴素 PCA 算法描述:
1.$\,$选择一个方向 作为新的坐标轴,使得方差沿着该坐标轴是最大化的
2.$\,$选择下一个方向 / 坐标轴垂直于当前所有的坐标轴,使得(余下的)方差着该坐标轴是最大化的
3.$\,$重复步骤 2,直到你得到了和原始数据中同样数量的坐标轴(即,维度)
4.$\,$将原始数据 投影 到这些新的坐标轴上,从而得到新的坐标(“PCA 坐标”)
5.$\,$对于每个数据点,仅保留 前 $l$ 个坐标
如果可以直接实现,那么该算法是有效的,但是,我们还有其他更好的解决方案
2.3 问题描述
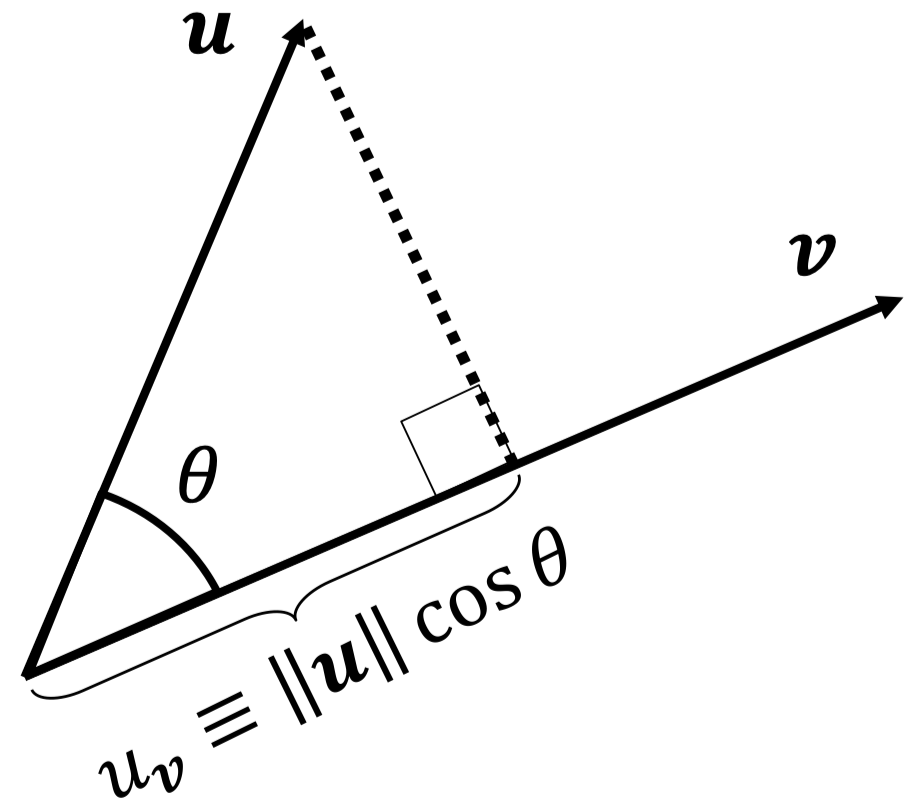
- PCA 的核心是寻找一个新的坐标系,使得大部分方差都被 “早先的” 几个坐标轴捕获到
- 现在,让我们将这一目标的正式形式写出来,看一下如何实现
- 首先,回忆点积的几何定义 $\boldsymbol u\cdot \boldsymbol v=u_{\boldsymbol v}\|\boldsymbol v\|$
- 假设 $\|\boldsymbol v\|=1$,那么 $\boldsymbol u\cdot \boldsymbol v=u_{\boldsymbol v}$
- 向量 $\boldsymbol v$ 可以被视为一个候选的坐标 轴,$u_{\boldsymbol v}$ 可以被视为点 $\boldsymbol u$ 的 坐标
2.4 数据变换
- 所以,新的 坐标系 是一个向量的集合 $\boldsymbol p_1,…,\boldsymbol p_m$,其中每个 $\|\boldsymbol p_i\|=1$
- 考虑一个原始的数据点 $\boldsymbol x_j\;(j=1,…,n)$ 和一个主轴 $\boldsymbol p_i\;(i=1,…,m)$
- 第一个数据点在经过变换之后,其对应的第 $i$ 个坐标为 $(\boldsymbol p_i)’(\boldsymbol x_1)$
- 对于第二个数据点,则为 $(\boldsymbol p_i)’(\boldsymbol x_2)$,以此类推
-
将所有这些数字整理为一个向量
\[\left[(\boldsymbol p_i)'(\boldsymbol x_1),...,(\boldsymbol p_i)'(\boldsymbol x_n)\right]'=\left((\boldsymbol p_i)'\boldsymbol X\right)'=\boldsymbol X'\boldsymbol p_i\]其中,$\boldsymbol X$ 的列中具有原始的数据点
2.5 复习:基础统计知识
-
考虑一个随机变量 $U$ 和相应的样本 $\boldsymbol u=[u_1,…,u_n]’$
-
样本均值为:$\overline u \equiv \dfrac{1}{n}\sum_{i=1}^{n}u_i\qquad$ 样本方差为:$\dfrac{1}{n-1}\sum_{i=1}^{n}(u_i-\overline u)^2$
-
假设事先已经减掉了均值(即样本是 居中的),在这种情况下,方差是一个经过缩放的点积 $\dfrac{1}{n-1}\boldsymbol u’\boldsymbol u$
-
类似地,如果我们有一个来自另一个随机变量的居中随机样本 $\boldsymbol v$,那么样本方差为 $\dfrac{1}{n-1}\boldsymbol u’\boldsymbol v$
-
最后,如果我们的数据为 $\boldsymbol x_1=[u_1,v_1]’,…,\boldsymbol x_n=[u_n,v_n]’$,将其整合为一个矩阵 $\boldsymbol X$,其中列是数据,行是居中变量。我们可以得到 协方差矩阵 为 $\mathbf \Sigma_{\boldsymbol X}\equiv \dfrac{1}{n-1}\boldsymbol X\boldsymbol X’$
2.6 PCA 的目标
- 我们应当假设数据是居中的
- 让我们从第一个主轴的目标开始,数据在这个主轴上的投影为 $\boldsymbol X’\boldsymbol p_1$
-
因此,沿该主轴的方差为
\[\dfrac{1}{n-1}\left(\boldsymbol X'\boldsymbol p_1\right)'\left(\boldsymbol X'\boldsymbol p_1\right)=\dfrac{1}{n-1}\boldsymbol p_1'\boldsymbol X\boldsymbol X'\boldsymbol p_1=\boldsymbol p_1'\mathbf \Sigma_{\boldsymbol X}\boldsymbol p_1\]- 这里,$\mathbf \Sigma_{\boldsymbol X}$ 是原始数据的协方差矩阵
- 因此,PCA 应该找到使得 $\boldsymbol p_1’\mathbf \Sigma_{\boldsymbol X}\boldsymbol p_1$ 最大化的 $\boldsymbol p_1$,其中 $\|\boldsymbol p_1\|=1$
2.7 解决这个优化问题
-
PCA 的目标是找到 $\boldsymbol p_1$ 使得 $\boldsymbol p_1’\mathbf \Sigma_{\boldsymbol X}\boldsymbol p_1$ 最大化,其中 $\|\boldsymbol p_1\|=\boldsymbol p_1’\boldsymbol p_1=1$
-
约束 $\to$ 拉格朗日乘子
\[L=\boldsymbol p_1'\mathbf \Sigma_{\boldsymbol X}\boldsymbol p_1-\lambda_1(\boldsymbol p_1'\boldsymbol p_1-1)\] \[\dfrac{\partial L}{\partial \boldsymbol p_1}=2\mathbf \Sigma_{\boldsymbol X}\boldsymbol p_1-2\lambda_1\boldsymbol p_1=0\] \[\mathbf \Sigma_{\boldsymbol X}\boldsymbol p_1=\lambda_1\boldsymbol p_1\]
引入拉格朗日乘子 $\lambda_1$,令拉格朗日函数的一阶导数为零,求解 -
定义 $\boldsymbol p_1$ 为 特征向量,$\lambda_1$ 为对应的 特征值
2.8 复习:特征向量
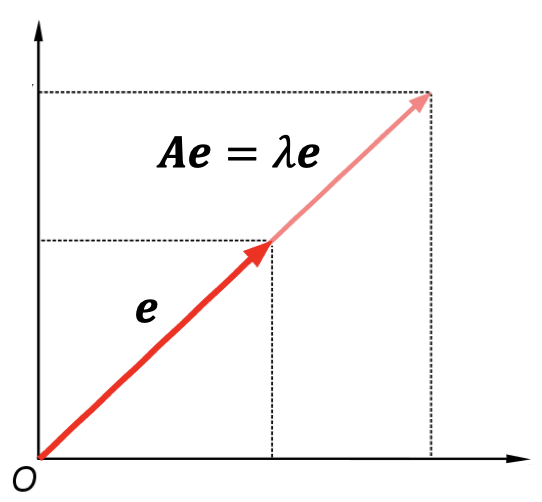
-
给定一个方阵 $\boldsymbol A$,一个列向量 $\boldsymbol e$
如果满足 $\boldsymbol {Ae}=\lambda \boldsymbol e$
那么向量 $\boldsymbol e$ 被称为 方阵 $\boldsymbol A$ 的特征向量
这里,$\lambda$ 是对应的特征值 -
几何解释:将 $\boldsymbol {Ae}$ 与前面的 $\boldsymbol {px}_i$ 进行对比。这里,对于某个向量 $\boldsymbol e$ 而言,$\boldsymbol A$ 是一个变换矩阵(“新轴”),使得向量 $\boldsymbol e$ 在经过变换后仍然指向相同的方向。
2.9 复习:特征值
- 代数解释:如果 $\boldsymbol {Ae}=\lambda \boldsymbol e$,那么 $(\boldsymbol A-\lambda \boldsymbol I)\boldsymbol e=0$,其中 $\boldsymbol I$ 是单位矩阵
- 当且仅当行列式 $|\boldsymbol A-\lambda \boldsymbol I|=0$ 时,上面的等式具有非零解 $\boldsymbol e$
而方程 $|\boldsymbol A-\lambda \boldsymbol I|=0$ 被称为特征方程,该方程的根 $\lambda$ 被称为特征值 - 特征向量和特征值是线性代数中的重要概念,并出现在许多实际应用中
- 矩阵的 谱(Spectrum)是其特征值的集合
- 有一些用于高效计算特征向量的算法
2.10 主成成分捕捉到的方差
- 总结:我们选择 $\boldsymbol p_1$ 作为中心协方差矩阵 $\mathbf \Sigma_{\boldsymbol X}$ 的最大特征值的特征向量
- 被 $\boldsymbol p_1$ 所捕获的数据的方差:
- 注意,我们已经表明了 $\lambda_1=\boldsymbol p_1’\mathbf \Sigma_{\boldsymbol X}\boldsymbol p_1$
- 但是,$\boldsymbol p_1’\mathbf \Sigma_{\boldsymbol X}\boldsymbol p_1$ 是投影数据的方差
$\to$ 第一 特征值 是捕获到的 方差
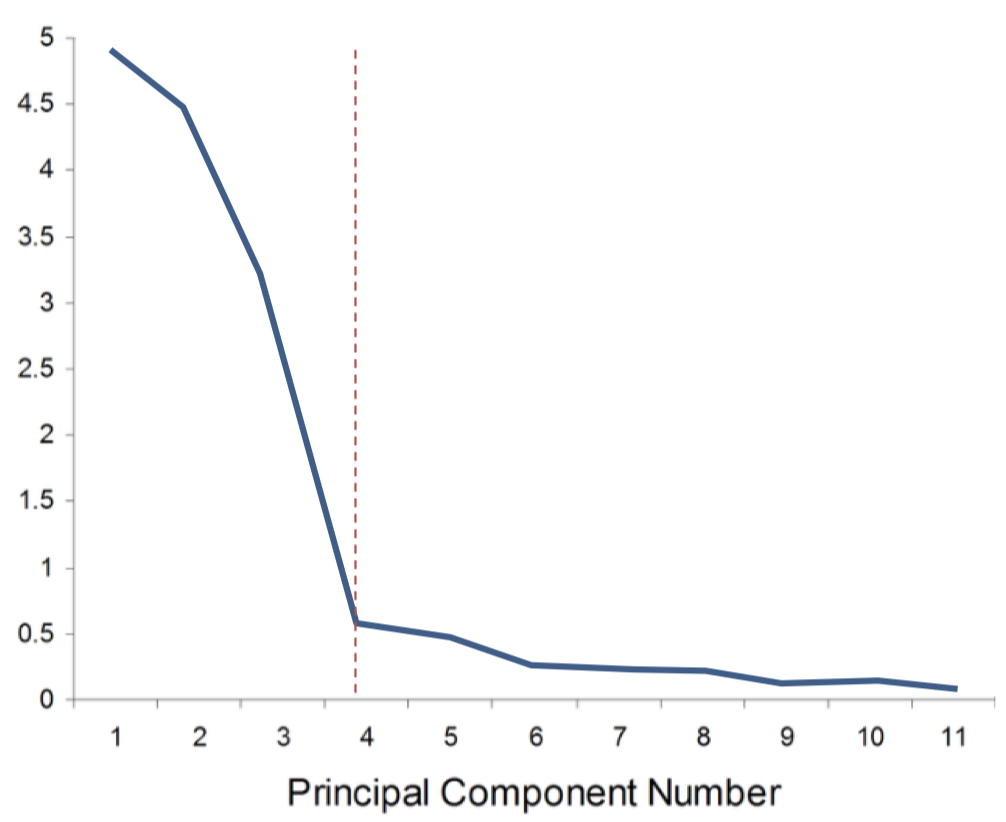
-
选择维度位于 碎石图(scree plot) 中的 “拐点” 处
2.11 PCA 的高效求解
- 相同的模式可以用来寻找所有的主成成分
- 约束 $\|\boldsymbol p_i\|=1$ 避免了方差 $\boldsymbol p_i’\mathbf \Sigma_{\boldsymbol X}\boldsymbol p_i$ 因为重新缩放 $\boldsymbol p_i$ 导致的发散
- 每次我们都会增加额外的约束,使得下一个主成成分与所有先前的主成成分正交。等效地,我们搜索它们的补集。
- 方法是:将 $\boldsymbol p_i$ 设为中心数据协方差矩阵 $\mathbf \Sigma_{\boldsymbol X}$ 的 所有特征向量,按照 特征值降序排列
- 真的对于任何 $\mathbf \Sigma_{\boldsymbol X}$ 都可行吗?
- 引理: 一个 $m\times m$ 的实对称矩阵有 $m$ 个实特征值,并且它们对应的特征向量都正交。
- 引理: 一个 PSD(半正定)矩阵还具有非负特征值。
2.12 PCA 总结
- 假设数据点被排列在矩阵 $\boldsymbol X$ 的列中,这意味着变量在矩阵的行中。
- 确保数据是居中的:从每一行中减去平均行(数据中心)
- 我们寻找一组正交基 $\boldsymbol p_1,…,\boldsymbol p_m$
- 每个基向量都具有单位长度,并且它们彼此之间互相垂直
- 寻找中心数据协方差矩阵 $\mathbf \Sigma_{\boldsymbol X}\equiv \dfrac{1}{n-1}\boldsymbol X\boldsymbol X’$ 的特征值
- 总是可行的,并且相当高效
- 将特征值从大到小排列
- 每个特征值都等于数据沿着对应主成成分方向上的方差
- 将 $\boldsymbol p_1,…,\boldsymbol p_m$ 设为对应的特征向量
- 将数据 $\boldsymbol X$ 投影到这些新的坐标轴上,从而得到变换数据的坐标
- 仅保留前 $s$ 个坐标实现降维
- PCA 的另一种视角:$s$-维的平面 最小化了数据的残差平方和(该平面其实就是由所选择的 $s$ 个主成成分所张成的线性空间)
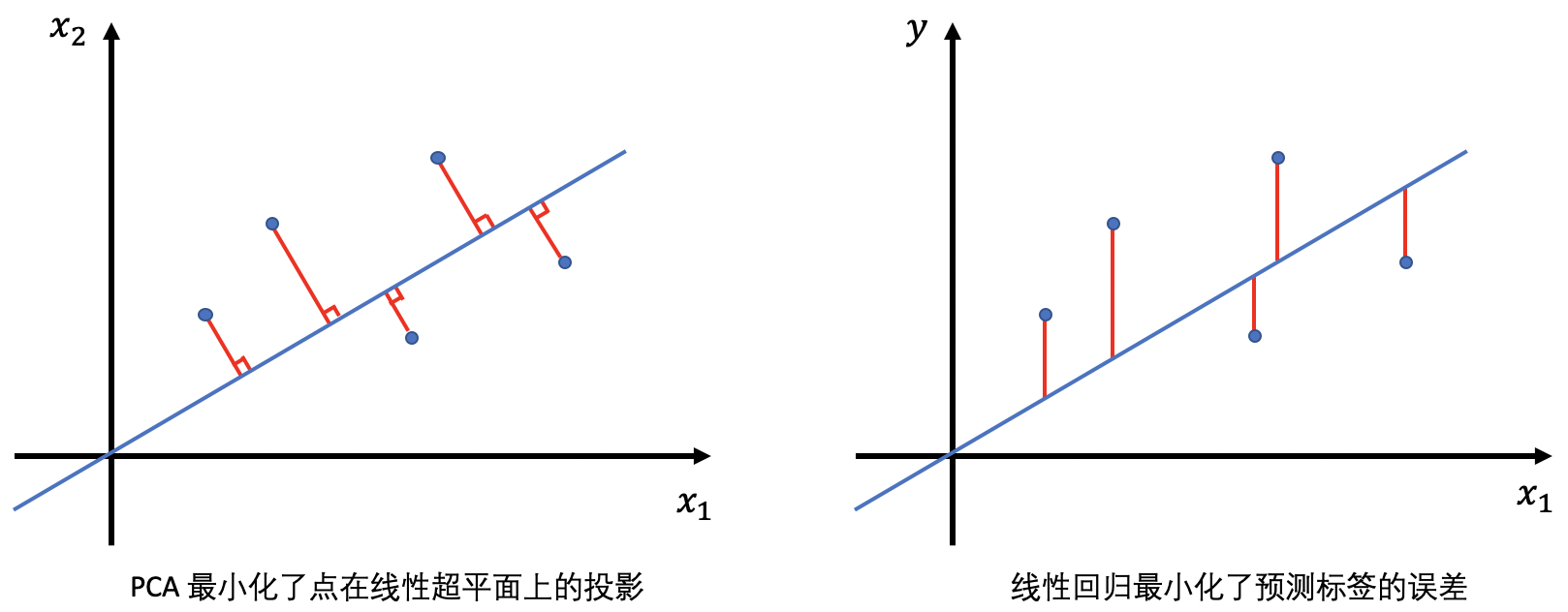
2.13 PCA vs. 线性回归
2.14 PCA 的额外效应
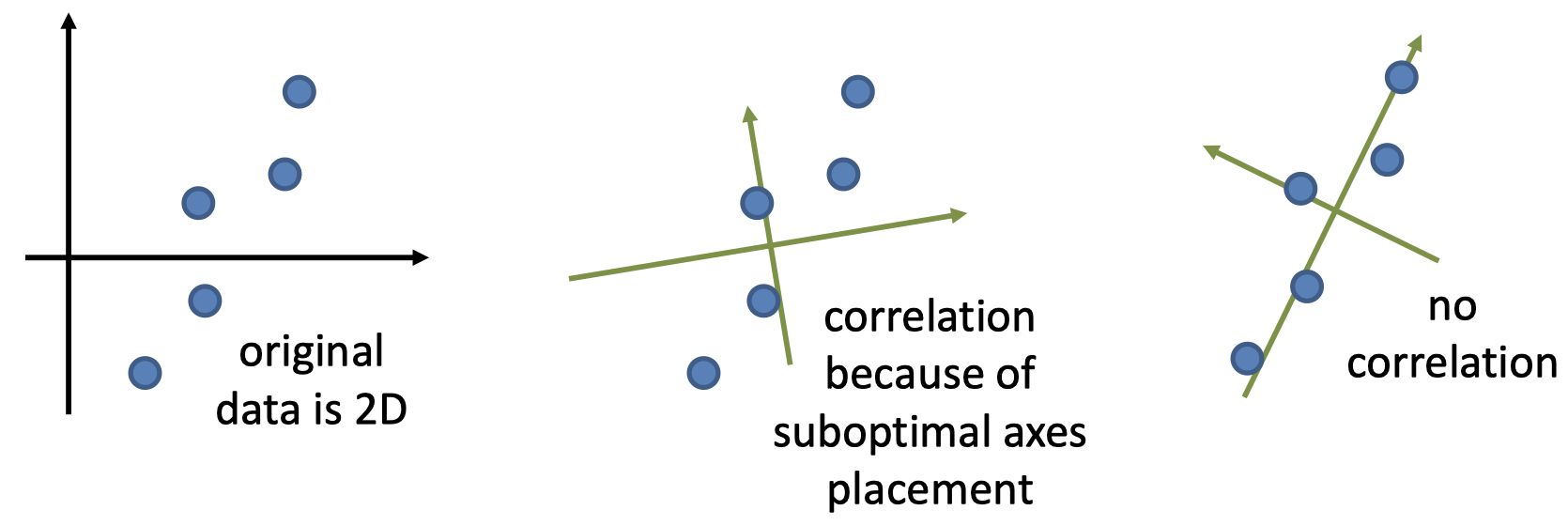
- PCA 的目的是寻找坐标轴,使得沿每个后续坐标轴的方差最大化
- 考虑两个候选坐标轴 $i$ 和 $(i+1)$。非正式地,如果它们之间存在相关性,那么意味着轴 $i$ 可以进一步旋转以捕获更多方差
- PCA 应该最终找到新的坐标轴(即变换),使得 变换后的数据不相关
2.15 对称矩阵的谱定理
- 为了进一步探讨这种效应,我们需要参考线性代数的基本结果之一
- 相关证明超出了范围,不在这里讨论
- 这是奇异值分解(SVD)定理的一个特例
- 定理: 对于任何实对称矩阵 $\mathbf \Sigma_{\boldsymbol X}$,总是存在一个行向量由 $\mathbf \Sigma_{\boldsymbol X}$ 的特征向量组成的实正交矩阵 $\boldsymbol P$,以及一个由 $\mathbf \Sigma_{\boldsymbol X}$ 的特征值组成的对角矩阵 $\boldsymbol \Lambda$,使得 $\mathbf \Sigma_{\boldsymbol X}=\boldsymbol P’ \boldsymbol \Lambda \boldsymbol P$
2.16 对角化协方差矩阵
- 构造变换矩阵 $\boldsymbol P$,其行向量是特征向量(新的坐标轴)
- 通过我们的问题表述,$\boldsymbol P$ 是一个正交矩阵
- 注意到 $\boldsymbol P’\boldsymbol P=\boldsymbol I$,其中 $\boldsymbol I$ 是单位矩阵
- 关于这点,可以回想一下,矩阵乘法结果中的每个元素都是对应行和列的点积
- 所以,$\boldsymbol P’\boldsymbol P$ 中的元素 $(i,j)$ 是点积 $\boldsymbol p_i’\boldsymbol p_j$,如果 $i=j$ 则其值为 $1$,否则为 $0$
- 变换后的数据为 $\boldsymbol P\boldsymbol X$
- 和上面类似,注意到 $\boldsymbol P\boldsymbol X$ 中的元素 $(i,j)$ 是点积 $\boldsymbol p_i’\boldsymbol x_j$,也就是 $\boldsymbol x_j$ 在轴 $\boldsymbol p_i$ 上的投影,即第 $j$ 个点的新的第 $i$ 个坐标
-
变换后的数据的协方差为
\[\mathbf \Sigma_{\boldsymbol{PX}}\equiv \dfrac{1}{n-1}(\boldsymbol{PX})(\boldsymbol{PX})'=\dfrac{1}{n-1}(\boldsymbol{PX})(\boldsymbol X'\boldsymbol P')=\boldsymbol P\mathbf \Sigma_{\boldsymbol{X}}\boldsymbol P'\] - 根据谱分解定理,我们可以得到 $\mathbf \Sigma_{\boldsymbol{X}}=\boldsymbol P’\boldsymbol \Lambda \boldsymbol P$
-
因此
\[\mathbf \Sigma_{\boldsymbol{PX}}=\boldsymbol P\boldsymbol P'\boldsymbol \Lambda \boldsymbol P\boldsymbol P'=\boldsymbol \Lambda\] - 变换后的数据的协方差矩阵是对角矩阵,其对角线上的元素就是矩阵 $\boldsymbol \Lambda$ 对角线上的特征值
- 变换后的数据是不相关的
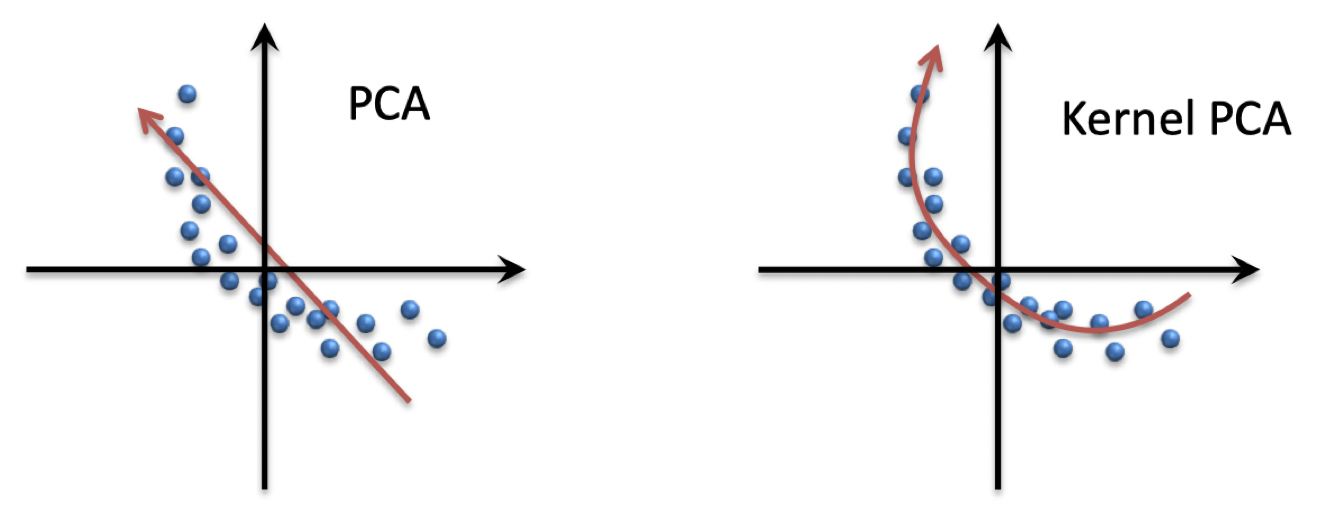
2.17 非线性数据和核化 PCA
- 低维近似不必是线性的
- 核化 PCA:将数据映射到特征空间,然后使用 PCA
- 用数据点表示主成成分。求解过程利用了 $\boldsymbol X’\boldsymbol X$ 可以被核函数化 $(\boldsymbol X’\boldsymbol X)_{ij}=K(\boldsymbol x_i,\boldsymbol x_j)$
- 求解策略不同于常规 PCA
- 模块化:更改核函数会导致不同的特征空间变换
总结
- 主成成分分析
- 线性降维方法
- 对角化协方差矩阵
- 核化 PCA
本作品采用知识共享署名-非商业性使用-相同方式共享 4.0 国际许可协议进行许可。 欢迎转载,并请注明来自:YEY 的博客 同时保持文章内容的完整和以上声明信息!