Lecture 00-01 概率论基础
参考资料:Natural Language Processing: Appendix A (p.475-483) —— by Eisenstein, Jacob
引言
概率论为推理随机事件提供了一种方法。通常用于解释概率论的随机事件包括:抛硬币、抽纸牌和天气。将选择单词和抛硬币进行类比似乎是很奇怪的,特别是,如果你是那种对于选择单词特别认真的人。但是,无论随机与否,语言都是一种很难对其进行确定性建模的东西。概率论为语言数据的建模和处理提供了一种强大的工具。
可以通过 随机结果 来思考概率:例如,单个硬币抛掷会产生两种可能的结果,正面或背面。所有可能结果的集合被称为 样本空间,而 样本空间 的一个子集就是一个 事件。对于连续抛两次硬币,有四种可能的结果:\(\{HH,HT,TH,TT\}\),分别代表 “正面-正面”、“正面-背面”、“背面-正面” 和 “背面-背面” 的有序序列。刚好得到一个正面的事件包括两种结果:\(\{HT,TH\}\)。
形式上,概率是一个将事件映射到 $0$ 到 $1$ 之间的区间的函数:$\Pr:\,\mathcal F \to[0,1]$,其中 $\mathcal F$ 是所有可能事件的集合。一个可以确定的事件的概率为 $1$,一个不可能发生的事件的概率为 $0$。例如,在连续两次抛硬币中,得到正面少于三次的概率为 $1$。每个结果也是一个事件(一个只包含一个元素的集合),对于连续两次抛一枚公平硬币,每种结果的概率为
\[\Pr(\{HH\})=\Pr(\{HT\})=\Pr(\{TH\})=\Pr(\{TT\})=\dfrac{1}{4} \tag{1}\]1. 事件组合的概率
因为事件是结果的集合,所以我们可以使用集合论的一些操作(例如补集、交集和并集)来推理事件及其组合的概率。
对于任何事件 $A$,都存在一个 补集 $\neg A$,使得:
- 并集 $A \cup \neg A$ 的概率为 $\Pr(A \cup \neg A)=1$
- 交集 $A \cap \neg A=\varnothing$ 是空集,其概率为 $\Pr(A \cup \neg A)=0$
在抛硬币的例子中,连续两次抛掷硬币后得到一次正面朝上的事件对应于结果集合 \(\{HT,TH\}\);补集事件则包含了另外两种结果 \(\{TT,HH\}\)。
1.1 不相交事件的概率
当两个事件的交集为空集时,即 $A \cap B=\varnothing$,它们是 不相交的。两个不相交事件的并集的概率等于二者概率的和
\[A \cap B=\varnothing \quad \Rightarrow \quad \Pr(A\cup B)=\Pr(A)+\Pr(B) \tag{2}\]这是 概率的第三公理,它可以推广到任何可数的不相交事件序列。
在抛硬币的例子中,该公理可以推导出抛两次硬币得到一次正面朝上的事件的概率。此事件是结果集合 \(\{HT,TH\}\),它是两个更简单的事件的并集 \(\{HT,TH\} = \{HT\}\cup \{TH\}\)。事件 \(\{HT\}\) 和 \(\{TH\}\) 是不相交的。因此,
\[\begin{align} \Pr(\{HT,TH\})=\Pr(\{HT\}\cup \{TH\}) &= \Pr(\{HT\})+\Pr(\{TH\}) \tag{3}\\ &= \dfrac{1}{4} +\dfrac{1}{4}=\dfrac{1}{2} \tag{4} \end{align}\]通常情况下,两个事件并集的概率为:
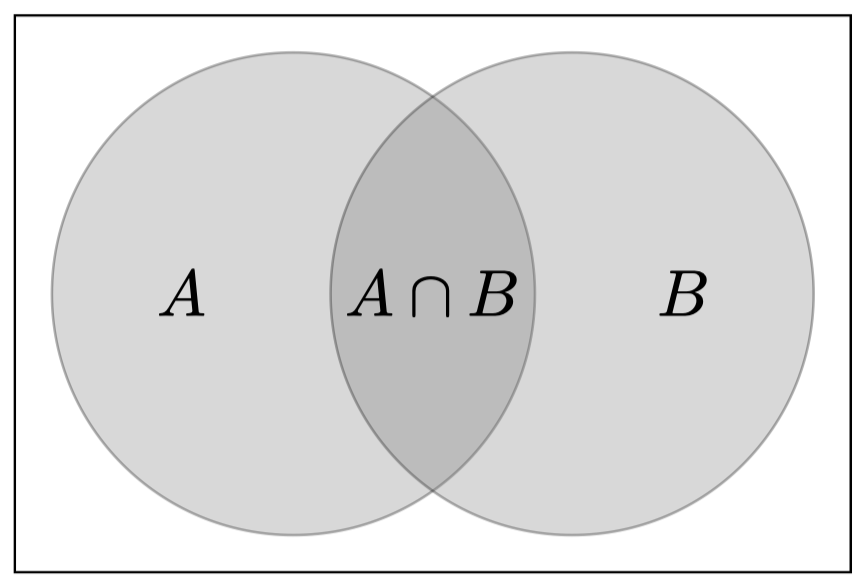
\[\Pr(A\cup B)=\Pr(A)+\Pr(B)-\Pr(A\cap B) \tag{5}\label{(5)}\]这可以从 图 1 中直观地看到,并且可以根据概率的第三公理推导出来。考虑一个由所有那些在 $B$ 中但是不在 $A$ 中的结果组成的事件,记为 $B-(A\cap B)$。通过构造,使得该事件与 $A$ 不相交。因此,我们可以应用加法原则,
\[\Pr(A\cup B)=\Pr(A)+\Pr(B-(A\cap B)) \tag{6}\label{(6)}\]此外,事件 $B$ 是两个不相交事件的并集:$A\cap B$ 和 $B-(A\cap B)$
\[\Pr(B)=\Pr(B-(A\cap B))+\Pr(A\cap B) \tag{7}\]移项后,代入公式 $\eqref{(6)}$,我们就可得到之前公式 $\eqref{(5)}$ 中的结果:
\[\Pr(B-(A\cap B))=\Pr(B)-\Pr(A\cap B) \tag{8}\] \[\Pr(A\cup B)=\Pr(A)+\Pr(B)-\Pr(A\cap B) \tag{9}\]1.2 全概率法则
一个事件的集合 \(\mathcal B=\{B_1,B_2,...,B_N\}\) 是样本空间的一个 划分,当且仅当其中每对事件都互不相交($B_i\cap B_j=\varnothing$),并且这些事件的并集就是整个样本空间。
全概率法则表明我们可以通过下面的公式在这些事件上进行 边缘化:
\[\Pr(A)=\sum_{B_n\in \mathcal B}\Pr(A\cap B_n) \tag{10}\]对于任何事件 $B$,并集 $B \cup \neg B$ 是样本空间的一个划分。因此,全概率法则的一个特例是
\[\Pr(A)=\Pr(A\cap B)+\Pr(A\cap \neg B) \tag{11}\]2. 条件概率和贝叶斯规则
条件概率 是一个类似于 $\Pr(A\mid B)$ 的表达式,它是假设事件 $B$ 也发生了的前提下,事件 $A$ 发生的概率。例如,我们可能会对某个随机选择的人回应我们的英语问候电话的概率感兴趣,前提是这个人说英语。条件概率被定义为一个比率
\[\Pr(A\mid B)=\dfrac{\Pr(A\cap B)}{\Pr(B)} \tag{12}\label{(12)}\]概率的链式法则 告诉我们 $\Pr(A\cap B)=\Pr(A\mid B)\times \Pr(B)$,而实际上这就是等式 $\eqref{(12)}$ 移项后得到的结果。链式法则可以重复应用:
\[\begin{align} \Pr(A\cap B \cap C) &= \Pr(A\mid B\cap C)\times \Pr(B\cap C)\\ &= \Pr(A\mid B\cap C)\times \Pr(B\mid C)\times \Pr(C) \end{align}\]贝叶斯规则(有时也称 “贝叶斯法则” 或 “贝叶斯定理”)给了我们一种在 $\Pr(A\mid B)$ 和 $\Pr(B\mid A)$ 之间转换的方式。它来自于条件概率和链式法则的定义:
\[\Pr(A\mid B)=\dfrac{\Pr(A\cap B)}{\Pr(B)}=\dfrac{\Pr(B\mid A)\times \Pr(A)}{\Pr(B)} \tag{13}\]贝叶斯规则中的每项都有一个名称,我们偶尔会使用该名称:
- $\Pr(A)$ 是 先验,因为它是在我们不知道 $B$ 是否发生的情况下,事件 $A$ 的概率
- $\Pr(B\mid A)$ 是 似然,它是在给定事件 $A$ 已经发生的情况下,事件 $B$ 的概率
- $\Pr(A\mid B)$ 是 后验,它是在已知 $B$ 发生的情况下,事件 $A$ 的概率
例子: 贝叶斯法则有一个经典例子涉及对罕见病的检验,但是 Manning 和 Schütze (1999)在语言学背景下重构了这个例子。假设你对一种罕见的句法构造感兴趣,例如寄生间隙 (parasitic gaps),这种间隙平均每 $100,000$ 个句子中出现一次。这里是一个寄生间隙的示例:
\[\textit{Which class did you attend _ without registering for _?}\]语言学家 Lana 开发了一种复杂的模式匹配器,试图识别带有寄生间隙的句子。它表现不错,但并不完美:
- 如果一个句子中存在一个寄生间隙,那么这个模式匹配器能够找出它的概率为 $0.95$。(这是 召回率,它等于 $1$ 减去 假阴性率。)
- 如果该句子中不存在寄生间隙,那么这个模式匹配器有 $0.005$ 的概率会误判为存在寄生间隙。(这是 假阳性率,它等于 $1$ 减去 精度。)
假设 Lana 的模式匹配器声称某个句子中存在一个寄生间隙。这个声明为真的概率是多少?
令 $G$ 表示某个句子带有一个寄生间隙的事件,$T$ 表示测试结果为阳性的事件。现在,已知测试结果为阳性,我们想知道句子中实际存在寄生间隙的概率。这是一个条件概率 $\Pr(G\mid T)$,可以通过贝叶斯规则计算:
\[\Pr(G\mid T)=\dfrac{\Pr(T\mid G)\times \Pr(G)}{\Pr(T)} \tag{14}\]我们已经知道了分子中的两项:召回率 $\Pr(T\mid G)=0.95$ ;先验 $\Pr(G)=10^{-5}$。
我们不知道分母,但是可以利用之前介绍过的工具来计算。首先对划分 $\{G,\neg G\}$ 应用全概率法则:
\[\Pr(T)=\Pr(T\cap G)+\Pr(T \cap \neg G) \tag{15}\]这表示测试结果为阳性的概率等于 真阳性 $(T\cap G)$ 的概率与 假阳性 $(T\cap \neg G)$ 的概率之和。其中,每个事件的概率都可以通过链式法则来计算:
\[\Pr(T\cap G)=\Pr(T\mid G)\times \Pr(G)=0.95\times 10^{-5} \tag{16}\] \[\Pr(T\cap \neg G)=\Pr(T\mid \neg G)\times \Pr(\neg G)=0.005\times (1-10^{-5})\approx 0.005 \tag{17}\] \[\begin{align} \Pr(T) &= \Pr(T\cap G)+\Pr(T \cap \neg G) \tag{18}\\ &= 0.95\times 10^{-5}+0.005 \tag{19} \end{align}\]将这些项插入贝叶斯规则中,可以得出所要求的后验概率
\[\begin{align} \Pr(G\mid T) &= \dfrac{\Pr(T\mid G)\Pr(G)}{\Pr(T)} \tag{20}\\ &= \dfrac{0.95\times 10^{-5}}{0.95\times 10^{-5}+0.005\times (1-10^{-5})} \tag{21}\\ &\approx 0.002 \tag{22} \end{align}\]Lana 的模式匹配器看上去很准确,假阳性率和假阳性率都低于 $5%$。然而,考虑到这种寄生间隙的现象极为罕见,这意味着当检测器给出一个阳性结果时,它很有可能是错误的。
3. 独立性
如果两个事件交集的概率等于它们各自概率的乘积,那么这两个事件是相互独立的:$\Pr(A\cap B)= \Pr(A)\times \Pr(B)$。例如,对于将一枚公平硬币连续抛两次,在第一次抛掷中正面朝上的概率与在第二次抛掷中正面朝上的概率之间互相独立:
\[\Pr(\{HT,HH\})=\Pr(HT)+\Pr(HH)=\dfrac{1}{4}+\dfrac{1}{4}=\dfrac{1}{2} \tag{23}\] \[\Pr(\{HH,TH\})=\Pr(Hh)+\Pr(TH)=\dfrac{1}{4}+\dfrac{1}{4}=\dfrac{1}{2} \tag{24}\] \[\Pr(\{HT,HH\})\times \Pr(\{HH,TH\})=\dfrac{1}{2}\times \dfrac{1}{2}=\dfrac{1}{4} \tag{25}\] \[\begin{align} \Pr(\{HT,HH\}\cap \{HH,TH\}) &= \Pr(HH)=\dfrac{1}{4} \tag{26}\\ &= \Pr(\{HT,HH\})\times \Pr(\{HH,TH\}) \tag{27} \end{align}\]如果 $\Pr(A\cap B\mid C)=\Pr(A\mid C)\times \Pr(B\mid C)$,则事件 $A$ 和 $B$ 之间是 条件独立 的关系,记为 $A \perp B\mid C$。条件独立性在概率模型(如朴素贝叶斯)中扮演着重要的角色。
4. 随机变量
随机变量 是将事件映射到 $\mathbb R^n$ 的函数,其中 $\mathbb R$ 是实数集。这包含了几种有用的特殊情况:
-
指示器随机变量 是将事件映射到 $\{0,1\}$ 集合的函数。在抛硬币的例子中,我们可以将 $Y$ 定义为一个指示器随机变量,当硬币至少出现一次正面朝上时该变量取值为 $1$。这将包括三种不同的结果 $\{HH,HT,TH\}$。概率 $\Pr(Y = 1)$ 等于这些结果的概率之和,$\Pr(Y = 1)=\frac{1}{4}+\frac{1}{4}+\frac{1}{4}=\frac{3}{4}$。
-
离散随机变量 是将事件映射到 $\mathbb R$ 的离散子集的函数。考虑抛硬币的例子:两次抛硬币中正面朝上的次数 $X$ 可以视为一个离散随机变量,$X\in 0,1,2$。事件概率 $\Pr(X=1)$ 可以通过将全部刚好有一次正面朝上的事件,$\{HT,TH\}$,的概率进行求和来计算,$\Pr(X=1)=\frac{1}{4}+\frac{1}{4}=\frac{1}{2}$。
一个随机变量的每个可能的取值都与样本空间的一个子集相关。在抛硬币的例子中,$X = 0$ 与事件 $\{TT\}$ 相关联,$X = 1$ 与事件 $\{HT,TH\}$ 相关联,而 $X = 2$ 与事件 $\{HH\}$ 相关联。假设硬币是公平的,则这些事件的概率分别为 $1/4$、$1/2$ 和 $1/4$。这一列数字代表了 $X$ 上的 概率分布,记为 $\text{p}_X$,它将 $X$ 的可能取值映射到非负实数。对于某个特定的值 $x$,我们记为 $\text{p}_X(x)$,它等于事件概率 $\Pr(X = x)$。如果 $X$ 是离散的,则函数 $\text{p}_X$ 称为 概率质量函数(pmf);如果 $X$ 是连续的,则称为 概率密度函数(pdf)。无论哪种情况,函数求和的结果都必须为 $1$,并且所有的值都必须为非负:
\[\begin{align} \int_x \text{p}_X(x)dx &=1 \tag{28} \\ \forall x,\text{p}_X(x) &\ge 0 \tag{29} \end{align}\]注: 通常,我们用大写字母(例如,$X$)表示随机变量,用小写字母(例如,$x$)表示特定的值。当分布已经在上下文中交代很清楚时,我们可以简记为 $\text{p}(x)$。
多个随机变量上的概率可以写为 联合概率,例如,$\text{p}_{A,B}(a,b)=\Pr(A=a\cap B=b)$。事件概率的一些性会延伸到随机变量的概率分布中:
-
边缘概率分布 为 $\text p_A(a)=\sum_b \text p_{A,B}(a,b)$
-
条件概率分布 为 $\text p_{A\mid B}(a\mid b)=\frac{\text p_{A,B}(a,b)}{\text p_B(b)}$
-
随机变量 $A$ 和 $B$ 相互独立,当且仅当 $\text p_{A,B}(a,b)=\text p_{A}(a)\times \text p_{B}(b)$
5. 期望
有时我们想知道某个函数的 期望,例如 $E[g(x)]=\sum_{x\in \mathcal X}g(x)\text p(x)$。而说到期望,最容易联想到的就是离散事件的概率分布:
- 如果是晴天,Lucia 将吃三个冰淇淋
- 如果是雨天,她将只吃一个冰淇淋
- 有 $80\%$ 的概率是晴天
- 她将吃掉的冰淇淋的数量的期望为 $0.8\times 3+0.2\times 1=2.6$
如果随机变量 $X$ 是连续的,期望是一个积分:
\[E[g(x)]=\int_{\mathcal X}g(x)\text p(x)dx \tag{30}\]例如,魁北克的一家快餐店在寒冷的日子有一个特别优惠:温度每往零下降一度,他们就会给肉汁乳酪薯条在价格上多提供 $1\%$ 的折扣。假设有一个可以无限精确的温度计,那么在所有可能的温度下,期望的价格将会是一个积分:
\[E[\text{price}(x)]=\int_{\mathcal X}\min(1,1+x/100)\times \text{original-price} \times \text p(x)dx \tag{31}\]6. 建模与估计
概率模型 提供了一种推理随机事件和随机变量的原则方法。让我们考虑抛硬币的例子,每一次投掷都可以建模为一个随机事件,事件 $H$ 的概率为 $\theta$,互补事件 $T$ 的概率为 $1-\theta$。如果我们用随机变量 $X$ 表示在三次抛硬币过程中得到的正面朝上的总次数,则 $X$ 的分布取决于 $\theta$。在这种情况下,$X$ 是一个 二项式随机变量,这意味着它来自一个二项式分布,参数为 $(\theta,N=3)$。记为
\[X\sim \text{Binomial}(\theta,N=3) \tag{32}\]二项式分布的性质使我们能够对 $X$ 进行描述,例如它的期望值,以及它的值将落入某个区间内的似然。
现在假设 $\theta$ 是未知的,但是我们进行了一个实验,在实验中我们进行了 $N$ 次尝试,并且得到了 $x$ 次正面朝上的结果。我们可以通过 最大似然 原理来 估计 $\theta$:
\[\hat \theta=\mathop{\operatorname{arg\,max}} \limits_{\theta} \text p_X(x;\theta,N) \tag{33}\]这表示估计 $\hat \theta$ 应该是使得数据似然最大化的值。分号表示 $\theta$ 和 $N$ 是概率函数的参数。似然 $\text p_X(x;\theta,N)$ 可以根据二项式分布计算出来:
\[\text p_X(x;\theta,N)=\dfrac{N!}{x!(N-x)!}\theta^x(1-\theta)^{N-x} \tag{34}\]这个似然和各个单独结果的概率乘积成正比:例如,序列 $T,H,H,T,H$ 的概率为 $\theta^3(1-\theta)^2$。系数项 $\frac{N!}{x!(N-x)!}$ 来自于 $N$ 次试验中得到 $x$ 次正面朝上的许多种可能的顺序。该项不依赖于 $\theta$,因此在进行估计时可以忽略。
在实际应用中,我们最大化对数似然,它是似然的一个单调函数。在二项式分布下,对数似然是 $\theta$ 的一个 凸函数,因此可以通过对其求导并将导数设为零来使其最大化。
\[\begin{align} \ell(\theta) &= x\log \theta+(N-x)\log (1-\theta) \tag{35}\\\\ \dfrac{\partial \ell(\theta)}{\partial \theta} &= \dfrac{x}{\theta}-\dfrac{N-x}{1-\theta} \tag{36}\\\\ \dfrac{N-x}{1-\theta} &= \dfrac{x}{\theta} \tag{37}\\\\ \dfrac{N-x}{x} &= \dfrac{1-\theta}{\theta} \tag{38}\\\\ \dfrac{N}{x}-1 &= \dfrac{1}{\theta}-1 \tag{39} \\\\ \hat \theta &= \dfrac{x}{N} \tag{40} \end{align}\]在这种情况下,最大似然估计等于 $\frac{x}{N}$,即出现的正面朝上的次数与总的试验次数的比值。这种直观的求解方法也称为 相对频率估计,因为它等于结果的相对频率。
最大似然估计总是正确的选择吗?假设你进行了一次试验,并且得到了正面朝上的结果。你能够得出 $\theta= 1$ 的结论,即可以保证在抛该硬币时一定能得到正面朝上的结果吗?如果不是,那么你必须有某种关于 $\theta$ 的 先验期望。为了囊括这一先验信息,我们可以将 $\theta$ 视为一个随机变量,并使用贝叶斯规则:
\[\begin{align} \text p(\theta \mid x;N) &= \dfrac{\text p(x\mid \theta)\times \text p(\theta)}{\text p(x)} \tag{41}\\ &\propto \text p(x\mid \theta)\times \text p(\theta) \tag{42} \end{align}\] \[\hat \theta = \mathop{\operatorname{arg\,max}} \limits_{\theta} \text p(x\mid \theta)\times \text p(\theta) \tag{43}\]这是 最大后验估计(MAP)。给定 $\text p(\theta)$ 的形式,你可以使用与最大似然估计相同的推导方法推导出 MAP 估计。
下节内容:数值优化基础
本作品采用知识共享署名-非商业性使用-相同方式共享 4.0 国际许可协议进行许可。 欢迎转载,并请注明来自:YEY 的博客 同时保持文章内容的完整和以上声明信息!