Lecture 02 导论 (2)

4. 拟合一个关于 gavote 的线性模型

4.1 最小二乘估计

一个线性模型 $\mathbf y=X\boldsymbol \beta+\boldsymbol \varepsilon$ 可以利用 最小二乘法（Least Squares method，LS） 来拟合数据。据此得到的参数 $\boldsymbol \beta$ 的 最小二乘估计量（LS estimator） 为：

最小二乘法通过最小化残差和来对模型参数 $\boldsymbol \beta$ 进行估计，从而拟合数据：

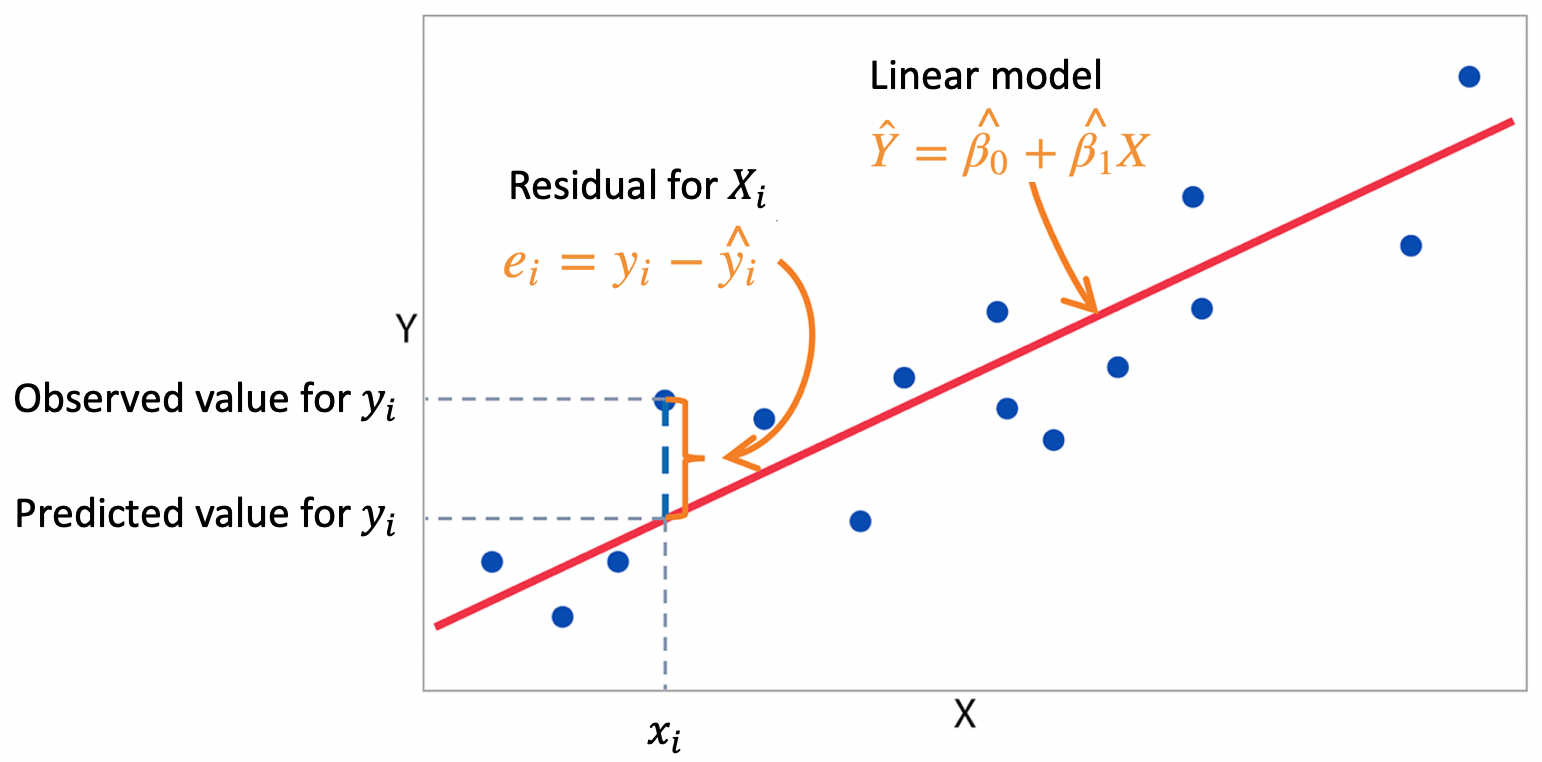
在 $\hat {\boldsymbol \beta}$ 的最小二乘估计量中，$X^{\mathrm{T}}X$ 的结果是一个 $p\times p$ 的矩阵，在大多数情况下（即当 $X$ 为一个满秩矩阵时），该矩阵是可逆的；而当 $X$ 为一个降秩矩阵时，$X^{\mathrm{T}}X$ 不可逆。

假设我们在建模时将 undercount 作为响应变量（response variable），将支持 Gore 的选民占比 pergore 和非裔美国人占比 perAA 作为预测变量（predictor variables），则对应的回归方程为：

R 代码：

1
lmod <- lm(undercount ~ pergore + perAA, gavote); coef(lmod)

输出结果：

1
2
(Intercept)     pergore       perAA
 0.03237600  0.01097872  0.02853314

所以，在上面的例子中，三个参数的最小二乘估计分别为：

然而，最小二乘法说到底只是一种计算数学方法，它还不足以好到对所估计的参数给出评判。所以人们可能会问：为什么要采用最小二乘法进行参数估计呢？通过它所得到的参数估计的优度如何？要回答这个问题需要一些统计学方法作为支持。

高斯-马尔可夫定理（Gauss–Markov theorem） 表明一个线性回归模型的参数的最小二乘估计量 $\hat{\boldsymbol \beta}$ 是一个 最佳线性无偏估计量（best linear unbiased estimator, BLUE）。

首先，最小二乘估计量是 无偏的（unbiased），即它的期望等于真实参数的期望。其次，它是 最佳的（best），即它的方差在所有的无偏估计量中是最小的。最后，它是 线性的（linear）。因此，高斯-马尔可夫定理为评价线性模型下的最小二乘估计的优度提供了理论支撑。注意，这里我们强调了是线性模型，对于后面即将扩展到的非线性模型而言，高斯-马尔可夫定理将不再适用。

4.2 最大似然估计

对于非线性的情况，我们需要另外的理论来评价参数估计的优度。因此，我们将采用一种不同的方法，即纯粹的概率统计方法：最大似然估计。在线性模型中，响应变量 $Y$ 被假设为服从独立的正态分布，所以我们可以写出观测值 $\boldsymbol y$ 的联合概率密度函数，然后我们可以得到该线性模型的一个对数似然函数。这种情况下，参数的估计量应为能够使对数似然函数最大化的值。

如果 $\varepsilon$ 被假设为正态，那么可以证明 $\boldsymbol \beta$ 的 最大似然估计量（maximum likelihood estimator, MLE） 等于其最小二乘估计量，即 $\hat{\boldsymbol \beta}=(X^{\mathrm{T}}X)^{-1}X^{\mathrm{T}}\mathbf y$。

在线性模型下，我们得到的最大似然估计的结果将和最小二乘估计给出的结果一致。但是，最大似然估计的方法要更好一些，因为它建立在 $Y$ 的概率分布上；而最小二乘估计并不涉及任何关于 $Y$ 的分布，它只是一种纯粹从几何角度出发寻找能够穿过尽可能多的数据点的直线，所以它只能从几何上给出解释。而当 $Y$ 服从其他分布的时候，显然，这种数据点的几何关系会发生变化，所以最小二乘估计不适用于当 $Y$ 服从非正态分布的情况。而最大似然估计在这种情况下仍然适用，因为它只依赖对数似然函数，只要我们能写出模型的对数似然函数，我们就可以利用最大似然估计方法得到参数的 MLE 估计量。

4.3 相关概念

模型的预测值或者 拟合值（fitted values） 为 $\hat{\mathbf y}=X\hat{\boldsymbol \beta}$

R 代码：

1
predict(lmod)

输出结果：

1
2
      APPLING      ATKINSON         BACON         BAKER       BALDWIN         BANKS  ...
   0.04133661    0.04329088    0.03961823    0.05241202    0.04795484    0.03601558  ...

模型的 残差（residuals） 为 $\hat{\boldsymbol \varepsilon}=\mathbf y-X\hat{\boldsymbol \beta}=\mathbf y-\hat{\mathbf y}$

R 代码：

1
residuals(lmod)

输出结果：

1
2
      APPLING      ATKINSON         BACON         BAKER       BALDWIN         BANKS  ...
 3.694660e-02 -6.994927e-03  6.555058e-02  2.348407e-03  3.589940e-03  1.426726e-02  ...

模型的 残差平方和（residual sum of squares, RSS），这里也可以称为为 偏差（deviance），为 $\mathsf{RSS}=\hat{\boldsymbol \varepsilon}^{\mathrm{T}}\hat{\boldsymbol \varepsilon}$，它衡量了模型对数据的拟合程度（注意：在线性模型中，残差平方和与偏差是相等的，但是在更一般的模型中，这两者是不相等的）。

R 代码：

1
deviance(lmod)

输出结果：

1
[1] 0.09324918

假如一共有 $n$ 个数据点，那么一共将会有 $n$ 个残差。所有的 $n$ 个 $y_i$ 之间是相互独立，对应的 $n$ 个随机误差项 $\varepsilon_i$ 之间也是相互独立的，但是残差 $\hat \varepsilon_i$ 之间则不需要满足相互独立。因为在残差的计算公式中，我们用到了所有的观测到的 $\mathbf y$，所以这 $n$ 个残差之间不再相互独立，它们可能彼此之间存在一些依赖关系。而为了衡量这种依赖的程度，或者说为了扩展这种残差之间的依赖，我们将引入自由度的概念。

残差的 自由度（degrees of freedom, df） 为 $n-p$。

自由度的计算公式第一眼看上去可能不太容易理解为什么要这样计算。我们可以这样理解：
假设一共有 $n$ 个独立的观测，由于彼此互相独立，它们之间可以随意变化，所以 $y_1,\dots,y_n$ 的自由度为：

现在假设 $y_i$ 对应的均值为 $\mu_i$，那么，同样地，$y_1-\mu_1,\dots,y_n-\mu_n$ 的自由度为：

接下来，我们用 $y_i$ 的样本均值（即均值的估计值） $\overline y$ 替换其均值 $\mu_i$，这样得到 $n$ 个残差 $y_1-\overline y,\dots,y_n-\overline y$ 的自由度为：

因为存在一个约束条件要求这 $n$ 个残差之和为零：$\sum_{i=1}^{n}(y_i-\overline y)=0$

现在，假设在线性回归模型下，我们用 MLE 替代均值 $\mu_i$，然后我们来看 $n$ 个残差 $y_1-\hat y_1,\dots,y_n-\hat y_n$ 的自由度。由上面的推导可知，该自由度实际上取决于这 $n$ 个残差所包含的线性约束条件的数量。回忆一下之前关于最小二乘估计量的内容：

其中，$\hat{\boldsymbol \beta}$ 是一个 $p\times 1$ 的向量，而这个向量中的每一行（即每一个元素）都是 $\mathbf y$ 的一个线性组合，这也意味着存在 $p$ 个线性约束方程。可见，约束条件的数量就等于参数的数量。因此，上面提到的 $n$ 个残差 $y_1-\hat y_1,\dots,y_n-\hat y_n$ 的自由度为：

R 代码：

1
df.residual(lmod)

输出结果：

1
[1] 156

R 代码：

1
nrow(gavote)-length(coef(lmod))

输出结果：

1
[1] 156

令 $\sigma^2=\mathrm{Var}(\boldsymbol \varepsilon)$。我们通过 残差标准误（residual standard error） 来估计 $\sigma$：

注意：当 $p=1$ 时，模型中仅包含一个参数，即截距项 $\beta_0$，此时：

我们称之为 样本标准差（sample standard deviation）。

可以看到，线性回归模型是对 描述性分析（descriptive analysis） 的扩展。在描述性分析中，我们用样本均值来估计总体均值；而在线性模型中，我们用拟合值来估计总体均值，这也将导致自由度的变化。类似地，对于标准差的估计将由样本标准差扩展到残差标准误。

R 代码：

1
sqrt(deviance(lmod)/df.residual(lmod))

输出结果：

1
[1] 0.02444895

R 代码：

1
lmodsum <- summary(lmod); lmodsum$sigma

输出结果：

1
[1] 0.02444895

偏差（deviance） 衡量的是模型在绝对意义上的拟合程度，而不是相对意义上的。一般而言，使用相对差异会更好一些，因为相对差异是无量纲的（dimensionless），我们不需要考虑量纲的影响。模型的相对拟合优度（relative goodness-of-fit）由 决定系数（coefficient of determination），也称解释方差百分比（percentage of variance explained），$R^2$ 衡量：

其中， RSS 是模型残差平方和（residual sum of squares）；而 TSS 是完全平方和（total sum of squares），它等于观测值 $\mathbf y$ 和样本均值之差的平方和。我们可以将 RSS 视为残差的完全方差，将 TSS 其视为观测值 $\mathbf y$ 的完全方差。所以，二者之比 $\frac{\mathsf{RSS}}{\mathsf{TSS}}$ 代表了观测值 $\mathbf y$ 的完全方差中由残差解释的部分所占的比重。而 $(1-\frac{\mathsf{RSS}}{\mathsf{TSS}})$ 则代表了观测值 $\mathbf y$ 的完全方差中可以由模型解释的部分所占的比重，我们将其称为决定系数（coefficient of determination），记为$R^2$，和偏差（deviance）相比，它是一个相对度量。

$R^2$ 也等于 $\hat {\mathbf y}$ 和 $\mathbf y$ 之间相关系数的平方。

关于这点可以通过线性代数相关知识进行证明，不过，更重要的是如何从统计学的直觉上来理解它。我们用 $\hat {\mathbf y}$ 来估计 $\mathbf y$，所以二者必须是相关的，因为如果我们用一些和 $\mathbf y$ 毫不相关的东西来预测它从道理上讲不通，所以一般我们会选择和 $\mathbf y$ 最相关的一些东西来预测它。因为拟合值 $\hat {\mathbf y}$ 是从模型中得出的，而决定系数 $R^2$ 衡量了该模型的拟合优度，所以 $\hat {\mathbf y}$ 和 $\mathbf y$ 之间的实际相关系数应当与 $R^2$ 存在某种关联。

R 代码：

1
summary(lmod)$r.squared

输出结果：

1
[1] 0.05308861

R 代码：

1
cor(predict(lmod),gavote$undercount)^2

输出结果：

1
[1] 0.05308861

虽然决定系数 $R^2$ 是一个相对度量，但是仍然存在一些局限。可以看到，我们现在拟合的模型有 3 个参数（$\beta_0,\beta_1,\beta_2$）和 2 个预测变量（支持 Gore 的选民占比 pergore 和非裔美国人占比 perAA ）。假如我们在模型中加入更多的预测变量 $X$，模型的 RSS 也将变得更小，这样就可以使决定系数 $R^2$ 越来越大。但是由于存在过拟合的风险，引入过多的预测变量 $X$ 并不是一个好的选择，因为这将导致模型预测能力的下降。可见，决定系数 $R^2$ 并不能帮我们修正模型的预测能力，我们需要对 $R^2$ 进行修正。

为此，我们引入 修正决定系数（adjusted coefficient of determination），记为 $R_a^2$。它并不用于模型拟合优度的衡量，而是作为模型（预测变量）选择的标准之一。可以看到，它是通过在 $R^2$ 的基础上对分子分母项分别除以各自的自由度得到：

R 代码：

1
summary(lmod)$adj.r.squared

输出结果：

1
[1] 0.04094872

关于 $R_a^2$ 的修正作用可以这样理解：

• 对于决定系数 $R^2$：随着参数数量 $p$ 的增加，$R^2$ 将单调递增，导致的结果就是模型容易引入过多的参数而产生过拟合。
• 而对于修正决定系数 $R_a^2$：初始时，$p$ 很小，此时 $R_a^2$ 将随着 $p$ 的继续增加而增大；而当 $p$ 变得很大时，$R_a^2$ 将随着 $p$ 的继续增加而减小。这样，我们就能够为模型选择合适的参数数量 $p$。

4.4 查看模型拟合结果

更多关于模型拟合的结果可以通过 faraway package 中的 summary(lmod) 或者 sumary(lmod) 查看：

R 代码：

1
2
lmodsum <- summary(lmod);
attributes(lmodsum)

输出结果：

1
2
3
4
5
6
7
$names
 [1] "call"          "terms"         "residuals"     "coefficients"  "aliased"      
 [6] "sigma"         "df"            "r.squared"     "adj.r.squared" "fstatistic"   
[11] "cov.unscaled" 

$class
[1] "summary.lm"

R 代码：

1
summary(lmod)

输出结果：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
Call:
lm(formula = undercount ~ pergore + perAA, data = gavote)

Residuals:
      Min        1Q    Median        3Q       Max 
-0.046013 -0.014995 -0.003539  0.011784  0.142436 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)  
(Intercept)  0.03238    0.01276   2.537   0.0122 *
pergore      0.01098    0.04692   0.234   0.8153  
perAA        0.02853    0.03074   0.928   0.3547  
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 0.02445 on 156 degrees of freedom
Multiple R-squared:  0.05309,	Adjusted R-squared:  0.04095 
F-statistic: 4.373 on 2 and 156 DF,  p-value: 0.01419

R 代码：

1
sumary(lmod)

输出结果：

1
2
3
4
5
6
            Estimate Std. Error t value Pr(>|t|)
(Intercept) 0.032376   0.012761  2.5370  0.01216
pergore     0.010979   0.046922  0.2340  0.81531
perAA       0.028533   0.030738  0.9283  0.35470

n = 159, p = 3, Residual SE = 0.02445, R-Squared = 0.05

可以看到，对于该模型的两个预测变量 pergore 和 perAA，它们的 p 值（0.8153 和 0.3547）都大于 0.05，所以这个结果并没有告诉我们太多信息。

5. 线性模型中的定性 / 分类预测变量

定性（qualitative，即 categorical 分类） 预测变量和 定量（quantitative，即 numerical 数值） 预测变量都可以用于线性模型。在 R 中，定性预测变量也被称为 因子（factors）。

这会带来一些实践上的问题，我们不能直接将一个定性预测变量应用于线性模型之中，如果我们这样做了，我们将只能看到该定性预测变量对于响应变量 $Y$ 的正面或负面的效应，因为定性变量之间的相关系数只有正负两种类型。但事实上，一个定性预测变量对于响应变量的效应不仅仅只是简单的正面或者负面，它可能刚开始是正面的，然后变为负面的，之后再变为正面的等等。因此，我们不能直接将一个定性预测变量引入我们的线性模型之中。

当我们向一个线性模型中引进一个定性预测变量时，它将会被编码为一个数值变量（numerical variables）的集合，称为 contrasts（对照）。

关于如何编码一个定性变量，存在很多种可能的 contrasts，R 使用了其中的 5 种：

R 代码：

1
2
3
4
5
6
7
contr.helmert(n, contrasts = TRUE, sparse = FALSE)
contr.poly(n, scores = 1:n, contrasts = TRUE, sparse = FALSE)
contr.sum(n, contrasts = TRUE, sparse = FALSE)
contr.treatment(n, base = 1, contrasts = TRUE, sparse = FALSE)
contr.SAS(n, contrasts = TRUE, sparse = FALSE)

options()$contrasts

输出结果：

1
2
        unordered           ordered
"contr.treatment"      "contr.poly"

在 R 中，名义因子（nominal factor，也叫 unordered factor 无序因子） 的默认编码方式为 contr.treatment，而 有序因子（ordinal factor 或者 ordered factor） 的默认编码方式为 contr.poly。

contr.treatment 将一个 factor 编码为 虚拟变量（dummy variables，也称 “哑变量”），在实践中，这种方式的解释性最强。

对于一个具有 $k$ 个等级（levels）的因子 $d$，R 会默认将 因子 $d$ 中（按照字母顺序排序）的第 1 个 level 作为 base level，而将其余的 $k-1$ 个 level 用 contr.treatment 编码为 $k-1$ 个虚拟变量 $d_2,\dots,d_k$，其中

这种编码方式会给模型解释带来很多便利。

之前的线性模型中已经包含了 pergore 和 perAA 两个数值预测变量。假设现在我们希望再引入一个包含 3 个 levels 的预测因子 d。我们可以通过下面的 R 代码拟合一个包含 pergore、perAA 和 d 的线性模型，其中 perAA:d 是一个 交互项（interaction term）：

R 代码：

1
2
d <- factor(sample(c("1","2","3"), size=dim(gavote)[1], replace=TRUE))
head(d)

输出结果：

1
2
[1] 2 2 3 1 3 1
Levels: 1 2 3

R 代码：

1
2
lmodI <- lm(undercount ~ pergore + perAA + d + perAA:d, gavote)
lmodI

输出结果：

1
2
3
4
5
6
Call:
lm(formula = undercount ~ pergore + perAA + d + perAA:d, data = gavote)

Coefficients:
(Intercept)     pergore       perAA           d2          d3    perAA:d2    perAA:d3
  0.0314180   0.0155487   0.0113981   -0.0025059   0.0003797   0.0067606   0.0425796

该模型对应的回归方程为：

因为 d 包含 3 个 levels，所以我们需要 2 个虚拟变量（即下面的 d2 和 d3）来编码它。同样，交互项 perAA:d 也被编码为 perAA:d2 和 perAA:d3。

6. 解释线性模型

6.1 模型拟合

让我们拟合一个线性模型，看一下可以如何解释其中的各项。

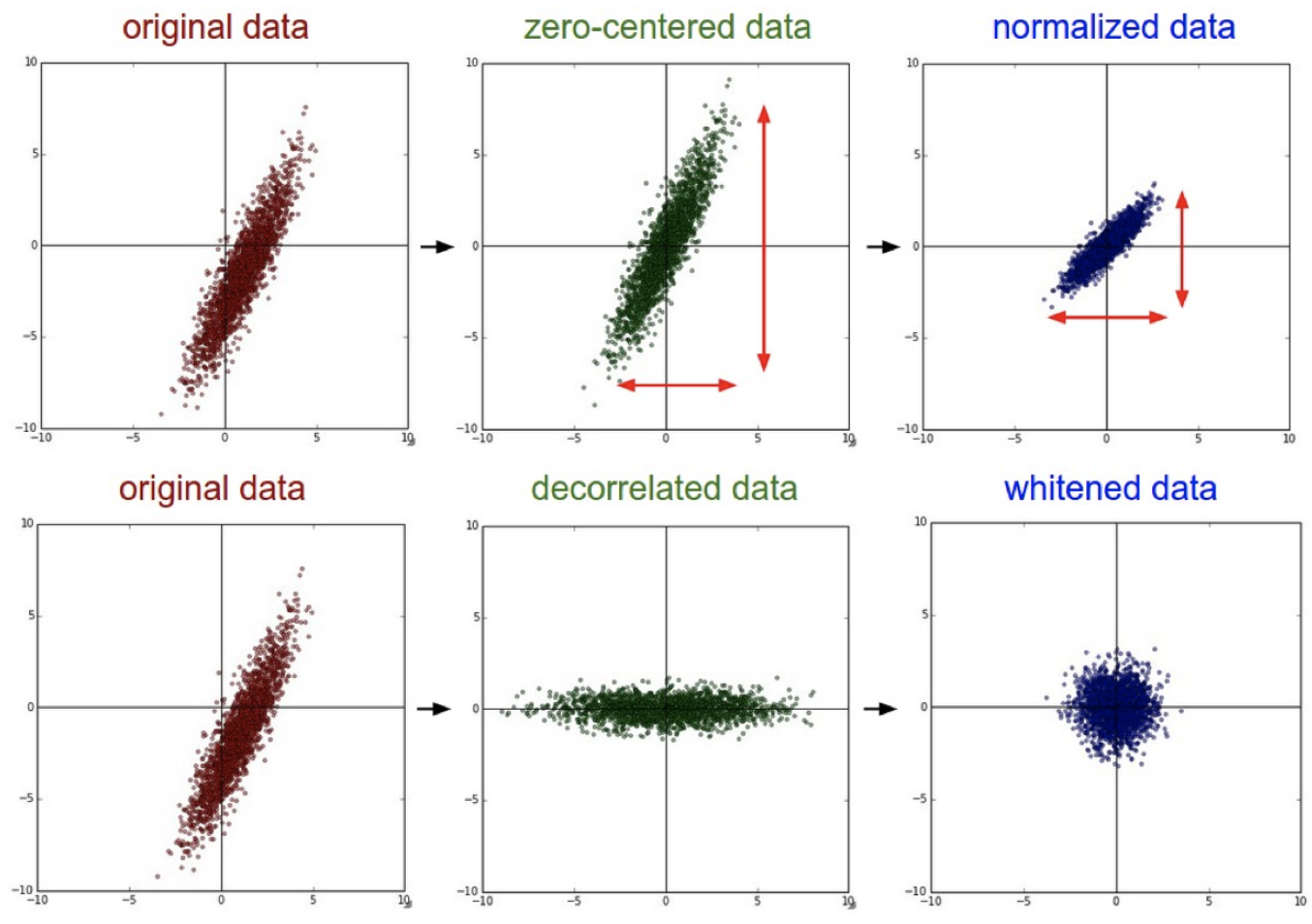
为了便于解释，我们利用 mean() 函数对 pergore 和 perAA 进行了 中心化（centered，也叫 “零均值化”） 处理，得到了两个新的变量 cpergore 和 cperAA。而 usage（即原始数据中的 rural）和 equip 都是因子。在建模时，我们还引入了一些交互项：cpergore*usage 等价于 cpergore + usage + cpergore:usage。

R 代码：

1
2
3
4
gavote$cpergore <- gavote$pergore - mean(gavote$pergore)
gavote$cperAA <- gavote$perAA - mean(gavote$perAA)
lmodi <- lm(undercount ~ cperAA+cpergore*usage+equip, gavote)
sumary(lmodi)

输出结果：

1
2
3
4
5
6
7
8
9
10
11
12
                      Estimate Std. Error t value  Pr(>|t|)
(Intercept)          0.0432973  0.0028386 15.2529 < 2.2e-16
cperAA               0.0282641  0.0310921  0.9090  0.364786
cpergore             0.0082368  0.0511562  0.1610  0.872299
usageurban          -0.0186366  0.0046482 -4.0095 9.564e-05
equipOS-CC           0.0064825  0.0046799  1.3852  0.168060
equipOS-PC           0.0156396  0.0058274  2.6838  0.008097
equipPAPER          -0.0090920  0.0169263 -0.5372  0.591957
equipPUNCH           0.0141496  0.0067827  2.0861  0.038658
cpergore:usageurban -0.0087995  0.0387162 -0.2273  0.820515

n = 159, p = 9, Residual SE = 0.02335, R-Squared = 0.17

我们来看一下模型 lmodi 的参数数量 $p$ 应该是多少：

• 首先，截距项 Intercept 包含 1 个参数；
• 然后，数值变量 cperAA 和 cpergore 各包含 1 个参数；
• 接下来，因子 usage 包含 2 个 levels（rural 和 urban），所以这里将 rural 作为 base level，再用 1 个虚拟变量 usageurban 来编码 usage，因此也包含 1 个参数；
• 同理，因子 equip 包含 5 个 levels，将第 1 个作为 base level，然后用 4 个虚拟变量（equipOS-CC, equipOS-PC, equipPAPER 和 equipPUNCH ），所以包含 4 个参数；
• 最后，对于截距项 cpergore:usage，由于 usage 已经用虚拟变量 usageurban 编码过了，所以它也被编码为 cpergore:usageurban，所以也包含 1 个参数。

所以，该模型的参数数量为：$p=1+1+1+1+4+1=9$

模型 lmodi 的数学形式为：

其中，如果 usage $=$ urban，那么虚拟变量 usaageurban $=1$；如果 usage $\ne$ urban，那么 usaageurban $=0$。其他的虚拟变量如 equipOS-CC 等皆同理。

模型 lmodi 的估计（estimate）为：

参数 $\boldsymbol \beta$ 的估计（estimates）的标准误（standard errors）可以通过 sumary(lmodi) 查看。

如果建模时还引入了交互项 cpergore:equip，那么模型还会增加 4 个额外的交互项：cpergore:equipOS-CC $,…,$ cpergore:equipPUNCH。

6.2 模型解释

考虑一个 usage 的 level 为 rural 的郡，该郡支持 Gore 的选民占比 pergore 和非裔美国人占比 perAA 在所有的郡中处于平均水平，另外，该郡采用的投票机器 equip 型号为 LEVER。

R 代码：

1
sumary(lmodi)

输出结果：

1
2
3
4
5
6
7
8
9
10
11
12
                      Estimate Std. Error t value  Pr(>|t|)
(Intercept)          0.0432973  0.0028386 15.2529 < 2.2e-16
cperAA               0.0282641  0.0310921  0.9090  0.364786
cpergore             0.0082368  0.0511562  0.1610  0.872299
usageurban          -0.0186366  0.0046482 -4.0095 9.564e-05
equipOS-CC           0.0064825  0.0046799  1.3852  0.168060
equipOS-PC           0.0156396  0.0058274  2.6838  0.008097
equipPAPER          -0.0090920  0.0169263 -0.5372  0.591957
equipPUNCH           0.0141496  0.0067827  2.0861  0.038658
cpergore:usageurban -0.0087995  0.0387162 -0.2273  0.820515

n = 159, p = 9, Residual SE = 0.02335, R-Squared = 0.17

由于 rural 和 LEVER 是作为 usage 和 equip 这两个分类变量的 reference levels（即 base levels），因此，它们对于 undercount 的预测值并没有什么贡献。另外，由于我们已经对数值变量 pergore 和 perAA 在各自的均值上进行了中心化处理，所以这两个变量也不会被引入模型之中。注意，中心化的意义在于：如果没有经过中心化处理，那么我们需要将这些变量设置为 $0$，使其脱离预测方程; 而 $0$ 并不是这些预测变量的典型值。假设所有其他项均被删除，则 undercount 的预测值仅由截距项（intercept）$\hat \beta_0$ 给出，即 $4.33\%$。

现在可以相对于该基准来对系数进行解释。我们看到，在所有其他预测变量都不变的情况下，除了使用具有区域计数的光学扫描设备（OS-PC）之外，预测的 undercount 增加了 $1.56\%$。其他的 equip 型号也可以采用类似的解释。请注意，我们需要对这种解释保持谨慎。给定两个郡，它们除了投票设备 equip 不同之外，其他的预测变量的取值都一样，我们 预测 采用OS-PC 的郡的 undercount 将比采用 LEVER 的郡的 undercount 的值高出 $1.56\%$。但是，我们不能这么说：如果我们去了一个采用 LEVER 的郡，并将其更改为 OS-PC，就将使 undercount 增加 $1.56\%$。

在所有其他预测变量保持不变的情况下，我们可以预测某个郡从没有非洲裔美国人的情况转变到全部为非洲裔美国人的情况时，undercount 将增长 $2.83\%$。有时一个单位的预测变量的变化可能太大或太小，我们可以对解释进行重新调整。例如，对于非裔美国人比例增长了 $10\%$ 的情况，我们可以预测 undercount 将增加 $0.283\%$。当然，这种解释不应该太当真。请注意，我们已经知道非裔美国人占比 perAA 和支持 Gore 的选民占比 pergore 之间强相关，因此，其中某一方占比上升将导致另一方占比也随之上升。这种被称为 共线性（collinearity） 的问题将使得对回归系数的解释更加困难。并且，非裔美国人的比例 perAA 很可能与其他社会经济变量有关，而这些变量也可能与 undercount 有关。这进一步阻碍了得出一个 因果结论（causal conclusion） 的可能性。

对于 usage 和 pergore 这两个变量的解释不能被割裂开来，因为在模型 lmodi 中存在一个这两者的交互项。我们可以看到，对于一个支持 Gore 选民占比的平均数字，我们预测一个 urban 的郡的 undercount 会比一个 rural 的郡要低 $1.86\%$。在一个 rural 的郡，我们预测随着 Gore 支持者占比 pergore 上升 $10\%$，undercount 将上升 $0.08\%$。而在一个 urban 的郡，我们预测随着 pergore 上升 $10\%$，undercount 将上升 $(0.00824-0.00880)\times 10=-0.0056\%$，而一个负增长实际上就意味着下降。这说明当某个变量存在一个与之相关的交互项时，我们在对该变量的效应进行预测时必须小心一些 潜在的陷阱。我们不能对 Gore 支持者占比 pergore 对于响应变量 undercount 的效应直接给出一个简单独立的解释。事实上，pergore 这个变量的效应体现在：对于 rural 的郡，undercount 会随着该变量的上升而上升；而对于 urban 的郡，undercount 则会随着该变量的上升而下降。

下节内容：导论 (3)

本作品采用知识共享署名-非商业性使用-相同方式共享 4.0 国际许可协议进行许可。 欢迎转载，并请注明来自：YEY 的博客 同时保持文章内容的完整和以上声明信息！

• Previous
  数据科学统计建模 01：导论 (1)
• Next
  自然语言处理 Workshop 01：利用 NLTK 进行预处理