Lecture 08 蒙特卡洛树搜索：利用和探索的权衡

这节课我们将学习 蒙特卡洛树搜索（Monte Carlo Tree Search, MCTS）。蒙特卡洛树搜索是一种用于解决强化学习问题的新方法。

MCTS 通常用于 在线决策（online decision） 或者 在线学习（online learning）。

与之相对的被称为 离线学习（offline learning），在离线学习中，我们提前完成所有的规划，当执行行动的时候，我们执行之前规划的所有行动，例如：在经典规划中，我们先规划好了一个行动序列，然后依次执行它们，我们也可能从中提取策略，并按照策略行动。

相反，在在线学习中，行动和选择是交错进行的，例如：在 MCTS 中，我们在每一次规划都会用来选择下一个行动，然后在执行该行动后，我们将重新进行下一轮的规划。

在实际解决规划问题时，我们可以自行选择采用在线学习或者离线学习的方式，有些技术基于在线学习，有些基于离线学习。例如：价值评估将提供一个完全收敛的策略，它更适用于离线规划；MCTS 则更倾向于在线规划；而经典规划中的启发式搜索既可用于在线学习，也可用于离线学习。在这里，我们将看到很多经典规划应用于我们的问题，我们可以选择忽略转移概率，直接选择行动直到目标状态；或者考虑转移概率，中途可能到达某个状态，然后将该状态作为初始状态重新规划。

本节课主要内容如下：

问题
蒙特卡洛树搜索 —— 基础
多臂老虎机
蒙特卡洛树搜索和多臂老虎机
总结

学习成果：

解释 MDP 的离线规划与在线规划之间的区别。
应用 MCTS 手动解决小规模 MDP 问题，并编写 MCTS 算法的代码来自动解决中等规模的 MDP 问题。
根据 MCTS 算法生成的 $Q$-函数来构造策略。
选择并应用多臂老虎机算法。
将多臂老虎机算法（包括 UCB）集成到 MCTS 算法。
将 MCTS 与价值/策略迭代进行比较和对比。
讨论 MCTS 系列算法的优缺点。

相关阅读：

Chapters 2 and 5 of Reinforcement Learning: An Introduction, second edition. Freely downloadable at: http://www.incompleteideas.net/book/RLbook2020.pdf
A Survey of Monte Carlo Tree Search Methods by Browne et al. IEEE Transactions on Computational Intelligence and AI in Games, 2012.
$\to$ 很好的入门资源，里面涵盖了大量的开创性的论文。
Regret Analysis of Stochastic and Nonstochastic Multi-armed Bandit Problems by S. Bubeck and N. Cesa–Bianchi, 2012. Freely downloadable at: https://arxiv.org/pdf/1204.5721v2.pdf
$\to$ 几乎涵盖了所有你想知道的关于后悔分析和多臂老虎机的相关研究。

1. 问题

1.1 MDP 上的离线规划与在线规划

在上一讲中，我们学习了价值迭代和策略迭代。它们都属于 离线规划 方法，我们对所有可能的状态进行离线求解问题，然后在线使用解决方案（策略）。这些离线规划策略 $\pi$ 使得：

我们可以方便地定义适用于任何状态的策略，
尽管通常会由于状态空间 $S$ 太大而无法精确地确定 $V(s)$ 或 $\pi$。
有一些方法可以通过降低 $S$ 的维度来近似 MDP，但是我们将暂时不对此进行讨论。

在 在线规划 中，规划是在执行行动之前立即进行的。一旦执行了一个行动（或者可能是一个行动序列），我们便从当前状态开始规划。因此，规划和执行是交错进行的。

对于访问过的每个状态 $s$，将评估许多策略 $\pi$（部分地）。
每个 $\pi$ 的质量将通过重复模拟 $r(s,a,s’)$ 获得的 $S$ 上的轨迹的期望回报来近似估计。
选择策略 $\hat \pi$，并执行行动 $\hat \pi(s)$。

问题是：我们如何进行重复模拟？蒙特卡洛方法是迄今为止使用最广泛的方法。

2. 蒙特卡洛树搜索 —— 基础

2.1 蒙特卡洛

蒙特卡洛树搜索（MTCS）是一个算法集合的名称，其中的所有算法都基于同一思想。在这里，我们将重点介绍使用一种算法在线求解单个 agent 的 MDP 问题。

蒙特卡洛（Monte Carlo）是摩纳哥（法国里维埃拉的一个小公国）内的地区，以其 Extravagent 赌场而闻名。由于赌博和赌场在很大程度上与机率相关，因此在线求解 MDP 的方法通常被称为蒙特卡洛方法，因为它们使用 随机性（randomness）来搜索 行动空间（action space）。

2.2 基础：MDP 作为 ExpectiMax 树

为了理解 MCTS 的思想，我们注意到 MDP 可以被表示为树（或者图），称为 ExpectiMax 树：

字母 $a$ 到 $e$ 表示行动，字母 $s$ 到 $x$ 表示状态。白色结点是状态结点，较小的黑色结点表示概率的不确定性：“环境” 基于转移函数从发生的行动中选择哪种结果。

可以看到，在根结点 $s_0$ 处，我们有 2 种行动可以选择：$a$ 和 $b$。而当我们选择行动 $a$ 后，我们来到黑色结点，此时我们发现有 2 种可能的结果状态：$t$ 和 $t’$，其中，有 $P_a(t\mid s_0)$ 的概率到达状态 $t$，而有 $P_a(t’\mid s_0)$ 的概率到达状态 $t’$。

所以，我们可以用这样一种树形结构表示 MDP。ExpectiMax 背后的思想是，当我们试图在 MDP 中寻找最优行动时，我们可以从叶子结点一层一层向上回溯来查看期望回报，并选择最优行动，所以，ExpectiMax 的结构和期望回报之间存在非常好的对应关系。在 MCTS 中，我们将学习如何增量式地构建这些树，以及如何探索这些树以得到最优规划。

2.3 蒙特卡洛树搜索：概览

MCTS 算法是一种在线规划算法，这意味着行动选择与行动执行是交错进行的。因此，agent 在每次访问一个新状态时都会调用 MCTS。

基本特征：

每个状态的价值 $V(s)$ 通过 随机模拟（random simulation）来近似。
ExpectiMax 搜索树是增量式地构建的。
当一些预定义的计算预算用完时（例如：超出时间限制或扩展的结点数），搜索将终止。
因此，它是一种 任意时间 算法，因为它可以随时终止并且仍然给出一个答案。
算法将返回表现最好的行动。

$\to$ 如果没有陷入僵局，则该算法的完整性可以保证。

$\to$ 如果可以执行一个完整搜索（这种情况比较少见 —— 如果问题如此小的话，我们就应该仅仅使用价值/策略迭代来求解）。

2.4 蒙特卡洛树搜索：框架

使用模拟来构建一个 MDP 树。评估状态存储在一个搜索树中。评估状态集合是通过迭代以下四个步骤 增量式 地构建的：

选择：在树中选择一个 未完全扩展 的单结点。这意味着它至少有一个子结点尚未被探索。
扩展：通过从该节点应用一个可用的行动（由 MDP 定义）来扩展该结点。
模拟：从一个新结点中，对 MDP 进行一个完整的随机模拟，使其达到终止状态。因此，这种做法假设搜索树是有限的，但是也存在无限大的树的版本，我们可以只在其中执行一段时间，然后估计结果。
反向传播：最后，将结点的价值 反向传播 到根结点，使用期望价值更新途中经过的每个祖先结点的价值。

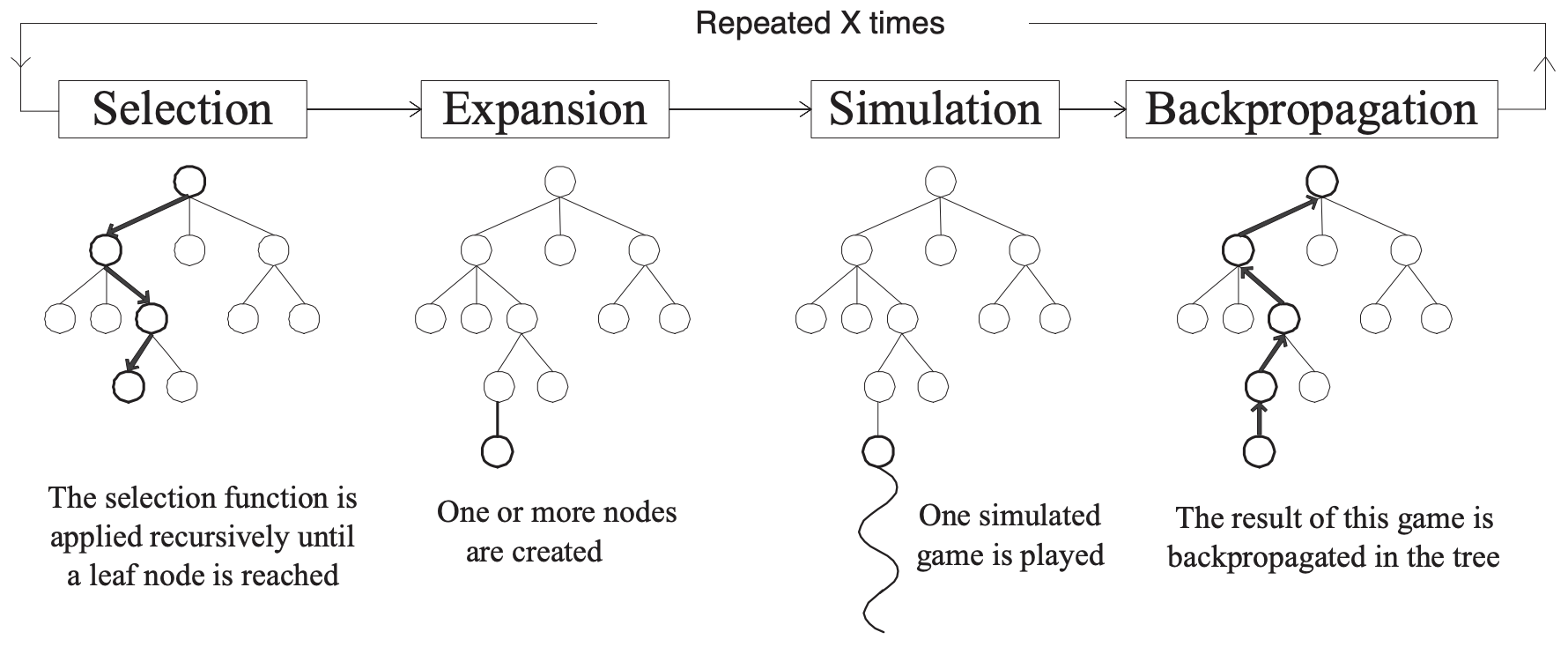
来源： Monte-Carlo Tree Search: A New Framework for Game AI. by Chaslot et al. In AIIDE. 2008. https://www.aaai.org/Papers/AIIDE/2008/AIIDE08-036.pdf

2.5 蒙特卡洛树搜索：流程

选择（Selection）

从根结点开始，然后依次选择一个子结点，直到我们到达一个未完全扩展的结点。

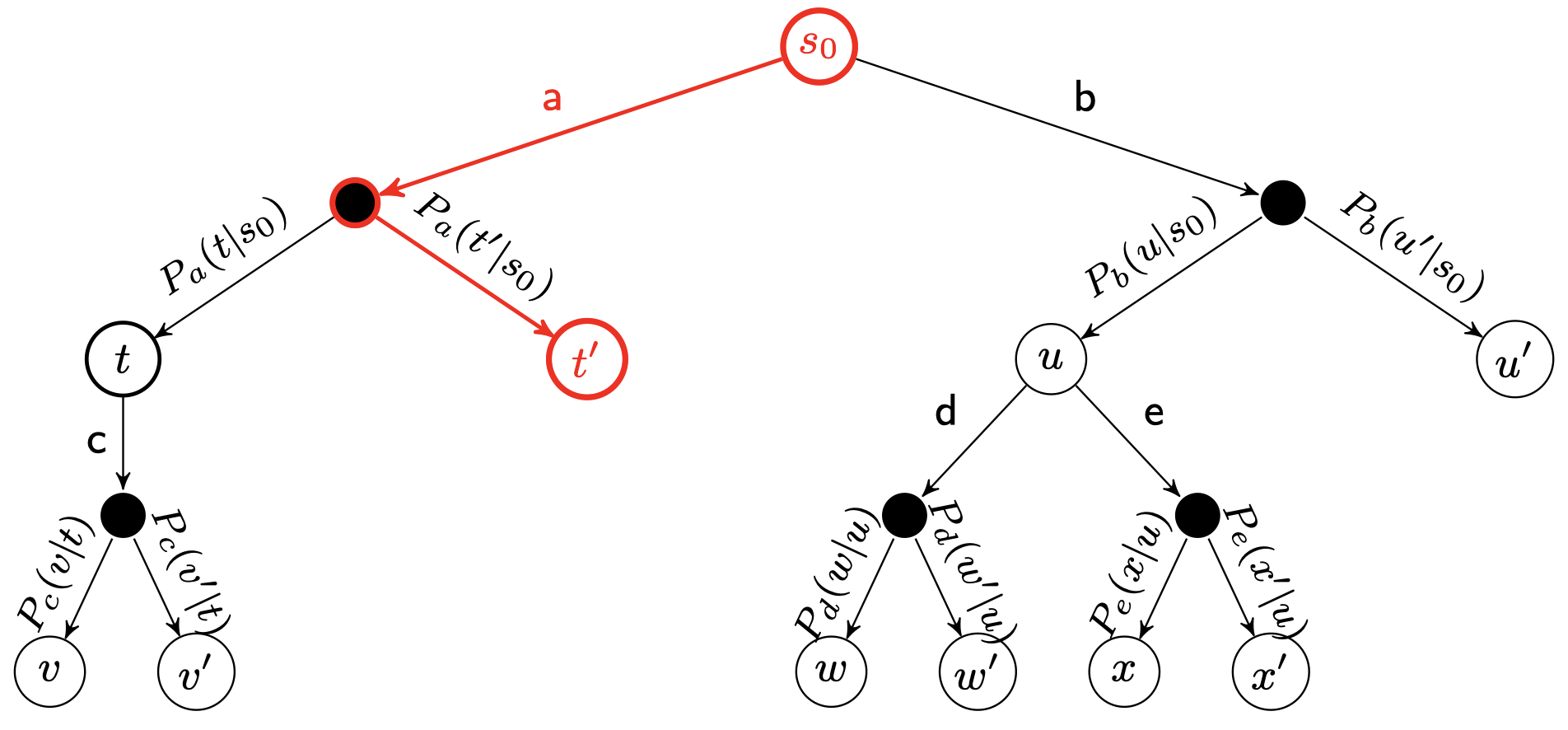
扩展（Expansion）

除非我们最终到达的结点是一个终止状态，否则我们将对选结点的子结点进行扩展，即通过选择一个行动并使用该行动的结果创建一些新的结点。

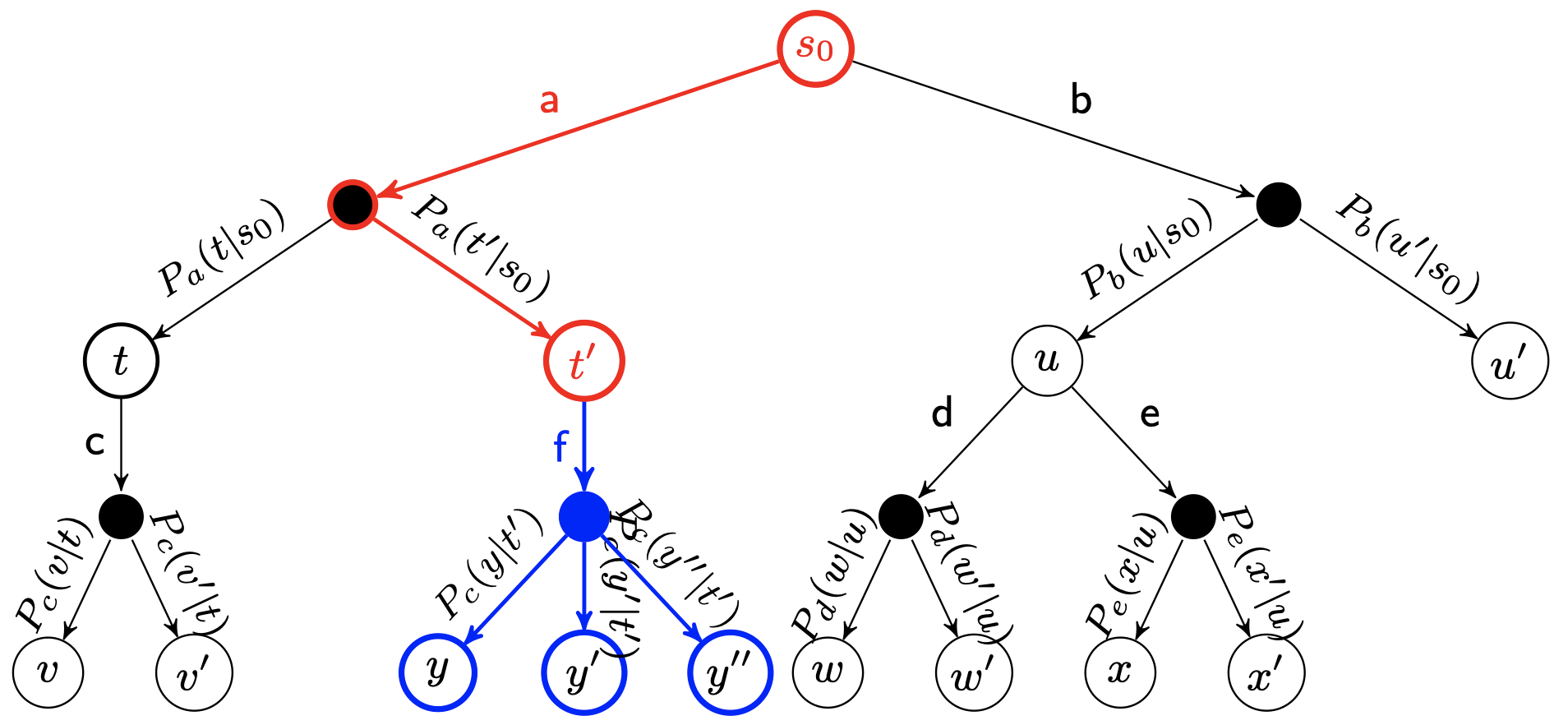
模拟（Simulation）

从这些新的结点中选择一个，并对 MDP 进行随机模拟，使其到达终止状态：

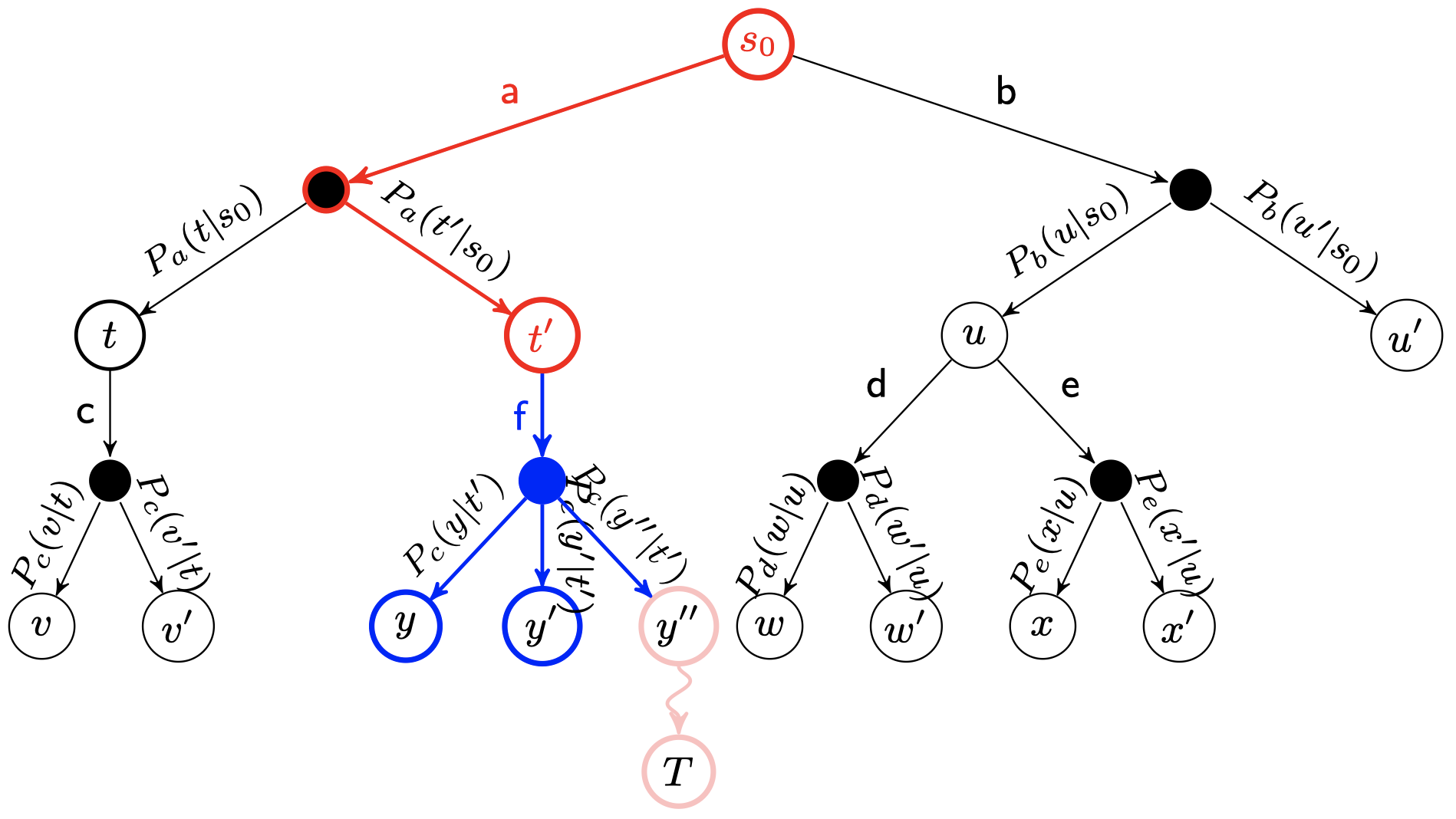
反向传播（Backpropagation）

给定处于终止状态时的回报 $r$，对其进行反向传播，以计算沿路径上的每个状态的价值 $V(s)$。

2.6 蒙特卡洛树搜索：算法

输入：

MDP $M$
初始状态 $s_0$
时间限制 $T$

每个结点存储：

该结点对应状态的 $V(s)$（该状态价值的一个估计）
该状态被访问的次数
一个指向其父结点的指针

$\text{S}\scriptsize \text{ELECT}\small(\textit{root})$
$\color{blue}{\to}$ 使用一些概率策略来递归选择下一个结点（我们将在稍后的 “多臂老虎机” 中看到更多相关内容），直到我们到达一个未完全扩展的结点为止。
$\color{blue}{\to}$ 在每个选择点，选择树中的一条边。
$\color{blue}{\to}$ 然后，使用 $P_a(s’\mid s)$ 选择该行动的结果。因此，我们的模拟遵循基础模型的概率转移。

$\text{E}\scriptsize \text{XPAND}\small(\textit{expand_node})$
$\color{blue}{\to}$ 根据已选择的结点，随机选择一个适用于该状态且之前在该状态下未被选择的行动。
$\color{blue}{\to}$ 扩展该行动的所有可能的结果结点。
$\color{blue}{\to}$ 检查生成的结点是否已在树中。如果不在，则将这些结点添加到树中。
注意：$P_a(s’\mid s)$ 是随机的，因此可能需要多次访问 (理论上需要无限次数) 才能生成所有后继结点。

$\text{S}\scriptsize \text{IMULATE}\small(\textit{child})$
$\color{blue}{\to}$ 对 MDP 执行随机模拟，直到达到终止状态。即，在每个选择点，从 MDP 中随机选择一个适用行动，并使用转移概率 $P_a(s’\mid s)$ 为每个行动选择一个结果。
$\color{blue}{\to}$ 我们也可以通过一些启发式方法来使用非随机模拟，但这里我们不会对此进行介绍。
$\color{blue}{\to}$ $\textit{reward}$ 是在这个完整模拟中获得的回报。
$\color{blue}{\to}$ 为了避免内存爆炸，我们丢弃了从该模拟中生成的所有结点。在任何非平凡搜索中，我们都不太可能会再次需要它们。

$\text{B}\scriptsize \text{ACKUP}\small(\textit{expand_node, reward})$
$\color{blue}{\to}$ 来自模拟的回报会从扩展的结点递归地反向传播到其祖先。
$\color{blue}{\to}$ 注意一定不要忘记 折扣因子。
$\color{blue}{\to}$ 对于每个状态 $s$，从该结点获取所有行动的期望价值：

\[V(s):=\max \limits_{a\in A(s)}\sum_{s'\in \textit{children}}P_a(s'\mid s)[r(s,a,s')+\gamma V(s')]\]

看上去熟悉吗？
这就是为什么该树被称为 ExpectiMax 树：我们将期望回报最大化，并且计算过程分两层进行。求和（$\sum_{s’\in S}\dots$）计算的是树中较小的黑色结点的价值；而最大化（$\max_{a\in A(s)}$）计算的是较大的白色结点（状态结点）的价值。

2.7 蒙特卡洛树搜索：执行

一旦我们用尽了计算时间，我们选择能够使期望回报最大化的行动，简单来说，就是我们的模拟中具有最高 $Q$-值 的行动：

\[\mathop{\operatorname{arg\,max}}\limits_{a} Q(s_0,a)\]

也就是：

\[\mathop{\operatorname{arg\,max}}\limits_{a} \sum_{s'\in A(s_0)}P_a(s'\mid s_0)[r(s_0,a,s')+\gamma V(s')]\]

我们执行该动作，然后等待观察该动作对应的哪种结果会发生。一旦我们观察到结果，我们将其称为 $s’$，我们将重新开始这整个过程，唯一变化是此时 $s_0:= s’$。

但是，很重要的一点是，我们可以保留来自状态 $s’$ 的子树，因为我们已经从该状态进行了模拟。我们丢弃树中的其余部分（除了所选择的行动之外的其他所有 $s_0$ 的子树），并从 $s’$ 开始增量式地构建 MCTS。

2.8 蒙特卡洛树搜索：例子

在模拟步骤之后

假设 $\gamma= 0.9$，$r=X$ 表示在某个状态下收到的回报 $X$，$N$ 是该状态被访问的次数，并且模拟的长度为 $13$。在模拟步骤之后，但在反向传播之前，我们的树看起来将会是这个样子：

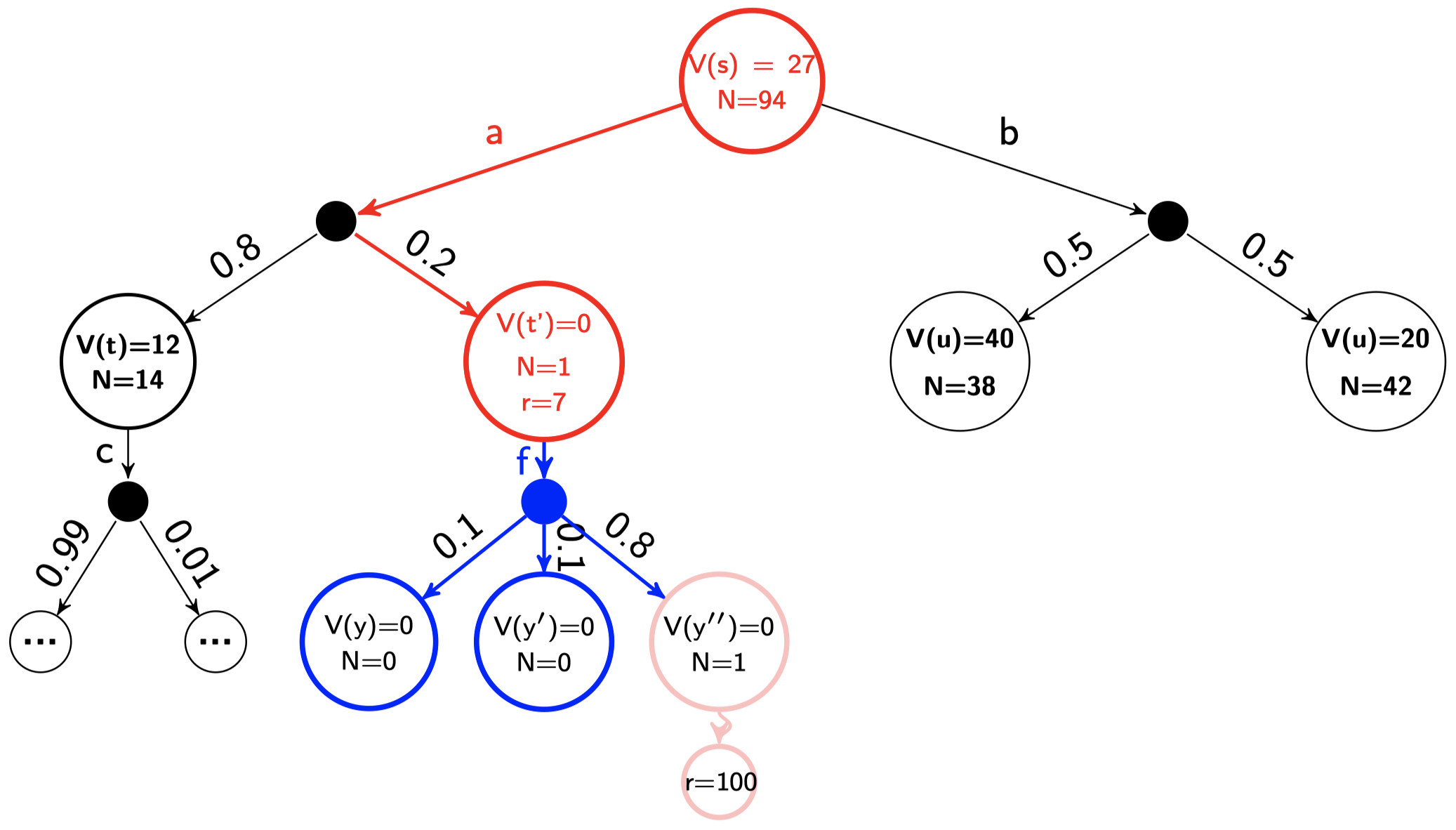
反向传播步骤

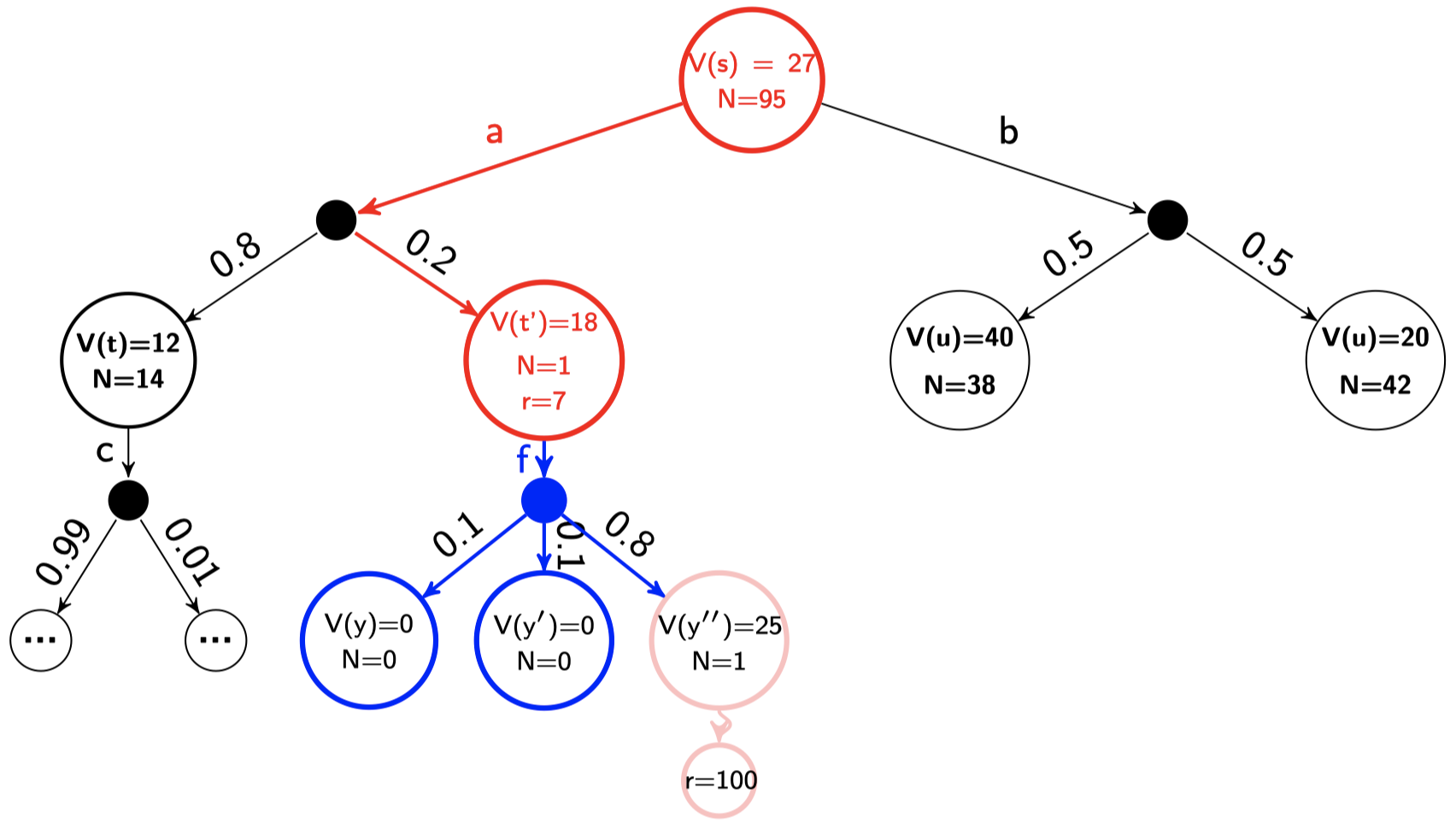
\[\begin{align*} V(y'') &= \max_{a\in A}\sum_{s'\in \textit{children}(y'')}P_a(s'\mid y'')[r(y'',a,s')+\gamma V(s')]\\ &= \gamma^{13}\times 100 \qquad \text{(模拟长度为 13 步，并且收到的回报为 100)}\\ &\approx 25\\\\ V(t') &= \max_{a\in \{f\}}\sum_{s'\in \textit{children}(t')}P_a(s'\mid t')[r(t',a,s')+\gamma V(s')]\\ &= 0.1\times (0+0)+0.1\times (0+0)+0.8\times (0+0.9\times 25)\\ &= 18\\\\ V(s) &= \max_{a\in \{a,b\}}\sum_{s'\in \textit{children}(s)}P_a(s'\mid s)[r(s,a,s')+\gamma V(s')]\\ &= \max (0.8\times(0+0.9\times 12)+0.2\times(7+0.9\times 18), \qquad (\text{行动 }a)\\ &\qquad \quad 0.5\times(0+0.9\times 40)+0.5\times(0+0.9\times 20)) \qquad (\text{行动 }b)\\ &= \max(8.64+4.62,18+9)\\ &= 27 \end{align*}\]

在反向传播步骤之后

$V(s)$ 的值没有变化，因为行动 $b$ 仍然会返回最大的折扣未来回报。

3. 多臂老虎机

关于有信息搜索，我们需要回答一个关键问题：我们应当如何选择下一个要扩展的结点？

事实证明，这种选择在 MCTS 上将导致非常不同的性能表现。

3.1 多臂老虎机：非正式定义

关于如何选择结点可以看作是 多臂老虎机（Multi-arm Bandits）问题的一个实例。该问题定义如下：

想象一下，你有 $N$ 台老虎机（或澳大利亚的扑克机），有时被称为单臂老虎机。随着时间的流逝，每台老虎机都会从未知的概率分布中返回一个随机回报。一些老虎机要比其他老虎机返回更高的回报。我们的目的是最大化一个老虎机摇臂序列的回报总和。

3.2 多臂老虎机：正式定义

一台 $N$-臂老虎机由一个随机变量 $X_{i,k}$ 的集合定义，其中：

$1\le i\le N$，令 $i$ 为老虎机的臂
$k$ 是臂 $i$ 被摇动的索引

连续摇臂 $X_{i,1},X_{j,2},X_{k,3},\dots$ 被假定为基于某个未知定律的独立分布。也就是说，我们并不知道这些随机变量的概率分布。

直觉上：适用于状态 $s$ 的行动 $a$ 可以视为 “老虎机的臂”，而 $Q(s,a)$ 对应随机变量 $X_{i,n}$。

3.3 平整蒙特卡洛（FMC）

由于我们不知道各个臂的回报分布，一个简单的策略就是简单地按照均匀分布选择摇臂。也就是说，我们以相同的概率选择每个臂。这就是 平整蒙特卡洛（Flat Monte Carlo，FMC），又称 均匀采样 (uniform sampling)。

然后，在给定状态 $s$ 下的行动 $a$ 的 $Q$-值可以通过以下公式来近似：

\[Q(s,a)=\dfrac{1}{N(s,a)}\sum_{t=1}^{N(s)} I_t(s,a)r_t\]

其中，
$N(s,a)$ 是在状态 $s$ 下，行动 $a$ 被执行的次数。
$N(s)$ 是状态 $s$ 被访问的次数。
$r_t$ 是来自状态 $s$ 的第 $t$ 次模拟得到的回报。
$I_t(s,a)$ 为 $1$，如果在状态 $s$ 的第 $t$ 次模拟中选择了行动 $a$；否则为 $0$。

$\to$ FMC 成功地在 Bridge（Ginsberg，01）和 Scrabble（Sheppard，02）上达到了世界冠军水平。

但是存在什么问题呢？使用均匀分布导致在所有行动中浪费了相同的采样时间。基于我们目前为止所获得的回报，为什么不将重点放在 最有前景的行动 上呢？

3.4 探索 vs. 利用

我们想要执行的仅仅是那些好的行动。因此，只要继续执行目前为止为我们带来最佳回报的行动即可。但是，我们的选择是随机的，所以如果我们并没有对最佳行动进行足够的采样呢？因此，我们希望策略能够 利用（exploit）我们认为的目前为止的最佳行动，但是仍然可以继续 探索（explore）其他行动。

但是，我们应该用多少次摇臂次数来利用，又应该用多少次摇臂次数来探索呢？
这被称为 探索 vs. 利用困境（exploration vs. exploitation dilemma）。

它是由 害怕错失的恐惧（The Fear of Missing Out, FOMO）驱动的。

3.5 害怕错失的恐惧（FOMO）

我们要寻找一种能够 最小化后悔（minimise regret）的策略 $\pi$。

后悔（Regret）：

\[\mathcal R_{N(s),b}=Q(\pi^*(s),s)N(s)-\mathbb E\left[\sum_{t}^{N(s)}Q(b,s) I_t(s,b)\right]\]

其中，
$Q(\pi^*(s),s)$ 是（未知的）最优策略 $\pi^*(s)$ 的 $Q$-值。 $N(s)$ 是状态 $s$ 被访问的次数。
$I_i(s,a)$ 为 $1$，如果在状态 $s$ 的第 $i$ 次模拟中选择了行动 $a$；否则为 $0$。
重要：对于每一个 $b$，都有 $\mathbb E\left[\sum_{t}^{N(s)}Q(b,s) I_t(s,b)\right]>0$。

重要：如果我们摇动臂 $b$，我们的后悔是 最大的可能期望回报 减去 摇动臂 b 的期望回报。如果我们摇动臂 $a$（最佳摇臂），我们的后悔是 $0$。

因此，后悔是由于没有采取最佳行动而造成的 期望损失。

$\to$ 在多臂老虎机算法中，探索 实际上 是由 FOMO 驱动的。

3.6 最小化后悔的解决方案

$\epsilon$-greedy：$\epsilon$ 是一个位于区间 $[0, 1]$ 之间的数。每次当我们需要选择一个臂时，我们以 $\epsilon$ 的概率随机选择一个臂，以 $1-\epsilon$ 的概率选择具有 $\max Q(s,a)$ 的臂。通常，$\epsilon$ 的值设在 $0.05$ 到 $0.1$ 时，效果较好。

$\epsilon$-decreasing：同 $\epsilon$-greedy 一样，唯一区别是 $\epsilon$ 将随时间衰减。参数 $\alpha$ 指定了 衰减率 (decay)，使得每次选择行动之后的 $\epsilon:=\epsilon \cdot \alpha$。

Softmax：这是 概率匹配策略，这意味着到目前为止所选择每个行动的概率都取决于其 $Q$-值。正式地：

\[\dfrac{e^{Q(s,a)/\tau}}{\sum_{b=1}^{n}e^{Q(s,b)/\tau}}\]

其中，$\tau$ 是 温度（temperature），它是一个正数，表明过去的数据对于决策有多大影响。

3.7 置信区间上界（UCB1）

一个更高效的（尤其是对于 MCTS 而言）多臂老虎机策略是 置信区间上界（Upper Conﬁdence Bounds，UCB1）策略。

UCB1 策略 $\pi(s)$

\[\pi(s):=\mathop{\operatorname{arg\,max}}\limits_{a\in A(s)}Q(s,a)+\sqrt{\dfrac{2\ln N(s)}{N(s,a)}}\]

其中，
$Q(s,a)$ 是估计的 $Q$-值。
$N(s)$ 是状态 $s$ 被访问的次数。
$N(s,a)$ 是在状态 $s$ 下，行动 $a$ 被执行的次数。

$\to$ 加号左侧的 $Q(s,a)$ 项鼓励利用：对于具有较高回报的行动，$Q$-值较高。
$\to$ 加号右侧的 $\sqrt{\frac{2\ln N(s)}{N(s,a)}}$ 项鼓励探索：对于被较少探索的行动，此项值较高。

4. 蒙特卡洛树搜索和多臂老虎机

4.1 上置信区间树（UCT）

上置信区间树（Upper Conﬁdence Trees，UCT）可以视为蒙特卡洛树搜索和多臂老虎机的结合：

UCT $=$ MCTS $+$ UCB1

Kocsis 和 Szepesvari 首次将 MCTS 中的扩展结点的选择视为一个多臂老虎机问题。

UCT 探索策略

\[\pi(s):=\mathop{\operatorname{arg\,max}}\limits_{a\in A(s)}Q(s,a)+2C_p\sqrt{\dfrac{2\ln N(s)}{N(s,a)}}\]

$C_p>0$ 是探索常数，该常数越大则鼓励更多探索，越小则鼓励更少探索。采用随机平局决胜制。

$\to$ 如果 $Q(s,a)\in [0, 1]$ 并且 $C_p=\frac{1}{\sqrt 2}$，那么在双人对抗游戏中，UCT 将收敛到著名的 Minimax 算法（如果你不知道 Minimax 是什么，请暂时忽略此方法，我们将在本课程后面提到。）

4.2 如果我们不知道 $P_a(s’\mid s)$ 会怎样？

在接下来的讲座中，我们将更多关注 $P_a(s’\mid s)$ 未知的情况，但重要的是要注意，即使我们不知道转移概率或者回报函数，我们仍然可以使用 MCTS ，前提是我们可以模拟它们；例如，使用基于代码的模拟器。这种新方法是对原始 MCTS 的一种简单修改：

选择步骤和之前一样。
在扩展步骤中，相比之前扩展一个行动的所有子结点，我们现在将模拟向前一步，它将根据 $P_a(s’\mid s)$ 选择结果（前提是模拟器是准确的）。
然后，我们像之前一样进行模拟，并在接收到回报时对其进行学习。
在 反向传播 步骤中，相比之前使用贝尔曼方程来计算期望回报，现在我们将简单地使用平均回报。如果我们对每一步都进行足够多次数的模拟，那么平均回报将收敛到期望回报。

这种方法的缺点是我们必须进行多次重复的模拟才能使平均值达到收敛，而当我们知道 $P_a(s’\mid s)$ 时，我们只需对一个行动扩展一次即可知道其即时效用。

该方法的优点是更具通用性：只要我们有一个问题模拟器，我们就可以应用它 —— 我们不需要明确的问题模型。对于许多问题，模拟器要比问题更容易生成。

4.3 带 UCB 树的 MCTS 的应用

游戏：

围棋：MoGo (2006), Fuego (2009), …, Alpha Go(2010–2016)
棋类游戏：Havannah, Y, Cataan, Othello, Arimaa…
视频游戏：Atari 2600

非游戏：

计算机安全：攻击树生成和渗透测试
深度学习：神经网络和特征选择的自动 “性能调整”
运营研究：优化公交时刻表，能源库存管理…

4.4 为什么它如此有效（有时）？

它全面解决了利用与探索的权衡问题。

UCT 是 系统性的：
- 策略评估在一定深度上是 彻底计算过的。
- 探索的目的是 最小化后悔（或者 FOMO）。

观看如何用 UCT 玩 马里奥兄弟（Mario Bros）：

UCT 表现不佳的情况：Atari 2600 游戏：高速公路（Freeway）：

UCT 在这里失败了，因为角色直到到达道路的另一侧才获得回报，因此 UCT 没有得到反馈而无法继续进行下去。

4.5 价值/策略迭代 vs. MCTS

通常，从初始状态 $s_0$ 使用最佳策略可以到达的状态集要远小于总的状态集。在这方面，价值迭代和策略迭代是计算彻底的：如果我们知道问题的初始状态，它们可以根据永远不会遇到的状态来计算行动。

对于 MCTS（和其他搜索方法）方法，仅仅通过从 $s_0$ 开始进行采样就可以使用。但是，其结果并不像使用价值/策略迭代那样通用：得到的解仅适用于已知的初始状态 $s_0$ 或者采用模型定义的行动能够从 $s_0$ 到达的任何状态。而价值/策略迭代方法得到的解适用于任何状态。

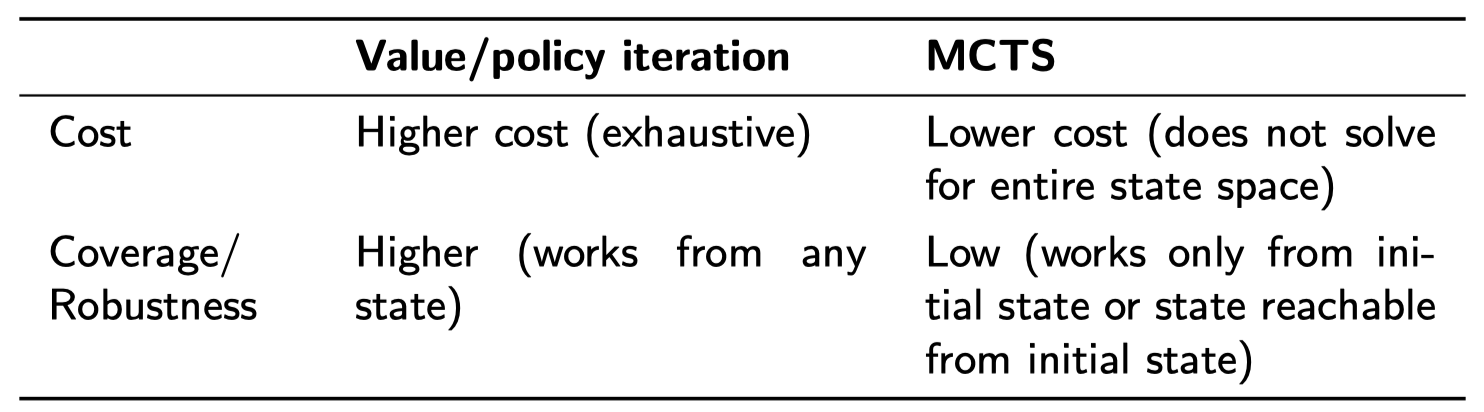
这一点很重要：因此，价值/策略迭代的成本更高，但是，对于在其环境中运行的 agent，我们可以通过仅仅一次彻底求解，然后，无论状态如何，我们都可以多次使用生成的策略。

而对于 MCTS，每当我们遇到之前没有考虑过的状态时，都需要在线求解。

5. 总结

蒙特卡罗树搜索（MCTS）是一种任意时间搜索算法，尤其适用于随机域，例如：MDP。
- 明智的选择策略对于取得良好的表现 至关重要。
多臂老虎机的置信区间上界（UCB1）是一个很好的选择策略。
- UCB1（稍作修改）可以很好地平衡利用和探索。
- 害怕错失的恐惧（FOMO）是探索的绝佳动力。
UCT 是 MCTS 和 UCB1 的结合，是一种 非常成功 的算法。
- 虽然它有明显的缺点。
- 除了 FOMO 外，还有其他替代方法可以激发探索，例如 $\epsilon$-greedy 和 softmax。

下节内容：无模型强化学习：Q-Learning 和 SARSA

本作品采用知识共享署名-非商业性使用-相同方式共享 4.0 国际许可协议进行许可。欢迎转载，并请注明来自：YEY 的博客同时保持文章内容的完整和以上声明信息！

人工智能自动规划 08：蒙特卡洛树搜索：利用和探索的权衡

墨尔本大学 COMP90054 课程笔记