Lecture 09 无模型强化学习：$Q$-学习和 SARSA

主要内容：

动机
强化学习
$Q$-学习
SARSA
总结

1. 动机

1.1 学习成果

识别在哪些情况下，无模型强化学习适用于求解 MDP 问题。
解释无模型规划与基于模型规划之间的差异。
应用 $Q$-学习和 SARSA 手动解决小规模 MDP 问题，并编写 $Q$-学习和 SARSA 算法代码自动求解中等规模 MDP 问题。
比较和对比非策略强化学习与策略强化学习。

1.2 规划与学习

到目前为止，我们已经学习了盲目/启发式搜索和价值/策略迭代。

搜索和价值/策略迭代都属于 基于模型 技术。这意味着我们需要知道模型；具体来说，我们知道 $P_a(s’\mid s)$ 和 $r(s,a,s’)$。
$Q$-学习和 SARSA 则属于 无模型 技术。这意味着我们不知道 $P_a(s’\mid s)$ 和 $r(s,a,s’)$。
如果我们不知道转移和回报，我们该如何计算策略呢？我们通过尝试行动并观察结果，从经验中学习，从而使它成为一个机器学习问题。
重要的是，在无模型强化学习中，我们不会尝试学习 $P_a(s’\mid s)$ 或 $r(s,a,s’)$ —— 我们将直接学习策略。
另外，有些技术则介于基于模型和无模型之间：基于模拟的技术。在这种情况下，我们将模型视为一个 模拟器，因此我们可以利用无模型技术来模拟 $P_a(s’\mid s)$ 和 $r(s,a,s’)$ 并学习策略。

2. 强化学习

2.1 例子：神秘游戏

游戏链接：该游戏的目的是通过实验了解计算机是如何学习的。游戏通过按键盘上的数字 $1$ 到 $6$ 键进行操作。你需要了解行动产生的结果以及如何赢得比赛。

当你做得很好或很差时，会出现一些回报值。当你完成游戏时，会出现一行短语 “ You Win :)” 。祝你好运！

你采取了什么程序？
你学到了什么？
你使用了什么假设？

$\to$ 想象一下，对于没有任何假设或直觉的计算机来说有多难！

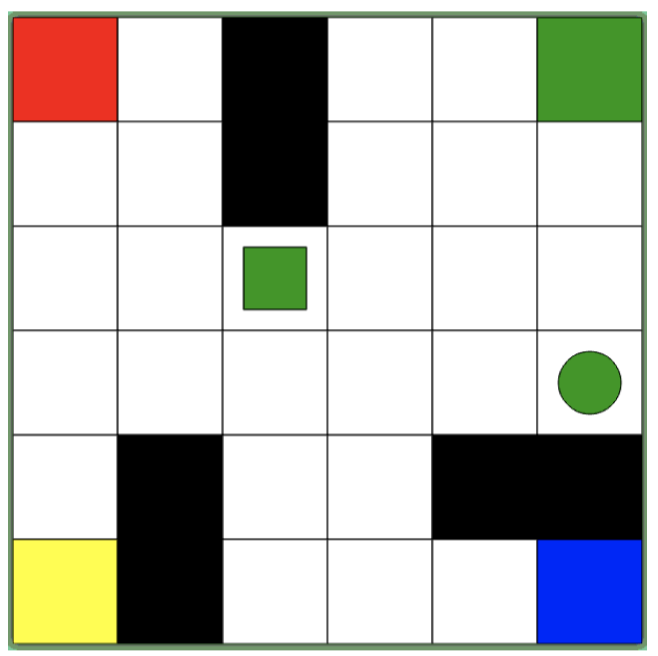
现在，我们来玩这个游戏。我们可以看到游戏界面是一个 $6\times 6$ 的网格组成，其中有一些不同颜色和形状的色块。刚开始，我们对于游戏规则、获胜条件等一无所知，我们只知道一共有 $6$ 种行动，分别对应键盘上的数字 $1$ 到 $6$，当我们按下这些数字键时，会执行一些行动。

这个游戏背后的思想是：我们并不知道应该做什么，我们要做的就是开始探索。所以，一开始我们可能只是随机地按下键盘上的数字 $1$ 到 $6$ 键，然后进行观察，我们发现，通过这些数字键，我们可以控制较小的绿色方块的行为：

$1$：向上移动
$2$：向左移动
$3$：向右移动
$4$：放下圆形色块
$5$：向下移动
$6$：拾取圆形色块

并且，我们发现，黑色色块和地图边缘起到了墙的作用（会阻挡方块移动），当我们成功拾取圆形色块时会得到 $+1$ 的回报，当我们在非指定区域放下圆形色块时会得到 $-1$ 的回报，而当我们将圆形色块运送到指定区域（四个角落上对应颜色区域，即右上角的绿色区）时，我们将获得胜利（“ You Win :)”）。

此外，当刷新页面重新开始游戏时，我们会发现可移动小方块和圆形色块的颜色发生了变化（例如：红色），作为人类，我们可以很容易推测此时指定区域也发生了相应的变化（即左上角的红色区），但是对于计算机而言，做到这点并不容易。

我们为什么玩这个游戏？这是在无模型环境下应用强化学习的一个例子。即，我们并不知道环境相关信息，我们只知道我们能够采取的行动，这有点类似于人类的学习过程：我们体验一些事物，尝试一些事物，有时结果比较理想，有时则不如预期，我们学习如何在这个世界中行事。

2.2 AI 规划和学习的方法

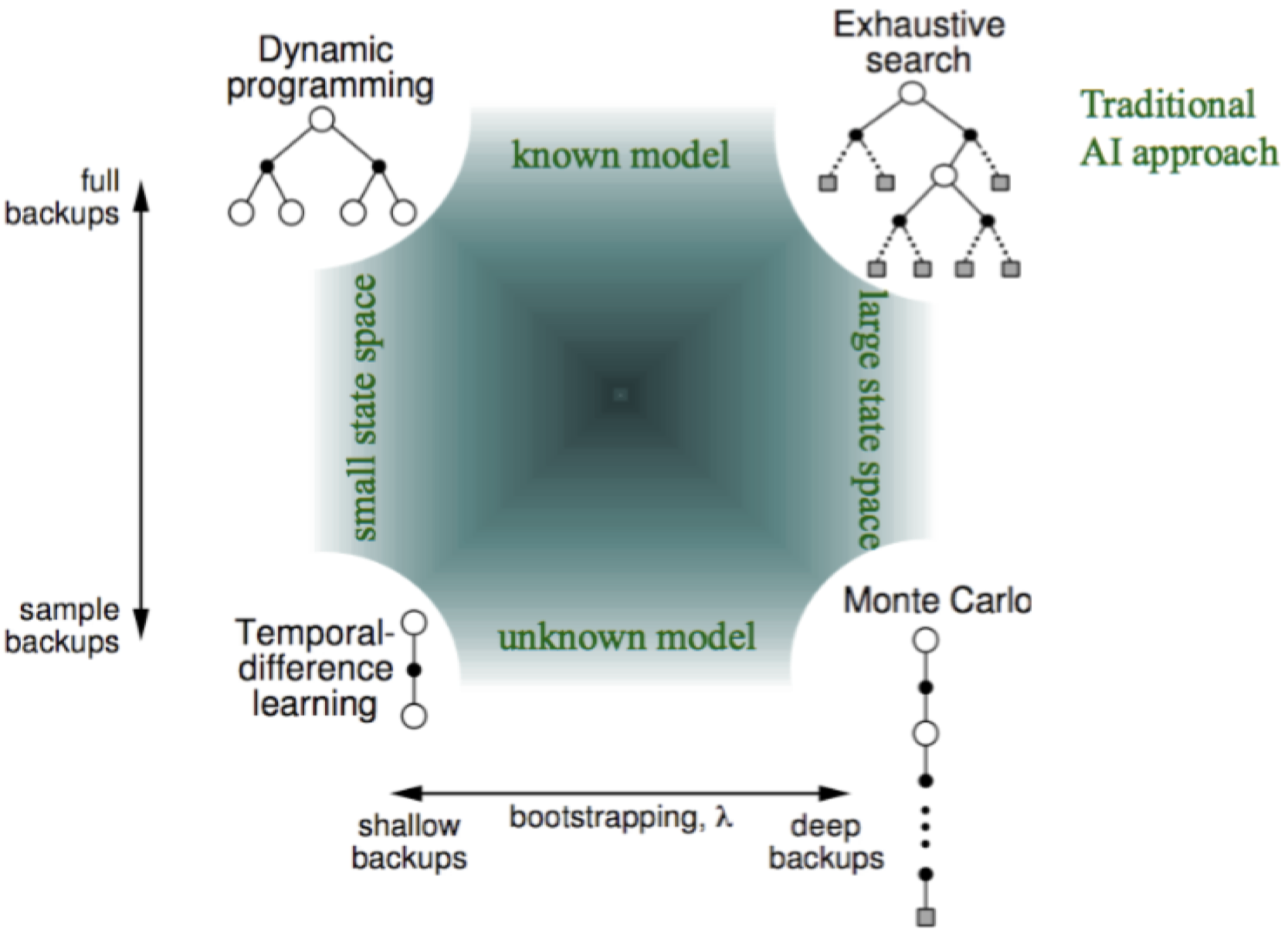
2.3 强化学习：基础

强化学习有许多不同的模型，它们都具有相同的基础：

我们对要解决的问题执行了许多不同的 episodes（注：agent 根据某个策略执行一系列行动到结束就是一个 episode），从中我们学习到一个策略。
在学习过程中，我们尝试学习在特定状态下应用特定行为的价值。
在每个 episode 中，我们需要执行一些行动。每次行动完成后，我们都会得到一个回报（可能为 $0$），并且我们可以看到新的状态。
由此，我们 强化（reinforce）了在先前状态下应用先前行动的估计。
我们在遇到以下情况时终止：（1）我们的训练时间用完了；（2）我们认为我们的策略已经收敛到了最优策略（对于每个新的 episode，我们不再看到任何改进）；或者（3）我们的策略已经 “足够好”（对于每个新的 episode，我们只能看到非常小的改进）。

2.3 基于模型 vs. 无模型

强化学习中一个非常重要的概念是 基于模型（model-based）和 无模型（model-free）的区别。

为了快速理解这点，我们回顾一下之前的马尔可夫决策过程（MDP），在 MDP 中，我们至少具备以下 4 点（当然，我们也可以再加一项初始状态 $s_0$）：

状态集合 $S$
转移概率 $P_a(s’\mid s)$
回报函数 $r(s,a,s’)$
折扣因子 $\gamma$

当我们在价值/策略迭代或者 MCTS 中谈论它们时，我们是确切知道转移概率 $P_a(s’\mid s)$ 和回报函数 $r(s,a,s’)$ 的，我们可以利用它们来计算期望回报。但是，在无模型环境下，这两项是未知的。

例如：在前面的神秘游戏的例子中，我们一开始并不知道我们能采取哪些行动，我们只知道总共可以采取 $6$ 种行动，我们并不知道什么时候可以采取哪种行动，以及相应的回报是什么。作为人类，我们已经具备了大量的先验知识来帮助我们发现其中的规则，我们实际上是在此基础上建立了一个该问题的模型：$1$ 表示向上移动、$6$ 表示拾取圆形色块等等。而在无模型强化学习中，我们实际上不会建立模型，我们所做的是从 经验（experience）直接映射到 策略（policy），而并非从动态的环境中学习任何事情。我们只知道采取某些行动后，我们将观察到一些特定的状态以及一些特定的回报，

此外，还有一种介于基于模型和无模型之间：基于模拟（simulation-based）。在这种情况下，我们并没有转移概率的显式模型，但是我们可以通过代码模拟估计转移概率。我们可以将无模型强化学习应用在模拟器上，从而学习到一个策略，如果我们模拟得很好，该策略应当表现不错。

2.4 时序差分学习

关于无模型强化学习，这里我们将主要关注 时序差分学习（Temporal Difference Learning）。它的基本思想是：当我们处于某个特定状态时，我们将进行利用和探索（就像之前的 MCTS 和多臂老虎机），来学习哪种行动是最优的，从而得到一个策略。

例如，我们从初始状态出发，随机选择一个行动（例如：向右移动），因为我们并不知道哪个行动更好。假设我们选择了向右移动，我们将尝试估计在之前的状态下，该行动真实的 $Q$-值是多少，但是这非常困难，因为我们并没有任何相关信息。但是，当我们每次按照时序差分进行移动之后，我们都试图对 $Q$-值进行估计，我们可以根据即时回报和未来回报来估计 $Q$-值。对于即时回报，我们直接将这里得到的回报加到 $Q$-函数上；而对于未来回报，在 MCTS 中，我们将一路模拟达到终止状态，然后反向传播对 $Q$-值进行更新，而在时序差分学习中，我们在每个状态都对 $Q$-值进行更新（即，每经过一个时间步都更新一次）。

3. $Q$-学习

3.1 $Q$-学习算法

$Q$-学习 可能是最简单的强化学习方法，它的灵感源于动物如何从其周围环境中学习。这种直觉很简单直接。算法维护一个 $Q$-函数，该函数记录每个 “状态-动作” 对的 $Q(s,a)$。在每一步中：（1）使用多臂老虎机算法选择一个行动；（2）应用该行动并获得回报；（3）根据该回报更新 $Q(s,a)$。重复多次 episodes，直到……什么时候？

$Q$-学习算法：

3.2 更新 $Q$-函数

$Q$-函数 的更新发生在学习过程中（上面算法中的第 7 行）：

\[Q(s,a) \leftarrow \underbrace{Q(s,a)}_{旧的值} + \underbrace{\alpha}_{学习率} \cdot [\overbrace{\underbrace{r}_{回报} + \underbrace{\gamma}_{折扣因子}\cdot \underbrace{\max_{a'}Q(s',a')}_{最优未来价值的估计}}^{估计回报} \underbrace{-Q(s,a)}_{不再计算额外的 Q(s,a)}]\]

一个较高的学习率 $\alpha$ 将使较新信息的权重大于较旧信息（$Q(s,a)$）的权重。

注意，这里我们使用 $\max_{a’}Q(s’,a’)$ 来估计未来价值，这意味着它忽略了策略选择的行动，而是根据更新的最优行动的估计值进行更新。这被称为 脱离策略（off policy）学习，我们将在稍后对其进行介绍。

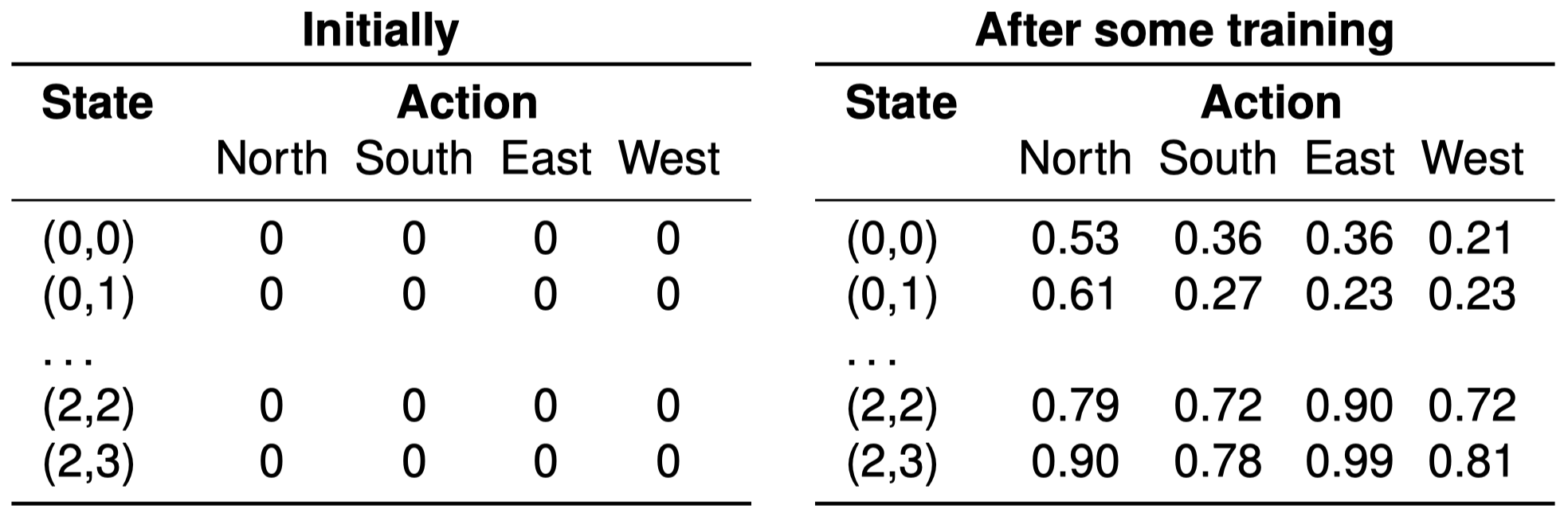
3.3 $Q$-函数：使用 $Q$-表

$Q$-表 是维护一个 $Q$-函数的最简单的方法。它是一个表，其中包含了每个 $Q(s,a)$ 的条目。因此，就像价值迭代中的价值函数一样，它们不会缩放到较大的状态空间。（在下一讲中，将涉及更多有关缩放的信息）。

3.4 $Q$-学习：例子

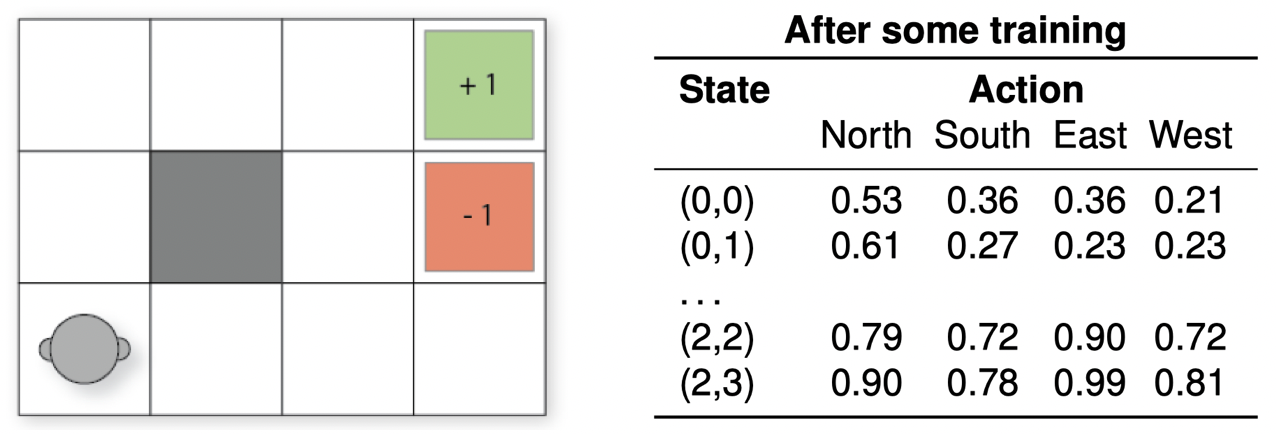
在状态 $(2,2)$ 中，行动 “North（向北移动）” 被选择并执行了，该行动将返回状态 $(2,2)$，因为在 $(2,2)$ 上方已经没有网格了。利用上面的 $Q$-表，我们可以更新 $Q$-值，如下所示：

\[\begin{align} Q((2,2),\text{North}) &\leftarrow Q((2,2),\text{North}) + \alpha[r + \gamma max_{a'}Q((2,2),a')-Q((2,2),\text{North})] \\ &\leftarrow 0.79+0.1\times[0 + 0.9\times Q((2,2),\text{East})-Q((2,2),\text{North})]\\ &\leftarrow 0.79+0.1\times[0 + 0.9\times 0.90-0.79]\\ &\leftarrow 0.792 \end{align}\]

3.5 利用 $Q$-函数

我们将迭代尽可能多的 episodes，或者直到每个 episode 都很难再提高我们的 $Q$-值。这为我们提供了一个（接近）最优 $Q$-函数。

一旦我们有了这样一个 $Q$-函数，我们将停止探索，而只进行利用。我们使用 策略提取，就像我们在价值迭代一样中所做的那样：

\[\pi(s)=\mathop{\operatorname{arg\,max}}\limits_{a\in A(s)}Q(s,a)\]

4. SARSA

4.1 SARSA：依附策略强化学习

SARSA $=$ State-action-reward-state-action

依附策略（On-Policy）：相比在更新期间对最优估计未来状态的 $Q(s’,a’)$ 进行估计，依附策略使用实际的下一个行动来更新：

依附策略学习（On-policy learning）会对当前行为策略 $\pi$ 的 “状态-行动” 对 $Q^{\pi}(s,a)$ 进行估计，而 脱离策略学习（off-policy learning）在估计策略时会独立于当前行为。

SARSA 算法：

4.2 $Q$-学习 vs. SARSA

依附策略：使用策略所选择的行动进行更新。

脱离策略：忽略策略所选择的行动，使用最优行动 $\mathop{\operatorname{arg\,max}}_{a’}Q(s’,a’)$ 进行更新。

依附策略的 SARSA 学习到的行动价值和它所遵循的策略有关，而脱离策略的 $Q$-学习和贪婪策略有关。

4.3 依附策略 vs. 脱离策略：在这里有什么区别？

区别仅仅在于：在循环体中，更新是如何发生的。

$Q$-学习：（1）选择一个行动 $a$；（2）执行该行动，并观察回报和下一个状态 $s’$；（3）通过假设未来回报是 $\max_{a’}Q(s’,a’)$ 乐观地 进行更新 —— 即，它假设未来行为是最优的（基于它的策略）。

SARSA：（1）为 下一次 循环迭代选择一个行动 $a’$；（2）在下一次迭代中，采取该行动，并观察回报和下一个状态 $s’$；（3）然后才为下一次迭代选择 $a’$；以及（4）使用估计的实际下一个行动（可能不是最贪婪的一个动作）进行更新（例如，可以对其进行选择以使其能够探索）。

4.4 SARSA：例子

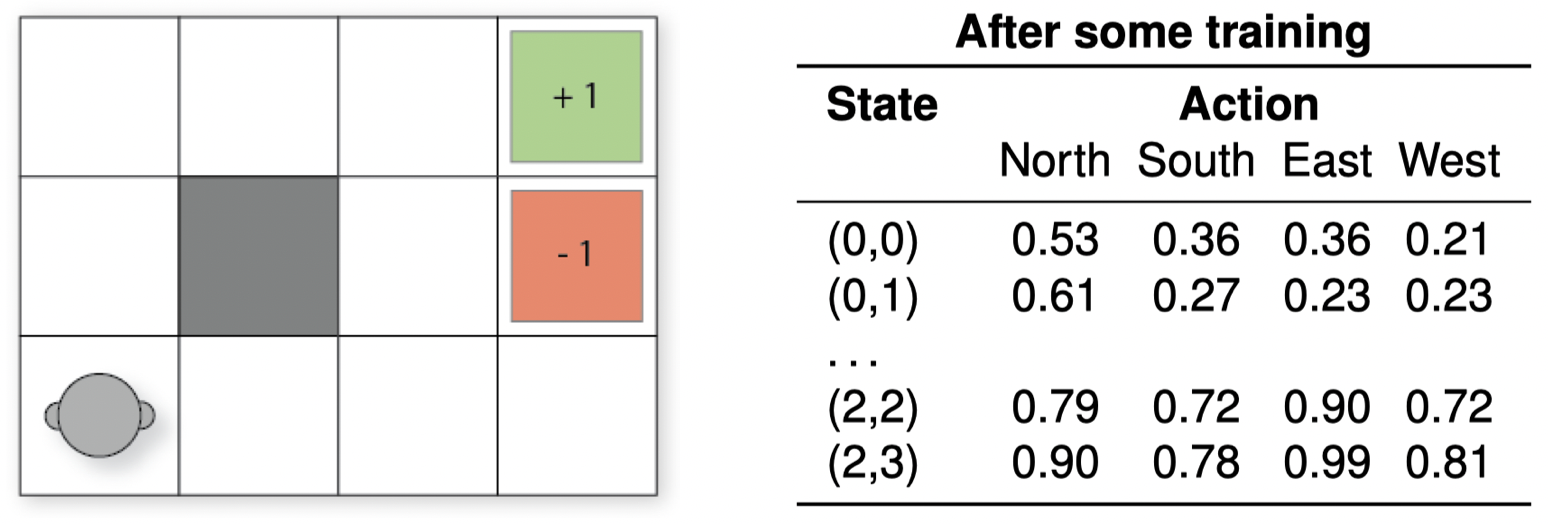
在状态 $(2,2)$ 中，成功选择并执行了 “North（向北移动）” 行动，该行动将返回状态 $(2,2)$，，因为在 $(2,2)$ 上方已经没有网格了。下一个选择的行动是 “West（向西移动）”。利用上面的 $Q$-表，我们可以使用 SARSA 更新 $Q$-值，如下所示：

\[\begin{align} Q((2,2),\text{North}) &\leftarrow Q((2,2),\text{North}) + \alpha[r + \gamma Q((2,2),\text{West})-Q((2,2),\text{North})] \\ &\leftarrow 0.79+0.1\times[0 + 0.9\times Q((2,2),\text{West})-Q((2,2),\text{North})]\\ &\leftarrow 0.79+0.1\times[0 + 0.9\times 0.72-0.79]\\ &\leftarrow 0.7758 \end{align}\]

4.3 依附策略 vs. 脱离策略：谁在乎？？

所以，依附策略和脱离策略这两者真正的区别在哪里？主要有以下两点：

$Q$-学习将收敛到与所遵循的策略无关的最优策略，因为它是 脱离策略的：它在更新过程中使用贪婪回报估计，而不是遵循诸如 $\epsilon$-greedy 之类的策略。如果使用随机策略，$Q$-学习仍将收敛到最优策略，但 SARSA 不会（或者说，不必要）。
$Q$-学习可以学习到一个最优策略，但这在 训练过程中 可能是 “不安全的” 或者冒险的。

4.4 SARSA vs. $Q$-学习：例子

考虑下面的网格。$S$ 是起点，状态 $G$ 会得到 $100$ 的回报。从悬崖上掉下来会得到 $-100$ 的回报。到达顶层的行（第一行）将得到 $-1$ 的回报。行动是确定性的，但在学习之前是未知的。

$Q$-学习沿着最优路径前进（沿着悬崖的边缘），但有时会由于 $\epsilon$-greedy 行动选择而跌落悬崖。SARSA 学习到的是安全路径，因为它是依附策略的，并且它在学习时会考虑选择行动的方法。下面右边的图显示了训练过程中 Sarsa 和 $Q$-学习每次尝试的回报：

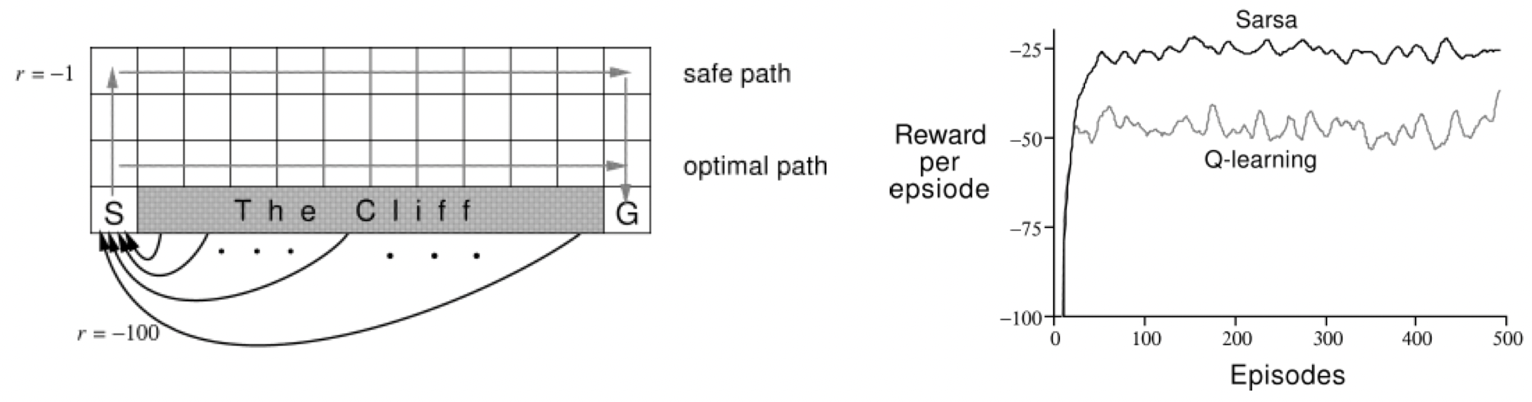
SARSA 在 每次试验 中获得的平均回报要高于 $Q$-学习，因为它在以后的 episodes 中跌落悬崖的次数要少一些。但是，$Q$-学习可以学习到最优策略。

4.5 依附策略 vs. 脱离策略：为什么我们会有这两种？

想象一下：有一个强化学习 agent，它管理着一个云平台的资源，并且我们之前没有数据可以提供策略相关信息。

当我们要优化一个 在其环境中运行期间 进行学习的 agent 的行为时，依附策略学习更为合适。

我们将需要运行我们的云平台来获取数据。这样一来，如果使用依附策略能够让 每次试验 的平均回报更高，那么与脱离策略学习相比，它将给我们带来更好的总体结果，因为 “试验” 不是实践（实践表示实际上影响了我们赚多少钱）。
而当我们有足够的机会在 agent 正式投入运行之前对其进行训练时，脱离策略学习更为合适。

如果在部署之前，我们能够在模拟环境中运行我们的强化学习算法（并且我们有理由相信模拟环境是准确的），那么脱离策略学习效果会更好，因为它可以遵循其最优策略。

简而言之：将依附策略的强化学习用于在线学习，将脱离策略的强化学习用于离线学习。

例子：如果我们将强化学习用于交通信号灯的优化问题，那么我们将使用依附策略的强化学习，因为考虑到策略会影响司机的行为，我们无法提前对其进行训练。

4.6 行动中的 $Q$-学习的例子

行动中：使用基于 $\epsilon$-greedy 的 $Q$-学习求解悬崖问题的例子：

该项目的源代码地址：https://github.com/alecKarfonta/Gridworld

例子：使用 $Q$-学习计算最佳路径的完整工作示例：
http://www.mnemstudio.org/path-finding-q-learning-tutorial.htm

5. 总结

如果我们知道 MDP：

离线：价值迭代、策略迭代。
在线：蒙特卡洛树搜索（MCTS）及其相关算法。

如果我们不知道 MDP：

离线：强化学习
在线：蒙特卡洛树搜索（MCTS）及其相关算法。

在 Python 中进行 pacman 的 $Q$-学习之后，我们可以在 OpenAI 的所有环境（用于开发和测试强化学习算法的工具包）上对其进行测试：https://gym.openai.com/

强化学习的应用：

Checkers (Samuel, 1959)
首次将强化学习应用于有趣的真实游戏中
(Inverted) Helicopter Flight (Ng et al. 2004)
表现超过人类
Computer Go (AlphaGo 2016)
AlphaGo 以 4:1 击败前世界围棋冠军李世乭
Atari 2600 Games (DQN & Blob-PROST 2015)
在超过 50 款游戏中，有半数以上达到人类玩家水准
Robocup Soccer Teams (Stone & Veloso, Reidmiller et al.)
1999 年，世界最佳模拟足球运动员；2000 年，亚军
Inventory Management (Van Roy, Bertsekas, Lee & Tsitsiklis)
在业界标准方法的基础上提升了 $10$-$15\%$
Dynamic Channel Assignment (Singh & Bertsekas, Nie & Haykin)
世界上最佳的移动电话无线电频道分配者
Elevator Control (Crites & Barto)
(可能是) 世界上最好的下行电梯控制器
Many Robots
导航、双足行走、抓取、技能之间的切换……
TD-Gammon and Jellyﬁsh (Tesauro, Dahl)
世界上最佳西洋双陆棋选手，宗师级水平。

6. 扩展阅读

Introduction to Reinforcement Learning [Sutton and Barto]
资源: https://webdocs.cs.ualberta.ca/~sutton/book/the-book.html
内容：由该领域奠基人编写的非常好的强化学习入门书籍。
Slides about Approximate Q-learning for PacMan
资源: https://www.cs.swarthmore.edu/~bryce/cs63/s16/slides/3-25_approximate_Q-learning.pdf
内容：如果你想利用强化学习参加竞赛，它将是非常好的技术参考资料。
Deep Q-learning for Atari
资源: http://www.davidqiu.com:8888/research/nature14236.pdf
内容：使用卷积神经网络（CNN）来估计 $Q(s,a)$，神经网络的输入为状态，输出为每个行动的估计回报。

下节内容：更高效的强化学习：回报设计和 $Q$-函数逼近

本作品采用知识共享署名-非商业性使用-相同方式共享 4.0 国际许可协议进行许可。欢迎转载，并请注明来自：YEY 的博客同时保持文章内容的完整和以上声明信息！

人工智能自动规划 09：无模型强化学习：Q-学习和 SARSA

墨尔本大学 COMP90054 课程笔记

Lecture 09 无模型强化学习：$Q$-学习和 SARSA

1. 动机

1.1 学习成果

1.2 规划与学习

2. 强化学习

2.1 例子：神秘游戏

2.2 AI 规划和学习的方法

2.3 强化学习：基础

2.3 基于模型 vs. 无模型

2.4 时序差分学习

3. $Q$-学习

3.1 $Q$-学习算法

3.2 更新 $Q$-函数

3.3 $Q$-函数：使用 $Q$-表

3.4 $Q$-学习：例子

3.5 利用 $Q$-函数

4. SARSA

4.1 SARSA：依附策略强化学习

4.2 $Q$-学习 vs. SARSA

4.3 依附策略 vs. 脱离策略：在这里有什么区别？

4.4 SARSA：例子

4.3 依附策略 vs. 脱离策略：谁在乎？？

4.4 SARSA vs. $Q$-学习：例子

4.5 依附策略 vs. 脱离策略：为什么我们会有这两种？

4.6 行动中的 $Q$-学习的例子

5. 总结

6. 扩展阅读

CATALOG

FEATURED TAGS

FRIENDS

Lecture 09 无模型强化学习：$Q$-学习 和 SARSA

1. 动机

1.1 学习成果

1.2 规划与学习

2. 强化学习

2.1 例子：神秘游戏

2.2 AI 规划和学习的方法

2.3 强化学习：基础

2.3 基于模型 vs. 无模型

2.4 时序差分学习

3. $Q$-学习

3.1 $Q$-学习算法

3.2 更新 $Q$-函数

3.3 $Q$-函数：使用 $Q$-表

3.4 $Q$-学习：例子

3.5 利用 $Q$-函数

4. SARSA

4.1 SARSA：依附策略强化学习

4.2 $Q$-学习 vs. SARSA

4.3 依附策略 vs. 脱离策略：在这里有什么区别？

4.4 SARSA：例子

4.3 依附策略 vs. 脱离策略：谁在乎？？

4.4 SARSA vs. $Q$-学习：例子

4.5 依附策略 vs. 脱离策略：为什么我们会有这两种？

4.6 行动中的 $Q$-学习的例子

5. 总结

6. 扩展阅读

CATALOG

FEATURED TAGS

FRIENDS

Lecture 09 无模型强化学习：$Q$-学习和 SARSA