Lecture 10 更高效的强化学习:回报设计和 $Q$-函数逼近
主要内容:
- 动机
- $Q$-函数逼近
- 回报设计和初始化 $Q$-函数
- 总结
1. 动机
1.1 学习成果
- 给定一些已知特征,手动应用线性 $Q$-函数逼近来求解小规模 MDP 问题。
- 选择合适的特征,设计并实现 $Q$-函数逼近,以实现无模型强化学习技术,从而自动求解中等规模的 MDP 问题。
- 比较各种函数逼近方法的优缺点。
- 比较和对比线性函数逼近与基于深度神经网络的函数逼近。
- 说明如何使用回报设计来帮助无模型强化学习方法达到收敛。
- 将回报设计手动应用于给定的潜在函数,以解决小规模 MDP 问题。
- 设计并实现潜在函数,以自动解决中等规模的 MDP 问题。
- 对比和比较回报设计与 $Q$-函数初始化。
1.2 强化学习:一些弱项
在之前的讲座中,我们了解了强化学习中基本的时序差分(TD)方法:$Q$-学习 和 SARSA。如前所述,这两种方法在以下一些基本方面存在一些缺点:
- 不同于蒙特卡洛方法中在获得回报后将该回报进行反向传播,TD 方法使用 bootstrapping(它们使用 $Q(s,a)$ 来估计未来折扣回报),这意味着对于回报稀疏问题,它可能需要很长时间才能将回报传播到整个 $Q$-函数。
- 两种方法都估计了一个 $Q$-函数 $Q(s,a)$,而对此最简单的建模方法是通过 $Q$-表。但是,这需要我们维护一个大小为 $|A|\times |S|$ 的表,而对于任何非平凡的问题来说,这样一张表都显得过于庞大了。
- 使用 $Q$-表 要求我们对于每个可到达的状态进行多次访问,并且对于每个行动应用多次以获得一个较好的 $Q(s,a)$ 的估计。因此,如果我们从未访问过某个状态 $s$,我们将无法估计 $Q(s,a)$,即便我们已经访问过一些与状态 $s$ 非常相似的状态。
- 回报可能非常稀疏,这意味着只有很少的状态/动作会得到非零回报。这显然是有问题的,因为初始时,强化学习算法的行为完全是随机的,并且很难发现那些较好的回报。还记得上一讲的 Freeway 游戏的演示吗?UCT 在那种情况下失效了。
1.3 强化学习:一些改进
为了克服这些限制,我们将看一下 3 种可以改进时序差分方法的简单方法:
- $n$-步时序差分学习:蒙特卡洛技术执行整个行动轨迹,然后反向传播回报;而基本的 TD 方法仅查看下一步的回报,来估计未来回报。相比之下,$n$-步方法在更新回报之前,将查看向前 $n$-步的回报,然后估算剩余部分。
- 逼近方法:相比计算一个精确的 $Q$-函数,我们可以使用简单方法来逼近它,这些方法既不需要大型 $Q$-表(因此方法的可扩展性更好),同时也可以用来提供合理的 $Q(s,a)$,即使我们之前从未在状态 $s$ 下应用过行动 $a$。
- 回报设计(Reward shaping)和 $Q$-值初始化:如果回报是稀疏的,我们可以通过修改/增强回报函数,来奖励那些我们认为能够使我们更接近解(目标状态)的行为,或者我们可以猜测最优 $Q$-函数 并将其设为初始 $Q(s,a)$。
2. $Q$-函数逼近
2.1 问题:大的状态空间
正如我们之前讨论的那样,问题在于:随着每增加一个变量,状态空间的大小将呈指数增长。这导致了两个主要问题:
- 为每个 $s$ 和 $a$ 存储 $Q(s,a)$ 值(例如:在 $Q$-表中)是不可行的。
- $Q$-值 的传播需要很长时间。
例子:在 Atari 2600 Freeway(高速公路)游戏中,假设一共有 $12$ 行 $40$ 列(这其实是被低估了,因为汽车是一次只移动几个像素,而不是按列移动),因此大约有 $480$ 个不同的位置。有两只鸡,另外我们还需要存储每个位置(至少)是否有汽车的状态。这导将致的状态空间大小为:
\[480^2 + 2^{480} = 3.12\times 10^{144}\]因此,我们可能需要一个 $Q$-表,该表的大小是上面的状态空间大小乘以可能的行动数(这里可能是四种行动:向左,向右,向上,向下)。
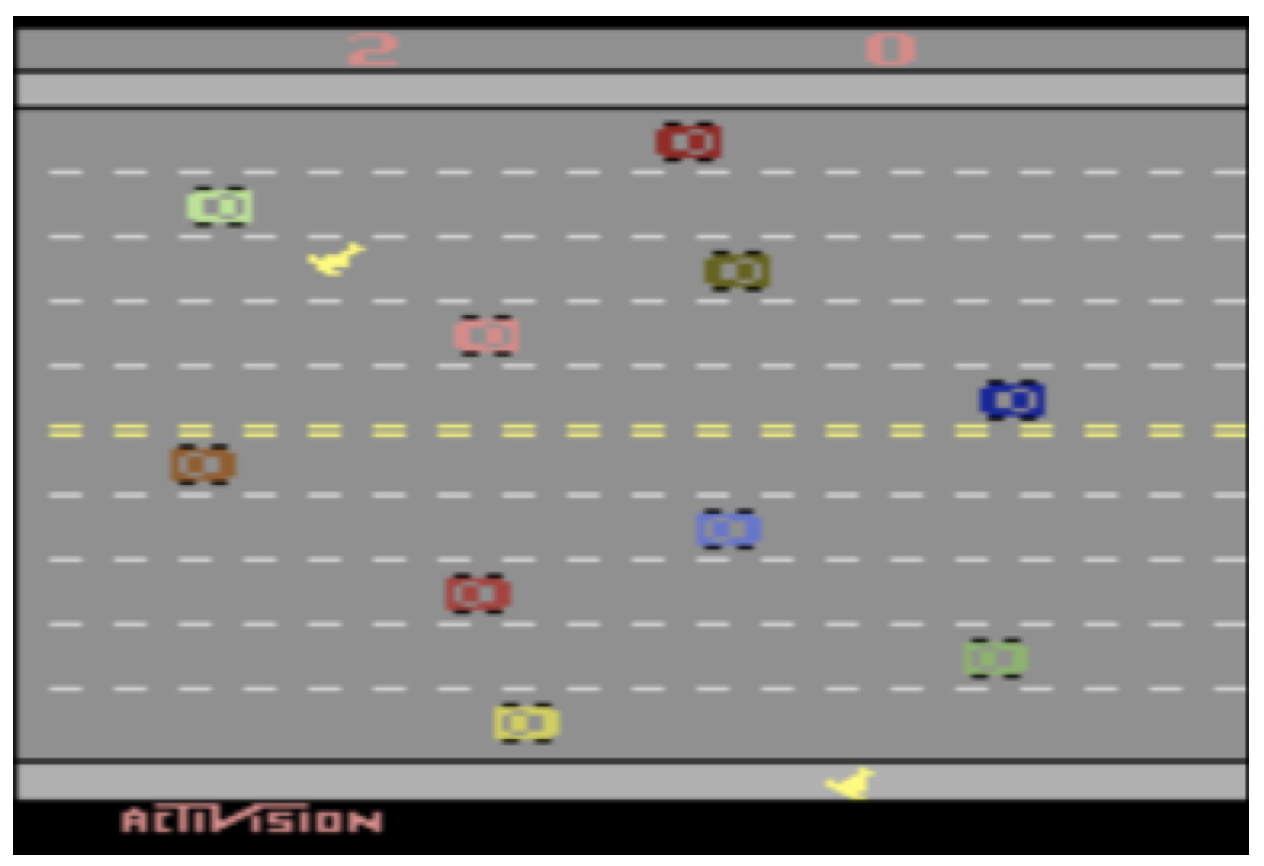
2.2 特征选择练习: Freeway 游戏
在 Atari 2600 Freeway(高速公路)游戏中,为了帮助我们的算法学习如何使鸡成功穿越高速公路,我们应该选择哪些可能的较好特征?
2.3 线性函数逼近
关键思想是使用 特征 及其权重的线性组合来近似 $Q$-函数。我们这里不会对其所有内容进行详细讨论,而是考虑其中最重要的部分,并对其建模。
整个过程如下:
- 对于状态,我们考虑能够确定其表示形式的特征是什么。
- 在学习过程中,我们的更新是基于 特征的权重 而非状态本身。
- 通过对特征进行加权求和来估计 $Q(s,a)$。
例子:在 Atari 2600 Freeway(高速公路)游戏中,相比之前我们记录两名玩家的位置以及地图上每个位置是否有汽车,现在我们只需记录每个玩家与道路另一侧的距离以及与每行中最近汽车的距离即可。这些信息可能已经足够了,而这只需要 $14$ 个特征。在近似 $Q$-学习 中,我们存储的是特征和权重,而非状态。我们需要学习的是每个特征对于每个行动的重要性(即,特征的权重)。
2.4 近似 $Q$-函数表示
如前所述,我们将使用特征及其权重而非 $Q$-表,来表示 $Q$-函数。
为了表示它,我们有两个向量:
-
特征向量 $f(s,a)$:它是一个由 $n\cdot |A|$ 个不同函数构成的向量,其中 $n$ 是状态特征数,$|A|$ 是行动数。每个函数都提取一个 “状态-行动” 对 $(s,a)$ 的特征值。我们说 $f_i(s,a)$ 从 “状态-行动” 对 $(s,a)$ 中提取了第 $i$ 个特征:
\[f(s,a)=\begin{pmatrix} f_1(s,a) \\ f_2(s,a) \\ \dots \\ f_n(s,a) \end{pmatrix}\]在 Atari 2600 Freeway(高速公路)的例子中,我们有一个向量,该向量具有 $14$ 个状态特征乘以 $4$ 个行动。函数 $f_i(s,\textit{Up})$ 返回的是:如果选择向上移动,第 $i+1$ 行(对于 $12$ 行中的每一行,即 $i=1,\dots,12$)中距离最近的汽车;而函数 $f_{13}(s,\textit{Up})$ 返回的是第 $1$ 只鸡离目标的距离;函数 $f_{14}(s,\textit{Up})$ 返回的是第 $2$ 只鸡离目标的距离。例如:$f_{13}(s,a)=\frac{row(s,chicken)}{max_row}$。
-
一个大小为 $n\times |A|$ 的 权重向量 $w$:每个 “特征-行动” 对都具有一个权重。$w_i^a$ 定义了特征 $i$ 对于行动 $a$ 的权重。
2.5 定义 “状态-行动” 特征
下节内容:更高效的强化学习:回报设计和 $Q$-函数逼近
本作品采用知识共享署名-非商业性使用-相同方式共享 4.0 国际许可协议进行许可。 欢迎转载,并请注明来自:YEY 的博客 同时保持文章内容的完整和以上声明信息!