Lecture 03 容错基础知识
参考教材:Transaction Processing: Concepts and Techniques, Jim Gray and Andreas Reuter, Morgan Kaufmann, 1993
这节课我们将介绍有关 容错 (Fault Tolerance) 的概念,该属性使系统在某些组件发生故障时能够继续正常运行。
1. 概率基础
在正式介绍容错之前,我们将先回顾一些概率相关知识。
-
$P(A)=$ 事件 $A$ 在 特定时期内 发生的概率
-
$P(A \cap B)=$ 在这段时期内事件 $A$ 和 $B$ 都发生的概率
\[P(A \cap B)=P(A)\times P(B)\]
如果 $A$ 和 $B$ 互为独立事件,那么 -
$P(A \cup B)= P(A) + P(B) - P(A\cap B)$
\[\begin{align} P(A \cup B) &= P(A)+P(B)-P(A)\times P(B) \\ &= P(A)+P(B)\qquad (如果\, P(A)\, 和\, P(B)\, 非常小)\end{align}\]
如果 $A$ 和 $B$ 互为独立事件,那么 -
事件发生的平均时间 $MT(A)=1/P(A)$
-
如果事件 $A$ 和 $B$ 的平均时间分别为 $MT(A)$ 和 $MT(B)$,那么到第一次事件发生的平均时间为
\[MT(A\cup B)=\dfrac{1}{P(A\cup B)}=\dfrac{1}{P(A)+P(B)-P(A\cap B)}\]假设 $P(A)$ 和 $P(B)$ 都非常小,那么我们可以认为 $P(A\cap B)\approx 0$。因此,在容错问题中,我们可以认为两个系统同时发生故障的概率非常低,此时
\[MT(A\cup B)=\dfrac{1}{P(A)+P(B)}\]
2. 可用性和失效率
2.1 模块可用性
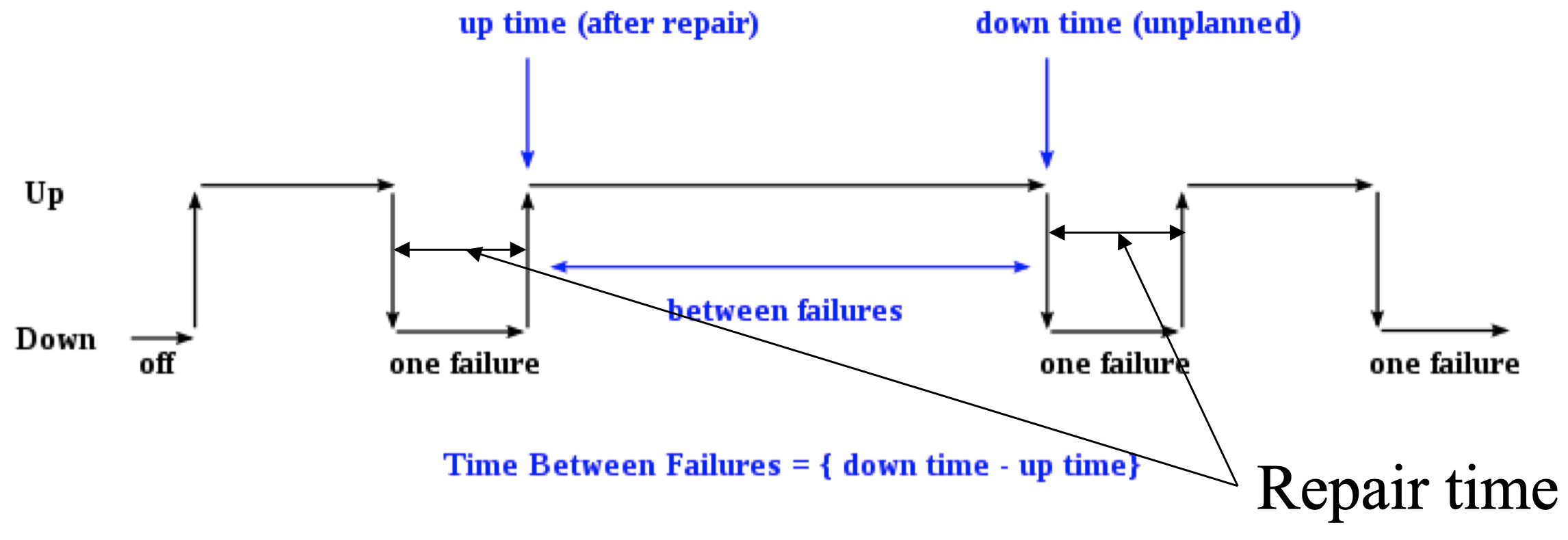
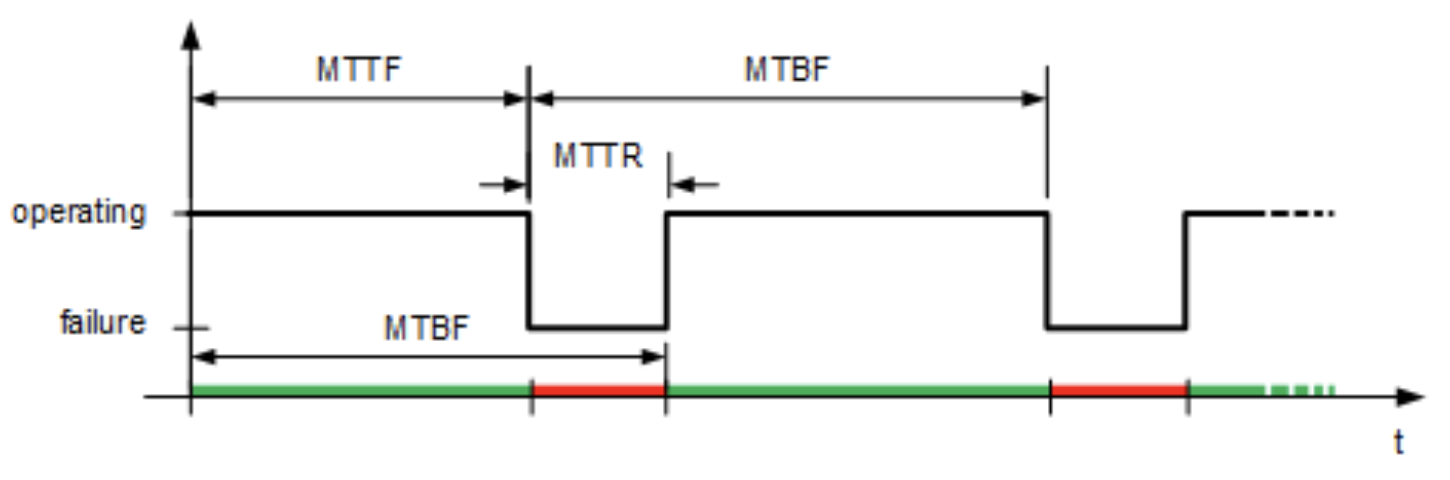
可以看到,在启动之后,系统先是正常运行,然后出现了一次故障使得系统宕机,然后经过一段时间修复,系统重新开始运行,一段时间后,系统再次由于故障宕机。
模块可用性 (Module availability):测量服务完成与消耗时间的比率。计算公式如下:
\[\dfrac{\text{Mean time to failure}}{\text{Mean time to failure} + \text{mean time to repair}}\]2.2 事件发生平均时间
如果所有的 $n$ 个事件都具有相同的平均时间 $m$,那么这些事件中的某一个第一次发生的平均时间为:$m/n$。
推导过程:
如果 $p$ 是一个事件在给定时间内发生的概率,那么其平均时间为:$m=\dfrac{1}{p}$
如果有 $n$ 个这样的概率相同的事件,那么这些事件中有一个发生的概率为 $np$,假设 $p$ 非常小。
因此,这些事件中有一个发生的平均时间为:
\[\dfrac{1}{np}=\dfrac{1}{p}\times \dfrac{1}{n}=\dfrac{m}{n}\]2.3 基于可用性的系统分类
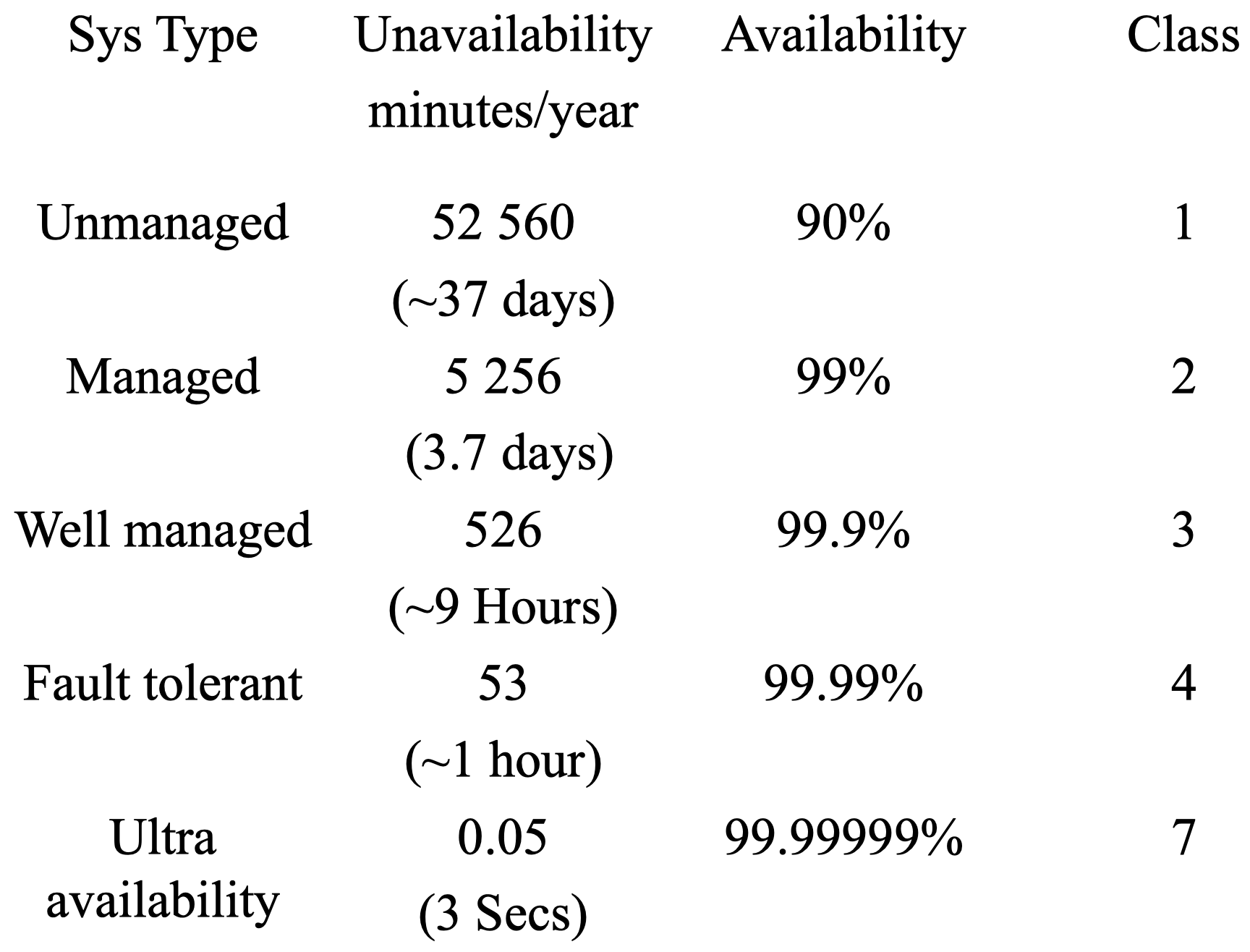
对于一个不具备容错性的系统,如果我们不采取任何措施来管理系统从崩溃中恢复或者保证在某些组件崩溃时数据仍然可用,那么该系统不可用的期望时间约为 37 年。而如果我们采取一些管理措施,那么这段时间将大大缩短。对于一个具备容错管理的系统,其期望宕机时间约为 1 小时。而对于可用性要求非常高的系统,其期望宕机时间仍然在 3 秒左右。根据不同系统的可用性和管理方式,可以将它们分为 7 个级别:完全无管理系统为 1 级,追求极端可用性系统为 7 级。
2.4 影响系统可用性的因素
- 环境方面:诸如冷却、电源、天气、数据通信线路、火灾、地震、海啸、战争、人为破坏等
- 操作方面:系统管理、系统配置和系统操作程序
- 维护:定期维护的程序、定期更换硬件
- 硬件:设备、冷却
- 软件:程序
- 流程:罢工、宕机管理决策
- 内战
2.5 失效率
浴缸失效率曲线
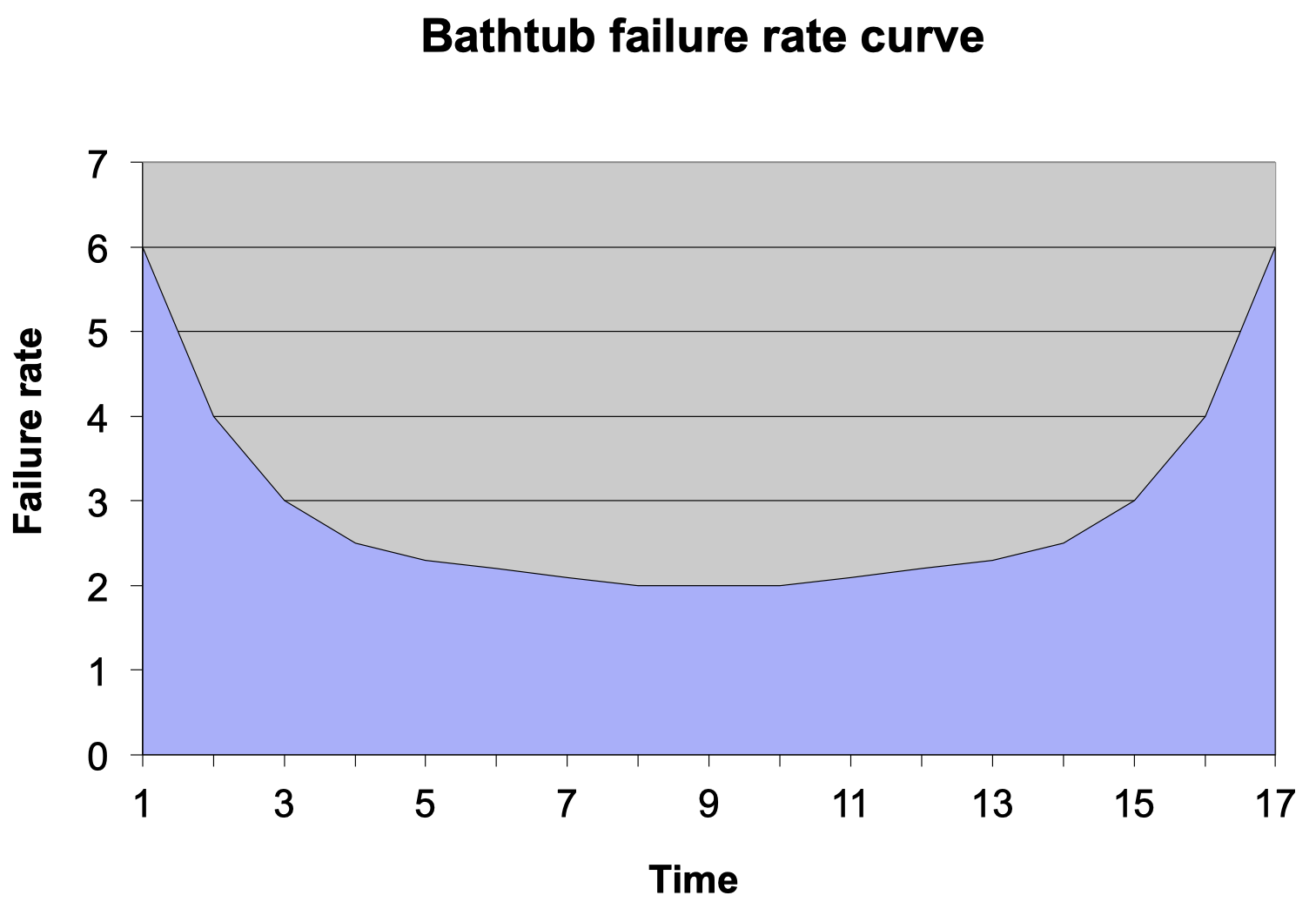
上图展示了大部分系统所遵循的浴缸失效率曲线。假设现在有一个正在运行的系统,其初始的失效率将较高,因为在初始阶段,可能有些硬件会失效,而当我们替换掉这些失效的硬件时,随着运行时间增加,失效率将逐渐下降。然后,经过某个时间点后,随着系统运行时间进一步增加,由于硬件过热或者一些其他原因,失效率又会逐渐上升。
失效频率 vs. 持续时间
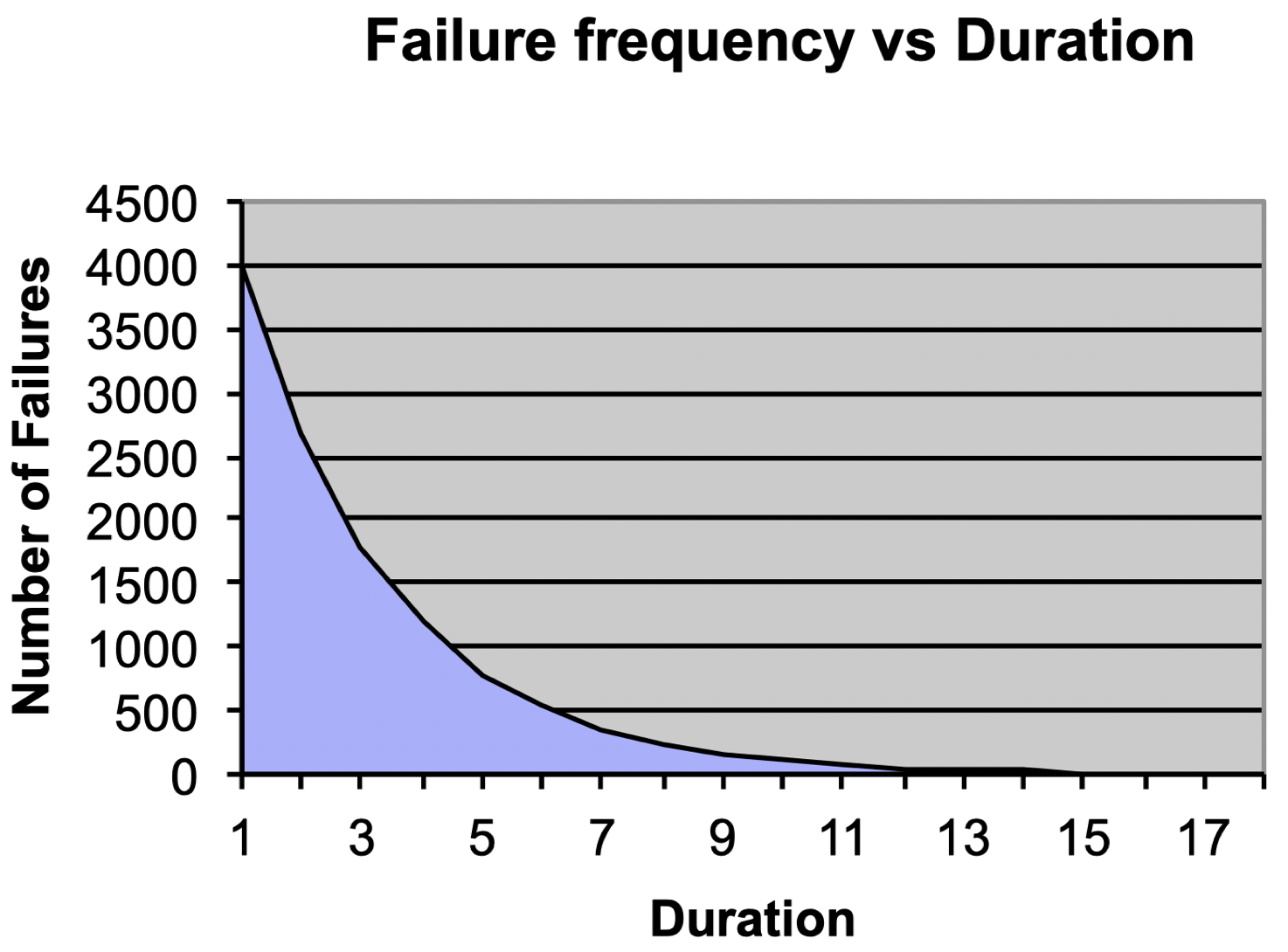
如果我们绘制出失效次数和持续时间二者之间的关系,一些小的失效问题的持续时间较短,可能只需要 1 个小时就能恢复正常,这类事件发生次数通常较高;而某些失效的修复时间可能需要 10 个小时以上,这类失效的发生率通常较低。
2.6 磁盘失效率

这里是一个磁盘失效率的例子。可以看到:软数据读取错误的 MTTF 约为 1 小时,无其他不良影响,恢复方式为重新尝试;可屏蔽的硬数据读取错误的 MTTF 约为 3 天,导致后果是重新映射到新的扇区,重写正确数据,恢复方式为 ECC (纠错编码);而导致设备需要修复的错误类型的 MTTF 约为 5 年,导致的结果为数据不可用,恢复方式为磁盘维修。
3. 投票 (Voting)
3.1 多数投票
现在,我们来看一个用于系统容错设计的基于多设备的简单策略:投票 (Voting)。
假设现在我们系统中有 3 台设备/模块,这被称为 三工 (3-plex) 系统 (如果有 $n$ 台设备即为 n 工 ($n$-plex) 系统)。如果其中一个磁盘上的数据发生错误,这 3 台设备将进行投票,其中 2 台上数据可以正常工作,那么根据 多数投票 (majority voting) 结果,即使某个设备发生数据错误,系统仍然能够正常运行。
根据多数投票的不同考虑方式,可以分为两类:Failvote (失败表决) 和 Failfast (失败即停)。
-
Failvote:在 所有模块 上实行多数表决。例如:对于 3-plex 系统,多数意味着 $2/3$;对于 5-plex 系统,多数意味着 $3/5$。
Failvote 使用两个或多个模块并比较其输出。如果没有多数输出达成一致,则停止。尽管包含重复 (一对) 模块的失败次数是单模块失败次数的两倍,但其提供了清晰的失败语义。
-
通过三工化,系统的 MTTF 降至单个模块的为 $5/6 = 1/3 + 1/2 = 0.83$
令 $M$ 为单个模块的 MTTF。三工系统中的任意一个模块的 MTTF 均为 $M/3$,然后,两个工作模块中的任意一个模块的 MTTF 为 $M/2$。整个系统总的 MMTF 为:
\[M \times(1/3 + 1/2)= 0.83M\]
-
-
Failfast (voting):此方案类似于 Failvote,区别在于 Failfast 系统会先检测哪些模块可用,然后在这些 可用模块 上实行多数表决。例如:对于 5-plex 系统,如果其中 2 个模块失效,这种情况下,系统的多数表决只需要剩下 3 个可用模块中的 2 个达成一致即可。
-
对于一个 10-plex Failfast 系统,直到其中 9 个模块都发生故障之前,它都将继续运行;而对于同样模块数的 Failvote 系统,当 5 个模块出现故障时,系统将停止运行。
-
Failfast 系统的可用性要优于 Failvote 系统 (因为在没有多数同意的情况下,后者将停止运行)。
-
例子:考虑一个多模块的 Failvote 系统,其中每个模块的 MTTF 为 $10$ 年,包括软故障。
-
对于一个双工 (Duplex) 系统:$MTTF = 10/2 = 5$ 年。
-
对于一个三工 (Triplex) 系统:$MTTF = 10/3$ (第一次故障) $+ 10/2$ (第二次故障) $= 8.3$ 年。
-
如果三工系统可以屏蔽所有瞬态/软故障,并且硬故障的 MTTF 为 $100$ 年,则系统的 MTTF 为:
\[100 \times(1/3 + 1/2)= 83.7 \text{ 年}\]
总体来看,多数表决策略提高了系统容错,但是和单模块系统相比,多模块系统的 MTTF 降低了。
3.2 Failvote 策略
Failvote 需要 全部设备中的多数 同意才能接受某项操作 (例如:读/写)
-
在三工系统中,我们有 3 台设备,我们至少需要其中 2 台设备同意才能继续进行操作。如果设备无法正常工作,并且我们没有多数表决,那么系统将停止。
-
方案 A:所有设备的都工作,所有设备都同意,那么接受操作($3/3$ 同意)
-
方案 B:其中两台设备正常工作,并且这两台设备都同意,那么接受操作($2/3$ 同意)
-
方案 C:其中两台设备正常工作,但这两台设备都不同意,那么不接受该操作,因为同意占比没有达到 $2/3$。
-
如果我们有 10 台设备,那么需要其中 6 台能够工作并就该决定达成共识,才能够继续运行。而当第 5 台设备失效时,系统将停止,因为剩余的能够进行同意表决的工作设备不足 6 台。
3.3 Failfast 策略
在 Failfast 中,我们只关心 工作设备中的多数 表决。我们假设我们能够知道哪些设备正在工作,因此,我们可以继续进行操作,直到只剩下 2 个工作设备为止,此时如果双方都同意,那么可以继续采取行动,但是如果二者表决结果不同,则系统将停止。
对于一个 10-plex 的 Failfast 系统:
- 0 台设备有故障,我们有 10 台设备在工作,至少需要 6 台同意才能接受操作
- 1 台设备有故障,我们有 9 台设备在工作,至少需要 5 台同意才能接受操作
- 2 台设备有故障,我们有 8 台设备在工作,至少需要 5 台同意才能接受操作
- 3 台设备有故障,我们有 7 台设备在工作,至少需要 4 台同意才能接受操作
- 4 台设备有故障,我们有 6 台设备在工作,至少需要 4 台同意才能接受操作
- 5 台设备有故障,我们有 5 台设备在工作,至少需要 3 台同意才能接受操作
- 6 台设备有故障,我们有 4 台设备在工作,至少需要 3 台同意才能接受操作
- 7 台设备有故障,我们有 3 台设备在工作,至少需要 2 台同意才能接受操作
- 8 台设备有故障,我们有 2 台设备在工作,那么需要这 2 台都同意才能接受操作
- 9 台设备有故障,我们有 1 台设备在工作,那么系统将停止,因为没有可用的多数表决
3.4 相关概率
N-plex 修复:在这种配置下,设备故障一旦被检测到,其修复的平均时间为 MTTR (平均修复时间)。有时 MTTR 只是需要更换设备的时间。
最新磁盘设备的典型值:
- $MTTR =$ 几小时 (假设我们有备用磁盘) 到 1 天
- $MTTF =$ 750000 小时 (大约 86 年)
系统中单个模块/设备不可用的概率为:
\[P_1 = \dfrac{MTTR}{MTTF + MTTR}\cong \dfrac{MTTR}{MTTF} \quad (\text{如果}\; MTTF \gg MTTR)\]系统中 ($n-1$) 个模块不可用的概率为:
\[P_{n-1}=\left(\dfrac{MTTR}{MTTF}\right)^{n-1}\]系统中单个模块/设备失效的概率为:
\[P_f = \dfrac{1}{MTTF}\]对于一个多模块系统,如果其中一个模块失效了,整体系统仍然可能是可用的,例如:在 RAID 6 中,我们有多个磁盘,即使其中某个磁出现故障,我们仍然可以通过其余磁盘上的数据和校验位进行数据恢复,使得系统继续运行。
系统由于特定的第 $i$ 个模块失效而最终发生故障的概率为:
\[P_f \cdot P_{n-1}= \left(\dfrac{1}{MTTF}\right) \cdot \left(\dfrac{MTTR}{MTTF}\right)^{n-1}\]一个 n-plex 的 Failfast 系统失效的概率为:
\[P_{n-plex} = \left(\dfrac{n}{MTTF}\right) \cdot \left(\dfrac{MTTR}{MTTF}\right)^{n-1}\]一个 n-plex 的 Failfast 系统的 MTTF 为:
\[MTTF_n = \left(\dfrac{MTTF}{n}\right) \cdot \left(\dfrac{MTTF}{MTTR}\right)^{(n-1)}\]4. Old-New Master
我们已经介绍了基于 Voting 的容错技术,现在我们来学习另外一种容错技术:old-new master。这种方法很简单,但是在大部分数据库系统中很少应用。
- 将要执行的所有更新 (事务) 记录在单独的文件 (稳定存储) 中
- 在晚上 (通常) 使用旧 (前一天) 的母版和批量更新 (事务) 生成一个单独的新 (第二天) 母版。
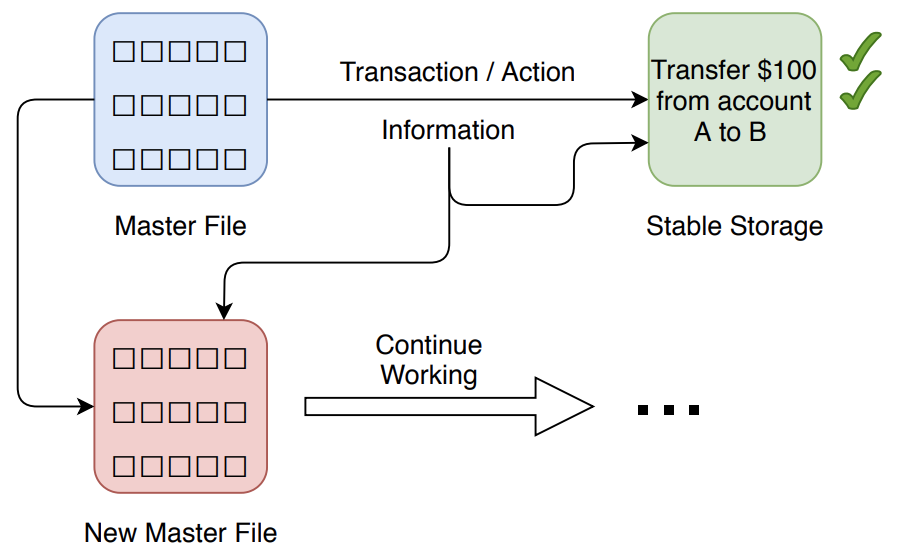
假设现在有一个银行系统,我们有一个 master 文件 (实际上它不是单个文件,而是一个文件集合),其中包含了所有我们需要的数据值,例如:账户名称、ID、余额等等。对于所有这些信息,有一些相应的事务/操作请求,例如:从一个银行账户转账到另一个账户。所有这些事务/操作相关信息都被存储在一个稳定存储 (stable storage) 中。然后,在某个事务发生率较低的时段 (例如:每天晚上),我们将创建一个新的 master 文件,其中包含了旧的 master 文件在经过事务/操作更新之后的信息 (例如:从账户 A 转账 100 美元到账户 B 之后, 两个账户余额将更新)。然后这个新的 master 文件将继续在系统中工作。这些事务/操作处理的过程是离线的,所以当出现任何问题时,我们并不知道发生了什么,直到第二天这些事务/操作实际上被完成之后。
这种更新模型为我们提供了容错能力,因为只要我们有旧的 master 文件和要执行的事务,我们就总是可以在第二天产生新的 master 文件。
但是,这种模式的问题是:它不是在线处理,如果事务失败,要等到第二天才会通知客户。
5. 软件可靠性
软件可靠性和硬件可靠性之间的主要区别:
- 硬件可靠性要求容忍 组件 故障。
- 软件可靠性要求容忍 设计和编码 错误。
- 硬件和软件之间的区别越来越小,因为大多数硬件单元都具有大量的软件组件。这些系统通常称为 嵌入式系统 (embedded systems)。
5.1 N 版本程序设计
N 版本程序设计 (N-version programming):为程序设计 $n$ 个版本,仔细地测试每个版本,然后并行地运行所有 $n$ 个版本的程序,选择 $n$ 个结果中占大多数的作为最终结果,利用这种设计差异就能够屏蔽许多故障。
- 使用 n 个并行运行的程序,对每个答案进行多数表决
- 优点是设计和编码的多样性可以屏蔽许多故障
5.2 事务
事务 (Transactions):把每个程序当成一个具有一致性检查的 ACID 状态转换来写。事务的最后,如果一致性检查不满足,终止事务并重新开始。第二次重新运行事务就会工作起来。
- 每个程序都被编写为带有一致性检查的 ACID 状态事务。
- 在没有适当恢复 (修复) 的情况下重新启动应用程序会使系统非常不可靠。
- 甚至一个事务处理系统也无法容忍应用程序错误。
- Bohrbug:以物理学家 Niels Bohr 命名,这些是确定性的 bug,相对容易处理。
- Heisenbug:以物理学家 Werner Heisenberg 命名,这些 bug 是偶然出现的瞬时 (非确定性) 软件错误,通常与负载条件和定时 (竞争条件) 有关。
5.3 故障
设计容错程序需要一个模型,模型包括三种实体类型:进程、消息 和 存储。每个实体有期望行为集合和故障行为集合。
故障行为可以分为 预期故障 (设计中可容错的故障) 和 非预期故障 (设计中不可容错的故障)。其中,非预期故障可以描述为稠密故障和拜占庭式故障。
-
稠密故障 (Dense Faults):算法是 $n$ 容错,系统在一段时间内最多可以容忍 $n$ 个故障。如果故障数超过 $n$,则系统可能会中断服务。
-
拜占庭式故障 (Byzantine Faults):这类故障不是模型的一部分,并且在设计时没有考虑到容忍此类故障。例如:设计模型时一般不考虑诸如地震之类的环境问题。
5.4 如何提高软件可靠性
数据定期传输 (Periodic Transfer of data):建立进程对。一个名为 主进程 (Primary Process) 的进程将完成所有工作,直到其失败。然后,另一个进程,称为 备份进程 (Backup Process),将接管主进程的工作,继续计算。为了做到这一点,主进程需要周期性地发送消息给后备进程,表明自己还处于活动状态,并且还需要将其状态传输给后备进程。如果后备进程在两个消息周期中没有从主进程接收到该消息,它就假设主进程已经失败,并且接管主进程的工作,接管分为以下三种形式:
-
检查点重启 (Checkpoint-restart):主进程将自己的状态记录在一个双工存储模块上。在接管时,后备进程从双工存储中读取主进程状态,然后恢复应用程序。
-
检查点消息 (Checkpoint messages):主进程将其状态更改作为消息发送给后备进程。 接管时,备份将从最近的检查点消息中获取其当前状态。
-
持久进程 (Persistent):后备进程以空状态重新启动,并允许事务处理机制清除所有尚未提交的事务。这是大部分数据库系统所采用的方法。
高可用存储 (Highly available storage)
- 写入多个存储模块
- 具有某种校验和,以确保以很高的概率正确读取数据
- 磁盘镜像就是一个例子
- 阴影化是另一种镜像技术,允许原子写操作
高可用进程 (Highly available Processes)
- 进程配对
- 基于事务的重启
- 检查点重启
6. 如何提高通信可靠性
我们已经介绍了如何提高硬件和软件的容错机制,现在我们将介绍有关通信的容错机制。除了前面提到的备份进程中的消息传递之外,不同系统之间还存在一些其他类型的消息传递,例如:分布式系统。
通常,存在两种类型的消息:发送消息 (messages sent) 和 接收消息 (messages received)。然后,为了提升通信可靠性,我们还引入了另一种消息类型:确认消息 (acknowledge messages)。
假设现在我们有一个分布式系统,它包含两个子系统:

其中:
- Out $=$ number of messages sent
- In $=$ number of messages received
- Ack $=$ number of acknowledgements
现在,右侧子系统往左侧子系统发送了一条消息。可以看到右侧子系统中 Out 数量从之前的 $6$ 增加到了 $7$,然后,消息 $7$ 被传递给左侧子系统:

如果左侧子系统成功接收到该消息,那么,其中的 In 数量将从之前的 $6$ 增加到 $7$。而由于成功接收,左侧子系统将发送一条确认消息给右侧子系统,告知其消息 $7$ 已经收到:

而在右侧子系统接收到左侧子系统发送过来的确认消息后,其 Ack 数量将从之前的 $6$ 增加到 $7$。当整个过程完成之后,最初的消息发送方将知道消息已经成功送达:

这些通信信息可能需要存储在一些诸如硬盘之类的稳定存储中。例如:为了确保后备进程能够正确运行,进程之间的通信信息需要保存在稳定存储中,我们来看一下这个过程是如何完成的。首先,为后备进程创建一个检查点,因此,它可以从该检查点状态开始接管主进程:
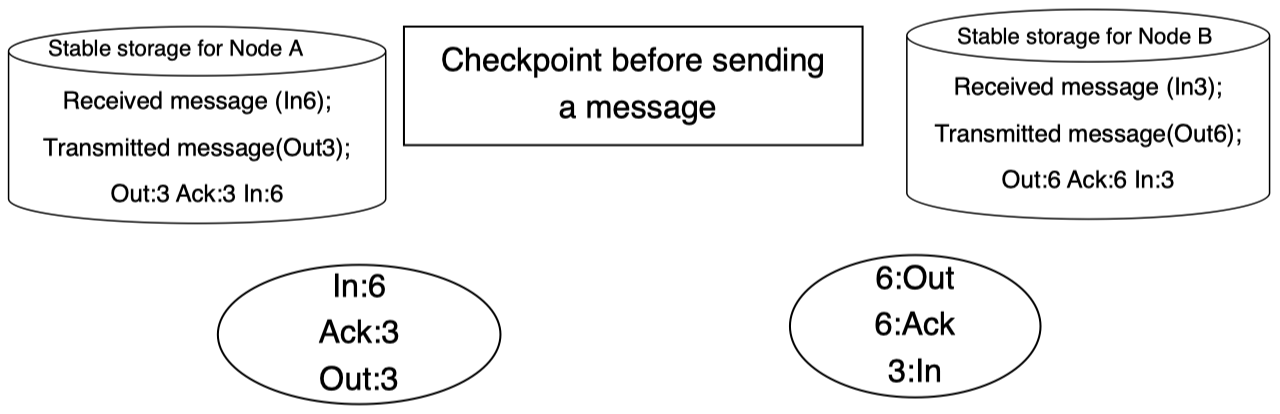
当右侧子系统发送消息时,需要对应的存储来记录该事务消息及其对应 ID:
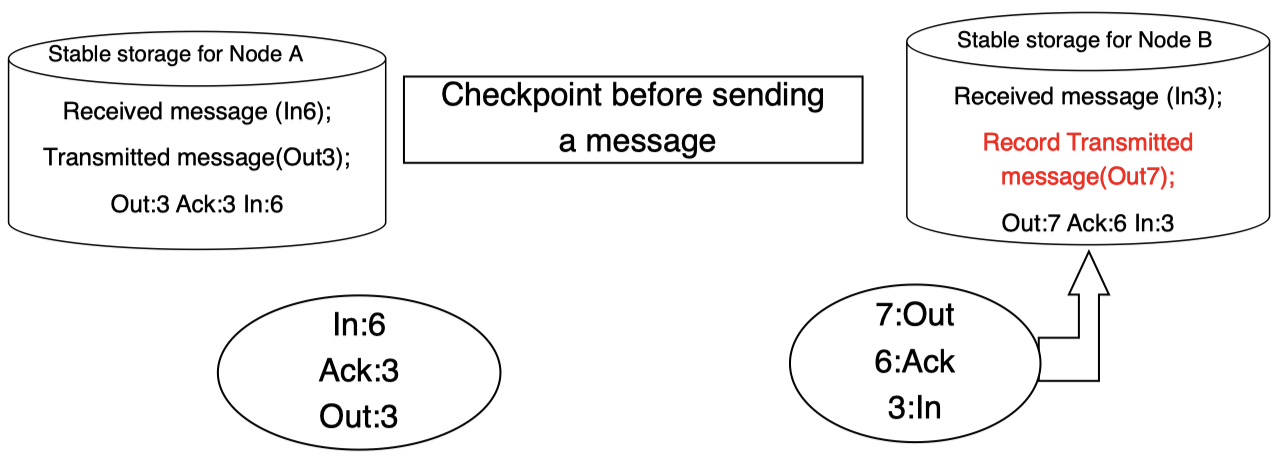
然后,消息将被发送:
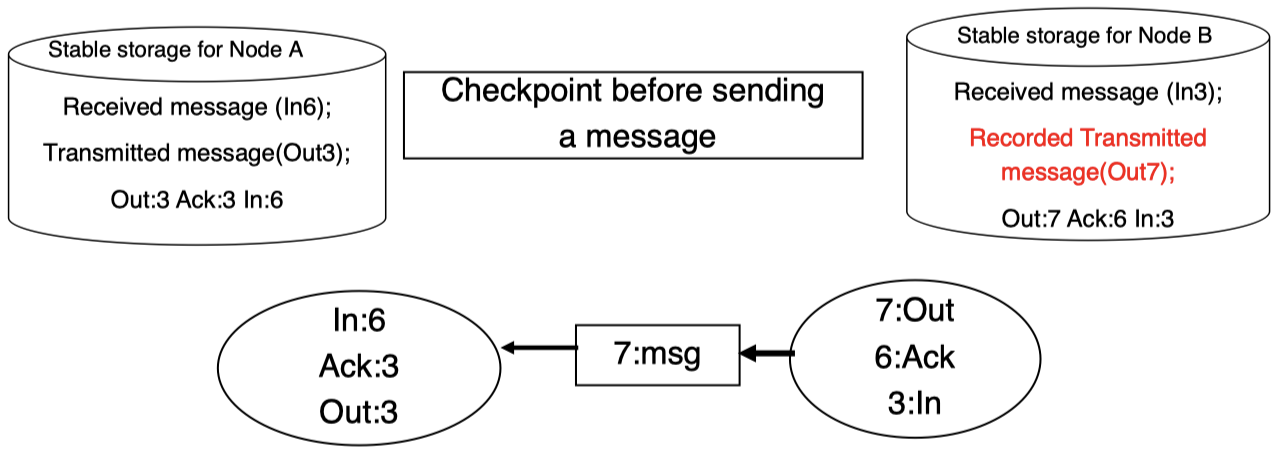
当左侧子系统接收该消息时,同样,在其对应存储中对该消息及其 ID 进行记录:
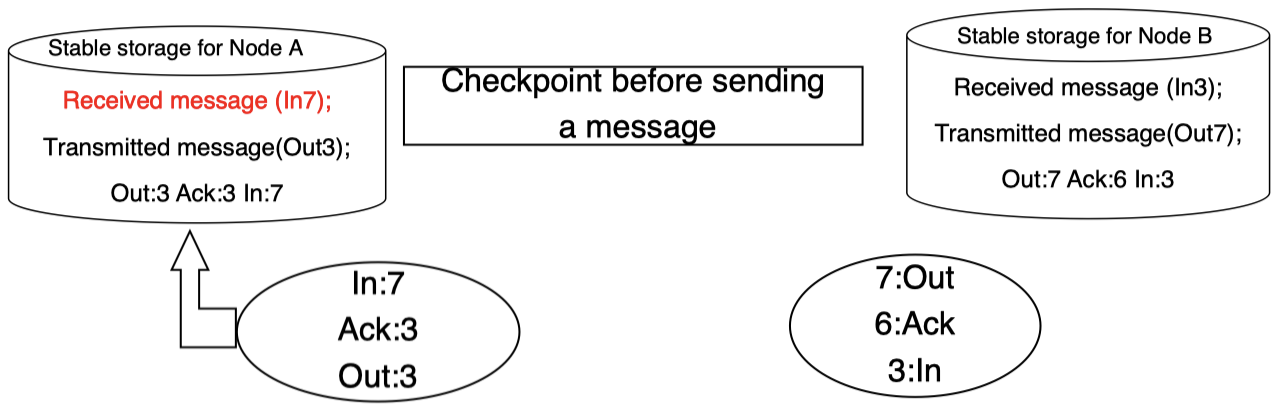
然后,接收方将发送确认信息给发送方:
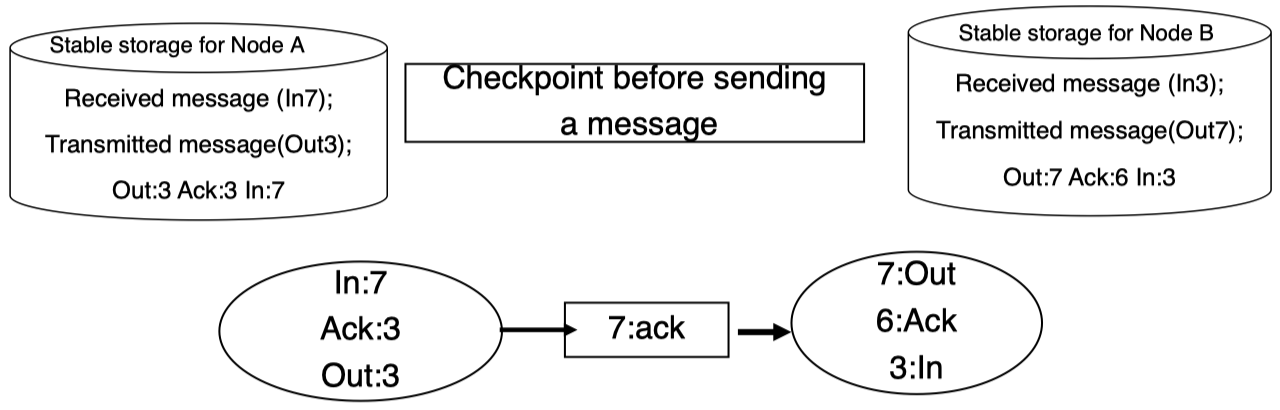
发送方接收确认信息并根据其 ID 更新 Ack 的值:
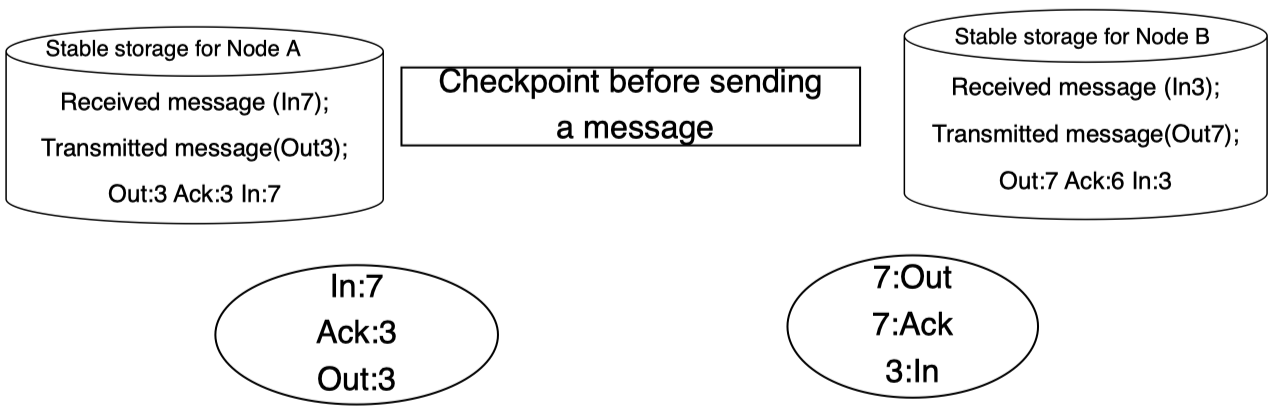
最后,同步更新其稳定存储中的 Ack 的值:
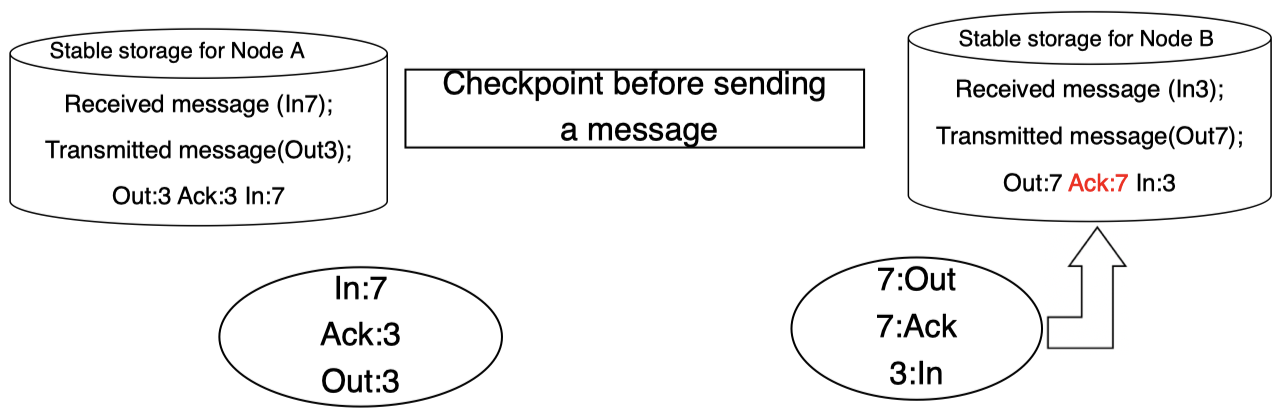
这两个稳定存储为每个对应的后备进程创建检查点,以确保接管正确。
7. 总结
提高系统的可靠性,具体性能方面涉及:
- 提高 CPU、内存和存储单元的硬件可靠性。这可以通过采用大量冗余实现,例如:N-plex 系统。
- 通过采用进程对或者基于事务的恢复,可以提高软件可靠性。
- 通信系统的可靠性不仅需要硬件冗余,而且还需要保证消息的发送和接收,这可以通过使用稳定存储,以及采用重传和重复确认机制实现:直到消息被传递和确认为止。
下节内容:面向事务的计算
本作品采用知识共享署名-非商业性使用-相同方式共享 4.0 国际许可协议进行许可。 欢迎转载,并请注明来自:YEY 的博客 同时保持文章内容的完整和以上声明信息!