高级数据库系统 COMP90050 课程笔记

高级数据库系统 05：并发控制

墨尔本大学 COMP90050 课程笔记

Posted by YEY on July 14, 2020

Lecture 05 并发控制

参考教材：Transaction Processing: Concepts and Techniques, Jim Gray and Andreas Reuter, Morgan Kaufmann, 1993

1. 并发

1.1 并发问题

本节课中，我们将讨论当多个事务同时访问某个共享数据资源时的一个常见问题：并发问题 (Concurrency Problems)。

这里，共享资源可以是一个变量、一些数据，或者一个磁盘块。

下面是一个相关例子，其中共享资源是一个名为 counter 的变量，其初始值为 $100$。

第一个事务 Task1 在 counter 上加了 $10$，第二个事务 Task2 在 counter 上加了 $30$。那么，由于这些事务是并发运行的，在 Task1 和 Task2 都执行完毕后，counter 变量的最终值将是多少呢？

上面的 (a)、(b)、(c) 三个选项对应了三种可能的情况，具体取决于最终的 counter 值是由哪个 Task 返回的。下图给出了这三种情况对应的操作序列：

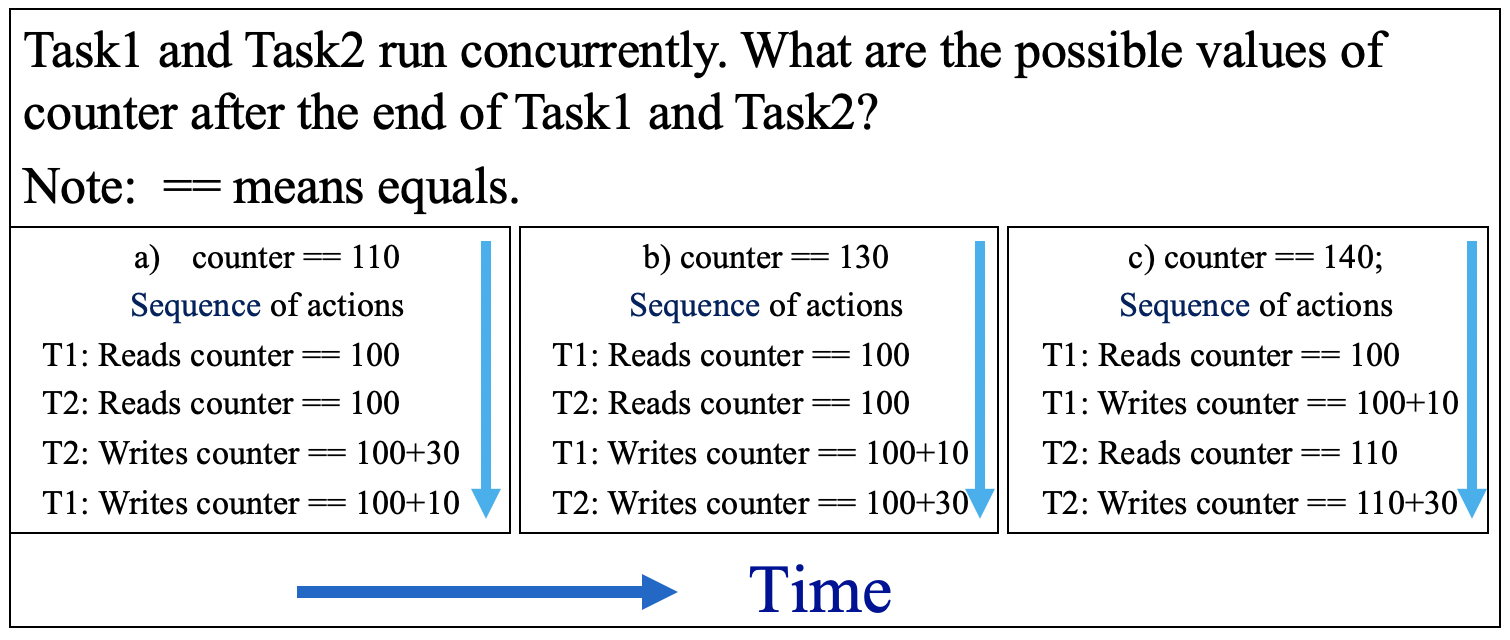
如果不同的 Task 执行顺序将导致得到的变量 counter 的最终值不同，那么对于这种多个事务并发访问某个共享资源时存在的不确定性问题，我们需要采取某种解决方案。

一种保证并发事务正确执行的策略是：当 Task1 和 Task2 同时访问某个共享变量时，我们可以强制要求当其中一个事务正在对该共享资源进行更改时，另一个事务不能对该资源做出任何更改。

1.2 并发控制的目的

  • 在相互冲突的事务之间进行强制隔离 (通过独占机制)。
  • 通过保持事务执行的一致性来保持数据库的一致性。
  • 解决 “读-写” 和 “写-写” 冲突。

2. 并发控制：独占访问的实现

有许多不同的方法来保证对于共享资源的独占访问：

  • Dekker 算法 (使用代码)
  • 操作系统支持的 原语 (primitives)，例如 锁 (Lock) 和 解锁 (Unlock) (通过中断调用)
  • 原子机器指令 (Atomic machine instructions)，例如 test and set 或者 swap 指令 (自旋锁)，所有现代处理器都支持某种形式的 自旋锁 (Spin Locks)。

2.1 独占访问的实现：Dekker 算法

Dekker 算法

这里我们有两个事务 T1 和 T2，然后有三个全局变量 c1、c2、turn，这些变量都可以被 T1 和 T2 访问。利用这些全局变量，我们可以检查某个事务是否在对这些共享资源进行独占访问。

例如对于 T1，它试图更改某些全局变量的值，并且在成功更改之前会反复尝试。假设现在 c1 和 turn 的值被更改了，算法将检查 c2 和 turn 的值是否已经被另一个事务 T2 更改为了满足条件的值。如果满足条件，则说明在 T1 成功更改之前，另一个事务 T2 已经得到了独占访问，然后，算法将进入循环直到 T1 成功得到独占访问。一旦成功，T1 将使用资源，变量 counter 记录了资源使用的次数。在使用资源后，T1 将全局变量 c1 的值设置为 0，以确保另一事务 T2 能够满足成功使用共享资源的所需条件。当 T2 试图对全局变量进行更改时，算法将判断条件 {c1 == 0 or turn == 2} 是否满足，如果条件满足，说明 T1 此时没有使用共享资源，然后 T2 可以独占使用这些资源。同理，当 T2 使用完资源后，它将 c2 设置为 0，以确保 T1 能够满足独占访问资源的前提条件。

优点：

  • 几乎不需要硬件支持
  • 如果锁争用 (即访问锁的频率) 低，则该算法将很高效

缺点：

  • 需要对主内存进行原子读写，这是一个内存访问时间周期的独占访问
  • 当涉及两个以上的事务/进程时，代码的实现将非常复杂
  • 对于两个以上的进程，该算法将难以理解
  • 占用大量存储空间
  • 使用繁忙等待 (即当 T2 处于运行过程中时，T1 由于不满足使用资源的前提条件而陷入长时间的循环中)

为了克服 Dekker 算法的缺点，另一种策略是使用锁和解锁，具体包含两种形式：(1) 操作系统支持的原语；(2) 自旋锁。

2.2 独占访问的实现：操作系统支持的原语

操作系统支持的原语，例如锁和解锁：

优点：

  • 通过中断调用，将请求传递到操作系统以实现所需的锁请求
  • 不需要特殊硬件
  • 不使用繁忙等待，因此如果锁争用较高，则更高效
  • 解决方案与进程数无关
  • 与先前的方案不同，该方案与机器无关

缺点：

  • 通常非常昂贵 (由于实现涉及中断调用，需要保存请求过程的上下文，因此需要执行数百至数千条指令)
  • 如果系统具有对称多处理器，则需要使用自旋锁在内核中实现 OS 原语

2.3 独占访问的实现： 原子机器指令

原子机器指令，例如：test and set 或者 swap 指令 (自旋锁)。所有现代处理器都支持某种形式的 自旋锁。

优点：

  • 实现非常简单
  • 与 Dekker 算法不同，该算法不依赖进程数
  • 如果锁争用较低，则非常高效：所有数据库系统都使用它们
  • 在对称多处理器计算机中是必需的

缺点：

  • 需要硬件支持–需要能够锁定总线 (CPU 和内存 + 任何其他设备之间的通信通道) 长达两个内存周期 (一个用于读取，一个用于写入)。在此期间，不允许其他设备访问此存储位置。
  • 使用繁忙等待

3. 信号量

你可能听说过一个和锁机制相关的术语：信号量 (Semaphores)。它源自用于火车的相应机制：仅当信号灯熄灭时，火车才允许通过一段轨道。当火车通过轨道时，将亮起信号灯，直到火车驶离该路段为止。

计算机信号量具有一个 get() 例程 (routine)，用于获取信号量 (可能等待直到其处于空闲状态)，以及一个对偶的 give() 例程，用于使该信号量返回到空闲状态 (可能通知/唤醒一个等待进程)。

信号量是非常简单的锁。实际上，它们被用于通用锁的实现。

4. 原子操作的实现

4.1 原子操作的实现：test and set

第一种原子操作实现被称为 test and set。

黄色方框部分以原子方式执行，内存总线将被锁定长达两个周期 (一个用于读，一个用于写)。如果变量 lock 值为 1，那么将其值重置为 0，并返回 True，这意味着独占锁 授予 (granted)。

在 T1 中，首先通过一个 while 循环获取锁：如果 testAndSet() 返回的值为 fasle，则将继续进行循环；如果为 true，则独占锁被授予给 T1。如果成功得到授予，T1 将对共享资源进行独占访问，变量 counter 记录了访问次数。访问结束后，T1 独占锁将被释放，并且将 lock 的值重置为 1，以确保其他事务 (例如 T2) 现在能够获取独占授予。

那么，这个过程中，黄色方框部分的原子性是如何实现的呢？

假设现在 T1 要获取独占锁，现在 lock 值为 1，if 条件满足，如果在 lock = 0 语句执行后，程序崩溃，那么后续的 return (true) 将不会被执行 (并且之前的 lock = 0 更改将被清空)。这种情况下，T1 在调用 testAndSet 时不会得到任何返回值，而由于该调用发生在 while 循环中，T1 将继续对其进行调用。如果在下一次循环中，成功返回 true，那么 T1 将被授予独占访问权。因此，函数 testAndSet() 的中途崩溃不会对 T1 造成任何影响。通常，如果一个程序在执行中途崩溃，那么在恢复时将清空之前已执行的操作。

4.2 原子操作的实现：compare and swap

现在，我们来看一下第二种原子操作：compare and swap。它被用于多个事务需要对某个共享变量进行更改的情况。

假设 counter 是一个共享变量，它可以被事务 T1、T2 访问和更改。

如果我们按照黄色方框中的顺序进行更改，那么某些赋值或者更新操作将有可能丢失。例如，白色方框中，T2 写入 counter == 100+30 后，T1 又重新写入了 counter == 100+10，那么，之前 T2 的写入将丢失。

为了防止这种丢失情况发生，我们可以采用自旋锁中的 compare and swap 操作：

函数 cs() 接受三个参数：cell 是我们希望更改的共享变量，old 是该变量先前的值，new 是更改后的值。其中的语句以原子方式执行。如果条件 cell == old 满足，说明此时其他事务还没有更改 cell 的值，那么当前事务可以进行 cell == new 更改；否则，我们将当前 cell 的值赋给 old，并且返回 FALSE 以告知有其他事务已经对 cell 进行过更改。

另外，这里的 cs() 的原子操作的实现机制和之前 test and set 中同理。

5. 独占模式信号量的实现

5.1 独占模式信号量的实现

目前为止，我们介绍了涉及两个事务/进程的独占实现，但通常可以有任意数量的事务/进程访问共享资源。对于通用锁的实现，我们有：

  • 一个指向进程队列的指针
  • 如果信号量处于繁忙状态，说明当前有一个进程在使用该共享资源，则指针指向的是拥有该信号量的进程的地址。
  • 如果还有其他等待进程，则信号量指向这些等待进程的一个链表。拥有信号量的进程在此列表的末尾。
  • 使用后，所有者进程唤醒队列中最旧的进程 (先进先出调度程序；当然，还存在其他形式的调度或者没有调度，我们将在之后讨论)

下面是这种模式的一个实现例子：

1
2
3
4
5
6
7
8
9
10
11
12

type long PID

type struct Process{
    PID pid; /*process ID*/
    PCB * sem_wait; /* waiting process are put in the queue */
}

PCB;
PID MyPID (void); /* returns the caller’s process ID */
PCB * MyPCB(void); /* returns pointer to caller’s process descriptor */
void wait (void); /* suspends calling process */
void wakeup( PCB * him) wakes him.

其中，wait() 函数将等待需要被释放的资源，而一旦该资源被释放，wakeup() 函数将唤醒另一个等待进程。

5.2 独占锁信号量操作的实现

进程 结构：

1
2
3
4
5
6
7
8
9
10
11
12

type struct Process{
    PID pid;
    PCB * sem_wait;
}

PCB;
typedef PCB *Xsemaphore

Void initialise( Xsemaphore *sem){
    *sem = NULL;
    return;
}

我们先来看一下第一个实现：锁机制

1
2
3
4
5
6
7
8
9
10

void lock(Xsemaphore *sem){
    PCB * new = myPCB();
    PCB * old = NULL; /*put the process in the semWait queue*/
    do{
        new ->semWait = old;
    } while( ! cs(sem, &old, &new));
    /*if queue not null then this process must wait for a wakeup from the semaphore owner*/
    if (old != NULL) wait(); % OS call
    return;
}

这里，一个新的进程试图获取锁，该进程将被添加进一个进程链表中。如果该进程是该链表中唯一的进程，说明除它之外，没有其他进程，那么该进程将被授予访问和使用共享资源；否则，如果还有其他进程正在使用该资源，则该进程需要保持等待，直到被 wakeup() 唤醒。

下面是 解锁机制 的实现：

1
2
3
4
5
6
7
8
9
10
11

void unlock(Xsemphore *sem){
    PCB * new = NULL;
    PCB * old = myPCB();
    if(cs(sem, &old, &new)) return;
    while(old->semWait !=myPCB()){
        old = old->semWait
    };
    old->semWait = NULL;
    /*wake up the oldest process (first in, first out scheduler)*/
    wakeup(old); % OS Call
}

采用一些更改以确保资源是否处于锁定或者解锁状态。否则，将唤醒最旧的进程，即最早进入队列的进程。

下面是独占信号量数据结构的转换图：

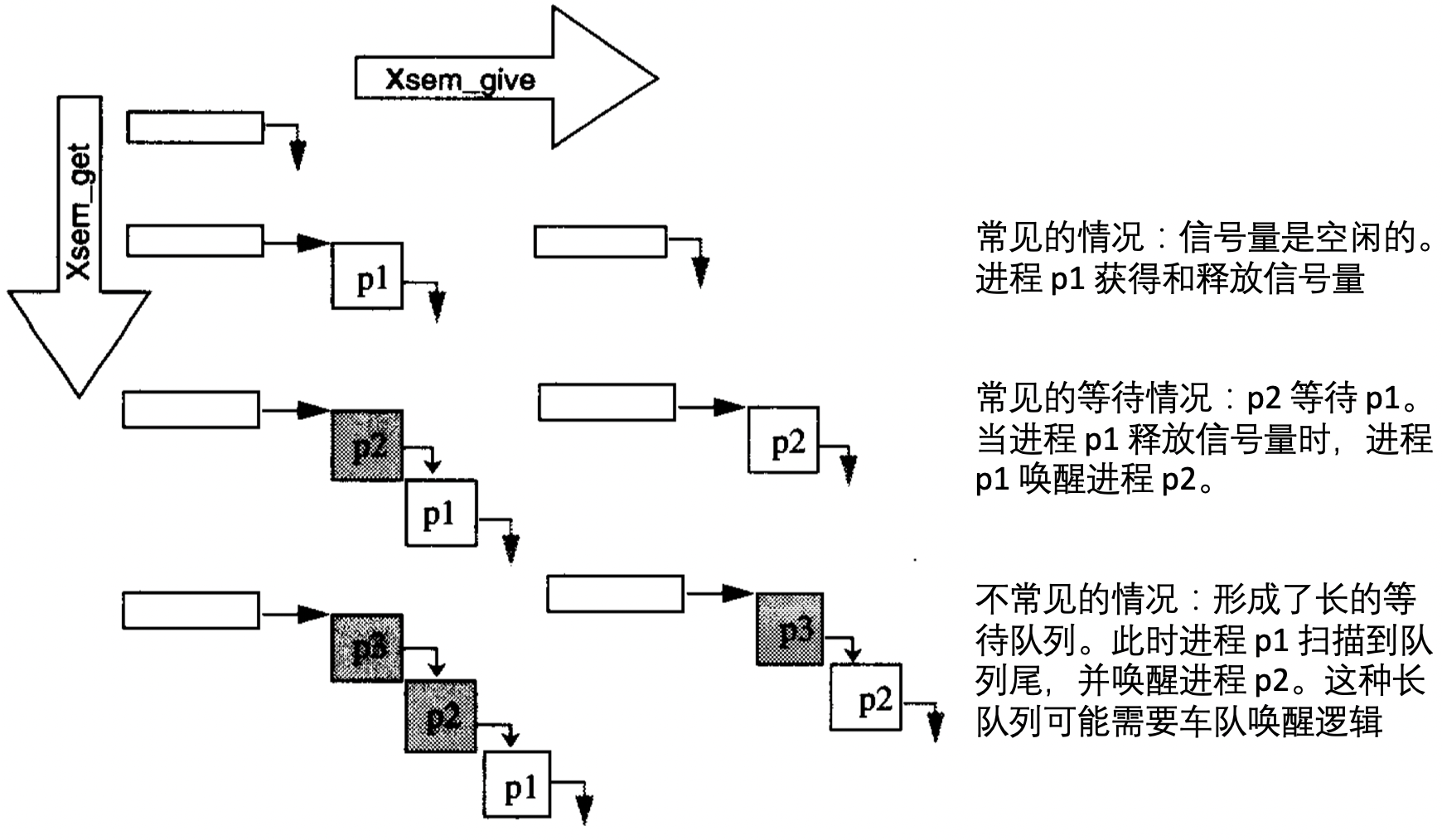
垂直方向转换是由 Xsem_get 调用引起，水平方向转换是由 Xsem_give 调用引起。通常情况下，信号量是空闲的，并且路径是 Xsem_get，Xsem_give。但是，如果进程 p2 在 进程 p1 调用 Xsem_give 之前调用 Xsem_get，等待的情况就发生了。也有一种较为少见的情况：p1 占有信号量很长时间，从而形成了一个很长的进程队列。这种情况下，每个进程都将按照 FIFO 顺序被授予，然后唤醒它的后继进程 (即它在队列中的前驱)。

5.3 车队避免信号量

  • 先前的实现可能会导致一长串等待进程，称为 车队 (Convoy)。
  • 为了避免出现麻烦，进程可以 简单地释放信号量 (将队列设置为 null)，然后在使用后唤醒列表中的每个进程。
  • 在这种情况下，这些进程中的每一个都必须重新执行获取信号量的例程。

下面是相关代码实现，和之前相比，红色字体标出了变化的部分：

如果一个进程没有成功获取到锁，它将等待一段时间，然后将再次请求获取锁。

当解锁完成后 (即进程完成了对资源的使用)，它将唤醒所有等待队列中的进程，所有这些进程将再次请求获取锁，而最早发出请求的进程将成功获得锁。

6. 死锁

6.1 死锁问题

由于锁和解锁机制的实现方式，会存在一种被称为 死锁 (Deadlock) 的情况。尽管死锁不常发生，但是一旦发生，将很难解决。

在死锁情况下，死锁进程中的每个成员都在等待另一个成员释放其所需的资源。

下面是一个非常简单的死锁的例子：

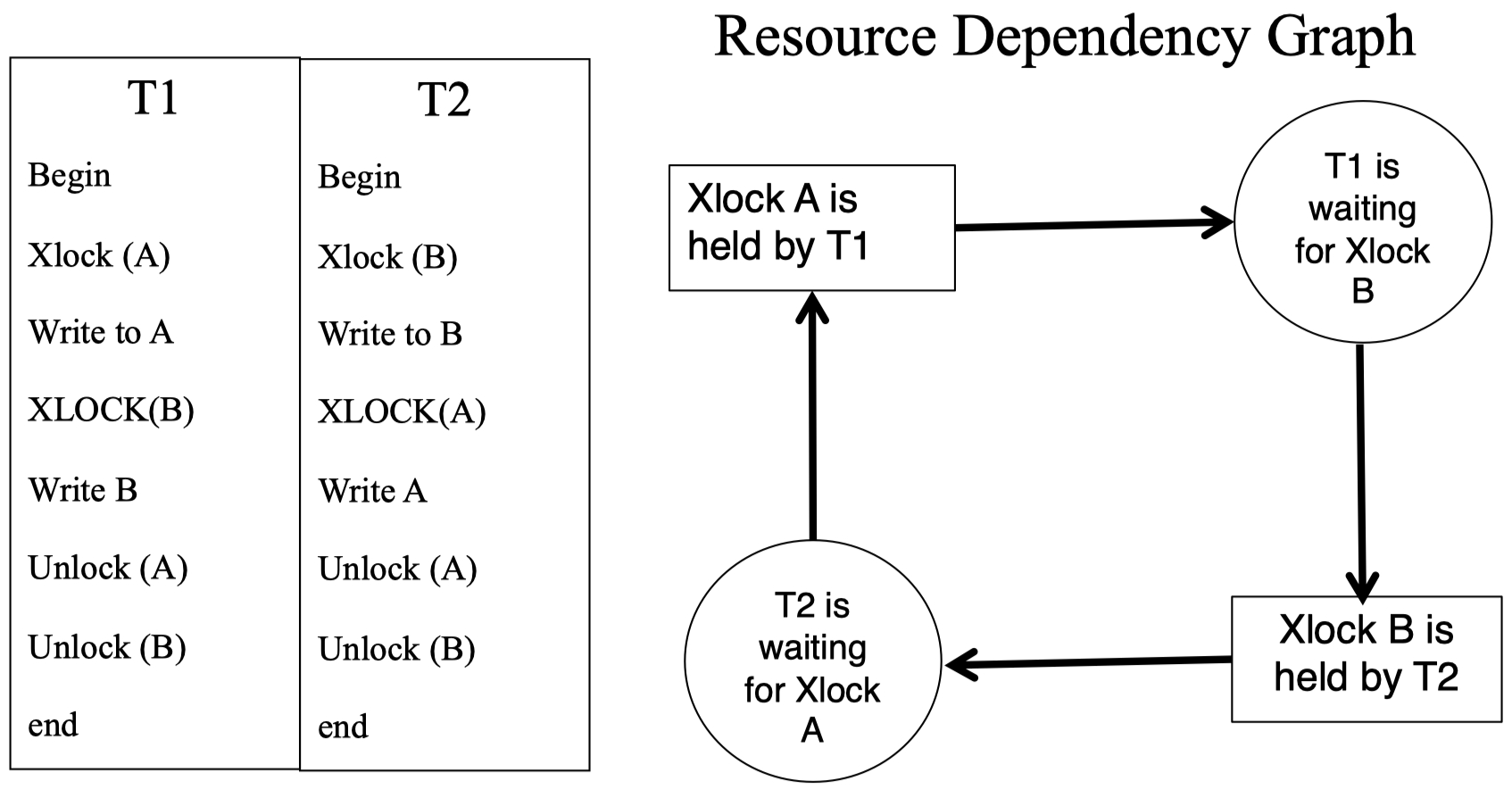
T1 获取了一个独占锁 A，然后 T1 在等待访问独占锁 B 控制的资源；与此同时，独占锁 B 由另一个进程 T2 持有，而 T2 也在等待访问独占锁 A 控制的资源。左边的表格显示了 T1 和 T2 的指令列表。从右图可以看到，这种情况下，整个过程形成了一个封闭环，其中的进程 T1 和 T2 都在等待对方释放相应的共享资源。

6.2 解决方案

对于死锁，通常有以下一些 解决方案：

  • 拥有 足够的资源，因此不会出现等待的情况。
  • 可以简单地 禁止长时间进程等待，如果一个进程等待时间过长，我们只需将其 回滚 (就像杀死该进程一样)。但是，如果这个过程中，日志没有被清除或者回滚出现错误，那么将会创建一个比死锁更糟糕的问题，称为 活锁 (live locks)，活锁无法被解锁因为进程并没有被杀死。因此，通常不会采用这种方案。
  • 资源线性排序，对资源的请求应遵循此顺序。即一个事务可以在请求完第 $I$ 个资源后，再请求第 $J$ 个资源，如果 $J>I$。这种类型的分配可以保证事务之间没有循环依赖性。

下面是一个关于资源线性排序方案的例子：

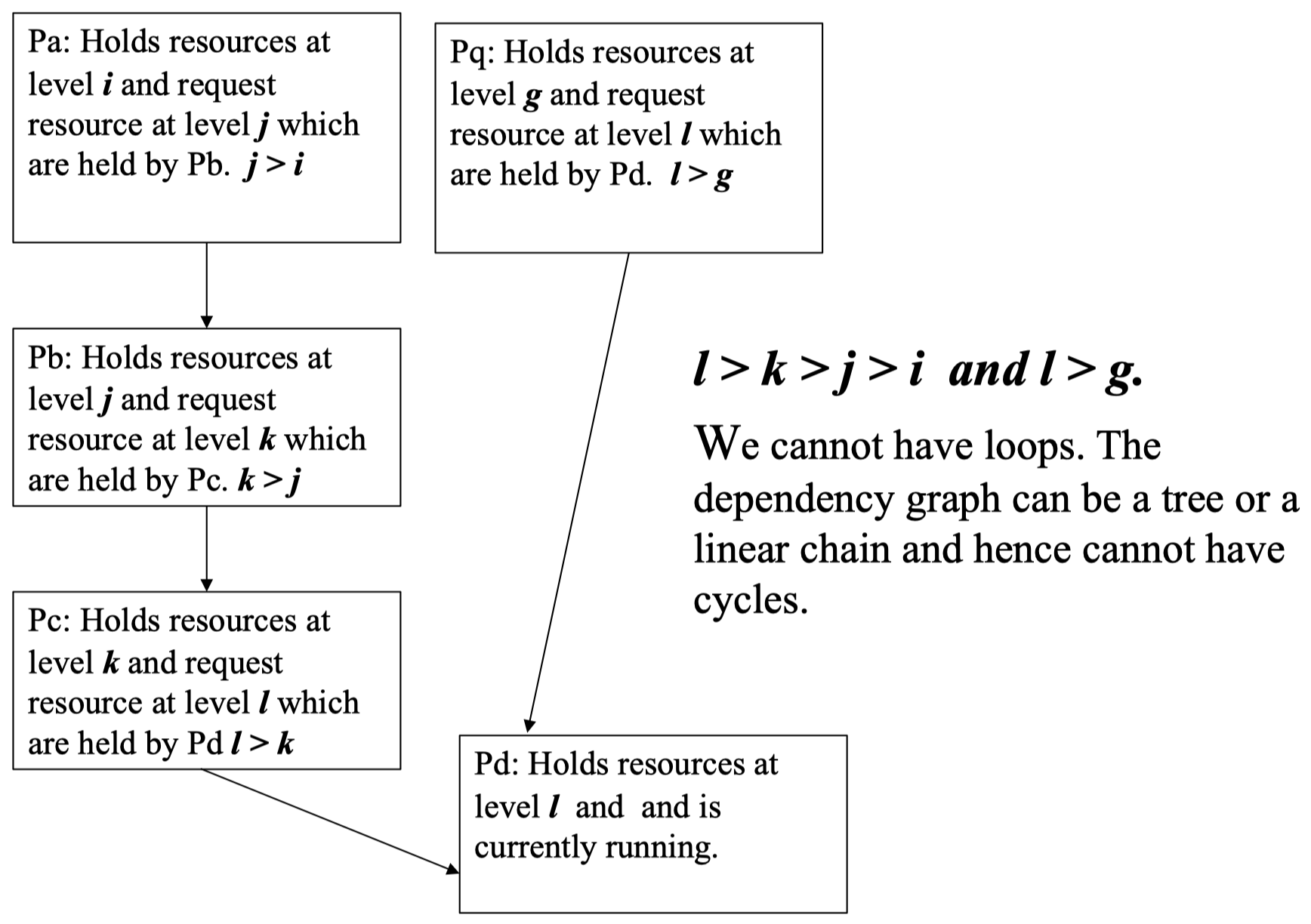
进程 Pa 占用资源 $i$，然后它请求由进程 Pb 正在占用的资源 $j$，并且 $j>i$。根据资源线性排序方案，这种情况是允许的。然后，进程 Pb 占用资源 $j$，并请求由进程 Pc 正在占用的资源 $k$，并且 $k>j$。同理，这也是允许的。类似地，如果我们有一个由很多资源请求组成的长链，并且某个进程正在占用其中最高级别的资源 $l$，当该资源 $l$ 被释放时，占用比其低一级的资源并且正在请求资源 $l$ 的进程将被唤醒。例如这里，资源 $l$ 的级别要比资源 $k$ 和 $g$ 都高，无论后两者中谁的级别更高，进程 Pd 都将唤醒进程 Pe 和 Pq，并且将资源 $l$ 释放。

这种方式保证了进程/事务之间不会出现循环依赖性，依赖关系可能是无环的树状结构或者线性链。因此，这种方式可以避免死锁问题。

6.3 避免/缓解死锁

  • 预声明所有的所需资源，并在单个请求中分配所有资源。
  • 允许一个事务在某个锁上等待一段特定的最长时间，然后如果超时，则将其强制回滚。许多成功的系统 (IBM，Tandem) 都选择了这种方法。
  • 定期检查资源依赖关系图，查看是否存在闭环。如果存在闭环，则回滚 (即终止) 一个或多个事务以消除闭环 (死锁)，并更新依赖关系图 (无环)。所选的事务应该成本较低 (例如，它们不会消耗太多资源)。
  • 许多分布式数据库系统仅维护本地依赖关系图，并对全局死锁采取超时策略。
  • Phantom 死锁：如果我们无法在许多独立的数据库系统之间构建一致的依赖关系图，则会发生 Phantom 死锁。

6.4 相关概率

虽然死锁这种情况很少见，但偶尔确实会发生，这种情况下，数据库需要处理死锁问题。

那么，一个死锁发生的概率是多少呢？

我们假设：

  • 事务数量 $=n+1\cong n\;$ (当 $n$ 非常大时)
  • 每个事务独占访问 $r$ 个锁，即它将连续获取独占锁
  • 数据库中的记录的总条数 $=R$，即总共可以有 $R$ 个锁
  • 平均而言，每个事务持有大约 $\frac{r}{2}$ 个锁 (最小为 $0$，最大为 $r$，所以平均是 $\frac{r}{2}$)
  • 刚刚开始的交易不持有任何交易，而即将完成的交易则持有其中的r个交易
  • 平均而言，其余 $n$ 个事务持有的锁的数量为 $n \cdot (\frac{r}{2})=\frac{nr}{2}$

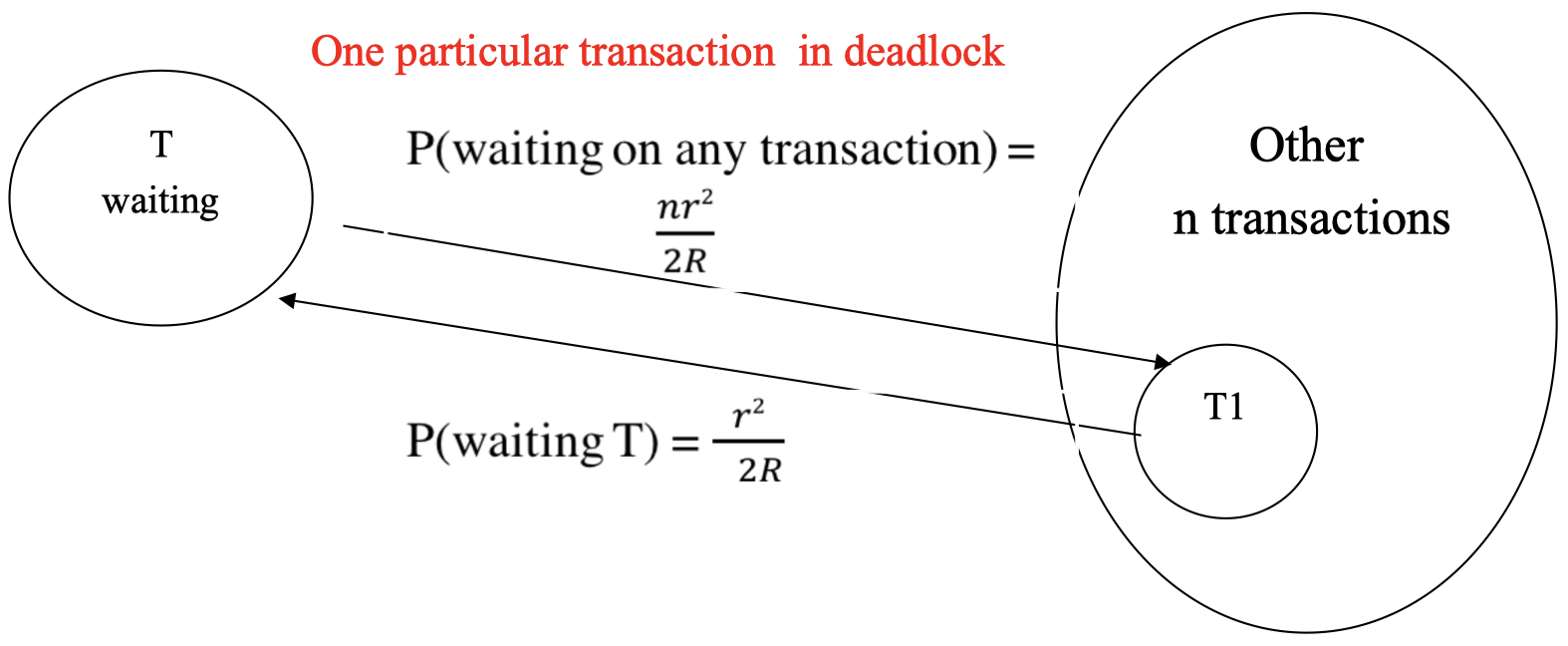
一个特定事务等待某个锁，意味着它需要从被其他 $n$ 个事务独占的 $\frac{nr}{2}$ 个锁中请求一个独占锁，而锁的总数为 $R$。因此，在总共的 $R$ 个锁中，有 $\frac{nr}{2}$ 个锁在请求时将引发等待。

所以，一个特定事务等待某个锁的概率为：

\[PW=\dfrac{nr}{2R}\]

一个事务 (访问 $r$ 个锁) 不需要等待的概率为：

\[\sim PW(T)=\left(1-\dfrac{nr}{2R}\right)^r \approx 1-\dfrac{nr^2}{2R}\]

注意：当 $\varepsilon$ 非常小时，$(1+\varepsilon)^r \approx 1+ r\varepsilon$

一个事务在其生命周期内需要等待的概率为：

\[PW(T)=1-\left(1-\dfrac{nr^2}{2R}\right)=\dfrac{nr^2}{2R}\]

一个特定事务 $T$ 等待某个事务 $T1$，而同时 $T1$ 也在等待 $T$ 的概率为：

\[PW(T)\times \dfrac{PW(T1)}{n}=\dfrac{nr^4}{4R^2}\]

任意两个事务产生死锁的概率为：

$n\times \dfrac{nr^4}{4R^2}=\dfrac{n^2r^4}{4R^2}$

发生死锁的概率：随访问锁的数量 $r$ 以 $O(r^4)$ 增加，随并发事务数 $n$ 以 $O(n^2)$ 增加，并且随数据库大小 $R$ 以 $O(R^2)$ 成反比。

7. 总结

  • 并发问题：为什么我们需要并发控制
  • 独占访问的实现：Dekker 算法、操作系统原语、自旋锁
  • 信号量：获取锁、释放锁、维护进程队列
  • 获取和释放锁的原子操作
  • 信号量队列，避免长时间排队
  • 死锁

下节内容：隔离性

知识共享许可协议本作品采用知识共享署名-非商业性使用-相同方式共享 4.0 国际许可协议进行许可。 欢迎转载，并请注明来自：YEY 的博客 同时保持文章内容的完整和以上声明信息！
CATALOG
    FEATURED TAGS
    随笔 课程笔记 统计机器学习 COMP90051 学习笔记 自然语言处理 COMP90042 PyTorch 人工智能伦理 COMP90087 数据科学多元统计学 MAST90138 AI 自动规划 COMP90054 数据分析 计算统计学与数据科学 MAST90083 高级数据库系统 COMP90050 统计建模 MAST90139 读书 📚 MySQL 学习索引 Hive 技术问题 Jekyll Workshop
    FRIENDS