Lecture 03 线性回归
参考教材:
- Gareth, J., Daniela, W., Trevor, H., & Robert, T. (2013). An intruduction to statistical learning: with applications in R. Spinger.
- Hastie, T., Tibshirani, R., & Friedman, J. (2009). The elements of statistical learning: data mining, inference, and prediction. Spinger Science & Business Media.
1. 线性回归
1.1 什么是线性回归
线性回归是一种简单的监督学习方法,它假设 $Y$ 和 $X_1, X_2,\dots, X_p$ 之间的依赖关系是线性的。
注意:真实的回归函数永远不会是线性。
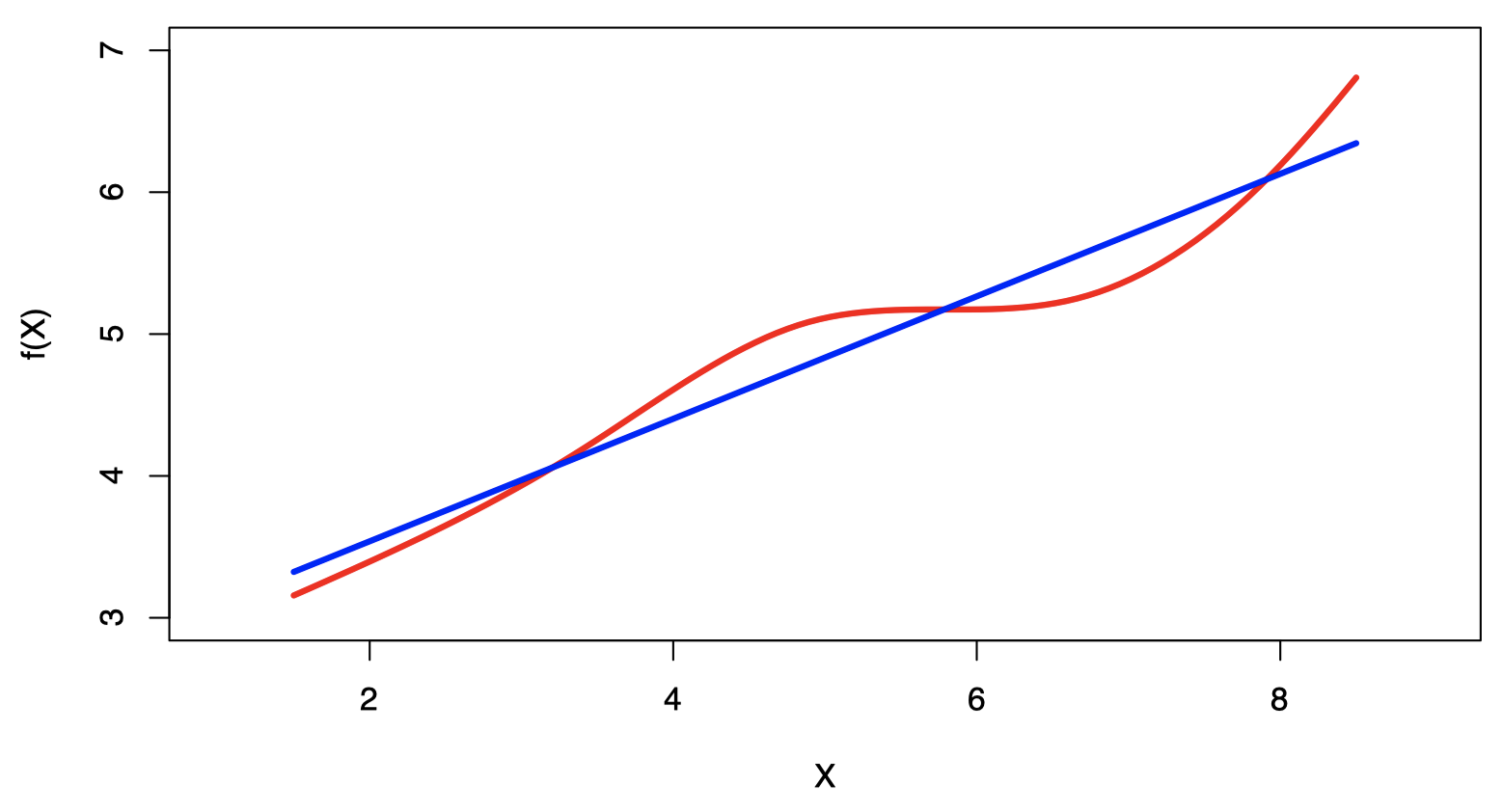
尽管看起来似乎过于简单,但线性回归在概念上和实践中都非常有用。
1.2 例子:广告数据的线性回归
回顾上节课中的广告数据的例子,我们可能会关心以下问题:
- 广告预算和销售额之间是否有关系?
- 广告预算和销售额之间的相关性有多强?
- 哪些媒体有助于提升销售额?
- 我们如何准确地预测未来的销售额?
- 二者之间的关系是线性的吗?
- 不同广告媒体之间是否存在协同作用?
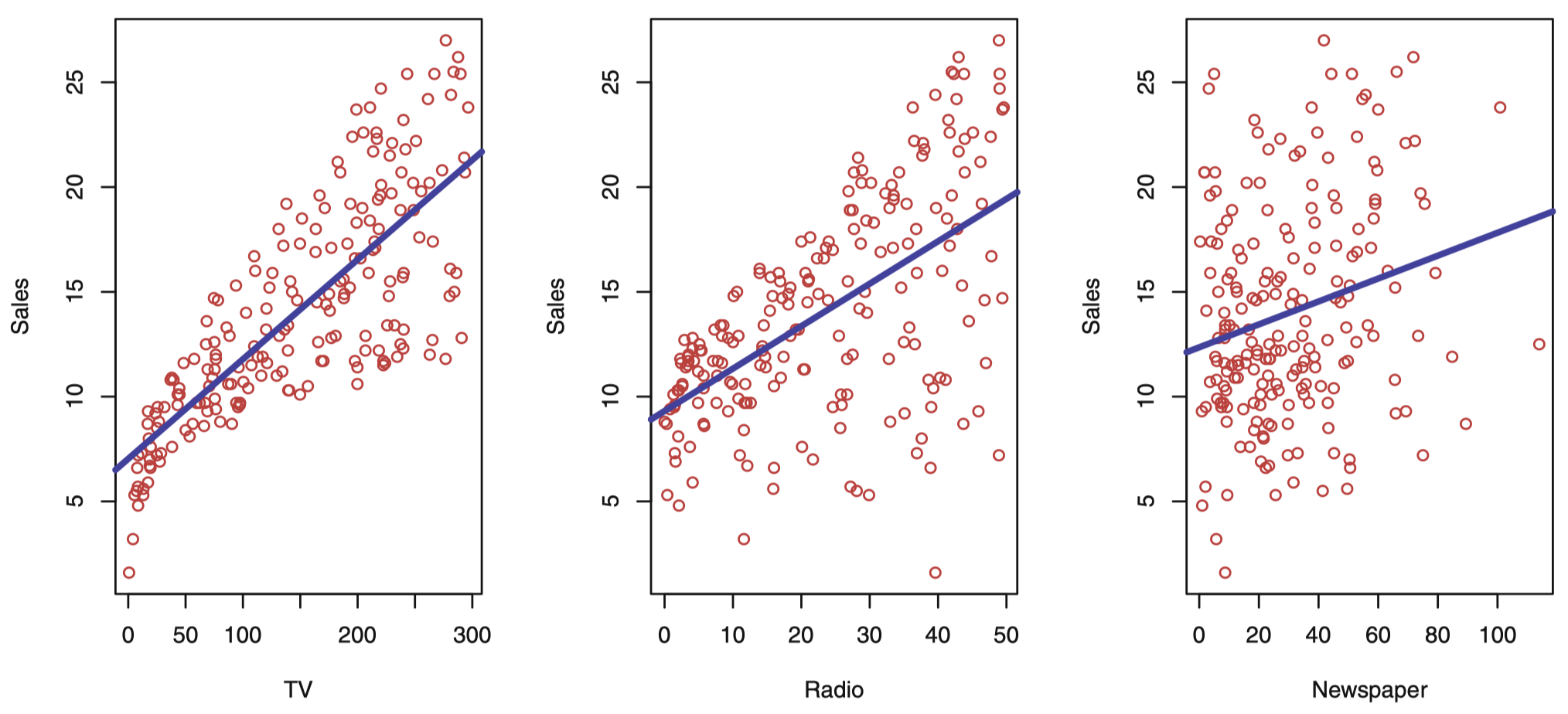
图 2:Advertising (广告) 数据集。这个散点图绘制了 200 个不同市场的 sales (单位: 千) 关于 TV、radio 和 newspager 三种媒体广告预算 (单位: 千美元) 的函数。每个散点图我们都给出了 sales 这个变量通过普通最小二乘法的拟合线,拟合的这个结果将在下节课详解。换句话说,在每个图中的蓝线代表一个线性回归模型,可以用来预测 TV、radio 和 newspager 的 sales。
2. 简单线性回归
我们假设一个模型:
\[Y=\beta_0 + \beta_1 X +\epsilon\]其中,$\beta_0$ 和 $\beta_1$ 是两个未知常数,分别代表 截距 (intercept) 和 斜率 (slope),也被称为 系数 (coefficients) 或 参数 (parameters),$\epsilon$ 代表 误差项 (error term)。
给定模型系数的估计值 $\hat \beta_0$ 和 $\hat \beta_1$,我们可以根据下式预测未来的销售额:
\[\hat y=\hat \beta_0 +\hat \beta_1 x\]其中,$\hat y$ 表示在 $X=x$ 的基础上对 $Y$ 的预测。通常,我们用帽子符号 “^” 表示估计值。
2.1 最小二乘参数估计
令 $\hat y_i=\hat \beta_0 +\hat \beta_1 x_i$ 表示根据 $X$ 的第 $i$ 个值预测的 $Y$,且 $e_i=y_i-\hat y_i$ 代表第 $i$ 个 残差 (residual)。
我们定义 残差平方和 (residual sum of squares, RSS) 为:
\[\mathrm{RSS}=e_1^2+e_2^2+\cdots +e_n^2\]或者等价地定义为:
\[\mathrm{RSS}=(y_1-\hat \beta_0 - \hat \beta_1 x_1)^2 + (y_2-\hat \beta_0 - \hat \beta_1 x_2)^2+\cdots + (y_n-\hat \beta_0 - \hat \beta_1 x_n)^2\]最小二乘法会选择 $\hat \beta_0$ 和 $\hat \beta_1$ 使得 $\mathrm{RSS}$ 最小化。通过计算可知,使 $\mathrm{RSS}$ 最小化的参数估计值为:
\[\begin{align} \hat \beta_1 &= \dfrac{\sum_{i=1}^n (x_i-\overline x\,)(y_i-\overline y\,)}{\sum_{i=1}^{n}(x_i-\overline x\,)^2} \\[2ex] \hat \beta_0 &= \overline y - \hat \beta_1 \overline x \end{align}\]其中,$\overline y\equiv \frac{1}{n}\sum_{i=1}^n y_i$ 和 $\overline x\equiv \frac{1}{n}\sum_{i=1}^n x_i$ 是样本均值。
例子:广告数据
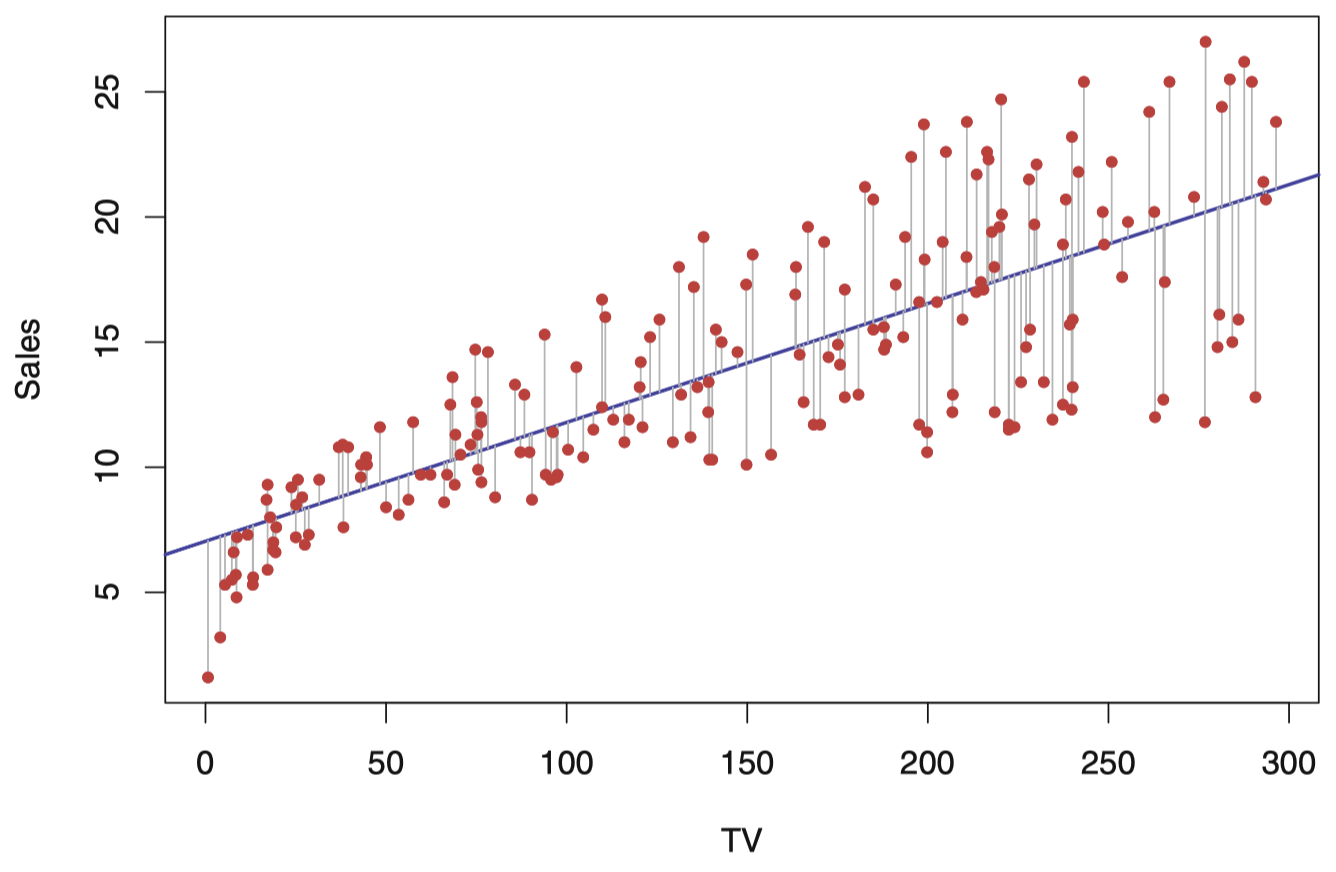
图 3:对于 Advertising 数据集,最小二乘法拟合 sales 关于 TV 的回归,如图所示。这种拟合是通过使残差平方和最小化得到的。每条灰色线段代表一个残差,拟合模型是对误差平方和取均值折中的结果。这里的线性拟合抓住了变量间关系的本质,尽管它对图中左侧区域的拟合稍有缺陷。
2.2 评价系数估计值的准确性
标准误
一个估计量的 标准误 (standard error) 反映了它在重复采样下的变化情况。我们有:
\[\begin{align} \mathrm{SE}(\hat \beta_1)^2 &= \dfrac{\sigma^2}{\sum_{i=1}^{n}(x_i-\overline x\,)^2}\\[2ex] \mathrm{SE}(\hat \beta_0)^2 &= \sigma^2 \left[\dfrac{1}{n} + \dfrac{\overline x\,^2}{\sum_{i=1}^{n}(x_i-\overline x\,)^2}\right] \end{align}\]其中,$\sigma^2=\mathrm{Var}(\epsilon)$。
置信区间
这些标准误可以用来计算 置信区间 (confidence intervals)。一个 $95 \%$ 置信区间被定义为一个取值范围:该范围有 $95\%$ 的概率会包含未知参数的真实值。它具有形式:
\[\hat \beta_1 \pm 2\cdot \mathrm{SE}(\hat \beta_1)\]也就是说,下述区间
\[\left[\hat \beta_1 - 2\cdot \mathrm{SE}(\hat \beta_1), \hat \beta_1 + 2\cdot \mathrm{SE}(\hat \beta_1)\right]\]有约 $95\%$ 的概率会包含 $\beta_1$ 的真实值 (在我们能够通过重复采样得到类似当前样本的情况下)。
对于前面的广告数据的例子,$\beta_1$ 的 $95\%$ 置信区间为 $[0.042, 0.053]$。
假设检验
标准误也可以用于对系数进行 假设检验 (hypothesis test)。最常用的假设检验包括对 零假设 (null hypothesis):
和 备择假设 (alternative hypothesis):
数学上来说,这就相当于检验
\[H_0: \beta_1=0 \qquad \mathrm{vs.} \qquad H_a: \beta_1 \ne 0\]因为如果 $\beta_1=0$,那么模型将简化为 $Y=\beta_0 + \epsilon$,而 $X$ 与 $Y$ 将不再相关。
为了检验零假设,我们会按照下式计算一个 $t$ 统计量:
\[t=\dfrac{\hat \beta_1 - 0}{\mathrm{SE}(\hat \beta_1)}\]它将服从一个自由度为 $n-2$ 的 $t$ 分布,假设 $\beta_1=0$。
使用统计软件,很容易计算任意观测值大于等于 $\lvert t \rvert$ 的概率,我们称此概率为 $p$ 值 (p-value)。
例子:广告数据的结果
表 1 提供了 Advertising 数据集中销量对电视广告预算的最小二乘回归模型的细节。可以看出,与它们的标准误相比,系数 $\hat \beta_0$ 和 $\hat \beta_1$ 的值很大,所以 t 统计量也很大。如果 $H_0$ 为真,出现这样的值的概率几乎为零。因此,我们可以得出结论 $\beta_0 \ne 0$ 和 $\beta_1 \ne 0$。
表 1:对于 Advertising 数据,销量对电视广告预算的最小二乘回归模型的系数。电视广告预算每增加 $1000$ 美元,销量增加约 $50$ 个单位。(sales 变量是以一千台为单位,而 TV 变量 是以一千美元为单位。)
| 系数 | 标准误 | t 统计量 | p 值 | |
|---|---|---|---|---|
Intercept |
$7.0325$ | $0.4578$ | $15.36$ | $< 0.0001$ |
TV |
$0.0475$ | $0.0027$ | $17.67$ | $< 0.0001$ |
2.3 评价模型的准确性
一旦我们拒绝零假设,并倾向于接受备择假设,就会很自然地想要量化模型对数据的拟合程度。判断线性回归的拟合质量通常使用两个相关的量:残差标准误 和 $R^2$ 统计量。
残差标准误
我们可以通过下式计算 残差标准误 (residual standard error, RSE):
\[\mathrm{RSE}=\sqrt{\dfrac{1}{n-2}\mathrm{RSS}}=\sqrt{\dfrac{1}{n-2}\sum_{i=1}^{n}(y_i-\hat y_i)^2}\]其中,残差平方和 为 $\mathrm{RSS}=\sum_{i=1}^{n}(y_i-\hat y_i)^2$。
$R^2$ 统计量
$R^2$ 或者方差分数被定义为:
\[R^2=\dfrac{\mathrm{TSS} - \mathrm{RSS}}{\mathrm{TSS}}=1-\dfrac{\mathrm{RSS}}{\mathrm{TSS}}\]其中,$\mathrm{TSS}=\sum_{i=1}^{n}(y_i-\overline y\,)^2$ 被称为 总平方和 (total sum of squares, TSS)。
可以证明,在简单线性回归模型中,$R^2 = r^2$,其中 $r$ 是 $X$ 和 $Y$ 之间的 相关性 (correlation):
\[r=\mathrm{Cor}(X,Y)=\dfrac{\sum_{i=1}^{n}(x_i-\overline x\,)(y_i-\overline y\,)}{\sqrt{\sum_{i=1}^{n}(x_i-\overline x\,)^2}\sqrt{\sum_{i=1}^{n}(y_i-\overline y\,)^2}}\]例子:广告数据的结果
表 2 显示了售出的单位数目在电视广告预算的线性回归中的残差标准误、$R^2$ 统计量和 $F$ 统计量。
表 2:关于 Advertising 数据集上销量对于电视广告预算的最小二乘回归模型的更多信息。
| 量 | 值 |
|---|---|
| 残差标准误 | $3.26$ |
| $R^2$ | $0.612$ |
| $F$ 统计量 | $312.1$ |
3. 多元线性回归
例子:广告数据集
简单线性回归是用单个预测变量预测响应变量的一种有用的方法。然而在实践中,常常有不止一个预测变量。例如,在 Advertising 数据集中,我们已经检查了销量与电视广告之间的关系。同时,我们还有广播广告和报纸广告的花费数据,我们可能想知道这两个媒体是否分别与销售相关。如何扩展对广告数据集的分析,来将这两个额外的预测变量纳入模型呢?
一种选择是建立 3 个独立的简单线性回归模型,其中每一个都用不同的广告媒体作为预测变量。例如,可以用广播和报纸广告费建立简单的线性回归模型以预测销量,结果如表 3 和表 4 所示。
表 3:对于 Advertising 数据,销量对广播广告预算的最小二乘回归模型的系数。广播广告预算每增加 $1000$ 美元,销量增加约 $203$ 个单位。(sales 变量是以一千台为单位,而 radio 变量 是以一千美元为单位。)
| 系数 | 标准误 | t 统计量 | p 值 | |
|---|---|---|---|---|
Intercept |
$9.312$ | $0.563$ | $16.54$ | $< 0.0001$ |
radio |
$0.203$ | $0.020$ | $9.92$ | $< 0.0001$ |
表 4:对于 Advertising 数据,销量对报纸广告预算的最小二乘回归模型的系数。报纸广告预算每增加 $1000$ 美元,销量增加约 $55$ 个单位。(sales 变量是以一千台为单位,而 newspaper 变量 是以一千美元为单位。)
| 系数 | 标准误 | t 统计量 | p 值 | |
|---|---|---|---|---|
Intercept |
$12.351$ | $0.621$ | $19.88$ | $< 0.0001$ |
newspaper |
$0.055$ | $0.017$ | $3.30$ | $0.00115$ |
然而,这种为每个预测变量单独建立一个简单回归模型的方法是不能完全令人满意的。首先,若给定三个广告媒体的预算,我们并不清楚如何对销量做出一个单一的预测,因为每种广告媒体预算都有一个单独的回归方程。其次,在形成对回归系数的估计时,每个回归方程都忽略了其他两种媒体。我们即将看到,如果在构成数据集的 200 个市场上,三种媒体的预算存在相关性,那么我们对销量受某种媒体的影响的估计可能是极有误导性的。
与单独为每个预测变量建立简单线性回归模型相比,更好的方法是扩展简单线性回归模型,使其可以直接包含多个预测变量。
多元线性回归
在一般情况下,假设有 $p$ 个不同的预测变量。则多元线性回归模型的形式为:
\[Y=\beta_0 + \beta_1 X_1 + \beta_2 X_2 +\cdots + \beta_p X_p +\epsilon\]其中,$X_j$ 代表第 $j$ 个预测变量,$\beta_j$ 代表第 $j$ 个预测变量和响应变量之间的关联。
$\beta_j$ 可解释为在 所有其他预测变量保持不变 的情况下,$X_j$ 增加一个单位对 $Y$ 产生的 平均 (average) 效应。以广告数据集为例,模型为:
\[\mathtt{sales}=\beta_0 + \beta_1 \times \mathtt{TV} + \beta_2 \times \mathtt{radio} + \beta_3 \times \mathtt{newspaper} + \epsilon\]解释回归系数
- 理想的情况是预测变量之间是不相关的 —— 一种 平衡的设计:
- 每个系数可以被单独估计和测试。
- 这样的解释是可能的,例如 “当所有其他变量保持不变时,$X_j$ 的一个单位的变化关联于 $Y$ 的一个 $\beta_j$ 的变化”。
- 预测变量之间的关联性会导致一些问题:
- 所有系数的方差趋于增加,有时会急剧增加。
- 解释变得困难:当 $X_j$ 改变时,其他预测变量也会发生改变。
- 对于观测数据,应避免关于 因果关系 的断言。
(解释) 回归系数的困境
Data Analysis and Regression, Mosteller and Tukey 1977
- 回归系数 $\beta_j$ 估计了在同时固定所有其他预测变量的情况下,$X_j$ 变化一个单位导致的 $Y$ 的期望变化。但是,预测变量通常会一起改变。
- 例子:$Y=$ 口袋里的零钱总额;$X_1=$ 硬币数量;$X_2 =$ 1 美分、5 美分和 10 美分的硬币数量。就其本身而言,$Y$ 在 $X_2$ 上的回归系数将 $>0$。但是在模型中使用 $X_1$ 会怎样?
- $Y =$ 一个赛季中一名足球运动员的铲球数量;$W$ 和 $H$ 是该运动员的体重和身高。拟合回归模型为 $\hat Y = b_0 + 0.5 W - 0.1 H$。 我们如何解释 $\hat \beta_2<0$?
引用两位著名统计学家的话
“Essentially, all models are wrong, but some are useful.”
George Box
“The only way to find out what will happen when a complex system is disturbed is to disturb the system, not merely to observe it passively.”
Fred Mosteller and John Tukey, paraphrasing George Box
3.1 多元回归的估计和预测
对于给定的估计系数 $\hat \beta_0,\hat \beta_1,\dots,\hat \beta_p$,我们可以使用以下公式进行预测:
\[\hat y=\hat \beta_0 + \hat \beta_1 x_1 + \hat \beta_2 x_2+\cdots + \hat \beta_p x_p\]与在简单线性回归中相同,多元线性回归同样采用最小二乘法进行参数估计。选择 $\beta_0,\beta_1,\dots,\beta_p$ 的估计值以最小化残差平方和:
\[\begin{align} \mathrm{RSS} &= \sum_{i=1}^{n}(y_i - \hat y_i)^2 \\[2ex] &= \sum_{i=1}^{n} (y_i- \hat \beta_0 - \hat \beta_1 x_{i1} - \hat \beta_2 x_{i2} - \cdots - \hat \beta_p x_{ip})^2 \end{align}\]计算过程可以通过标准统计软件完成。使得 $\mathrm{RSS}$ 最小化的 $\hat \beta_0, \hat \beta_1, \dots, \hat \beta_p$ 的值就是多元最小二乘回归系数估计。
图 4 是用 $p=2$ 个预测变量对一个玩具数据集进行最小二乘拟合的一个例子。
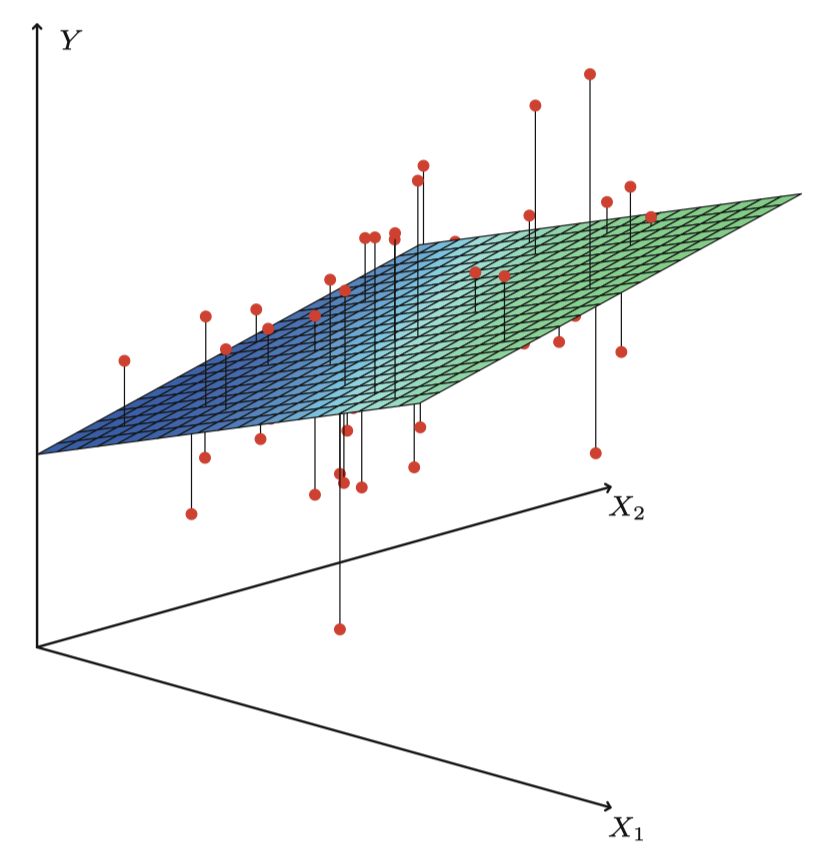
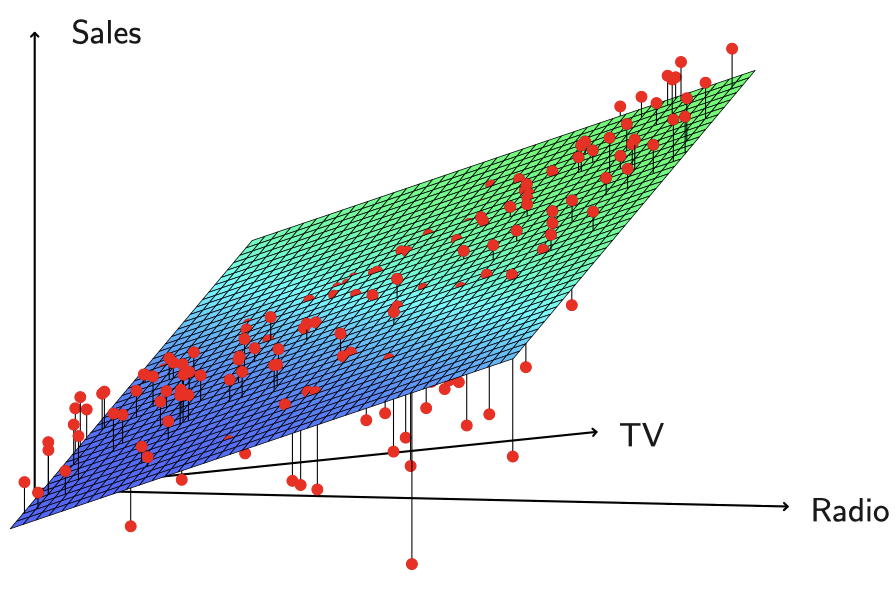
图 4:这个三维图中有两个预测变量和一个响应变量,最小二乘回归直线变成了一个平面。这个平面使得每个观测值 (由图中红点表示) 与平面之间的垂直距离的平方和尽可能小。
例子:广告数据的结果
表 3 显示了在 Advertising 数据中,用电视、广播和报纸广告预算预测产品销量的多元回归系数估计。我们对这些结果的解释如下:在电视和报纸广告预算给定的情况下,在广播广告上多投入 $1000$ 美元将使销量增加约 $189$ 个单位。
表 5:在 Advertising 数据集中,sales 关于 radio、TV 和 newspaper 的多元线性回归的最小二乘估计系数。
| 系数 | 标准误 | t 统计量 | p 值 | |
|---|---|---|---|---|
Intercept |
$2.939$ | $0.3119$ | $9.42$ | $< 0.0001$ |
TV |
$0.046$ | $0.0014$ | $32.81$ | $< 0.0001$ |
radio |
$0.189$ | $0.0086$ | $21.89$ | $< 0.0001$ |
newspaper |
$-0.001$ | $0.0059$ | $-0.18$ | $0.8599$ |
将这些系数估计值与表 1、3、4 中的相比较,可以看出,TV 和 radio 这两个变量的多元回归系数估计与简单线性回归系数估计非常相似。然而,newspaper 在表 4 中的回归系数估计值是显著不为零的,但在多元回归模型中的系数估计值却接近于零且不再显著,相应的 $p$ 值显著,约为 $0.86$。
这说明 简单回归系数和多元回归系数可能差异极大。这种差异的根源在于:简单回归 中的斜率表示在 忽略 其他预测变量 (如 TV 和 radio) 的情况下,报纸广告费用增加一千美元的平均效果。而在 多元回归 模型中,newspaper 的系数表示在 TV 和 radio 保持不变 的情况下,报纸广告费用增加一千美元所产生的平均效果。
多元回归的结果表明商品 sales 与 newspaper 无关,而简单线性回归的结论则相反,那么多元回归的结论是否还有意义呢?答案是肯定的。我们考虑由响应变量和三个预测变量构成的相关性矩阵,如表 6 所示。
表 6:在 Advertising 数据集中,TV、radio、newspaper 和 sales 的相关性矩阵。
TV |
radio |
newspaper |
sales |
|
|---|---|---|---|---|
TV |
$1.0000$ | $0.0548$ | $0.0567$ | $0.7822$ |
radio |
$1.0000$ | $0.3541$ | $0.5762$ | |
newspaper |
$1.0000$ | $0.2283$ | ||
sales |
$1.0000$ |
表中可见 radio 和 newspaper 之间的相关性为 $0.35$。这表明在报纸广告费更高的市场上,对广播广告的投入也趋于更高。现假设多元回归是正确的,报纸广告对销售没有直接影响,但广播广告能增加销量。那么在广播广告费较高的市场上,商品销量将趋于更高,而相关性矩阵显示,我们在这些市场上的报纸广告投入往往也会更高。
因此,尽管报纸广告实际上并不影响销售,由于简单线性回归中只检查 sales 和 newspaper 之间的关系,于是导致了在简单线性回归中观察到商品的高销量与报纸广告的高投入之间的相关关系。因此,newspaper 是 radio 广告对销量的影响的一个替代品,newspaper 通过 radio 对 sales 的影响来获得 “认可”。
3.2 一些重要问题
在进行多元线性回归时,我们通常有兴趣回答一些重要的问题:
- 预测变量 $X_1,X_2,\dots,X_p$ 中是否至少有一个可以用来预测响应变量?
- 所有的预测变量都有助于解释 $Y$ 吗?或者仅仅是预测变量的一个子集对预测有用?
- 模型对数据的拟合程度如何?
- 给定一组预测变量的值,响应值应预测为多少?所作预测的准确程度如何?
现在我们依次解决这些问题。
问题 1:响应变量和预测变量之间是否存在关系?
与简单线性回归类似,我们用假设检验回答这个问题:
\[H_0:\beta_1=\beta_2=\dots =\beta_p =0 \qquad \text{vs.} \qquad H_a: \text{at least one }\beta_j \text{ is non-zero}\]为此,我们需要计算 $F$ 统计量:
\[F=\dfrac{(\mathrm{TSS}-\mathrm{RSS})/p}{\mathrm{RSS}/(n-p-1)} \sim F_{p,n-p-1}\]其中,$\mathrm{TSS}=\sum_{i=1}^{n}(y_i - \overline y)^2$,$\mathrm{RSS}=\sum_{i=1}^{n}(y_i - \hat y_i)^2$。
如果线性回归假设是正确的,可知 $E[ \mathrm{RSS}/(n-p-1)]=\sigma^2$;进一步地,若 $H_0$ 为真,则有 $E[(\mathrm{TSS}-\mathrm{RSS}) / p]=\sigma^2$。
因此,当响应变量与预测变量无关,$F$ 统计量应该接近 $1$。否则,如果 $H_a$ 为真,那么 $E[(\mathrm{TSS}-\mathrm{RSS}) / p] > \sigma^2$,所以我们预计 $F$ 大于 1。
如果 $n$ 很大,即使 $F$ 统计量只是略大于 $1$,可能也仍然提供了拒绝 $H_0$ 的证据。相反,若 $n$ 较小,则需要较大的 $F$ 统计量才能拒绝 $H_0$。
事实上,每个变量的 $t$ 检验都等价于不含该变量,但包含所有其他变量的模型的 $F$ 检验。
既然我们已经通过 $t$ 检验得到各个变量的 p 值,为什么还需要看整体的 $F$ 统计量呢?毕竟现在看来似乎是这样:如果任一变量的 p 值很小的,那么至少有一个预测变量与响应变量相关。然而,这种逻辑存在缺陷的,特别是当预测变量的数目很大的时候。
如果我们用单独的 $t$ 统计量及相应的 p 值确定预测变量与响应变量是否相关,很有可能错误地得出有相关性的结论。而 $F$ 统计量不存在这个问题,因为它会根据预测变量个数进行调整。因此,如果 $H_0$ 为真,那么无论预测变量个数或观测个数是多少,$F$ 统计量的 p 值小于 $0.05$ 概率只有 $5\%$。
当 $p< n$ 时,我们可以使用 $F$ 统计量检验预测变量和响应变量是否相关。然而,有时候变量数目非常大,即 $p > n$,此时待估计的系数 $\beta_j$ 的个数比可用于估计的观测个数还多。在这种情况下,我们甚至无法用最小二乘法拟合多元线性模型,因此无法使用 $F$ 统计量,以及前面提到的一些 $R^2$ 等概念。当 $p$ 很大时,可以使用一些其他方法,如 前向选择 (forward selection)。在后面课程中,我们会更详细地讨论这种 高维 (high-dimensional) 情况。
问题 2:选择重要的变量
如前面所讨论的,多元回归分析的第一步是计算 $F$ 统计量并检查相应的 p 值。如果检验结果表明至少有一个预测变量与响应变量相关,那么我们希望知道 哪些变量是和响应变量相关。当然,我们可以查看各个变量的 p 值,但正如前面讨论的,如果预测变量的数目 $p$ 很大,很可能得出错误结论。
所有的预测变量都与响应变量相关是可能的,但更常见的情况是响应变量仅与预测变量的某个 子集 (subset) 相关。确定哪些预测变量与响应变量相关,以建立只包含相关预测变量的模型的任务被称为 变量选择 (variable selection)。
所有子集/最优子集回归 (All subsets/Best subsets regression)
通常,一种最直接的方式是:我们计算所有可能子集的最小二乘拟合,然后根据一些能在训练误差与模型大小之间取得较好平衡的准则,从所有可能子集中选择出最优的变量子集。
但是,我们通常无法检查所有可能的模型,因为存在 $2^p$ 种组合。例如,当 $p = 40$ 时,就有十亿多个可能的模型。因此,我们需要一种自动方法在其子集中进行搜索。接下来将讨论两种常用方法。
前向选择 (Forward selection)
- 从 空模型 (null model) 开始,即一个仅包含截距项,但不包含任何预测变量的模型。
- 拟合 $p$ 个简单线性回归,然后将能够最小化 RSS 的变量添加到空模型中。
- 然后再考虑加入一个变量,考察所有包含两个变量的模型,将能够使 RSS 最小化的变量添加到上一步得到的模型中。
- 继续按照上面的过程添加变量,直到满足某些停止规则为止,例如,当所有剩余变量的 p 值都超过某个阈值时。
后向选择 (Backward selection)
- 从包含所有变量的模型开始。
- 删除 p 值最大的变量,即具有最低统计显著性的变量。
- 拟合包含 $(p - 1)$ 个变量的新模型,再从中删除 p 值最大的变量。
- 继续按照上面的过程删除变量,直到满足某些停止规则为止,例如,当所有剩余变量的 p 值都小于某个阈值时。
稍后,我们将讨论在通过前向或后向逐步选择所产生的模型的路径中选择出 “最佳” 模型的更系统的标准。
其中包括 Mallow’s $C_p$、Akaike 信息标准 (AIC)、贝叶斯信息标准 (BIC)、修正 $R^2$ 和 交叉验证 (CV)。
问题 3:模型拟合
两个最常见的衡量模型拟合优劣的指标是 RSE 和 $R^2$ (方差的解释比例)。它们在多元回归中的计算和解释与在简单线性回归中相同。
在简单回归中,$R^2$ 是响应变量和预测变量的相关系数的平方。在多元线性回归中,$R^2$ 等于 $\mathrm{Cor}(Y,\hat Y)^2$,是响应值和线性模型拟合值的相关系数的平方。事实上,线性拟合模型的一个特性就是:在所有可能的线性模型中,它使上述相关系数最大。
若 $R^2$ 值接近 $1$ ,则表明该模型能解释响应变量的大部分方差。,当更多的变量进入模型时,即使新加入的变量与响应变量的关联很弱,$R^2$ 也一定会增加。这是因为在最小二乘方程中添加变量必然会使我们能更准确地拟合训练数据 (尽管对于测试数据未必如此)。因此,根据训练数据计算出的 $R^2$ 统计量也必然增加。
另外,为什么当某些变量加入模型时,在 RSS 必然减少的情况下,RSE 反而会增加?
我们知道,RSE 一般被定义为:
\[\mathrm{RSE}=\sqrt{\dfrac{1}{n-p-1}\mathrm{RSS}}\]在简单线性模型中,可简化为:
\[\mathrm{RSE}=\sqrt{\dfrac{1}{n-2}\mathrm{RSS}}=\sqrt{\dfrac{1}{n-2}\sum_{i=1}^{n}(y_i-\hat y_i)^2}\]因此,如果相对于变量数量 $p$ 的增加来说,RSS 的减少量较小,那么,变量较多的模型可能反而具有更高的 RSE。
问题 4:预测
一旦拟合出多元回归模型,应该根据预测变量 $X_1,X_2,\dots,X_p$ 直接用下式预测响应变量 $Y$:
\[\hat y=\hat \beta_0 + \hat \beta_1 x_1 + \hat \beta_2 x_2 +\cdots + \hat \beta_p x_p\]但是,预测也存在以下三类不确定性:
-
系数估计值 $\hat \beta_0, \hat \beta_1, \hat \beta_2, \dots, \hat \beta_p$ 是对 $\beta_0, \beta_1, \beta_2, \dots, \beta_p$ 的估计。也就是说,最小二乘平面 (least squares plane)
\[\hat Y=\hat \beta_0 + \hat \beta_1 X_1 + \hat \beta_2 X_2 +\cdots + \hat \beta_p X_p\]只是对 真实总体回归平面 (true population regression plane)
\[f(X)=\beta_0 + \beta_1 X_1 + \beta_2 X_2 +\cdots + \beta_p X_p\]的一个估计。系数估计的不准确性与上节课中提到的 可减小误差 (reducible error) 有关。我们可以计算 置信区间 (confidence interval) 以确定 $\hat Y$ 与 $f(X)$ 的接近程度。
-
当然,实践中假设的线性模型 $f(X)$ 几乎总是对现实的一种近似,所以存在改进可减小误差的机会。线性模型相关假设就是可减小误差的来源之一,我们将这类误差称为 模型偏差 (model bias)。所以在使用线性模型时,我们其实是在对真实平面进行最佳线性近似。但在这里我们将忽略这种差异,并假定线性模型是正确的。
-
即使 $f(X)$ 己知,即 $\beta_0, \beta_1, \beta_2, \dots, \beta_p$ 的真实值已知,我们依然无法对响应值作出完美预测,因为模型中还存在随机误差 $\epsilon$。在上节课中,我们将其称为 不可减小误差 (irreducible error)。$\hat Y$ 与 $Y$ 会相差多少呢?我们用 预测区间 (prediction interval) 来回答这个问题。预测区间总是比置信区间宽,因为预测区间既包含 $f(X)$ 的估计误差 (可减小误差),也包含单个点偏离总体回归平面程度的不确定性 (不可减小误差)。
4. 回归模型中的其他注意事顶
4.1 定性预测变量
某些预测变量不是 定量的 (quantitative) 而是 定性的 (qualitative),其取值为一组离散值。这类变量也称为 分类预测变量 (categorical predictors) 或 因子变量 (factor variables)。
例如,在信用卡数据的例子中,除了下面散点图矩阵中显示的 $7$ 个定量变量外,还有 $4$ 个定性变量:gender (性别)、student (学生)、status (婚姻状况) 和 ethnicity (种族:高加索白人、非裔美国人、亚洲人)。

图 5:Credit 数据集包含一些潜在客户的 balance、age、cards、education、income、limit 和 rating 等信息。
二值预测变量
假如我们希望调查男性和女性之间信用卡余额的差异,并且暂时忽略其他变量。
如果一个定性预测变量 (也被称为因子) 只有两个水平 (levels) 或可能的取值,那么将它纳入回归模型是非常简单的。我们只需给二值变量创建一个指标,或称 虚拟变量 (dummy variable)。例如,我们可以基于 gender 变量创建一个新变量:
并在回归方程中使用这个变量。从而得到以下模型:
\[y_i=\beta_0 + \beta_1 x_i + \epsilon_i = \begin{cases}\beta_0 + \beta_1 + \epsilon_i & \text{if }i\text{-th person is female}\\[2ex] \beta_0 + \epsilon_i & \text{if }i\text{-th person is male}\end{cases}\]那么,这种情况下得到的回归系数应该如何解释呢?
这里,$\beta_0$ 可以解释为男性的平均信用卡余额,$\beta_0 + \beta_1$ 为女性的平均信用卡余额,所以,$\beta_1$ 是男性和女性之间信用卡余额的平均差异。
表 7:Credit 数据集中 balance 对 gender 回归的最小二乘估计系数。线性模型如上式所示,这里,性别被编码为一个虚拟变量。
| 系数 | 标准误 | t 统计量 | p 值 | |
|---|---|---|---|---|
Intercept |
$509.80$ | $33.13$ | $15.389$ | $< 0.0001$ |
gender[Female] |
$19.73$ | $46.05$ | $0.429$ | $0.6690$ |
表 7 列出了系数估计值和与模型相关的其他信息。男性的平均信用卡余额估计值为 $509.80$ 美元,而女性的余额估计值比男性多 $19.73$ 美元,共为 $19.73 + 509.80 = 529.53$ 美元。然而,我们注意到虚拟变量的 $p$ 值是非常高的。这表明,两种性别之间的平均信用卡余额差异并无显著的统计学证据。
具有两个以上水平的定性预测变量
当一个定性预测变量具有两个以上的水平时,一个单独的虚拟变量无法代表所有可能的值。这种情况下,我们可以创建更多的虚拟变量。例如,我们对于 ethnicity 变量创建两个虚拟变量。第一个虚拟变量是:
第二个虚拟变量是:
\[x_{i2}=\begin{cases}1 & \text{if }i\text{-th person is Caucasian}\\[2ex] 0 & \text{if }i\text{-th person is not Caucasian}\end{cases}\]然后,这两个变量都可以用于回归方程中,得以下模型:
\[y_i=\beta_0 + \beta_1 x_{i1} +\beta_2 x_{i2} + \epsilon_i = \begin{cases}\beta_0 + \beta_1 + \epsilon_i & \text{if }i\text{-th person is Asian}\\[2ex] \beta_0 + \beta_2 + \epsilon_i & \text{if }i\text{-th person is Caucasian}\\[2ex] \beta_0 + \epsilon_i & \text{if }i\text{-th person is African American}\end{cases}\]虚拟变量个数总是比水平数少 $1$。没有相对应的虚拟变量的水平 (即这里的 African American) 被称为 基准水平 (baseline)。
表 8:Credit 数据集中 balance 对 ethnicity 回归的最小二乘估计系数。线性模型如上式所示,这里,种族被编码为两个虚拟变量。
| 系数 | 标准误 | t 统计量 | p 值 | |
|---|---|---|---|---|
Intercept |
$531.00$ | $46.32$ | $11.464$ | $< 0.0001$ |
ethnicity[Asian] |
$-18.69$ | $65.02$ | $-0.287$ | $0.7740$ |
ethnicity[Caucasian] |
$-12.50$ | $56.68$ | $-0.221$ | $0.8260$ |
从表 8 中可以看到,基准水平 (非裔美国人) 的余额估计值为 $531.00$ 美元。据估计,亚洲人的余额比非裔美国人少 $18.69$ 美元,高加索白人的余额比非裔美国人少 $12.50$ 美元。然而,两个虚拟变量系数估计的 $p$ 值非常大,这意味着信用卡余额的种族差异没有显著的统计学证据。这里基准水平类的选择也是任意的,不管如何选择基准,对每一类人的最终预测是一定的。但变量的系数及相应的 $p$ 值依赖于虚拟变量的编码。我们可以用 $F$ 检验而不是基于系数对 $H_0: \beta_1=\beta_2=0$ 进行检验,$F$ 检验的结果与编码方式无关。此 $F$ 检验的 p 值是 $0.96$,这表明我们无法拒绝 balance 和 ethnicity 无关的零假设。
4.2 线性模型的扩展
标准线性回归模型提供了可解释的结果,并且被应用于许多现实问题中。但是,它附加了一些高度限制性的假设,这些假设在实践中经常被违背。两个最重要的假设是预测变量和响应变量的关系是 可加的 (additive) 和 线性的 (linear)。
可加性假设是指预测变量 $X_j$ 的变化对响应变量 $Y$ 产生的影响与其他预测变量的取值无关。线性假设是指无论 $X_j$ 取何值,$X_j$ 变化一个单位引起的响应变量 $Y$ 的变化是恒定的。本课程中考察了一些复杂的模型来放宽这两个假设。在这里,我们将对几种常见的扩展线性模型的经典方法进行简要介绍。
移除可加性假设
交互作用 (Interactions):在先前对广告数据的分析中,我们的线性模型假设一种媒体的广告支出增加引起的 sales 变化与其他媒体的广告支出无关。例如,对于线性模型
可以发现,无论在 radio 上花费多少,TV 增加一个单位对 sales 的平均效应总是 $\beta_1$。
然而,这个简单的模型可能并不正确。假设对广播广告的投入事实上增强了电视广告的有效性,这时 TV 的斜率项应随着 radio 的增加而增加。在这种情况下,给定 $10$ 万美元的预算,将资金平均分配给两种媒体可能要比全部投到其中一种上对销售帮助更大。这种现象在营销中被称为 协同效应 (synergy),而在统计学中被称为 交互作用 (interaction)。
注意到,当 TV 或 radio 其中之一较低时,真实 sales 总是低于线性模型的预测。但当两种媒体共享广告费时,模型往往会低估 sales。
一种扩展该模型,使其能够考虑交互作用的方法是加入第三个预测变量,名为 交互项 (interaction term),由二者的乘积构成。这里,我们可以用包含 radio、TV 以及两者之间的交互项的线性模型来预测 sales:
表 9:Advertising 数据集中,sales 关于 TV、radio 和交互项的回归模型的最小二乘系数估计。
| 系数 | 标准误 | t 统计量 | p 值 | |
|---|---|---|---|---|
Intercept |
$6.7502$ | $0.248$ | $27.23$ | $< 0.0001$ |
TV |
$0.0191$ | $0.002$ | $12.70$ | $< 0.0001$ |
radio |
$0.0289$ | $0.009$ | $3.24$ | $0.0014$ |
TV $\times$ radio |
$0.0011$ | $0.000$ | $20.73$ | $< 0.0001$ |
表 9 中的结果表明,交互项在这里是一个重要的预测变量。交互项 TV $\times$ radio 的 p 值非常低,这强有力地证明了 $H_a : \beta_3\ne 0$。这说明真实关系明显是不可加的。
另外,包含交互项的模型的 $R^2$ 为 $96.8\%$ ,而不含交互项的模型只有 $89.7\%$。这意味着在拟合完可加性模型后,交互项的加入解释了 sales 的剩余变化的 $(96.8 -89.7)/(100 -89.7) =69\%$。
表中的系数估计表明:
-
\[(\hat \beta_1 +\hat \beta_3\times \mathtt{radio})\times 1000=19+1.1 \times \mathtt{radio} \quad \text{units}\]TV广告费用每增加 $1000$ 美元,sales将增加 -
\[(\hat \beta_2 +\hat \beta_3\times \mathtt{TV})\times 1000=29+1.1 \times \mathtt{TV} \quad \text{units}\]radio广告费用每增加 $1000$ 美元,sales将增加
在这个例子中,TV、radio 和交互项的 p 值都是统计显著的,因此这三个变量显然都应包含在模型中。但在少数情况下,交互项的 p 值很小,而相关的主效应 (例如,这里的 TV 和 radio) 的 p 值却不然。
实验分层原则 (hierarchical principle) 规定:如果模型中含有交互项,那么即使主效应的系数的 p 值不显著,也应包含在模型中。
换句话说,如果 $X_1$ 和 $X_2$ 之间的交互作用是重要的,那么即使 $X_1$ 和 $X_2$ 的系数估计的 p 值较大,这两个变量也应该被包含在模型中。这一准则的合理性在于,如果 $X_1 \times X_2$ 与响应变量相关,则 $X_1$ 或 $X_2$ 的系数不论是否为零,意义都不大。而且 $X_1 \times X_2$ 通常与 $X_1$ 和 $X_2$ 相关,因此删除它们将改变交互作用的意义。
在前面的例子中,我们考虑了 TV 和 radio 之间的交互作用,二者都是定量变量。然而,交互作用的概念也同样适用于变量为定性变量,或者定量和定性变量皆有的情况。事实上,定量变量和定性变量之间的交互作用同样具有很好的可解释性。
考虑之前的 Credit 数据集,假设我们希望用 income (定量) 和 student (定性) 预测 balance。在没有交互项的情况下,模型为:
请注意,这相当于为数据拟合了两条平行线,一条反映学生的情况,另一条反映非学生的情况。如图 6 的左图所示,两条直线有着不同的截距,分别是 $\beta_0 + \beta_2$ 和 $\beta_0$,但它们都有相同的斜率 $\beta_1$。事实上,两条线平行说明 income 增加对 balance 的影响不依赖于信用卡持有者是否 为学生。这意味着模型可能存在严重的局限性,因为事实上对学生与非学生来说,income 变化对信用卡余额的影响可能差别很大。
该模型局限可以通过增加交互项来解决,交互项由 student 的虚拟变量乘以 income 构成,这样模型就变为:
我们再一次对学生和非学生生成了两条不同的回归直线,但现在两条回归直线具有不同的截距 $\beta_0+\beta_2$ 和 $\beta_0$,以及不同的斜率 $\beta_1+\beta_3$ 和 $\beta_1$。收入变动可能对学生和非学生的信用卡余额产生不同的影响。
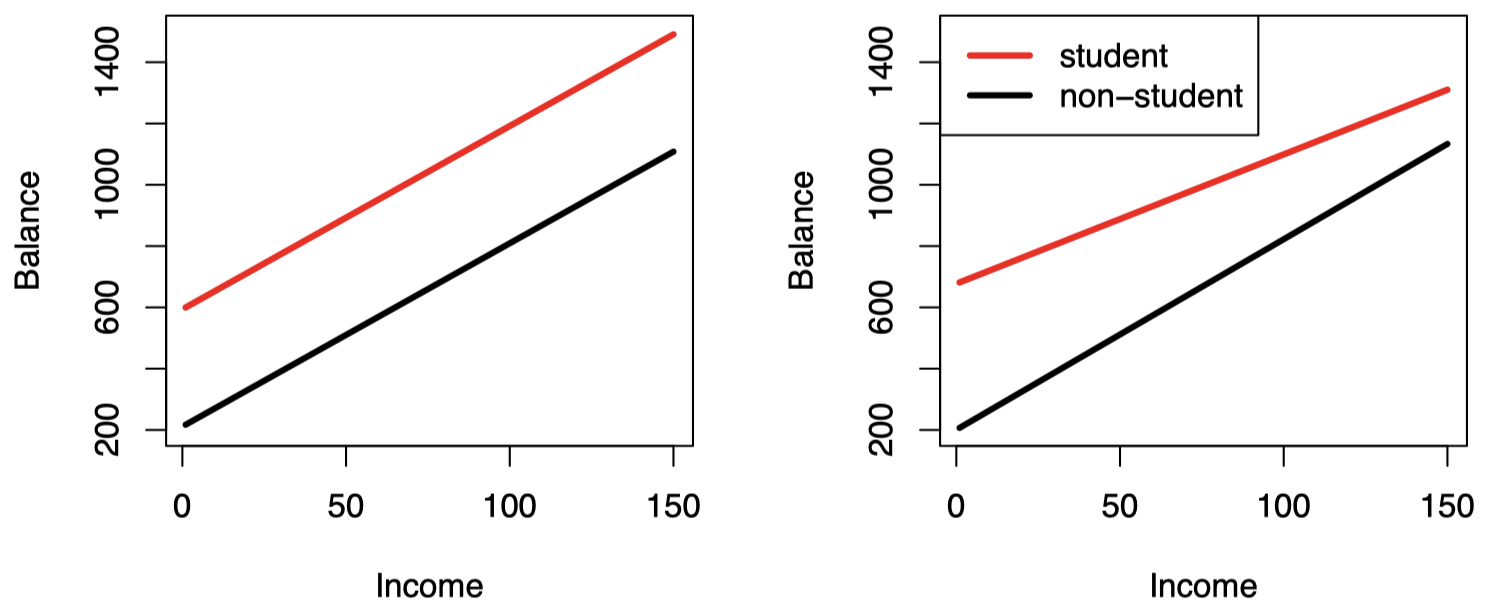
图 6:在 Credit 数据集上,用 income 预测学生和非学生的 balance 的最小二乘线。左图:不包含 income 和 student 交互项的模型的拟合结果。右图:包含 income 和 student 交互项的模型的拟合结果。
图 6 中的右图展示了包含交互项的模型对学生及非学生的 income 和 balance 之间关系的估计。我们注意到,学生回归线的斜率要小于非学生回归线的斜率。这表明与非学生群体相比,收入增加在学生群体中引起的信用卡余额增加要更小一些。
非线性关系
如前所述,线性回归模型假设响应变量和预测变量之间存在线性关系。但在某些情况下,响应变量和预测变量的真实关系可能是非线性的。这里,我们给出一个非常简单的方法来直接扩展线性模型,使之能对非线性关系进行拟合,这就是 多项式回归 (polynomial regression)。在后面课程中,我们将介绍一些更复杂的方法,以便在更一般的情况下建立非线性拟合模型。
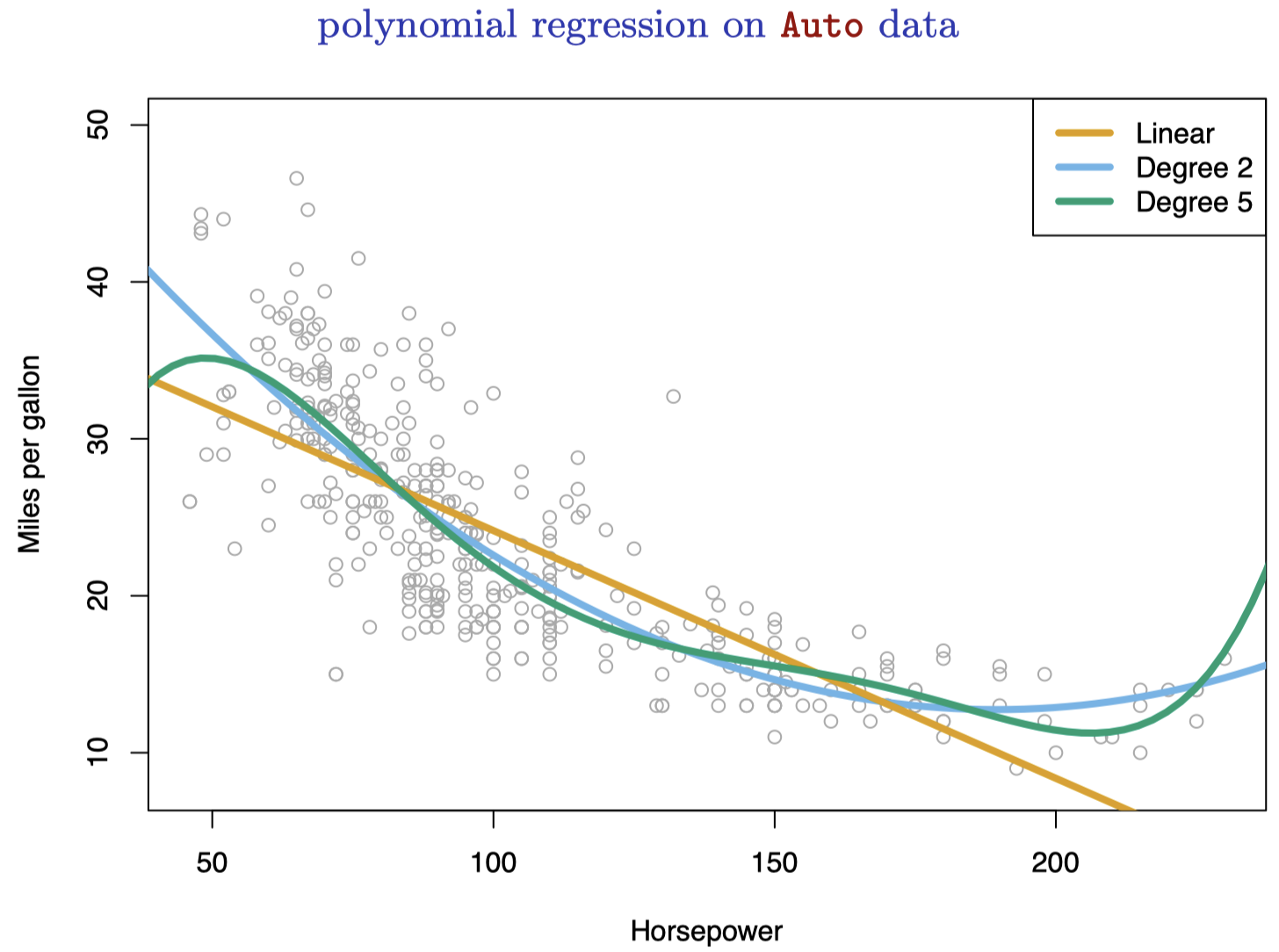
图 7:Auto 数据集,一些汽车的油耗 (mpg) 和马力 (horsepower)。橙色线是线性回归的拟合线。蓝色线是包含 horsepower 二次项的线性回归拟合线。绿色线是包含 horsepower 所有五次以内项的线性回归拟合线。
图 7 显示了 Auto 数据集中一些汽车的 mpg (英里每加仑,即油耗) 和 horsepower (马力)。橙色的线代表线性回归拟合。mpg 和 horsepower 无疑是相关的,但它们的关系明显是非线性的:数据呈现出一种曲线关系。使用预测变量的转换形式 是一种将非线性因素纳入线性模型的简单方法。例如,图 7 中的点似乎有 二次方 (quadratic) 的形状特征,这表明模型
可能会提供更好的拟合,这里我们用 horsepower 的非线性函数预测 mpg,但它仍然是一个 线性模型。事实上,这是一个多元线性回归模型,其中 $X_1=\mathtt{horsepower}$,$X_2=\mathtt{horsepower}^2$。因此,我们可以用标准线性回归软件来估计 $\beta_0$、$\beta_1$ 和 $\beta_2$ 以得到非线性拟合。
表 10:Auto 数据集中,mpg 关于 horsepower 及其平方项的回归模型的最小二乘系数估计。
| 系数 | 标准误 | t 统计量 | p 值 | |
|---|---|---|---|---|
Intercept |
$56.9001$ | $1.8004$ | $31.6$ | $< 0.0001$ |
horsepower |
$-0.4662$ | $0.0311$ | $-15.0$ | $< 0.0001$ |
horsepower$^2$ |
$0.0012$ | $0.0001$ | $10.1$ | $< 0.0001$ |
图 7 中的蓝色曲线显示了由此得到的二次拟合,可以看到,二次拟合要明显优于线性拟合。这里,二次拟合的 $R^2$ 为 $0.688$,而线性拟合的 $R^2$ 只有 $0.606$,而且表 10 中二次项的 p 值是高度显著的。
如果将 horsepower 的平方项纳入模型能带来如此大的改进,为什么不将 horsepower 的三次、四次甚至五次方项也纳入模型呢?图 7 中的绿色曲线表示包含 horsepower 所有不超过五次项的模型的拟合结果。由此产生的拟合似乎存在不必要的波动。也就是说,目前并不清楚添加的项是否真的带来了更好的数据拟合。
这里的建模方法被称为 多项式回归 (polynomial regression),它因为在回归模型中加入了预测变量的多项式函数而得名。我们将在后面课程中进一步探索该方法以及线性模型的其他非线性扩展方式。
线性模型的泛化
在本课程的其余大部分内容中,我们将讨论扩展线性模型范围以及如何拟合的方法:
- 分类问题:逻辑回归,支持向量机
- 非线性:核平滑、样条和广义加性模型;最近邻方法。
- 相互作用:基于树的方法、bagging、随机森林和 boosting (这些方法同样可以捕获非线性)
- 正则拟合:岭回归和 lasso
下节内容:分类
本作品采用知识共享署名-非商业性使用-相同方式共享 4.0 国际许可协议进行许可。 欢迎转载,并请注明来自:YEY 的博客 同时保持文章内容的完整和以上声明信息!