Lecture 05 主成分分析 (二)
参考教材:
- Hardle, W. and Simar, L (2015). Applied multivariate statistical analysis, 4th edition.
- Hastie, T. Tibshirani, R. and Friedman, J. (2009). The elements of statistical learning, 2nd edition
1. 主成分的解释
请记住,我们的目的是通过尽可能少的 PC 来解释 $X_i$ 尽可能多的变化 (低维投影,以便于数据可视化)。
并且,我们有
\[\mathrm{Var}(Y_{ij}) = \lambda_j, \quad \text{for}\; j=1,\dots,p\]以及
\[\sum_{j=1}^{p}\lambda_j = \sum_{j=1}^{p} \mathrm{Var}(Y_{ij}) = \mathrm{tr}(\Sigma) = \sum_{j=1}^{p} \mathrm{Var}(X_{ij})\]所以,前 $q$ 个主成分能够在多大程度上解释数据的变化可以通过以下比例来度量:
\[\psi_q = \dfrac{\sum_{j=1}^{q}\lambda_j}{\sum_{j=1}^{p}\lambda_j}\]在上节课的瑞士纸币的例子中,我们有:
表 1:瑞士纸币数据:特征值、解释方差比例和累积比例。

因此,我们有
\[\psi_1 = 0.668, \;\psi_2 = 0.876,\; \psi_3 = 0.930,\; \psi_4 = 0.973,\; \psi_5 = 0.992,\; \psi_6 = 1.000\]也就是说,第一个主成分解释了数据中 $66.8\%$ 的变化,前两个主成分一起解释了 $87.6\%$ 的变化,前三个主成分一起解释了 $93\%$ 的变化。
通常,我们会将 $\psi_q$ 绘制在图中,称为 碎石图 (scree plot),它将按照 $\lambda_1 \ge \lambda_2 \ge \cdots \ge \lambda_p$ 显示,这使我们能够查看哪些成分贡献最大。
在 R 中,我们可以通过 prcomp 获得 PCA 结果,并用 screeplot 来绘制碎石图:
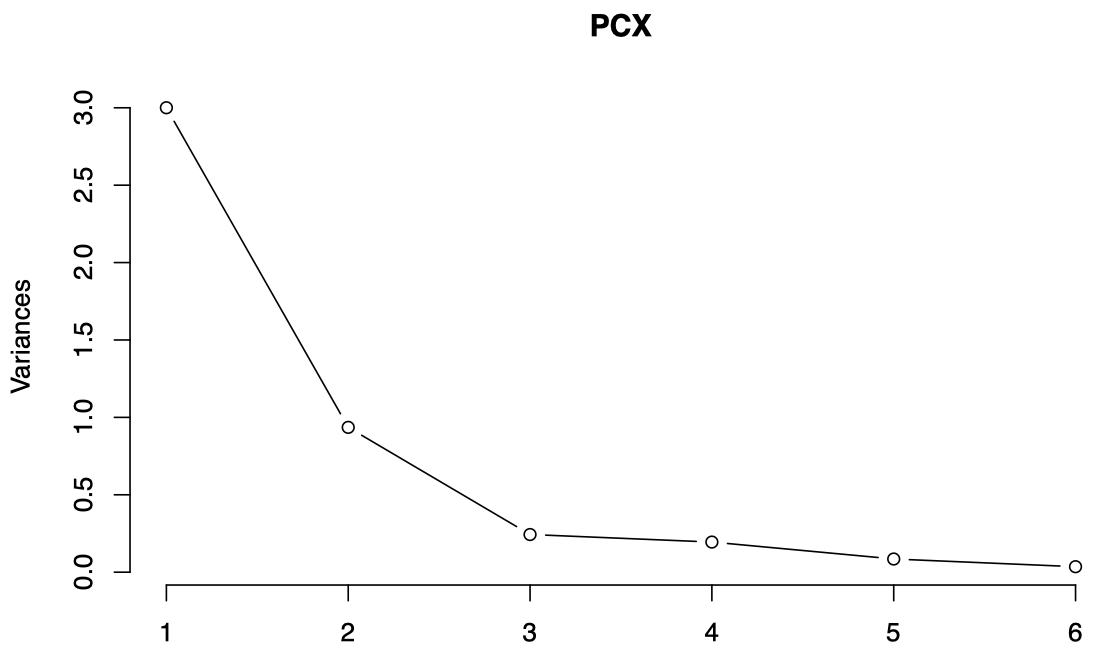
图 1:瑞士纸币数据的碎石图,横轴表示 PC,纵轴表示该 PC 解释的方差 (即特征值)。
通过观察碎石图,我们可以决定需要考虑的 PC 数量:
- 考虑全部 PC 是没有意义的,因为这样无法实现降维 (总共有 $p$ 个 PC)。
- 另一方面,我们应保留足够数量的 PC,以获取有关数据的大量信息。
- 我们需要保留足够数量的 PC,使得它们所解释的累计方差百分比足够大。
- 通常,我们会找到碎石图中的某个 拐点 (elbow) 并停在那里:以瑞士纸币为例,我们可以停在第 3 个 PC 处。
在瑞士纸币的例子中,前两个 PC 一起解释了 $87.6\%$ 的数据方差,理论上看已经足够;但是前 3 个 PC 一起解释了 $93\%$ 的数据方差,要比之前更好一些。
然而,第三个 PC 也只是增加了少量额外信息 (在某些情况下,少量信息实际上可能包含了之前的 PC 无法捕获到的关于数据的一些有趣的方面,因此我们需要对其进行检查)。
通常,最初的几个 PC 共同解释了数据可变性的很大一部分,并且可以很容易从碎石图中看到。如果最初的 3 个或 4 个 PC 无法解释数据的大部分可变性,则意味着我们无法通过 PC 方法有效实现降维 (这种情况下,如果显著减小维数,则会丢失有关数据的太多信息)。
我们可以计算每个主成分变量 $Y_{ik}$ 和原始数据向量 $X_i$ 之间的协方差。
由于我们可以构造多达 $p$ 个主成分,我们可以将 $X_i$ 的 $p$ 个 PC 表示为:
\[Y_i = (Y_{i1},\dots, Y_{ip})^{\mathrm T}\]其中,$Y_{ik} = \gamma_k^{\mathrm T} (X_i - \mu)$。
我们可以通过两个向量之间的协方差矩阵来计算 $X_i$ 和 $Y_i$ 中的所有成对元素之间的协方差:
-
令 $\Gamma = (\gamma_1,\dots,\gamma_p)$,它包含了 $\Sigma$ 的 $p$ 个特征向量。
-
令 $\Lambda = \mathrm{diag}(\lambda_1,\dots,\lambda_p)$,它包含了 $p$ 个对应的降序排列的特征值,并且令 $\gamma_{jk}$ 表示 $\gamma_j$ 的第 $k$ 个分量。并且,回忆一下,我们用 $\sigma_{jk}$ 表示 $\Sigma$ 中的第 $(j,k)$ 个元素。
-
我们有
\[\mathrm{Cov}(X_i,Y_i) = \Gamma \Lambda\]所以
\[\mathrm{Cov}(X_{ij}, Y_{ik}) = \gamma_{kj}\lambda_k\]因此,
\[\rho_{X_{ij}, Y_{ik}} = \dfrac{\gamma_{kj}\lambda_k}{(\sigma_{jj}\lambda_k)^{1/2}} = \gamma_{kj} \dfrac{\lambda_k^{1/2}}{(\sigma_{jj})^{1/2}}\]注意:在实践中,这些量均由其经验版本代替。
-
然后,我们有
\[\sum_{k=1}^{p} \rho_{X_{ij}, Y_{ik}}^2 = \dfrac{\sum_{k=1}^{p}\gamma_{kj}^2 \lambda_k}{\sigma_{jj}} = \dfrac{\sigma_{jj}}{\sigma_{jj}} = 1\]推导过程:
我们用 $Y$ 表示 PC 向量,$X$ 表示原始数据向量:
\[Y = \begin{pmatrix}Y_1 \\ \vdots \\ Y_p \end{pmatrix}\quad \text{and} \quad X = \begin{pmatrix}X_1 \\ \vdots \\ X_p \end{pmatrix}\]$\Gamma$ 表示特征向量矩阵:
\[\Gamma = (\gamma_1,\dots,\gamma_p) \quad \text{where} \; \gamma_j = \begin{pmatrix}\gamma_{j1} \\ \vdots \\ \gamma_{jp} \end{pmatrix}\]由于 $\Gamma$ 是一个正交矩阵,$\Gamma \Gamma^{\mathrm T} = \mathcal I_p$,我们有
\[Y = \Gamma^{\mathrm T} X \quad \Longrightarrow \quad X = \Gamma Y \quad \Longrightarrow \quad X_j = \sum_{k=1}^{p} \gamma_{kj} Y_k\]所以,
\[\sigma_{jj} = \mathrm{Var}(X_j) = \sum_{k=1}^{p}\gamma_{kj}^2 \mathrm{Var}(Y_k) = \sum_{k=1}^{p} \gamma_{kj}^2 \lambda_k\]因此,$X_j$ 的方差中可以由 $Y_k$ 解释的部分所占比例为:
\[\dfrac{\gamma_{kj}^2 \lambda_k}{\sum_{k=1}^{p} \gamma_{kj}^2 \lambda_k} = \dfrac{\gamma_{kj}^2 \lambda_k}{\sigma_{jj}}\] -
所以,相关系数的平方
\[\rho_{X_{ij},Y_{ik}}^2 = \dfrac{\gamma_{kj}^2 \lambda_k}{\sigma_{jj}}\]可以被解释为 $X_j$ 的方差中由 $Y_k$ 解释的部分所占的比例。
由于 $\sum_{k=1}^{p} \rho_{X_{ij}, Y_{ik}}^2 = 1$,我们有
\[\rho_{X_{ij}, Y_{i1}}^2 + \rho_{X_{ij}, Y_{i2}}^2 \le 1\]所以,相关系数对 $(\rho_{X_{ij}, Y_{i1}},\rho_{X_{ij}, Y_{i2}})$ 落在一个半径为 $1$ 的圆内。如果 $X_{ij}$ 与 $(Y_{i1},Y_{i2})$ 强相关,那么 $(\rho_{X_{ij}, Y_{i1}},\rho_{X_{ij}, Y_{i2}})$ 将落在非常接近圆周的地方。
通过将所有 $j=1,\dots,p$ 的相关系数对 $(\rho_{X_{ij}, Y_{i1}},\rho_{X_{ij}, Y_{i2}})$ 绘制在同一张图中,我们可以看到 $X_i$ 的哪些分量与 $Y_{i1}$ 和 $Y_{i2}$ 相关性最强。
注意:对于一个给定的 $j$,只有一个 $(\rho_{X_{ij}, Y_{i1}},\rho_{X_{ij}, Y_{i2}})$,对于所有的 $i$ 都是一样的。回忆一下,$\rho_{X_{ij}, Y_{ik}}$ 与 $i$ 无关:
\[\rho_{X_{ij}, Y_{ik}} =\gamma_{kj} \dfrac{\lambda_k^{1/2}}{(\sigma_{jj})^{1/2}}\]在实践中,我们通过使用经验协方差矩阵 $S$ 代替理论上的 $\Sigma$ 得到的经验估计量来代替 $\gamma_{kj}$、$\lambda_k$ 和 $\sigma_{jj}$,从而计算相关系数。
回忆一下,在之前瑞士纸币的例子中,我们有
\[\begin{align} Y_{i1} &= 0.044X_{i1}− 0.112X_{i2}− 0.139X_{i3}− 0.768X_{i4}− 0.202X_{i5}+ 0.579X_{i6} \\[2ex] Y_{i2} &= −0.011X_{i1} − 0.071X_{i2} − 0.066X_{i3} + 0.563X_{i4} − 0.659X_{i5} + 0.489X_{i6} \end{align}\]其中,$X_{i1}$ 到 $X_{i6}$ 分别是 Length、Left、Right、Bottom、Top、Diagonal:
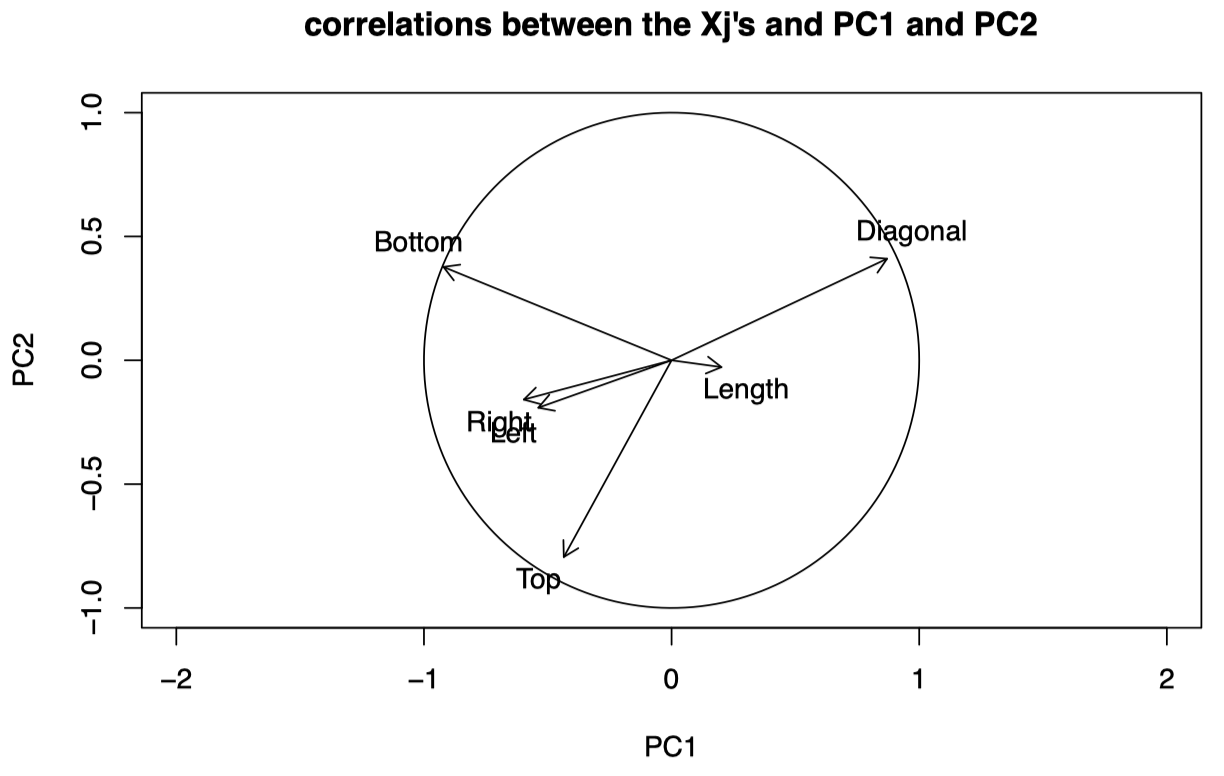
图 2:瑞士纸币数据:$X_j$ 与 PC1 和 PC2 之间的相关系数图。
我们看到 Diagonal、Top 和 Bottom 是与前两个 PC 最相关的三个原始变量。也就是说,前两个 PC 很好地解释了这些变量。
对于靠近圆周的变量:
- 指向相同方向的变量呈正相关。
- 指向相反方向的变量呈负相关。
- 与坐标轴成小角度的变量与相应的 PC 紧密相关。
我们知道 PC1 在 $X_4$ (Bottom) 和 $X_6$ (Diagonal) 上的权重最大,它们的系数符号不同。从图 2 可以看到,两者都靠近相关系数圆的圆周,并且 Bottom 与 PC1 呈负相关,而 Diagonal 与 PC1 呈正相关:它们对于 PC1 具有相反的效应。
对于 PC2,其在 $X_4$ (Bottom)、$X_6$ (Diagonal) 和 $X_5$ (Top) 上的权重最大,其中前两个系数为正,第三个系数为负。我们看到 $X_4$ 和 $X_6$ 与 PC2 正相关,而 $X_5$ 与 PC2 负相关。
表 2 证实了我们刚才所说的内容。另外,我们可以看到 $X_1$、$X_2$ 和 $X_3$ 与前两个 PC 的相关性不强,而前两个 PC 共同解释的方差百分比很小。
表 2:瑞士纸币数据:原始变量与 PC 之间的相关系数。
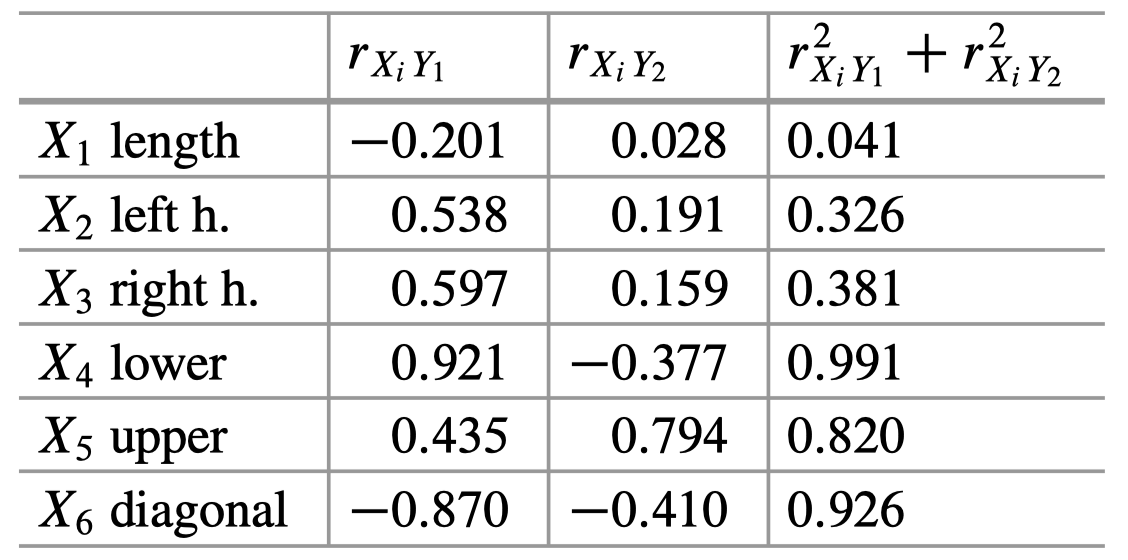
注意:表 2 来自教材 (Hardle and Simar),按照我们之前的计算,这里的符号应该全部取反。教材中,在构造前两个 PC 时采用了特征向量的负版本。
大致来说,对于靠近圆周的变量,如果前两个 PC 占了数据可变性的很大百分比,则:
- 我们可以看到哪些变量倾向于影响个体的坐标。
- 示例:如果某个个体的 PC1 较大 (与其他个体相比),则意味着它与 PC1 相关的变量倾向于具有较大值。
- PC2 同理。
- 但是我们在解释图形时需要谨慎,因为它们只是粗略的近似,而且,我们只能使用那些可以由前两个 PC 很好地表示的变量。
我们可以结合之前的投影数据的散点图一起观察:
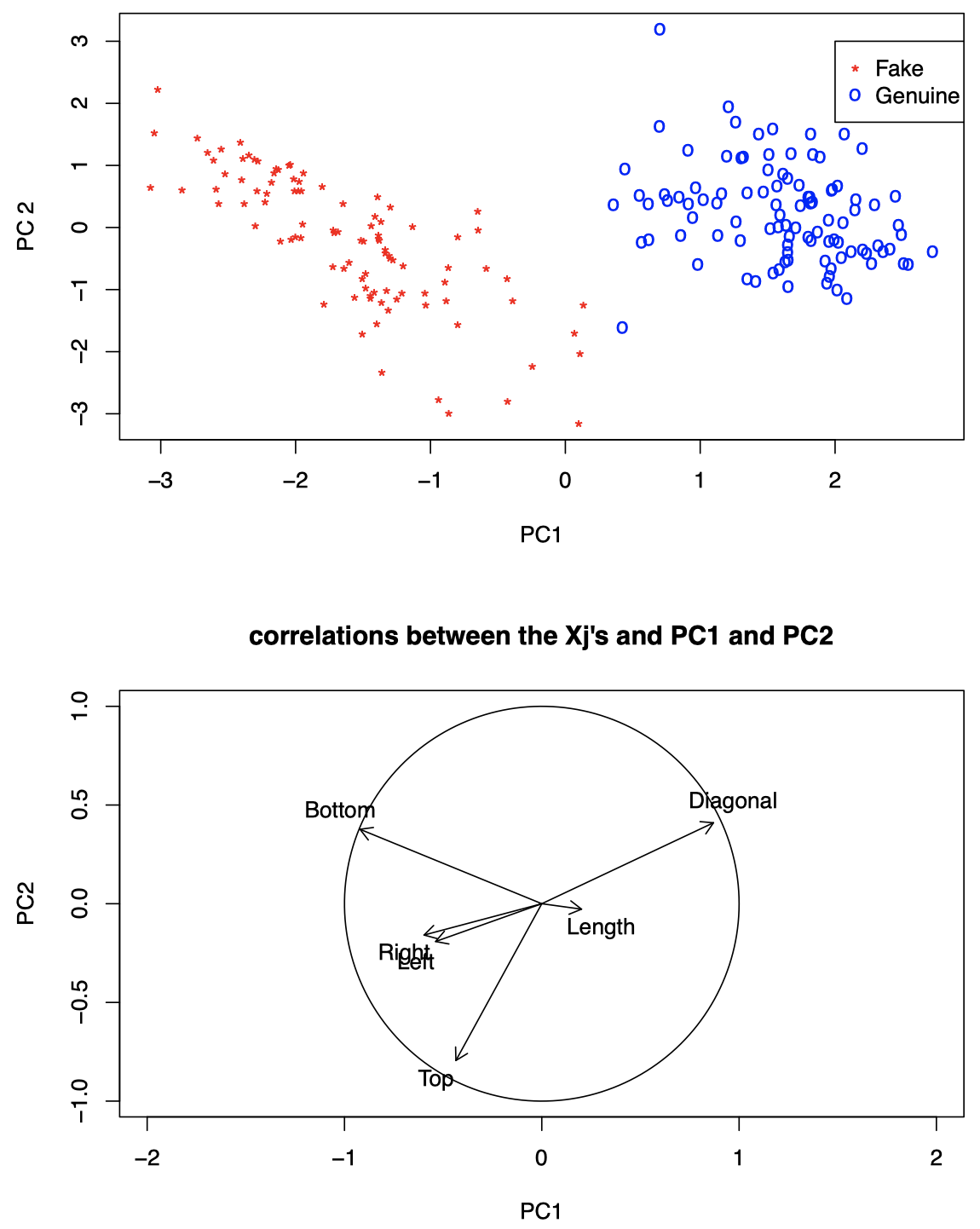
图 3:瑞士纸币数据。上图:将原始数据投影到前两个 PC 上的散点图。下图:$X_j$ 与 PC1 和 PC2 之间的相关系数图。
可以看到:
Diagonal、Bottom和Top似乎在区分假钞和真钞方面起着重要作用。- PC1 与
Diagonal高度正相关 $\quad \Longrightarrow \quad$ 较大的 PC1 往往与较大的Diagonal一起出现。 - PC1 与
Bottom高度负相关 $\quad \Longrightarrow \quad$ 较小的 PC1 往往与较大的Bottom一起出现 - PC2 与
Top高度负相关 $\quad \Longrightarrow \quad$ PC2 的值越大,Top值往往越小。
我们发现,真钞倾向于具有较大的 Diagonal 和较小的 Bottom,而伪钞倾向于具有较大的 Top 和 Bottom。
我们可以通过观察 Diagonal、Bottom 和 Top 这三个原始变量的散点图验证这一点:
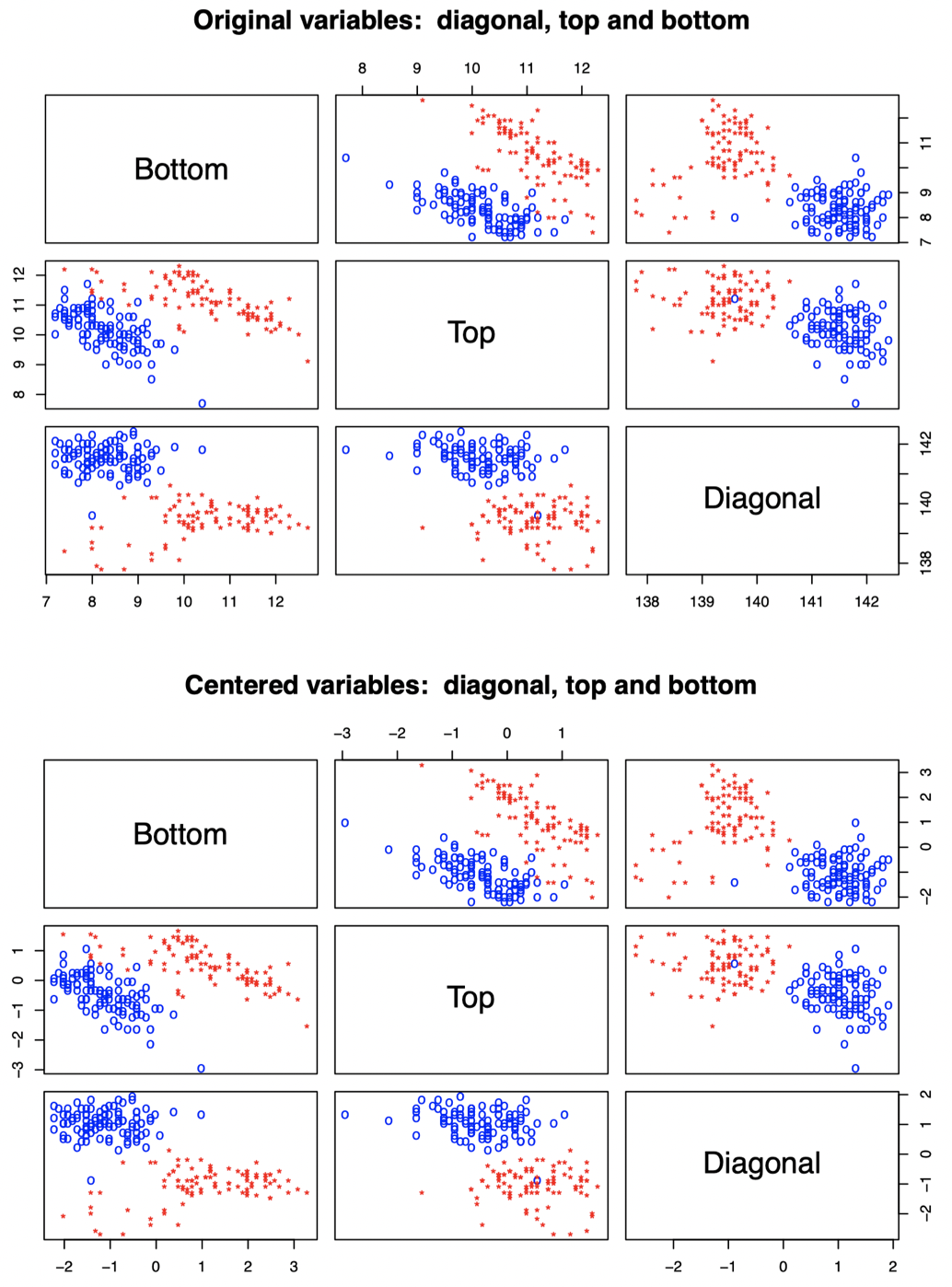
图 4:瑞士纸币数据。上图:原始数据散点图。下图:原始数据中心化后的散点图。红色代表伪钞,蓝色代表真钞。
2. 归一化 PCA
在某些情况下,原始变量的标度可能差异非常大。由于 PCA 试图捕获数据的大部分可变性,因此 PC1 将仅关注因其规模而变化最大的变量。
回到瑞士纸币的例子,根据我们之前的分析,真钞和伪钞的区分主要与 $X_4$ (Bottom)、$X_5$ (Top)、$X_6$ (Diagonal) 这三个变量有关。假如我们将 $X_1$ (Length) 乘以 $100$,那么 PC1 将只关注 $X_1$。
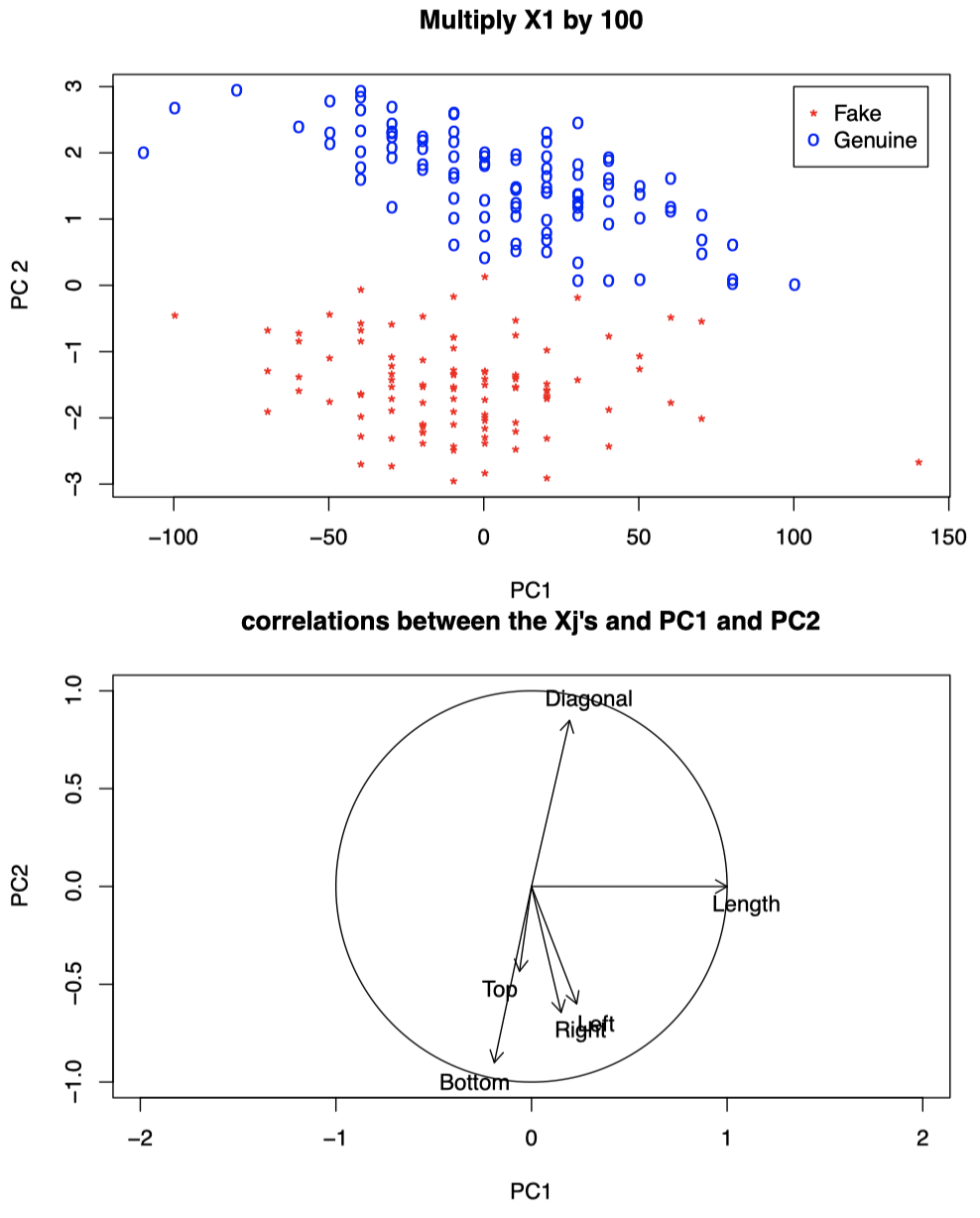
图 5:瑞士纸币数据,将 $X_1$ 乘以 $100$。上图:将数据投影到前两个 PC 上的散点图。下图:$X_j$ 与 PC1 和 PC2 之间的相关系数图。
可以看到,当我们将 $X_1$ 乘以 $100$ 后,PC1 与 Length 呈现强正相关,此时仅靠 PC1 将无法很好地区分真钞和伪钞 (对比之前的图 3)。
如果我们将 $X_1$ (Length) 和 $X_2$ (Left) 都乘以 $100$,那么 PC1 和 PC2 将只关注 $X_1$ 和 $X_2$,我们将无法从数据中学习到任何能够区分真钞和伪钞的信息 (即我们丢弃了两个 PC 的区分能力,对比之前的图 3)。

图 6:瑞士纸币数据,将 $X_1$ 和 $X_2$ 都乘以 $100$。上图:将数据投影到前两个 PC 上的散点图。下图:$X_j$ 与 PC1 和 PC2 之间的相关系数图。
当各变量的标度非常不同时,为了避免前几个 PC 将时间浪费在仅捕获少数几个变量的标度,更好的做法是在执行 PC 分析之前对所有变量进行重新缩放使其方差为 $1$:即将 $X_i =(X_{i1},\dots,X_{ip})^{\mathrm T}$ 替换为
\[D^{-1/2} X_i\]其中,$D = \mathrm{diag}(\sigma_{11},\dots,\sigma_{pp})$。
等效地,我们对相关系数矩阵而不是协方差矩阵进行特征分析:
\[\mathrm{Var}(D^{-1/2} X_i) = D^{-1/2} \mathrm{Var}(X_i) D^{-1/2} = D^{-1/2} \Sigma D^{-1/2} = P\]我们可以计算该相关系数矩阵,然后执行 PC 分析。
3. 其他例子:波士顿住房
波士顿住房 (Boston housing) 数据 (教材 Hardle and Simar, section 22.1) 来自 Harrison and Rubinfeld (1978)。
对于波士顿都会区的每个人口普查区,我们有 $n=506$ 个观测值,包含 $p = 14$ 个变量:
- $X_1$:人均犯罪率 (
crim) - $X_2$:大块占地住宅区比例 (
zn) - $X_3$:非零售商业占地比例 (单位:英亩) (
indus) - $X_4$:查尔斯河 (虚拟变量,靠近河流为
1,其他情况为0) - $X_5$:氮氧化物浓度 (
nox) - $X_6$:每户平均房间数 (
rm) - $X_7$:1940 年之前建造的户主所有房比例 (
age) - $X_8$:与五个波士顿劳动力聚集区的加权距离 (
dis) - $X_9$:与辐射式公路的接近指数 (
rad) - $X_{10}$:每 $1$ 万美元的全值财产税 (
tax) - $X_{11}$:学生/教师比例 (
ptratio) - $X_{12}$:$1000(B − 0.63)^2 I(B < 0.63)$,其中 $B$ 为非裔美国人比例 (
b) - $X_{13}$:低社会地位人口的百分比 (
lstat) - $X_{14}$:户主拥有住房价值的中位数 (单位:千美元) (
medv)
在执行 PCA 之前,需要对数据进行一些转换 (请参见 Hardle and Simar, chapter 1)。我们对除第 4 个二元变量之外的所有其他变量执行 PCA。
在本例中,各变量的标度完全不同,因此我们在执行分析之前需要将变量标准化。以下是图表和相关结果的解释:
表 3:波士顿住房数据:特征值和解释方差的百分比。
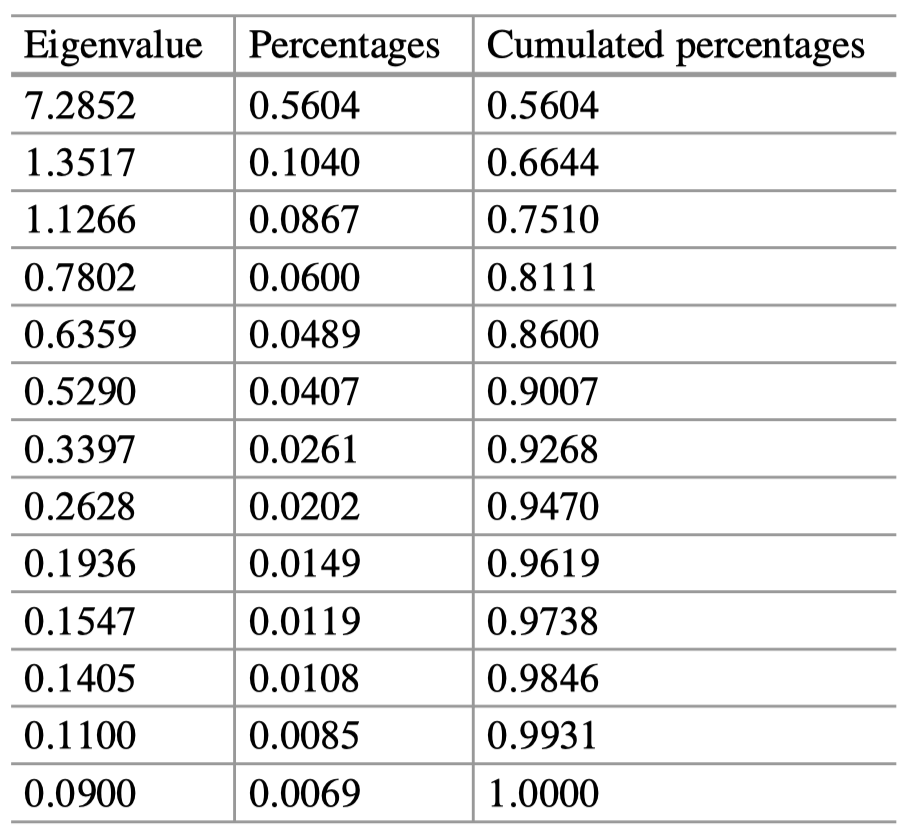
由于这里我们有许多变量,因此前几个 PC 只解释了 $80\%$ 的数据可变性也就不足为奇了,值得一看的是这些数据生成的图像。
表 4:波士顿住房数据:各标准化变量 $X_j$ 与各 PC 之间的相关系数。
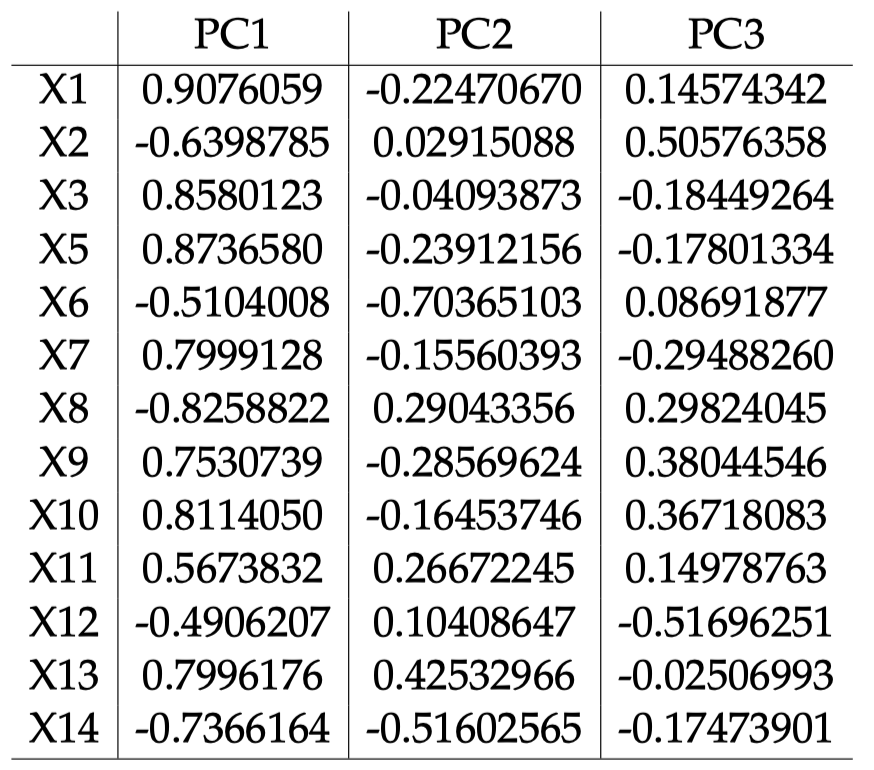

图 7:波士顿住房数据:各标准化变量 $X_j$ 与 PC1 和 PC2 之间的相关系数。
可以看到,除了 $X_{12}$ (b) 和 $X_2$ (zn) 之外,其余大多数变量都靠近圆周,并且与 PC1 之间的相关性最大。PC1 与 dis ($X_8$)、mdev ($X_{14}$)、rm ($X_6$) 呈高度负相关,与除 b 和 zn 之外的所有其他变量均呈高度正相关。PC1 轴上,与 PC1 呈正相关的变量和呈负相关的变量的箭头方向相反,它可以大致解释为生活质量和房屋指标。
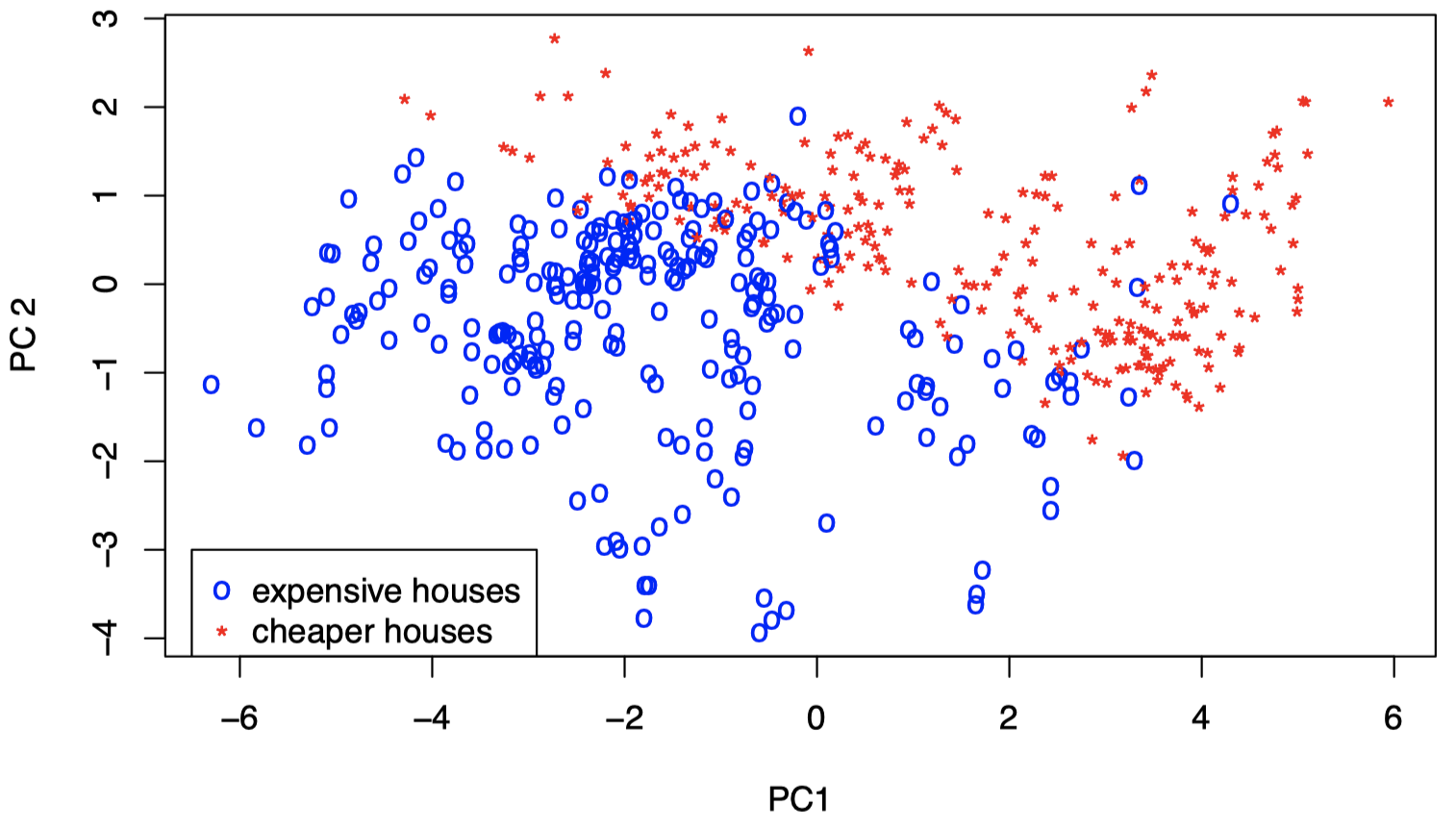
图 8:波士顿住房数据:标准化数据在 PC1 和 PC2 上投影的散点图。红色表示低价房屋,蓝色表示高价房屋。
图中颜色代码:$X_{14} >$ 中位数为蓝色,否则为红色。可以看到,PC1 和 PC2 似乎与房屋价值有关。对于高价值房屋个体,其与 PC1 和 PC2 呈负相关的变量往往具有较高的值;对于低价值房屋个体,其与 PC1 和 PC2 呈正相关的变量往往具有较高的值。但是,这需要进一步研究并通过回到原始变量进行确认 (我们需要进行更详细的研究,并提供更多详细信息)。
从表 4 中可以看到,对于 PC2,其与 $X_8$ (dis)、$X_{11}$ (ptratio)、$X_{13}$ (lstat) 之间相关系数和与 $X_6$ (rm)、$X_{14}$ (medv) 之间相关系数的符号相反,这可以解释为社会因素仅解释了 $10\%$ 的总方差。同样,我们还需要更多相关调查。
PC3 由 zn ($X_2$) 和 b ($X_{12}$) 之间的极性主导,但其相关系数点距离圆周较远,因此如果我们像对 PC1 和 PC2 那样将它与个体联系起来,则风险要更大一些。
4. PCA 用于回归
通常,我们也会将 PC 用作降维工具,用于执行其他统计分析。例如,PCA 也经常用于回归分析,以及分类和聚类问题中。在这些问题中,我们不是将分析技术应用于原始数据,而是将其应用于数据的某些 PC。
例如,考虑一个线性回归问题,对于一个变量 $Z$ 和一个 $p$ 维向量 $X$,我们假设一个线性模型
\[Z = m(X) + \epsilon\]其中,
\[m(x) = E(Z\mid X=x) = \alpha + \beta^{\mathrm T}x\]是回归函数,$E(\epsilon)=0$,并且 $X$ 和 $\epsilon$ 相互独立。
出于简化考虑,这里我们假设 $Z$ 和 $X$ 都已经 中心化,因此上面的模型中不再有截距项 $\alpha$,我们有
\[Z=m(X) + \epsilon\; , \quad m(x)= E(Z\mid X=x) = \beta^{\mathrm T}x\]其中,$\beta \in \mathbb R^p$ 是未知的。
假设我们从上面的模型中观测到一组 i.i.d. 数据
\[(X_1,Z_1),\dots, (X_n,Z_n)\]并且 $\beta$ 是未知的。通常在这种情况下,我们想要估计 $\beta$,从而提供回归函数 $m$ 的估计,并且能够根据新的 $X$ 值预测 $Z$ 值。
从之前的统计课程中,我们知道根据观测数据计算得到的 $\beta$ 的最小二乘估计为:
\[\hat \beta = \mathop{\operatorname{arg\,min}}\limits_{b\in \mathbb R^p}\sum_{i=1}^{n}(Z_i - b^{\mathrm T}X_i)^2 = (\mathcal X^{\mathrm T}\mathcal X)^{-1}\mathcal X^{\mathrm T}\mathcal Z\]其中,$\mathcal X$ 是 $n \times p$ 的数据矩阵,$\mathcal Z = (Z_1,\dots,Z_n)^{\mathrm T}$ 是一个 $n$ 维向量。
当 $p$ 很大时,$\mathcal X^{\mathrm T}\mathcal X$ 通常是不可逆的 (或者几乎不可逆,因此在实践中很难很好地估计其逆矩阵)。
例如,当 $p > n$ 时就会发生这种情况:由于 $\mathcal X$ 是一个 $n \times p$ 的矩阵,然后
- 根据线性代数知识,我们知道 $\mathrm{rank}(\mathcal X)\le \min(n, p)$;
- 并且,$\mathrm{rank}(\mathcal X^{\mathrm T} \mathcal X)=\mathrm{rank}(\mathcal X)\le \min(n, p) = n < p$;
- 由于 $\mathcal X^{\mathrm T} \mathcal X$ 是一个 $p \times p$ 的矩阵,它不可能是满秩的 $\quad \Longrightarrow \quad$ 它不是可逆的。
另外,即使 $p < n$,也有可能发生这种情况:某些变量可以写为其他变量的线性组合,这种情况下,$\mathcal X^{\mathrm T} \mathcal X$ 也是不可逆的。
更一般地,只要一个变量可以近似地写为其他变量的线性组合,那么 $\mathcal X^{\mathrm T} \mathcal X$ 将几乎不可逆,因此在实践中我们很难很好地估计该矩阵的逆。
这种情况下,
\[\hat \beta = (\mathcal X^{\mathrm T}\mathcal X)^{-1}\mathcal X^{\mathrm T}\mathcal Z\]对于 $\beta$ 而言可能是一个非常差的估计量。
这将导致 $\hat \beta$ 失去作用:如果它与 $\beta$ 相差很远,那么它所做的就是带给我们一些关于 $X$ 和 $Z$ 之间关系的误导性信息。
由于我们无法以可靠的方式估算上面的线性模型,因此我们采用该模型的改进版本,可以很好地对其进行近似,并且可以从数据中进行合理估算。
一种方法是对 $X$ 的某些 PC,而不是 $X$ 本身,执行线性回归。
为什么我们可以这么做呢?这是因为如果某些变量可以写为其他变量的线性组合,则 $\Sigma$ 的某些特征值将等于零。
例如,如果 $X=(X_1,X_2)^{\mathrm T}$,并且 $X_2 =c X_1$,其中 $c$ 是一个常数,那么我们有
\[\Sigma = \begin{pmatrix}\mathrm{Var}(X_1) & c\cdot \mathrm{Var}(X_1) \\ c\cdot \mathrm{Var}(X_1) & c^2 \cdot \mathrm{Var}(X_1)\end{pmatrix}\]所以,$\Sigma$ 中的第二列等于第一列乘以 $c$。因此,$|\Sigma |=0$,并且 $\Sigma$ 有一个零特征值。
更一般地,假设 $\Sigma$ 中只有前 $q$ 个特征值非零,并且回忆一下,对于 $j=1,\dots,p$,$X$ 的 PC 的方差满足
\[\mathrm{Var}(Y_j) =\lambda_j\;, \quad \text{for}\; j=1,\dots,p\]所以,
\[\mathrm{Var}(Y_j) = 0\;, \quad \text{for}\; j=q+1,\dots,p\]现在,回忆一下,当 $E(X)=0$ 时,我们可以将 $p$ 维 PC 向量写为
\[Y=\Gamma^{\mathrm T}X\]结合上面的 $\Sigma$,由于 $Y_j$ 之间是不相关的,我们有
\[\mathrm{Var}(Y) = \Lambda\]其中,
\[\Lambda = \begin{pmatrix}\Lambda_1 & 0 \\ 0 & 0\end{pmatrix}\]这里的 $0$ 都表示零矩阵,并且
\[\Lambda_1 = \begin{pmatrix}\lambda_1 & 0 & \cdots & 0\\ 0 & \lambda_2 & \cdots & 0\\ \vdots & \vdots & \ddots & \vdots \\ 0 & \cdots & 0 & \lambda_q\end{pmatrix}\]换而言之,
\[Y \sim (0,\Lambda)\]所以,$Y$ 具有零均值,并且 $Y$ 的最后 $p-q$ 个分量具有零方差。
如果我们将 $p$ 维向量 $Y$ 写为
\[Y^{\mathrm T} = (Y_{(1)}^{\mathrm T}, Y_{(2)}^{\mathrm T})\]其中,
\[Y_{(1)}= (Y_1,\dots,Y_q)^{\mathrm T} \quad \text{and} \quad Y_{(2)}= (Y_{q+1},\dots,Y_p)^{\mathrm T}\]那么,我们有
\[Y_{(1)} \sim (0,\Lambda_1) \quad \text{and} \quad Y_{(2)} \sim (0,0)\]换而言之,$Y_{(2)}$ 是一个具有零均值和零方差的向量 $\quad \Longrightarrow \quad$ 它退化为一个零向量。
现在,由于
\[Y= \Gamma^{\mathrm T}X\]并且 $\Gamma$ 是正交的,然后我们有
\[X=\Gamma Y = \Gamma_{(1)} Y_{(1)} + \Gamma_{(2)} Y_{(2)}\]其中,
\[\Gamma_{(1)} = (\gamma_1,\dots,\gamma_q) \;, \;\; \Gamma_{(2)} = (\gamma_{q+1},\dots,\gamma_p)\]并且
\[\Gamma_{(2)} Y_{(2)} \sim (0,0)\]因此,$X$ 可以直接表示为
\[X= \Gamma_{(1)} Y_{(1)}\]这意味着 $X$ 包含了很多冗余信息,我们只需要使用前 $q$ 个 PC 的向量 $Y_{(1)}$ 即可。
现在,回到我们的线性回归问题:
\[Z=m(X) + \epsilon = \beta^{\mathrm T}X + \epsilon\]我们希望在 $Z$ 和 $X$ 均值为零且 $X$ 的成分之间接近共线性的情况下,对 $m$ 进行估计。
在上面我们讨论过的精确共线性的情况下,我们看到如果 $\Sigma$ 仅具有 $q$ 个非零特征值,则
\[X= \Gamma_{(1)} Y_{(1)}\]其中,$Y_{(1)}$ 是由前 $q$ 个 PC 组成的向量。
然后,我们可以将回归模型写为
\[Z = m_{\mathrm{PC}} (Y_{(1)}) + \epsilon\]其中,
\[m_{\mathrm{PC}} (Y_{(1)}) = \beta_{\mathrm{PC}}^{\mathrm T} Y_{(1)} \quad \text{and} \quad \beta_{\mathrm{PC}}^{\mathrm T} = \beta^{\mathrm T} \Gamma_{(1)}\]换而言之,如果 $\Sigma$ 只有 $q < p$ 个非零特征值,那么相比求解一个关于 $p$ 维向量 $X$ 的线性模型,我们可以求解一个关于 $q$ 维向量 $Y_{(1)}$ 的线性模型作为替代。
的确,我们刚才看到了
\[\beta^{\mathrm T}X = m(X) = m_{\mathrm{PC}}(Y_{(1)}) = \beta_{\mathrm{PC}}^{\mathrm T} Y_{(1)}\]这里,$m_{\mathrm{PC}}$ 要比 $m$ 更容易估计一些,因为现在我们只需要估计一个 $q$ 维参数 $\beta_{\mathrm{PC}}$,而不是一个 $q$ 维参数 $\beta$。
为了估计 $\beta_{\mathrm{PC}}$,我们可以使用最小二乘估计量
\[\hat \beta_{\mathrm{PC}} = \mathop{\operatorname{arg\,min}}\limits_{b\in \mathbb R^q} \sum_{i=1}^{n}(Z_i - b^{\mathrm T}Y_{(1),i})^2 = (\mathcal Y_{(1)}^{\mathrm T}\mathcal Y_{(1)})^{-1} \mathcal Y_{(1)}^{\mathrm T} \mathcal Z\]其中,$Y_{(1),i} = (Y_{i1},\dots,Y_{iq})^{\mathrm T}$ 表示第 $i$ 个个体的 $Y_{(1)}$ 版本,并且
\[\mathcal Y_{(1)} = \begin{pmatrix}Y_{11} & \cdots & Y_{1q}\\ \vdots & \ddots & \vdots \\ Y_{n1} & \cdots & Y_{nq} \end{pmatrix}\]更常见的情况是,$p$ 个分量中只有某几个分量之间接近共线性,因此 $\Sigma$ 的特征值可能全部非零,但其中某些可能接近于零。
假设 $\lambda_{q+1},\dots,\lambda_p$ 都非常小,并且令
\[Y^{\mathrm T} = (Y_{(1)}^{\mathrm T}, Y_{(2)}^{\mathrm T})\, , \;\; Y_{(1)}= (Y_1,\dots,Y_q)^{\mathrm T} \, , \;\; Y_{(2)}= (Y_{q+1},\dots,Y_p)^{\mathrm T}\]然后,$Y_{q+1},\dots,Y_p$ 的方差都将非常小:
\[\mathrm{Var}(Y_{q+1}) = \lambda_{q+1} \, , \dots,\, \mathrm{Var}(Y_{p}) = \lambda_{p}\]这种情况下,移除特征值很小的 PC 只能得到一个近似结果:
\[X=\Gamma Y = \Gamma_{(1)}Y_{(1)} + \Gamma_{(2)}Y_{(2)} \approx \Gamma_{(1)}Y_{(1)}\]回忆一下,
\[Y=(Y_1,\dots,Y_p)^{\mathrm T} = \Gamma^{\mathrm T}X \, , \;\; Y_{(1)}=(Y_1,\dots,Y_q)^{\mathrm T}\]并且对于任何 $x\in \mathbb R^p$,令
\[y=(y_1,\dots,y_p)^{\mathrm T} = \Gamma^{\mathrm T}x \, , \;\; y_{(1)}=(y_1,\dots,y_q)^{\mathrm T}\]现在,我们考虑关于 $Y_{(1)}$ 而不是关于 $X$ 的线性模型:
\[Z = m_{\mathrm{PC}}(Y_{(1)}) + \eta\]其中,
\[m_{\mathrm{PC}}(y_{(1)})= E(Z \mid Y_{(1)}=y_{(1)}) = \beta_{\mathrm{PC}}^{\mathrm T} y_{(1)}\]并且 $E(\eta)=0$。
$m_{\mathrm{PC}}$ 要比 $m$ 更容易估计,因为 $\beta_{\mathrm{PC}}$ 的维度要比 $\beta$ 更低。然而,这里由于我们只有 $X\approx \Gamma_{(1)} Y_{(1)}$,所以我们只能得到
\[m(x) \approx m_{\mathrm{PC}}(y_{(1)})\]如上所述,$\beta_{\mathrm{PC}}$ 的最小二乘估计量等于
\[\hat \beta_{\mathrm{PC}} = \mathop{\operatorname{arg\,min}}\limits_{b\in \mathbb R^q} \sum_{i=1}^{n}(Z_i - b^{\mathrm T}Y_{(1),i})^2 = (\mathcal Y_{(1)}^{\mathrm T}\mathcal Y_{(1)})^{-1} \mathcal Y_{(1)}^{\mathrm T} \mathcal Z\]我们希望这种近似能得到较好的结果,因此我们就可以将 $m(x)$ 估计为
\[\hat m_{\mathrm{PC}}(y_{(1)}) = \hat \beta_{\mathrm{PC}}^{\mathrm T} y_{(1)}\]那么,应该如何选择 $q$ 呢?选择能够使最小二乘估计量最小化的 $q$ 将无法工作 (这会造成过拟合,我们选择的 $q$ 太大了)。
通常使用的一种选择要使用的 PC 数量 $q$ 的标准是交叉验证 (CV)。在最简形式下,它将选择
\[q = \mathop{\operatorname{arg\,min}}\limits_{k=1,\dots,p} CV(k)\]其中,
\[CV(k)=\sum_{i=1}^{n}(Z_i - \hat \beta_{\mathrm{PC},k}^{-i} Y_{(1),i})^2\]并且 $\hat \beta_{\mathrm{PC},k}^{-i}$ 表示按照之前给出的公式取 $q=k$ 计算出的 $\beta_{\mathrm{PC}}$ 的 LS 估计量,只是这里我们将第 $i$ 个个体从 $\mathcal Z$ 和 $\mathcal Y_{(1)}$ 中移除了。
在实践中我们经常这样做:对少量的 $q$ 个 PC (而不是大量的 $p$ 个原始变量) 进行线性回归。
问题:在回归中,由于我们的目标并非仅仅解释 $X$,而是需要解释 $Z$ 和 $X$ 之间的关系,因此选择前几个 PC 并非最佳选择。
- 实际上,我们所知道的是,前几个 PC 可以解释 $X$ 的大部分可变性,但我们的目标是解释 $Z$ 与 $X$ 之间的关系。
- 如果目标是进行回归,则前几个 PC 可能并非最佳选择。使用几个 PC 可能仍然是一个好主意,但并非特定的前几个 PC。
- 相反,我们可以选择少数几个能够解释 $Z$ 和 $X$ 之间大部分关系的 PC。
- 事实上,我们可以做到这一点,有些人也的确是这样做的,但是对于这种情况有没有更好地对 $X$ 进行降维的方法呢?也就是说,我们可以在降维的同时捕获到 $Z$ 和 $X$ 之间的关系吗?答案是肯定的,下节课我们将介绍相关方法 PLS。
下节内容:主成分分析 (三)
本作品采用知识共享署名-非商业性使用-相同方式共享 4.0 国际许可协议进行许可。 欢迎转载,并请注明来自:YEY 的博客 同时保持文章内容的完整和以上声明信息!