Lecture 06 线性模型选择与正则化
参考教材:
- Gareth, J., Daniela, W., Trevor, H., & Robert, T. (2013). An intruduction to statistical learning: with applications in R. Spinger.
- Hastie, T., Tibshirani, R., & Friedman, J. (2009). The elements of statistical learning: data mining, inference, and prediction. Spinger Science & Business Media.
1. 引言
回忆一下标准的线性回归模型:
\[Y=\beta_0 + \beta_1 X_1 +\cdots + \beta_p X_p + \epsilon\]它通常用于描述响应变量 $Y$ 和一系列预测变量 $X_1,X_2,\dots,X_p$ 之间的线性关系。并且我们在之前课程中介绍了一种用于拟合此模型的经典方法:最小二乘法。
在接下来的课程中,我们将考虑一些扩展线性模型框架的方法。在第 7 章的课程中,我们对线性模型进行了推广,以使其适用于关系为 非线性 (non-linear),但形式仍然 可加 (additive) 的情况。在第 8 章的课程中,我们将考虑一些更通用的 非线性模型。
尽管线性模型非常简单,但其在可解释性方面具有明显优势,并且通常显示出良好的预测性能。因此,在正式介绍非线性模型之前,我们将先介绍几种可替代普通最小二乘拟合的一些其他拟合方法,这些方法是对简单线性模型的改进。
那么,为什么要采用其他拟合方法替代最小二乘法呢?
因为与最小二乘法相比,其他拟合方法具有更高的 预测准确率 (prediction accuracy) 和更好的 模型可解释性 (model interpretability)。
-
预测准确率:若响应变量和预测变量的真实关系近似线性,则最小二乘估计的偏差较低。若 $n\gg p$,即观测个数 $n$ 远大于变量个数 $p$,则到最小二乘估计的方差通常较低,从而在测试样本集上有较好表现。然而,在不满足 $n$ 远大于 $p$ 的情况下,最小二乘拟合可能会发生较大变化,发生过拟合,从而使模型在测试样本集上表现较差。此外,若 $p > n$,最小二乘法得到的系数估计结果不唯一:此时方差为 无穷大 (infinite),这种情况下最小二乘法会失效。通过 限制 (constraining) 或 收缩 (shrinking) 待估计系数,以牺牲偏差为代价,显著减小估计量方差。这种方法可以显著提高模型在测试样本集上的预测准确率。
-
模型可解释性:通过删除不相关的特征,即通过将相应的系数估计设置为零,我们可以获得更易于解释的模型。 我们将介绍一些自动执行特征选择的方法
在多元回归模型中,常常存在一个或多个预测变量与响应变量不存在线性关系的情况,包括一些增加了模型的复杂性、却与模型 无关 (irrelevant) 的变量。通过移除这些无关变量,即将其系数设置为 $0$,可以使模型的可解释性更强,但运用最小二乘法很难将系数缩减至 $0$。本节课中,我们将介绍几种自动进行 特征选择 (feature selection) 或 变量选择 (variable selection) 的方法,以便将无关变量从多元回归模型中剔除。
除了最小二乘法,还有多种方法可用于拟合线性模型,其中既有经典方法又有现代方法。本节课中我们主要讨论以下三类重要的方法:
-
子集选择 (Subset selection):该方法从 $p$ 个预测变量中挑选出与响应变量相关的变量,构建一个变量子集,再对这个缩减后的变量集合应用最小二乘法拟合模型。
-
收缩 (Shrinkage):该方法基于全部 $p$ 个变量进行模型拟合。但是,与最小二乘估计相比,该方法的估计系数可以缩减为 $0$。这种收缩,也称 正则化 (regularization),具有减少方差的效果。根据收缩的类型,某些系数估计可以正好为 $0$。因此,收缩法也可以用于变量选择。
-
降维 (Dimension reduction):此方法将 $p$ 个原始预测变量投影到一个 $M$-维子空间中,其中 $M< p$。这是通过计算原始变量的 $M$ 个不同的 线性组合 (linear combination) 或者 投影 (projections) 实现的。然后,我们将这 $M$ 个投影作为新的预测变量,用最小二乘法拟合线性回归模型。
本节课中,我们将详细介绍上述方法及其优缺点。虽然这里我们讨论的是之前线性回归模型的扩展,但其中涉及的概念同样适用于其他方法,例如之前介绍的分类模型。
2. 子集选择
这里我们将介绍几种选择预测变量子集的方法,包括最优子集选择和逐步模型选择。
2.1 最优子集选择
最优子集选择 (best subset selection):对 $p$ 个预测变量的所有可能组合分别使用最小二乘回归进行拟合。即拟合包含一个变量所有 $p$ 个的模型;拟合包含两个变量的所有 ${p \choose 2} = p(p-1)/2$ 个模型,以此类推。最后在所有可能模型中选取一个最优模型。
最优子集选择算法:
- 令 $\mathcal M_0$ 表示 零模型 (null model),即不包含任何预测变量的模型。该模型只是简单预测各观测的样本均值。
- 对于 $k=1,2,\dots,p$:
(a) 拟合正好包含 $k$ 个预测变量的所有 ${p \choose k}$ 个模型。
(b) 从这 ${p \choose k}$ 个模型中选择具有最小 $\mathrm{RSS}$ 或者最大 $R^2$ 的模型作为最优模型,记为 $\mathcal M_k$。 - 根据 $\mathrm{CV}$ 预测误差、$C_p\, (\mathrm{AIC})$、$\mathrm{BIC}$ 或者调整 $R^2$,从 $\mathcal M_0,\dots, \mathcal M_p$ 中选出一个最优模型。
例子:信用卡数据集
图 1 是应用最优子集选择的一个例子。图中的每个点都对应一个用 Credit 数据集的 $11$ 个预测变量的不同子集建立的最小二乘回归模型。其中,ethnicity 是一个包含三个水平的分类变量,因此将其编码为两个虚拟变量。图中横坐标表示模型中包含的变量个数,在散点圈中绘制每个模型对应的 $\mathrm{RSS}$ 和 $R^2$ 值,用红色折线将不同模型复杂度下的 $\mathrm{RSS}$ 和 $R^2$ 对应的点联结起来。
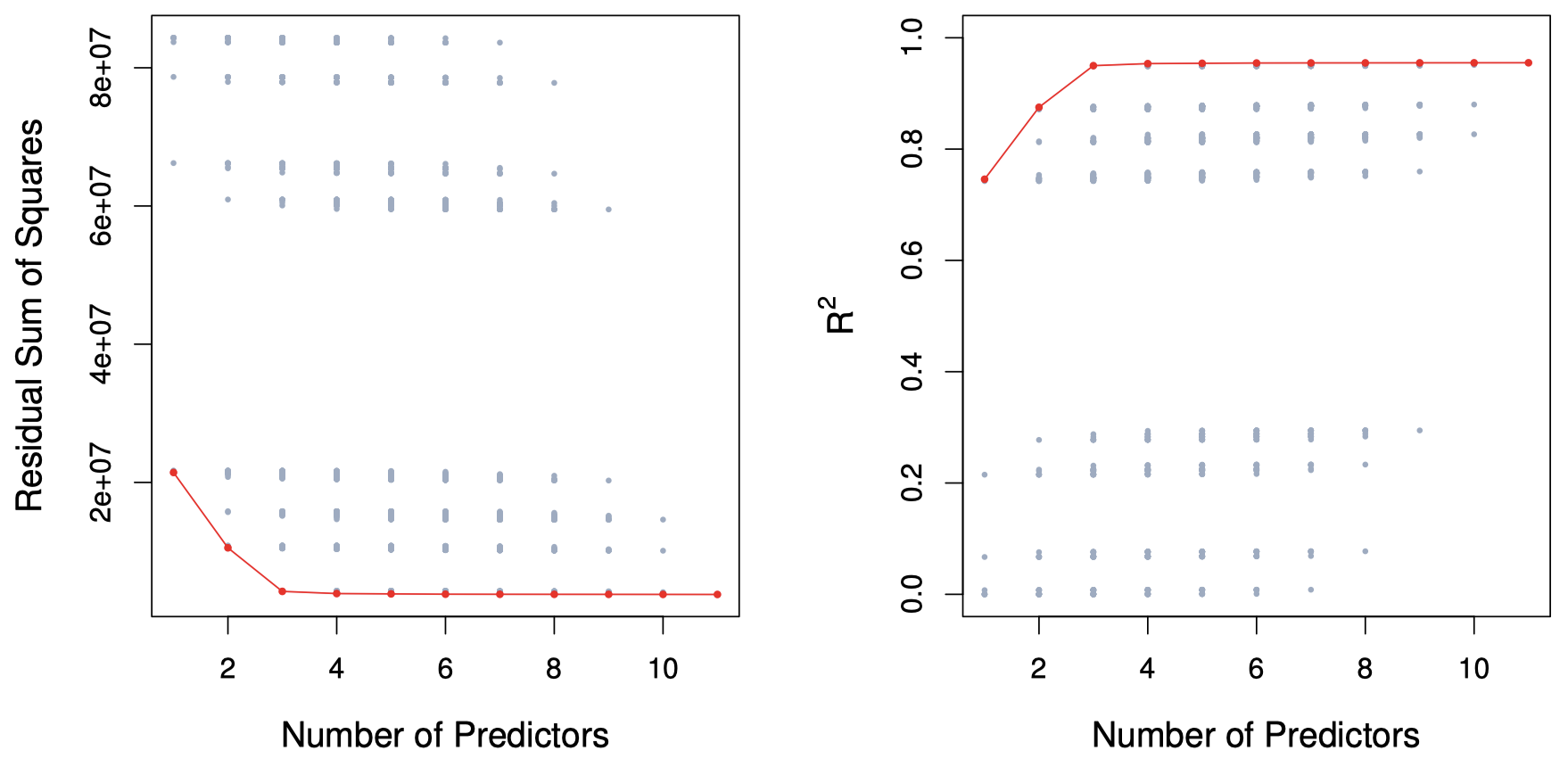
图 1:图中展示了 Credit 数据集中 $10$ 个预测变量所有可能子集构成的模型的 $\mathrm{RSS}$ 和 $R^2$ 值。红色折线表示给定预测变量个数的情况下,最优模型的 $\mathrm{RSS}$ 和 $R^2$ 值轨迹。数据集包含 $10$ 个预测变量,而 $x$ 轴的范围在 $1$ 到 $11$ 之间,这是由于其中有一个包含三种水平的分类变量,将其编码后引入了两个虚拟变量。
可以看到,随着变量个数增加,统计量得到改善。然而,在模型引入第三个变量之后,继续增加变量对于模型 $\mathrm{RSS}$ 和 $R^2$ 值的改善幅度将变得非常小。
尽管我们在这里为最小二乘回归提供最优子集选择,但是相同的思想也适用于其他类型的模型,例如逻辑回归。在逻辑回归中应用最优子集选择时,算法的步骤 2 中的 $\mathrm{RSS}$ 应当用 偏差 (deviance) 代替,两者的作用相同,但偏差的适用范围更广。偏差定义为负 $2$ 倍的最大似然函数,偏差越小,拟合优度越高。
2.2 逐步选择
当 $p$ 很大时,最优子集选择算法存在以下两方面的问题:
-
由于 运算效率 的限制,最优子集选择方法不再适用。
-
另外,还存在一些统计学上的问题:随着搜索空间的增大,通过最优子集法找到的模型虽然在训练数据上有较好表现,但对新数据并不具备良好的预测能力。从一个巨大搜索空间中得到的模型通常会存在 过拟合 和 系数估计方差高 的问题。
基于上述的两大原因,与最优子集选择相比,逐步选择的优点是限制了搜索空间,从而提高了运算效率。
前向逐步选择
前向逐步选择 (Forward stepwise selection) 从不包含任何预测变量的模型开始,然后每次添加一个预测变量到模型中,直到所有预测变量都被添加到模型中。特别地,在每一步中,算法将能够对拟合带来 最大额外提升 的变量添加到模型中。
前向逐步选择算法:
- 令 $\mathcal M_0$ 表示 零模型 (null model),即不包含任何预测变量的模型。
- 对于 $k=0,1,2,\dots,p-1$:
(a) 考虑所有 $p-k$ 个模型,其中每个模型都在模型 $\mathcal M_k$ 的基础上增加一个变量。
(b) 从这 $p-k$ 个模型中选择具有最小 $\mathrm{RSS}$ 或者最大 $R^2$ 的模型作为最优模型,记为 $\mathcal M_{k+1}$。 - 根据 $\mathrm{CV}$ 预测误差、$C_p\, (\mathrm{AIC})$、$\mathrm{BIC}$ 或者调整 $R^2$,从 $\mathcal M_0,\dots, \mathcal M_p$ 中选出一个最优模型。
与最优子集选择相比,前向逐步选择在运算效率上具有明显优势。
虽然前向逐步选择在实际中有很好的应用,但它无法保证找到的模型是所有 $2^p$ 个模型中最优的。
例如,在给定的包含三个变量的数据集中,最优的单变量模型只包含变量 $X_1$,最优的双变量模型包含 $X_2$ 和 $X_3$。这种情况下,通过前向逐步选择方法无法得到包含双变量的最优模型,因为 $\mathcal M_1$ 包含变量 $X_1$,从而 $\mathcal M_2$ 只能包含 $X_1$ 及另一变量,$X_2$ 或 $X_3$。
例子:信用卡数据集
表 1 给出了在 Credit 数据集上使用最优子集选择和前向逐步选择的前四个模型的结果。
表 1:对 Credit 数据使用最优子集选择和前向逐步选择的前四个模型的结果。前三个模型选择结果相同,第四个模型选择结果不同。

可以看到,最优子集选择和前向逐步选择在最优单变量模型中都引入了 rating 变量,紧接着在双变量和三变量模型中依次引入了 income 和 student 变量。但是,最优子集选择在四变量模型中将 rating 变量替换为 cards 变量,而在前向逐步选择中必须要在四变量模型中依然保留 rating 变量。从之前的图 1 来看,三变量和四变量模型之间在 $\mathrm{RSS}$ 值上并没有太大差别,因此,这两种方法选出的四变量模型都是可用的。
在高维数据中,甚至 $n < p$ 的情况下,依然可以使用前向逐步选择方法;在这种情况下,可以建立子模型 $\mathcal M_0,\dots,\mathcal M_{n-1}$,因为每个子模型都使用最小二乘法拟合,若 $p\gg n$,结果将是不唯一的。
后向逐步选择
与前向逐步选择一样,后向逐步选择 (backward stepwise selection) 为最优子集选择提供了一种有效的替代方法。
但是,与前向逐步选择不同,它从包含所有 $p$ 个预测变量的最小二乘模型开始,然后每次删除一个作用最小的预测变量。
后向逐步选择算法:
- 令 $\mathcal M_p$ 表示 全模型 (full model),即包含全部 $p$ 个预测变量的模型。
- 对于 $k=p,p-1,\dots,1$:
(a) 考虑所有 $k$ 个模型,其中每个模型都在模型 $\mathcal M_k$ 的基础上减少一个变量,即每个模型都包含 $k-1$ 个变量。
(b) 从这 $k$ 个模型中选择具有最小 $\mathrm{RSS}$ 或者最大 $R^2$ 的模型作为最优模型,记为 $\mathcal M_{k-1}$。 - 根据 $\mathrm{CV}$ 预测误差、$C_p\, (\mathrm{AIC})$、$\mathrm{BIC}$ 或者调整 $R^2$,从 $\mathcal M_0,\dots, \mathcal M_p$ 中选出一个最优模型。
与前向逐步选择类似,后向逐步选择方法只需要对 $1+p(p+1)/2$ 个模型进行搜索。因此,当 $p$ 太大导致最优子集选择不适用时,可以采用该方法。
同样,与前向逐步选择类似,后向逐步选择方法无法保证得到的模型在 $p$ 个预测变量的所有 $2^p$ 个可能子集中是最优的。
后向逐步选择要求 样本数 $n$ 要大于变量数 $p$ (保证全模型可以被拟合)。相反,前向逐步选择在 $n < p$ 的情况下依然适用,因此当 $p$ 非常大的时候,前向逐步选择是唯一可行的子集选择方法。
2.3 选择最优模型
最优子集选择、前向逐步选择和后向逐步选择等方法产生了一系列由 $p$ 个预测变量的子集所构建的模型。为了实现这些方法,需要找到一种确定最优模型的方法。
如前所述,包含所有预测变量的模型总是具有最小的 $\mathrm{RSS}$ 和最大的 $R^2$,因为这些统计量与 训练误差 有关。然而,我们希望找到具有 最小测试误差 的模型。回想一下,训练误差通常不能很好地评估测试误差。
因此,$\mathrm{RSS}$ 和 $R^2$ 并不适用于从一系列具有不同预测变量数量的模型中选择出最优模型。
为了达到基于测试误差选择最优模型的目的,我们需要估计测试误差。通常有两种方法:
- 根据过拟合导致的偏差对训练误差进行 调整,从而间接地估计测试误差。
- 通过验证集方法或交叉验证方法,直接 估计测试误差。
接下来,我们将对以上两种方法进行说明。
$C_p$、$\mathrm{AIC}$、$\mathrm{BIC}$ 和调整 $R^2$
这些方法可以根据模型大小对训练误差进行调整,并且可以用于选择包含不同变量数量的模型。
这里,我们对最优子集选择在 Credit 数据集上产生的不同大小的模型,应用三种方法从中选出最优模型:$C_p$、$\mathrm{BIC}$ 和调整 $R^2$。
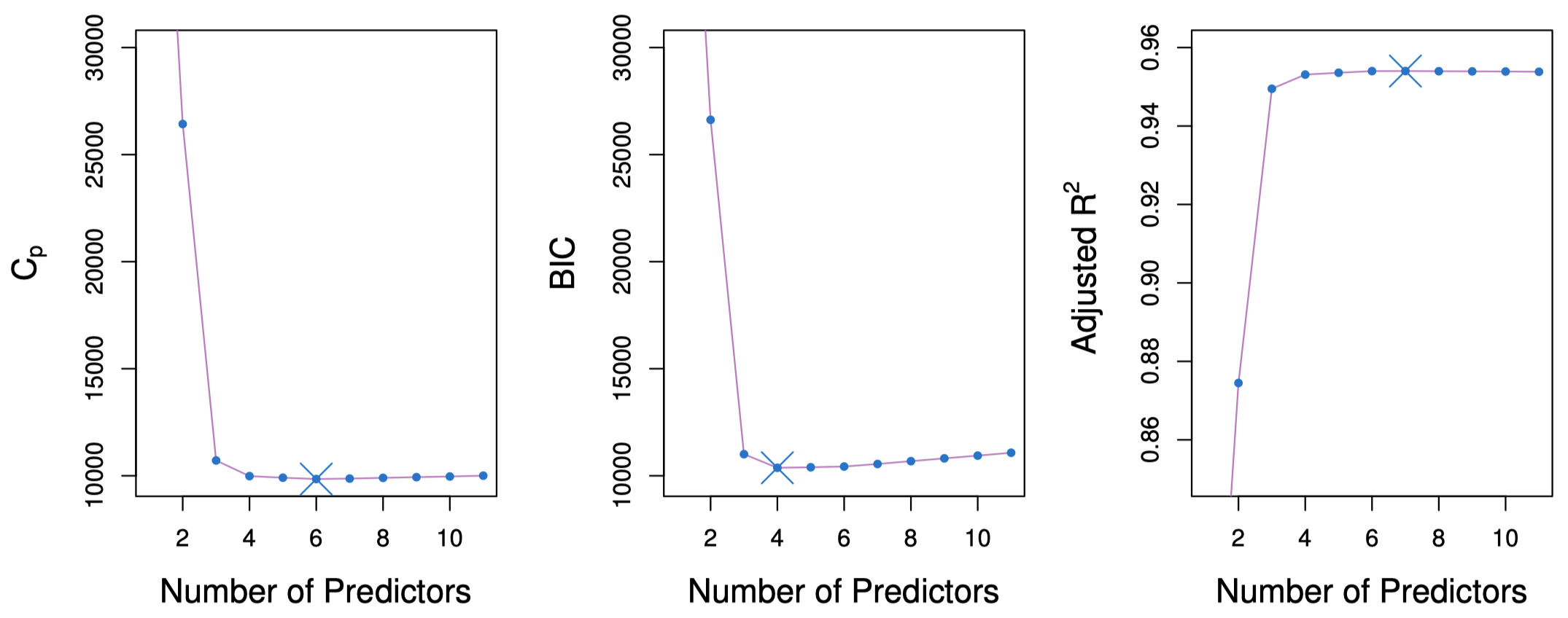
图 2:图中显示了在 Credit 数据集上应用 $C_p$、$\mathrm{BIC}$ 和调整 $R^2$ 对不同大小的模型进行最优子集选择的结果。$C_p$ 和 $\mathrm{BIC}$ 是测试均方误差的估计。中图显示,$\mathrm{BIC}$ 作为测试误差的估计在模型引入四个变量后开始增加。左图和右图中,$C_p$ 和调整 $R^2$ 在模型引入四个变量后开始变得相对平缓。
Mallow’s $C_p$
用最小二乘法拟合模型,$C_p$ 值的计算公式如下:
\[C_p= \dfrac{1}{n}(\mathrm{RSS} + 2d \hat \sigma^2)\]其中,$d$ 是模型包含的预测变量的数量,$\hat \sigma^2$ 是与各响应变量测量相关的误差项 $\epsilon$ 的方差估计。
$\mathrm{AIC}$ 准则
$\mathrm{AIC}$ 准则适用于许多使用最大似然法进行拟合的模型:
\[\mathrm{AIC} = -2 \log L + 2\cdot d\]其中,$L$ 是估计模型的似然函数的最大值。
在具有高斯误差的线性模型的情况下,最大似然估计和最小二乘估计是等价的,并且 $C_p$ 和 $\mathrm{AIC}$ 相等。我们可以证明这一点。
$\mathrm{BIC}$ 准则
$\mathrm{BIC}$ 是从贝叶斯观点中衍生出来的,然而最终也和 $C_p$ (以及 $\mathrm{AIC}$) 非常相似。对于包含 $d$ 个变量的最小二乘模型,$\mathrm{BIC}$ 通常由下式给出:
\[\mathrm{BIC} = \dfrac{1}{n}(\mathrm{RSS} + \log (n)d \hat \sigma^2)\]类似 $C_p$,测试误差较低的模型的 $\mathrm{BIC}$ 值也较低,因此通常我们选择具有最低 $\mathrm{BIC}$ 值的模型作为最优模型。
请注意,$\mathrm{BIC}$ 用 $\log (n)d \hat \sigma^2$ 代替了 $C_p$ 中的 $2d\hat \sigma^2$,其中 $n$ 是观测数。
由于对于任意的 $n> 7$,都有 $\log n > 2$,所以 $\mathrm{BIC}$ 统计量通常会对包含多个变量的模型施加较大的惩罚。因此,与 $C_p$ 相比,$\mathrm{BIC}$ 选择的模型通常要小一些。
调整 $R^2$
对于包含 $d$ 个变量的最小二乘模型,调整 $R^2$ 统计量由下式计算得到:
\[\text{Adjusted } R^2=1- \dfrac{\mathrm{RSS}/(n-d-1)}{\mathrm{TSS}/(n-1)}\]其中,$\mathrm{TSS}=\sum_{i=1}^{n}(y_i - \overline y)^2$ 是响应变量的总平方和。
与 $C_p$、$\mathrm{AIC}$、$\mathrm{BIC}$ 越小表示模型测试误差越低不同,调整 $R^2$ 越大,模型测试误差越低。
最大化调整 $R^2$ 等价于最小化 $\frac{\mathrm{RSS}}{n-d-1}$。虽然 $\mathrm{RSS}$ 总是随模型中的变量数量的增加而减小,但是由于分母项中包含 $d$,所以 $\frac{\mathrm{RSS}}{n-d-1}$ 有可能增大也有可能减小。
不同于 $R^2$ 统计量,调整 $R^2$ 统计量对加入非必要变量的模型 引入了惩罚。
验证集法与交叉验证法
这两种方法都会返回一系列由模型大小 $k=0,1,2,\dots$ 索引的模型 $\mathcal M_k$。我们的目标是选择一个 $\hat k$,然后返回模型 $\mathcal M_{\hat k}$。
我们将为所考虑的每个模型 $\mathcal M_k$ 计算验证集误差或者交叉验证误差,然后选择使估计测试误差最小的 $k$。
与 $C_p$、$\mathrm{AIC}$、$\mathrm{BIC}$ 和调整 $R^2$ 相比,这种方法有一个好处,它提供了测试误差的一个直接估计,而 无需估计误差项的方差 $\sigma^2$。
这种方法可以用于更广泛的模型选择任务中,即使对于难以精确确定模型自由度 (例如,模型中的预测变量个数) 或者难以估计误差项方差 $\sigma^2$ 的情况,该方法同样适用。
图 3 显示了 Credit 数据集包含 $d$ 个变量的最优模型,曲线表示 $\mathrm{BIC}$、验证集误差和交叉验证误差作为 $d$ 的函数的取值。验证集误差通过随机选择四分之三的观测作为训练集,其余观测作为验证集计算得到。交叉验证误差按 $k= 10$ 折进行计算。在这种情况下,验证集方法和交叉验证方法得到的模型都包含 $6$ 个变量。然而,所有这三种方法表明,分别包含 $4$、$5$、$6$ 个变量的模型的测试误差都大致相等。
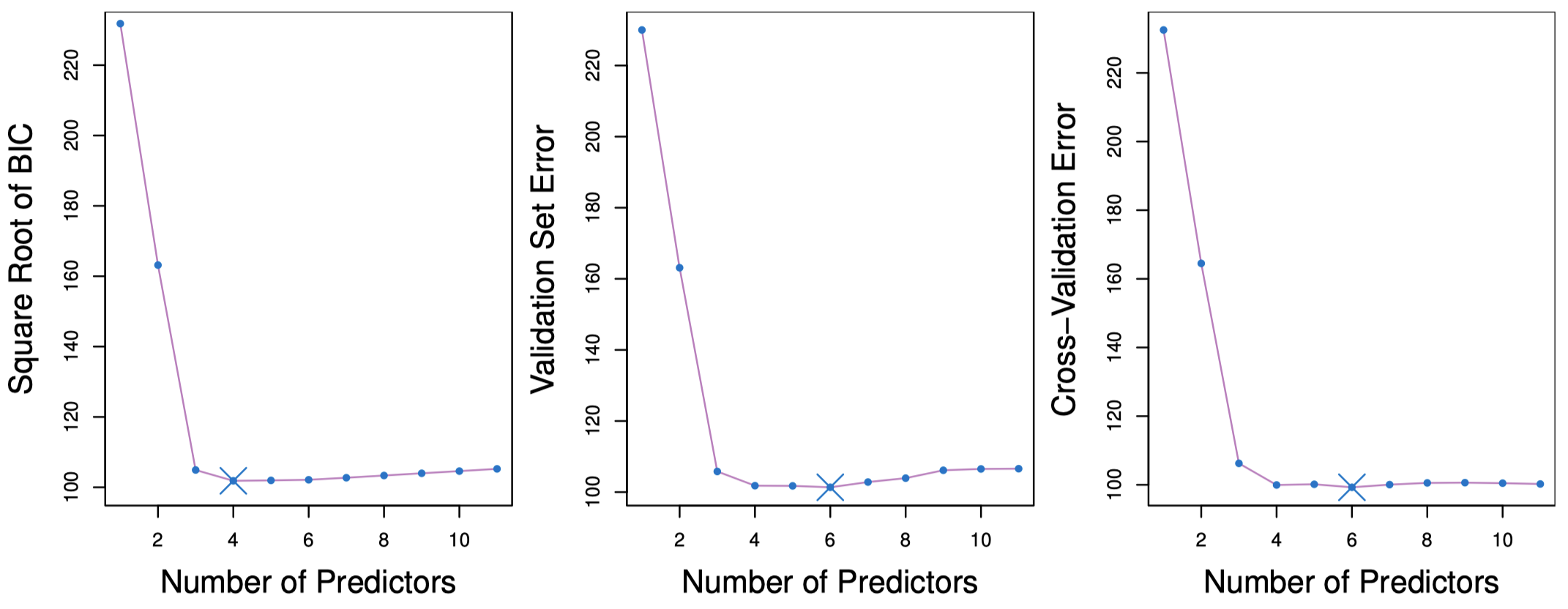
图 3:图中显示了 Credit 数据集包含 $d$ 个变量的最优模型的三种统计量的值,$d$ 的范围在 $1$ 到 $11$ 之间。基于各统计量得到的全局最优模型用 “$\times$” 表示。左图:$\mathrm{BIC}$ 的平方根。中图:验证集误差。右图:交叉验证误差。
事实上,图 3 的中图与右图的测试误差估计曲线均比较平坦。与两变量模型相比,三变量模型具有明显更低的测试误差估计,而当模型中变量个数在 $3$ 到 $11$ 之间变化时,测试误差估计值的差别不大。
此外,如果对不同的训练集和验证集划分重复使用验证集方法,或者对于不同的折数重复使用交叉验证方法,会得到不同的具有最低测试误差的精确模型。
针对这种情况,可以使用 一个标准误原则 (one-standard-error rule) 进行模型选择:首先计算不同大小的模型的测试均方误差估计值的标准误,然后选择测试误差估计值在曲线最低点附近一个标准误范围内且预测变量数最少的模型。这种做法的原因是在一系列效果近似相同的模型中,总是倾向于选择最简单的模型。
上面的例子中,对验证集方法和交叉验证方法使用一个标准误原则选择出的模型包含三个变量。
3. 收缩方法
前面介绍的子集选择方法使用最小二乘法对包含预测变量子集的线性模型进行拟合。除此之外,我们还可以使用对系数进行 约束 (constrains) 或 正则化 (regularizes) 的技术来对包含所有 $p$ 个预测变量的模型进行拟合,也就是说,将系数估计值向 $0$ 的方向压缩。至于为什么这种约束条件可以改善拟合效果,其原理并非显而易见。但事实证明,收缩系数可以显著减小其方差。
接下来,我们将介绍两种最常见的收缩方法:岭回归 (Ridge regression) 和 Lasso。
3.1 岭回归
回忆一下,最小二乘拟合通过最小化下式来估计 $\beta_0,\beta_1,\dots,\beta_p$:
\[\mathrm{RSS}=\sum_{i=1}^{n}\left(y_i - \beta_0 - \sum_{j=1}^{p}\beta_j x_{ij}\right)^2\]相比之下,岭回归的估计系数 $\hat \beta^R$ 通过最小化下式得到:
\[\sum_{i=1}^{n}\left(y_i - \beta_0 - \sum_{j=1}^{p}\beta_j x_{ij}\right)^2 + \lambda \sum_{j=1}^{p}\beta_j^2 = \mathrm{RSS} + \lambda \sum_{j=1}^{p}\beta_j^2\]其中,$\lambda \ge 0$ 是一个 调节参数 (tuning parameter),需要单独确定。
与最小二乘法一样,岭回归通过使 $\mathrm{RSS}$ 很小,来寻找能够较好拟合数据的系数估计。
然而,岭回归还增加了一个被称为 收缩惩罚 (shrinkage penalty) 的项 $\lambda \sum_{j=1}^{p}\beta_j^2$。当 $\beta_1,\dots,\beta_p$ 接近 $0$ 时,该项会变得很小。因此,它具有将回归系数 $\beta_j$ 的估计向 $0$ 的方向 压缩 的效应。
调节参数 $\lambda$ 的作用是控制这两项对回归系数估计的相对影响程度。当 $\lambda=0$ 时,收缩惩罚项不会产生作用,岭回归与最小二乘估计结果相同。随着 $\lambda \to \infty$,收缩惩罚项的影响力增加,岭回归系数估计值越来越接近 $0$。
与最小二乘法得到一个唯一的估计结果不同,岭回归得到的系数估计 $\hat \beta_{\lambda}^R$ 会随 $\lambda$ 的变化而变化。选择一个合适的 $\lambda$ 值非常重要,我们可以使用交叉验证法进行选择。
例子:信用卡数据集
图 4 显示了 Credit 数据集的岭回归系数估计值的变化情况:
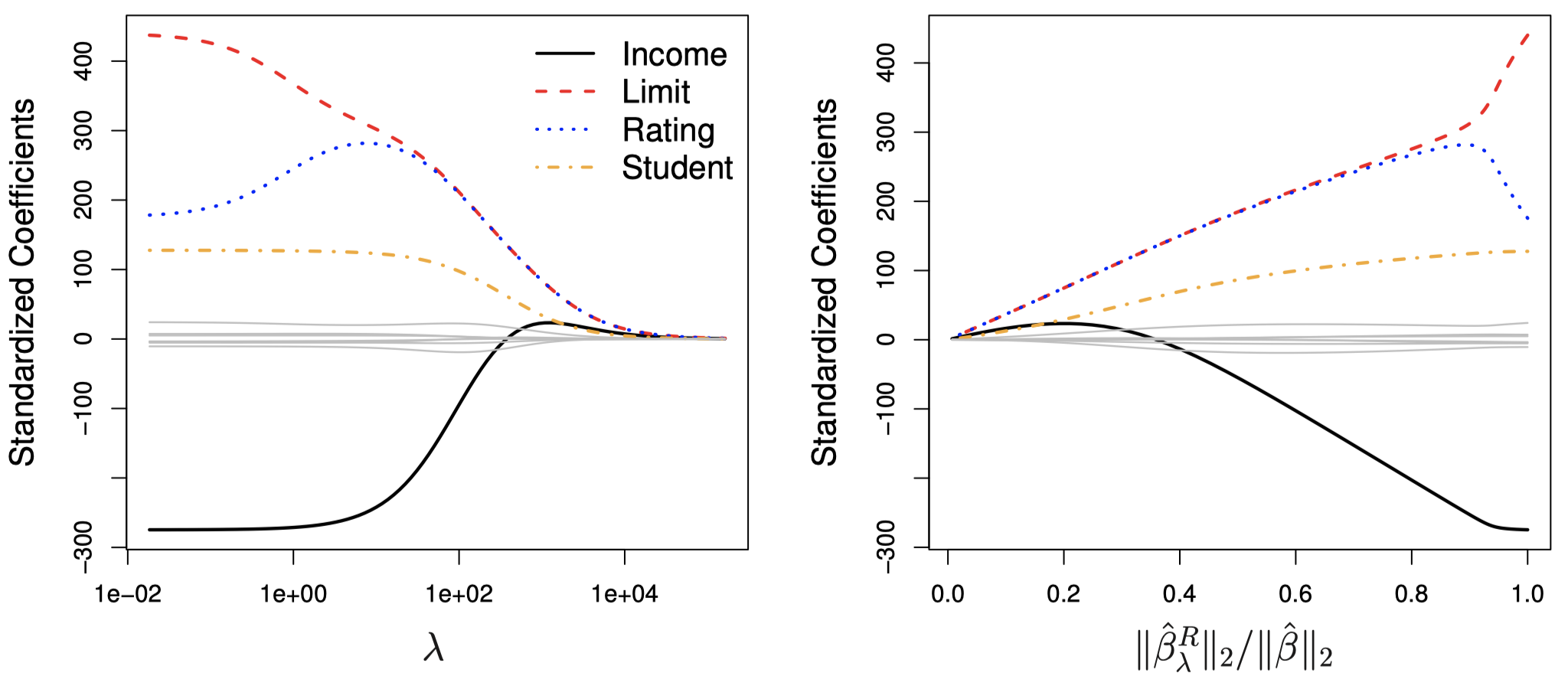
图 4:图中显示了 Credit 数据集上的标准化岭回归系数随着 $\lambda$ 和 $\|\hat \beta_{\lambda}^R\|_2 / \|\hat \beta\|_2$ 的变化情况。
在图 4 的左图中,每条曲线都代表 (全部 $10$ 个变量中的) 一个变量的岭回归系数估计,并且被绘制为一个关于 $\lambda$ 的函数。这里,不同颜色和类型的曲线代表不同变量的岭回归估计系数随 $\lambda$ 变化而变化的情况。当 $\lambda=0$ 时 (即左图中的最左边),此时各变量的岭回归系数估计和最小二乘回归估计值相同。但是,随着 $\lambda$ 的增加,岭回归系数估计朝着 $0$ 的方向收缩。当 $\lambda \to \infty$ 时,所有变量的岭回归系数估计都接近 $0$,此时得到的模型相当于不包含任何变量的零模型。
图 4 中的右图与左图一样,都显示了岭回归估计系数的变化。不过,这里的 $x$ 轴由之前的 $\lambda$ 变为了 \(\|\hat \beta_{\lambda}^R\|_2 / \|\hat \beta\|_2\),其中,$\hat \beta$ 表示最小二乘估计系数的向量。\(\|\beta\|_2\) 表示某个向量 $\beta$ 的 \(\ell_2\) 范数,其定义为 \(\|\beta\|_2 = \sqrt{\sum_{j=1}^{p}\beta_j^2}\),它衡量了向量空间中 $\beta$ 到原点的距离。随着 $\lambda$ 增加,\(\hat \beta_{\lambda}^R\) 的 \(\ell_2\) 范数降低,从而 \(\|\hat \beta_{\lambda}^R\|_2 / \|\hat \beta\|_2\) 也降低。后者的取值范围在 $1$ (当 $\lambda=0$ 时,岭回归系数估计与最小二乘估计结果相同,二者的 \(\ell_2\) 范数也相同) 到 $0$ (当 $\lambda =\infty$ 时,岭回归系数估计是一个零向量,其 \(\ell_2\) 范数值也为 $0$) 之间。因此,可以图 4 中右图的 $x$ 轴看作是岭回归系数估计值向 $0$ 方向收缩的程度,数值较小意味着系数估计值已经压缩得非常接近于 $0$。
变量缩放
我们之前讨论过,最小二乘系数估计是 尺度等变的 (scale equivariant):将 $X_j$ 乘以一个常数 $c$,最小二乘系数估计的结果将乘以一个因子 $1/c$。换而言之,无论第 $j$ 个预测变量如何按比例缩放,$X_j\hat \beta_j$ 始终保持不变。
相比之下,如果将预测变量乘以一个常数,岭回归系数估计值可能会发生 显著改变。这是由岭回归目标函数中惩罚项部分的系数平方和导致的。也就是说,$X_j \hat \beta_{j,\lambda}^R$ 的值不只取决于 $\lambda$,还取决于第 $j$ 个变量的尺度,甚至还可能受到其他预测变量的尺度的影响。
因此,在使用岭回归之前,最好先将 预测变量标准化 (standardizing the predictors):
\[\tilde x_{ij} = \dfrac{x_{ij}}{\sqrt{\dfrac{1}{n}\sum_{i=1}^{n}(x_{ij}- \overline x_j)^2}}\]为什么岭回归要比最小二乘回归效果更好?
与最小二乘相比,岭回归的优势在于 偏差-方差权衡 (bias-variance trade-off)。随着 $\lambda$ 的增加,岭回归拟合的灵活度降低,这将导致方差降低,偏差增加。
图 5 使用了一个包含 $p=45$ 个预测变量和 $n=50$ 个观测的模拟数据集。
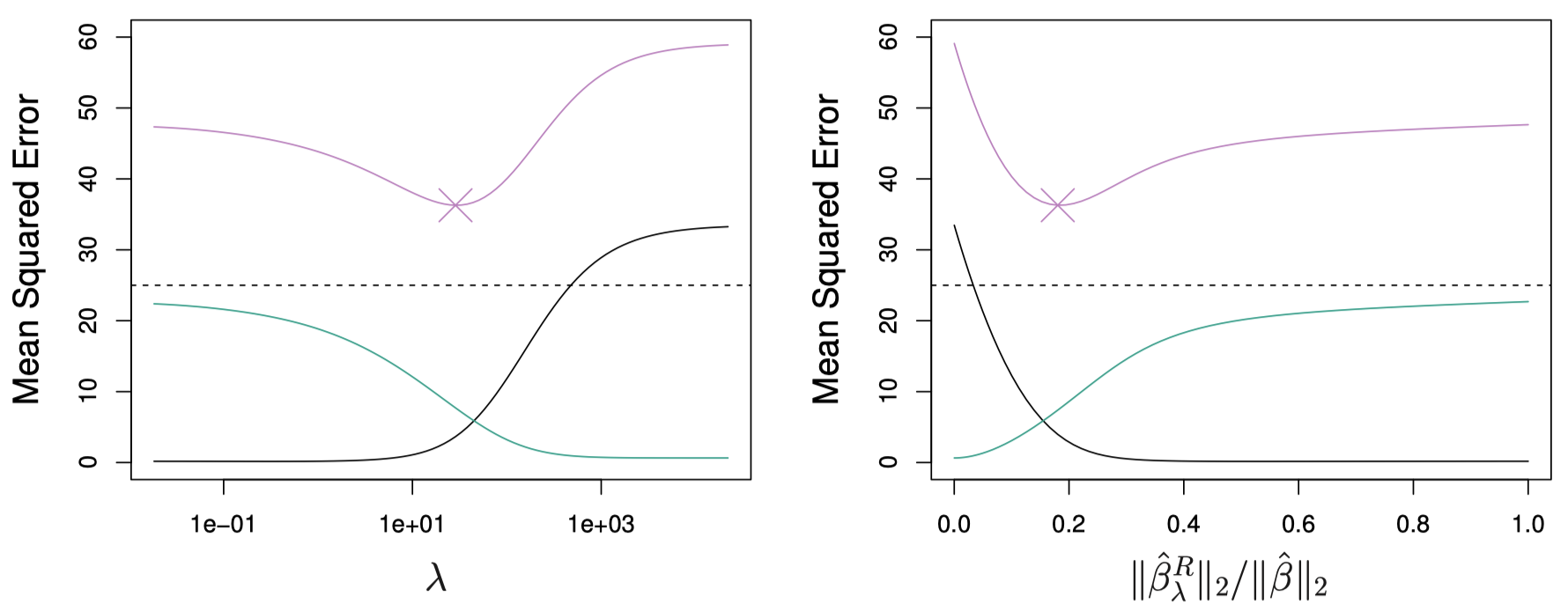
图 5:图中且示了岭回归在模拟数据集上预测结果的偏差平方 (黑色)、方差 (绿色) 和测试均方误差 (紫色),随 $\lambda$ 和 $\|\hat \beta_{\lambda}^R\|_2 / \|\hat \beta\|_2$ 的变化情况。水平虚线表示 $\mathrm{MSE}$ 可能的最低水平。紫色曲线上的 “$\times$” 代表具有最小 $\mathrm{MSE}$ 的岭回归模型。
通常来说,当响应变量和预测变量关系近似线性时,最小二乘估计将具有较低的偏差和较高的方差。这意味着训练集数据一个微小改变可能会导致最小二乘系数的较大变化。特别地,当变量个数 $p$ 和观测个数 $n$ 差不多大的时候 (如图 5 中的情况),最小二乘估计的方差会很大。如果 $p > n$,则最小二乘估计没有唯一解,此时岭回归仍然能够通过小幅度增加偏差换取方差的大幅下降,并通过这种权衡获得比较好的模型效果。因此,当最小二乘估计的方差很大时,岭回归的效果更好。
另外,与需要搜索 $2^p$ 个模型的最优子集选择方法相比,岭回归在运算上也具有显著优势。如前所述,即使对于变量数 $p$ 不大的情况,全局搜索方式在运算上也不可行。相比之下,对于任意给定的 $\lambda$,岭回归仅拟合单个模型,并且模型拟合过程可以非常快速地执行。实际上,可以证明,对于所有 $\lambda$ 值,同时求解岭回归目标函数所需的计算量与使用最小二乘法拟合模型的计算量几乎相同。
3.2 Lasso
然而,岭回归有一个明显的缺点:与子集选择不同,子集选择通常会选择仅涉及变量子集的模型,而岭回归的最终模型将包含全部的 $p$ 个预测变量。
尽管在岭回归的目标函数中,惩罚项 $\lambda \sum_{j=1}^{p}\beta_j^2$ 可以将系数朝 $0$ 的方向进行压缩,但并不会把任何一个变量的系数完全压缩到 $0$ (除非 $\lambda = \infty$)。虽然这种设定不影响预测精度,但是当变量个数 $p$ 非常大时,不利于模型解释。因此,我们希望建立一个仅包含部分变量的模型。虽然在岭回归中增加 $\lambda$ 可以减小系数的绝对值,但依然无法剔除任何变量。
Lasso 是一种最近非常流行的用于克服岭回归缺点的方法。Lasso 的估计系数 $\hat \beta_{\lambda}^L$ 可以通过最小化下式得到:
\[\sum_{i=1}^{n}\left(y_i - \beta_0 - \sum_{j=1}^{p}\beta_j x_{ij}\right)^2 + \lambda \sum_{j=1}^{p} |\beta_j | = \mathrm{RSS} + \lambda \sum_{j=1}^{p} |\beta_j |\]可以看到,Lasso 与岭回归具有相似的目标函数,唯一区别在于,Lasso 使用 \(\ell_1\) 范数而不是 $\ell_2$ 范数作为惩罚项。某个向量 $\beta$ 的 $\ell_1$ 范数被定义为:$\|\beta\|_1 = \sum_{j=1}^{p} |\beta_j |$。
与岭回归一样,Lasso 也将系数估计值往 $0$ 的方向进行压缩。但是,在 Lasso 中,当调节参数 $\lambda$ 足够大时,$\ell_1$ 惩罚项具有将其中某些系数估计值强制设定为 $0$ 的作用。因此,与最优子集选择类似,Lasso 也可以实现变量选择,所以与岭回归相比,Lasso 选择的模型更易于解释。可以说 Lasso 产生的是 稀疏模型 (sparse models),即仅涉及全部变量的一个子集的模型。与在岭回归中一样,选择一个合适的 $\lambda$ 值对于 Lasso 非常重要,可以通过交叉验证做到这点。
例子:信用卡数据集
图 6 显示了在 Credit 数据集上运用 Lasso 进行拟合得到的系数曲线:
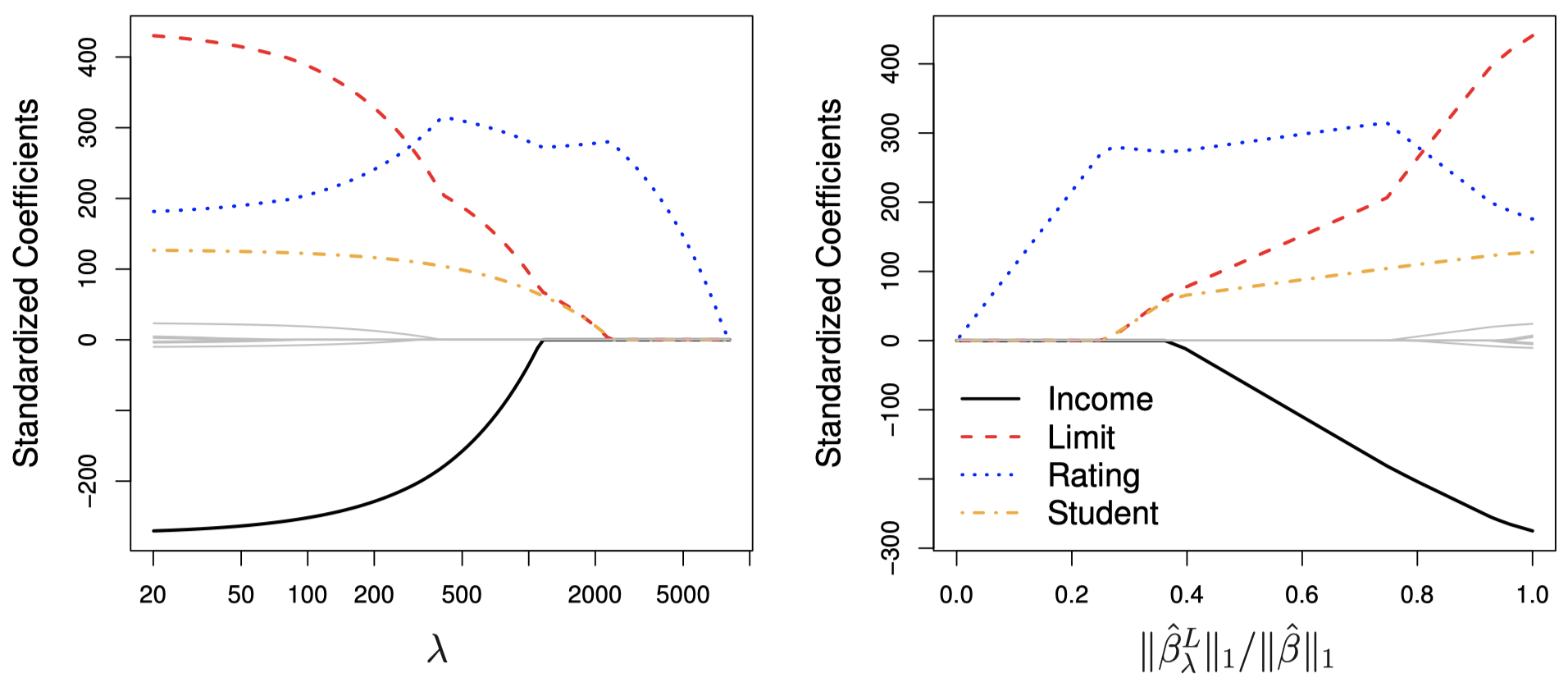
图 6:图中显示了 Credit 数据集上的标准化 Lasso 系数随着 $\lambda$ 和 $\|\hat \beta_{\lambda}^L\|_1 / \|\hat \beta\|_1$ 的变化情况。
可以看到,当 $\lambda=0$ 时,Lasso 与最小二乘法等价。当 $\lambda$ 足够大时,Lasso 估计会得到一个零模型,所有系数估计值均为 $0$。然而,在这两个极端之间,岭回归和 Lasso 模型的表现具有很大差异。在图 6 的右图中,从左至右可以看到,Lasso 首先得到一个仅包含变量 rating 的模型,student 和 limit 紧随 income 之后几乎同时进入模型。最后其余变量也进入模型。于是,根据不同的 $\lambda$ 取值,Lasso 可以得到包含不同变盘个数的模型。而岭回归得到的模型自始至终都包含所有变量,虽然其系数估计值的大小会随 $\lambda$ 变化。
3.3 岭回归和 Lasso 的其他形式
为什么 Lasso 与岭回归不同,可以导致系数估计精确地等于零呢?
可以证明,Lasso 和岭回归系数估计分别等价于求解以下问题:
\[\mathop{\operatorname{minimize}} \limits_{\beta} \sum_{i=1}^{n}\left(y_i - \beta_0 - \sum_{j=1}^{p}\beta_j x_{ij}\right)^2 \quad \text{subject to}\quad \sum_{j=1}^{p} |\beta_j| \le s\]和
\[\mathop{\operatorname{minimize}} \limits_{\beta} \sum_{i=1}^{n}\left(y_i - \beta_0 - \sum_{j=1}^{p}\beta_j x_{ij}\right)^2 \quad \text{subject to}\quad \sum_{j=1}^{p} \beta_j^2 \le s\]当 $p=2$ 时,上面两个式子分别表示:在 $|\beta_1| + |\beta_2| \le s$ 所确定的 菱形 区域里,Lasso 系数估计可以得到最小的 $\mathrm{RSS}$;同样,在 $\beta_1^2 + \beta_2^2 \le s$ 所确定的 圆形 区域里,岭回归系数估计可以得到最小的 $\mathrm{RSS}$。
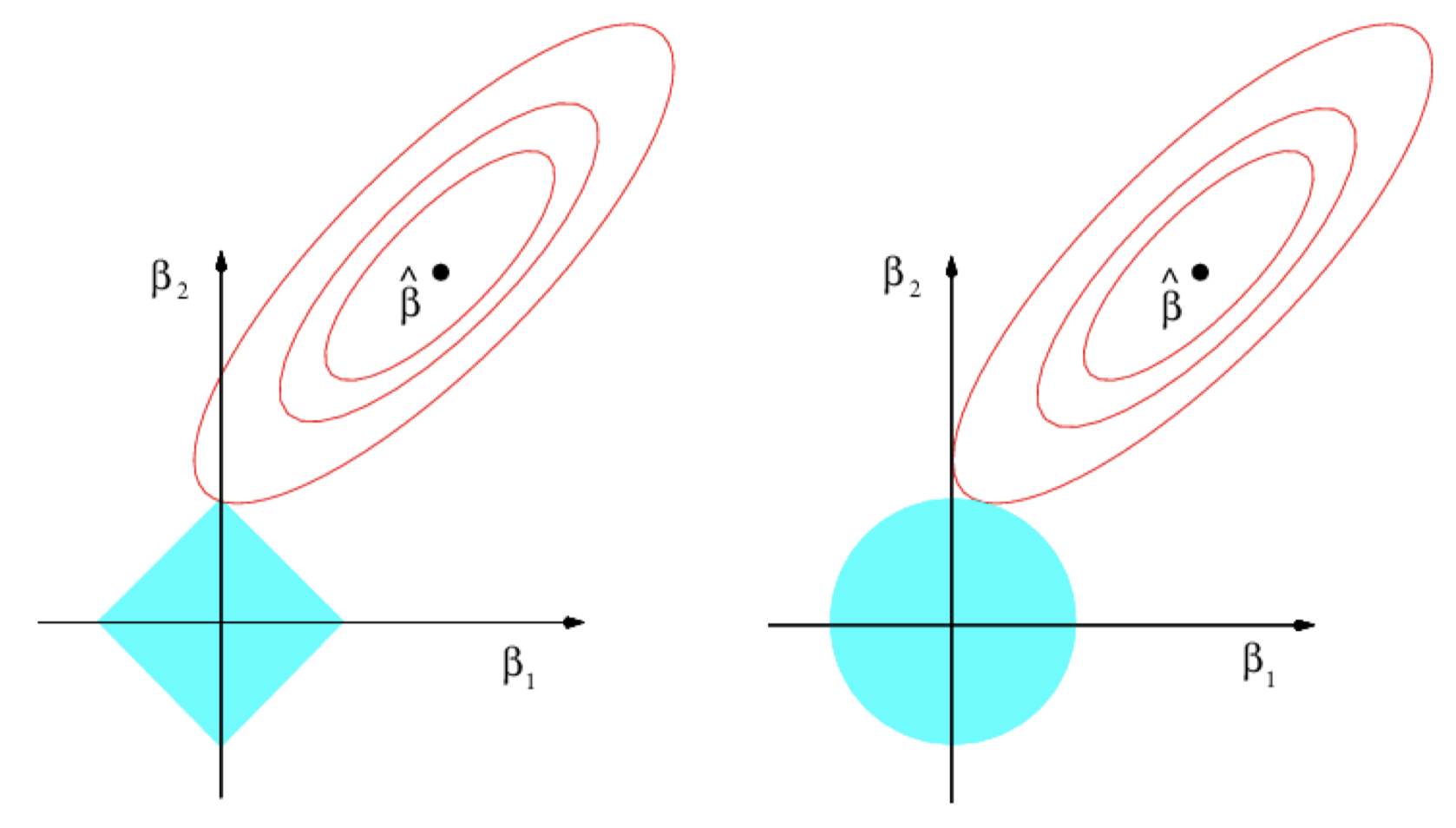
图 7:误差等高线和限制条件区域 (左图:Lasso;右图:岭回归)。蓝色阴影区域分别代表限制条件:$|\beta_1| +| \beta_2| \le s$ 和 $\beta_1^2 + \beta_2^2 \le s$。红色椭圆曲线代表 $\mathrm{RSS}$ 等高线。
当 $p =3$ 时,岭回归的限制条件区域将变成 球体 (sphere),而 Lasso 的限制条件区域将变成 多面体 (polyhedron)。当 $p > 3$ 时,岭回归的限制条件区域将变成 超球面 (hypersphere),而 Lasso 的限制条件区域将变成 多胞形 (polytope)。
3.4 对比 Lasso 和岭回归
很明显,Lasso 与岭回归相比具有较大优势,因为它可以得到只包含部分变量的简单易解释模型。但是,哪种方法得到的模型的预测精度更高呢?
图 8 展示了之前图 5 中的模拟数据在 Lasso 上的应用,包括偏差平方和、方差和测试均方误差:
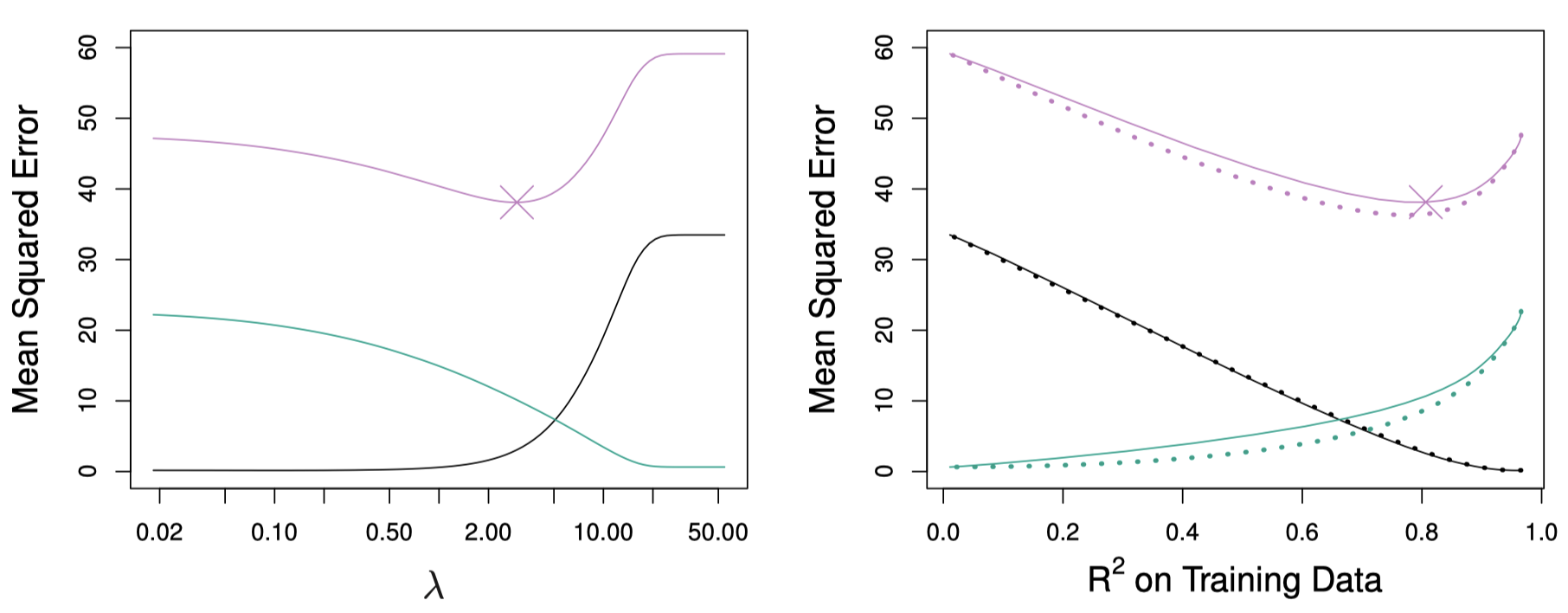
图 8:左图:模拟数据集上 Lasso 得到的偏差平方和 (黑色)、方差 (绿色) 和测试均方误差 (紫色)。右图:对比 Lasso (实线) 和岭回归 (虚线) 的偏差平方和、方差和测试均方误差。两图都是根据训练数据集的 $R^2$ 作图,这是一个很常见的指标。图中紫色曲线上的 “$\times$” 代表具有最小 $\mathrm{MSE}$ 的 Lasso 模型。
显然,Lasso 的结果和岭回归在性质上相似,随着 $\lambda$ 增大,方差减小而偏差平方和增大。在图 8 的右图中,虚线代表岭回归。这里,我们画出了两种方法在训练数据上的 $R^2$,这是另一种描述模型的有效方法,可以用来对比采用不同正则化方法的模型。然而,岭回归的方差稍小于 Lasso 的方差,导致其最小均方误差同样稍小于 Lasso。
然而,图 8 数据中的 $45$ 个预测变量是模拟生成的,它们与响应变量真实相关。也就是说,任何一个真实系数 $\beta_1,\dots,\beta_{45}$ 都不等于 $0$,而 Lasso 会潜在地假设一些系数的真实值为 $0$。因此,从误差角度来看,这里岭回归的表现要比 Lasso 好。
图 9 解释了类似的情况:真实响应变量只是 $45$ 个预测变量中的 $2$ 个变量的函数。这种情况下,Lasso 在偏差、方差和均方误差等方面的表现要优于岭回归。
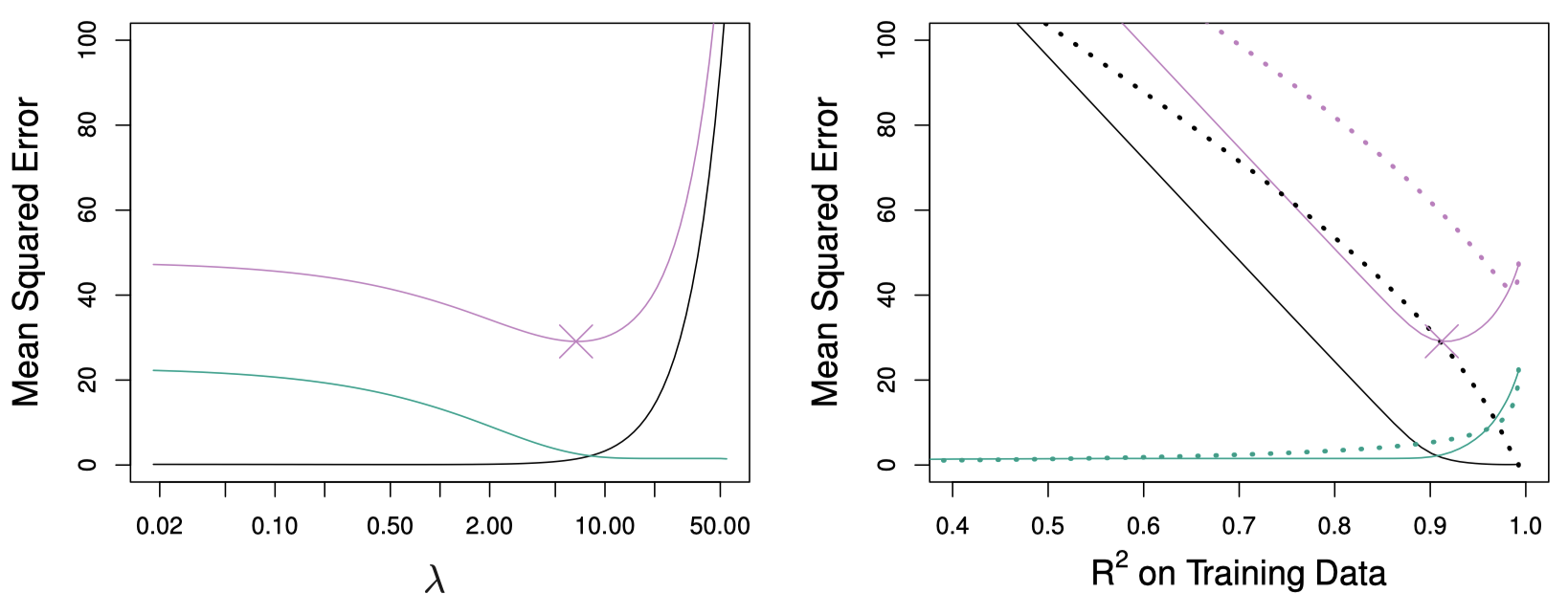
图 9:左图:Lasso 的偏差平方和 (黑色)、方差 (绿色) 和测试均方误差 (紫色)。这里,模拟数据只有两个预测变量与响应变量有关,其余与图 8 中的数据一样。右图:对比 Lasso (实线) 和岭回归 (虚线) 的偏差平方和、方差和测试均方误差。两图都是根据训练数据集的 $R^2$ 作图。图中紫色曲线上的 “$\times$” 代表具有最小 $\mathrm{MSE}$ 的 Lasso 模型。
结论
上面两个例子说明岭回归和 Lasso 二者中并没有哪一个在任何情况下都是最好的。一般情况下,当真实响应变量只与一小部分变量相关或者其余变量的系数都非常小时,Lasso 表现通常更好;而当真实响应变量与大部分变量都相关,并且这些变量的系数都比较接近时,岭回归表现通常更好。
然而,对于一个真实数据集,与响应变量相关的预测变量个数永远不会是一个已知先验。为此,我们可以采用诸如交叉验证之类的技术来确定哪种方法对于特定数据集更好。
与岭回归类似,当最小二乘估计出现较大方差时,Lasso 以牺牲偏差为代价去降低方差,从而得到更为精确的预测结果。不同于岭回归,Lasso 能够进行变量选择,因此得到的模型更容易解释。
事实上,存在可以同时拟合岭回归和 Lasso 的高效算法;每个算法的系数估计的运算量都与一个最小二乘拟合的运算量的基本一致。
3.5 选择岭回归和 Lasso 的调节参数
与子集选择类似,对于岭回归和 Lasso,我们也需要一种方法来确定所考虑的模型中哪个最好的。也就是说,我们需要一种方法来选择调节参数 $\lambda$ 的值,或者等价地,选择约束 $s$ 的值。
交叉验证 是一种解决此问题的简单方法:
-
首先,选择一个由不同 $\lambda$ 值组成的网格,并且为其中的每个 $\lambda$ 值计算交叉验证错误率。
-
然后,选择交叉验证误差最小的调节参数值。
-
最后,使用所有可用的观测值和选定的调节参数值重新拟合模型。
图 10 显示了用岭回归对 Credit 数据集进行留一交叉验证的结果。这里,$\lambda$ 相对较小,说明相对于最小二乘拟合,这里的最优拟合只进行了少量的压缩。此外,下降并不显著也说明存在很多种系数取值情况都可以得到很小的误差。在这种情况下,我们可以简单地使用最小二乘拟合。
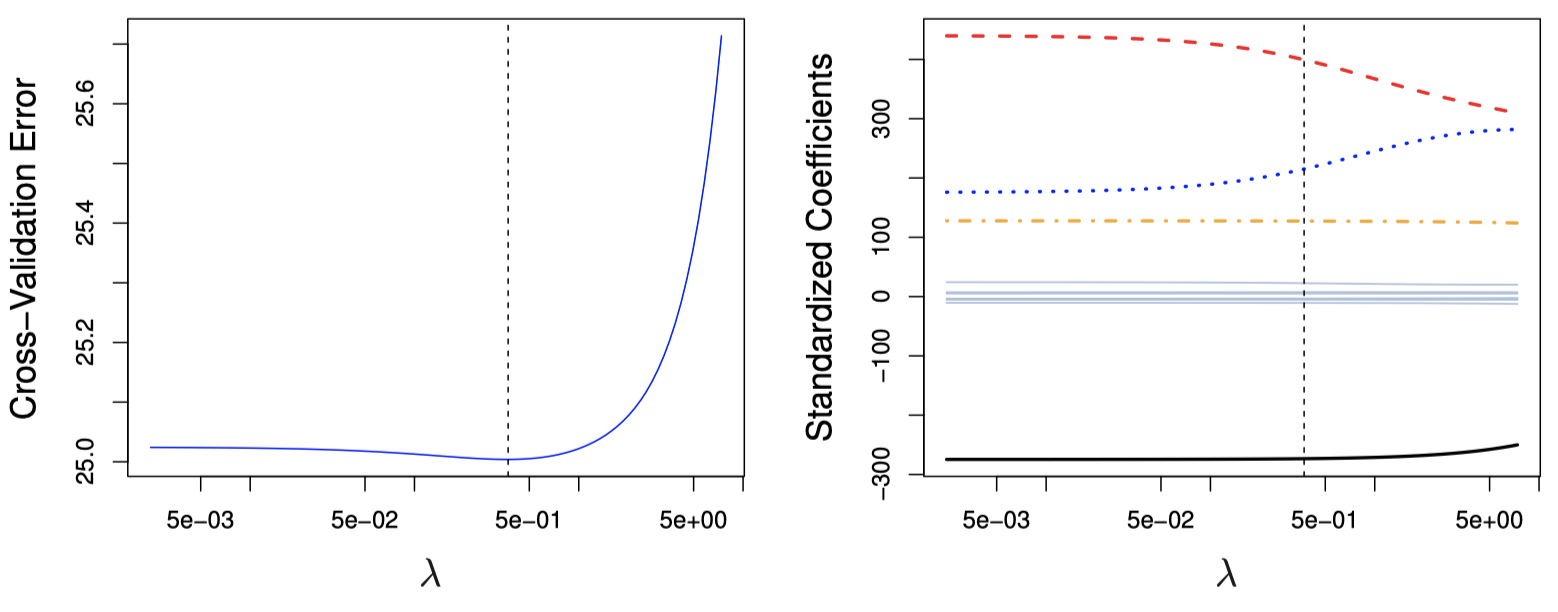
图 10:左图:对 Credit 数据集应用岭回归的交叉验证误差,$\lambda$ 取各种不同值。右图:系数估计作为 $\lambda$ 的函数。竖直虚线表示根据交叉验证选择的参数 $\lambda$。
图 11 显示了用 Lasso 对之前图 9 中的稀疏模拟数据进行$10$-折交叉验证的得到的结果。右图中两条彩色曲线代表与响应变量最相关的两个预测变量,称为 信号变量 (signal variable);其余灰色曲线代表与响应变量无关的预测变量,称为 噪声变量 (noise variable)。
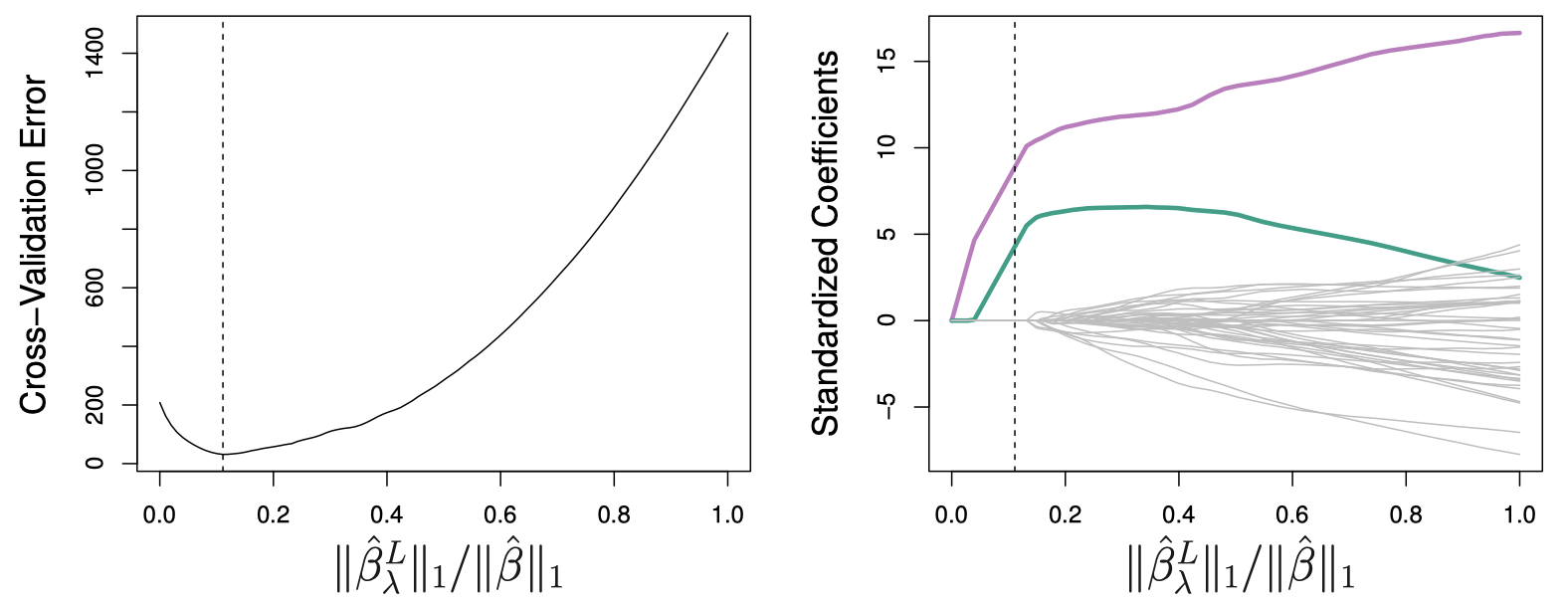
图 11:左图:用 Lasso 对之前图 9 中的稀疏模拟数据进行 $10$-折交叉验证的均方误差。右图:相应的 Lasso 系数。竖直虚线代表使得交叉验证误差最小的系数。
可以看到,Lasso 不仅正确地给予两个信号变量较大的系数,而且在具有最小验证误差的模型中只有信号变量的系数不为 $0$。因此,交叉验证和 Lasso 的结合可以正确地识别出真实模型中的两个信号变量,即使这是在一个具有 $p=45$ 个预测变量而仅有 $n=50$ 个观测的困难问题下。相反,从图 11 的右图中最右边可以看到,最小二乘估计的结果中只有一个信号变量的系数较大。
4. 降维方法
目前为止,我们讨论的方法都涉及通过最小二乘法或者收缩方法对原始变量 $X_1,\dots,X_p$ 拟合线性回归模型。现在,我们将探索一类新的方法:对预测变量进行 转换 (transform),然后使用转换后的变量拟合最小二乘模型。这类技术被称为 降维 (dimension reduction) 方法。
令 $Z_1,Z_2,\dots,Z_M$ 表示 $M$ 个原始预测变量的 线性组合 ($M < p$,总共有 $p$ 个原始预测变量)。即
\[Z_m=\sum_{j=1}^{p}\phi_{jm}X_j\]其中,$\phi_{1m},\phi_{2m},\dots,\phi_{pm}$ 是常数,$m=1,\dots,M$。
然后,我们用 普通最小二乘法 (ordinary least squares, OLS) 拟合线性回归模型:
\[y_i = \theta_0 + \sum_{m=1}^{M}\theta_m z_{im} + \epsilon_i, \quad i=1,\dots,n\]注意,这里回归系数由 $\theta_0,\theta_1,\dots,\theta_M$ 给出。如果常数 $\phi_{1m},\phi_{2m},\dots,\phi_{pm}$ 选择合适,那么这种降维方法的效果通常要优于 OLS 回归。
降维 是指某种方法可以使本来需要估计 $p + 1$ 个系数 $\beta_0,\beta_1,\dots,\beta_p$ 的问题简化为估计 $M+1$ 个系数 $\theta_0,\theta_1,\dots,\theta_M$ 的问题,这里 $M < p$。也就是说,问题的维度从 $p +1$ 降至 $M+1$。
由前面的 $Z_m$ 的定义可知,
\[\sum_{m=1}^{M}\theta_m z_{im} = \sum_{m=1}^{M}\theta_m \sum_{j=1}^{p}\phi_{jm}x_{ij}= \sum_{j=1}^{p} \sum_{m=1}^{M} \theta_m \phi_{jm} x_{ij} = \sum_{j=1}^{p} \beta_j x_{ij}\]其中,
\[\beta_j = \sum_{m=1}^{M} \theta_m \phi_{jm}\]因此,前面拟合出的线性回归模型可以视为原始线性回归模型的一个特例。这里,降维的作用是约束系数 $\beta_j$ 的估计,所以 $\beta_j$ 必须满足上述形式。
这种方法可以获得更好的偏差-方差权衡:对于系数形式上的约束很可能使估计结果有偏。但是,当 $p \gg n$ 时,选择一个 $M\ll p$ 可以显著地降低拟合系数的方差。如果 $M=p$,并且所有的 $Z_m$ 都是线性无关的,那么上述 $\beta_j$ 形式其实没有施加任何约束,这种情况下并没有实现降维,其等同于在原先 $p$ 个变量上进行最小二乘拟合。
4.1 主成分回归
这里,我们应用 主成分分析 (principal components analysis, PCA) 来定义预测变量的线性组合,以用于回归分析:
- 第一个主成分是具有最大方差的 (经过归一化的) 变量线性组合。
- 第二个主成分是与第一主成分不相关的、具有最大方差的变量线性组合。
- 以此类推。
因此,对于许多彼此存在相关性的原始变量,我们将其替换为能够捕获其联合变化的一个较小的主成分集合。在第一主成分的方向上,数据的变化最大。
图 12 显示了 $100$ 个不同城市中,人口规模 (pop) 和广告支出 (ad) 之间的关系。绿色实线代表数据的第一主成分方向,在这个方向上数据的波动性最大。也就是说,如果把 $100$ 个观测投影到此方向,那么投影的方差是最大的,而投影到其他方向上的方差只会比这个小。将一个点投影到一条线上可以简单地理解为在这条线上寻找距离这个点最近的位置。
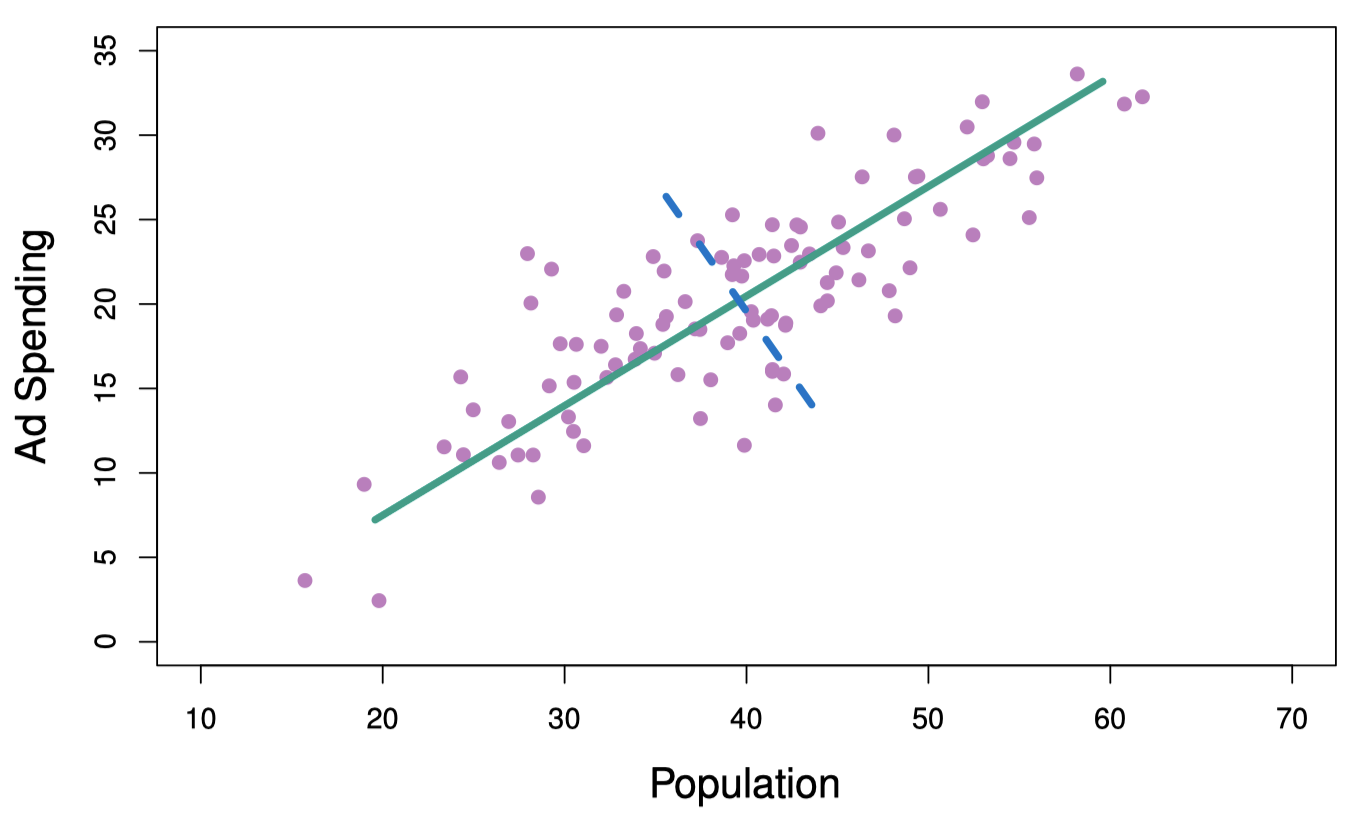
图 12:紫色圆点代表了 $100$ 个不同城市的人口规模 (pop) 和广告支出 (ad)。绿色实线表示第一个主成分,蓝色虚线表示第二个主成分。
第一主成分的图形表示如图 12 中的绿色实线所示,其数学描述为:
\[Z_1= 0.839 \times (\mathtt{pop} - \overline{\mathtt{pop}}) + 0.544 \times (\mathtt{ad} - \overline{\mathtt{ad}})\]这里,$\phi_{11}=0.839, \phi_{21}=0.544$ 是主成分载荷,它定义了上面提到的主成分方向。$\overline{\mathtt{pop}}$ 代表数据集中所有人口规模的均值,$\overline{\mathtt{ad}}$ 代表了所有广告支出的均值。在满足 $\phi_{11}^2 + \phi_{21}^2 = 1$ 的条件下所有可能的 $\mathtt{pop}$ 和 $\mathtt{ad}$ 线性组合里,将使方差 $\mathrm{Var}(\phi_{11} \times (\mathtt{pop} - \overline{\mathtt{pop}}) + \phi_{21} \times (\mathtt{ad} - \overline{\mathtt{ad}}))$ 最大化。注意,必须满足$\phi_{11}^2 + \phi_{21}^2 = 1$ 这一条件,否则可以通过人为增大 $\phi_{11}$ 和 $\phi_{21}$ 来增加方差。
由于这里 $n=100$,$\mathtt{pop}$ 和 $\mathtt{ad}$ 都是长度为 $100$ 的向量,所以 $Z_1$ 也是长度为 $100$ 的向量。例如:
\[z_{i1} = 0.839 \times (\mathtt{pop}_i - \overline{\mathtt{pop}}) + 0.544 \times (\mathtt{ad}_i - \overline{\mathtt{ad}})\]这里,$z_{11},\dots,z_{n1}$ 被称为 主成分得分 (principal component scores),如图 13 中的右图所示。
主成分分析还有另一种解释:第一主成分向定义了与数据最接近的那条直线。例如在图 13 中,第一主成分线使得所有数据点到该线的垂直距离平方和最小。图 13 的左图中的虚线部分表示这些距离,虚线与实线的交点就是这些数据点在第一主成分方向上的投影。第一主成分的选择使得投影得到的观测与原始观测最为接近。
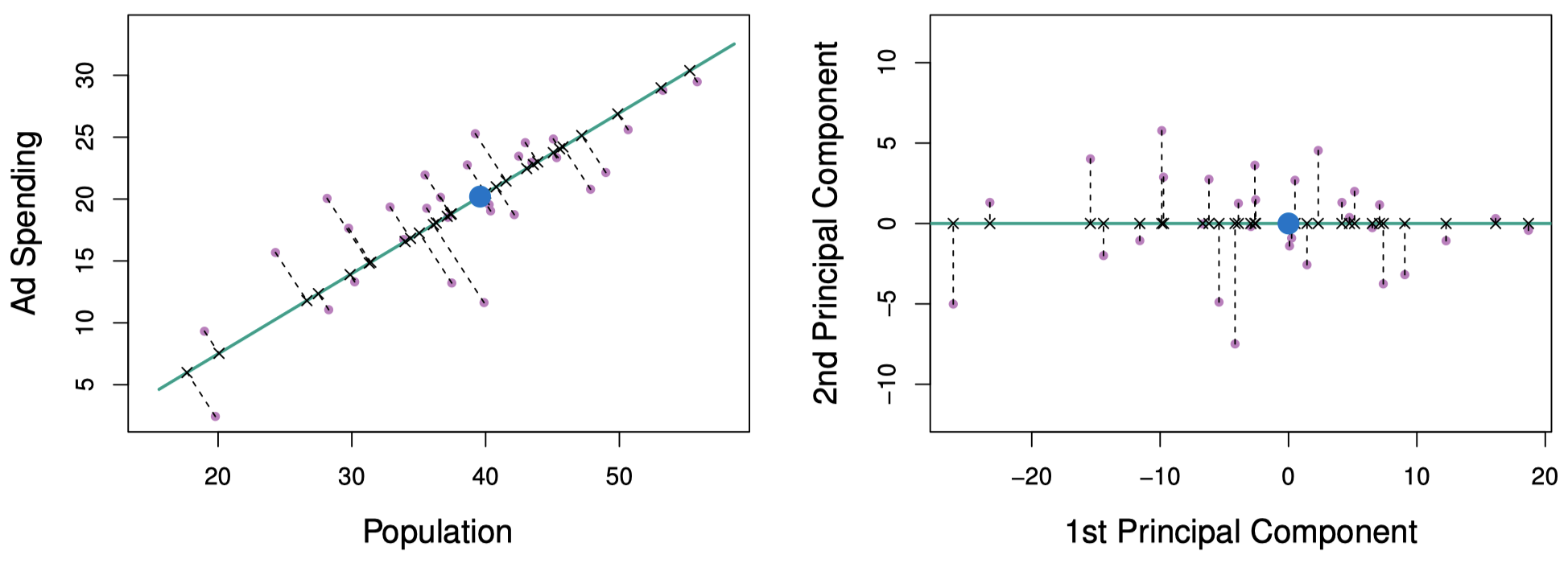
图 13:广告数据集的一个子集。蓝色圆点代表 pop 和 ad 的均值。左图:绿色实线代表第一主成分方向,这是数据波动最大的维度,同时它定义了与全部 $n$ 个观测最接近的直线。每个观测到主成分的距离用黑色虚线表示。蓝色圆点表示 $(\overline{\mathtt{pop}},\overline{\mathtt{ad}})$。右图:对左图进行旋转,使得第一主成分方向与 $x$ 轴一致。
图 13 的右图是将左图旋转,使第一主成分方向同 $x$ 轴一致。可以看到,前面公式中第 $i$ 个观测的第一主成分得分 $z_{i1}$ 就是在 $x$ 方向上第 $i$ 个投影点到原点的距离。
可以将主成分 $Z_1$ 看作是在每个位置上对 pop 和 ad 的 数值摘要 (number summary)。在这个例子中,如果 $z_{i1} < 0$,表明该城市的人口规模和广告支出低于平均水平,如果主成分得分大于 $0$ 则情况相反。为什么这里我们可以用一个数值来表示 pop 和 ad 两个变量呢?在这个例子中,从图 12 可以看出,pop 和 ad 之间存在近似线性的关系,因此得到一个有效的数值摘要是有可能的。
图 14 显示了 $z_{i1}$ 与 pop 和 ad 的关系。可以看到,第一主成分与两个变量高度相关。也就是说,第一主成分捕捉到了 pop 和 ad 这两个变量所包含的大部分信息。
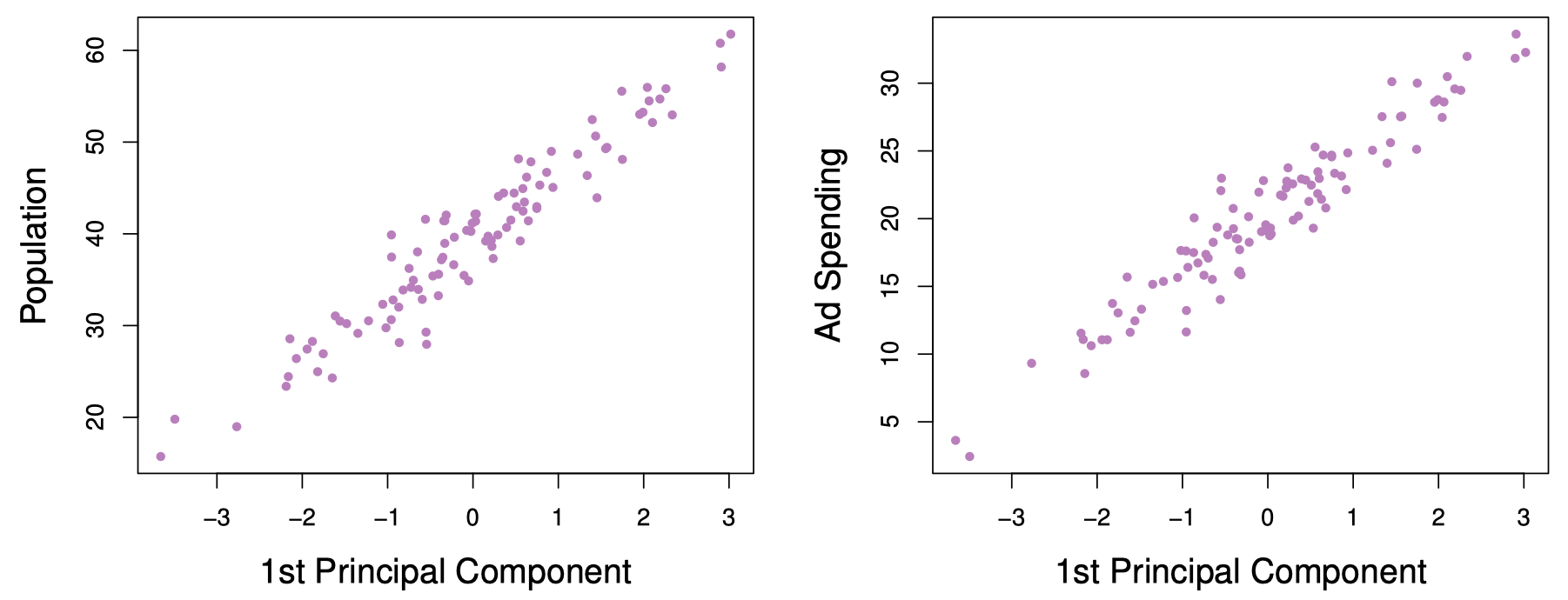
图 14:第一主成分得分 $z_{i1}$ 与 pop 和 ad 高度相关。
目前为止,我们所有讨论都是关于第一主成分。通常,我们可以构造 $p$ 个不同的主成分。第二主成分 $Z_2$ 是所有与 $Z_1$ 无关的原始变量的线性组合中方差最大的。图 12 中的蓝色虚线表示第二主成分方向。$Z_1$ 与 $Z_2$ 之间的零相关关系等价于 $Z_2$ 的方向垂直或正交于 $Z_1$。这个例子中,第二主成分由下式给出:
\[Z_2= 0.544 \times (\mathtt{pop} - \overline{\mathtt{pop}}) - 0.839 \times (\mathtt{ad} - \overline{\mathtt{ad}})\]由于这里的广告数据集中只有这两个预测变量,所以前两个主成分包含了 pop 和 ad 的全部信息。然而,构造过程使得第一主成分包含了大部分信息。例如,图 13 的右图中,$z_{i1}$ 方向 ($x$ 轴方向) 上的方差要比 $z_{i2}$ 方向 ($y$ 轴方向) 上的方差更大。事实上,第二主成分得分更接近零也表示其携带的信息量较少。另一种解释是第二主成分与两个变量的相关性很小,正如 图 15 中 $z_{i2}$ 与 pop 和 ad 的散点图所示。这也再次证明了这里只需要第一主成分就可以准确地表示 pop 和 ad。
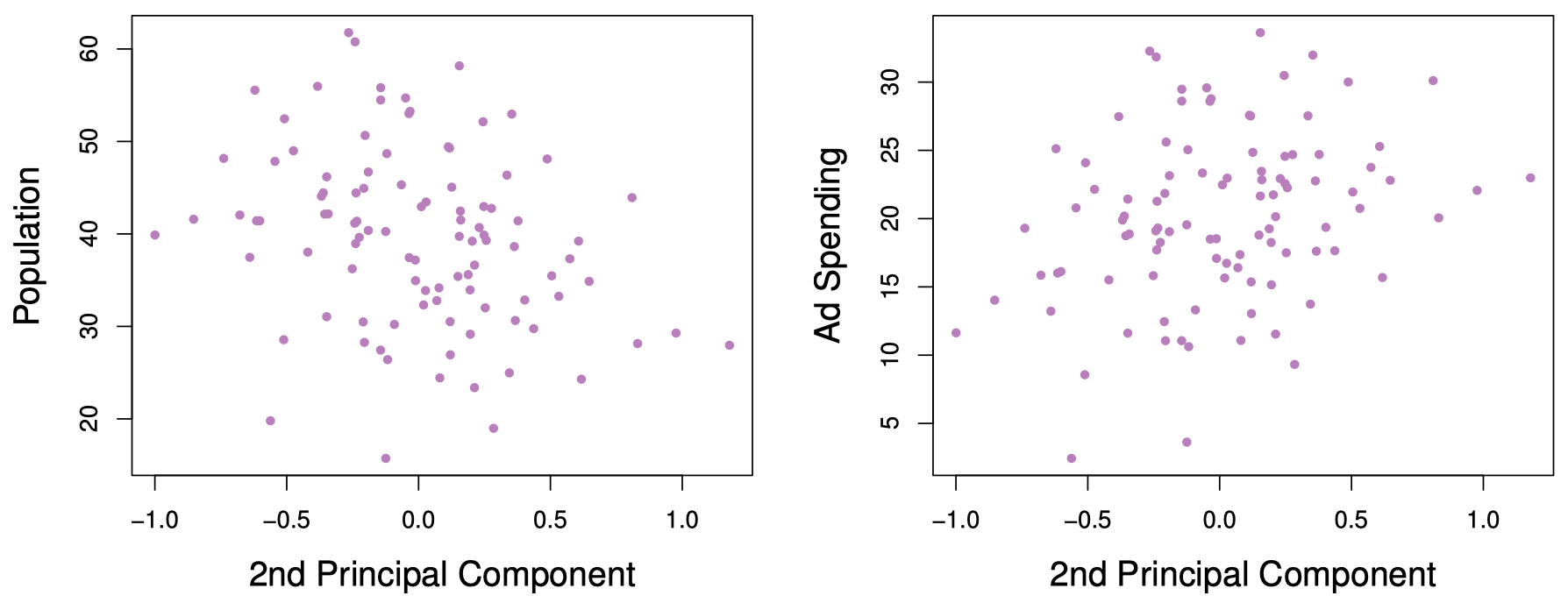
图 15:第二主成分得分 $z_{i2}$ 与 pop 和 ad 的散点图。可以看到,它们之间的相关性很弱。
这里,像广告数据这样的二维数据至多可以构造两个主成分。然而,当数据中包含有更多变量时,比如人口年龄、收入水平、教育等,我们就可以构造更多的主成分。它们需要使方差最大化,并且必须满足与之前各主成分不相关这一限制条件。
主成分回归的应用
主成分回归 (principal components regression, PCR) 是指构造前 $M$ 个主成分 $Z_1,\dots,Z_M$,然后以这些主成分作为预测变量,用最小二乘拟合线性回归模型。其主要思想是,少量的主成分足以解释大部分的数据波动以及数据和响应变量之间的关系。即假设响应变量 $Y$ 的方向就是预测变量 $X_1,\dots,X_p$ 变动最为剧烈的方向,但我们无法确保这个假设始终成立,所以为了得到良好的结果,常常需要合理的近似。
如果 PCR 的假设条件成立,那么用 $Z_1,\dots,Z_M$ 拟合一个最小二乘模型的结果要优于用 $X_1,\dots,X_p$ 拟合的结果,因为大部分甚至全部与响应变量相关的数据信息都包含 $Z_1,\dots,Z_M$ 中,而只需估计 $M \ll p$ 个系数可以减轻过拟合的风险。在广告数据集中,第一主成分解释了 pop 和 ad 的大部分变动信息,所以这个单变量的 PCR 模型用来预测诸如 sales 这样的响应变量时,会表现得更好。
图 16 展示了 PCR 模型在之前图 8 和 图 9 中的模拟数据集上的拟合结果。两个数据集都有 $n=50$ 个观测和 $p=45$ 个变量。然而,第一个数据集中的响应变量是所有预测变量的函数,而第二个数据集中的响应变量只与两个预测变量有关。
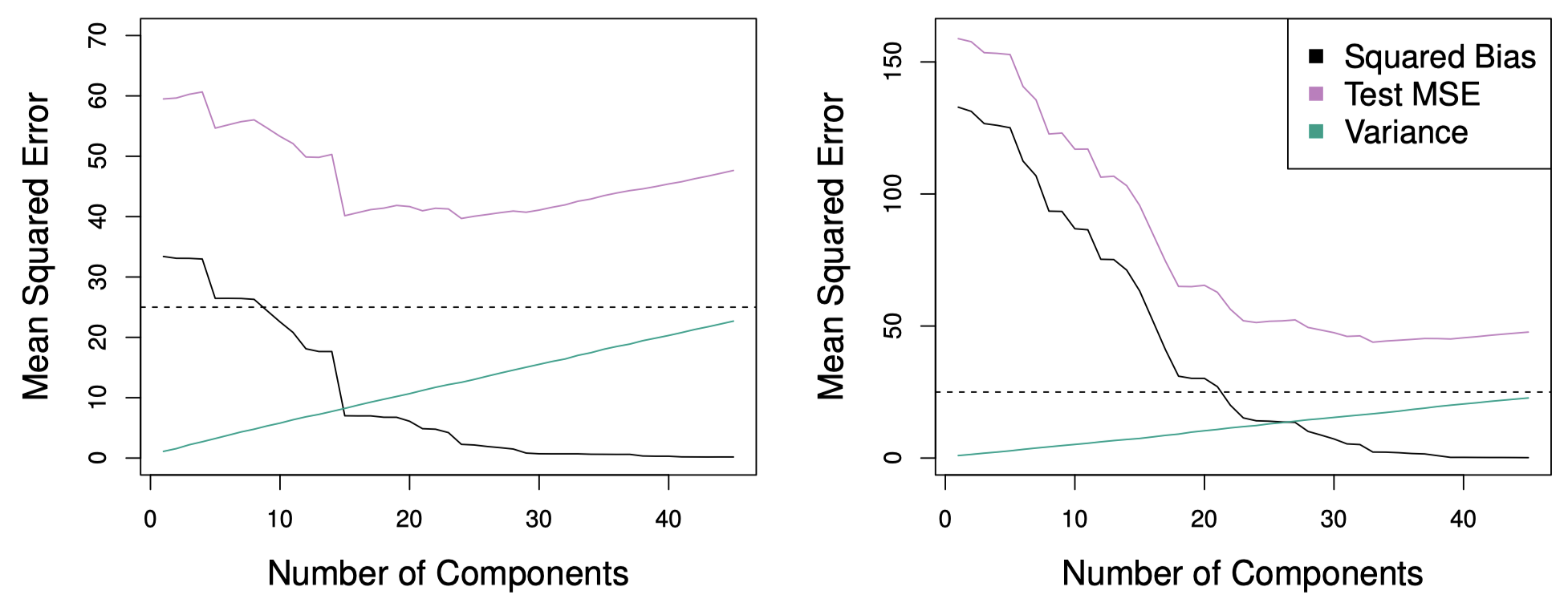
图 16:PCR 在两个模拟数据集上的应用。左图:之前图 8 中的模拟数据。右图:之前图 9 中的模拟数据。
图中的每条曲线都是一个关于 $M$ 的函数,即作为回归模型预测变量的主成分个数的函数。随着引入回归模型的主成分越来越多,偏差逐渐减小,方差逐渐增大。这使得均方误差呈现出 U 形。当 $M=p=45$ 时,PCR 将等价于简单地用所有原始变量进行最小二乘拟合。图 16 中的左图表明,在 PCR 中选择一个合适的 $M$ 可以明显提升最小二乘法的拟合效果。
然而,对比之前图 5、图 8 和图 9 中的岭回归和 Lasso 的结果,可以发现在这个例子中,PCR 并没有比前两种方法的效果更好。其原因可能是:这里的数据生成机制导致需要很多主成分才能对响应变量进行充分建模。相反,如果对于某个数据集,只需要前几个主成分就可以充分捕捉预测变量的变动及其与响应变量之间的关系,那么 PCR 的效果通常会更好。
图 17 显示了在另一个数据集上的结果,该数据集更适合 PCR。这里,响应变量仅由前五个主成分决定。随着主成分个数 $M$ 的增大,偏差迅速降为零。均方误差明显在 $M=5$ 时达到最低。图 17 中的右图展示了岭回归和 Lasso 在该数据集上的结果。与最小二乘相比,三种方法的结果都有显著提升,其中,PCR 和岭回归比 Lasso 更好一些。
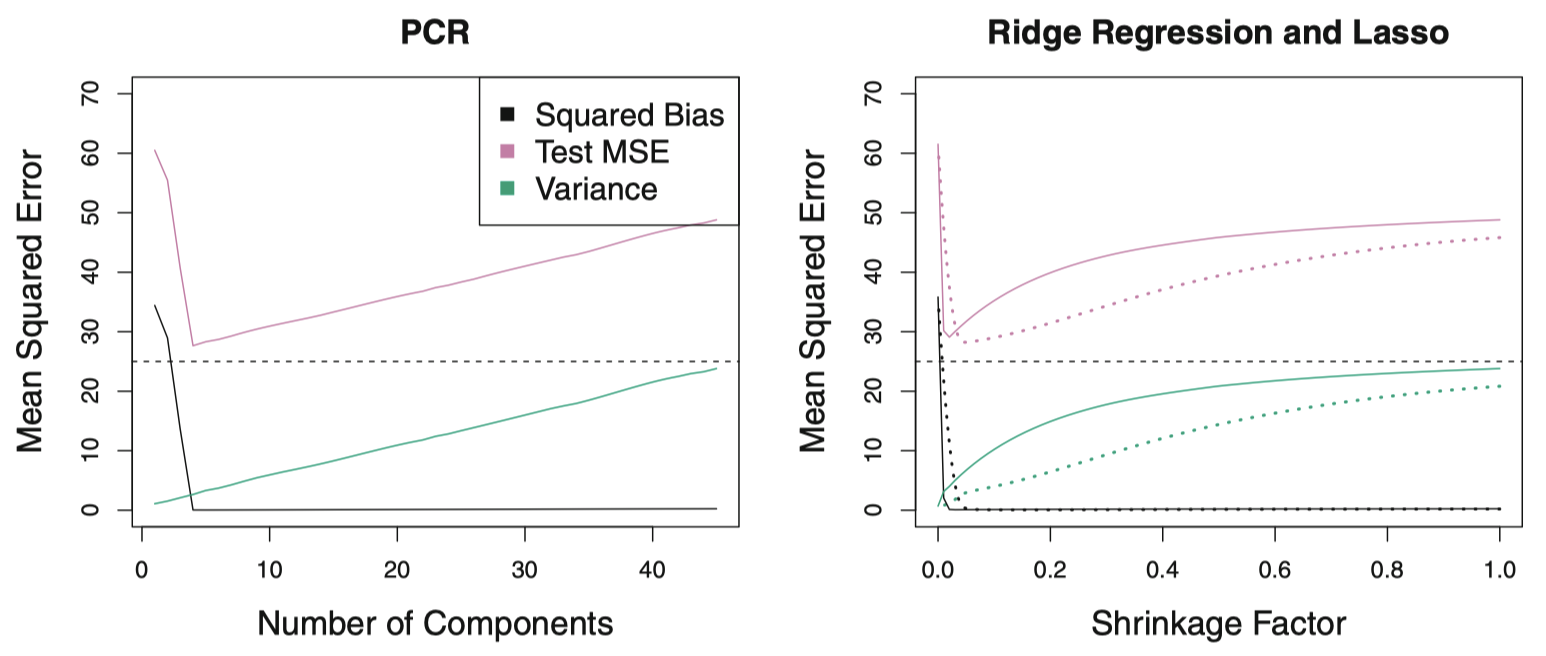
图 17:PCR、岭回归和 Lasso 应用于模拟数据集。该数据集中,$X$ 的前五个主成分包含了关于响应变量 $Y$ 的全部信息。图中水平虚线表示不可减小误差 $\mathrm{Var}(\epsilon)$。左图:PCR 结果。右图:Lasso (实线) 和岭回归 (虚线) 的结果。$x$ 轴表示系数估计的收缩因子,定义为收缩后系数估计的 $\ell_2$ 范数除以最小二乘系数估计的 $\ell_2$ 范数。
注意,虽然 PCR 提供了一种用 $M< p$ 个预测变量进行回归的简单方法,但它不属于特征提取方法。因为回归中 $M$ 个主成分中的每一个都是全部 $p$ 个原始变量的线性组合。例如在之前的广告数据中,$Z_1$ 是 pop 和 ad 的线性组合。因此,尽管 PCR 在许多实际情况下通常表现良好,但它并不会生成仅依赖于原始特征的一个小子集的模型。从这个意义上讲,PCR 更接近岭回归,而不是 Lasso。实际上,可以证明 PCR 和岭回归非常相似,我们甚至可以将岭回归视为 PCR 的连续版本。
在 PCR 中,主成分数量 $M$ 一般通过交叉验证确定。图 18 显示了将 PCR 应用于 Credit 数据集上的结果,右图表示交叉验证误差,它是一个关于 $M$ 的函数。在该数据集上,最小交叉验证误差出现在主成分数量 $M=10$ 的情况下,这里几乎没有实现降维,因为当 $M=11$ 时,PCR 与简单的最小二乘拟合等价。
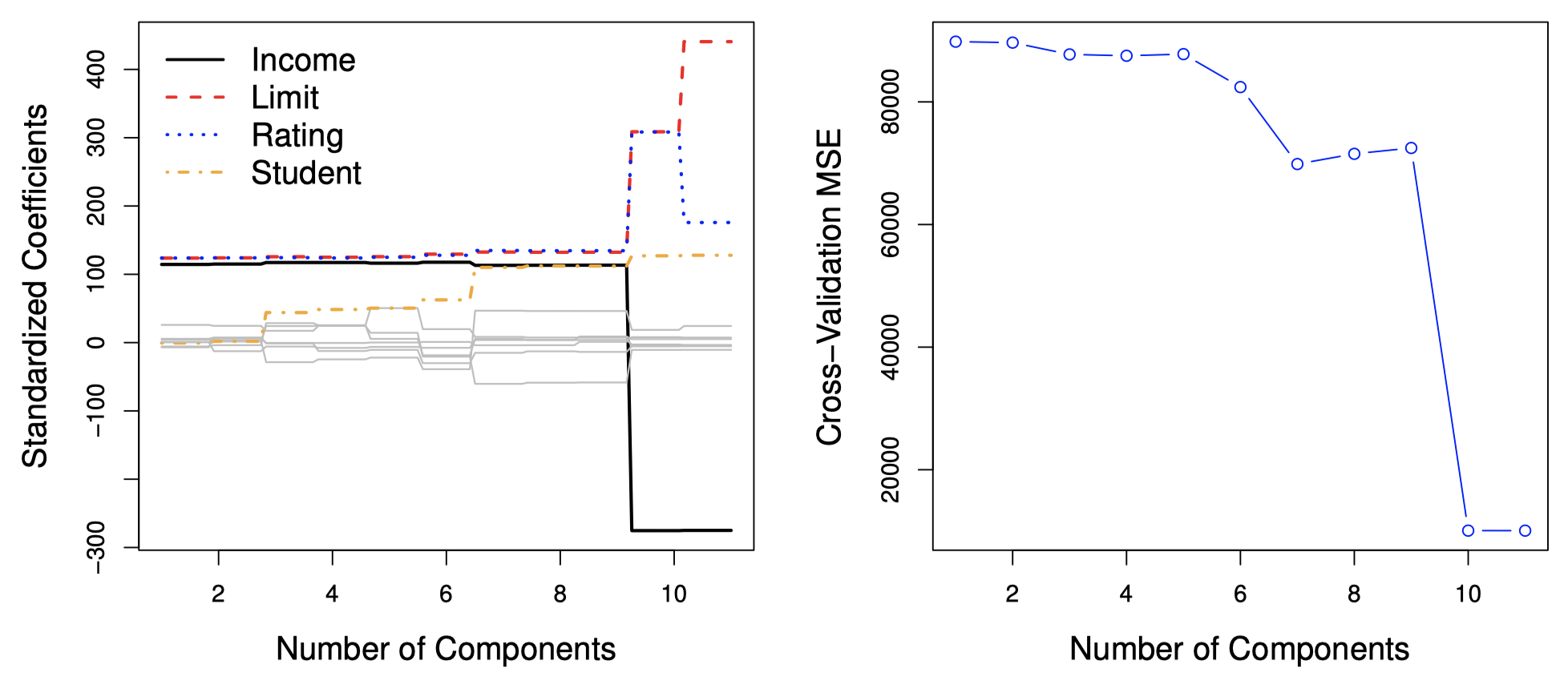
图 18:左图:Credit 数据集上不同 $M$ 值下 PCR 标准化系数估计。右图:用 PCR 进行 $10$-折交叉验证的均方误差随 $M$ 的变化。
应用 PCR 时,通常建议在构造主成分之前,对每个变量进行标准化处理。标准化保证了所有变量处在相同尺度上。如果没有进行标准化处理,方差较大的变量将在主成分中占主导地位,变量的尺度将最终影响 PCR 模型的效果。如果所有变量均使用同一计量单位 (例如:千克或英寸),则可以不进行标准化处理。
4.2 偏最小二乘法
PCR 方法需要确定能够最大限度地代表预测变量 $X_1,\dots,X_p$ 的线性组合或方向。这些方向是通过 无监督 (unsupervised) 方法确定的,因为该过程中没有使用响应变量 $Y$ 来帮助确定主成分方向。也就是说,响应变量没有指导主成分的构造过程。因此,PCR 存在一个潜在的严重缺陷:我们无法保证那些能够很好地解释预测变量的方向同样可以很好地帮助预测响应变量。
现在,我们将介绍一种 PCR 的替代方法,它是一种有监督方法,称为 偏最小二乘法 (partial least squares, PLS)。
和 PCR 类似,PLS 也是一种降维方法,它将原始变量的线性组合 $Z_1,\dots,Z_M$ 作为新的变量集,然后通过 OLS 对这 $M$ 个新变量拟合一个线性模型。但是与 PCR 不同,PLS 以一种新的有监督方式来构造这些新特征,即利用了响应变量 $Y$ 的信息来构造新变量,使得不仅很好地近似了原始变量,并且也 与响应变量相关。大致来说,PLS 方法试图找到那些同时有助于解释响应变量和预测变量的方向。
具体来说,在对全部 $p$ 个原始预测变量进行标准化后,PLS 在计算第一个方向 $Z_1$ 时,将之前 $Z_m$ 公式中的每个 $\phi_{j1}$ 设置为等于 $Y$ 对 $X_j$ 进行简单线性回归的系数。可以证明,此系数与 $Y$ 和 $X_j$ 之间的相关系数成比例。因此,在计算 $Z_1=\sum_{j=1}^{p}\phi_{j1}X_j$ 时,PLS 会将最大权重赋予与响应变量相关性最强的预测变量。
为确定第二个 PLS 方向,首先用 $Z_1$ 中的每个变量对 $Z_1$ 做回归,取其残差来调整每个变量。残差可以视为没有被第一 PLS 方向解释的剩余信息。然后利用这些正交数据计算 $Z_2$,形式上同之前基于原始数据计算 $Z_1$ 完全一致。重复迭代此过程 $M$ 次以生成多个 PLS 成分 $Z_1,\dots,Z_M$。最后,与 PCR 一样,用 $Z_1,\dots,Z_M$ 拟合线性最小二乘模型来预测 $Y$。
同 PCR 一样,PLS 方向的个数 $M$ 也是一个需要调节的参数,一般通过交叉验证选择。 通常,应用 PLS 之前需要对预测变量和响应变量进行标准化处理。
PLS 在化学统计学领域应用广泛,许多变量是数字化的光谱数据。在实践中,其表现通常没有岭回归或 PCR 好。作为有监督降维技术,PLS 虽然可以减小偏差,但同时可能会增大方差,所以总体而言,PLS 与 PCR 各有优劣。
5. 总结
-
模型选择方法是进行数据分析的重要工具,尤其是对于涉及许多预测变量的大型数据集。
-
关于 稀疏 (sparsity) 方法 (例如:Lasso) 的研究是一个非常热门的领域。
-
在后面课程中,我们将更详细地介绍稀疏性,包括诸如 弹性网 (elastic net) 之类的相关方法。
下节内容:非线性模型
本作品采用知识共享署名-非商业性使用-相同方式共享 4.0 国际许可协议进行许可。 欢迎转载,并请注明来自:YEY 的博客 同时保持文章内容的完整和以上声明信息!