Lecture 06 主成分分析 (三)
参考教材:
- Hardle, W. and Simar, L (2015). Applied multivariate statistical analysis, 4th edition.
- Hastie, T. Tibshirani, R. and Friedman, J. (2009). The elements of statistical learning, 2nd edition
1. 主成分回归
在上节课中,我们介绍了 主成分回归 (principal component regression, PCR) (参见教材 Elements of Statistical Learning, section 3.5),下面我们对其进行一些简单的回顾:
对于中心化的 $\underbrace{Z}_{1\times 1}$ 和 $\underbrace{X}_{p\times 1}$,我们希望将回归模型
\[\begin{align} Z &= \beta^{\mathrm T}X + \epsilon \\[2ex] &= \beta^{\mathrm T}\Gamma Y + \epsilon \\[2ex] &= \beta^{\mathrm T}\underbrace{\Gamma_{(1)}}_{p\times q} \underbrace{Y_{(1)}}_{q\times 1} + \beta^{\mathrm T} \underbrace{\Gamma_{(2)}}_{p\times (p-q)\;} \underbrace{Y_{(2)}}_{\;(p-q)\times 1} + \epsilon \end{align}\]用以下模型近似
\[Z = \beta_{\mathrm{PC}}^{\mathrm T} Y_{(1)} + \eta\]并且我们相信来自 $Y_{(2)}$ 的可变性是可以忽略不计的 (即 $X\approx \Gamma_{(1)}Y_{(1)}$)。
当然,在实践中,我们只能基于样本协方差矩阵 $S$ 获得 $\Gamma$ 和 $Y$ 的 “经验版本”。基于一般的最小二乘公式,我们可以计算出一个 $\hat \beta_{\mathrm{PC}}$ 估计。然后,我们可以将 $\beta$ 的 “PCR 估计” 定义为
\[\hat \beta^{\mathrm{PCR}}(q) = \hat \Gamma_{(1)} \hat \beta_{\mathrm{PC}}\]其中,$\hat \Gamma_{(1)}$ 是 $\Gamma_{(1)}$ 在实践中的估计版本。
回忆一下,如果 $\mathcal X^{\mathrm T}\mathcal X$ 是可逆的但特征值较小,那么
\[\hat \beta_{\mathrm{LS}} = (\mathcal X^{\mathrm T}\mathcal X)^{-1}\mathcal X^{\mathrm T} \mathcal Z\]可以具有较大的 (协) 方差。
可以证明,当 $q < p$ 时,
\[\mathrm{Cov}(\hat \beta_{\mathrm{LS}}) - \mathrm{Cov}(\hat \beta^{\mathrm{PCR}}(q)) \ge 0\](回忆一下,这意味着 “正定”)
参见 https://en.wikipedia.org/wiki/Principal_component_regression
但是请注意,与 $\hat \beta_{\mathrm{LS}}$ 不同,$\hat \beta^{\mathrm{PCR}}(q))$ 是有偏的。因此,我们通过增加一些偏差为代价,减小了估计量的方差。
2. 偏最小二乘法
考虑一个具有 $E(X)=0$ 和 $E(Z)=0$ 的线性回归模型:
\[Z=m(X) + \epsilon\; , \quad m(x)= E(Z\mid X=x) = \beta^{\mathrm T}x\]其中,$\beta$、$X=(X_1,\dots,X_p)^{\mathrm T}$ 和 $x$ 都是 $p$ 维向量,并且 $\beta$ 是未知的。
在 PCA 中,我们构造了一个关于 $X_j$ 的特定线性组合:
\[Y_j = \gamma_j^{\mathrm T}X \, , \;\; Y=\Gamma^{\mathrm T}X\]其中,权重矩阵 $\Gamma$ 仅仅通过 $\Sigma=\mathrm{Var}(X)$ 构造。
我们希望前几个 $Y_j$ 包含 关于 $X$ 的大部分信息,然后我们取以下近似:
\[m(x) = \beta^{\mathrm T}x \approx m_{\mathrm{PC}}(y_{(1)}) = \beta_{\mathrm{PC}}^{\mathrm T}y_{(1)}\]问题:这种方式分解得到的连续 PC $Y_1,\dots,Y_p$ 仅基于 $\mathrm{Var}(X)$ 的特征向量,而完全忽略了 $Z$。
在 偏最小二乘法 (partial least squares, PLS) 中,我们选择将 $X$ 分解为连续的线性投影
\[T_1,T_2,\dots,T_p\]并且它们试图保留 关于 $Z$ 和 $X$ 之间关系 的大部分信息。
由于我们的目标是估计 $X$ 和 $Z$ 之间的关系,因此这种方法似乎要更好一些。
-
在 PCA 中,第一个成分 $Y_1$ 通过下式构造:
\[Y_1 = \gamma_1^{\mathrm T} X\]其中,\(\|\gamma_1\| = 1\),并且 $\mathrm{Var}(Y_1)$ 尽可能大。
-
在 PLS 中,第一个成分 $T_1$ 通过下式构造:
\[T_1 = \phi_1^{\mathrm T} X\]其中,$\|\phi_1 \| = 1$,并且 $|\mathrm{Cov}(Z,T_1) |$ 尽可能大。
注意:$Z$ 和 $T_1$ 都是 $1$ 维的,而 $\phi_1$ 是一个 $p$ 维向量。
-
然后,对于 $k=2,\dots,p$,第 $k$ 个成分 $T_k$ 通过下式构造:
\[T_k = \phi_k^{\mathrm T} X\]其中,$\|\phi_k \| = 1$,
\[\phi_k^{\mathrm T} \Sigma \phi_j =0 \quad \text{for}\; j=1,\dots,k-1\]并且 $|\mathrm{Cov}(Z,T_k) |$ 尽可能大。
注意:$Z$ 和 $T_k$ 都是 $1$ 维的,而 $\phi_k$ 是一个 $p$ 维向量。
$X$ 在 $T_j$ 上的投影被构造为仍然保持 $X$ 的线性组合的形式,并且这些线性组合解释了 $Z$ 和 $X$ 之间的大部分线性关系。
令 $\Phi = (\phi_1,\dots,\phi_p)$ 为一个 $p\times p$ 的矩阵。我们希望 $p$ 维向量 $T=(T_1,\dots,T_p)^{\mathrm T} = \Phi^{\mathrm T}X$ 的前几个 (例如前 $q$ 个) 成分包含了与 $X$ 相关并且能够用于估计 $X$ 和 $Z$ 之间线性关系 $m(X)$ 的大部分信息。
然后,我们对 $T_1,\dots,T_q$ (而不是对 $X_1,\dots,X_p$) 进行线性回归。
特别地,回忆一下,对于 $x$、$X$ 和 $\beta \in \mathbb R^p$,我们的线性模型为
\[m(x) = E(Z\mid X=x) = \beta^{\mathrm T}x\]将 $p$ 维向量 $t$ 定义为
\[t=(t_1,\dots,t_p)^{\mathrm T} =\Phi^{\mathrm T} x\]并且对于 $q < p$,定义 $q$ 维向量
\[T_{(1)} = (T_1,\dots,T_q)^{\mathrm T} \quad \text{and} \quad t_{(1)} = (t_1,\dots,t_q)^{\mathrm T}\]我们采用以下近似:
\[m(x) = \beta^{\mathrm T}x \approx E(Z\mid T_{(1)}=t_{(1)}) \equiv m_{\mathrm{PLS}}(t_{(1)}) = \beta_{\mathrm{PLS}}^{\mathrm T} t_{(1)}\]$\beta_{\mathrm{PLS}}$ 的最小二乘估计量等于
\[\hat \beta_{\mathrm{PLS}} =\mathop{\operatorname{arg\,min}}\limits_{b\in \mathbb R^q} \sum_{i=1}^{n}(Z_i - b^{\mathrm T} T_{(1),i})^2 = (\mathcal T_{(1)}^{\mathrm T}\mathcal T_{(1)})^{-1} \mathcal T_{(1)}^{\mathrm T} \mathcal Z\]其中,$\mathcal Z=(Z_1,\dots,Z_n)^{\mathrm T}$ 是一个 $n$ 维向量,而
\[T_{(1),i} = (T_{i1},\dots,T_{iq})^{\mathrm T}\]是一个 $q$ 维向量,对应于第 $i$ 个个体,并且
\[\mathcal T_{(1)} = \begin{pmatrix}T_{11} & \cdots & T_{1q} \\ \vdots & \ddots & \vdots \\ T_{n1} & \cdots & T_{nq}\end{pmatrix}\]和 PCA 一样,我们可以通过交叉验证来选择 $q$:
\[q=\mathop{\operatorname{arg\,min}}\limits_{k=1,\dots,p} CV(k)\]其中,
\[CV(k) = \sum_{i=1}^{n} \{Z_i - \hat \beta_{\mathrm{PLS},k}^{-i} T_{(1),i}\}^2\]并且 $\hat \beta_{\mathrm{PLS},k}^{-i}$ 表示 $\beta_{\mathrm{PLS}}$ 的 LS 估计量
表示按照上面公式取 $q=k$ 计算出的 $\beta_{\mathrm{PLS}}$ 的 LS 估计量,只是这里我们将第 $i$ 个个体从 $\mathcal Z$ 和 $\mathcal T_{(1)}$ 中移除了。
到此为止,我们已经在总体级别上展示了 PLS 的所有内容。请参阅 ESL 中的算法 3.3,以了解在实践中如何实现 PLS (经验版本)。

3. 讨论:PCA vs. PLS
PCA 和 PLS 也可以用于非线性回归模型,我们同样可以将 $m(x) = E(Z\mid X=x)$ 近似为:
\[m_{\mathrm{PLS}}(t_{(1)}) = E(Z\mid T_{(1)} = t_{(1)}) \quad \text{or} \quad m_{\mathrm{PC}}(y_{(1)}) = E(Z\mid Y_{(1)} = y_{(1)})\]对于回归估计,如前所述,通过 PLS 降维通常要比通过 PCA 降维更好。
通常情况下,要么 $m_{\mathrm{PLS}}(t_{(1)})$ 比 $m_{\mathrm{PC}}(y_{(1)})$ 对 $m(x)$ 近似得更好,或者如果它们达到相同的近似效果,那么 PLS 使用的成分数量通常要比 PC 使用的成分数量更少 $\quad \Longrightarrow \quad$ 计算效率更高。
例子:音素数据 (Phoneme data)
来源:http://www-stat.stanford.edu/ElemStatLearn
$X_i \in \mathbb R^{256}$ 代表由音素 “aa” (例如 “dark”) 和 “ao” (例如“water”) 录音构成的对数周期。
对于每个 $i$,我们将 $Z_i$ 模拟为
\[Z_i = m(X_i) + \epsilon_i = \beta^{\mathrm T}X_i + \epsilon_i\]其中,$\epsilon_i \sim N(0,\sigma^2)$,并且对于构造的各种 $p$ 维向量 $\beta$,使得 $X$ 和 $Z$ 之间的所有交互作用仅取决于 5 个PC (其余不起作用)。
注意:回忆一下,$X_i =\Gamma Y_i$,因此通过选择合适的 $\beta$,可以使得 $\beta^{\mathrm T}\Gamma$ 仅具有五个非零坐标。
- 情况 (i):信息包含在前 5 个 PC 中
- 情况 (ii):信息包含在第 6 到第 10 个 PC 中
- 情况 (iii):信息包含在第 11 到第 15 个 PC 中
- 情况 (iv):信息包含在第 16 到第 20 个 PC 中
该数据集有 $N = 1717$ 个观测值。我们随机创建了 $200$ 个大小为 $n = 30$ 或 $n = 100$ 的子样本,并从每个子样本中计算了 PLS 回归估计量和 PCA 回归估计量。
然后在每种情况下,对于未用于计算回归估计量的其余 $N-n$ 个观测值,我们计算了其预测量
\[\hat Z_{i}^{\mathrm{PLS}} = \hat m_{\mathrm{PLS}}(T_{(1),i}) \quad \text{or} \quad \hat Z_{i}^{\mathrm{PC}} = \hat m_{\mathrm{PC}}(Y_{(1),i})\]$\text{for} \; q=1,2,\dots,10$.
对于 $\hat Z_i$ 的表示 $\hat Z_{i}^{\mathrm{PLS}}$ 或者 $\hat Z_{i}^{\mathrm{PC}}$,我们计算其 均方预测误差 (average squared prediction error):
\[PE = \dfrac{1}{N-n}\sum_{i=1}^{N-n}(Z_i - \hat Z_i)^2\]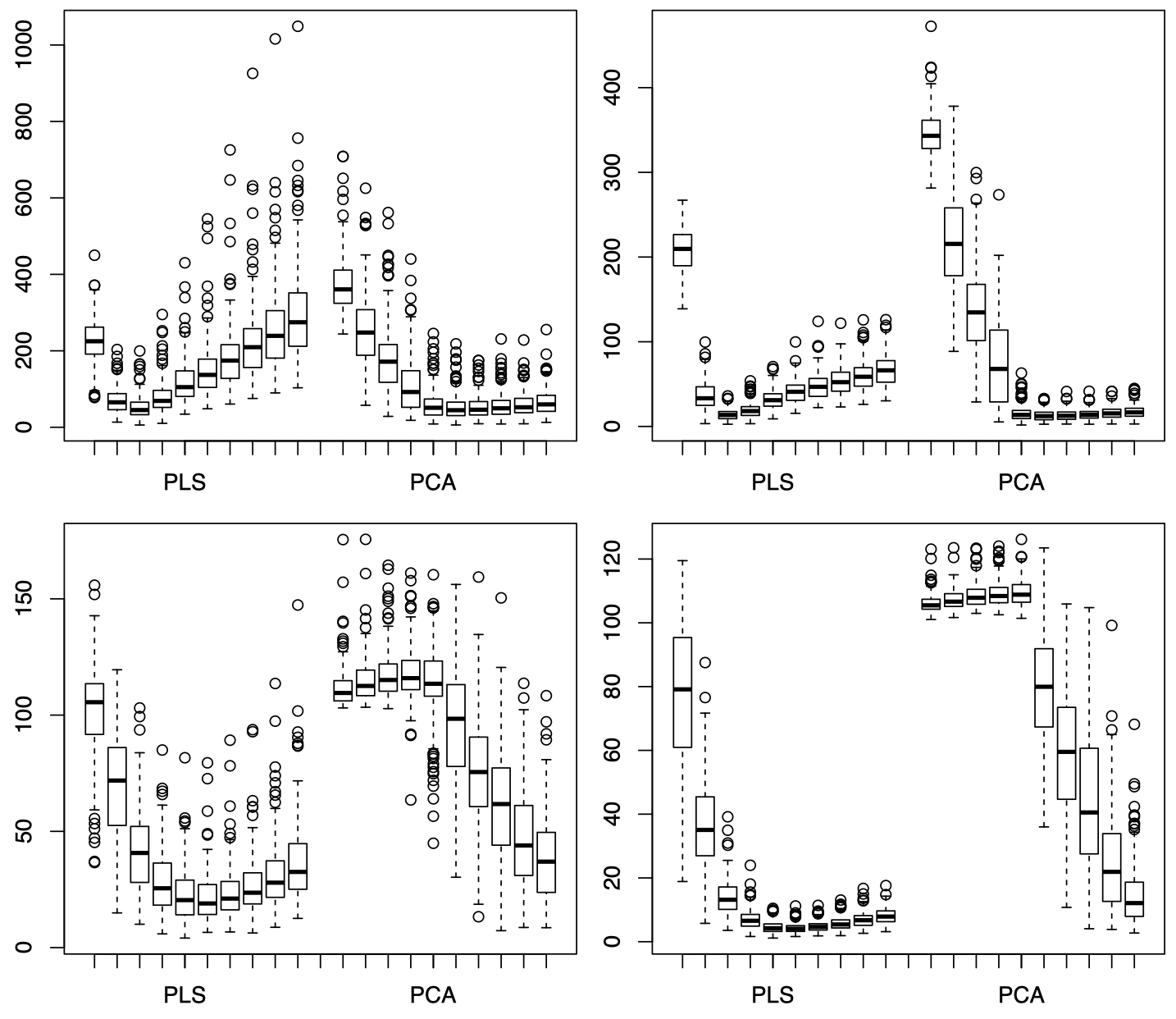
图 1:左上:当 $n=30$ 时,情况 (i)。右上:当 $n=100$ 时,情况 (i)。左下:当 $n=30$ 时,情况 (ii)。右下:当 $n=100$ 时,情况 (ii)。每张图中,左侧是 PLS 模型,右侧是 PCA 模型,每一侧从左到右依次为 $q=1,\dots,10$ 时,均方预测误差 PE 的箱型图。
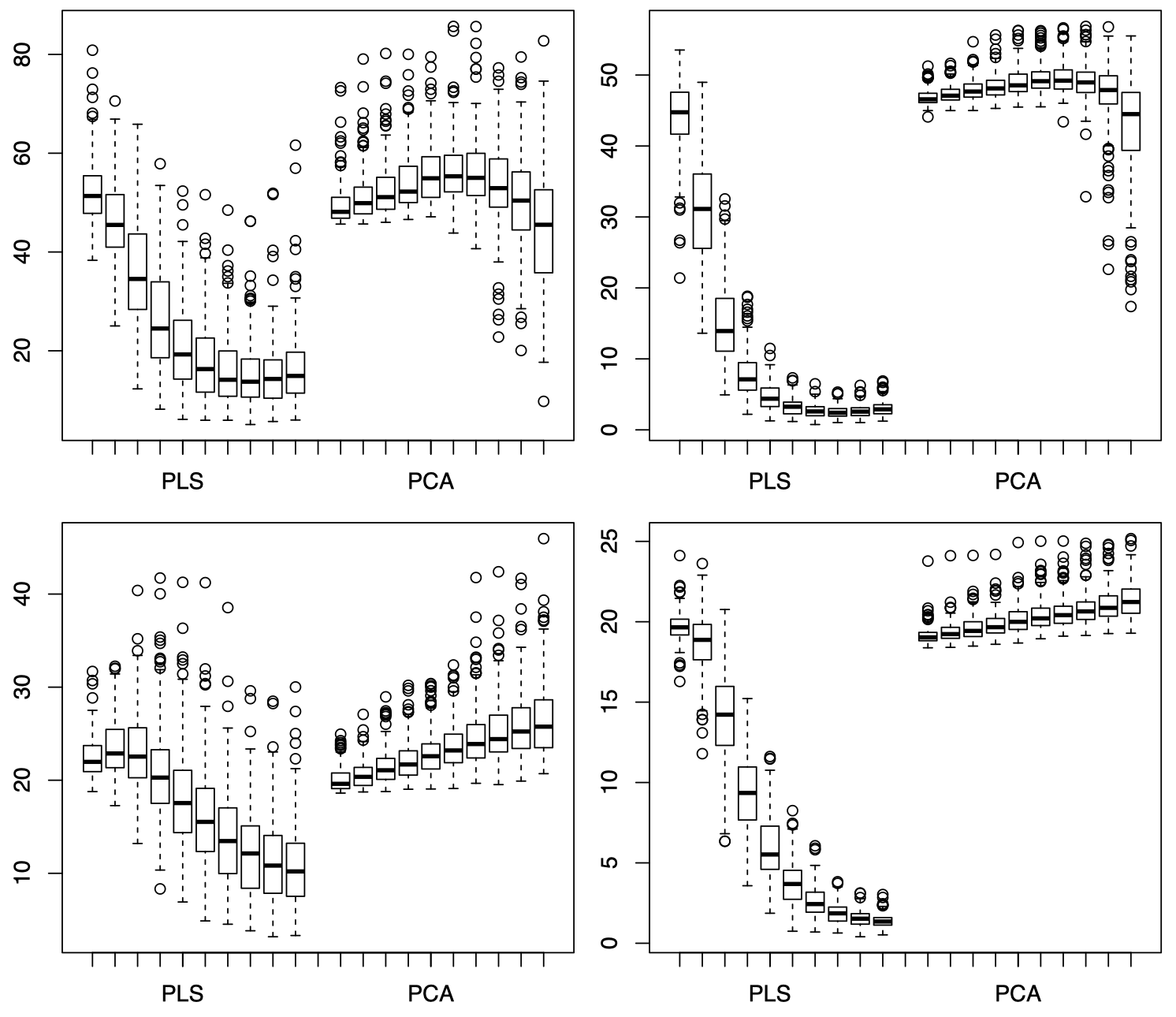
图 2:左上:当 $n=30$ 时,情况 (iii)。右上:当 $n=100$ 时,情况 (iii)。左下:当 $n=30$ 时,情况 (iv)。右下:当 $n=100$ 时,情况 (iv)。每张图中,左侧是 PLS 模型,右侧是 PCA 模型,每一侧从左到右依次为 $q=1,\dots,10$ 时,均方预测误差 PE 的箱型图。
可以看到,PCA 的均方预测误差的走势与四种情况下的 PC 有着非常直接的关系,当 PC 中包含 $X$ 和 $Z$ 的交互信息时,PCA 的均方预测误差将呈现下降趋势。例如,图 1 中上面两张图对应情况 (i),即 $X$ 和 $Z$ 的交互信息包含在前 5 个 PC 中,因此当 $q$ 从 $1$ 增加到 $5$ 时,PCA 的均方预测误差呈现下降趋势,随后逐渐平稳,或者可能略微上升 (后面引入的 PC 对模型的损害大于帮助);而图 1 中下面两张图对应情况 (ii),即 $X$ 和 $Z$ 的交互信息包含在第 6 到第 10 个 PC 中,因此当 $q$ 从 $1$ 增加到 $5$ 时,PCA 的均方预测误差没有变化,或者略微上升,而当 $q$ 从 $6$ 增加到 $10$ 时,PCA 的均方预测误差呈现明显下降趋势。图 2 中,由于情况 (iii) 和 (iv) 中,$X$ 和 $Z$ 的交互信息都包含在第 $10$ 个之后的 PC 中,所以图中当 $q$ 从 $1$ 增加到 $10$ 的过程中,PCA 的均方预测误差的变化并不显著。
而对于 PLS,由于它和 PC 并不直接相关,而是取决于线性投影 $T_j$。因此,PLS 的均方预测误差的走势与四种 PC 情况之间的关系并不像 PCA 那样明显。以图 1 中左上图为例,随着 $q$ 从 $1$ 增加到 $10$,PLS 的均方预测误差先下降后上升,最低点位于 $q=3$ 处,这意味着前 $3$ 个 PC 中已经包含了大部分 $X$ 和 $Z$ 的交互信息,后面再增加的 PC 只是给模型引入了不必要的方差。总体来看,对于达到相同的均方预测误差,PLS 需要的成分数量通常要比 PCA 更少,这也表明 PLS 的计算效率通常要高于 PCA。
下节内容:因子分析
本作品采用知识共享署名-非商业性使用-相同方式共享 4.0 国际许可协议进行许可。 欢迎转载,并请注明来自:YEY 的博客 同时保持文章内容的完整和以上声明信息!