PyTorch 学习笔记

PyTorch 16：损失函数 (二)

PyTorch 学习笔记

Posted by YEY on December 19, 2020

Lecture 16 损失函数 (二)

上节课中，我们学习了损失函数的概念以及四种不同的损失函数。这节课我们继续学习 PyTorch 中提供的另外十四种损失函数。

1. PyTorch 中的损失函数

首先我们来看在回归任务中常用的两个损失函数 nn.L1Loss 和 nn.MSELoss：

nn.L1Loss

功能：计算 inputs 与 target 之差的绝对值。

1
2
3
4
5

nn.L1Loss(
    size_average=None,
    reduce=None,
    reduction='mean'
)

主要参数：

  • reduction：计算模式，可为 none/sum/mean。
    • none：逐个元素计算。
    • sum：所有元素求和，返回标量。
    • mean：加权平均，返回标量。

计算公式：

\[l_n = |x_n - y_n |\]

nn.MSELoss

功能：计算 inputs 与 target 之差的平方。

1
2
3
4
5

nn.MSELoss(
    size_average=None,
    reduce=None,
    reduction='mean'
)

主要参数：

  • reduction：计算模式，可为 none/sum/mean。
    • none：逐个元素计算。
    • sum：所有元素求和，返回标量。
    • mean：加权平均，返回标量。

计算公式：

\[l_n = (x_n - y_n )^2\]

代码示例：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

import torch
import torch.nn as nn
import matplotlib.pyplot as plt
import numpy as np
from tools.common_tools import set_seed

set_seed(1)  # 设置随机种子

inputs = torch.ones((2, 2))
target = torch.ones((2, 2)) * 3

# ------------------------------------ L1 loss ----------------------------------
loss_f = nn.L1Loss(reduction='none')
loss = loss_f(inputs, target)

print("input:{}\ntarget:{}\nL1 loss:{}".format(inputs, target, loss))

# ------------------------------------ MSE loss ---------------------------------
loss_f_mse = nn.MSELoss(reduction='none')
loss_mse = loss_f_mse(inputs, target)

print("MSE loss:{}".format(loss_mse))

输出结果：

1
2
3
4
5
6
7
8

input:tensor([[1., 1.],
        [1., 1.]])
target:tensor([[3., 3.],
        [3., 3.]])
L1 loss:tensor([[2., 2.],
        [2., 2.]])
MSE loss:tensor([[4., 4.],
        [4., 4.]])

可以看到，这里我们的每个神经元的输入为 $x_i = 1$，输出为 $y_i=3$。所以，每个神经元的 L1 loss 为 $|x_i - y_i| = |1-3| = 2$，MSE loss 为 $(x_i - y_i)^2 = (1-3)^2 = 4$。

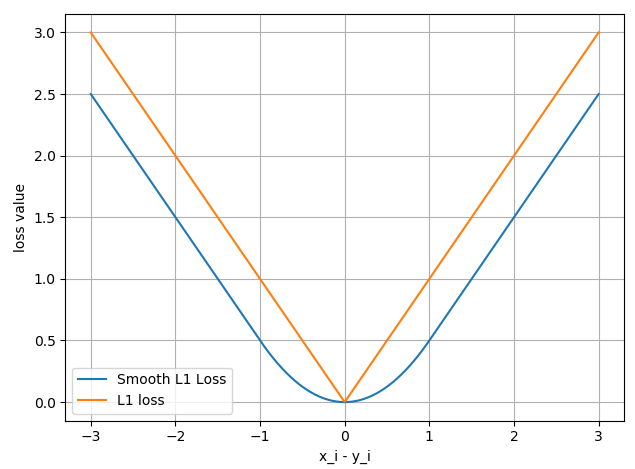
nn.SmoothL1Loss

功能：平滑的 L1 Loss，可以减轻离群点带来的影响。

1
2
3
4
5

nn.SmoothL1Loss(
    size_average=None,
    reduce=None,
    reduction='mean'
)

主要参数：

  • reduction：计算模式，可为 none/sum/mean。
    • none：逐个元素计算。
    • sum：所有元素求和，返回标量。
    • mean：加权平均，返回标量。

计算公式：

\[\mathrm{loss}(x,y) = \dfrac{1}{n}\sum_{i=1}^n z_i\]

其中，

\[z_i = \begin{cases}0.5(x_i - y_i)^2\;, & \text{if } |x_i - y_i|< 1 \\[2ex] |x_i - y_i| - 0.5\;, & \text{otherwise}\end{cases}\]

代码示例：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

inputs = torch.linspace(-3, 3, steps=500)
target = torch.zeros_like(inputs)

loss_f = nn.SmoothL1Loss(reduction='none')
loss_smooth = loss_f(inputs, target)

loss_l1 = np.abs(inputs.numpy())

plt.plot(inputs.numpy(), loss_smooth.numpy(), label='Smooth L1 Loss')
plt.plot(inputs.numpy(), loss_l1, label='L1 loss')
plt.xlabel('x_i - y_i')
plt.ylabel('loss value')
plt.legend()
plt.grid()
plt.show()

输出结果：

PoissonNLLLoss

功能：泊松分布的负对数似然损失函数。

1
2
3
4
5
6
7
8

nn.PoissonNLLLoss(
    log_input=True,
    full=False,
    size_average=None,
    eps=1e-08,
    reduce=None,
    reduction='mean'
)

主要参数：

  • log_input：输入是否为对数形式，决定计算公式。
  • full：计算所有 loss，默认为 False。
  • eps：修正项，避免 input 为 $0$ 时，log(input) 为 nan 的情况。

计算公式：

  • 当 log_input=True 时：

    \[\mathrm{loss}(x_n, y_n) = e^{x_n} - x_n \cdot y_n\]

  • 当 log_input=False 时：

    \[\mathrm{loss}(x_n, y_n) = x_n - y_n \cdot \log(x_n + \mathrm{eps})\]

代码示例：

1
2
3
4
5
6
7

inputs = torch.randn((2, 2))
target = torch.randn((2, 2))

loss_f = nn.PoissonNLLLoss(log_input=True, full=False, reduction='none')
loss = loss_f(inputs, target)

print("input:{}\ntarget:{}\nPoisson NLL loss:{}".format(inputs, target, loss))

输出结果：

1
2
3
4
5
6

input:tensor([[0.6614, 0.2669],
        [0.0617, 0.6213]])
target:tensor([[-0.4519, -0.1661],
        [-1.5228,  0.3817]])
Poisson NLL loss:tensor([[2.2363, 1.3503],
        [1.1575, 1.6242]])

下面我们以第一个神经元的 loss 为例，通过手动计算来验证我们前面的公式是否正确：

1
2
3
4

idx = 0
loss_1 = torch.exp(inputs[idx, idx]) - target[idx, idx]*inputs[idx, idx]

print("第一个元素的 loss 为:", loss_1)

输出结果：

1

第一个元素的 loss 为: tensor(2.2363)

可以看到，由于这里我们的 log_input=True，默认输入为对数形式，计算出的第一个神经元的 loss 为 $2.2363$，与前面 PyTorch 中 nn.PoissonNLLLoss 的计算结果一致。

nn.KLDivLoss

功能：计算 KL 散度 (KL divergence, KLD)，即相对熵。

1
2
3
4
5

nn.KLDivLoss(
    size_average=None,
    reduce=None,
    reduction='mean'
)

主要参数：

  • reduction：计算模式，可为 none/sum/mean/batchmean。
    • none：逐个元素计算。
    • sum：所有元素求和，返回标量。
    • mean：加权平均，返回标量。
    • batchmean：batchsize 维度求平均值。

计算公式：

\[\begin{aligned} D_{\mathrm{KL}}(P,Q) = \mathrm{E}_{X\sim P}\left[\log \dfrac{P(X)}{Q(X)}\right] &= \mathrm{E}_{X\sim P}[\log P(X) - \log Q(X)] \\[2ex] &= \sum_{i=1}^{n} P(x_i)(\log P(x_i) - \log Q(x_i)) \end{aligned}\]

其中，$P$ 为数据的真实分布，$Q$ 为模型拟合的分布。

PyTorch 中的计算公式：

\[l_n = y_n \cdot (\log y_n - x_n)\]

由于 PyTorch 是逐个元素计算的，因此可以移除 $\Sigma$ 求和项。而括号中第二项这里是 $x_n$，而不是 $\log Q(x_n)$，因此我们需要提前计算输入的对数概率。

注意事项：需提前将输入计算 log-probabilities，例如通过 nn.logsoftmax() 计算。

代码示例：

1
2
3
4
5
6
7
8
9
10
11
12
13

inputs = torch.tensor([[0.5, 0.3, 0.2], [0.2, 0.3, 0.5]])
inputs_log = torch.log(inputs)
target = torch.tensor([[0.9, 0.05, 0.05], [0.1, 0.7, 0.2]], dtype=torch.float)

loss_f_none = nn.KLDivLoss(reduction='none')
loss_f_mean = nn.KLDivLoss(reduction='mean')
loss_f_bs_mean = nn.KLDivLoss(reduction='batchmean')

loss_none = loss_f_none(inputs, target)
loss_mean = loss_f_mean(inputs, target)
loss_bs_mean = loss_f_bs_mean(inputs, target)

print("loss_none:\n{}\nloss_mean:\n{}\nloss_bs_mean:\n{}".format(loss_none, loss_mean, loss_bs_mean))

输出结果：

1
2
3
4
5
6
7

loss_none:
tensor([[-0.5448, -0.1648, -0.1598],
        [-0.2503, -0.4597, -0.4219]])
loss_mean:
-0.3335360586643219
loss_bs_mean:
-1.000608205795288

由于我们的输入是一个 $2\times 3$ 的 Tensor，所以我们的 loss 也是一个 $2\times 3$ 的 Tensor。在 mean 模式下，我们得到 6 个 loss 的均值为 $-0.3335$；而 batchmean 模式下是 6 个 loss 相加再除以 $2$，所以得到 $-1.0006$。

下面我们以第一个神经元的 loss 为例，通过手动计算来验证 PyTorch 中的公式是否和我们之前提到的一致：

1
2
3
4

idx = 0
loss_1 = target[idx, idx] * (torch.log(target[idx, idx]) - inputs[idx, idx])  #  注意，这里括号中第二项没有取 log

print("第一个元素的 loss 为:", loss_1)

输出结果：

1

第一个元素的 loss 为: tensor(-0.5448)

可以看到，手动计算的结果与前面 PyTorch 中的 nn.KLDivLoss 的结果一致。

nn.MarginRankingLoss

功能：计算两个向量之间的相似度，用于 排序任务。该方法计算两组数据之间的差异，返回一个 $n\times n$ 的 loss 矩阵。

1
2
3
4
5
6

nn.MarginRankingLoss(
    margin=0.0,
    size_average=None,
    reduce=None,
    reduction='mean'
)

主要参数：

  • margin：边界值，$x_1$ 与 $x_2$ 之间的差异值。
  • reduction：计算模式，可为 none/sum/mean。

计算公式：

\[\mathrm{loss}(x,y)= \max (0, -y \cdot (x_1 - x_2) + \mathrm{margin})\]
  • 当 $y=1$ 时，我们希望 $x_1$ 比 $x_2$ 大，当 $x_1 > x_2$ 时， 不产生 loss。
  • 当 $y=-1$ 时，我们希望 $x_2$ 比 $x_1$ 大，当 $x_2 > x_1$ 时，不产生 loss。

代码示例：

1
2
3
4
5
6
7
8
9

x1 = torch.tensor([[1], [2], [3]], dtype=torch.float)
x2 = torch.tensor([[2], [2], [2]], dtype=torch.float)

target = torch.tensor([1, 1, -1], dtype=torch.float)

loss_f_none = nn.MarginRankingLoss(margin=0, reduction='none')
loss = loss_f_none(x1, x2, target)

print(loss)

输出结果：

1
2
3

tensor([[1., 1., 0.],
        [0., 0., 0.],
        [0., 0., 1.]])

由于这里我们的输入是两个长度为 $3$ 的向量，所以输出的是一个 $3\times 3$ 的 loss 矩阵。该矩阵中的第一行是由 x1 中的第一个元素与 x2 中的三个元素计算得到的 loss。当 $y=1$ 时，$x_1 =1$，$x_2=2$，$x_1$ 并没有大于 $x_2$，因此会产生 loss 为 $\max (0, -1\times (1 - 2)) = 1$，所以输出矩阵中第一行的第一个元素为 $1$；第一行中的第二个元素同理。对于第一行中的第三个元素，$y = -1$，$x_1 =1$，$x_2=2$，满足 $x_2 > x_1$，因此不会产生 loss，即 loss 为 $\max (0, 1\times (1 - 2)) = 0$，所以输出矩阵中第一行的第三个元素为 $0$。

nn.MultiLabelMarginLoss

功能：多标签边界损失函数。例如四分类任务，样本 $x$ 属于第 $0$ 类和第 $3$ 类，注意这里标签为 $[0,3,-1,-1]$，而不是 $[1,0,0,1]$。

1
2
3
4
5

nn.MultiLabelMarginLoss(
    size_average=None,
    reduce=None,
    reduction='mean'
)

主要参数：

  • reduction：计算模式，可为 none/sum/mean。

计算公式：

\[\mathrm{loss}(x,y) = \sum_{ij}\dfrac{\max(0, 1-x[ y [j] ] - x[i])}{x.\mathrm{size}(0)}\]

其中，$i=0,\dots,x.\mathrm{size}(0)\;,\;j=0,\dots,y.\mathrm{size}(0)$，对于所有的 $i$ 和 $j$，都有 $y[j] \ge 0$ 并且 $i \ne y[j]$。

代码示例：

1
2
3
4
5
6
7

x = torch.tensor([[0.1, 0.2, 0.4, 0.8]])  # 一个四分类样本的输出概率
y = torch.tensor([[0, 3, -1, -1]], dtype=torch.long)  # 标签，该样本属于第 0 类和第 3 类

loss_f = nn.MultiLabelMarginLoss(reduction='none')
loss = loss_f(x, y)

print(loss)

输出结果：

1

tensor([0.8500])

下面我们通过手动计算来验证前面计算公式的正确性：

1
2
3
4
5
6
7

x = x[0]
item_1 = (1-(x[0] - x[1])) + (1 - (x[0] - x[2]))    # 第 0 类标签的 loss
item_2 = (1-(x[3] - x[1])) + (1 - (x[3] - x[2]))    # 第 3 类标签的 loss

loss_h = (item_1 + item_2) / x.shape[0]

print(loss_h)

输出结果：

1

tensor(0.8500)

可以看到，手动计算的结果与 PyTorch 中的 nn.MultiLabelMarginLoss 的结果一致。

nn.SoftMarginLoss

功能：计算二分类的 logistic 损失。

1
2
3
4
5

nn.SoftMarginLoss(
    size_average=None,
    reduce=None,
    reduction='mean'
)

主要参数：

  • reduction：计算模式，可为 none/sum/mean。

计算公式：

\[\mathrm{loss}(x,y) = \sum_i \dfrac{\log(1 + \exp (-y[i] \cdot x[i]))}{x.\mathrm{nelement()}}\]

其中，$x.\mathrm{nelement()}$ 为输入 $x$ 中的样本个数。注意这里 $y$ 也有 $1$ 和 $-1$ 两种模式。

代码示例：

1
2
3
4
5
6
7

inputs = torch.tensor([[0.3, 0.7], [0.5, 0.5]])  # 两个样本，两个神经元
target = torch.tensor([[-1, 1], [1, -1]], dtype=torch.float)  # 该 loss 为逐个神经元计算，需要为每个神经元单独设置标签

loss_f = nn.SoftMarginLoss(reduction='none')
loss = loss_f(inputs, target)

print("SoftMargin: ", loss)

输出结果：

1
2

SoftMargin:  tensor([[0.8544, 0.4032],
        [0.4741, 0.9741]])

下面我们以第一个神经元的 loss 为例，采用手动计算来验证上面公式的正确性：

1
2
3
4
5
6
7

idx = 0
inputs_i = inputs[idx, idx]
target_i = target[idx, idx]

loss_h = np.log(1 + np.exp(-target_i * inputs_i))

print(loss_h)

输出结果：

1

tensor(0.8544)

可以看到，手动计算的结果与 PyTorch 中的 nn.SoftMarginLoss 的结果一致。

nn.MultiLabelSoftMarginLoss

功能：SoftMarginLoss 的多标签版本。

1
2
3
4
5

nn.MultiLabelSoftMarginLoss(
    weight=None,
    size_average=None,
    reduce=None,
    reduction='mean')

主要参数：

  • weight：各类别的 loss 设置权值。
  • reduction：计算模式，可为 none/sum/mean。

计算公式：

\[\mathrm{loss}(x,y)= - \dfrac{1}{C} \cdot \sum_i y[i] \cdot \log\left(\dfrac{1}{1+\exp(-x[i]))} \right) + (1-y[i]) \cdot \log \left(\dfrac{\exp(-x[i])}{1+\exp(-x[i]))} \right)\]

其中，$C$ 是标签类别的数量，$i$ 表示第 $i$ 个神经元，这里标签取值为 $0$ 或者 $1$，例如在一个四分类任务中，某样本标签为第 $0$ 类和第 $3$ 类，那么该样本的标签向量为 $[1,0,0,1]$。

代码示例：

1
2
3
4
5
6
7

inputs = torch.tensor([[0.3, 0.7, 0.8]])
target = torch.tensor([[0, 1, 1]], dtype=torch.float)

loss_f = nn.MultiLabelSoftMarginLoss(reduction='none')
loss = loss_f(inputs, target)

print("MultiLabel SoftMargin: ", loss)

输出结果：

1

MultiLabel SoftMargin:  tensor([0.5429])

下面我们通过手动计算验证上面公式的正确性：

1
2
3
4
5
6
7

i_0 = torch.log(torch.exp(-inputs[0, 0]) / (1 + torch.exp(-inputs[0, 0])))
i_1 = torch.log(1 / (1 + torch.exp(-inputs[0, 1])))
i_2 = torch.log(1 / (1 + torch.exp(-inputs[0, 2])))

loss_h = (i_0 + i_1 + i_2) / -3

print(loss_h)

输出结果：

1

tensor(0.5429)

可以看到，手动计算的结果与 PyTorch 中的 nn.MultiLabelSoftMarginLoss 的结果一致。

nn.MultiMarginLoss

功能：计算多分类的折页损失。

1
2
3
4
5
6
7
8

nn.MultiMarginLoss(
    p=1,
    margin=1.0,
    weight=None,
    size_average=None,
    reduce=None,
    reduction='mean'
)

主要参数：

  • p：可选 1 或 2。
  • weight：各类别的 loss 设置权值。
  • margin：边界值。
  • reduction：计算模式，可为 none/sum/mean。

计算公式：

\[\mathrm{loss}(x,y) = \dfrac{\sum_i \max(0,\mathrm{margin}-x[y] + x[i])^p}{x.\mathrm{size(0)}}\]

其中，$x\in \{0,\dots,x.\mathrm{size}(0)-1\}\;,\; y\in \{0,\dots,y.\mathrm{size}(0)-1\}$，并且对于所有的 $i$ 和 $j$，都有 $0 \le y[j] \le x.\mathrm{size}(0)-1$，以及 $i \ne y[j]$。

代码示例：

1
2
3
4
5
6
7

x = torch.tensor([[0.1, 0.2, 0.7], [0.2, 0.5, 0.3]])
y = torch.tensor([1, 2], dtype=torch.long)

loss_f = nn.MultiMarginLoss(reduction='none')
loss = loss_f(x, y)

print("Multi Margin Loss: ", loss)

输出结果：

1

Multi Margin Loss:  tensor([0.8000, 0.7000])

下面我们以第一个样本的 loss 为例，通过手动计算验证上面公式的正确性：

1
2
3
4
5
6
7
8
9

x = x[0]
margin = 1

i_0 = margin - (x[1] - x[0])
i_2 = margin - (x[1] - x[2])

loss_h = (i_0 + i_2) / x.shape[0]

print(loss_h)

输出结果：

1

tensor(0.8000)

可以看到，手动计算的结果与 PyTorch 中的 nn.MultiMarginLoss 的结果一致。

nn.TripletMarginLoss

功能：计算三元组损失，常用于人脸识别验证。

三元组损失：

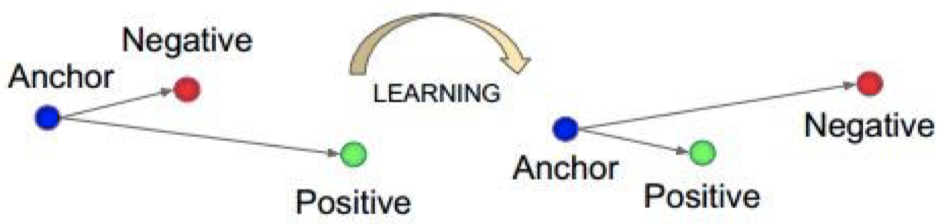
我们希望通过学习，使得 Anchor 与 Posttive 之间的距离小于 Anchor 与 Negative 之间的距离。

1
2
3
4
5
6
7
8
9

nn.TripletMarginLoss(
    margin=1.0,
    p=2.0,
    eps=1e-06,
    swap=False,
    size_average=None,
    reduce=None,
    reduction='mean'
)

主要参数：

  • p：范数的阶，默认为 2。
  • margin：边界值。
  • reduction：计算模式，可为 none/sum/mean。

计算公式：

\[L(a,p,n) = \max \{d(a_i, p_i) - d(a_i, n_i) + \mathrm{margin}, 0\}\]

其中，$d(x_i, y_i) = \|\mathbf{x}_i - \mathbf{y}_i \|_p$。

代码示例：

1
2
3
4
5
6
7
8

anchor = torch.tensor([[1.]])
pos = torch.tensor([[2.]])
neg = torch.tensor([[0.5]])

loss_f = nn.TripletMarginLoss(margin=1.0, p=1)  # 范数为 1，即计算两者之差的绝对值
loss = loss_f(anchor, pos, neg)

print("Triplet Margin Loss", loss)

输出结果：

1

Triplet Margin Loss tensor(1.5000)

下面我们通过手动计算验证上面公式的正确性：

1
2
3
4
5
6
7
8
9

margin = 1
a, p, n = anchor[0], pos[0], neg[0]

d_ap = torch.abs(a-p)
d_an = torch.abs(a-n)

loss = d_ap - d_an + margin

print(loss)

输出结果：

1

tensor([1.5000])

可以看到，手动计算的结果与 PyTorch 中的 nn.TripletMarginLoss 的结果一致。

nn.HingeEmbeddingLoss

功能：计算两个输入的相似性，常用于非线性 embedding 和半监督学习。

1
2
3
4
5
6

nn.HingeEmbeddingLoss(
    margin=1.0,
    size_average=None,
    reduce=None,
    reduction='mean'
)

主要参数：

  • margin：边界值。
  • reduction：计算模式，可为 none/sum/mean。

计算公式：

\[l_n = \begin{cases}x_n\, , & \text{if } y_n = 1 \\[2ex] \max\{0,\Delta - x_n\}\, , & \text{if } y_n = -1\end{cases}\]

注意事项：输入 $x$ 应为两个输入之差的绝对值。

代码示例：

1
2
3
4
5
6
7

inputs = torch.tensor([[1., 0.8, 0.5]])
target = torch.tensor([[1, 1, -1]])

loss_f = nn.HingeEmbeddingLoss(margin=1, reduction='none')
loss = loss_f(inputs, target)

print("Hinge Embedding Loss", loss)

输出结果：

1

Hinge Embedding Loss tensor([[1.0000, 0.8000, 0.5000]])

下面我们通过手动计算验证上面公式的正确性：

1
2
3
4
5
6

margin = 1.
loss_0 = inputs.numpy()[0, 0]
loss_1 = inputs.numpy()[0, 1]
loss_2 = max(0, margin - inputs.numpy()[0, 2])

print(loss_0, loss_1, loss_2)

输出结果：

1

1.0 0.8 0.5

可以看到，手动计算的结果与 PyTorch 中的 nn.HingeEmbeddingLoss 的结果一致。

nn.CosineEmbeddingLoss

功能：采用余弦相似度计算两个输入的相似性。

1
2
3
4
5
6

nn.CosineEmbeddingLoss(
    margin=0.0,
    size_average=None,
    reduce=None,
    reduction='mean'
)

主要参数：

  • margin：可取值 $[-1, 1]$，推荐为 $[0, 0.5]$。
  • reduction：计算模式，可为 none/sum/mean。

计算公式：

\[\mathrm{loss}(x,y) = \begin{cases}1-\cos(x_1,x_2)\, , & \text{if } y = 1 \\[2ex] \max\{0,\cos(x_1,x_2)-\mathrm{margin}\}\, , & \text{if } y = -1\end{cases}\]

其中，

\[\cos(\theta) = \dfrac{A\cdot B}{\|A\| \|B\|} = \dfrac{\sum_{i=1}^{n}A_i \times B_i}{\sqrt{\sum_{i=1}^{n}(A_i)^2} \times \sqrt{\sum_{i=1}^{n}(B_i)^2}}\]

代码示例：

1
2
3
4
5
6
7
8

x1 = torch.tensor([[0.3, 0.5, 0.7], [0.3, 0.5, 0.7]])
x2 = torch.tensor([[0.1, 0.3, 0.5], [0.1, 0.3, 0.5]])
target = torch.tensor([[1, -1]], dtype=torch.float)

loss_f = nn.CosineEmbeddingLoss(margin=0., reduction='none')
loss = loss_f(x1, x2, target)

print("Cosine Embedding Loss", loss)

输出结果：

1

Cosine Embedding Loss tensor([[0.0167, 0.9833]])

下面我们通过手动计算验证上面公式的正确性：

1
2
3
4
5
6
7
8
9
10
11

margin = 0.

def cosine(a, b):
    numerator = torch.dot(a, b)
    denominator = torch.norm(a, 2) * torch.norm(b, 2)
    return float(numerator/denominator)

l_1 = 1 - (cosine(x1[0], x2[0]))
l_2 = max(0, cosine(x1[0], x2[0]) - margin)

print(l_1, l_2)

输出结果：

1

0.016662120819091797 0.9833378791809082

可以看到，手动计算的结果与 PyTorch 中的 nn.CosineEmbeddingLoss 的结果一致。

nn.CTCLoss

参考文献：A. Graves et al.: Connectionist Temporal Classification: Labelling Unsegmented Sequence Data with Recurrent Neural Networks

功能：计算 CTC (Connectionist Temporal Classification) 损失，用于解决时序类数据的分类。

1
2
3
4
5

torch.nn.CTCLoss(
    blank=0,
    reduction='mean',
    zero_infinity=False
)

主要参数：

  • blank：blank label。
  • zero_infinity：无穷大的值或梯度值为 $0$。
  • reduction：计算模式，可为 none/sum/mean。

代码示例：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

T = 50      # Input sequence length
C = 20      # Number of classes (including blank)
N = 16      # Batch size
S = 30      # Target sequence length of longest target in batch
S_min = 10  # Minimum target length, for demonstration purposes

# Initialize random batch of input vectors, for *size = (T,N,C)
inputs = torch.randn(T, N, C).log_softmax(2).detach().requires_grad_()

# Initialize random batch of targets (0 = blank, 1:C = classes)
target = torch.randint(low=1, high=C, size=(N, S), dtype=torch.long)

input_lengths = torch.full(size=(N,), fill_value=T, dtype=torch.long)
target_lengths = torch.randint(low=S_min, high=S, size=(N,), dtype=torch.long)

ctc_loss = nn.CTCLoss()
loss = ctc_loss(inputs, target, input_lengths, target_lengths)

print("CTC loss: ", loss)

输出结果：

1

CTC loss:  tensor(7.5385, grad_fn=<MeanBackward0>)

2. 总结

到这里，我们已经学习完了 PyTorch 中的 18 种损失函数：

  1. nn.CrossEntropyLoss
  2. nn.NLLLoss
  3. nn.BCELoss
  4. nn.BCEWithLogitsLoss
  5. nn.L1Loss
  6. nn.MSELoss
  7. nn.SmoothL1Loss
  8. nn.PoissonNLLLoss
  9. nn.KLDivLoss
  10. nn.MarginRankingLoss
  11. nn.MultiLabelMarginLoss
  12. nn.SoftMarginLoss
  13. nn.MultiLabelSoftMarginLoss
  14. nn.MultiMarginLoss
  15. nn.TripletMarginLoss
  16. nn.HingeEmbeddingLoss
  17. nn.CosineEmbeddingLoss
  18. nn.CTCLoss

下节课中，我们将学习 PyTorch 中的优化器。

下节内容：优化器 (一)

知识共享许可协议本作品采用知识共享署名-非商业性使用-相同方式共享 4.0 国际许可协议进行许可。 欢迎转载，并请注明来自：YEY 的博客 同时保持文章内容的完整和以上声明信息！
CATALOG
    FEATURED TAGS
    随笔 课程笔记 统计机器学习 COMP90051 学习笔记 自然语言处理 COMP90042 PyTorch 人工智能伦理 COMP90087 数据科学多元统计学 MAST90138 AI 自动规划 COMP90054 数据分析 计算统计学与数据科学 MAST90083 高级数据库系统 COMP90050 统计建模 MAST90139 读书 📚 MySQL 学习索引 Hive 技术问题 Jekyll Workshop
    FRIENDS