Lecture 17 PGM 的概率推断和统计推断
主要内容
- PGM 的概率推断
- PGM 的统计推断
1. PGM 的概率推断
利用贝叶斯规则和边缘化,根据一个 PGM 的联合分布,计算边缘和条件分布。这里我们将学习如何有效地做到这一点。
1.1 两个熟悉的例子
-
朴素贝叶斯(频率学家 / 贝叶斯人)
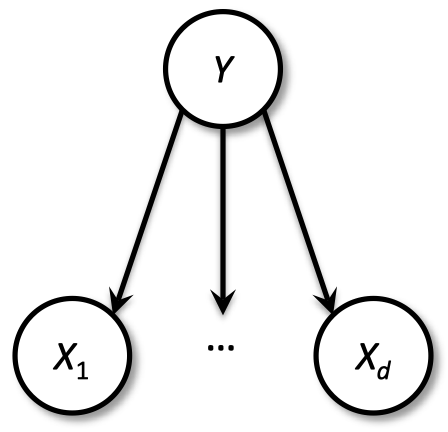
- 根据给定数据选择最有可能的类别
- $\Pr(Y|X_1,…,X_d)=\dfrac{\Pr(Y,X_1,…,X_d)}{\Pr(X_1,…,X_d)}=\dfrac{\Pr(Y,X_1,…,X_d)}{\sum_y\Pr(Y=y,X_1,…,X_d)}$
-
数据 $X|\theta \sim N(\theta,1)$,其中先验 $\theta \sim N(0,1)$ (贝叶斯人)
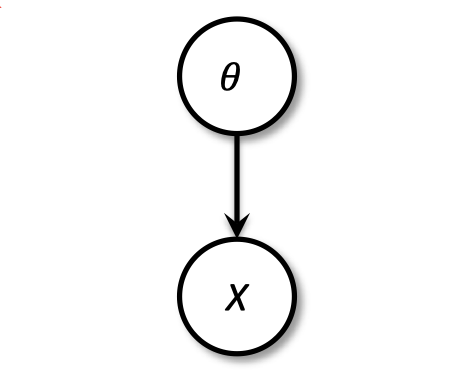
- 给定观测 $X=x$,更新后验
- $\Pr(\theta |X)=\dfrac{\Pr(\theta,X)}{\Pr(X)}=\dfrac{\Pr(\theta,X)}{\sum_{\theta}Pr(\theta,X)}$
- 联合分布 + 贝叶斯规则 + 边缘化 $\to$ 任何东西
1.2 继续 Lecture 16 中核电站的例子
-
问题: 已知警报响了,最终核电站仍然由于高温熔毁的概率是多少?
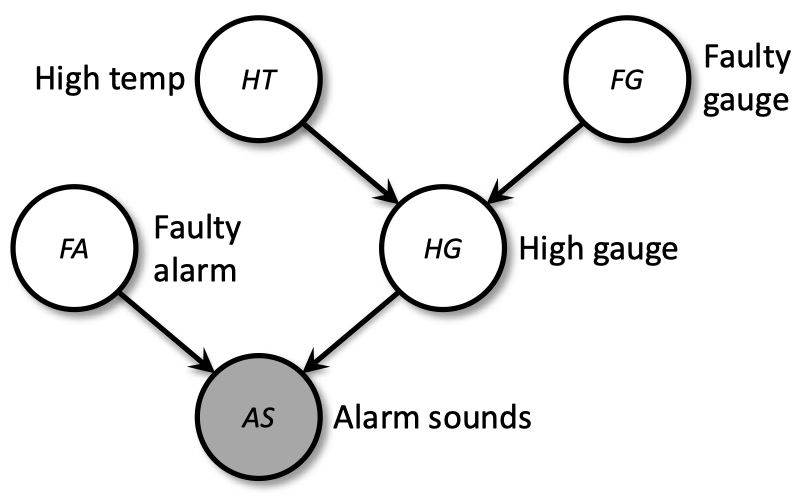
-
需要求解的概率为
\(\begin{align} \Pr(HT|AS=t) &= \dfrac{\Pr(HT,AS=t)}{\Pr(AS=t)} \\ &= \dfrac{\sum_{FG,HG,FA}\Pr(AS=t,FA,HG,FG,HT)}{\sum_{FG,HG,FA,HT'}\Pr(AS=t,FA,HR,FG,HT')}\\ \end{align}\) -
分子部分(分母部分类似)
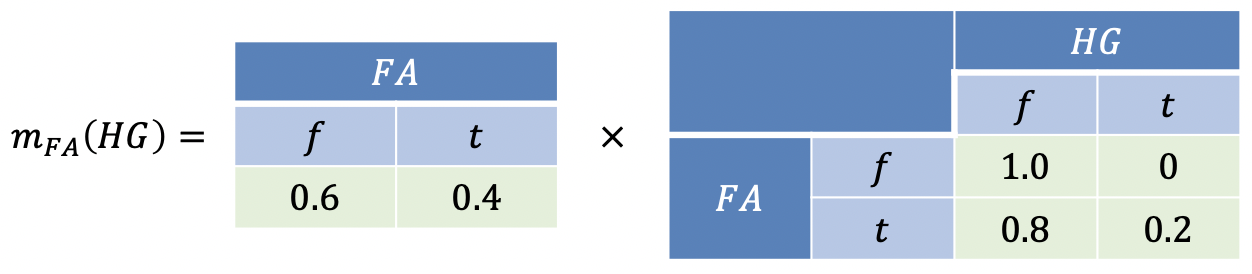
\(\begin{align} & 展开累加求和项,联合 \,\color{red}{2^5 \,个表格的累加求和}\\ &= \sum_{FG}\sum_{HG}\sum_{FA}\Pr(HT)\Pr(HG|HT,FG)\Pr(FG)\Pr(AS=t|FA,HG)\Pr(FA) \\\\ & 将累加求和分配到 \color{red}{\,尽可能小的几张表上}\\ &= \Pr(HT)\sum_{FG}\Pr(FG)\sum_{HG}\Pr(HG|HT,FG)\sum_{FA}\Pr(FA)\color{red}{\Pr(AS=t|FA,HG)}\\ & \color{red}{消除 \,AS}:由于\, AS \,为已观测到的变量,所以实际上无需操作\\\\ &= \Pr(HT)\sum_{FG}\Pr(FG)\sum_{HG}\Pr(HG|HT,FG)\sum_{FA}\color{red}{\Pr(FA)m_{AS}(FA,HG)}\\ & \color{red}{消除 \,FA}:将 \,1\times 2\,的表格和 \,2\times 2\,的表格相乘\\\\ &= \Pr(HT)\sum_{FG}\Pr(FG)\sum_{HG}\color{red}{\Pr(HG|HT,FG)m_{FA}(HG)}\\ & \color{red}{消除 \,HG}:将 \,2\times 2\times 2\,的表格和 \,2\times 1\,的表格相乘\\\\ &= \Pr(HT)\sum_{FG}\color{red}{\Pr(FG)m_{hg}(HT,FG)}\\ & \color{red}{消除 \,FG}:将 \,1\times 2\,的表格和 \,2\times 2\,的表格相乘\\\\ &= \Pr(HT)m_{FG}(HT) \end{align}\)
表格相乘,然后相加,实际上相当于矩阵乘法:
1.3 消除算法

1.4 消除算法的运行时
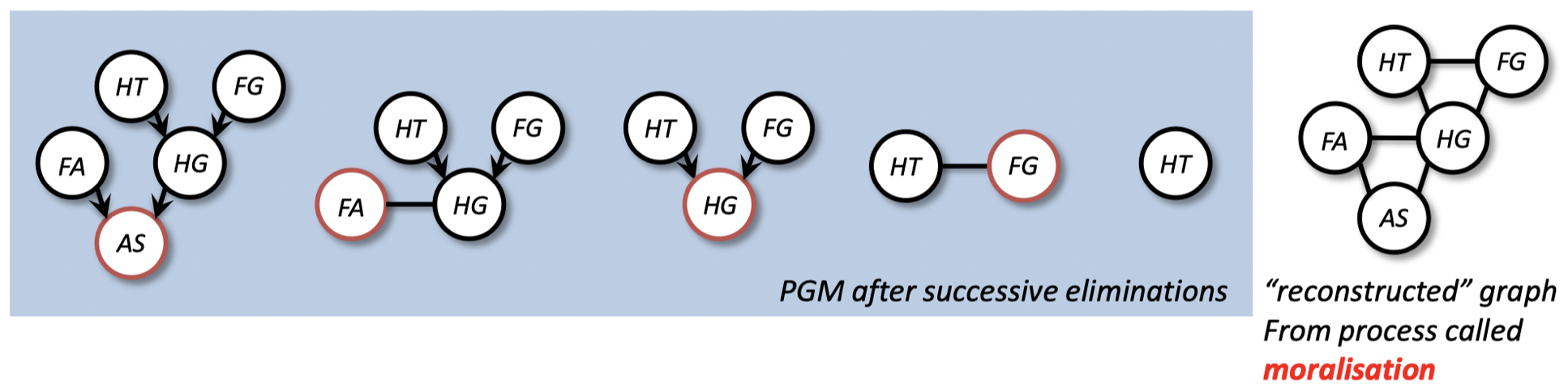
- 在消除的每一步
- 移除一个节点
- 连接该节点剩下的相邻节点 $\to$ 在 “重构的” 图中 形成一个 clique(cliques 就是包含在每个累加求和里的随机变量)
- 最大 clique 中的时间复杂度是 指数级的
- 不同的消除顺序将产生不同的 cliques
- 树的宽度:最大 clique 顺序的最小值
- 最好的可能的时间复杂度与树的宽度呈指数关系
1.5 通过模拟进行概率推断
- 精确的概率推断可能(在计算上)成本高昂 / 不可能实现
- 我们可以对其在数值上近似求解吗?
- 思路:抽样方法
- 从所需分布中获取样本(计算成本低)
-
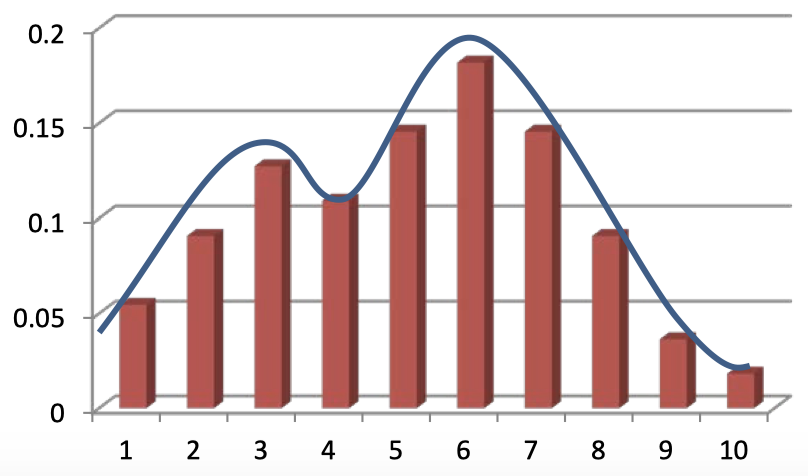
通过 样本直方图 得到概率的 近似分布
1.6 蒙特卡洛近似概率推断
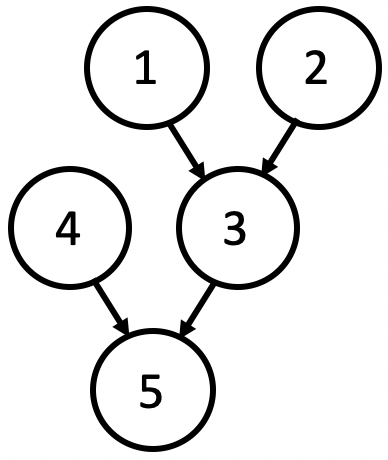
-
算法:从联合分布中采样一次
1.$\,$在子节点之前,先对父母节点排序(拓扑排序)
2.$\,$重复:
$\qquad$ a. 对于每个节点 $X_i$:
$\qquad \qquad$ I.$\;$ 用父母节点的值来索引到 $\Pr(X_i|parents(X_i))$
$\qquad \qquad$ II. 从该分布中采样 $X_i$
$\qquad$ b. 合并后的 $\boldsymbol X=(X_1,…,X_d)$ 是一个来自联合分布的样本 -
算法:从 $\Pr(X_Q|X_E=x_E)$ 中采样
1.$\,$在子节点之前,先对父母节点排序
2.$\,$初始化一个空集 $S$,重复:
$\qquad$ a. 从联合分布中采样 $\boldsymbol X$
$\qquad$ b. 如果 $X_E=x_E$,那么将 $X_Q$ 加进 $S$
3.$\,$返回:$S$ 的直方图,通过除以 $|S|$ 对数量进行归一化 -
其他采样方法:Importance weighting 采样、Gibbs 采样、Metropolis-Hastings 采样
1.7 概率推断的替代形式
- 消除算法产生单个边缘化
- 树上的 和-积 算法
- 2 倍的成本,满足所有边缘化
- 名称:边缘化只是表格 乘积的累加求和
- “完全相同” 的变体:最大乘积,用于MAP 估计
- 总的来说,这些都属于 消息传递算法
- 可以推广到树以外(超出范围):连接树算法、循环信念传播
- 变分贝叶斯:通过优化进行近似
2. PGM 的统计推断
从数据中学习 —— 用概率表对观测值进行拟合(例如,作为一个频率学家;一个贝叶斯人可能仅仅使用概率推断来将先验更新为后验)
2.1 重新梳理一下
- 联合概率的表示
- PGM 编码了条件独立性
- 独立性,d-分割
- 概率推断
- 根据联合分布计算其他分布
- 消除算法、采样算法
- 统计推断
- 从数据中学习参数
2.2 给定 PGM 和一些观测,表格未知
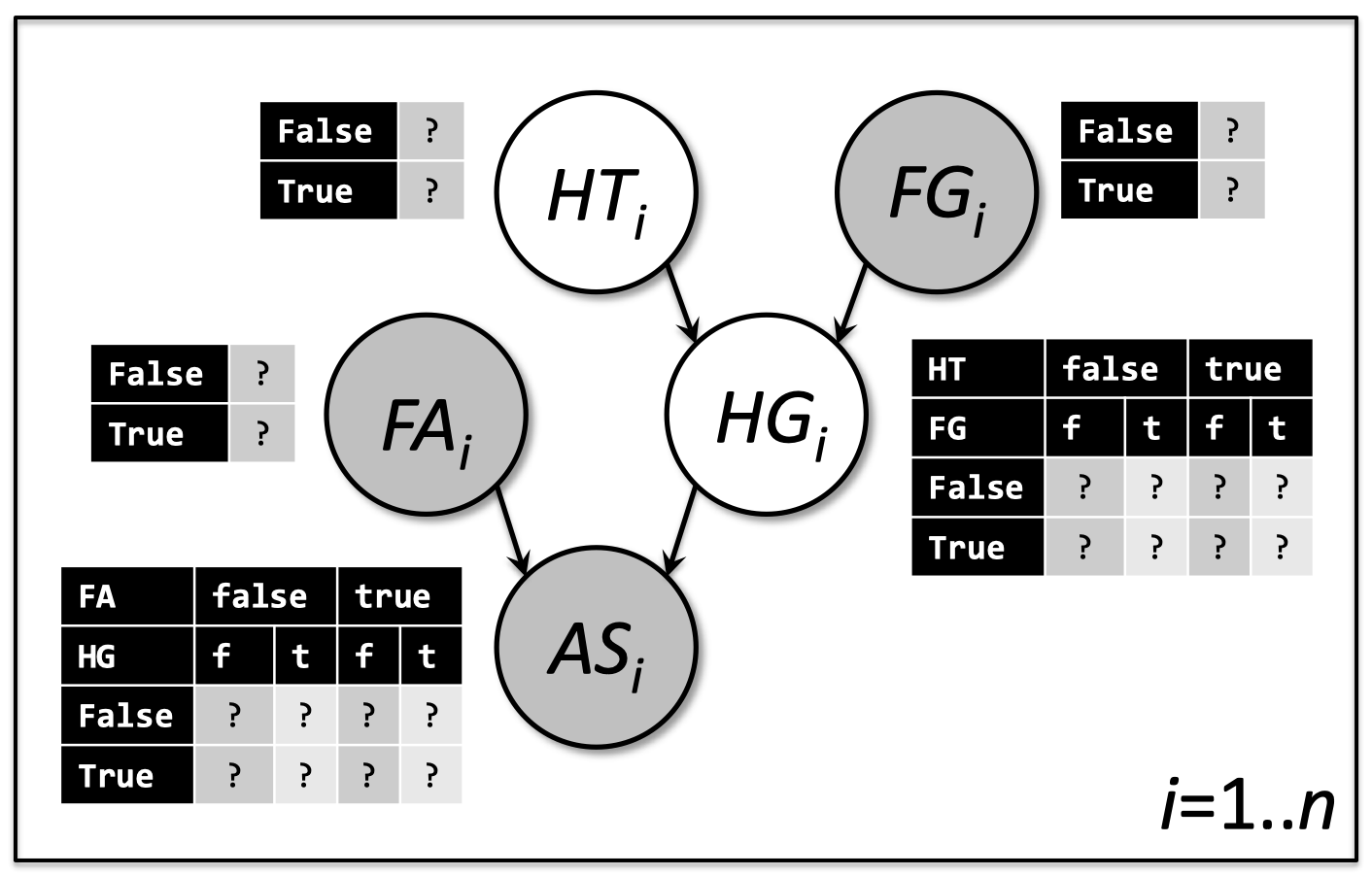
2.3 完全观测的情况比较简单
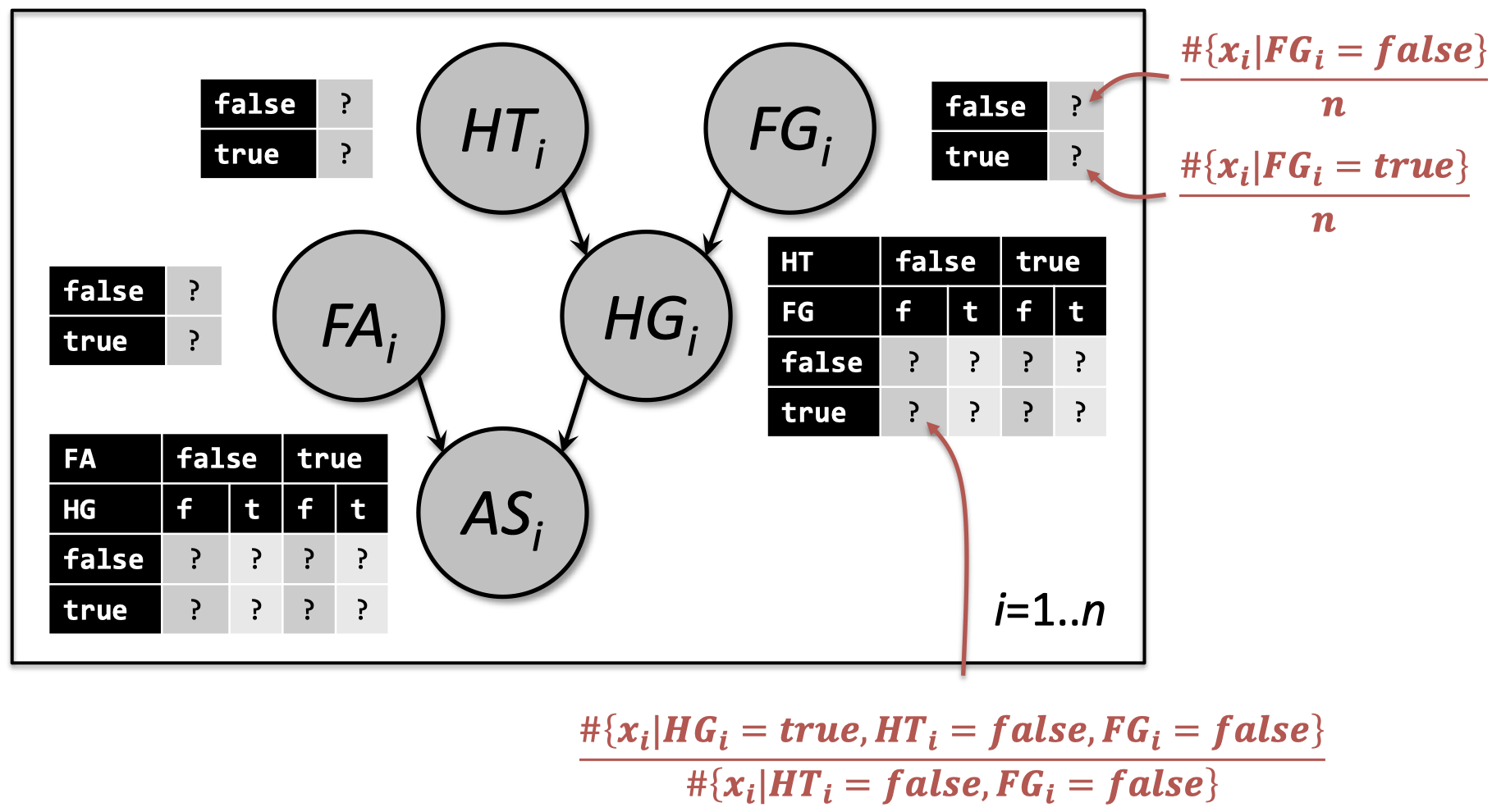
- 最大似然估计(MLE)表明
- 如果在一个 PGM 中,我们可以观测到 所有的 随机变量 $\boldsymbol X$,进行 $n$ 次独立观测 $\boldsymbol x_i$
-
那么,最大化 完全的 联合分布
\[\mathop{\operatorname{arg\,max}}\limits_{\theta \in \Theta}\prod_{i=1}^{n}\prod_{j}p\left(X^j=x_i^j|X^{parents(j)}=x_i^{parents(j)}\right)\]
- 容易分解,推导出基于计数的估计
-
用最大化对数似然替代,转化为求对数的和
\[\mathop{\operatorname{arg\,max}}\limits_{\theta \in \Theta}\sum_{i=1}^{n}\sum_{j}\log p\left(X^j=x_i^j|X^{parents(j)}=x_i^{parents(j)}\right)\] -
将一个所有参数一起的最大化的大问题,分解为几个小的独立问题
-
- 例如,训练一个朴素贝叶斯分类器
2.4 例子:完全观测的情况
2.5 不可观测变量的存在更加棘手

- 但是,我们以后将碰到的大部分 PGM 都会包含 隐变量 或者 未观测到的变量
- 这种情况下,MLE 会导致什么问题?
- 只能最大化观测数据的似然函数
- 通过边缘化完全联合分布来得到我们所期望的 “部分” 联合分布
- $\,$
\(\mathop{\operatorname{arg\,max}}\limits_{\theta \in \Theta}\prod_{i=1}^{n}\sum_{\text{latent } j}\prod_{j}p\left(X^j=x_i^j|X^{parents(j)}=x_i^{parents(j)}\right)\)
$\,$ - 上面这个式子不能被分解
- 解决方法:使用 EM 算法
总结
- PGM 的概率推断
- 什么是 PGM 的概率推断?我们为什么要研究它?
- 消除算法;用 cliques 量化复杂度
- 蒙特卡洛方法作为精确积分的近似替代
- PGM 的统计推断
- 什么是 PGM 的统计推断?我们为什么要研究它?
- 对于完全观测数据,直接使用 MLE
- 对于 隐变量 / 观测变量混合的数据,使用 EM 算法
下节内容:高斯混合模型(GMM)和期望最大化(EM)
本作品采用知识共享署名-非商业性使用-相同方式共享 4.0 国际许可协议进行许可。 欢迎转载,并请注明来自:YEY 的博客 同时保持文章内容的完整和以上声明信息!