Lecture 00-02 数值优化基础
参考资料:Natural Language Processing: Appendix B (p.485-488) —— by Eisenstein, Jacob
引言
无约束数值优化涉及到求解具有以下形式的问题:
\[\min \limits_{\boldsymbol x\in \mathbb R^D}f(\boldsymbol x) \tag{1}\]其中,$x\in \mathbb R^D$ 是一个由 $D$ 个实数构成的向量。
微分是数值优化的基础。假设在某个点 $\boldsymbol x^*$ 处,$f$ 的每个偏导数都等于 $0$:形式上,$\left. \frac{\partial f}{\partial x_i}\right| _{\boldsymbol x^*}=0$。那么 $\boldsymbol x^*$ 被称为 $f$ 的一个 临界点。 如果 $f$ 是一个 凸函数,那么 $f(\boldsymbol x^*)$ 的值等于 $f$ 的全局最小值,当且仅当 $\boldsymbol x^*$ 是 $f$ 的临界点时。
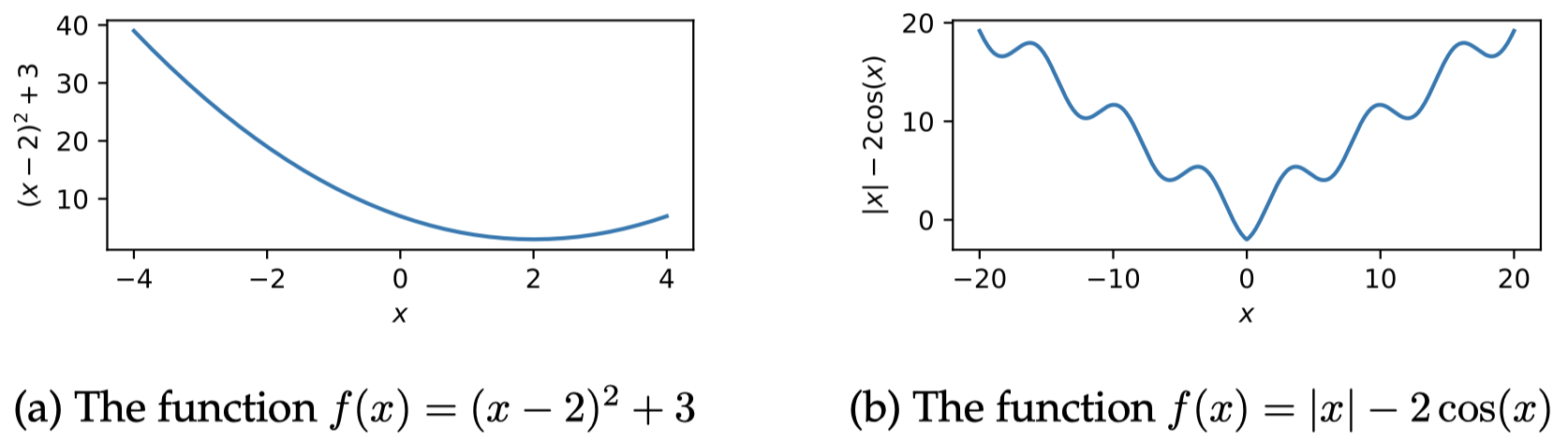
例如,考虑一个凸函数 $f(x)=(x-2)^2+3$,如 图 1(a) 所示。其导数为 $\frac{\partial f}{\partial x}=2x-4$。通过将导数设置为零并求解 $x$,可以得到一个唯一的最小值 $x^* = 2$。现在考虑一个多元凸函数 $f(\boldsymbol x)=\frac{1}{2}\|\boldsymbol x-[2,1]^{\mathrm{T}}\|^2$ ,其中 $\|\boldsymbol x \|^2$ 是平方欧几里得范数。偏导数为:
\[\dfrac{\partial d}{\partial x_1}=x_1-2 \tag{2}\] \[\dfrac{\partial d}{\partial x_2}=x_2-1 \tag{3}\]唯一最小值为 $\boldsymbol x^*=[2,1]^{\mathrm{T}}$。
对于非凸函数,临界点不一定是全局最小值。一个局部最小值 $\boldsymbol x^*$ 意味着函数在该点处的取值小于在其所有近邻点的取值:形式上,$\boldsymbol x^*$ 是一个局部最小值,如果存在某个正值 $\epsilon$ 使得 $f(\boldsymbol x^*)\le f(\boldsymbol x)$ 对于所有和 $\boldsymbol x^*$ 距离在 $\epsilon$ 以内的 $\boldsymbol x$ 都成立。图 1(b) 描绘了函数 $f(x)=|x|-2\cos(x)$,它具有许多局部最小值,并且在 $x = 0$ 处还具有一个唯一的全局最小值。临界点也可以是函数的局部最大值或者全局最大值;它也可以是一个 鞍点,至少在一个坐标方向上是最小值,而在至少一个其余的坐标方向上是最大值;它还可以是一个 拐点,既不是最小值,也不是最大值。如果可以的话,$f$ 的二阶导数可以帮助区分这些情况。
1. 梯度下降
对于许多凸函数,我们不可能求得 $\boldsymbol x^*$ 的闭合解。在梯度下降中,我们计算一系列的解,$\boldsymbol x^{(0)},\boldsymbol x^{(1)},…$ 方法是通过沿着局部梯度 $\nabla_{\boldsymbol x^{(t)}}f$ 的方向一步步前进,这里的梯度是在点 $\boldsymbol x^{(t)}$ 处求得的函数 $f$ 的偏导数构成的向量。每个解 $\boldsymbol x^{(t+1)}$ 可以根据下式计算得到:
\[\boldsymbol x^{(t+1)} \leftarrow \boldsymbol x^{(t)} - \eta^{(t)}\nabla_{\boldsymbol x^{(t)}}f \tag{4}\]其中,$\eta^{(t)}>0$ 是一个 步长。如果适当选择步长,那么此过程将会找到一个可微凸函数的全局最小值。对于非凸函数,梯度下降将找到一个局部最小值。
2. 约束优化
很多时候,优化必须在约束条件下进行:例如,当对一个概率分布的参数进行优化时,所有事件的概率之和必须等于 $1$。约束优化问题可以写成如下形式:
\[\min \limits_{\boldsymbol x}f(\boldsymbol x) \tag{5}\] \[\text{s.t.} \quad g_c(\boldsymbol x)\le 0,\qquad \forall c=1,2,...,C \tag{6}\]其中,每个 $g_c(\boldsymbol x)$ 都是 $\boldsymbol x$ 的一个标量函数。例如,假设 $\boldsymbol x$ 必须为非负,并且其总和不能超过预设的 $b$。然后,存在 $D+1$ 个不等式约束:
\[\begin{align} g_i(\boldsymbol x) &= -x_i,\qquad \forall i=1,2,...,D \tag{7}\\ g_{D+1}(\boldsymbol x) &= -b+\sum_{i=1}^{D}x_i \tag{8} \end{align}\]不等式约束可以与原始目标函数 $f$ 结合起来,这可以通过构造一个 拉格朗日方程 实现:
\[L(\boldsymbol x,\boldsymbol \lambda)=f(\boldsymbol x)+\sum_{c=1}^{C}\lambda_c g_c(\boldsymbol x) \tag{9}\]其中,$\lambda_c$ 是一个 拉格朗日乘子。对于任何拉格朗日函数,都存在一个对应的对偶形式,它是一个关于 $\boldsymbol \lambda$ 的函数:
\[D(\boldsymbol \lambda)=\min \limits_{\boldsymbol x} L(\boldsymbol x,\boldsymbol \lambda) \tag{10}\]我们可以将拉格朗日函数 $L$ 称为问题的原始形式。
3. 例子:被动攻击在线学习
有时可以通过改造拉格朗日方程来解决约束优化问题。一个例子是朴素贝叶斯概率模型的最大似然估计。在这种情况下,不必显式计算拉格朗日乘子。另一个例子是用于在线学习的 被动攻击算法(passive-aggressive algorithm)(Crammer 等,2006)。该算法与感知器类似,但其在每一步的目标是进行最保守的更新,使得当前样本上的边缘损失为零。(这是该算法名称的基础:当损失为零时它是被动的,但在必要时会主动出击使损失为零。)每次更新都可以表述为一个权重 $\boldsymbol \theta$ 上的约束优化:
\[\min \limits_{\boldsymbol \theta}\dfrac{1}{2}\|\boldsymbol \theta-\boldsymbol \theta^{(i-1)}\|^2 \tag{11}\] \[\text{s.t.}\quad \ell^{(i)}(\boldsymbol \theta)=0 \tag{12}\]其中,$\boldsymbol \theta^{(i-1)}$ 是先前的权重集合,$\ell^{(i)}(\boldsymbol \theta)$ 是实例 $i$ 上的边缘损失。该损失定义为:
\[\ell^{(i)}(\boldsymbol \theta)=1-\boldsymbol \theta \cdot \boldsymbol f(\boldsymbol x^{(i)},y^{(i)})+\max \limits_{y\ne y^{(i)}}\boldsymbol \theta \cdot \boldsymbol f(\boldsymbol x^{(i)},y) \tag{13}\]当 $\boldsymbol \theta^{(i-1)}$ 的边缘损失为零时,最优解为 $\boldsymbol \theta^*= \boldsymbol \theta^{(i-1)}$,因此,我们将主要关注 $\ell^{(i)}(\boldsymbol \theta^{(i-1)})>0$ 的情况。该问题的拉格朗日方程为:
\[L(\boldsymbol \theta,\lambda)=\dfrac{1}{2}\|\boldsymbol \theta-\boldsymbol \theta^{(i-1)}\|^2 + \lambda \ell^{(i)}(\boldsymbol \theta) \tag{14}\]保持 $\lambda$ 不变,我们可以通过微分来求解 $\boldsymbol \theta$:
\[\nabla_{\boldsymbol \theta}L=\boldsymbol \theta-\boldsymbol \theta^{(i-1)}+\lambda \dfrac{\partial}{\partial \boldsymbol \theta}\ell^{(i)}(\boldsymbol \theta) \tag{15}\] \[\boldsymbol \theta^*=\boldsymbol \theta^{(i-1)}+\lambda \boldsymbol \delta \tag{16}\]其中,$\boldsymbol \delta=\boldsymbol f(\boldsymbol x^{(i)},y^{(i)})-\boldsymbol f(\boldsymbol x^{(i)},\hat y)$,并且 $\hat y=\mathop{\operatorname{arg\,max}}_{y\ne y^{(i)}}\boldsymbol \theta \cdot \boldsymbol f(\boldsymbol x^{(i)},y)$
拉格朗日乘子 $\lambda$ 的作用相当于感知器中更新 $\boldsymbol \theta$ 的学习率。我们可以通过将 $\boldsymbol \theta^*$ 回代入拉格朗日方程中,得到对偶函数来求解 $\lambda$:
\[\begin{align} D(\lambda) &= \dfrac{1}{2}\|\boldsymbol \theta^{(i-1)}+\lambda \boldsymbol \delta -\boldsymbol \theta^{(i-1)}\|^2+\lambda \left(1-(\boldsymbol \theta^{(i-1)}+\lambda \boldsymbol \delta)\cdot \boldsymbol \delta \right) \tag{17}\\ &= \dfrac{\lambda^2}{2}\|\boldsymbol \delta\|^2-\lambda^2 \|\boldsymbol \delta\|^2 +\lambda (1-\boldsymbol \theta^{(i-1)}\cdot \boldsymbol \delta) \tag{18}\\ &= -\dfrac{\lambda^2}{2}\|\boldsymbol \delta\|^2+\lambda \ell^{(i)}(\boldsymbol \theta^{(i-1)}) \tag{19} \end{align}\]微分,求解 $\lambda$:
\[\dfrac{\partial D}{\partial \lambda}=-\lambda\|\boldsymbol \delta\|^2+ \ell^{(i)}(\boldsymbol \theta^{(i-1)}) \tag{20}\] \[\lambda^*=\dfrac{\ell^{(i)}(\boldsymbol \theta^{(i-1)})}{\|\boldsymbol \delta\|^2} \tag{21}\]因此,完整的更新公式为:
\[\boldsymbol \theta^*=\boldsymbol \theta^{(i-1)}+\dfrac{\ell^{(i)}(\boldsymbol \theta^{(i-1)})}{\|\boldsymbol f(\boldsymbol x^{(i)},y^{(i)})-\boldsymbol f(\boldsymbol x^{(i)},\hat y)\|^2}\left(\boldsymbol f(\boldsymbol x^{(i)},y^{(i)})-\boldsymbol f(\boldsymbol x^{(i)},\hat y)\right) \tag{22}\]该学习率具有直觉上的意义。分子随着损失函数增长。分母随着特征向量与正确标签和预测标签相关的特征函数之差的范数增长。如果此范数较大,则针对每个特征的步长应较小,反之亦然。
下节内容:线性分类器
本作品采用知识共享署名-非商业性使用-相同方式共享 4.0 国际许可协议进行许可。 欢迎转载,并请注明来自:YEY 的博客 同时保持文章内容的完整和以上声明信息!