Lecture 03 N-gram 语言模型

1. 引言

本节课我们将学习 语言模型（Language Models），我们之前在第 1 节课中提到过它。

为什么我们关心语言模型？

因为 NLP 中有很大一部分研究都是关于如何 解释语言（explaining language） 的。

为什么有些句子比其他句子更 流畅（fluent），或者说 更自然（natural）？
我们为什么关心这个问题呢？
因为在很多应用中，我们很关心语言的流畅性与自然性。
例如，在语音识别中，你听到一句话，并且想将它转换成文本，所以你需要区分这段语音可能对应的不同文本，并从中选择更加流畅和自然的版本。比如下面两个句子的发音很接近：
\[\textit{recognise speech > wreck a nice beach}\]
从流畅和自然的角度考虑，显然，左边的句子更有可能代表了讲话者的本意。而语言模型可以帮你做到这一点，它会告诉你 “recognise speech” 是人们更倾向表达的意思。
那么，我们如何衡量这种 “优度（goodness）”（或者说流畅度、自然度）呢？
我们用概率来衡量它，而语言模型提供了一种很自然的方式来估计句子的概率。
在此基础上，一旦你构建了一个语言模型，你还可以用它来 生成（generation） 语言。

如果你还有印象，我们之前提到过这个名为 Talk to Transformer 的网站。现在，我们尝试通过这个小的语言模型来完成一个段落。我们在用户输入提示框中输入一句话：“Today we have a lecture on Natural Language Processing.” 然后点击 GENERATE ANOTHER 按钮，我们将看到这个在线语言模型自动生成了一些看上去相当不错的相关段落：

语言模型可以用于哪些任务呢？

主要用于：
- 语音识别（Speech recognition）
- 拼写纠错（Spelling correction）
- 查询补全（Query completion）
- 光学字符识别（Optical character recognition）
其他生成任务：
- 机器翻译（Machine translation）
- 概括（Summarisation）
- 对话系统（Dialogue systems）

本节课程大纲

推导 n-gram 语言模型
平滑（Smoothing）处理稀疏性（sparsity）
生成语言
评估语言模型

2. N-gram 语言模型

2.1 概率：从联合概率到条件概率

我们的目标是得到一个由 $m$ 个单词组成的任意序列（即一个包含 $m$ 个单词的句子）的概率：

\[P(w_1,w_2,\dots,w_m)\]

第一步是利用链式法则（chain rule）将联合概率转换成条件概率的连乘形式：

\[P(w_1,w_2,\dots,w_m)=P(w_1)P(w_2\mid w_1)P(w_3\mid w_1,w_2)\cdots P(w_m\mid w_1,\dots,w_{m-1})\]

2.2 马尔可夫假设（The Markov Assumption）

目前，这仍然是一个比较棘手的问题，因为随着上下文的不断增加，我们构建的模型中将包含越来越多的参数。所以这里，我们采用一种称为 “马尔可夫假设” 的简化假设：某个单词出现的概率不再依赖于全部上下文，而是取决于离它最近的 $n$ 个单词。因此，我们得到：

\[P(w_i\mid w_1,\dots,w_{i-1})\approx P(w_i\mid w_{i-n+1},\dots,w_{i-1})\]

对于某个很小的 $n$：

当 $n=1$ 时，一个 unigram 模型：
\[P(w_1,w_2,\dots,w_m)=\prod_{i=1}^{m}P(w_i)\]
在 unigram 模型中，我们假设一个句子出现的概率等于其中每个单词单独出现的概率的乘积，这意味着每个单词出现的概率之间相互独立，即我们并不关心每个单词的上下文。
当 $n=2$ 时，一个 bigram 模型：
\[P(w_1,w_2,\dots,w_m)=\prod_{i=1}^{m}P(w_i\mid w_{i-1})\]
在 bigram 模型中，我们假设句子中每个单词出现的概率都和它前一个单词出现的概率有关。
当 $n=3$ 时，一个 trigram 模型：
\[P(w_1,w_2,\dots,w_m)=\prod_{i=1}^{m}P(w_i\mid w_{i-2},w_{i-1})\]
在 trigram 模型中，我们假设句子中每个单词出现的概率都和它前两个单词出现的概率有关。

2.3 最大似然估计

我们如何计算这些概率？

非常简单，我们只需要一个大的用于训练的语料库（corpus），然后我们就可以根据语料库中各个单词的计数（counts），利用最大似然估计来估计该单词出现的概率：

对于 unigram 模型：
\[P(w_i)=\dfrac{C(w_i)}{M}\]
其中，$C$ 是一个计数函数，$C(w_i)$ 表示单词 $w_i$ 在语料库中出现的次数，$M$ 表示语料库中所有单词 tokens 的数量。
对于 bigram 模型：
\[P(w_i\mid w_{i-1})=\dfrac{C(w_{i-1},w_i)}{C(w_{i-1})}\]
其中，$C(w_{i-1},w_i)$ 表示单词 $w_{i-1}$ 和单词 $w_i$ 前后相邻一起出现的次数。
对于 n-gram 模型：
\[P(w_i\mid w_{i-n+1},\dots,w_{i-1})=\dfrac{C(w_{i-n+1},\dots,w_i)}{C(w_{i-n+1},\dots,w_{i-1})}\]
同理，我们计算 n-gram 出现的次数，除以 (n-1)-gram（即上下文）出现的次数。

2.4 序列的开头和结尾表示

在我们进入例子之前，我们需要用一些特殊的记号表示一个序列的开始和结束：

$\texttt{<s>}$ 表示句子的开始（对应于课本 E18 中的 $\square$）
$\texttt{</s>}$ 表示句子的结束（对应于课本 E18 中的 $\blacksquare$）

2.5 Trigram 例子

现在，让我们来看一个玩具例子，假设我们有一个只包含两个句子的语料库。

语料库：
$\texttt{<s> <s> } \textit{yes no no no no yes}\texttt{ </s>}$
$\texttt{<s> <s> } \textit{no no no yes yes yes no}\texttt{ </s>}$

可以看到，每个句子开头有两个起始标记，因为我们采用的是 trigram 模型。
我们希望知道下面的句子在一个 trigram 模型下的概率是多少？
\[\texttt{<s> <s> } \textit{yes no no yes}\texttt{ </s>}\] \[\begin{align} P(\text{sent} =\textit{yes no no yes}) &= P(\textit{yes}\mid \texttt{<s>},\texttt{<s>})\times P(\textit{no}\mid \texttt{<s>},\textit{yes})\times P(\textit{no}\mid \textit{yes},\textit{no})\\ &\quad \times P(\textit{yes}\mid \textit{no},\textit{no}) \times P(\texttt{</s>} \mid \textit{no},\textit{yes})\\ &= \dfrac{1}{2} \times 1 \times \dfrac{1}{2} \times \dfrac{2}{5} \times \dfrac{1}{2} \\ &= 0.1 \end{align}\]
说明：
- 首先，我们对要计算的句子的概率按照 trigram 模型拆分成条件概率的连乘形式。
- 然后，对于等式右边的每一个条件概率项，按照 trigram 模型中的条件概率计算公式，分别统计 “当前单词连同它的上下文” 以及 “单独的上下文部分” 在语料库中出现的次数，并将两者相除，得到该项的计算结果。
  例如，对于上面等式右边第一个条件概率项，我们考虑句子中第一个单词 “$\textit{yes}$” 及其相邻的 bigram 上下文 “$\texttt{<s>}\, \texttt{<s>}$”：
  \[P(\textit{yes}\mid \texttt{<s>},\texttt{<s>})=\dfrac{C(\texttt{<s>},\texttt{<s>},\textit{yes})}{C(\texttt{<s>},\texttt{<s>})}=\dfrac{1}{2}\]
  可以看到，子序列 “$\texttt{<s>}\, \texttt{<s>} \,\textit{yes}$” 在语料库中只出现过 $1$ 次；而子序列 “$\texttt{<s>} \,\texttt{<s>}$” 在语料库中一共出现了 $2$ 次，所以第一个条件概率项的结果为 $\frac{1}{2}$。其余各条件概率项的计算方式同理，另外请注意，在计算第四个条件概率项时，bigram 上下文 “$\textit{no}\,\textit{no}$” 在语料库中一共出现了 $5$ 次。

2.6 N-gram 语言模型的一些问题

语言通常具有长距离效应 —— 需要设置较大的 $n$ 值
有些词对应的上下文可能出现在句子中距离该词很远的地方，这意味着如果我们采用固定长度的上下文（例如：trigram 模型），我们可能无法捕捉到足够的上下文相关信息。例如：
\[\textit{The }\color{red}{\textit{lecture/s }}\textit{that took place last week } \color{red}{\textit{was/were }}\textit{on processing.}\]
在上面的句子中，假如我们要决定系动词 $be$ 是应该用第三人称单数形式 $was$ 还是复数形式 $were$，我们需要回头看句子开头的主语是 $lecture$ 还是 $lectures$。可以看到，它们之间的距离比较远，如果我们采用 bigram 或者 trigram 模型，我们无法得到相关的上下文信息来告诉我们当前位置应该用 $was$ 还是 $were$。这是所有有限上下文语言模型（finite context language models）的一个通病。
计算出的结果的概率通常会非常小
你会发现，一连串条件概率项连乘得到的结果往往会非常小，对于这个问题，我们可以采用取对数计算 log 概率来避免数值下溢（numerical underflow）。
对于不存在于语料库中的词，无法计算其出现概率
如果我们要计算概率的句子中包含了一些没有在语料库中出现过的单词（例如：人名），我们应该怎么办？
一种比较简单的技巧是，我们可以用某种特殊符号（例如：$\texttt{<UNK>}$）来表示这些所谓的 OOV 单词（out-of-vocabulary，即不在词汇表中的单词），并且将语料库中一些非常低频的单词都替换为这种表示未知单词的特殊 token。
出现在新的上下文（context）中的单词
默认情况下，任何我们之前没有在语料库中见过的 n-gram 的计数都为 $0$，这将导致计算出的 整个句子的概率为 $0$。

这个问题和前面的 OOV 单词的问题类似，我们的语料库中可能已经包含了这些单词，但是并没有包含该单词在新句子中对应的特定的 n-gram（即上下文信息）。这意味着该单词在新的句子中对应 n-gram 对于语言模型来说是全新的，而且因为 n-gram 的组合存在如此多的可能性，以至于语料库很难将所有的可能性都覆盖到。

例如：假设我们构建了一个 five-gram 语言模型，我们的语料库中一共有 20000 个词汇，那么一共存在多少种可能的 five -gram 组合？

答案是：$20000^5$。这是一个非常非常大的数字，以至于无论我们的训练语料库有多大，都不可能捕捉到所有的可能性组合。

这是一个相当常见的问题，并且很重要。如果我们回顾一下链式法则，可以看到所有的条件概率都连乘在一起，所以只要其中某一项在计算子序列时 n-gram 的计数为 $0$，那么最终计算出的整个句子的概率就会为 $0$。

为此，我们需要对语言模型进行 平滑处理（smoothing）。

3. 平滑处理

基本思想：给之前没有见过的事件赋予概率。
必须附加一个约束条件：$P(\text{everything})=1$
有很多不同种类的平滑处理方法：
- 拉普拉斯平滑（Laplacian smoothing，又称 Add-one smoothing，即 “加一” 平滑）
- “加 k” 平滑（Add-k smoothing）
- Jelinek-Mercer 插值（又称线性插值平滑）
- 卡茨回退法（Katz backoff）
- 绝对折扣（Absolute discounting）
- Kneser-Ney
- ……

3.1 拉普拉斯平滑（“加一” 平滑）

简单思想：假装我们看到的每一个 n-gram 都比它们实际出现的次数多 $1$ 次。

这意味着即使是那些我们在语料库中没有见过的 n-gram，我们也将它们出现的次数记为 $1$ 次。所以对于一个新句子中的任何东西都至少有 $1$ 次计数。
对于 unigram 模型（$V=$ 词汇表）：
\[P_{\text{add}1}(w_i)=\dfrac{C(w_i)+1}{M+|V|}\]
在之前的模型中，我们只是简单的计算单词 $w_i$ 在语料库中出现的次数 $C(w_i)$ ，然后除以语料库中所有单词 tokens 的数量 $M$。

现在，对于分子而言，我们总是在它此前的基础上加上 $1$。然后，为了保证它仍然是一个合法的概率分布，即单词 $w_i$ 遍历词汇表中所有可能情况的的概率之和 $\sum_{i=1}^{|V|}P(w_i)=1$，我们需要在此前分母 $M$ 的基础上加上词汇表的长度 $|V|$（即语料库中所有单词 types 的总数）。
对于 bigram 模型：
\[P_{\text{add}1}(w_i\mid w_{i-1})=\dfrac{C(w_{i-1},w_i)+1}{C(w_{i-1})+|V|}\]
同样地，我们在之前分子的基础上加 $1$，在分母的基础上加 $|V|$。

所以现在，我们解决了之前新句子中的未知单词或者 n-gram 的计数为 $0$ 从而导致最终计算出的概率为 $0$ 的问题。接下来，让我们来看一个 “加一” 的例子。

3.2 拉普拉斯（“加一”）平滑的例子

假设现在我们的语料库中只有一个简单的句子：

\[\texttt{<s>} \textit{ the rat ate the cheese } \texttt{</s>}\]

所以，词汇表为：

\[V=\{\textit{the, rat, ate, cheese, }\texttt{</s>}\}\]

也许你会问：为什么词汇表中只包含了特殊结束标记 $\texttt{</s>}$，而没有包含特殊起始标记 $\texttt{<s>}$？
这是因为我们永远不会预测起始标记 $\texttt{<s>}$，起始标记仅仅用于条件概率项中的条件部分。如果你回忆之前的 trigram 的例子，可以发现我们实际上在最后一个条件概率项中预测了（以句子中最后两个单词作为条件时）结束标记 $\texttt{</s>}$ 的概率，但我们从来没有预测过起始标记 $\texttt{<s>}$ 的概率，因此我们不需要为其计数。

所以，在 “加一” 平滑下，bigram 条件概率 $P(\textit{ate}\mid \textit{rat})$ 为：
\[P_{\text{add}1}(\textit{ate}\mid \textit{rat})=\dfrac{C(\textit{rat},\textit{ate})+1}{C(\textit{rat})+|V|}=\color{red}{\dfrac{2}{6}}\]
可以看到，对于分子而言，bigram “$\textit{rat ate}$” 在语料库中出现过 1 次，所以 $C(\textit{rat},\textit{ate})=1$，然后我们在其基础上再加上 $1$，结果为 $2$。对于分母而言，单词 “$\textit{rat}$” 在语料库中出现过 1 次，所以 $C(\textit{rat})=1$，然后我们在其基础上再加上 $|V| = 5$，结果为 $6$。
同理，在 “加一” 平滑下，bigram 条件概率 $P(\textit{ate}\mid \textit{cheese})$ 为：
\[P_{\text{add}1}(\textit{ate}\mid \textit{cheese})=\dfrac{C(\textit{cheese},\textit{ate})+1}{C(\textit{cheese})+|V|}=\color{red}{\dfrac{1}{6}}\]
对于分子而言，“$\textit{cheese ate}$” 从来没有在语料库中出现过，所以 $C(\textit{cheese},\textit{ate})=0$，然后我们在其基础上再加上 $1$，结果为 $1$。对于分母而言，单词 “$\textit{cheese}$” 在语料库中出现过 1 次，所以 $C(\textit{cheese})=1$，然后我们在其基础上再加上 $|V| = 5$，结果为 $6$。所以，通过简单的 “加一” 平滑，我们永远不会遇到计数为 $0$ 的问题。

3.3 “加 k” 平滑

“加一” 往往太多了
但是很多时候，加 $1$ 会显得太多了，我们并不想每次都加 $1$，因为这会导致原本的罕见事件可能变得有点过于频繁了。并且我们丢弃了所观测的 n-gram 的太多有效计数。
用 “加 k” 来代替 “加一”
这种方式也被称为 Lidstone 平滑（Lidstone Smoothing）。
对于 trigram 模型，公式如下：
\[P_{\text{add}k}(w_i\mid w_{i-1},w_{i-2})=\dfrac{C(w_{i-2},w_{i-1},w_{i})+k}{C(w_{i-2},w_{i-1})+k|V|}\]
可以看到，和 “加一” 平滑类似，只是我们将分子中的加 $1$ 变成了加 $k$，并且为了满足单词 $w_i$ 遍历词汇表中所有可能情况的概率之和为 $1$，我们在分母中的 $|V|$ 前面乘了一个系数 $k$。
必须选择一个 $k$
事实上，如何选择一个合适的 $k$ 值对于模型影响非常大。$k$ 在这里实际上是一个超参数，我们需要尝试对其进行调整以便找到一个使模型表现比较好的 $k$ 值。

3.4 Lidstone 平滑（“加 k”）的例子

现在，让我们来看一个简单的例子：

context $= \textit{alleged}$
$5$ observed bi-grams
$2$ unobserved bi-grams

表 1：Lidstone 平滑（“加k” 平滑）的例子

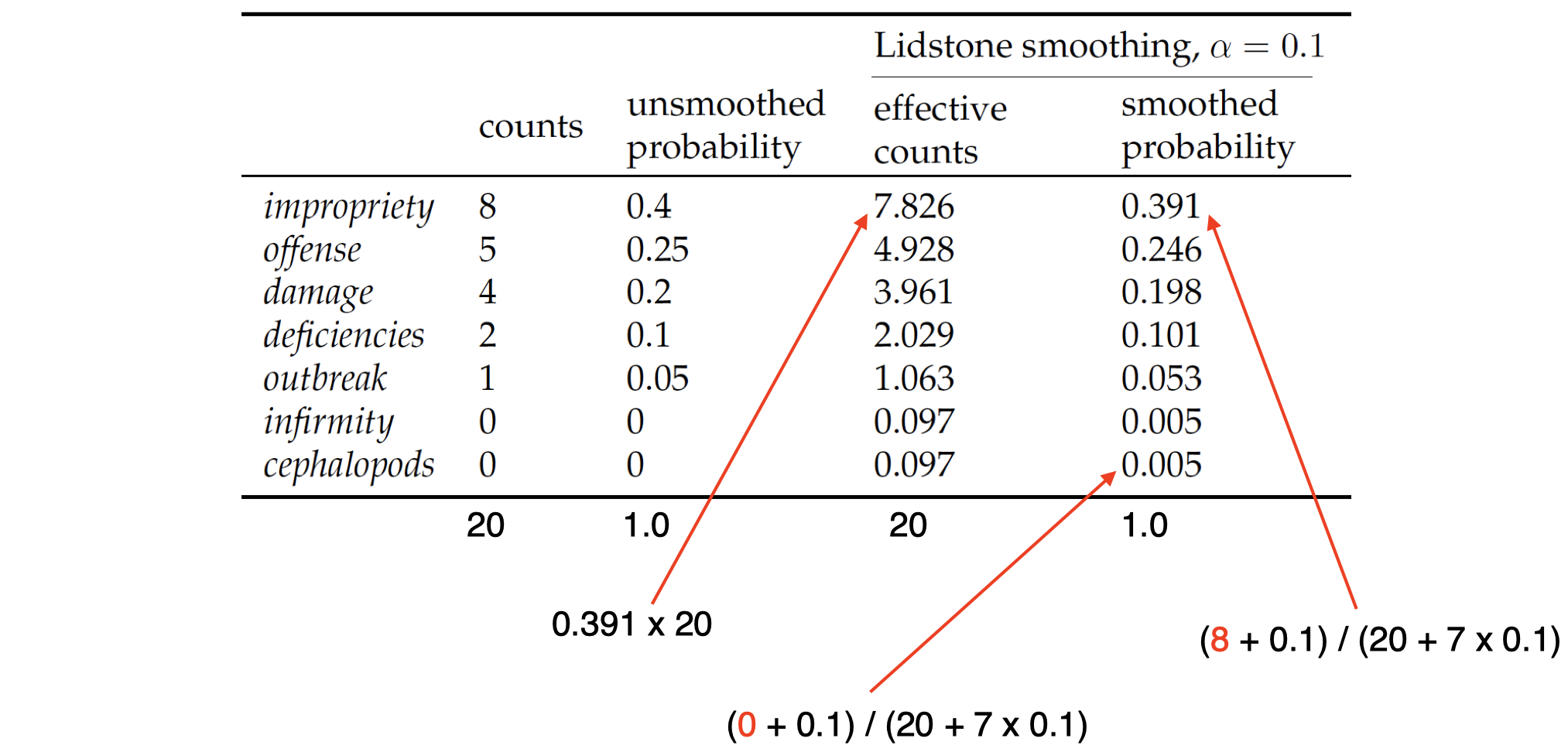
假设我们收集了一些 bi-grams，其中上下文（context）单词是 “$\textit{alleged}$”，其后面跟随的相邻单词请见表 1 中的第 1 列（例如：“$\textit{impropriety}$”、“$\textit{offense}$” 等，这些词都是出现在 “$\textit{alleged}$” 后面的词）。其中我们有 $5$ 个观测到的 bi-grams（表格中前 5 行，可以看到它们的计数都大于 $0$）和 $2$ 个未观测到的 bi-grams（表格中最后 2 行，也就是说 “$\textit{alleged infirmity}$” 和 “$\textit{alleged cephalopods}$” 这两个 bi-grams 并不在我们的语料库中，所以它们的计数都是 $0$）。

我们希望计算这些 bi-grams 没有经过平滑处理的概率（unsmoothed probability），即表 1 中的第 3 列：我们只需要计算每个 bi-gram 的计数 $\text{counts}$，然后除以上下文 “$\textit{alleged}$” 在语料库中出现的总次数 $20$。例如，对于第一个 bi-gram “$\textit{alleged impropriety}$”，其未平滑概率为：

\[P(\textit{impropriety}\mid \textit{alleged}) = \dfrac{C(\textit{alleged}, \textit{impropriety})}{C(\textit{alleged})}= \dfrac{8}{20}= 0.4\]

假如我们希望计算这些 bi-grams 的 平滑概率（smoothed probability），即表 1 的最后一列：我们只需要在前面未平滑概率的基础上，对分子加上一个 Lidstone 平滑系数 $\alpha=0.1$（即 “加 k” 平滑中的 $k$），对分母加上一个词汇表长度 $|V|=7$ 和平滑系数 $\alpha=0.1$ 的乘积。例如，对于上面的 bi-gram “$\textit{alleged impropriety}$”，其平滑概率为：：

\[P_{\text{add}k}(\textit{impropriety}\mid \textit{alleged}) = \dfrac{C(\textit{alleged}, \textit{impropriety})+\alpha}{C(\textit{alleged})+|V|\times \alpha}= \dfrac{\color{red}{8}+0.1}{20+7\times 0.1}= 0.391\]

注意，这里词汇表为：

\[V=\{\textit{impropriety},\textit{offense},\textit{damage},\textit{deficiencies},\textit{outbreak},\textit{infirmity},\textit{cephalopods}\}\]

其长度为 $|V|=7$。

同理，对于最后一行中未观测到的 bi-gram “$\textit{alleged cephalopods}$”，其概率为：

\[P_{\text{add}k}(\textit{cephalopods}\mid \textit{alleged}) = \dfrac{C(\textit{alleged}, \textit{cephalopods})+\alpha}{C(\textit{alleged})+|V|\times \alpha}= \dfrac{\color{red}{0}+0.1}{20+7\times 0.1}= 0.005\]

另外，表格中第 4 列的 “$\text{effective counts}$”（有效计数）等于其平滑概率乘以上下文 “$\textit{alleged}$” 在语料库中出现的总次数。例如，对于第一个 bi-gram “$\textit{alleged impropriety}$”，其有效计数为：

\[\begin{align}C_{\text{effect-add}k}(\textit{alleged}, \textit{impropriety}) &= P_{\text{add}k}(\textit{impropriety}\mid \textit{alleged})\times C(\textit{alleged})\\\\ &=0.391\times 20=7.826 \end{align}\]

所以，从效果上来看，我们可以看到在经过平滑处理后，第一个 bi-gram “$\textit{alleged impropriety}$” 的计数由原来的 $8$ 移动到了 $7.826$，而第二个 bi-gram “$\textit{alleged offense}$” 的计数由原来的 $5$ 移动到了 $4.928$，其余的 bi-grams 同理。

3.5 Absolute Discounting 平滑

另外一种更好的方法是采用 绝对折扣平滑（Absolute Discounting）：

从每个 观测到的 n-gram 计数中 “借” 一个 固定的概率质量（a fixed probability mass） $d$。
然后将其 重新分配（redistributes） 到 未知的 n-grams 上。

让我们再回到之前那个例子：

context $= \textit{alleged}$
$5$ observed bi-grams
$2$ unobserved bi-grams

表 2：Lidstone 平滑 vs. Absolute Discounting 平滑

那么，Absolute Discounting 平滑到底是如何工作的呢？

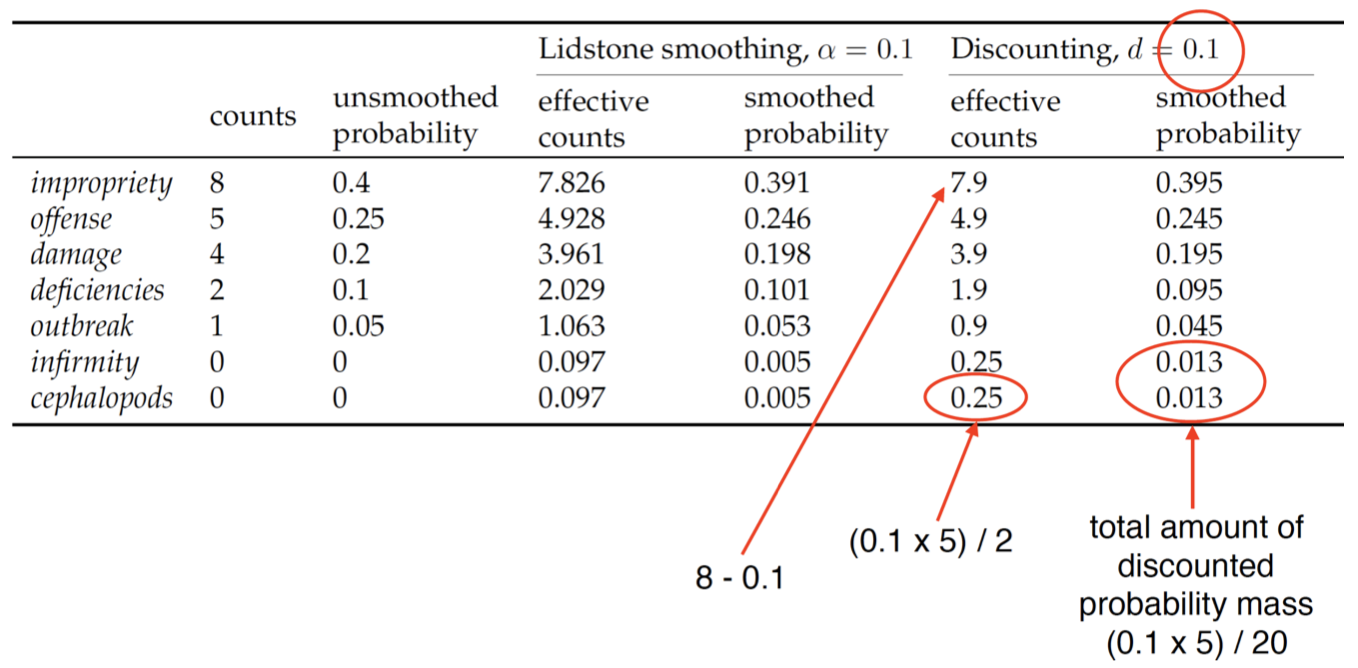
回忆刚才提到过的 有效计数（effective counts），其中第一个 bi-gram “$\textit{alleged impropriety}$” 的计数由原来的 $8$ 减少到了 $7.826$，前后相差 $0.174$。可以看到，对于不同的观测到的bi-grams 的有效计数，它们在原计数的基础上减少的量各不相同，例如对于第二个 bi-gram “$\textit{alleged offense}$” 的计数由原来的 $5$ 减少到了 $4.928$，前后相差只有 $0.072$。

现在，我们不希望看到这样的情况。我们希望 “借到的” 概率质量总是一个 固定的（fixed） 值。在上面表 2 的例子中，我们设置一个 Discounting 系数 $d=0.1$，也是是说我们希望总是从观测到的 n-grams 中 “借” 一个固定的概率质量 $0.1$。所以，这里第一个 bi-gram “$\textit{alleged impropriety}$” 的计数由原来的 $8$ 减少到了 $7.9$，前后相差 $0.1$：

\[C_{\text{effect-AD}}(\textit{alleged}, \textit{impropriety})=C(\textit{alleged}, \textit{impropriety})-d=8-0.1=7.9\]

那么，对于未观测到的 n-grams，我们怎样计算其 Absolute Discounting 平滑的有效计数呢？

其实也很简单，以最后两个未观测到的 bi-grams “$\textit{alleged infirmity}$” 和 “$\textit{alleged cephalopods}$” 为例，我们将 “借” $5$ 次 $0.1$（因为总共有 $5$ 个观测的 bi-grams，我们向其中的每个 bi-gram 都 “借” $0.1$），所以我们会看到 “借到的” 总的概率质量是 $0.5$，然后我们将其平均分配给这两个原始计数为 $0$ 的未知 bi-grams，即每个未观测到的 bi-gram 分配到的有效计数为 $0.25$：

\[\begin{align} C_{\text{effect-AD}}(\textit{alleged}, \textit{infirmity}) &= C_{\text{effect-AD}}(\textit{alleged}, \textit{cephalopods})\\\\ &=\dfrac{5\times d}{2}=\dfrac{5\times 0.1}{2}=0.25 \end{align}\]

然后，和前面的 Lidstone 平滑一样，如果我们想计算 Absolute Discounting 平滑概率，只需要用 Absolute Discounting 平滑下的有效计数除以上下文在语料库中出现的总次数即可。

例如，对于第一个观测到的 bi-gram “$\textit{alleged impropriety}$” 和最后一个未观测到的 bi-gram “$\textit{alleged cephalopods}$”，两者对应的 Absolute Discounting 平滑概率分别为：

\[P_{\text{AD}}(\textit{impropriety}\mid \textit{alleged})=\dfrac{C_{\text{effect-AD}}(\textit{alleged}, \textit{impropriety})}{C(\textit{alleged})}=\dfrac{7.9}{20}=0.395\] \[P_{\text{AD}}(\textit{cephalopods}\mid \textit{alleged})=\dfrac{C_{\text{effect-AD}}(\textit{alleged}, \textit{cephalopods})}{C(\textit{alleged})}=\dfrac{0.25}{20}=0.0125\]

总的来说，我们先计算一个 n-gram 的有效计数，然后再据此计算其对应的平滑概率。在实践中，通常 Absolute Discounting 平滑的效果要比 Lidstone 平滑（“加 k”）的效果好一些。

3.6 Backoff 平滑

基本上，我们会按照不断改进的顺序来介绍各种平滑处理方式的变体，由此，我们可以看到对于这些平滑方式的评估。现在，我们继续介绍另一种更好的平滑方式：Backoff 平滑。

在之前的 Absolute Discounting 平滑中，我们从观测到的每个 n-gram 计数中 “借来” 一个固定的概率质量，并将它们重新平均分配给所有的未知 n-grams。
Katz Backoff：概率质量的重新分配是基于一个 低阶（lower order） 模型（例如：unigram 模型）

例如，假设我们现在有一个 bigram 模型，当我们将概率质量重新分配到未知的 bi-grams 时，我们将基于上下文单词的 unigram 概率进行重新分配。因为比例很简单，如果我们看到上下文出现次数越多，我们就给它更高的权重。

对于一个 bigram 模型，它的 Katz Backoff 平滑的概率公式 如下：

\[P_{\text{katz}}(w_i\mid w_{i-1})=\begin{cases}\dfrac{C(w_{i-1},w_i)-D}{C(w_{i-1})}\;, & \text{if } C(w_{i-1},w_i)>0\\\\ \alpha(w_{i-1})\dfrac{P(w_i)}{\sum_{w_j:C(w_{i-1},w_j)=0}P(w_j)}\;, & \text{otherwise} \end{cases}\]

其中，$\alpha(w_{i-1})$ 表示从上下文 $w_{i-1}$ 中扣除的概率质量；
$\quad\quad$ $P(w_i)$ 表示单词 $w_i$ 的 unigram 概率；
$\quad\quad$ $\sum_{w_j:C(w_{i-1},w_j)=0}P(w_j)$ 表示所有没有和上下文 $w_{i-1}$ 共现的单词的 unigram 概率之和。

对于观测到的 bi-grams，即 $C(w_{i-1},w_i)>0$ 的情况，Katz Backoff 平滑概率就等于之前的 Absolute Discounting 平滑概率，其中 $D$ 代表 Discounting。
Katz Backoff 平滑的关键之处在于：对于其他未观测到的 bi-grams 的情况，$\alpha(w_{i-1})$ 表示上下文单词 $w_{i-1}$ 分配到的概率质量（即之前例子中的 $5\times 0.1=0.5$），而 $P(w_i)$ 表示当前单词 $w_{i}$ 的 unigram 概率。

让我们回到之前的例子，假设这里 “$\textit{infirmity}$” 比 “$\textit{cephalopods}$” 出现得更频繁，那么我们就给 “$\textit{infirmity}$” 以更高的权重。

我们为什么将这种方式称为 Backoff（回退）呢？

因为我们在碰到未知的 n-grams 的时候会将原来的模型回退到一个更低阶的 (n-1)-gram 模型：对于一个 bigram 模型，我们在计算未知 bi-grams 的概率时将回退到 unigram 模型；而对于一个 trigram 模型，我们在计算未知 tri-grams 的时候将回退到 bigram 模型。所以，我们总是只回退一步。

3.7 Katz Backoff 存在的问题

所以，Katz Backoff 存在什么问题呢？

考虑我们现在有一个句子：

\[\textit{I can't see without my reading __}\]

我们需要构建一个语言模型来预测 “$\textit{reading}$” 后面出现的单词是什么。假设我们有一个用于训练的语料库，并且语料库中没有 “$\textit{reading glasses}$” 和 “$\textit{reading Francisco}$” 这两个 bi-grams，这将使得它们的计数都为 $0$，即：

\[C(\textit{reading},\textit{glasses})=C(\textit{reading},\textit{Francisco})=0\]

另外，我们还假设在语料库中，单独的 uni-gram “$\textit{Francisco}$” 出现的频率要比单独的 uni-gram “$\textit{glasses}$” 出现的频率高得多，即：

\[C(\textit{Francisco})>C(\textit{glasses})\]

这种情况下，如果我们采用 Katz Backoff 平滑，它会给 “$\textit{Francisco}$” 更高的概率。因为我们没有见过前面两个 bi-grams，当我们重新为它们分配概率质量时，Katz Backoff 会根据这两个 bi-grams 各自对应的 uni-gram 概率分配不同的权重，而由于语料库中 “$\textit{Francisco}$” 出现的频率要比 “$\textit{glasses}$” 出现的频率高得多，所以 Katz Backoff 会预测 “$\textit{reading}$” 后面缺失的单词是 “$\textit{Francisco}$”。尽管根据常识我们知道在当前语境下，“$\textit{reading glasses}$” 明显才是更好的选择。

3.8 Kneser-Ney 平滑

现在，我们将介绍一种比 Katz Backoff 更好的平滑处理方式：Kneser-Ney 平滑

概率质量分配基于当前单词 $w$ 出现在 不同上下文 中的次数。
对于概率质量重新分配的问题，相比 Katz Backoff 中只是简单地基于低阶模型，Kneser-Ney 平滑采用的方法是基于当前单词 $w$ 在多少个 不同的上下文 中出现过，或者说是基于该单词的 多功能性（versatility）。
回忆前面 “$\textit{glasses}$” 和 “$\textit{Francisco}$” 的例子，其中，“$\textit{Francisco}$” 是一个非常特殊的词，它的 versatility 非常低，因为它很可能只在上下文单词 “$\textit{San}$” 后面出现过。因此，对于其他绝大多数的上下文单词，它们后面都不太可能出现 “$\textit{Francisco}$” 这个词。而相比之下，“$\textit{glasses}$” 这个词具有较高的 versatility，它可能在很多不同的上下文单词之后都出现过。
这种度量被称为 多功能性（versatility） 或者 延续概率（continuation probability）

对比 Katz Backoff 的概率公式，在 Kneser-Ney 平滑概率公式中，只有一项不同：

\[P_{\text{KN}}(w_i\mid w_{i-1})=\begin{cases}\dfrac{C(w_{i-1},w_i)-D}{C(w_{i-1})}\;, & \text{if } C(w_{i-1},w_i)>0\\\\ \alpha(w_{i-1})\color{red}{P_{\text{cont}}(w_i)}\;, & \text{otherwise} \end{cases}\]

其中，

\[P_{\text{cont}}(w_i)=\dfrac{|\{w_{i-1}:C(w_{i-1},w_i)>0\}|}{\sum_{w_i}|\{w_{i-1}:C(w_{i-1},w_i)>0\}|}\]

可以看到，对于观测到的 n-grams，Kneser-Ney 概率和 Katz Backoff 概率两者是相同的。而对于那些未知的 n-grams，Kneser-Ney 概率中从观测 n-grams 中 “借来” 的概率质量 $\alpha(w_{i-1})$ 与之前一样保持不变，而之前关于低阶模型 $P(w_i)$ 的部分则由我们所说的延续概率 $P_{\text{cont}}(w_i)$ 来替代。

在延续概率 $P_{\text{cont}}(w_i)$ 的计算公式中：分子部分计算的是一共有多少个唯一的上下文单词 $w_{i-1}$ 和当前单词 $w_i$ 共同出现过（co-occurrence）；而分母部分就是将所有可能的单词 $w_i$ 对应的不同共现上下文单词数量（即分子部分）进行一个累加。

现在，让我们再次回到之前 “$\textit{glasses}$” 和 “$\textit{Francisco}$” 的例子：

对于单词 “$\textit{glasses}$”，我们很可能会计算出一个很高的延续计数（continuation counts），因为 “$\textit{glasses}$” 这个单词可能出现在很多不同的上下文中，例如：“$\textit{men’s glasses}$”、“$\textit{black glasses}$”、“$\textit{buy glasses}$”、“$\textit{prescription glasses}$” 等等
而对于单词 “$\textit{Francisco}$” 的延续概率，我们极有可能计算出一个比 “$\textit{glasses}$” 中要小得多的分子部分，因为 “$\textit{Francisco}$” 这个单词几乎只可能出现在上下文单词 “$\textit{San}$” 后面，这意味着其对应的延续概率的分子部分很有可能只有 $1$。

在实践中，Kneser-Ney 平滑通常要比 Katz Backoff 平滑的效果更好。

3.9 Interpolation

我们将介绍最后一种也是最好的一种平滑处理方式：插值（Interpolation）

将不同阶数的 n-gram 模型结合起来 的更好的平滑方式。
我们在前面提到过的 Katz Backoff 平滑：对于一个 trigram 模型，如果我们遇到了一些未知的 tri-grams，我们将回退到一个低阶模型。
但是一种更好的做法是：将不同阶数的 n-gram 模型结合起来。
逐步缩短的上下文的概率加权求和
例如，对于一个 trigram 模型，我们计算未知 tri-grams 的平滑概率时会贯穿 trigram、bigram 和 unigram 三种阶数的模型。
一个 trigram 模型下的 Interpolation 平滑概率：
\[\begin{align} P_{\text{Interpolation}}(w_m\mid w_{m-1},w_{m-2}) &= \lambda_3 \times P_3^{*}(w_m\mid w_{m-1},w_{m-2})\\ &+ \lambda_2 \times P_2^{*}(w_m\mid w_{m-1})\\ &+ \lambda_1 \times P_1^{*}(w_m) \end{align}\]
其中，$\lambda_1,\lambda_2$ 和 $\lambda_3$ 是根据留存数据学习到的，并且 $\sum_{n=1}^{n_{\max}}\lambda_n=1$

我们可以按照下面的步骤计算单词 $w_m$ 在上下文单词 “$w_{m-2}$” 和 “$w_{m-1}$” 之后出现的 Interpolation 平滑概率：
- 首先计算 trigram 概率 $P_3^{*}$，并将其乘以一个系数 $\lambda_3$；
- 然后计算 bigram 概率 $P_2^{*}$，并将其乘以一个系数 $\lambda_2$；
- 然后计算 unigram 概率 $P_1^{*}$，并将其乘以一个系数 $\lambda_1$；
- 最后，将三者相加得到最终结果。
并且，为了保证所得到的仍然是一个合法的概率分布，我们需要满足所有 $\lambda$ 之和为 1。此外，这些 $\lambda$ 的值甚至并不需要我们手动设置，而是由模型通过一些留存数据学习到的，因为我们想知道对于这些不同阶数的模型，什么样的 Interpolation 方式是最高效的。

3.10 Interpolated Kneser-Ney 平滑

基于 Interpolation，我们得到了 Kneser-Ney 的最后一种版本：Interpolated Kneser-Ney 平滑。

Interpolation 替代 back-off：

\[P_{\text{IKN}}(w_i\mid w_{i-1})=\dfrac{C(w_{i-1},w_i)-D}{C(w_{i-1})}+\beta{(w_{i-1})}P_{\text{cont}}(w_i)\]

其中，$\beta{(w_{i-1})}$ 是一个归一化常数。

这里，我们所做的唯一改变就是：将之前观测 n-grams 和未知 n-grams 两种情况加在一起，取代了之前的 back-off 操作。所以，相比之前二选一的情况，现在我们都合并在一个公式里。

另外，相比之前的固定概率质量 $\alpha(w_{i-1})$，这里我们替换为归一化常数 $\beta(w_{i-1})$，以确保上下文 $w_{i-1}$ 对应的所有可能的 $w_i$ 的概率 $P_{\text{IKN}}(w_i\mid w_{i-1})$ 之和为 1。

这就是我们到目前为止介绍过的最有效的平滑方式，在实际应用中有很多 n-gram 语言模型都是基于 Interpolated Kneser-Ney 平滑实现的。

3.11 实践应用

在实践中，我们通常采用 Kneser-Ney 语言模型并将 5-grams 作为最高阶数。
对于每个 n-gram 阶数都有不同的 discount 值。
当我们试图学习如何在它们之间进行 Interpolation 时，我们将从数据中学习。

4. 生成语言

在最后一部分中，我们将介绍如何利用语言模型来 生成语言（Generating Language）。

4.1 生成（Generation）

我们这里讨论的是利用语言模型生成语言的一种通用的方法，并不仅仅局限于 n-gram 语言模型。

但是我们还是会以 n-gram 语言模型作为例子：

给定一个初始单词，从语言模型定义的概率分布中抽取一个词作为下一个出现的单词。
在我们的 n-gram 语言模型中包含 $(n-1)$ 个起始 tokens，用于提供生成第一个单词所需的上下文。
- 永远不会生成起始标记 $\texttt{<s>}$，它只作为初始单词的生成条件
- 生成 $\texttt{</s>}$ 来结束一个序列

例子：Bigram 语言模型

$\,$ Sentence $=\texttt{<s>}$
$\,$ $P(?\mid <s>)=“\textit{a}”$

这里是一个很简单的例子，我们有一个 bigram 语言模型。现在有一个空句子，即只包含一个起始标记 $\texttt{<s>}$。我们试图预测在给定一个起始标记 $\texttt{<s>}$ 的条件下，下一个最有可能出现的单词是什么。所以，我们会利用 bigram 语言模型来逐个检查词汇表中每个单词 $w$ 的条件概率 $P(w\mid \texttt{<s>})$，并选择其中概率最大的那个单词作为我们的预测结果。这里，我们可以看到单词 “$\textit{a}$” 出现在一个句子开头的概率最大，我们将它添加到句子中。

$\,$ Sentence $=\texttt{<s> }\textit{a}$
$\,$ $P(?\mid \textit{a})=“\textit{cow}”$

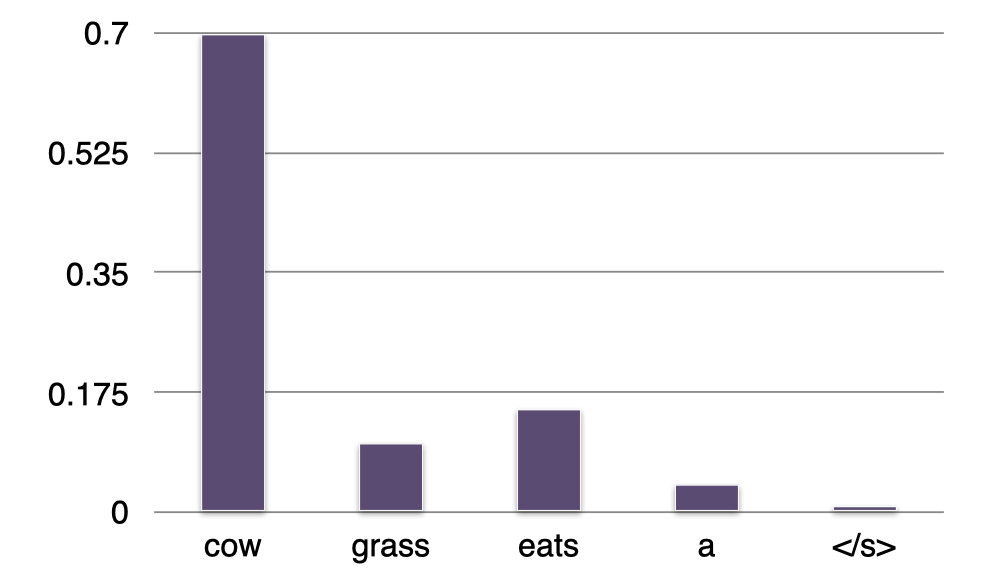
现在我们的句子有了第一个单词 “$\textit{a}$”，我们想知道下一个最有可能出现的单词是什么。还是和之前一样，我们逐一检查词汇表中各个词在给定上下文单词 “$\textit{a}$” 的情况下，哪个词对应的条件概率最大。可以看到，这里单词 “$\textit{cow}$” 出现在单词 “$\textit{a}$” 之后的概率最大，所以我们将它添加到句子中。

$\,$ Sentence $=\texttt{<s> }\textit{a cow}$
$\,$ $P(?\mid \textit{cow})=“\textit{eats}”$

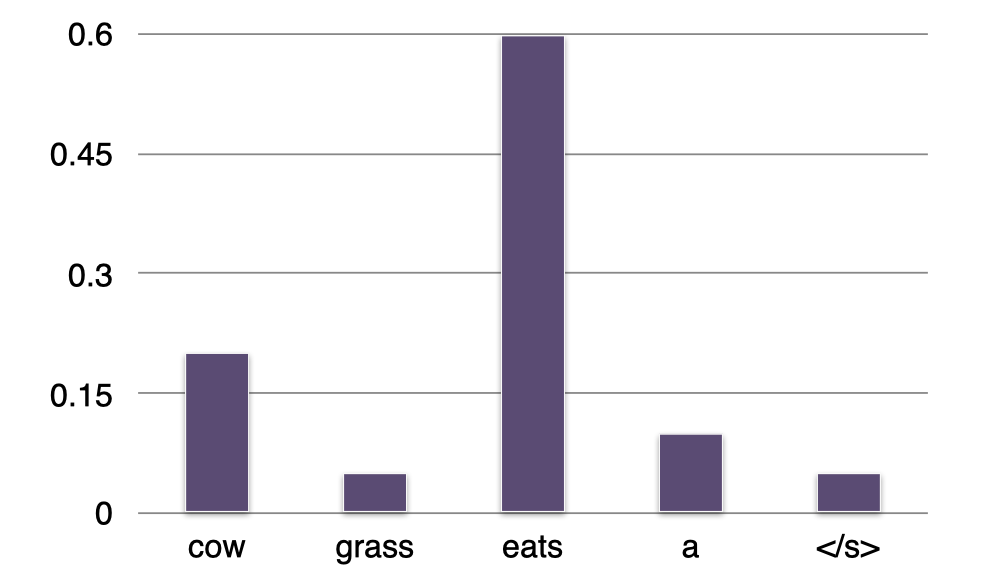
重复上面的步骤，我们得到了下一个最有可能的单词 “$\textit{eats}$” 并将它添加到句子中。

$\,$ Sentence $=\texttt{<s> }\textit{a cow eats}$
$\,$ $P(?\mid \textit{eats})=“\textit{grass}”$

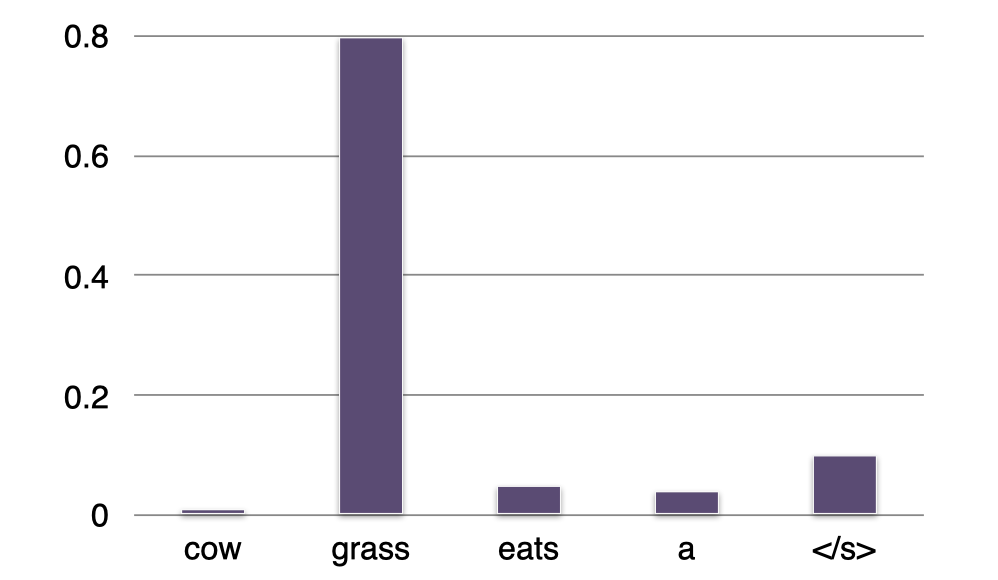
继续，我们得到单词 “$\textit{grass}$” 并将它添加到句子中。

$\,$ Sentence $=\texttt{<s> }\textit{a cow eats grass}$
$\,$ $P(?\mid \textit{grass})=“\texttt{</s>}”$

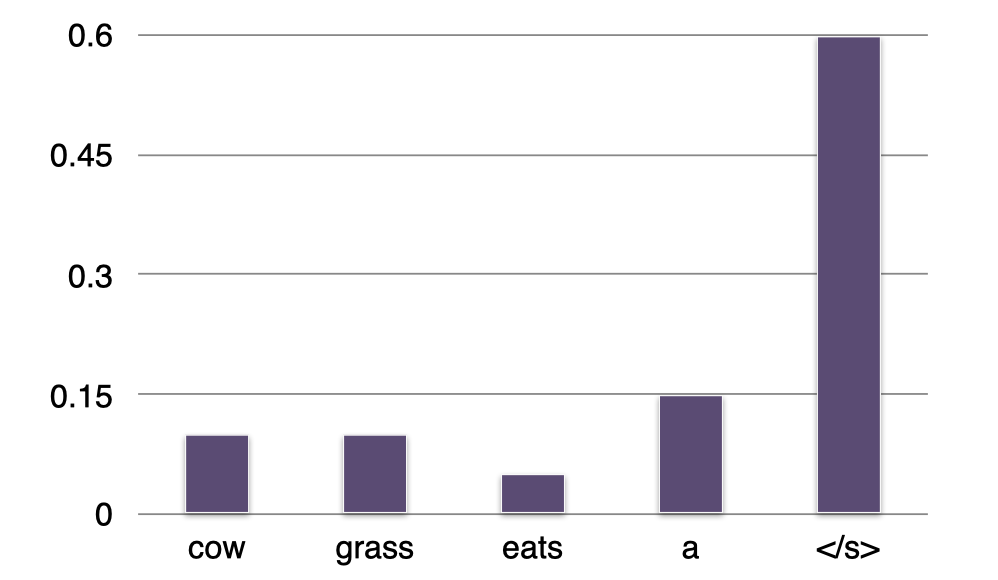
最终，我们预测单词 “$\textit{grass}$” 后面最有可能出现的是结束标记 “$\texttt{</s>}$”，我们将它添加到句子中。

$\,$ Sentence $=\texttt{<s> }\textit{a cow eats grass }\texttt{</s>}$
完成

现在我们得到了一个由这个 bigram 语言模型生成的句子：$\textit{a cow eats grass}$

4.2 如何选择下一个单词

Argmax：在每一轮中选择与上下文共现概率最高的那个单词。
- 贪婪搜索（Greedy search ）
  这其实是一种贪婪搜索策略，因为即使在每一步中我们都选择概率最高的那个单词，也无法保证最终生成的句子具有最优的概率。
Beam search decoding
一种更好的方法是 Beam search decoding，它在机器翻译中应用非常广泛。
- 在每轮中，我们跟踪概率最高的前 $N$ 个单词
- 我们总是检查这几个候选单词给出的完整句子的概率
- 这种方法可以生成具有 近似最优（near-optimal） 概率的句子
从分布中随机抽样
另一种方法是从语言模型给出的概率分布中随机抽样，例如：temperature sampling

5. 评估语言模型

在最后一部分，我们将学习如何评估一个语言模型的质量。

5.1 评估

语言模型的评估通常有两种范式：

外部的（Extrinsic）
这种评估范式常见于下游应用中，我们根据其反馈来评估语言模型的表现。比如对于机器翻译中的某些任务，我们可以比较不同语言模型在完成该任务上的表现。
- 例如：拼写纠错、机器翻译
内部的（Intrinsic）
在这种评估范式下，我们不依赖任何下游应用，而是观察我们的语言模型在保留测试集上的 Perplexity。
- 在保留测试集（held-out test set）上的 Perplexity
- Perplexity（困惑） 衡量的是我们对于模型在测试数据上给出的预测的置信度。置信度越高，对应的 Perplexity 就越低，代表我们的模型越好。

5.2 Perplexity

整个测试集的逆概率（Inverse probability）
- 通过单词 tokens（包括结束标记 $\texttt{</s>}$）的数量实现归一化（Normalization）
假设我们保留的测试集语料库是一个由 $m$ 个单词 $w_1,w_2,\dots,w_m$ 组成的序列，我们用 $PP$ 表示 Perplexity。从下面的公式可以看到，它是通过对整个测试集的概率 $P(w_1,w_2,\dots,w_m)$ 取倒数，然后再开 $m$ 次方得到的：
\[PP(w_1,w_2,\dots,w_m)=\sqrt[\uproot{10} \leftroot{-2} m]{\dfrac{1}{P(w_1,w_2,\dots,w_m)}}\]
等同于：
\[PP(w_1,w_2,\dots,w_m)=2^{-\frac{\log_2 P(w_1,w_2,\dots,w_m)}{m}}\]
如果我们遇到未知单词（OOV），我们通常是直接忽略掉，因为我们没有办法表示它们。
Perplexity 越低，模型表现越好。
假如我们模型的 Perplexity 只有 $1$，那么这是最好的情况。因为当我们的测试集语料库上的概率 $P(w_1,w_2,\dots,w_m)=1$ 时，$PP(w_1,w_2,\dots,w_m)=\sqrt[m]{1}=1$。而对于一个非常差的语言模型，可能在测试集上的概率 $P(w_1,w_2,\dots,w_m)=0$，此时模型的 Perplexity 将趋近 $\infty$。所以，最理想的情况是 Perplexity 等于 $1$，当然，我们永远不可能达到这个值。

5.3 Perplexity 得分的例子

让我们来看一个关于 Perplexity 得分的例子：

	Unigram	Bigram	Trigram
Perplexity	962	170	109

语料库：$\textit{Wall Street Journal}$（华尔街日报）
训练区：3800 万个单词 tokens，接近 2 万个单词 types（即词汇表）
测试区：150 万个单词 tokens

我们训练了三个模型：unigram、bigram 和 trigram 模型。语料库来自 $\textit{Wall Street Journal}$。其中，相比训练集中的 3800 万个单词 tokens，测试数据包含的单词 tokens 比较少，只有 150 万个，这属于正常情况。

可以看到，对于 unigram 模型，Perplexity 得分非常高，到达了 962，这不是我们希望看到的情况。在模型阶数从 unigram 增加到 bigram，再增加到 trigram 的过程中，模型的 Perplexity 得分也在逐渐降低。当模型的复杂度增加时，即 n-gram 模型中的 $n$ 增大时，我们将得到一个更好的语言模型。

6. 总结

N-gram 模型在捕捉语言的可预测性方面是一种简单且高效的方法。
模型的构建很容易：我们只需要一个大的语料库，并且对单词和上下文进行计数即可。
信息可以通过无监督的方式推导得出，可以扩展到大型语料库。
由于稀疏性的存在，需要进行平滑处理才能保证有效性。
我们需要一些工程上的技巧处理稀疏性问题，例如：smoothing、back-off、interpolation 等。

虽然 n-gram 模型非常简单，但是它在实践中的效果非常好。所以，在构建语言模型时，我们通常会选择将 n-gram 模型作为 baseline，尽管目前有很多模型都采用了深度学习。

7. 思考

思考： Interpolation、Interpolated Kneser-Ney 和 Kneser-Ney 之间有什么区别？我们应当如何判断应该采用哪种方法？

首先，我们应该明确一点：Interpolated（插值）、Smoothing（平滑）和 Backoff（回退）都是用来解决数据稀疏问题（sparsity）的方法。我们在这节课中讨论的前 3 种平滑方法（拉普拉斯、“加 k” 和 Lidstone）都是在 和原先的 N-gram 模型相同的阶数 内重新分配概率，将概率质量从常见情况向罕见情况进行偏移。

Interpolation 和 Backoff 都是通过 结合不同阶数的 N-gram 模型 来解决这个问题。对于 Backoff 而言，如果高阶 higher-gram 的计数为 $0$，那么它将完全落回低阶 lower-gram；而 Interpolation 则是通过将我们所有的 N-gram 模型加权求和来将它们结合起来。

现在，当我们采用低阶模型时又会带来一个新的问题。例如，对于单词 “$\textit{Old}$” 和 “$\textit{Zealand}$”，很可能它们的 bi-gram “$\textit{Old Zealand}$” 计数为 $0$，所以我们需要依赖 unigram 模型提供的概率。想象一下，如果单词 “$\textit{Zealand}$” 具有一个非常高的 unigram 概率，那么对于这两个词的 bi-gram，我们还是可以得到一个相对较高的共现概率，而这不是我们希望看到的。

Kneser-Ney Smoothing 中引入了所谓 延续计数（continuation count） 的概念。因为在大多数情况下，单词 “$\textit{Zealand}$” 只出现在上下文单词 “$\textit{New}$” 的后面，所以对于单词 “$\textit{Zealand}$” 出现在上下文单词 “$\textit{Old}$” 后面这种情况（即 bi-gram “$\textit{Old Zealand}$”）的延续计数会非常低。到这里，我们通过 在不同上下文中的频率计数 解决了上述例子中的问题。

回到原问题中提到的哪种方法更好，我们可以在 Backoff 或者 Interpolation 二者中选择一种来使用 Kneser-Ney Smoothing。通常来说，Interpolation 可能更合适，因为这种方式更灵活（因为我们考虑了所有阶数的 N-gram 模型）。

8. 扩展阅读

Natural Language Processing, Draft 15/10/18, by Eisenstein
- Chapter 6 (skip 6.3)

下节内容：文本分类

本作品采用知识共享署名-非商业性使用-相同方式共享 4.0 国际许可协议进行许可。欢迎转载，并请注明来自：YEY 的博客同时保持文章内容的完整和以上声明信息！

自然语言处理 03：N-gram 语言模型

墨尔本大学 COMP90042 课程笔记